Performance of cork-based thermal protection material P50 exposed to air plasma

Abstract

Cork P50 thermal protection material was characterized under the Earth atmospheric entry conditions in the framework of the in-flight experiment QARMAN. A total of 25 P50 samples were exposed to air plasma ranging the chamber static pressure values of 1500, 4100, 6180, and 20,000 Pa and heat fluxes between 280 and 3250 kW/m$^2$. The sample radius was also varied between 11 and 25 mm radius to investigate the effects of the stagnation line velocity gradient. The experimental results on heat flux, pressure, surface and in-depth temperatures, surface emissivity, swelling and recession rates, and computed boundary layer profiles as well as the mass blowing rates are presented. A material characterization data suite is also provided including thermogravimetric analysis, specific heat, and thermal conductivity. Overall, a wide range of experimental data of Cork P50 material in Earth atmospheric entry conditions is made available to modelers and engineers for improved material response models and heat shield design consolidation.

1 Introduction

Spacecraft, returning back to Earth or landing on a planet, experiences a very harsh environment during the encounter with the atoms and molecules of the atmosphere. One of the major issues of the atmospheric entry is the extreme aerodynamic heating and the exothermic chemical reactions due to the gas–surface interaction at hypersonic-free stream velocities. The safety and efficiency of the spacecraft during this phase rely heavily on the performance of their thermal protection systems (TPS). Their design requires accurate prediction tools that are used during pre-flight mission. In particular, the numerical instruments are based on material response models, which are validated with experimental data. Thus, there is a need of high-quality data in the aerospace community to build and improve the models [12].

Cork-based materials are highly used in the aerospace industry both in launchers and in entry vehicles, either in the rocket boosters or in heat shields [6], including the heat shield of Mars entry capsule Schiaparelli of European Space Agency [18]. Specifically, the Cork P50 flew onboard the Intermediate eXperimental Vehicle (IXV) in the sideward and leeward regions [26]. At this occasion, the ablative material was tested in the VKI Plasmatron to consolidate the design of IXV. The experimental campaign discussed here was originated from the QARMAN mission [21], which has its front TPS made of Cork P50. The experimental conditions reported here are much wider than the QARMAN’s entry trajectory, with the aim of a more extensive material characterization of Cork P50, as it is a widely used material with interesting characteristics, such as swelling. QARMAN, a flight demonstrator on a 3-Unit CubeSat platform, was to perform a series of aerothermodynamic experiments during its entry to Earth’s atmosphere. Its front heat shield is equipped with three thermal plugs of 14 thermocouples in total, three absolute pressure ports and a miniature emission spectrometer. These data were to be used to flight-qualify numerical and material models as well as the experimental methodologies for ground testing. QARMAN was successfully launched to ISS on December 5th, 2019 and was released from ISS on March 24th, 2020. Although its atmospheric entry was expected at the end of August 2020, the last telemetry from the spacecraft was received in July 2020 before it was lost [27].

Unlike lower density fibrous ablators like ASTERM [25], cork-based materials tend to expand volumetrically (mechanically and pyrolysis-triggered) prior to its recession, thus making it very difficult to model. The swelling is often ignored in published studies [1, 4] with the exception of the attempt by Pinaud and van Eekelen [19]. As it will also be discussed in the next section, the duplication of the stagnation region during an Earth entry relies not only on the correct pressure, heat flux but also on the adequate velocity gradient which is dictated by the spacecraft and sample geometries. Along with valuable experimental data on numerous test conditions, the effects of these three parameters are further discussed in the following sections. This study aims to provide modelers, through experimental data of the cork-based P50 material from plasma wind tunnel tests inline with the entry trajectory of an Earth entry mission.

2 Flight-to-ground duplication methodology

Due to the lack of existing cork P50 response model, the thermal design of the QARMAN vehicle was based on plasma wind tunnel experiments. To do so, an accurate methodology was needed to duplicate the flight conditions of QARMAN in the plasma wind tunnel, also because QARMAN nose geometry is rectangular unlike regular spherical entry vehicles. Such “Flight-to-Ground Duplication” methodology was developed and applied to QARMAN geometry and entry trajectory by Sakraker et al. [23] for subsonic plasma wind tunnels testing, i.e., VKI Plasmatron facility. The outcomes of the duplication procedure lead to extensive testing, caring for three parameters, namely, enthalpy, pressure, and velocity gradient explained further in this section, and their effects on the ablation phenomena.

The stagnation heating and the boundary layer chemistry are crucial quantities in the hypersonic entry and it is important to reproduce the flight conditions in the ground test facility as accurately as possible. Several correlations for heat transfer at stagnation point are given in the literature; Fay and Riddell [8], which is one of the first to be derived, are given as example here

$$\begin{aligned}&\dot{q}_w = 0.763 \text {Pr}^{-0.6} \left( \rho _e \mu _e \right) ^{0.4} \left( \frac{du_e}{dx} \bigg | _{\text {edge}} \right) ^{1/2} \left( \rho _w \mu _w \right) ^{0.1} \nonumber \\&\quad \times \left( h_{0,e} - h_w \right) \left[ 1+\left( Le^\alpha -1 \right) \left( \frac{h_{D,e}}{h_{0,e}} \right) \right] , \end{aligned}$$

(1)

where $\rho$ is the mass density, $\mu$ is the absolute viscosity, $du_e / dx$ is the velocity gradient, h is the enthalpy per unit mass, Pr is the Prandtl number and the subscripts 0, e and w describe the total, the conditions at the edge of the boundary layer edge and at the wall, respectively. Le is the Lewis number¹; $h_{D,e}$ is the dissociation enthalpy. It is expressed as the product of the enthalpy of formation, $\Delta h_{F,i}^0$, of species i with its mass fraction $y_{i,e}$

$$\begin{aligned} h_{D,e}= \sum \limits _{i=1}^N y_{i,e} \Delta h_{F,i}^0. \end{aligned}$$

(2)

Studying Eq. (1), the density $\rho$, the velocity gradient du/dx, also called $\beta$, the total enthalpy $h_0$ and the chemical composition at the boundary layer edge (contained in the $h_{D,e}$ term) as well as the wall conditions of enthalpy and catalycity can be treated as the duplication parameters.

At the wall, the same enthalpy, and catalycity should be provided. The wall catalycity is the same if the actual flight TPS is used; given the sample is exposed to the same stagnation flow environment.

When the same wall conditions are assured, to reproduce the stagnation point boundary layer of the flight and the corresponding heat flux in the test chamber, there are four independent parameters to be determined at the boundary layer edge: $\rho _e$, $\beta _e$, $h_{0,e}$ and $y_{i,e}$. To have a reference in the free stream conditions, one could assume local thermodynamic equilibrium (LTE). Then, the species concentration, $y_{i,e}$, the density, $\rho _e$, and the viscosity, $\mu _e$, at the boundary layer edge, become functions of pressure and enthalpy only.

In these conditions, there are only three independent variables left at LTE: p, h, and $\beta$. This is expressed as Local Heat Transfer Simulation (LHTS) by Kolesnikov [11]. If these three independent parameters at the boundary layer edge of a hypersonic vehicle are duplicated in a ground facility on the TPS sample probe, then the heat flux and the boundary layer aerothermochemistry are the same. The stagnation point of a specific spacecraft on a given entry trajectory point is fully duplicated.

Unfortunately, duplicating these three parameters is not direct for nonaxisymmetric vehicles such as QARMAN and an iterative procedure involving CFD computations and experiments was needed [23]. It was shown in previous publications [23] that each trajectory point has a unique combination of pressure, enthalpy, and velocity gradient. This lead to the interest of plasma testing for the Cork P50 material in a range of pressure, heat flux (thus enthalpy), and sample sizes (thus velocity gradient). The ranges were primarily based on QARMAN entry trajectory; however, wider testing conditions had been considered to provide a broader behavior analysis of the material as it will be shown in the following sections.

Finally, it should be noted here that the sample geometry can be chosen freely as long as it satisfies the duplication requirements. Hemispherical sample geometries were chosen in this study as it is a widely used geometry in high-enthalpy facilities worldwide to give a better comparative set of experimental data. Additionally, hemispherical samples allow for a better visualization of the external recession/swelling behavior and for an easier probe manufacturing process.

3 Material description and properties

The Cork P50 material is manufactured by Amorim Cork Composites [7]. It consists of high percentages of premium quality cork granules agglomerated with a phenolic resin, and plasticized with a glycol, to improve flexibility of the material.

3.1 Thermogravimetric analysis (TGA)

TGA was performed at VKI on two cork P50 samples to observe its decomposition and reactions as it was heated. Argon is used to prevent any oxidation or nitridation, and to isolate the pyrolysis mechanisms of the cork. The initial sizes of the samples were $1.8\times 2.2\times 3$ mm and $2\times 2.5\times 2.3$ mm. Both samples were heated with a rate of 10 K/min in Argon. The virgin densities of the two samples, $\rho _v$ were 466.66 and 464.53 $\mathrm {kg/m}^3$, while the char densities, $\rho _c$ were 298.38 and 279.90 $\mathrm {kg/m}^3$. (The 6% variation in the char density can be explained by the heterogeneous volumetric phenomena.)

Figure 1 shows the change of mass of both samples in temperature. It can be seen that the pyrolysis begins around 430 K with the mass reduced to 98% and the samples are fully charred at 780 K with the mass down to 24.5%. The char mass is then constant at 20% until the end of the test at 1650 K. The derivative of the mass loss rate is also computed to see the major reactions that would appear in the slope changes and is depicted in Fig. 1. There is a slight change at around 350 K which is attributed to moisture volatilization by Smith et al. [24]. Then, a larger reaction occurs at 488–500 K according to the two sample data. Finally, at 700 K, the major reaction takes place. These reaction locations are consistent with data for a similar material cork P45 [1], which has the same constituents but a different elemental composition.

Fig. 1

TGA data for two samples with 10 K/min heating rate. The thick lines show the data of sample 1 and the thin lines of sample 2. The normalized mass loss profiles for both samples are very similar

The ablators decompose chemically when exposed to heat, and as a result, the mass density is decreasing. This can be described by multiple Arrhenius laws, which relate the chemical reactions with temperature (by the notation of [19])

$$\begin{aligned} \partial _i \alpha _i = A_i \left[ \frac{\rho _v - \rho _c}{\rho _v} \right] ^{N_i-1} \left( 1- \alpha _i \right) ^{N_i} e^{\frac{-E_i}{RT}}, \end{aligned}$$

(3)

where $\alpha _i$ is the advancement of the $i\mathrm {{th}}$ pyrolysis reaction, $A_i$ is the frequency or the pre-exponential factor of the $i\mathrm {{th}}$ Arrhenius law, $\rho$ is the mass density with subscripts v and c for virgin and char, N is the order of reaction, $E_i$ is the activation energy of the $i^\text {th}$ Arrhenius law, R is the perfect gas constant, and T is the temperature.

Two Arrhenius laws can be fit to the two distinctive reactions happening at 488 and 700 K. The coefficients that are determined by this fitting procedure are the pre-exponential factor A, the density difference term $d \rho = \frac{\rho _v -\rho _c}{\rho _v}$, the order of the reaction N, and finally the activation energy of the chemical reaction E. The fitting results for both reactions for both TGA tests are given in Table 1.

Table 1 Arrhenius law coefficients fitted on the TGA data shown in Fig. 1

3.2 Specific heat measurements

Specific heat tests were conducted by Amorim Cork Composites to determine the specific heat, $C_p$, of P50 material by Differential Scanning Calorimetry (DSC).

The tests were performed for three samples and the results are averaged in temperature range of 2–500$\,{^\circ }$C, at a scan rate of 10$\,{^\circ }$C/min under nitrogen atmosphere 99,996% purity at 20 and 40 mL/min flow rate. It was used a temperature equilibrium time of 2 min and three tests were performed for each sample. The samples were conditioned at room temperature in an inert atmosphere for a period of 48 h prior to encapsulation in an aluminum crucible for analysis. The results are plotted in Fig. 2.

Fig. 2

Specific heat of P50 samples. The average is computed from three sample test results

3.3 Thermal conductivity

The thermal conductivity, k, of P50 is measured by NETZSCH LFA 457 MicroFlash, and the results are shown in Fig. 3. Three Cork P50 samples were tested and the results are shown together with an average curve.

Fig. 3

Thermal conductivity measurements on three samples by NETZSCH LFA 457 MicroFlash

4 Plasma experiment results

4.1 VKI plasmatron facility

The plasmatron facility [5] is a high-enthalpy wind tunnel in which a plasma discharge is generated by electromagnetic induction and blown in the form of a subsonic plasma jet inside a test chamber. The facility uses a high frequency, high power, high voltage (400 kHz, 1.2 MW, 2 kV) solid state (Metal Oxyde Semiconductor, MOS, technology) generator, feeding the single-turn inductor of the 160 mm diameter plasma torch. The testing gas can be argon, air, N$_2$, and CO$_2$.

The test matrices usually consist of static pressure and heat flux ranges. After the plasma onset, the static pressure in the test section is adjusted with the vacuum pumps. The operating ranges are 10–800 mbar of pressure and 50 kW/m${^2}$–16 MW/m${^2}$ of heat flux. For a generic TPS test configuration, the heat flux probe is injected and the facility power is regulated until the required heat flux is measured. Finally, the TPS sample is injected from the cooling box in the upper sample holder.

4.2 Experimental setup

The experimental setup consists of a number of measurement techniques and is depicted in Fig. 4. The heat flux is measured by the 25 mm hemisphere cylinder probe with a water-cooled copper calorimeter. The dynamic pressure is measured by the Pitot probe.

Fig. 4

Experimental setup of VKI plasmatron TPS testing. Courtesy of: Bernd Helber

The surface temperature evolution during the plasma exposure is recorded with a two-color pyrometer. The Raytek Marathon (RAYTEK MR1S-C) two-color pyrometer performs measurements in a wavelength range of 0.75–1.1 ${\upmu}$m and 0.95–1.1 ${\upmu}$m and a temperature range of 1000–3000 $^\circ$C. The infrared Heitronics KT19 radiometer functions in the wavelength range of 0.6–39 ${\upmu}$m and provides as output the integrated thermal radiation over this spectrum, within a temperature range of 0–3000$\,^\circ$C. Even though the combination of pyrometer and radiometer data may allow determining surface emissivity [17], due to the high uncertainties associated, the authors decided to report only the pyrometer temperature data.

The samples geometries were hemisphere cylinders of 48 mm in length with, respectively, 11, 15, and 25 mm radii. These three radii are chosen in accordance with the computed sample radius of QARMAN vehicle along its trajectory [23]. Each sample is mounted on a cooled probe arm of its size, as depicted in Fig. 5, for the 25 mm radius example. All samples were equipped with three thermocouples along the centerline at 4, 8, and 12 mm away from the surface. While the first two thermocouples were type K, the third ones were type E, as shown in Fig. 5b. It was seen that the cork is very insulating and the noise-sensitive type K thermocouples could be avoided at the depth of 12 mm.

Fig. 5

Hemispherical cork sample and the plasmatron probe arm configuration

The mass change and char-pyrolysis layer thicknesses are determined for each case after the experiments by weighing and sectioning. A high-speed camera is used to determine the swelling and recession rates at ten frames per second. Additionally, a high-resolution photo camera, positioned interchangeably with the spectrograph, is used at 2 Hz acquisition to monitor the surface and check for mechanical erosions. The spectrograph data are not included here, as they were only used for some test cases and qualitatively only.

4.3 Testing conditions

The testing conditions are determined primarily based on the QARMAN trajectory; however, the heat flux and pressure envelopes are extended to generate a larger database to be able to build a more general model, from which the QARMAN trajectory points can later be interpolated. Figure 6 shows a comparison of the free stream enthalpy of the QARMAN trajectory and the testing conditions. The chamber static pressure values are 1500, 4100, 6180, and 20,000 Pa. VKI plasmatron was operated in the subsonic plasma regime; hence, the dynamic pressure levels are negligible when compared to the uncertainties caused by plasma fluctuations. Therefore, the static pressure values can be considered as total pressure for modeling. On the other hand, the reference heat fluxes, measured by the hemispherical 25 mm probe, are between 280 and 3250 kW/m$^2$.

Fig. 6

QARMAN re-entry trajectory and the experimental campaign testing conditions in terms of free stream enthalpy and pressure from [22]

For each test case, the total heat load is fixed to 48,000 kJ/m${^2}$, which is the heat load expected during QARMAN re-entry flight. Therefore, the test durations are determined according to the impinging cold wall heat fluxes on the given sample geometry. Even though the reference heat fluxes are measured with a 25 mm calorimeter probe radius, a heat flux database containing different probe dimensions is used to determine the impinging heat fluxes [22], thus the test durations.

The testing conditions and the plasma exposure durations are given in Table 2. It should be noted that this paper aims to provide modelers an as wide as possible data range, which is not constrained by QARMAN mission. Some of the tests were unsuccessful due to loss of major data and those are not included here. In some cases, even if some data are marked as “Not Available (N/A)”, the authors think that the rest of the data set can still be useful, hence are included here.

Table 2 Test matrix and the summary of experimental results

4.4 Boundary layer edge conditions

Prior to present the experimental data from the plasmatron experiments, it is important to provide the free stream conditions at the edge of the boundary layer, since they will be useful to characterize the flow in front of the sample stagnation point and to determine the heat transfer coefficients. The edge conditions are rebuilt using the VKI code CERBOULA [2]. The rebuilt enthalpies, temperatures, and species concentrations at the boundary layer edge can be found in Table 3.

Table 3 Boundary layer edge enthalpy, density, temperature, and species concentrations rebuilding with copper catalytic efficiencies using CERBOULA [2]

4.5 Visual inspection and in-depth layers

During plasma exposure, the test samples were also monitored with a photo camera in addition to the high-speed camera. All the samples first swelled when they were exposed to plasma and then started receding. Moreover, it was observed that for most cases, the samples are bigger at the end of the test, so the sample swelled and then recessed, but the test was stopped before it recessed further. The reason was that the test matrix is built in a way that all the samples are exposed to the same heat load which resulted in different test durations. No significant mechanical erosion was observed except very small-scale spallation.

Fig. 7

Change of cork P50 surface topology from virgin (left) to char cracks (right) after Test 9R

The test sample surfaces notably changed after the plasma tests. An example image is given for virgin material and tested material for Test 9R in Fig. 7. It is observed that as soon as the sample is in the plasma jet, the cracks occur suddenly. The surfaces between the cracks (called cells from here on) do not change geometry but move away from each other as the sample swells and then get back closer as the sample recedes. Moreover, it is seen by the high-speed camera images that the cell surfaces start as concave and later during char recession become convex. This means that the crack contours are higher and the center is lower. This suggests that the pyrolysis gas products are still traveling toward the surface along these cracks, and due to the cooling effect of the pyrolysis blowing, there is less recession in these adjacent areas.

This is an important feature when thermal plugs are considered for the front TPS, as it is the case for QARMAN mission [21].

The dimensions of the samples were also measured before and after the plasma tests. From the outer dimension measurements, it is seen that the swelling is a volumetric phenomenon, since the diameter of the sample is also changing along the height. All the test samples were sectioned to identify the char layer thickness as well as in-depth layers of pyrolysis and virgin thicknesses. From Fig. 8, it can directly be noticed that there is still a very large amount of virgin material inside and the ablation thicknesses are much smaller.

Table 4 shows the layer thicknesses for all tests.

Fig. 8

Cross sections of Tests 14R (left) and 26 (right) with radii of 25 and 15 mm, respectively. 11 mm radius samples were completely charred and could not be removed intact from the sample holder

Table 4 Sample dimensions before and after test, and char, pyrolysis, and virgin thicknesses

4.6 Surface and in-depth temperatures

For all test cases, the pyrometer was pointed at the stagnation point. Each surface temperature profile indicated a sharp increase shortly after plasma exposure and then reached a steady temperature. The mean steady temperatures taken at the plateau are given in Table 5. It is important to note that the pyrometer device has a measurement error of ${\pm 10}$ K. Furthermore, the measurements fluctuate in time. The fluctuations in time, as one standard deviation from the mean values, are also given in Table 5.

Table 5 Surface temperature measurements and the measurement fluctuations in time in terms of one standard deviation

The in-depth temperatures provide comparison datasets for the solution of the material response equations. All samples were equipped with three in-depth thermocouples. They were mounted at 4, 8, and 12 mm away from the surface of the virgin sample. As the sample swells or recesses, the surface position changes and the sample may slightly move from the sample holder. However, the thermocouples stay where they initially were, since the thermocouple extensions were fixed to the sample holder. Therefore, throughout the test, the thermocouple depths may change with respect to the surface, but in the plots presented in this study, they will be named after the initial positions. For future campaigns, it is suggested that the thermocouples are fixed to the back of the sample instead of the sample holder. Figure 9 shows the in-depth temperature profiles of some test cases. It should be noted that in-situ material testing with a coupled X-Ray imaging such as in an X-Ray Synchrotron facility [20] proves to be very useful especially for swelling materials such as cork, to determine temperature at exact 3D locations during plasma exposure. However, such experiments require dedicated portable plasma facilities that are not as powerful as fixed facilities such as Plasmatron, in addition to the fact that sample sizes are very limited due to the limited field of view of X-Ray Synchrotron measurements. At the time of the presented campaign here, such facility was not available.

The in-depth temperatures can be compared to the TGA data which showed pyrolysis temperatures. For most cases, the temperatures immediately at 4 mm depth are much lower than the surface temperatures given in Table 5. This suggests that the thermocouples are not in the ablating char layer. For example, in the case of Test 23 shown in Fig. 9h, the final char thickness is 2.7 mm as given in Table 4. It is also seen that the final sample height is larger than the original. Assuming the thermocouples do not change position when the sample is swelling or recessing, the first thermocouple is still in the pyrolysis layer. Indeed the TGA data showed that the pyrolysis is apparent above 430 K, which is the measured temperature range by this thermocouple.

For the cases where the char layer is thicker and there is a thermocouple in it, the temperature rises above the measurement range of type K to a value closer to the surface temperature. A good example of this is the Test 22, plotted in Fig. 9g, where the sample almost completely charred and broke into pieces while removing from the sample holder. The first two thermocouples were in the char layer and TC1 failed to provide data above limit temperature. One can guess that the measurement junction opens when the temperature rises above its operational limit, and later, when the sample cools down, the two thermocouple wires are soldered back together and start giving a signal again as can be seen after 125 s.

Coming back to the Test 23 example, the first and although not very visible, the second thermocouple data show a “hump” after a certain time as if a thermal wave arrived. This behavior has also been reported for other materials such as NASA’s PICA, Phenolic Impregnated Carbon Ablators [16]. The term “hump” is also used by Milos and Chen [16] referring to the treatment of PICA data first in arcjet tests and later the real flight data from Mars Science Laboratory thermal plugs by Mahzari et al. [14].

It can be seen that a certain exothermic reaction occurs at those moments with an incoming thermal wave. One possibility of exothermic reactions would be the oxidation reactions reaching subsurface areas due to the cracks or the charring surface which changes the surface porosity. By definition, the pyrolysis reactions are endothermic, which is the main reason for the ablative materials to be good insulators. To cross check, TGA data are considered; apparent reactions had occurred at 488 and 700 K. The hypothesis is that the endothermic reactions observed during the TGA analysis are responsible for “cooling down” the material and decreasing the in-depth temperatures.

The location and the timing of these humps were also examined as the pressure and sample radii were changed. Figure 10 shows the 4 mm thermocouple data for two cases having the same sample radius and the same reference heat flux suggesting same surface temperatures. Regardless of the pressure, the three humps occurred almost at the same time and temperature. A similar behavior is seen when the reference heat flux is kept constant and the sample radius is changed, as depicted in Fig. 10. In both cases, a hump occurs around 41 s but at different temperatures. For all the test cases, humps are seen around 490 K and for those that increases enough, at 700 K. These data are consistent with the TGA data. However, during the plasma tests, an additional hump occurred consistently around 430–440 K, as well.

Fig. 9

In-depth temperatures, “TC1” at 4 mm, “TC2” at 8 mm and “TC3” at 12 mm from the surface

Fig. 10

The “humps” in thermocouple data at 4 mm depth for two cases of different pressures but the same radius and same reference heat flux (left); and for two cases of different radii (also different test duration) but the same pressure and same reference heat flux (right). Note that the 15 mm radius samples could not fit in the cooling box, and therefore are subjected to a pre-heating

4.7 Swelling and recession profiles

The swelling and recession profiles were captured with a high-speed camera throughout the plasma exposure. The time evolution of the stagnation point along the horizontal line is tracked with an edge detection algorithm, as shown in Fig. 11 during the swelling and recessing processes of Test 19 given as example. All the swelling and recession profiles are given in Figs. 12 and 13. The recession rates were determined from the linear slopes once the swelling is over and there is an apparent recession. These rates are given in Table 2. Due to the fixed-heat load approach of the test matrix here, not all recession rates could be determined accurately due to the fact that the plasma was stopped before the sample stops swelling.

Fig. 11

Determination of swelling and recession of Test 19 by high-speed camera. The sample is exposed to plasma at t = 0.04 s; it swells until t = 24.85 s and recedes until the end of the test, t = 99.85 s. Each pixel shown in the axes correspond to 0.23 mm

During the tests, it is observed that the material surface directly chars and the surface temperatures stay constant after a very short time for all tests. From here, it can be assumed that the char layer at the surface ablates constantly, even though the sample is overall swelling as seen by the high-speed camera. Therefore, the high-speed camera cannot determine the recession rate until the sample stops swelling. This steady ablation is also assumed when the mass loss of each sample is further analyzed in Sect. 4.8. This assumption has recently been proved by Boehrk [3] by exposing a cork-based TPS to radiative heat flux while monitoring the sample with an X-ray. The 2D images show clearly that the char front propagates linearly inward in the contrast of the swelling outer sample shape. The constant recession rate assumption has also been confirmed in a secondary campaign by Sakraker et al. [20], at the X-Ray synchrotron facility of Karlsruhe Institute of Technology in Germany.

Fig. 12

Swelling and recession profiles by high-speed camera. Positive values correspond to recession and negatives to swelling behavior

Fig. 13

Swelling/recession profiles of the rest of the test cases. Negative values mean swelling, while positive values mean recession

4.8 Mass blowing rates

The mass loss rates of ablators, as well as the the non-dimensional pyrolysis and char blowing rates, $B'_g$ and $B'_c$, respectively, are useful parameters when modeling their response. The first assumption is that the ablation, thus the mass loss, is only due to thermo-chemical processes, thus to pyrolysis outgassing and char ablation. Indeed, no mechanical failure is observed for any of the test cases.

The mass loss rate computation methods differ in the literature based on the materials. If the $B'_g$ and $B'_c$ are not known, as it is the case for P50, Smith et al. [24], who studied the cork P45 material, preferred to compute the total mass loss rate as follows:

$$\begin{aligned} \dot{m}_{\text {tot}} = \frac{m_{i}-m_{f}}{\tau \, A}, \end{aligned}$$

(4)

where $\tau$ is the test duration, $m_{i}$ and $m_{f}$ are the initial and final mass, and A is the total surface area of the hemispherical sample.

Since the first assumption is that all mass loss is due to pyrolysis and the oxidation of the char, this could be treated as the total value. To analyze which portion of the total mass loss comes from which process, the dimensional char blowing rates are computed. One approach is to consider that the recession occurs at a constant rate since the beginning of the test, even though it is not visible on the high-speed camera images initially due to swelling. This assumption agrees well with the constant surface temperature during the whole test. Equation (5) could be used to determine the char blowing rates, $\dot{m}_c$ [10]

$$\begin{aligned} \dot{m}_c =\dot{s}\, \rho _c, \end{aligned}$$

(5)

where $\dot{s}$ is the recession rate and $\rho _c$ is the char density. The char density was measured after the TGA, using the final volume of the charred sample and the final mass measured by the TGA. The char recession rates are taken as the linear slopes of high-speed camera data after the swelling finishes. However, due to the varying test durations of the test matrix presented here, some recession rates cannot be determined accurately, e.g., Test 26 in Fig. 13c.

Fig. 14

The normalized total and char mass rates with surface temperatures. The ordinates are normalized as: ${\dot{\text{m}}\sqrt{R_m / p_e}}$

The total mass loss and the char mass rates are plotted in Fig. 14, and provided in Table 2. Following the literature convention [15], it is also normalized with the sample radius and the pressure at the boundary layer edge. The difference between the total mass loss rates and the char rates can be attributed to the pyrolysis blowing rates. For some cases, the total mass loss has almost the same value with the char rates, so the char blowing rates could not be determined accurately. The reason is attributed to the volumetric swelling which prevents accurate recession measurements.

According to Metzger et al. [15], when the mass loss rate is normalized by radius and pressure, the term is a function of temperature. Metzger et al. [15] studied the non-pyrolyzing graphite; therefore, the char ablation was only due to the oxidation processes. They observed a reaction limited process up to 1500 K where the mass loss rate increases gradually depending on the sample radius; then, the rates reach a plateau until 2800 K where the radius and pressure no longer affects the mass loss rate even with increasing surface temperature, suggesting a diffusion-limited process. After 2800 K, sublimation starts and the mass loss is increasing again as a function of temperature and also pressure. Metzger et al. suggest for graphite that the smaller sample radius and higher pressures move the curves toward higher temperatures. However, for cork P50, these trends are the opposite: as sample radius gets smaller, the temperatures are lower and higher pressures have the same effect. Overall, it can be stated that as the surface temperature increases, the mass loss rate also increases by an order of magnitude and no plateau is observed as for graphite ablation shown by Metzger et al. [15].

In summary, it was seen that the swelling behavior and the pyrolysis effects changed significantly the complexity of the measurements and the results deviated a lot from the expected behavior in the absence of pyrolysis. A dedicated campaign in the future could be performed by exposing the samples for longer times to plasma to increase the accuracy of the recession rate measurements.

For flight safety, it can be concluded that even when the samples lost considerable amount of mass during the test, they have not recessed much so to increase the temperatures at the back. One could also say that the volumetric swelling, in practice although it cannot be put in an accurate prediction model yet, would keep the hot char layer away from the back surface, which would protect the back shell for a longer time.

5 Discussion on Local Heat Transfer Simulation (LHTS) parameters

5.1 Effect of reference heat flux or edge enthalpy

The first duplication parameter of the LHTS methodology is the enthalpy at the edge of the boundary layer. At a fixed pressure, increasing the power of the facility directly increases the resulting heat flux and, therefore, the free stream enthalpy increases as well. At this point, to analyze the direct effect of the enthalpy, thus heat flux, the experiment results are evaluated for fixed geometry, thus velocity gradient at a given free stream. Figure 15 shows how the surface temperature increases linearly with increasing heat flux, so enthalpy, at fixed pressure levels. The rebuilt boundary layer edge enthalpies are shown in Table 3.

In addition to the surface temperatures, the effect of increasing enthalpy can be seen on swelling/recession profiles, as depicted in Fig. 12a. It is seen that at higher heat fluxes, thus surface temperatures, the recession rates are higher. It is also seen that the apparent swelling takes longer time at lower heat fluxes.

Another observation can be made on the total mass blowing rates, given in Table 2. The mass loss rates of the test cases 13, 15, and 18 increase with increasing heat flux, at fixed pressure and sample geometry.

Fig. 15

Change of surface temperature with heat flux for a fixed pressure and sample geometry of 15 mm radius

5.2 Effect of pressure

The effect of pressure on surface temperature is investigated by fixing the sample radius and reference heat flux. The 15 mm sample is chosen as more data are available at different pressures and heat fluxes. To fix the heat fluxes, the previously discussed fits are used, because not all experiments were conducted at the exact same heat flux. Figure 16 shows the change of surface temperature with pressure at a number of fixed heat flux values. It can be seen that at a constant heat flux, the effect of pressure is quite small. At lower heat fluxes, the maximum difference is about 45 K, while at high heat fluxes, the maximum difference is 150 K. As expected, the effect of pressure is quite smaller than increasing the heat flux at a constant pressure, as shown in Fig. 15. It is also seen that there is a decrease of temperature of about maximum 80 K when the pressure is increased from 1500 Pa to 20,000 Pa. This is consistent with other low density ablator experimental data where a decrease between 60 and 160 K was observed [9] for 1500 and 20,000 Pa pressures.

Fig. 16

Effect of pressure for 15 mm radius sample tests at fixed reference heat fluxes. The error bars indicate the maximum of the measurement and the fitting

Fig. 17

Effect of pressure with boundary layer edge enthalpies for 15 mm radius samples. The error bars indicate the maximum of the measurement and the fitting

Figure 17 shows the boundary layer edge enthalpy values for three heat fluxes as the models often require them. Each of the pressure and heat flux couples corresponds to a boundary layer edge enthalpy. As the pressure increases, the amount of power that should be given to the plasma gets higher if we want to keep the heat flux the same. This is simply because there are more gas particles in the chamber. Thus, at constant heat flux, at high pressures, the edge enthalpy is also higher, while the velocity gradient becomes smaller.

Another observation is that although the recession rates are not changing, the total swelling and recession thicknesses and the swelling durations are different. For Test 15 and 25, it is seen that the lower pressure, Test 15, swells during 19 s for 1.5 mm while the swelling time for higher pressure, Test 25, is 23 s and swells for 3 mm. The recession slopes are then the same for both cases. The same two behaviors are observed in Fig. 12b for three tests. This suggest that the swelling thickness and duration are dependent on pressure, thus enthalpy if the heat flux is kept constant. A different trend in the in-depth temperature is also observed, as shown in Fig. 10.

5.3 Effect of sample radius

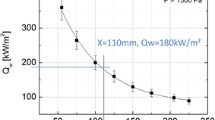
After analyzing the effect of pressure, how the velocity gradient affects the surface temperature of the ablator is also investigated. The cases where different sized samples are exposed to the same free stream having the same pressure and reference heat flux are chosen. Figure 18 shows how the temperature changes with different radii. It should be noted that since the free stream is the same, thus the samples are exposed to the same pressure and enthalpy at the boundary layer edge. However, when the impinging heat flux is measured with a heat flux probe that has the same geometry as the sample, the heat flux gets higher with smaller sample radius. It is seen that, in the ablative tests, the velocity gradient affects only by a maximum of 82 K except the high-pressure high heat flux case where the difference between the mean temperatures is 150 K. The error margins however are observed to be large at the points with high differences.

Fig. 18

Effect of radius for fixed reference heat fluxes and pressures.$\dot{q}_{\text {ref}}$ always corresponds to cold wall heat flux measured by 25 mm radius probe.

The boundary layer profiles of temperature and oxygen are plotted for a cold wall in Fig. 19 for Test 14R, 15, and 16. These are cases exposed to the same pressure and reference heat flux, thus free stream enthalpy; however, they have 25, 15, and 11 mm probe radii, respectively. As the radius gets smaller, the conduction in the fluid phase is increasing as given by the temperature profiles. The diffusion on the other hand is also increasing as shown by the species profiles. Indeed, this confirms the higher impinging heat flux on the smaller sample sizes, since the conduction measured by the calorimeter is equal to the conduction in the fluid and diffusion.

Fig. 19

The boundary layer temperature and oxygen mass concentration profiles, for tests 14R, 15, and 16 which are exposed to the same free stream pressure and enthalpy but having different probe radii of 25, 15, and 11 mm, respectively

In addition to the surface temperature analysis, it is also important to note the effect of radius on the recession/swelling profiles. It was shown in Fig. 12c that the smaller radii resulted in a bigger recession, although the swelling durations were comparable. This may be due to the side heating of the smaller samples, but it necessitates further investigation before conclusion.

6 Conclusions

The experimental results of Cork P50 characterization campaign were presented. The effects of the Flight-to-Ground duplication parameters enthalpy, pressure, and velocity gradient were investigated by exposing Cork P50 samples of different radii to air plasma in VKI Plasmatron facility. It was seen that for a fixed sample geometry and pressure, the surface temperature linearly increased with the reference cold wall heat flux, so the free stream enthalpy. Furthermore, for a fixed sample geometry and given heat flux, the change of pressure is investigated. Note that to reach the same heat flux at a higher pressure, one must operate the facility at a higher power that leads to higher free stream enthalpy to compensate the contribution of the lower velocity gradient. It was seen that the surface temperatures did not change as much as the previous comparison of changing heat fluxes. A maximum decrease of 80 K is observed when going from 1500 to 20,000 Pa. The effect of velocity gradient is also investigated by exposing different sized samples to the same free stream pressure, enthalpy, and reference heat flux. If the cold wall heat fluxes were to measure at the given sample radii, one would measure higher cold wall heat flux with the small sample. It was seen that reducing the sample size from 25 to 11 mm, the surface temperature only increased by 82 K.

Finally, it is the intention of the authors to provide the aerospace community thorough and valuable experimental data on a swelling ablative thermal protection material, for material response model development or as validation cases.