Abstract
Two electric propulsion concepts have been developed at Technische Universität Dresden as spin-off devices of regular hollow cathodes and initial testing has been conducted. Both devices represent millinewton thrusters that take advantage of thermionic electron emission using the low work function materials C12A7, LaB6, and thoriated tungsten in different design configurations. The first concept represents an electrothermal thruster which generates thrust by expanding and accelerating a heated propellant in a nozzle. Initial thrust measurement tests were carried out which showed thrust levels well above cold gas thrust, but low thrust efficiencies. The influence of different geometric parameters on the discharge properties and the performance is investigated and presented. The second thruster concept is a novel electromagnetic device in which charge carriers in a plasma discharge are accelerated by an applied magnetic field that is orthogonally oriented to the discharge current. Initial tests with C12A7 were not successful, but the functionality of the concept was shown by thrust measurements using a thoriated tungsten wire as an electron emitter.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Hollow cathodes are an essential part of electric propulsion systems and have been the subject of extensive theoretical and experimental research for decades. Although the physics of hollow cathodes are complex, they prove to be reliable and efficient electron emitters with lifetimes generally exceeding tens of thousands of hours even at high extraction currents [1]. The technological maturity of hollow cathodes is attractive for stand-alone spin-off devices that could be of interest in various fields of application in the space industry. As part of the H2020 E.T.Pack project that aims at developing a de-orbit kit for spacecraft using an electrodynamic tether, research on hollow cathodes and spin-off devices using the low work function material C12A7 is being conducted at Technische Universität Dresden. In this context, two different propulsion concepts have been designed and realized that take advantage of the basic characteristics of hollow cathodes. The goal of this research effort is to benefit from the considerable advantages that come with heaterless hollow cathodes while relying on a vast body of theoretical literature to optimize the devices. This publication is intended to present the early development progress and first test series of two propulsion systems that will be continuously improved in the future. A third electrostatic hollow cathode thruster concept is currently under development but will be presented in a different publication. The first concept generates thrust electrothermally and has already been extensively studied at the University of Southampton with satisfactory results using and modifying the space-qualified hollow cathodes of the T5 and T6 ion thrusters [2]. The current research effort focuses on expanding the application envelope of these hollow cathode thrusters to C12A7 inserts and thus replacing the heater, and on investigating potential design optimizations by conducting a design parameter study. In Sect. 2, the operational principle and thruster development of the first concept is described. The second thruster type is an electromagnetic device that accelerates charged particles—both positive and negative—by means of the Lorentz force. In contrast to conventional magnetoplasmadynamic (MPD) thrusters, that are characterized by cylindrical discharge channels, the device presented in this work has a rectangular discharge channel in order to apply a homogenous and strong magnetic field, elaborated on in detail in Sect. 3. The results of the conducted test series of both concepts are presented in Sect. 4.
2 Hollow cathode thruster development
2.1 Previous work on hollow cathode thrusters
The idea of a hollow cathode thruster was based on early observations of high energetic ions produced in hollow cathodes [3, 4] and a high degree of ionization in the orifice region, that represent possible thrust production mechanisms, and thus could qualify hollow cathodes as simple stand-alone electric propulsion systems [5]. Efforts at the University of Southampton by Gessini et al. focused on examining the thrust produced by the T6 hollow cathode resulting in the derivation of specific thrust production mechanisms that govern the hollow cathode plasma discharge and could be exploited to improve thrust efficiency and optimize hollow cathode thruster design [6, 7]. This work was expanded to the T5 thruster by Grubisic who did not modify the cathode assembly but attached a nozzle-shaped anode to the hollow cathodes and provided the first benchmark of test results of hollow cathode thrusters [2]. Using the smaller T5 cathode with discharge currents up to 3.2 A, thrust levels on the order of 1 mN at an \({I}_{sp}\) on the order of 200–300 s using argon could be achieved, resulting in thrust efficiencies below 10% [2]. The larger T6 cathode was operated at currents up to 30 A and achieved \({I}_{sp}\) levels of about 1000 s using argon. However, the thrust efficiency was below 1% [2]. Frollani conducted the first effort to derive a performance model of a hollow cathode thruster and tested an optimized version of the T5 and T6 hollow cathode thrusters in which the keeper electrode was replaced by a nozzle-shaped anode [8]. The main work up to now has thus been conducted on the nozzle design and modelling.
2.2 Hollow cathode thruster operation
The principal of operation of hollow cathode thrusters is very straightforward. An electron-emitting insert is placed at the tip of a metal tube and electrically insulated from the keeper electrode—a metal plate with a small diameter hole in its center. Further downstream, a nozzle-shaped anode is attached and electrically insulated from the hollow cathode. The keeper electrode can be omitted and entirely replaced by the anode nozzle, as shown by Frollani [8]. In general, heating of the insert is necessary to enable the thermal emission of electrons. By engaging a gas flow through the tube and applying a sufficiently high voltage to the anode, a plasma discharge is engaged. The propellant is then heated mainly by the current that is drawn from the insert through the orifice to the anode. Due to the small dimensions, the plasma resistivity is highest in the orifice region, and thus the majority of heating takes place in the orifice by means of Joule heating. The small dimensions of the orifice generally prevent the measurement of data that could be used to validate model results. However, the background pressure is assumed to be sufficiently low for the heavy plasma species—namely ions and neutrals—to reach supersonic conditions in the orifice, which is also suggested by 2D hollow cathode model results [9]. The supersonic hot gas then enters the nozzle regions and is expanded and accelerated.
The main thrust production mechanism is the thrust due to particle momentum and pressure at the exit plane by the three plasma species, i.e., ions, neutrals, and electrons. The respective contributions can be expressed by the following, assuming a continuum fluid approach [8]:
where \(m\), \(n\), \(u\), and \(T\) are the species mass, density, velocity, and temperature, respectively. It is, however, difficult to determine the exit plane that needs to be considered to calculate the momentum contributions to the thrust, since the flow quickly transitions from a continuum in the cathode region to a rarefied gas as it is expanded [8]. High modelling efforts are thus required to accurately predict the thrust. Preliminary simulations of the nozzle section using a particle-in-cell code showed that the Knudsen number reaches 1 only a few millimeters downstream of the orifice, which is consistent with other publications on hollow cathode modelling [9].
There are additional potential thrust contributions that have been identified by the researchers at the University of Southampton. For example, high energetic ions have been found in hollow cathode discharges with energies above the discharge potential that might contribute to the thrust. The origins of these ions are manifold and described in detail in Ref. [8]. The thrust contribution of high energetic ions is:
where \({I}_{\mathrm{HEI}}\), \({E}_{\mathrm{HEI}}\), and \({u}_{\mathrm{HEI}}\) are the high energy ion current, energy, and velocity, respectively. To the knowledge of the author, there are no models that predict the current of high energetic ions in hollow cathodes, and thus measurement is necessary. At low discharge currents, however, the thrust contribution of high energetic ions is deemed negligible. The discharge current that is being drawn through the orifice to the anode also causes a net electromagnetic force on the plasma similar to that of a MPD thruster. By integrating the magnetic stress tensor, the famous Maecker's law can be derived and applied to the thruster, as shown in Ref. [8]:
where \({I}_{d}\), \({R}_{a}\), and \({R}_{or}\) are the discharge current, the effective anode radius, and the orifice radius, respectively. Again, at low discharge currents, the electromagnetic thrust contribution is deemed negligibly small. The expected thrust level is in the range of micronewton to the low millinewton range. If the outcome of the study is successful, the performance of the thruster concept is expected to be comparable to common electrothermal devices like resistojets. One advantage of the hollow cathode thruster is that it can serve as both a classic hollow cathode neutralizer and as a stand-alone thruster. A combined operation with a large-scale electric propulsion system is thus possible, where the large thruster can be used for high thrust operations and the hollow cathode thruster can be used for low thrust operations like station-keeping. Moreover, the presented device does not need a heater, and thus simplifies the power processing unit.
2.3 Hollow cathode thruster development
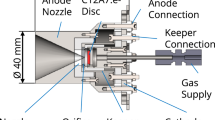
The thruster designed at Technische Universität Dresden focuses on a mostly experimental approach to identify important geometric and operational parameters that drive the performance of a hollow cathode thruster. The prototypes manufactured up to now are modular to quickly apply changes to the geometry of the thruster. One goal of this work is to replace the hollow cathode heater either by using the low work function material C12A7, that has been successfully used in a heaterless hollow cathode by Drobny [10], or by achieving a heaterless plasma ignition using LaB6. Not relying on thermally emitted electrons of a preheated insert necessitates a high electric field that needs to be applied at the surface of the insert in order to achieve a gas breakdown. This constraint leads to different hollow cathode geometries compared to heated hollow cathodes, summarized in Ref. [11]. One drawback using C12A7 is that material properties, like work function and thermal electron emission properties, are not yet fully investigated and understood. Therefore, this work also presents an investigation of the discharge properties of C12A7. A second goal of this research is to limit the discharge current to a maximum of 3 A, mainly to limit the power consumption and due to constraints by the thrust balance used for the current test series. This condition implies that the electromagnetic thrust according to Eq. 6 can be neglected, and high energetic ions will not significantly contribute to the thrust as well. Three baseline thruster modules have been tested that are shown in Figs. 1 and 2. The first version is shown in Fig. 1 consists of a metal tube with a cylindrical C12A7 hollow cylinder insert at the downstream end. A graphite nozzle is attached and electrically insulated by a ceramic spacer. Here, no keeper electrode was used. To facilitate heaterless plasma ignition, the orifice in the ceramic spacer was chosen to be sufficiently small to increase internal cathode pressure. The second version uses C12A7 tablets instead of hollow cylinders. It was decided to implement an additional molybdenum keeper electrode for the ignition phase. In the third baseline thruster, a cylindrical LaB6 insert was implemented. The conducted test series and test results are outlined in Sect. 4.2.
3 Magnetoplasmadynamic device
3.1 Principle of operation
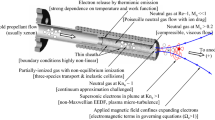
The operational principle of the second thruster concept presented in this work is illustrated in Fig. 3. Within a rectangular, electrically insulating discharge channel, two electrodes are placed on two opposing sides of the channel. An external magnetic field is applied perpendicularly to the expected current flow between the electrodes. Gas is then let into the channel and a breakdown must be achieved by applying a high voltage to the anode. By generating a plasma column in the channel, current flows between the electrodes. Due to the perpendicular magnetic field, the Lorentz force acts on the charge distribution in the channel, accelerating both electrons and ions in the downstream direction. The concept is based on magnetohydrodynamic drives that have mostly been developed for marine propulsion systems. In contrast to conventional MPD thrusters, in which the charge carriers are accelerated primarily by the self-induced magnetic field in an axisymmetric discharge channel, the rectangular design allows to explicitly apply a strong external magnetic field using permanent magnets that excel the self-induced magnetic fields of common MPDs. This allows for a significant reduction of the discharge current and discharge power. Moreover, the design is easily scalable, and the performance can be adjusted by altering the current and the magnetic field strength of the permanent magnets.
The thrust of the device can be estimated by means of a simple analytical model. Here, the current between the electrodes is assumed to be homogenously distributed along the electrode surfaces. The externally applied magnetic field \({{\varvec{B}}}_{\mathrm{ext}}\) is also homogeneous within the discharge channel and interacts with the charge distribution. A force density \({\varvec{f}}\) acts on the plasma volume and can be expressed by:
where \({\varvec{j}}\) is the current density and \({\varvec{B}}\) is the magnetic field. One approach to evaluate the total electromagnetic force acting on the plasma column is by means of the Maxwell stress tensor. Using the differential form of Ampère’s law:
Equation 7 can be rewritten as:
The expression above can be written in terms of the Maxwell stress tensor \({\varvec{T}}\):
Using Gauss’s law:
Equations 9 and 10 can be combined to obtain the total electromagnetic force acting on the plasma:
The above equation shows that the electromagnetic force on the plasma can be expressed by the flux of the Maxwell tensor across the boundary surfaces of the control volume that encloses the plasma column in the discharge channel, depicted in Fig. 4 for the presented thruster. The Maxwell tensor in cartesian coordinates for the magnetostatic case is defined as:
with \(B\) being the magnitude of the flux density. As first approximation, the current is considered as flowing through a perfectly homogeneous rectangular conductor of infinite length. The magnetic field induced by the current within the conductor can be determined by the Biot-Savart law [12]. An infinitesimal cross-section element of the conductor at the location \({\varvec{r}}\boldsymbol{^{\prime}}\) causes a magnetic field of strength \({\varvec{H}}\) at the distance \({\varvec{r}}\) from the element, as shown in Fig. 5.
The x- and y- components of \({\varvec{H}}({\varvec{r}})\) can be determined as follows:
with:
The magnetic field is zero in the direction of the current flow, so that \({H}_{z}=0\) is true throughout the domain. The magnetic field strength is obtained by integrating Eqs. 14 and 15 over the conductor surface:
Using the substitution:
The integrals in Eqs. 22 and 23 are analytically solvable. The magnetic flux density is then determined under the assumption that the relative magnetic permeability is equal to the vacuum permeability:
Since \({B}_{z}\) is zero, the Maxwell tensor is now simplified to:
Here, \({B}_{\mathrm{ext}}\) is included in the \({B}_{x}\) component. Integration of the tensor in Eq. 25 along the respective boundaries yields the force vector that acts on the plasma. The y-component of the force vector can be interpreted as an ideal electromagnetic thrust. In Fig. 6, the dependence of the thrust on different input parameters is summarized. As evident in Fig. 6, the thrust increases linearly with \({B}_{\mathrm{ext}}\), \({I}_{d}\) and \(z\), and is nearly invariant with changing \(a\) and \(b\). The current design aims at generating thrust levels of approximately 1 mN at an Isp of 1000 s to qualify as a potential candidate for attitude control systems and de-orbit manoeuvers of small satellites. For a target thrust level of 1 mN and easily realizable magnetic fields, Table 1 summarizes the determined thruster parameters. In addition to the electromagnetic force, the gas-dynamic force of the gas flow contributes to the overall thrust but was not considered for the design of the device.
The modelling approach presented above is equivalent to simply multiplying Eq. 7 by the discharge volume. However, the implementation of the presented approach allows considering possible inhomogeneities in the discharge parameters and magnetic field, which might be useful in future studies.
3.2 MPD thruster assembly
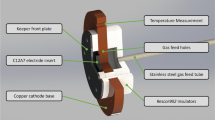
The MPD thruster prototype assembly is illustrated in Fig. 7. A rectangular alumina component serves as the discharge channel. A ceramic gas distributor is placed in the downstream direction of the gas inlet and two ceramic constrictors lead the gas into the channel. The magnetic field is established by an array of permanent magnets connected to two iron poles, acting as a horseshoe magnet.
4 Initial testing
4.1 Test facility
A compact torsion thrust balance developed by Neunzig [13] was used to obtain thrust measurements during operation. A movable aluminum frame serves as mounting for the thrusters and allows rotation about a vertical axis. The electrical connections are realized through liquid metal reservoirs filled with Galinstan along the thrust balance axis, enabling a frictionless connection. There are two ways of operating the balance. For the first method, the thruster's rotation is counterbalanced by an assembly of counterweights. A thrust thereby leads to a deflection of the thruster and a reaction of a torsion spring of known spring constant, which is used to translate the new resting position of the thruster into a thrust value. The deflection is measured using a laser interferometer. The operational principle of the thrust balance is illustrated in Fig. 8. Prior to each test cycle, the balance-thruster assembly is calibrated using a voice coil that applies a defined force to the assembly and leads to a distinct deflection. The second method is called “closed-loop operation”. In this case, the voice coil is used to keep the thruster in place and impede rotation. The necessary current through the voice coil to do so can be translated into a thrust value. For the electrothermal thruster, the closed-loop method was considered more suitable, because higher temperatures of the thruster bearing would affect the spring constant, and thus alter the thrust measurement. By impeding rotation, this source of error is eliminated.
Schematic of torsion thrust balance [13]
The tests were carried out in a 1.4 m × 1.7 m × 2.6 m rectangular vacuum chamber. A primary multi-stage Roots vacuum pump and a second stage cryopump with a total pumping speed of 10,000 l/s enabled a vacuum regime of approximately 1e–7 mbar during the tests without gas ballast. Two Delta Elektronika SM AR-11 power supplies were used for both thrusters. For the electrothermal thruster, preliminary tests showed significantly improved plasma ignition using a 100 Ω pre-resistor for the anode and a 2.2 kΩ pre-resistor for the keeper.
4.2 HCT test results
First tests with cylindrical C12A7 inserts showed promising results as the plasma discharge could be achieved nearly instantaneously by simply applying a voltage to the anode nozzle. Moreover, a clear thrust above cold gas level was observed. However, at currents exceeding 1 A, the C12A7 insert melted and thus clogged the cathode, shown in Fig. 9. The same phenomenon was observed in other early C12A7 hollow cathode test campaigns. C12A7 tablets in combination with a cathode body made of copper proved to be much more thermally stable [10]. Though evacuating excess heat from the insert to prevent overheating seems counterintuitive to an electrothermal device, post-test inspections of the tablet surfaces showed signs of melting, indicating sufficiently high temperatures in the plasma discharge. Inspections by Fraunhofer IKTS revealed that although the surface clearly experiences high temperatures, the thermal resistance is sufficiently high for the cathode assembly not to reach temperatures that are typical for common hollow cathodes. During the conducted test series, the temperature of the cathode backplate did not exceed 100 °C, which was measured using a K-type thermocouple attached to the backplate close to the gas connection. While the intended purpose of the copper cathode body was to prevent the insert from overheating and melting by evacuating excess heat by thermal conduction to the back of the thruster, the use of a highly thermally conductive material like copper might be unnecessary as only the surface of the insert heats up significantly while the base of the emitter stays cooler. Due to the melting of the hollow cylinder insert, it was decided to dismiss the cylindrical C12A7 configuration in favor of C12A7 tablets. For the presented study, two different nozzles and two different orifice dimensions have been tested, summarized in Table 2. Krypton was used as the primary propellant for the test series.
Heaterless ignition of the C12A7 cathode could almost instantaneously be achieved by simultaneously applying a high voltage to both the keeper and the anode at mass flow rates on the order of 1 mg/s. The discharge proved to be stable shortly after ignition independent of the orifice and nozzle dimensions. LaB6 showed a more complex ignition behavior. For most test configurations, no main discharge could be achieved. Using the smaller orifice, the anode discharge was achieved by applying the keeper and anode voltages, which more or less instantaneously led to a gas breakdown within the cathode and a current drawn to the keeper. After a timespan on the order of 300 s, the main discharge was automatically achieved. The keeper discharge thus serves as heating mechanisms for the insert. As soon as a sufficiently high temperature is achieved, thermally emitted electrons supply the main discharge. However, this procedure was only possible using the larger nozzle and the small orifice, no other combination resulted in a successful main discharge ignition. Figures 10 and 11 illustrate ignition processes for both insert materials.
Aside from ignition difficulties, the thrust measurement proved to be inaccurate in most cases, as the thrust signal showed large drifts, independent of the measuring method. This could be largely attributed to thermal drifts. The presented thrust data are thus preliminary and only consider those parameter combinations that showed an interpretable thrust signal at all. Nevertheless, valuable data can be drawn from the current–voltage characteristics (CVCs) of the different tests, shown in Figs. 12, 13, 14, 15 for C12A7 and Fig. 20 for LaB6. Using the smaller 0.25 mm diameter orifice and nozzle A enabled to maintain spot mode for currents up to 1.5 A for mass flow rates as low as 0.6 mg/s at 1.5 A, and well below 0.4 mg/s at 0.5 A. At higher currents, the discharge transitioned to a noisy plume mode even at high mass flow rates in excess of 1 mg/s. For the larger nozzle B, the discharge transitioned to plume mode at currents of 1 A and above. Increasing the orifice size significantly promoted spot mode. Here, the larger nozzle B showed a notable improvement to the smaller nozzle in terms of discharge noise and maintaining of spot mode even at currents up to 2.5 A and mass flow rates as low as 0.5 mg/s. The discharge voltage in spot mode operation was also slightly lower using the larger nozzle. In Fig. 15, the 0.5 A discharge unexpectedly transitions to a very high voltage of approximately 250 V at 0.625 mg/s, while higher currents could be maintained at lower mass flow rates. One possible cause of this phenomenon is the insufficient gas tightness of the prototype. In this case, the discharge might be starved of sufficient charge carriers and transition to plume mode at higher mass flow rates than expected.
The clearest thrust signal using C12A7 was obtained with the 0.25 mm diameter orifice and nozzle B. Here, the deflection signal of the thrust balance showed distinct plateaus as the operating parameters were changed. An exemplary deflection signal is shown in Figs. 16 and 17 for the C12A7 and LaB6 configurations, respectively. The measurement uncertainty was determined by taking the slope of the drift and the standard deviation of the measurement into account. The main systematic measurement uncertainty was due to the voice coil calibration and on the order of 1%. The uncertainties of power supplies and mass flow controllers have been neglected. The thrust and \({I}_{sp}\) as function of discharge current and mass flow rate are summarized in Figs. 18 and 19, respectively. The uncertainty of the thrust measurement is relatively high on the order of 10% for most operating points due to large standard deviations in the thrust signal, as the thrusters were mostly operated in noisy plume mode. However, the trend that can be seen in Fig. 18 is clear. The thrust rises nearly linearly with the discharge current. As the current is increased, the ohmic heating that takes place predominantly in the orifice increases and heats the propellant. The lowest mass flow rate of 0.625 mg/s shows the highest thrust and \({I}_{sp}\) values of the tested mass flow rates. This trend can be attributed to the increase in discharge voltage as the mass flow rate is reduced which leads to an increase in electron temperature, and thus the electron pressure term in Eq. 3 becomes more dominant. However, the depicted thrust and \({I}_{sp}\) values were obtained almost exclusively in plume mode operation, which significantly limits the lifetime of the cathode and is thus unsustainable. Moreover, the thrust and \({I}_{sp}\) obtained at current levels up to 2.5 A barely lie above cold gas thrust and are not competitive yet.
Operation of the LaB6 configuration could only be obtained using the 0.25 mm diameter orifice. As evident in Fig. 20, the cathode was operated in spot mode for current levels up to 1 A at relatively high voltages on the order of 50–70 V. Transition occurred at about 0.6 mg/s for the 0.5 A discharge. At currents above 1 A, the discharge operated in plume mode or in a transition regime at mass flow rates of 1 mg/s and below. The thrust signal for the LaB6 configuration, depicted in Fig. 21, showed a similar linear trend of increased thrust with discharge current. The \({I}_{sp}\) in Fig. 22 generally is higher compared to the C12A7 configuration but still is not competitive with comparable electric propulsion systems like resistojets and low-power arcjets. However, Fig. 22 indicates that notable heating of the propellant takes place even at low currents. Nevertheless, operation of the hollow cathode as presented is not sustainable due to the limited lifetime in plume mode operation. In post-test investigations of the LaB6 and the C12A7 cathodes, the 0.25 mm diameter orifice plates showed notable signs of melting, indicating local temperatures in excess of the melting point of molybdenum. Similar signs of deterioration could not be found for the larger orifice plate of the C12A7 cathode. The tests showed that a smaller orifice results in higher temperatures in the orifice and of the cathode in general, which is consistent with trends of hollow cathode models [14]. However, larger orifices facilitate operation in spot mode and lower the discharge voltages. The target design is thus a trade-off between making the orifice as small as possible to increase the temperature while making it large enough to maintain spot mode. The influence of the nozzle geometry on the thrust could not be identified in the current study but will be investigated in the future. However, Figs. 14 and 15 indicate that increasing the electron collecting area of the nozzle promotes a passive current collection by the anode, as stated by Grubisic [15], and thus widens the spot mode operation regime.
4.3 MPD test results
In preliminary tests, several methods of creating a plasma discharge in the MPD concept have been investigated. First efforts aimed at implementing C12A7 using rectangular inserts fixed on a metal plate as electron emitters. However, the ignition of a stable discharge could not be achieved. A test series using a radiofrequency (RF) voltage applied to a steel plate was then conducted to facilitate plasma generation. Here, a gas breakdown was achieved, and a clear thrust was seen in the thrust signal. However, the RF discharge led to substantial sputtering of the discharge channel and was thus dismissed. A discharge using carbon nanotube foil as electron emitter was not successful as well. Hence, a simple thoriated tungsten wire was implemented that served as an electron emitter. Initial tests were carried out using krypton with an electrode distance z of 10 mm. In Fig. 23, the electro-magnetic component of the measured thrust is shown as a function of the discharge current, the thrust caused by gas flow is not considered. A clear discrepancy is visible between the measured electromagnetic thrust and the ideal thrust in Fig. 23, which can be mainly attributed to the channel and electrode wall friction and possible inhomogeneities in the discharge and magnetic field. Magnetic field simulations of the thruster showed that the magnetic field within the channel is homogenous along the thrust axis but shows slight deviations in the direction orthogonal to the electrodes of approximately 2–3%. This can be source of slight inhomogeneities in the thrust. The channel was thus redesigned, and a second test series was carried out using argon as the propellant, a higher magnetic field of 0.1 T and an electrode distance of 20 mm. In Fig. 24, the electromagnetic component of the measured thrust is shown. The measured electromagnetic thrust shows very good agreement with the ideal Lorentz force. The main problem with the current thruster design is the filament which is sensible to melting. The maximum current that could be extracted with a magnetic field of 0.1 T to date is 0.3 A. Moreover, relatively high mass flow rates are necessary to operate the thruster, limiting the \({I}_{sp}\) to a maximum of 160 s to date. In order to increase thruster efficiency and performance, methods of increasing both the magnetic field and the discharge current are investigated. A new design using a hollow cathode as an electron source is currently being manufactured and will be presented in the future.
5 Conclusion
Two different thruster concepts have been realised, one electrothermal and one electro-magnetic concept. Performance measurements of the electrothermal device have not been satisfactory up to now due to strong drifts in the thrust measurements, but discharge properties of C12A7 are very attractive and will be further investigated and exploited in future device iterations. Although LaB6 showed a slightly better performance in the presented test series, ignition proved to be very difficult. The emphasis of future research on the electrothermal device will thus shift primarily to C12A7. In addition, using a lighter propellant than krypton generally leads to higher specific impulses for electrothermal devices. Early tests using argon as the propellant were promising and will be expanded as well. The current thruster design and test configuration will be revised to improve gas tightness of the thruster and thermal decoupling of the thrust balance from the thruster. The outcome of the upcoming testseries will be compared to a performance model that was developed at TUD to identify optimization potential especially regarding the anode design.
The electromagnetic concept proved to be able to generate thrust on the order of few millinewtons. However, the reliability of the presented design is insufficient. An upcoming design iteration using a C12A7 hollow cathode, a stronger and more homogeneous magnetic field, and a segmented anode will be tested in the near future. The test series will include variations in the cathode position, anode segment control, and cathode orifice geometries.
References
Goebel, D., Katz, I.: Fundamentals of electric propulsion: ion and hall thrusters. Jet Propulsion Laboratory California Institute of Technology (2008)
Grubišić, A.: Microthrusters based on the T5 and T6 hollow cathode. University of Southampton, PhD Thesis (2009)
Kameyama, I., Wilbur, P.J.: Measurements of ions from high-current hollow cathodes using electrostatic energy analyzer. J. Propuls. Power 16(3), 529–535 (2000)
Patterson, S.W., Fearn, D.G.: The generation of high energy ions in hollow cathode discharges. In: IEPC-99-125, 26th International Electric Propulsion Conference, Kitakyushu (1999)
Gessini, P., Gabriel, S.B., Fearn, D.G.: The hollow cathode as a micro-ion thruster. In: IEPC-01-233, 27th International Electric Proulsion Conference, Pasadena (2001)
Gessini, P., Gabriel, S.B., Fearn, D.G.: Thrust characterization of a T6 hollow cathode. In: IEPC-2005–257, 29th International Electric Proulsion Conference, Princeton (2005)
Gessini, P., Coletti, M., Grubišić, A., Gabriel, S.B., Wallace, N.C., Fearn, D.G.: Hollow cathode thruster for all-electric spacecraft. In: AIAA 2007-5195, 43rd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Cincinnati (2007)
Frollani, D.: Modelling and design optimisation of a hollow cathode thruster. University of Southampton, PhD Thesis (2014)
Mikellides, I.G., Katz, I.: Wear mechanisms in electron sources for ion propulsion, I: neutralizer hollow cathode. J. Propuls. Power 24(4), 855–865 (2008)
Drobny, C., Wulfkühler, J., Tajmar, M.: Development of a C12A7 electride hollow cathode and joint operation with a plasma thruster. In: IEPC-2019-629, 36th International Electric Propulsion Conference, Vienna (2019)
Lev, D., Appel, L.: Heaterless hollow cathode technology—a critical review. In: SP2016_3125366, 5th Space Propulsion Conference, Rome (2016)
Strütt, M.: Das magnetische Feld eines rechteckigen, von Gleichstrom durchflossenen Leiters. Archiv für Elektrotechnik 17, 533–535 (1926)
Neunzig, O.: Development of a compact milli-newton thrust balance and characterization of a miniature hall-effect thruster. In: IEPC-2017-375, 35th International Electric Propulsion Conference, Atlanta (2017)
Albertoni, R., Pedrini, D., Paganucci, F., Andrenucci, M.: A Reduced-order model for thermionic hollow cathodes. IEEE Trans. Plasma Sci. 41(7), 1731–1745 (2013)
Grubišić, A., Gabriel, S.B.: Thrust production mechanisms in hollow cathode microthrusters. In: 2010 IEEE Aerospace Conference, Big Sky, MT (2010)
Acknowledgements
This work has received funding from the European Unions Horizon 2020 research and innovation programme under grant agreement No 828902 (E.T.PACK project).
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gondol, N., Tajmar, M. Design of a hollow cathode thruster: concepts, parameter study and initial test results. CEAS Space J 14, 65–77 (2022). https://doi.org/10.1007/s12567-021-00369-1
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12567-021-00369-1