Orbit deployment and drag control strategy for formation flight while minimizing collision probability and drift

Abstract

The compact form factor of nanosatellites or even smaller satellites makes them predestined for distributed systems such as formations, constellations or large swarms. However, when it comes to orbit insertion of multiple satellites, these ride share payloads have constrains in the deployment parameters such as sequence, direction, velocity and time interval. Especially for formation flight missions without propulsion, where the satellites should minimize their relative distance drift either passively or by atmospheric drag control, the initial ejection parameters must find a proper trade-off between collision probability and relative drift. Hence, this article covers short-term (first orbit) collision analysis, long-term (30 days) drift analysis and atmospheric drag control strategy for long-term distance control of multiple satellites. The collision analysis considers various orbit deployment parameters such as insertion direction and tolerance, orbital elements of insertion and time span. To cover the parameter space, a Monte Carlo simulation was conducted to identify the impact of these parameters. It showed that for collision probability the major factor is the time span between two ejections and the precision of the deployment vector. For long-term drift analysis, orbit perturbation such as atmosphere and J2 terms are considered. The result showed that for drift minimizing, minimizing the along-track variation is more substantial than reducing the time span between ejections. Additionally, a drag control strategy to reduce the relative drift of the satellites is described. The results have been applied on the S-NET mission, which consists of four nanosatellites with the task to keep their relative distance within 400 km to perform intersatellite communication experiments. The flight results for orbital drift show equal or better performance (0.1–0.7 km/day) compared to the worst-case simulation scenario, implying that orbit perturbation was chosen correctly and all orbit injection tolerances were within specified range. The drag control maneuver showed good matching to the flight results as well with a deviation for the maneuver time of approximately 10%.

1 Introduction

The number of launches of small satellites, especially CubeSats and nanosatellites, has been increased exponentially over the last years. The increasing number of formation and swarm mission such as the Dove, Flock [1] or Lemur [2] constellation were heavily contributing to this trend. Still these small satellites are launched as secondary payload, and thus have constrains in orbital parameters and deployment conditions dictated either by the primary payload or launch vehicle upper stage.

Especially for satellite swarms/formation with strict requirements on relative distance (due to, e.g., communication, distributed measurement or proximity operation), a proper deployment strategy is crucial to minimize collision risk and set optimal (e.g., propellant saving) drift conditions. Since propulsion is not accommodated in most CubeSat missions, passively minimizing the relative drift by proper initial deployment could reduce system complexity of the satellites.

Hence, this article covers short-term (first orbit) collision analysis based on Monte Carlo simulation, long-term (30 days) drift propagation incorporating J2 and atmospheric density, and atmospheric drag control strategy for long-term distance control of multiple satellites. The analysis has been applied on the S-NET mission, which consists of four nanosatellites with the task to keep their relative distance within 400 km to perform (ISL) experiments [3]. The mission was launched in February 2018 to an 580 km (SSO).

2 Motivation

2.1 Considerations for piggy-back swarm deployment

In general, the orbit insertion condition of share-ride missions is not as flexible as the primary payloads and is constrained by the upper stage configuration and ejection mechanism. Hence, for optimal deployment of multiple spacecrafts, the following constraints must be considered:

• All piggy-back satellites of a launch are normally deployed in a single orbit (e.g., Dove satellites). Re-ignition capability of upper stage may allow for several orbits.

• The attitude determination and control accuracy of upper stage have to be considered when defining the ejection direction. Normally attitude determination of upper stage is performed by the integration of an IMU; thus, the attitude information depends on angular random walk and time since lift-off. Typical values of attitude determination accuracy are few degrees in orbit.

• CubeSats and nanosatellites are mostly separated from upper stage by a dispenser/container using a spring mechanism. Compared to the classical separation ring with pyro actuator, spring mechanism is beneficial in controlling the relative ejection velocity and direction.

• For precise deployment, even the mechanical tolerance of the dispenser mounted on the upper stage must be considered.

Primarily, the initial deployment condition is set to minimize collision risk with the upper stage or other spacecrafts of the deployment sequence. Depending on mission requirements, the secondary requirement would be to minimize the relative drift of satellites (e.g., distributed nanosatellites of mission (S-NET)) or maximize to achieve broad distribution in short time (e.g., 3U Dove constellation by Planet Inc.).

2.2 Existing deployment strategies for formations/swarms

Some deployment strategies have already been evaluated to reach the objectives of each mission. For example, Kılıç [4] analyzes the deployment strategy of a cluster of nanosatellites. Also from the space debris mitigation aspect, proper deployment is required to avoid fragmentation events [5]. A parametric study was utilized to test various deployment parameters and thus analyze the dispersion of the 50 CubeSats of the QB50 mission. Then, it is provided an insight about the collision risk between the CubeSats, as well as, the effect of the deployment strategy on the lifetime distribution of CubeSats.

For swarm deployment, the first couple of orbits right after the orbit injection are the most critical in terms of collision risk. Even if satellites are equipped with propulsion, especially for secondary payloads, a fixed waiting time for initial activation (e.g., 30 min for 6U CubeSats [6]) in order to protect the main payload prohibits active orbit control within that critical phase. Thus, the development of a right deployment strategy is crucial to minimize collision between the swarm members.

Dove satellites, a reference in this sector, have been deployed in different ways. For example, 8 Flock 2E and Flock 2E’ satellites were deployed from the (ISS) in May 2016. They were deployed in groups of two over four deployment windows by a spring deployer supplied by NanoRacks. The system was attached to the Multi-Purpose Experiment Platform of the Japanese Experiment Module. This is grappled and set in deployment position and orientation by the Japanese Remote Manipulator System [7].

3 Methodology

This section presents the propagator used and explains the perturbation sources taken into account for the development of this project. Afterward, the different methodologies considered for the collision and drift analyses are explained.

3.1 Orbital propagation

There are several classical special perturbation methods for orbit propagation such as Cowell, Encke and DROMO. In Cowell’s method, the equations are formulated in rectangular coordinates and integrated numerically. Encke’s method approximates the orbit as an conic section. Since differences grow with time, it becomes necessary to derive a new osculating orbit. This process is called rectification of the orbit. The DROMO method is especially appropriated to propagate complex orbits, e.g., comets and asteroids [8]. For the typical cases of this study (LEO satellites perturbed by atmospheric drag and J2), Cowell’s method offers optimal results in terms of time consumption and precision.

3.1.1 Cowell propagator

Cowell’s formulation for orbit propagation was initially proposed by P. H. Cowell (Cambridge, UK). It is the most direct approximation of all the perturbation’s methods available nowadays, since the (Newtonian) perturbation forces are simply summed. The equation of motion in ECI system is given in Eq. 1:

$$\begin{aligned} \ddot{x}&= - \mu \frac{x}{r^3} + a_{p_x}(t, x, y, z, {\dot{x}}, {\dot{y}},{\dot{z}})\nonumber \\ \ddot{y}&= - \mu \frac{y}{r^3} + a_{p_y}(t, x, y, z, {\dot{x}}, {\dot{y}}, {\dot{z}}) \nonumber \\ \ddot{z}&= - \mu \frac{z}{r^3} + a_{p_z}(t, x, y, z, {\dot{x}}, {\dot{y}}, {\dot{z}}), \end{aligned}$$

(1)

where $a_{p_x}$, $a_{p_y}$ and $a_{p_z}$ are the accelerations caused by perturbations. This work considers atmospheric drag which requires velocity information. Therefore, Cowell’s equation is reduced to a first-order system (Eq. 2), which allows for a broader class of integration methods. The used Cowell propagator integrates the motion equations with a Runge–Kutta–Fehlberg 7(8) numeric solver with variable step size, where perturbations are included:

$$\begin{aligned} {\mathbf {X}}& = \begin{bmatrix} {\mathbf {r}} \\ {\mathbf {v}} \end{bmatrix} \nonumber \\ {{\dot{\mathbf {X}}}}& = \begin{bmatrix} {\mathbf {v}} \\ - \mu \frac{{\mathbf {r}}}{r^3} + {\mathbf {a}}_{p} \end{bmatrix}. \end{aligned}$$

(2)

3.1.2 Orbital perturbation

For small satellites in LEO altitudes 400–800 km, J2 perturbation of the Earth’s oblateness is the dominant force, followed by lunar gravity and solar gravity. The atmospheric density strongly depends on the solar activity and can vary up to one order of magnitude [9]. The orbital perturbations implemented and applied for obtaining the results of this publication are J2 taken from (EAGF) and atmospheric drag using USSA76 as density model.

Non-spherical Earth Harmonics

The Cowell simulation considered the zonal harmonic term J2. The satellite’s acceleration due to the Earth’s non-spheric gravity field EAGF can be expressed as a function derived from the gradient of the geopotential function (Eq. 3):

$$\begin{aligned} {\mathbf {a}}_{\mathrm{{grav}}} ({\mathbf {r}},t)=\nabla \varPhi ({\mathbf {r}},t). \end{aligned}$$

(3)

Atmospheric Drag

The acceleration experienced by the satellite due to atmospheric drag is obtained by Eq. 4:

$$\begin{aligned} \begin{aligned} \mathbf {a}_{\mathbf {d}}&= - \frac{1}{2} \rho v^2_{\mathrm{{rel}}} \frac{C_{\mathrm{d}} A}{M_s} {{{\hat{\mathbf {v}}}}_{\mathbf{rel}}}\\&= - \frac{1}{2} \rho v^2_{\mathrm{{rel}}} BC^{-1} {{{\hat{\mathbf {v}}}}_\mathbf{rel}}, \end{aligned} \end{aligned}$$

(4)

where BC is the ballistic coefficient (Eq. 5), and ${{\hat{\mathbf {v}}}_{\mathbf{rel}}}$ is the unit vector of velocity of the satellite relative to the atmosphere:

$$\begin{aligned} BC & = \frac{M_s}{C_{\mathrm{d}} \cdot A} \end{aligned}$$

(5)

$$\begin{aligned} {{{\hat{\mathbf {v}}}}_\mathbf{rel}} & = {\mathbf {v}} - {\varvec{{\omega }}}_E \times {\mathbf {r}} - {\mathbf {v}}_w. \end{aligned}$$

(6)

In Eqs. 4, 5 and 6 , $C_{\mathrm{d}}$ is the drag coefficient of the satellite, A is its cross-sectional area normal to $\mathbf {v_{rel}}$, $\rho$ is the local atmospheric density, $M_s$ is the spacecraft mass, $\omega _E$ is the angular velocity vector of the central body, and ${\mathbf {v}}_w$ stands for the local wind velocity. $\rho$ is obtained from USSA76. ${\mathbf {v}}_w$ depends on the altitude, as empirical studies from satellites have shown [10]. For altitudes between 200 and 300 km, ${\mathbf {v}}_w$ might have up to 30% of $\omega _E$, but for altitudes above 500 km, it becomes reduced to a range where it can be neglected [10]. Additionally ${\mathbf {v}}_w$, which is dominantly eastward wind, mainly changes the i for high inclination orbits. Inclination change is not primary relevant for the drag analysis.

3.2 Collision analysis

As Florijn points out in [11], the reduction of the collision probability can be achieved through orbit design and determined by the satellite deployment method. The method he utilized to calculate the collision probability is based on the propagation of the nominal position of the satellites with an error ellipsoid that describes the position and velocities by a three-dimensional (PDF). It is concluded that the PDF-based method is more suitable when a large number of satellites are going to be evaluated and the Monte Carlo-based method to calculate collision probability is more suitable for a few number of satellites due to its intrinsic computational intensity.

Patera [12] calculates the probability of collision using a nonlinear approach. The proposed method is applicable to low-velocity space vehicle encounters that involve nonlinear relative motion. According to him, “the total probability of collision over a specified time is obtained by integrating the collision rate over the appropriate time interval.” The accuracy of this nonlinear model was verified with the comparison of a Monte Carlo simulation of 6000 runs, where the collision probability was only 2% greater than the result obtained by the Monte Carlo approach.

A Monte Carlo method is used to compute the collision of various deployment scenarios. In a Monte Carlo statistical method, the variable of interest is computed from a random input variable. In this study, ${\mathbb {V}}_{\mathrm{{RD}}}\ni \mathbf {v_R}$ represents the random set of deployment velocity vectors of each satellite w.r.t the upper stage. The random variation from the ideal ($\mathbf {v_D}$) is derived from the sum of the following uncertainties:

• $e_{\mathrm{{dis}}}$: variation of ejection velocity vector due to the ejection mechanism (generally spring or linear actuator) and mechanical tolerance of dispenser itself

• $e_{\mathrm{mech}}$: tolerance of the mechanical alignment between dispenser and upper stage

• $e_{\mathrm{us}}$: error in attitude control of upper stage

Assuming normal distribution, the random deployment vector $\mathbf {v_{R}}$ is given by:

$$\begin{aligned} \mathbf {v_{R}} \sim N(\mathbf {v_D},\sigma ^2) \end{aligned}$$

(7)

with $1 \sigma$ variation

$$\begin{aligned} \sigma ^2 = e_{\mathrm{dis}}+e_{\mathrm{mech}}+e_{\mathrm{us}}. \end{aligned}$$

(8)

Therefore, for every satellite, $\vert {\mathbb {V}}_{\mathrm{{RD}}} \vert = n_{\mathrm{{R}}}$. The permutation of each satellite pair $s_is_j \left( i,j=1\dots n_{\mathrm{{sat}}} \right)$ results in

$$\begin{aligned} n_{\mathrm{i}}= n_{\mathrm{R}} \cdot \left( n_{\mathrm{R}} -1 \right) /2 \end{aligned}$$

(9)

number of iterations that is required to obtain an acceptable amount of values for the minimum (${d}_{\mathrm{rel}}$), which is the parameter of interest. The bigger the $n_{\mathrm{{i}}}$, the more accurate is the result of the Monte Carlo approach. To find a trade-off between computing time and accuracy, the following equation is used to obtain the order for $(n_{\mathrm{i}})$ [13]:

$$\begin{aligned} \textit{n}_{\mathrm{i}} = \left( z_{\alpha /2} \frac{100s}{\varepsilon {\bar{Y}}}\right) ^2. \end{aligned}$$

(10)

$\varepsilon$ is the percentage error of the mean. s is the calculated standard deviation, ${\bar{Y}}$ is the calculated mean, and $z_{\alpha /2}$ is the z-score associated with $\alpha /2$ where $\alpha$ is the significance level.

Finally, collision is counted if ${d}_{\mathrm{rel}}\le d_{c}$ within orbit propagation. Therefore, the collision probability is simply obtained by

$$\begin{aligned} P_{\mathrm{c}} = \frac{n_{\mathrm{c}}}{n_{\mathrm{i}}}. \end{aligned}$$

(11)

3.3 Drift analysis

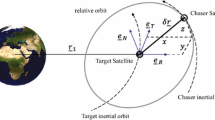
The study of drift can therefore estimate the lifetime of a mission, its different phases or the time between maneuvers for missions with active orbit control capabilities. If the drift can be estimated and minimized by controlling the initial deployment condition, even formation flight and proximity operations without propulsion could be feasible. Thus, herein the drift analysis investigated the effect of initial orbit insertion condition and orbit perturbation. For the direction of deployment, the three main directions to analyze correspond to the three axis of (LVLH) reference system:

• Zenith deployment impulses in radial direction change the shape (e) and in-plane orientation ($\omega$ and $\nu$) of the satellite, but not the size or plane of the orbit.

• Along-track deployment along-track impulses produce a change in the shape and size of the orbit (a, i and e), and also in the orientation in-plane ($\omega$ and $\nu$), but do not modify the plane.

• Cross-track deployment finally, impulses in cross-track direction will affect mainly the plane of the orbit, changing i and $\varOmega$.

To analyze the long-term drift behavior depending on initial condition of orbit insertion and orbit perturbation, a Monte Carlo method was applied. Similar to the collision analysis method, the ($n_{\mathrm{ED}}$) of the $\mathbf {V_{D, ED}}$ is selected. The set of ${\mathbf {V}}_{{\mathbf {D}}, {\mathbf {ED}}}$ is distributed around the nominal deployment velocity ${\mathbf {v}}_{\mathbf {D}}$. Each vector is propagated with Cowell propagator (Eq. 1), which returns $n_{\mathrm{ED}}$ propagated position sets for each satellite. These sets are combined to obtain the relative distances among the satellites. There are $n_{\mathrm{ED}} \cdot \left( n_{\mathrm{ED}}-1\right) /2$ combinations for each pair of satellites $s_is_j \left( i,j=1\dots n_{\mathrm{sat}} \right)$ and each drift between two satellites after a given amount of time.

3.4 Differential drag control

Differential drag is caused when the ballistic coefficients (Eq. 5) of the spacecraft in a formation are not equal. The magnitude of differential drag depends on the difference in ballistic coefficients and also the altitude of the spacecraft formation. Differential drag is a favorable method to compensate orbital energy difference, especially for small satellites who do not carry active propulsion. Mean motion of satellites could be matched by decreasing larger semi-major axes values using higher drag.

After S-NET satellites were launched in February, consistent secular drifts are observed in relative distances between satellites. As anticipated from Clohessy–Wiltshire equations [14], these drifts result from velocity component in along-track direction. Expressed in Keplerian orbit elements, those linear increases are caused by discrepancies in satellite’s orbital energies (i.e., semi-major axis disparities). Since mean motion of the satellites is a function of semi-major axis only, those differences affect the satellite’s angular velocity.

Fig. 1

Relative state $\theta$ in along-track direction

3.4.1 Differential drag controller

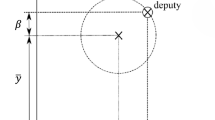
Since differential drag affects the in-plane dynamics only, six relative states in the LVLH frame could be reduced to a single angular distance $\theta$ and its derivative ${\dot{\theta }}$. The angle $\theta$ is defined w.r.t. the reference satellite as shown in Fig. 1. As shown, ${\dot{\theta }}$ is equivalent to the satellite’s mean motion for circular orbits. The reference satellite is the one which has the smallest semi-major axis, because drag could only generate negative acceleration and reduces the orbital energy.

The main idea of differential drag control is to accelerate each satellite’s ${\dot{\theta }}$ until it becomes the same as the reference value, by increasing cross-sectional area and adjusting $\ddot{\theta }$. $\ddot{\theta }$ is zero when the satellite faces the same amount of drag as the reference and has a nonzero value when the satellite is in high-drag mode [1, 15]. To derive $\ddot{\theta }$ caused by differential drag, induced $\varDelta V$ should be examined first. Since the cross-sectional area and corresponding ballistic coefficient in high-drag mode $\hbox {BC}_{H}$ are different from the low-drag value $\hbox {BC}_{L}$, $\varDelta V$ during the discretized time period $\varDelta t$ could be derived as in Eq. 12. To simplify the formulation, dynamic pressure $q_{ref}$ is set as an average value from the reference satellite:

$$\begin{aligned} \begin{aligned} \varDelta {V}&= \frac{1}{2}\overline{\rho {v^2_{\mathrm{{rel}}}}}(\hbox {BC}_L-\hbox {BC}_H)\varDelta {t}\\&= q_{\mathrm{{ref}}}(\hbox {BC}_L-\hbox {BC}_H)\varDelta {t} \end{aligned}. \end{aligned}$$

(12)

Considering the secular along-track term in CW equations only, mean relative velocity ${\dot{y}}$ could be approximately derived as a function of $\varDelta V$:

$$\begin{aligned} {\dot{y}}\approx -3\dot{y_0}=-3\triangle {V}=3q_{\mathrm{{ref}}}(\hbox {BC}_L-\hbox {BC}_H)\varDelta {t}. \end{aligned}$$

(13)

For the special case of circular orbits, angular acceleration $\ddot{\theta }$ could be converted from relative velocity ${\dot{y}}$ by using the reference satellite’s mean semi-major axis at epoch ${\bar{a}}_{\mathrm{{ref}}}$:

$$\begin{aligned} \ddot{\theta }=\frac{{\dot{y}}}{{\bar{a}}_{\mathrm{{ref}}}\varDelta {t}}=\frac{3q_{\mathrm{{ref}}}}{{\bar{a}}_{\mathrm{{ref}}}}(\hbox {BC}_H-\hbox {BC}_L). \end{aligned}$$

(14)

Required time interval to maintain high-drag mode can be obtained by dividing initial angular velocity offset with angular acceleration above:

$$\begin{aligned} \varDelta {t}=-\frac{({\dot{\theta }}-{\dot{\theta }}_{\mathrm{{ref}}})}{\ddot{\theta }}. \end{aligned}$$

(15)

4 Analysis setup

4.1 Mission S-NET overview

The mission goal of S-NET is to demonstrate intersatellite communication with distributed nanosatellites. The mission consists of four satellites, to test multi-hop communication with different protocols and routing algorithm. Four satellites allow for redundancy on satellite level, since the ISL can also be performed with some restrictions on three satellites.

To reduce system complexity of the space segment, a propulsion system was omitted, and therefore, the relative formation will be controlled by the initial separation parameters. The goal is to keep the satellites within a range of ${400}\,\hbox {km}$ to enable a stable ISL for at least four months. Therefore, the separation direction, angle, velocity and sequence will be the primary starting values for the formation drift. A summary of mission parameters is provided in Table 1.

Table 1 Overview of mission S-NET [16]

The four S-NET satellites were accommodated in dispensers (Fig. 2) and inserted into a ${580}\,\hbox {km}$ SSO via Soyuz/ Fregat. The re-ignition capability of Fregat upper stage allowed for a circular orbit even for secondary payloads. The nominal orbital elements for the upper stage at time of ejection are specified in Table 2. These values were used for both collision and drift analysis. Only for true anomaly of collision analysis, a different value of ${30}^\circ$ was used. Besides, for both analyses, the considered perturbations for the propagation with Cowell are listed in Table 3.

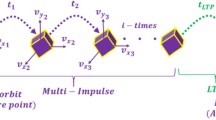
The considered distance from one dispenser to the next dispenser’s CoG is ${0.5}\,\hbox {m}$, and the time interval between consecutive separations $\varDelta t_{\mathrm{{SS}}}$ was set to $10\hbox {s}$ according to the simulation results in this article.

Fig. 2

Dispensers for S-NET mounted on Fregat upper stage. See Fig. 3 for dispenser orientation and naming conventions

Table 2 Initial nominal classical orbital elements of the upper stage ($\text {COE}_{A,US,t0}$) for the drift analysis

Table 3 Considered perturbations for the S-NET collision and drift analysis

Finally, the characteristics of the nominal deployment vector ${\mathbf {v}}_{\mathbf {D}}$ that generate both the random set of deployment vectors $V_{D,R}$ for the collision analysis and the equal distributed set of deployment vectors for the drift analysis $V_{D,ED}$ are summarized in Table 4.

Table 4 Deployment velocity vector and tolerance for S-NET

4.2 Collision analysis

From the nominal deployment parameters, the mean minimum relative distance between two consecutive satellites is obtained as 13.258 m with a standard deviation of 3.371 m, $z_{\alpha /2}$ = 2.58 (99% level of confidence) and $\varepsilon$ = 1%. Thus, according to Eq. 10, at least 4305 iterations are required to achieve 99% confidence level that the calculated value of the minimum $d_{\mathrm{{rel}}}$ between two satellites is within 1% of the true minimum distance’s value. Finally, a sample size of 250.000 provides an accurate level for the real mean and $n_{\mathrm{{R}}}$ is set to 500. The critical distance $d_{\mathrm{c}}$ is set to $0.30\,\hbox {m}$. To compare the effects of perturbations, two propagation methods were used to run the simulation: One refers to the Keplerian propagation without perturbations and the other uses the Cowell propagator to integrate the orbit, inclusive of J2 and atmospheric drag perturbations. Also, different deployment directions and separation sequences were considered to figure out the optimal deployment strategy.

4.2.1 Deployment direction

The direction of deployment is defined by the attitude control of the upper stage. The Euler rotation sequence from XYZ (along-track/cross-track/nadir) to the deployment direction assumed in this paper is pitch, followed by yaw and then by roll. The reference direction is positive along-track where the pitch is $0^\circ$ and yaw $0^\circ$ (P0Y0). Hence, to point a deployment toward the zenith direction, the rotation of the upper stage is $90^\circ$ in pitch and $0^\circ$ in yaw (P90Y0), as per schematic in Fig. 3. The cross-track direction is (P0Y90), respectively. The nominal deployment is shown in the schematic in Fig. 3, which is the baseline to compare other deployment parameters. The nominal ejection velocity vector ${\mathbf {v}}_{\mathbf {D}}$ has a magnitude of $1.5\,\hbox {ms}^{-1}$ and point toward zenith (P90Y0).

4.2.2 Deployment order

The deployment order changes the initial distances of satellites. Linear A configuration (P3–P1–P4–P2) means that S1 is deployed from position P3, then S2 from P1, then S3 from P4 and finally S4 from P2. Thus, the initial distance on the upper stage is maximized. Linear B configuration (P1–P2–P3–P4) implies that the directly neighboring satellites are ejected beginning from positions P1, P2, P3 and finally P4. A summary is given in Table 5.

Table 5 Setup for the collision simulation

Fig. 3

Schematic of the upper stage’s attitude for deployment toward zenith direction. Nominal deployment conditions: $COE_A$, Linear A, P90Y0

4.3 Drift analysis

For the drift analysis, all propagations (upper stage and deployed satellites) are carried out with the same set of perturbation forces that includes J2 and are propagated with Cowell. Atmospheric drag was not considered since the effect is negligible for the altitude of $580\,\hbox {km}$. The simulations have been carried out for the three main direction zenith, along-track and cross-track of the nominal deployment, to achieve results for $30\,\hbox {d}$ from insertion. Since the three main directions provide the worst and best cases for drift, parametrical exploration of those combinations was not done in this work. Especially for a nearly circular orbit, the result can be compared with the Clohessy–Wiltshire equations for relative motion.

To estimate the behavior of the four satellites after deployment with reduced computation load, a set of equally distributed worst-case deployment velocity vectors has been defined, based on the tolerance provided in Table 4.

The set of deployment velocity vectors ${\mathbb {V}}_{\mathrm{{ED}}}$ has been reduced by defining the maximum deviations from the nominal values for each case. Taking the full set of random vectors ${\mathbb {V}}_{\mathrm{{RD}}}$ would exceed acceptable computation time, especially for 35 days of drift propagation. Thus, ${\mathbb {V}}_{\mathrm{{ED}}}$ is defined as:

$$\begin{aligned} {\mathbb {V}}_{\mathrm{ED}} ={\mathbf {v}}_{\mathbf {D}}\cup {\mathbf {v'}}_{\mathbf {{ED}}} \cup {\mathbf {v''}}_{\mathbf {{ED}}} \end{aligned}$$

(16)

and illustrated in Fig. 4.

Fig. 4

Sketch of deployment vectors ${\mathbb {V}}_{\mathrm{{ED}}}$ used for the drift analysis

Thus, it results in 17 vectors and covers the most deviated cases from the nominal vector ${\mathbf {v}}_{\mathbf {D}}$ as:

• The nominal deployment vector ${\mathbf {v}}_{\mathbf {D}}$, refer to Table 4 for values

• ${\mathbf {v}}'_{\mathbf {{ED}}}$: magnitude: ${1.5}\,\hbox {ms}^{-1}+ 3\% \left( 1\sigma \right)$, angle offset $\theta = {2}^\circ \left( 1\sigma \right)$ w.r.t ${\mathbf {v}}_{\mathbf {D}}$, azimuth variation: $0, 45\dots 360^\circ$

• ${\mathbf {v}}''_{\mathbf {{ED}}}$: magnitude: $1.5\,\hbox {ms}^{-1} - 3\% \left( 1\sigma \right)$, angle offset $\theta = {2}^{\circ } \left( 1\sigma \right)$ w.r.t ${\mathbf {v}}_{\mathbf {D}}$, azimuth variation: $0, 45 \dots 360^\circ$

A summary of drift simulation setup is given in Table 6.

Table 6 Setup for the drift simulation

4.4 Drag control maneuver planning

For S-NET, S4 is at the very front and S2 has the slowest angular velocity. Obviously, S2 will be the one with high-drag mode, which has the maximum cross-sectional area.

The attitude of the following satellite is assumed to be tilted $45^{\circ }$, and the leading satellite is assumed to continuously tumble with respect to the velocity direction, which generates 17% of area difference.

Maximum cross-sectional area for S-NET is $\sqrt{3}$ times larger than the square cross section.

Although the area difference is small between two satellites, it is still sufficient for S-NET mission because secular drifts are gradual compared to general cases.

To calculate required $\varDelta t$ for drag control maneuver to stop relative drift, atmospheric density is set as a rough average based on the ephemeris, which is $\rho = 2.5 \times 10^{-14}\,\hbox {kg}/\hbox {m}^{3}$, and mean dynamic pressure of the reference satellite, i.e., S4, is derived as a function of reference velocity:

$$\begin{aligned} q_{\mathrm{{ref}}}=\frac{1}{2}\rho \times {v^2_{\mathrm{{rel}}}}. \end{aligned}$$

(17)

The drag coefficient depends on numerous factors such as shape of the satellite, momentum exchange with molecular particles, satellite surface temperature and chemical reactions at the satellites surface. Since satellites do not incorporate methods of measuring it, the numerical value must be estimated. Empirical values from orbital measurements given by [17] indicate a good estimation of $C_{\mathrm{d}}=2.3$ for the cube-shaped S-NET satellites at 580 km altitude. The only unknown parameters in the equation are semi-major axis and the reference velocity. Since two semi-major axes are almost identical to each other, semi-major axes value should be precisely determined. For instance, Brouwer mean conversion oscillates in $10^2$m level, and the semi-major axis difference is in $10^0$m order. To get accurate semi-major axes, (GMAT) propagation was conducted with 50x50 EGM96 gravitational model and the resulting positional differences were averaged over time.

Table 7 Semi-major axis of S4 and S2, based on flight data

The a difference (values given in Table 7) causes mean motion difference of approximately $1.182\times 10^{-9} s^{-1}$. This again results in $3.062 \times 10^{-3}$ rad angular drift in along-track after 30 days. This is equivalent to ${21}\,\hbox {km}$ range drift, which is similar to actual behavior from measurement data presented in Fig. 15. Once all the variables are prepared, mean dynamic pressure and the angular acceleration values could be achieved as follows:

$$\begin{aligned} q_{\mathrm{{ref}}}& = \frac{1}{2}\cdot \rho \cdot {\left( \sqrt{\frac{\mu }{a_{\mathrm{{ref}}}}}-\omega _{E}\cdot {a_{\mathrm{{ref}}}}\cdot cos{i}\right) ^2} \nonumber \\ & = 7.29 \cdot 10^{-7} \dfrac{\hbox {kg}}{\hbox {ms}^{2}}, \end{aligned}$$

(18)

and thus,

$$\begin{aligned} \ddot{\theta }=\frac{3q_{\mathrm{{ref}}}}{{\bar{a}}_{\mathrm{{ref}}}}(\hbox {BC}_H-\hbox {BC}_L)=1.06\cdot 10^{-15} \frac{1}{s^2}. \end{aligned}$$

(19)

And the angular velocity of each satellites is obtained by:

$$\begin{aligned} {\dot{\theta }}= \sqrt{\dfrac{\mu }{a^3}}. \end{aligned}$$

(20)

Required $\varDelta t$ estimation results to stop the drift are as given in Table 8.

Table 8 Required $\varDelta t$ for drag control maneuver to stop relative drift

5 Results for mission S-NET

5.1 Results for collision analysis

5.1.1 Cowell propagation

The Cowell propagation results are plotted in Fig. 5. The histogram shows that $90\%$ of the collision probability occurs within the first ${10}\,\hbox {min}$ after the deployment process starts. The next potential collision window is after half orbital period and then again after one full orbit, where the satellites approach the initial state. After one orbit, the cumulative probability reaches close to 1.

Fig. 5

Collision histogram and cumulative distribution of nominal deployment over a orbital period with J2 and atmospheric drag

5.1.2 Components of the deployment vectors that cause collision

Here, the collision cases are examined in detail. Figure 6 shows the distribution and mean values of azimuth, elevation and magnitude of the deployment velocity vectors that cause a collision for the satellite combination S3S4. The bottom figure verifies the influence of deploying with two different velocity magnitudes on the collision probability. From this graph, it is observed that it is more probable for a collision to occur when the deployment velocity’s magnitude of the second deployed nanosatellite is greater than the first one.

Fig. 6

Mean value of the components of the deployment velocity vectors that cause a collision, including J2 and atmospheric drag

5.1.3 Effect of deployment configuration

The linear A (P3–P1–P4–P2) configuration with an attitude of P90Y0 was originally proposed under the assumption that a greater distance between the slots of the satellite’s dispenser would generate a lower collision probability. However, the linear B (P1–P2–P3–P4) configuration (P90Y0) was tested in order to verify that assumption. From the results provided by the total cumulative collision graph, which is presented in graph Fig. 7, it is observed that the Linear A drives a $P_{\mathrm{c}}$ of $0.2048\%,$ while the $P_{\mathrm{c}}$ of Linear B (P90Y0) is $0.1788\%$. Therefore, the distance between slots is not the only parameter affecting collision probability, it is also influenced by the order in which they are deployed and the attitude of the upper stage. For example, a simulation with Linear A configuration and upper stage’s attitude of P90Y90 provides a $P_{\mathrm{c}}$ of $0.1748\%$, while Linear B with P90Y90 drives a $P_{\mathrm{c}}$ of $0.1800\%$, showing that a greater distance between the slots has more influence when the upper stage’s dispenser is oriented perpendicular to the orbital path.

Fig. 7

Comparison between Linear A and Linear B deployment configurations. Vertical red line marks one orbital period

5.1.4 Effect of deployment time span

Among the simulated deployment parameters, the span between the satellites insertion $\varDelta t_{\mathrm{{SS}}}$ results in the greatest variation of collision. Figure 8 provides the collision probabilities w.r.t $\varDelta t_{\mathrm{{SS}}}$ for two cases: without perturbation (Keplerian orbit) and with perturbation (J2 and atmospheric drag). The figure shows for $\varDelta t _{AB}=5$ s a collision probability difference of 0.23% (0.80% vs. 1.03%) only. According to the results, the propagation method and the perturbation effects are negligible. After $10\,\hbox {s}$, $P_{\mathrm{c}}$ converges to less than 1%.

Fig. 8

Effect on overall collision probability w.r.t time spans $\varDelta t_{AB}$ after one orbit with perturbation and without perturbation

5.1.5 Effect of deployment direction

The effect of the deployment direction is analyzed by varying the yaw and pitch angle depicted in Fig. 9. The red colored zone highlights the highest $P_{\mathrm{c}}$ and occurs in the cross-track direction (P0Y90) with value of $0.364\%$. In contrast, the lowest $P_{\mathrm{c}}$ of $0.204\%$ occurs in zenith direction (P90Y0) which is colored in dark blue. The along-track (P0Y0) is intermediate with $P_{\mathrm{c}}$ = 0.29%. Despite variations, the effect of deployment direction is rather small, since the majority of collisions occur within the first 600 s (see also Fig. 7), where the relative motion effect is not fully unfolded yet.

Fig. 9

Collision probability for six deployment directions including J2 and atmospheric drag, $\varDelta t_{\mathrm{{SS}}}$=10s. Cross-track (P0Y90) $P_{\mathrm{c}}$ = 0.364%, along-track (P0Y0) $P_{\mathrm{c}}$ = 0.29%, zenith (P90Y0) $P_{\mathrm{c}}$ = 0.204%

5.1.6 Effect of orbital elements of the upper stage

To analyze the effect of the orbit characteristic on $P_{\mathrm{c}}$, the orbital elements e and a of insertion orbit were varied in discrete steps. Figure 10 plots the results for a range of $e=0\dots 0.015$ and $a=6871\dots 7071$ km. It shows a variation of only 0.01% (min: 0.20%, max: 0.21%) for a nearly circular orbit. The dashed white rectangle highlights the tolerance window of the upper stage’s orbit insertion tolerance specification (values also given in Table 2). In this range, the $P_{\mathrm{c}}$ only changes $\pm 0.002\%$, indicating that a and e introduce negligible variability for nominal orbit insertion.

Fig. 10

Collision probability w.r.t variation of e and a shows a variation of 0.01%. White dotted rectangle represents orbit insertion nominal tolerance window

5.2 Drift behavior

Simulations were run for the four S-NET satellites with time span between satellites set to $\varDelta t$=10s, which resulted in sufficiently small $P_{\mathrm{c}}$ = 0.204%. For each direction, a set of pointing errors was added to the deployment vector, as discussed in Section 4.1. The results are presented in three subsections, depending upon the deployment direction employed. Since the purpose was to identify the extrema and along-track results in maximum drift (worst case), a parametrical exploration was not part of this paper.

5.2.1 Along-track deployment

The drift produced after along-track deployment is the largest among the three directions considered. Figure 11 shows the maximum drift obtained combining the sets of initial vectors for each combination of satellite pairs. The drift in this case is very large, reaching almost $780\,\hbox {km}$ for this maximum-drift case. The maximum drift corresponds in all cases to combinations with maximum difference in deployment speed (one satellite with an initial $1.45\,\hbox {ms}^{-1}$ and the other one with $1.55\,\hbox {ms}^{-1}$), which provoke the maximum variation in a and therefore in the orbital period.

Fig. 11

Maximum drift for each combination for along-track deployment

5.2.2 Cross-track deployment

The results for cross-track direction are obviously very different compared with along-track. Cross-track deployment causes mainly a change in an orbit’s plane (i) and not size (a). In Fig. 12, the maximum drift for each combination is shown, reaching about ${21}\,\hbox {km}$ drift after 30 days. Again, the results are very similar for the six pair combinations.

Fig. 12

Maximum drift for each combination for cross-track deployment

5.2.3 Zenith deployment

Observing Fig. 13, the maximum drift obtained for zenith deployment is of the same order as for cross-track, namely less than ${22}\,\hbox {km}$ for the worst case. Obviously, the closer the deployment order, the smaller the drift. The drift is caused by the along-track component of ${\mathbb {V}}_{\mathrm{{ED}}}$. It is thus important to minimize this component in the launch, to comply with the requirements of the mission.

Fig. 13

Maximum drift for each combination for zenith deployment

Finally, Fig. 14 shows the maximum drift after 30 days of propagation by varying $\varDelta t_{\mathrm{{SS}}}$. It presents an almost linear variation of drift versus time span; thus, to minimize the drift, it is necessary to deploy the satellites with minimum time span as possible. Thus, a trade-off between $P_{\mathrm{c}}$ (Fig. 8) and drift (Fig. 14) must be found by defining proper $\varDelta t_{\mathrm{{SS}}}$.

Fig. 14

Effect of different deployment time spans on total drift obtained after 30 days of propagation (J2 and drag), for the worst between satellites 1 and 4 in zenith deployment

5.2.4 Relative distance in orbit

The relative drift among the satellites was measured in orbit using the signal run time of the S-band radio during ISL sessions. The measurement was correlated with TLE data and ILRS data to increase the accuracy and is illustrated in Fig. 15. Interestingly, the maximum value of measured $d_{\mathrm{{rel}}}$ occurs between satellite S4 and S2 and coincides with the simulation result for zenith deployment, given in Fig. 13. All other satellite distances are smaller than the simulation case. Overall, it implies that the tolerance assumptions made for $\mathbf {v_D}$ (Table 4) were realistic and all launch requirements have been fulfilled.

Fig. 15

Simulation (worst case) vs. orbit data of relative drift shows that drift value is less or equal (S4-S2) compared to simulation results. This indicates that simulation assumptions regarding orbital perturbation and ejection vector tolerances were correct and that the real initial condition was within the specified tolerances

5.3 Drag control results

The graph in Fig. 16 shows the real relative distance plot. The experiment has been started at day 190. The most ahead flying S-NET A was put into nadir pointing mode, to allow other satellites to catch up. SNET-D is the slowest satellite, and it is following SNET-A and SNET-C which are randomly tumbling. The plots are from two-line elements analysis. The acceleration is $-3.8\, \hbox {m}/\hbox {d}^2$ between SNET-D and SNET-C and $-3.0\, \hbox {m}/\hbox {d}^2$ between SNET-D and SNET-A from the plot fitting. Average acceleration is about $-3.4\,\hbox {m}/\hbox {d}^2$. Due to some operational constraints, the accumulated drag control was performed for 247.8 h during 151 days. The expected acceleration for this case can be averaged as:

$$\begin{aligned} \ddot{y}= \ddot{\theta } \cdot a_{ref} = -55.3 \frac{m}{d^2}\cdot \frac{247.8h}{24h\cdot 151} = -3.78\frac{m}{d^2}. \end{aligned}$$

(21)

The calculated and scaled acceleration is consistent with the in-orbit result with an error of about 10%. This error could be cased by $C_{\mathrm{d}}$ estimation error, variable atmospheric density, irregular tumbling and attitude control error.

Fig. 16

Flight results of relative distance control. Nonlinear drift (red box) is a result of differential drag control started at day 190. Since SNET-A and D were controlled, the not involved pair B-C remains linear

Non-constant atmospheric density during propagation is surmised as a cause for vestigial secular behavior.

6 Conclusion

An analysis on various deployment conditions to develop an orbit deployment and drag control strategy to minimize the collision and drift rate for distributed space systems (e.g., swarms or formations) is presented. This analysis includes the impact of deployment conditions such as orbital elements, time span, deployment direction and order for multiple satellites on collision probability and relative drift. Due to the large number of relevant parameters to define the insertion condition, a Monte Carlo simulation was conducted. Only perturbations due to J2 and atmospheric drag ($\rho$ from USSA76) were considered. The parameter space was limited to a SSO LEO swarm mission assuming a near circular orbit, and as a baseline four satellites where simulated. The upper stage was assumed to provide flexible pointing and deployment configuration. At the end, the analysis was applied for the distributed nanosatellite mission S-NET. The following aspects can be concluded from the analysis:

• For $P_{\mathrm{c}}$ analysis, the variation of e and a is mostly negligible for nearly circular orbits (Fig. 10).

• For $P_{\mathrm{c}}$ analysis, the relevant time window to consider is in the order of few orbits after insertion (Fig. 7). In fact, approximately 90% of all collisions events occur within the first 600 s (Figs. 5, 9). After one orbit, the probability of collision approaches zero due. Thus, the deployment direction does not have significant impact for $P_{\mathrm{c}}$ since the effect of relative motion is not fully unfolded for the first 600 s.

• For $P_{\mathrm{c}}$ analysis, the major factor is the time span $\varDelta t_{\mathrm{{SS}}}$ and the precision of the deployment vector. Even the effect of drag and J2 perturbation can be neglected due to the short time window of relevance (Fig. 8).

• Long-term (few months) drift analysis considering J2 and atmospheric drag showed very good matching to flight results. The effect of sun and moon gravitation and solar pressure were not analyzed in this work.

• Cross-track and zenith deployment do not show significant differences in drift rate. However, cross-track deployment can generate a drift in the orbital plane due to differential (RAAN) rate, which could be more difficult to correct via differential drag. RAAN control could be achieved via differential lift, as introduced in [18].

• Along-track component does not significantly reduce $P_{\mathrm{c}},$ but is major cause of long-term drift. So these three main directions result in the extrema boundaries for drift. So to minimize drift, minimizing the along-track component is the key, more than reducing the time span $\varDelta t_{AB}$ (Figs. 12 and 14 ).

• The value of $C_{\mathrm{d}}$ to obtain BC has been estimated from [17], since direct measurement is not feasible. Even though drag control maneuver in order to stop the relative drift rate showed good matching to the flight results with a deviation for the maneuver time of approximately 11% (Section 5.3), this was good enough to apply the drag control maneuver successfully in orbit.

• Table 9 contains recommended deployment configuration, direction, time span and resulting collision probability and maximum drift rate for the mission S-NET.

Table 9 Selected parameters for the S-NET mission