The MASCOT separation mechanism

Abstract

The Mobile Asteroid Surface Scout (MASCOT), an Asteroid Lander carried by the Hayabusa2 spacecraft, successfully landed on the Near-Earth Asteroid (162173) Ryugu on October 03, 2018. Thereby accomplishing the first-ever landing of a European spacecraft on the surface of this type of celestial body. MASCOT was a prototype design of a new class of nano-size surface science packages for the exploration of small solar system bodies. The very low gravity (thus, very low escape velocity) of the target body required the design of a miniaturized deployment mechanism with a relatively small, well-reproducible separation velocity. In addition, the mechanism also had to safely restrain the lander to the mother spacecraft during the launch and its 3.5-year cruise phase. In this paper, we describe in detail the design, numerical analysis and test of this newly developed separation mechanism. Furthermore, we compare the mechanism to other existing deployment systems and verify its performance with two independent analysis methods using actual flight data taken during the ultimate flight activation event, which initiated the successful delivery and surface operation of the MASCOT asteroid lander.

Introduction

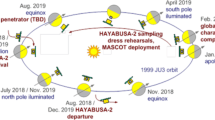
Launched on December 03, 2014, from the Tanegashima Space Center in Japan, the Japanese space probe Hayabusa2 (HY2), carrying the German–French (DLR/CNES) Lander MASCOT (Mobile Asteroid Surface Scount) [1, 2], reached its target asteroid (162173) Ryugu on June 27, 2018 [3]. After arrival, HY2 performed first a global mapping to characterize the asteroids global properties and to gather information for the selection of a suitable landing site for MASCOT based on local geology, thermal constraints and scientific interest. On October 03, 2018 at 03:58:15 UTC MASCOT was released during a dedicated HY2 descent and slow free-fall maneuver at a relative altitude of 41.3 m above the surface (Fig. 1). At this point, MASCOT was ejected out of its support frame with a controlled low velocity of a few cm/s. MASCOT then performed a slow tumbling free fall only under the influence of the weak gravitational field (Fig. 2) before touching down for the first time approximately 6 min later, bouncing multiple times across the surface and finally coming to rest in an arbitrary orientation. Thus, achieving the first European landing on an asteroid.

Fig. 1

Separation and landing sequence of MASCOT on asteroid Ryugu

Fig. 2

Snapshot of MASCOT (top right) and its path across the surface during its approach to Ryugu (indicated in yellow). Image credit: JAXA, University of Tokyo & collaborators. Flight reconstruction: DLR [4]

The separation process from the carrying mother spacecraft was a decisive factor. For such a prototype design driven by tight constraints in mass and volume, several odds could have impeded a successful deployment and had to be taken into account. In the following, the subsystem design of the MASCOT separation mechanism is outlined, giving details on its architecture, design criteria and functional performance as analyzed with multi-body simulation and as tested in microgravity test campaigns. In addition, we compare these results to the flight data collected during the landing event on October 03, 2018, supporting its TRL-9 maturity.

Deployment units: types and concepts

To introduce the peculiarities of the separation problem in a microgravity environment, this section shall provide an overview of the different requirements imposed onto the deployment of the MASCOT package to the Ryugu surface. Later we will investigate the suitability of common deployment mechanisms regarding these requirements and justify the chosen design to be described in a following chapter.

There are two key requirements, which satisfy mission success: (i) the lander shall survive the launch and cruise phase attached to the carrier spacecraft and (ii) the lander shall land safely on the surface of the asteroid. In combination with the given environment during launch, cruise and at the asteroid these yield a list of further broken down requirements as displayed in Table 1. A few derived requirements are worthwhile a closer investigation. In a microgravity environment, the landing or touchdown (TD) velocity is of high importance. This is not only true because of the need to sustain the landing from a structural point of view, but more importantly to assure a lander actually staying on the surface of the target body. Due to the low gravity of the body, the local escape velocity is very low, which could lead to eventual rebouncing of the lander in case it arrives with a velocity exceeding this local escape velocity. In case of deploying a passive lander without any propulsive means, the TD velocity is mainly driven by the separation height and any given delta-v. Thus, these aspects are the only parameters, which can be influenced to change the TD velocity and need to be tightly controlled in design and mission planning to guarantee successful landing. While the former is mainly determined by the carrier spacecraft, the latter can partially be influenced by the design of the separation system. This will be discussed in the following sections.

Table 1 System level requirements (SR) dedicated to the deployment of the lander

Based on these requirements, the following four basic functions need to be covered:

• 1. Secure and lock the system during launch.

• 2. Release the launch lock.

• 3. Deploy the system in a dedicated direction and with a defined velocity, i.e.

• i. Provide kinetic energy to the system.

• ii. Provide direction and guidance.

• 4. Provide deployment status information.

These functions are typically also required for the deployment of cubesats from larger satellites as well as for the deployment of secondary payloads from upper stages. The following section shall discuss some characteristics of common systems for these purposes.

Cubesat dispensers

A cubesat deployer is a rectangular box with a spring-loaded door/hatch and a spring platform mechanism, which could accommodate three 1U or one 3U cubesats (or any combination in between) for launch and up until deployment. Upon opening the hatch, a preloaded spring pushes the cubesat out of its box. Typically, rails inside the deployer guide the cubesat to ensure a reliable trajectory. One of the most frequently used systems is the P-POD (Poly Picosatellite Orbital Deployer) from Standford and CalPoly [5] (Fig. 3e). The P-POD system and similar solutions are in the mass range of 3 kg. The kinetic energy of, e.g. a 3 kg cubesat after separation is in the order of $E_\mathrm{kin} =$ 8 J. The door is held in place by a bolt and a non-explosive actuator, which is activated by the carrier. All other systems use a similar design and follow the cubesat dimensional standards. Main differences are to be found in the release mechanism of the door (e.g. using electro-thermal actuators/wire cutters) and in the general shape of the system. Similar concepts are available which accommodate 6U or even 12U cubesats [6], but without flight heritage yet.

Fig. 3

a Minerva-II-1 (JAXA) b MASCOT (DLR) c Philae (MPG) d M3S (ISIS) e P-POD Mk III (CalPoly/San Luis Obispo and SSDL/Stanford University) f Kaber–NanoRacks separation system (NRSS) g Lightband MkII (Planetary Systems Corporation)

For larger payloads, a containerized system provides no benefit. Micro- and nanosatellites in the range of larger than 12U and up to 300 kg are directly attached via discrete mounting points or standardized separation rings such as the Planetary Systems Corp Lightbands or other Clampbands. The Mk II motorized Lightband adapter (Fig. 3g) is a flexible space-vehicle separation system, which features low shock at separation and has a long flight heritage. It is produced in multiple diameters starting at 20 cm, 1.5 kg. The kinetic energy provided by the smallest lightband is in the order of $E_\mathrm{kin} =$ 8.7 J. An alternative to the Lightband with a similar design is provided by NanoRacks and its Kaber small satellite deployment system (Fig. 3f) providing release capability for payloads of up to 100 kg and velocities of 25–50 cm/s [7].

Customized solutions

The Philae lander onboard Rosetta was deployed in 2014 to land on the comet 67P/Churyumov–Gerasimenko. To guarantee separation, the lander mechanical separation system (MSS, Fig. 3c) contained two redundant release mechanisms: a belt-driven spindle drive and a spring eject system. The former could be preset to safe ejection velocities between 10 and 50 cm/s [accuracy of 1.3% and $0.3^{\circ }\,(1\sigma )]$, while the latter provided a fixed release velocity of 18.74 cm/s, [8]. The total MSS mass was 7.39 kg [9]. The spindle drive was the baseline system, whereas the spring eject was used as redundancy and back-up. Even in the case of a total loss of motor power, a mechanical jam or failure of the cruise latch mechanism, the lander could have been jettisoned.

The Minerva-I and Minerva-II-1a/b systems were stored and deployed in a similar fashion as the canisterized solutions for cubesats (Fig. 3a). Half the storage enclosure would be separated upon command and would give away the spring-loaded rovers. The total mass of the deployment structure was $\sim 1.1$ kg [10] and the deployment velocity was in the order of 20 cm/s [11].

Regarding other customized small satellite deployer alternatives, the M3S (Fig. 3d) developed by Innovative Solutions In Space (ISIS) provides a three point launch adapter with an integrated separation system. It is suitable for a mass of up to 100 kg, induces no shock and has been developed as a low mass alternative to the Light- and Clampband systems. It features separation switches and an adjustable deployment velocity.

Table 2 provides an overview over the discussed solutions. Most of the mechanisms are resettable, which is beneficial for verification purposes. Especially the Cubesat and Lightband separation systems are highly reliable as these are standardized systems which have been used in dozens to hundreds of applications. This would have naturally led to the choice of such a systems for any kind of similar problem. However, as can be seen in the table the add-on system mass for all of these solutions is very high. The same holds true for the separation velocities. And the unique combination of microgravity environment requiring very low separation velocities as well as low system mass and small volume led to the necessity of designing a completely new separation system for the MASCOT lander (Fig. 3b).

Table 2 Comparison of deployment mechanisms

System design of the MASCOT separation mechanism

This section shall describe the customized solution for the MASCOT deployment system in detail and trace to the requirements as defined above. To do this, we will analyze the system architecture in the next section, followed by a detailed design description of the subunits of the deployment system.

System architecture

The MASCOT space system (Fig. 5) as installed on the HY2 carrier consisted of two main elements: (i) the landing module (LM) and (ii) the mechanical electrical support system (MESS). These two elements were the compounds of the main system elements, which contributed to the deployment functionality. The physical breakdown (in terms of system blocks) and functional allocation is displayed in Fig. 4. To understand the peculiarities of the design of these elements, in addition to the functions as mentioned earlier, it is important to mention that the MASCOT system was bound to very strict volume and mass constraints given by JAXA responsible for the design of the carrier HY2.

Fig. 4

System architecture and functions of the MASCOT separation mechanism

To meet these, structural interfaces were minimized. The fixation of the LM to the MESS (Fig. 6) and its associated deployment functionality was based on four cup–cone-shaped stand-off elements shown in Fig. 7 (right), which were held in place by a single load-bearing bolt to be released at separation. In this way, the LM walls and edges were decoupled from the MESS-structure and no guiding rails were required which is common for regular CubeSat dispenser pods. Fig. 7 (left and center) shows a CAD sketch of the overall system and the physical locations of the main components contributing to the deployment functionality. The ejection energy resulting in a deployment velocity as required was realized by the MASCOT Separation Mechanism (MSM). To meet the tight mass and volume budget, this system was custom built and designed as a robust single-shot device with high reliability. This MSM consisted of four main subunits, namely the preload release mechanism (PRM, Fig. 8), a hold down and release mechanism (HDRM, Fig. 9), an umbilical connector (UMC, Fig. 10) and a miniaturized spring-loaded push-off mechanism (POM, Fig. 11). The PRM was designed to reduce the required preload for a save launch lock, but which were inherently stored in the CFRP-structure. The HDRM fulfilled the function of coupling and de-coupling the lander to the MESS. The UMC transmitted the decoupling signal to the HDRM and served also as a separation sense line, while the POM finally provided the delta-v of the release activity. In addition to these functionalities, the MESS structure served as a guidance while the lander made its way out of the cradle. It also provided the overall mounting interface towards the HY2 carrier system.

All elements were designed according to ECSS standards for the minimization of misalignment errors and cold welding risk and the total mass of the MSM was < 290 g, including PRM 85 g, HDRM 75 g, UMC 65 g, POM 52 g and harness respectively. The functionality and performance of the MSM has been verified by system level tests (presented in detail in [2]), extensive sub-unit tests (e.g. low temperature or even thermal-vacuum and shock/vibration for the PRM, UMC and POM), as well as in dedicated microgravity campaigns using parabolic flights and drop tower experiments (presented in Sect. 4). The design and operational principle of these four subunits are explained in more detail in the following.

Fig. 5

Left: MASCOT landing module (LM); right: mechanical and electronic support system (MESS)

Fig. 6

MASCOT LM attached to the MASCOT MESS

Fig. 7

CAD schematic of the MSM outlining its main components contributing to the deployment functionality (left and center) and a close-up on the MESS stand-off cup–cone interface principle (right)

Fig. 8

MASCOT preload release mechanism (PRM) comprising of two thermoplastic discs and three heating foils stacked inside two opposing titanium pans. Successful activation was monitored with four adjustable closing contacts

Fig. 9

MASCOT hold down and release mechanism (HDRM) comprising of a non-explosive actuator 9100 from NEA^® Electronics, Inc. and a custom made separation bolt

Fig. 10

MASCOT umbilical connector (UMC) comprising of two identical MIL standard matrix KJ type bodies equipped with spring-loaded pogo pins on one side and concave counter-pins on the other

Fig. 11

MASCOT push-off mechanism (POM) comprising of the V-shaped push-off plate (POP), a PTFE-coated inner bushing, a titanium-polished outer bushing and a heat-treated steel compression spring

Fig. 12

Simplified schematic of the MASCOT separation and release sequence. Left to right: (1) pre-loaded launch configuration, (2) relieved cruise configuration after PRM activation and release of pre-load, (3) final eject sequence after NEA activation, release of bolt and LM push-off, (4) free flight of LM guided by the MESS, (5) release of LM after clearing the MESS frame

Subunit description and operational principle

The MSM operated as a two-stage system. The first stage (preload release) was activated and controlled by MASCOT during one of the cruise check-out activities. The second stage (eject maneuver) was triggered by HY2 at the asteroid with an automated timer initiating the terminal separation sequence while being below 60 m above and on a free-fall trajectory towards the surface (cf. Figs. 1 and  12).

Preload release mechanism

To withstand the high stresses of shock and vibration during launch, the LM was “locked” with a high preload of approximately 2500 N. This was to ensure that the lander stayed in place within the MESS and neither to harm the main spacecraft nor changing the pre-adjusted configuration for the separation. However, through initial multi-body simulations (Sect. 5) it was found that the preload was elastically stored within the CFRP structure and would have been transferred to kinetic energy of the lander upon release. In this case, the separation velocity would have been too high which could have caused the LM to rebounce from the surface and drift off into space. To guarantee a smooth separation and to avoid an excessive eject velocity, the preload of the structure was required to be reduced by a dedicated mechanism.

The concept of the PRM (shown in Figs. 13, 14) was based on two polyacetal thermoplastic disks with heating foils in between stacked to a sandwich inside two opposing titanium pans. Two temperature sensors measured the heating process by which the discs were mechanically weakened. This initiated a fast creeping process and consequently a movement of the pans towards each other, which was driven by the initially set preload. To keep a small remaining load for the cruise phase and the following separation process, four adjustable closing contacts did stop the motion and at the same time detected electrically the successful preload release process. A successful activation was given, when contact was detected by two diagonal opposing contacts. The required activation time had to be pre-selected based on ground test results (Fig. 15)

After activation of the PRM, the LM was left with a minimal load of approximately 100 N. This assured physical contact within the stand-offs and was sufficient to compensate structural distortions due to temperature gradients during cruise.

Fig. 13

Electrical interfaces of the MASCOT PRM

Fig. 14

Section view of the MASCOT PRM and detailed description of its elements

Fig. 15

Remaining preload force and temperature profile during PRM final TVAC acceptance tests

Hold down and release mechanism

For releasing the LM from the MESS and therefore from its mother spacecraft HY2, the HDRM comprised of a non-explosive actuator (NEA) 9100 from $\hbox {NEA}^{\textregistered }$ Electronics, Inc. and a custom-made steel separation bolt. The NEA is based on a split spool principle. The operation involves a tensile load (preload) applied through a release rod held in place by two separable spool halves which are in turn held together by a tight winding of restraining wire. The restraint wire is held in place by redundant electrical fuse wires (Fig. 16 a). Actuation of either circuit allows release. When sufficient electrical current is applied, the restraint wire unwinds allowing the spool halves to separate (Fig. 16 b) releasing the rod and the associated preload (Fig. 16 c).

Fig. 16

Operational principle of the non-explosive actuator (courtesy of: NEA Electronics, Inc)

To initiate the terminal eject maneuver the NEA was triggered by a main-spacecraft command (Fig. 17). This command was sent by ground via the HY2 on-board Telemetry Command Interface Unit (TCIU). The TCIU delivered a pulsed command to the HY2 Igniter (IG) Box closing the redundant trigger channels and firing the redundant fuse wires of the NEA. A fuse current of approximately 3 A was needed on one of the channels and respective fuse filaments for roughly 30 ms to activate the release. But since the possible range of the IG box was given to be 2.65 – 5.55 A, the current was provided for 1 s to account for possible lower currents.

Fig. 17

Separation command and NEA actuation logic showing the main and redundant actuation lines/circuits and redundant fuse wires

Since the NEA was a commercial of the shelf product and has well demonstrated its performance and reliability on other missions, no dedicated qualification tests for this unit was necessary. However, its capability and environmental performance was confirmed during the MASCOT system level qualification tests presented in Sect. 4

Umbilical connector

The electrical interface for this command was the UMC which provided also a feedback signal to indicate MASCOT’s separation upon disconnect. The connector design (shown in Figs. 18, 19) was based on a MIL standard Matrix KJ type body with spring-loaded pins. The material selection (coatings) was determined by the prevention of cold welding during the 4-year cruise phase. Gold-coated pogo-type pins on the LM side (connector part B) and concave platinum counter-faces on the MESS side (connector part A). The combined force of the spring contacts was sufficient to push the two connector bodies apart at release. The design principle was taken from Philae lander heritage, but due to lack of a full comprehensive documentation, the connector had to be entirely re-engineered and a full qualification process was necessary including fit checks and mating cycles, push force and misalignment measurements as well as environmental testing in thermal vacuum and for shock and vibration.

Fig. 18

Position and interfaces of the MASCOT UMC including connector bodies, housing and spring-loaded contacts

Fig. 19

Detailed elements of the spring-loaded contacts within the MASCOT UMC

Push-off mechanism

When the NEA was triggered releasing its hold-down pressure, the compression spring drove the push-off plate (POP) which pushed the LM into its eject trajectory. The energy stored in the compressed spring needed to correspond to the LM’s required kinetic energy at ejection (completely leaving its support frame) of $v_{\mathrm{rel}} \approx$ 5 ± 0.5 cm/s. The POP was made of CFRP-foam sandwich, 4.5 mm in thickness. At the interface of the separation bush, the foam was replaced by an aluminum flange which provided a robust interconnection. The POP was shaped to fit on the struts of the LM to evenly distribute the pushing force. As long as the CoG of the LM resided within the effective area of the POP, the introduction of rotational moments was minimized.

A detailed sketch of the POM is seen in Fig. 21. The external support structure was placed in the MESS main truss and fixed with a washer on its top and a small collar at the bottom side. Placed within the moveable separation bushing was the separation spring with and unloaded length of $L_0=70\,\hbox {mm}$ (Fig. 20). When the bushing was put and locked in the external support structure, the spring was compressed and preloaded to $L_1=53.3\,\hbox {mm}$. When the LM was installed in the MESS, the spring was compressed further to $L_2=47.8\,\hbox {mm}$. The push length dl was, therefore, 4.5 mm (Fig. 20).

The spring stiffness k and actuation/push length ${\mathrm{dl}} = L_1-L_2 = s_0-s_1$ was estimated for the requirement, that the energy stored in the compressed spring shall not exceed the maximum allowed kinetic energy of the LM after deployment.

$$\begin{aligned} E_{\mathrm{spring}} \le E_{\mathrm{kin,max}} \Leftrightarrow \frac{1}{2} k \cdot {\mathrm{dl}}^2 \le \frac{1}{2} m v^2. \end{aligned}$$

(1)

The verification and necessary adjustment of the compression spring is further explained in Sect. 4.

Fig. 20

Schematic of force–displacement and corresponding potential energy of the push-off spring

Fig. 21

Detailed view of the push-off mechanism (POM) and its elements

The successful deployment of the lander out of its MESS cavity was key to mission success and the most critical activity in the functional chain between in-cruise activation and landing. For such mission-critical mechanisms, ECSS typically demands the avoidance of single point of failure, e.g. by implementing redundancy. As this was not possible within the given strict volume and mass budget, the MSM had to be designed non-redundantly. To keep risk at a minimum, the NEA was chosen as a highly reliable component with built-in redundancy. Further design guidelines included ECSS advised aspects of material selection, tribology, thermal and structural design and sizing for mechanisms.

As described above, the POM was designed as a linear motion system with the separation bush gliding within the external support structure. This relative movement was intended for integration and separation purposes, but not at other times. In launch configuration, the loaded spring pushed the separation bush with the attached POP against the fixed LM. But although the mechanism’s movable mass was low, micro-movements could not be excluded during launch phase. This could have led to cold welding of the external support structure with the separation bush and its corresponding guiding and end-stop bolts/pins, respectively (cf Fig. 21).

In accordance with the standards ECSS-E-ST-33-01C and ECSS-Q-ST-70C, potential material pairings shown in Table 4 were evaluated based on the requirements listed in Table 3 to prevent cold welding between the aforementioned parts of the POM.

Table 3 Sub-system requirements (SSR) driving the push-off mechanism design

The selected basic material pairing was titanium, 3.7035 (Ti99.4—Grade 2), for the External Support Structure and aluminum, EN-AW 5083 (AlMg4.5Mn0.7), for the separation bushing. Based on this, the aluminum part was suitable to receive various surface coatings and dry lubricants as listed in Table 4.

Table 4 Material parings traded for the application of parts with gliding contact (external support structure vs. separation bushing and bolts) *3.7035 (Ti99.4—Grade 2), **EN-AW 5083 (AlMg4.5Mn0.7)

Eventually, the last three material pairings from Table 4 were pre-selected for further investigation of possible cold welding and wear of the lubricated surface. In a dedicated experimental setup (cf. Fig. 22), a pin, made of titanium, was loaded with 9 N and moved in $50\,\upmu \hbox {m}$-long strokes over a flat disc, made of aluminum and treated by one of the three pre-selected surface coatings each. The pin movement was continued for 10 s with a frequency of 200 Hz, then the pin–disc contact was opened and the separation force measured. For each pin–disc pairing, this cycle was repeated consecutively 30 times at 1013 hPa, 30 times at 10 hPa and 30 times at high vacuum, to simulate the rocket launch. For reliability purposes, this was repeated for a second set of the same pin–disc material combinations and intervals. As described in [12], it was concluded that the material combination Ti + Al/Anodisation + PTFE performs the best under the given requirements. Hence, the QM and FM units of the external support structure were made of titanium, 3.7035 (Ti99.4—Grade 2), and the separation bushing as well the guiding pins were made of aluminum, EN-AW 5083 (AlMg4.5Mn0.7), coated by a sulfuric acid anodizing (SAA) layer with embedded PTFE (provided by: Fraunhofer Institute for Surface Engineering and Thin Films, Braunschweig).

Fig. 22

Sketch (left) and test setup (right) of the cold welding test [12]

Environmental tests in microgravity

To verify the design of this low force mechanism and to ensure its proper functionality in the expected microgravity at the asteroid, dedicated environmental tests had to be performed. Following the first development test during the 19th DLR Parabolic Flight Campaign (PFC) in Bordeaux, France, in February 2012, a consecutive series of three Drop Tower Campaigns (DTC) at the ZARM low-gravity facility in Bremen was conducted in March 2013 (DTC-1), February 2014 (DTC-2) and June 2014 (DTC-3), respectively. These tests took advantage of the close vicinity to the DLR Bremen Institute of Space Systems, where MASCOT has been developed and build, and the high grade of undisturbed microgravity level due to the 110 m free fall in an evacuated drop shaft.

Test setup and constraints

For DTC-2 and DTC-3 (equivalent to the Qualification and Acceptance Tests), a long capsule interface was used, compared to the short capsule used during DTC-1, with a direct build-in experimental setup (Fig. 23). This was done in favor for better observation possibilities as well as less restricted integration and handling space. The safe encapsulation of the experiment was achieved by placing aluminum plates directly between the four structural base trusses of the capsule. For measuring the release velocity high-speed image recoding (Photron Fastcam (MC2-10K) with 250–500 fps) was used. The release rotation was detected using an internal wireless IMU (x-IMU, with a data rate of 256 Hz). Additional action cams (GoPro Hero3) were used at selected locations to capture the global separation behavior (Fig. 25) as well as localize critical contact points between the LM and the MESS if necessary. To ensure a soft touchdown and capture of the LM within the experiment setup and to avoid an uncontrolled harmful rebounce of the LM, when the drop capsule gets decelerated (> 50 g) at the end of the drop shaft, a dedicated deceleration cushion was placed into the setup. This cushion was padded with a layer of a hook-and-loop fasteners, with the corresponding hook-and-loop fasteners attached to the top surface of the LM (the side which makes contact with the cushion).

Fig. 23

Separation experimental setup with attached MESS and LM integrated inside the drop capsule

Fig. 24

MASCOT-LM and MESS body fixed coordinate system

As mentioned above, the MSM was designed as a simple, robust and very lightweight unit. While through its simplicity its reliability increased, the drawback was found in (i) the predefined and non-adjustable separation velocity and (ii) a higher uncertainty for the eject trajectory and rotational rate after clearing its support frame. While the impact of the elastic energy stored for launch in the primary structure was limited with the PRM, the function of the UMC was more severe. The UMC was designed as a positive-force separation connector. As a consequence, it introduced a non-negligible amount of energy as all of its 49 spring contacts worked in parallel. The effective spring stiffness of the UMC was thus given with $k_{\mathrm{eff}} = 0.125$ N/mm $\cdot$$49 = 6.125$ N/mm. This impact was even aggravated since due to the compact volume of MASCOT it was necessary to place this connector a certain distance away from the landers CoG. As a consequence, a rotational moment was introduced. To overcome all of these side effects the push-off was adjusted to drive the lander by a short and relative strong impulse rather than a long gentle push. Due to the governing influence of the POM, the lander was driven forwards along the separation direction (z-axis), but due to the secondary effects of the structure and the UMC, lateral movements within the xy-plane could not be avoided (LM frame, cf. Fig. 24). Through the combined verification of numerical simulations (Sect. 5) and microgravity tests, it was possible to understand the systematic behavior of the lander during its separation process and to trim the mechanism parameters accordingly. However, due to this systematic pattern, lower separation speeds were not feasible or would have largely increased the risk of getting stuck within the frame. The analysis of the LM’s release velocity and release rotation is given in the following.¹

Fig. 25

Separation sequence of the MASCOT LM in microgravity during drop tower experiments

Release velocity

Figures 28 and 29 show the results of the LM’s release velocity relative to the MESS during DTC-2 and DTC-3, respectively. Since MASCOT and its CFRP structural parts were hand-crafted elements, the contact of the POP to the LM bottom side depended on manufacturing tolerances. Hence, the precise contact area and consequently the push force distribution could vary greatly. This situation was observed very drastically during DTC-2 in flights 1 and 2, where the eject velocity dropped from 5.5 cm/s down to 1.9 cm/s. To stabilize the POP and to minimize the influence of the manufacturing uncertainties, the tips of the two push arms where padded increasing slightly the thickness (Figs. 26 and 27). The resulting low pre-bending of the elastic arms ensured a reliable three-point contact from the POP to the LM. Comparing the following flights 3 and 4, the separation velocity remained relatively stable at 3.7 cm/s and 3.9 cm/s, respectively. However, even with the stabilized push-off, the LM still encountered many small contacts inside the MESS lowering the given energy. Identified as a major risk, the initial energy of the compression spring had to be adjusted.

Due to this, a slightly stiffer push spring was used during DTC-3. As can be seen in Fig. 29, the combined effects of the stabilized contact and the increased spring stiffness, enabled the system to produce reliable and reproducible release conditions. The POM propels the LM with an initial velocity of $v_{\mathrm{push}} = 8.7$ ± 0.6 cm/s out of its rest position. Due to a short but strong dissipating MESS contact within the first 0.5 s, this was systematically reduced by $\sim$ 40 %. Afterwards, the velocity remained relatively constant and the LM cleared the MESS frame safely with a higher eject velocity. The apparent velocity oscillations along the modules eject path were again due to soft contacts within the MESS following minor rotation changes as well as due to the one-axis optical measurement principle (rotation bias). However, as compared to the previous results in DTC-2, these contacts were less critical and did not lower the system’s kinetic energy further. The actual differences of the release velocity between individual flights could be argued with the uncertainty in the adjustment of the main preloading for each flight ($F_{\mathrm{pre}} = 250\,\pm$ 50 N).

Averaging the results for $t\ge$ 0.5 s, led to $v_{\mathrm{rel}}=$ 4.56 cm/s, 5.09 cm/s, 4.26 cm/s and 5.25 cm/s, for flights 1 – 4, respectively. The mean value is 4.79 cm/s with a standard deviation between values of 0.15 cm/s, thus giving a standard deviation of the mean of 0.08 cm/s corresponding to a random uncertainty. The standard deviation between the four flights, corresponding to the systematic uncertainty/repeatability, was ± 0.49 cm/s. Therefore, the mean release velocity for the test article was determined to be 4.79 ± 0.56 cm/s ($1\sigma$), or ± 1.69 cm/s ($3\sigma$). However, this absolute value referred to the test specimens used. Since these tests were performed prior to QM manufacturing some parameters deviated slightly from the flight model. Hence, the final value to be expected had to be estimated. The test model used during DTC-3, had a different eject spring constant k and a different mass m. Due to manufacturing issues for the FM springs, it was required to integrate a slightly stronger spring into the MASCOT FM, $k_{\mathrm{FM}} = 0.21$ N/mm, compared to $k_{\mathrm{DTC}} = 0.19$ N/mm used in DTC-3. Aging of the spring is neglected. Tests for the Philae Lander showed that the variance of k for a taut spring during 10 years of simulated cruise was < 1 % [R. Roll, MPS, priv. comm. to J. Biele, Oct 21, 2013]. The mass deviation was small, $m_{\mathrm{DTC}} = 9.29$ kg, compared to $m_{\mathrm{FM}} = 9.66$ kg. Accordingly, the final value could be estimated by

$$\begin{aligned} v_{\mathrm{FM}} = v_{\mathrm{DTC}}\sqrt{\frac{k_{\mathrm{FM}}\cdot m_{\mathrm{DTC}}}{k_{\mathrm{DTC}}\cdot m_{\mathrm{FM}}}} = v_{\mathrm{DTC}}\cdot \left( 1.031\pm 0.016\right) . \end{aligned}$$

(2)

The final estimate of the expected release velocity was, therefore, given to be 4.94 ± 0.08 ($1\sigma$ random) ± 0.49 cm/s ($1\sigma$ reproducibility) or 4.94 ± 1.7 cm/s ($3\sigma$). A summary can be found in Table 5. A first estimate of the release time (when the LM completely clears the MESS frame) was done by extrapolating the velocity profile towards a distance of 20 cm. Here we found $t_{\mathrm{rel}}=$ 4.18 s, 3.70 s, 4.42 s and 3.63 s (flights 1–4). This led to a rounded average of 4.0 ± 1.2 s ($3\sigma$) and scaled to the FM values of 3.9 ± 1.2 s ($3\sigma$).

Fig. 26

Push-off plate used for DTC-2 flights 1–2

Fig. 27

Push-off plate used for DTC-2 flight 3–4 and DTC-3 flights 1–4

Fig. 28

MASCOT-LM eject velocity profile during DTC-2 microgravity tests

Fig. 29

MASCOT-LM eject velocity profile during DTC-3 microgravity tests

Table 5 Comparison of eject spring parameters and corresponding calculated/measured/predicted values for test and flight

Release rotation

Fig. 30

IMU measurements during drop tower flights. The example is given for DTC-3 flight 2, angular velocities (left) and accelerations (right). Magnitudes are given in mean values for the respective event duration

The rotational motion was studied with respect to the DTC-3 tests (flights 2 – 4 only) as they had the most reliable and consistent IMU data across all the tests. The angular velocities and acceleration components along all the axes (cf. Fig. 24) had distinct edges and peaks corresponding to the different stages of the drop tower test as expected. Fig. 30 (left) shows the angular velocity readings of the LM for DTC-3 flight 2 along with the vertical acceleration of the drop capsule from its release to its deceleration within the drop shaft. Figure 30 (right) shows the corresponding acceleration forces present. Marked events (A)–(G) correspond to capsule release at (A) $0\,\hbox {s}$; NEA trigger and push-off at (B) $0.38\,\hbox {s}$; first bounce inside MESS at (C) $0.59\,\hbox {s}$; last bounce inside MESS at (D) $2.48\,\hbox {s}$; last contact with MESS and LM separation at (E) $2.86\,\hbox {s}$; LM capture by the cushion at (F) $3.45\,\hbox {s}$; capsule deceleration at (G) $4.72\,\hbox {s}$. For filtering out the experiment time from the raw data, time was set to zero when the acceleration along the z-axis rose sharply from − 1 g to − 0.2 g at (A). Similarly, the end of the test was marked when the acceleration fell sharply to the IMU’s limit of − 8 g at (G), which was constant for all flights at $4.72\,\hbox {s}$.

After the NEA was triggered (B), the LM experienced several impacts within the MESS. The first bounce (C) was a strong, single impact that is distinctly visible in the sharp rise of rotation rates. For flight 2, the lander spun with a maximum of $7.31\deg /\hbox {s}$ about the x-axis, $6.91\deg /\hbox {s}$ about the y-axis and $4.44\deg /\hbox {s}$ about the z-axis. The subsequent flights 3 and 4 had similar peaks for the first bounce with the same initial rise and following drop of rotation rates along the three axes. This was followed by several random soft bounces/contacts marked by dashed lines between (C) and (D). These occurred either as multiple contacts, such that there was no sharp edge in the rotation rates and having a gradual slope, or as single contacts observable as distinguishable steps. However, this movement within the MESS was unpredictable and varied for all three flights. The last contact (E) before the clearance of the MESS was again alike across all flights such that the angular separation rate about the x-axis had a greater magnitude than for the y-axis and the z-axis.

The eject time $t_{\mathrm{eject}}$, which was defined as the time from the trigger of the NEA (B) up until the final contact within the MESS (E), was observed to be $2.48\,\hbox {s}$, $3.51\,\hbox {s}$ and $2.21\,\hbox {s}$, flight 2 – 4 respectively. Taking the average led to $2.86\pm 0.65$ s. The difference between the flights varied in the same manner as the release velocity $v_{\mathrm{rel}}$ (compare again with Sect. 4.2). The faster the LM was pushed by the MSM, the shorter the eject time. This indicated that the relative position of this last contact from the LM to the MESS remained rather constant. But the intensity and directional change of this last contact remained unpredictable. However, for all the three flights an unperturbed and smooth angular velocity was observed along all axes [free-flight phase marked as gray area (E) to (F)]. Since this last contact, most probably occurred within the MESS envelope and not at its most outer edge, the eject time $t_{\mathrm{eject}}$ is not equal to the release time $t_{\mathrm{rel}}$, which is the time when the LM completely clears the MESS frame. The final angular velocity values were evaluated by taking the average of the free-flight phase from the peak of the rising edge to the beginning of the falling edge. Table 6 shows the measured angular velocities for the used test articles of LM, MESS and MSM in DTC-3 flights 2–4.

Table 6 Mean angular separation velocities for three micro-gravity separation tests for MASCOT

Numerical simulation of the separation and push-off event

The engineering of the separation and push-off mechanism was largely supported by a numerical multi-body simulation (MBS) to get early insight into the kinematics and dynamics of the mission critical lander deployment event. From the numerical investigations during the preliminary design phase it became evident that the eject velocities were too sensitive to its geometrical and material parameters. The simulation-supported engineering approach therefore was based on sensitivity analyses which lead iteratively to a more robust design with less sensitivity to off-nominal values of the critical design parameters. A direct quantification of the distributions of real off-nominal values was not possible in that early stage due to lack of time for substantial hardware representations. Without quantified dispersion parameters a full Monte Carlo campaign was not deemed beneficial. But with our approach we could minimize the propagation of the “known unknowns” into the eject behavior.

Simulation setup

The simulation environment used was the software tool SIMPACK [13]. According to the MBS topologies, the following modeling elements (Table 7 and Fig. 31) were used to realize a virtual representation of the MASCOT-LM/MESS push-off assembly.

Table 7 Simulation model setup elements

Fig. 31

Simulation model setup: body model elements (denoted with B) and force elements (denoted with F). The lander body B1 is shown as a wireframe to reveal its meshed surface being part of the polygonal contact model used for collision and contact detection. As counterpart, the MESS (B2) was meshed likewise, but shown here in semi-transparent view for better visibility

The polygonal contact model (PCM) of the multibody dynamics simulation was used to investigate especially the contact conditions and collisions between the LM body and the MESS assembly as well as the LM body and the push-plate. Therefore, the respective body surfaces were meshed and its faces were evaluated for mutually intersections to detect contact and collision events and to derive contact forces therefrom. The LM body in Fig. 31 is displayed in a wireframe to illustrate this. The underlying force law and its implementation were part of the MBS tool and is explained in detail in [14]. The parametrization of the simulation model considered geometry, mass, inertia and stiffness properties of MASCOT according to the respective design phase of the project. Gravity was set to 0, which represented the separation condition that the HY2 spacecraft would be in no-thrusting mode and a ballistic free-fall phase during the separation event of MASCOT.

Simulator application and results

Several push-off scenarios have been simulated during the preliminary design phase under variation of the following parameter: Preload of the bolt being the main load path for hold down during launch and cruise, center of mass (CoM) position and stiffness of LM-to-MESS contact. Critical effects under investigation were (i) kinetic energy of the LM after push-off (separation velocity shall not exceed 0.05 m/s), and (ii) deviations from the trajectory cone. A major finding in that phase was, that a release of the LM from a preload of 2500 N (required to accommodate the launch loads) led to the transfer of excessive elastic energy of $\sim$ 2.5 J, stored in 2 mm strain of LM’s CFRP baseplate, partly into added kinetic energy of the LM. The associated transient force and “snapping out” of the LM resulted in a velocity of $\sim$ 0.4 m/s. The simulation has been repeated with lower preloads, indicating that a remaining preload of 200 N or less would lead to acceptable eject velocities while maintaining the nominal trajectory. A new requirement to reduce the preload prior to push-off initiation was deduced from this finding.

Simulations with off-nominal CoM positions were used to determine tolerances between CoM with regard to the POP diameter. Deviation torques could be controlled by the diameter keeping the CoM within the perimeter of the plate. However, the resulting torque applied to the guide bearing became large, causing friction in the POP travel. The design solution resulting from this finding was to implement a force spring with a short travel distance to control the amount of energy transferred to the LM. The guide bushing was redesigned to provide more tolerance towards canting moments. The simulator has been updated during the post PDR phases to represent growing fidelity of the lander design.

The simulation example below refers to the design state similar to the physical model used in the DTC-3 test campaign (Sect. 4). Figure 32 is, therefore, the numerical counterpart to the test data shown in Fig. 29. The graph shows the lander body velocity $v_z$ in z-direction versus time and versus eject distance. The slight imbalance between the net push-off forces due to the umbilical connector and the asymmetric stand-off positions in y-axis direction led to bouncing contacts between the lander body and its MESS support frame. The initial velocity of $\sim$ 9 cm/s was reduced to $\sim$ 4 cm/s. After 2.55 s the body had traveled 15 cm and was clear of conflict with the MESS frame. Figure 33 depicts the still images from the associated animation. Starting at t = 0.00 s with the release-to-push and ending at t = 5.00 s into the flight. The intermediate images show the MASCOT-LM body at main touches with the MESS frame which can be also identified as “steps” in the trajectory plots in Fig. 32. Despite these touches, the MESS cavity restricted deviations from the nominal eject path along the z-axis. The LM showed some angular motion induced by the touches after leaving the MESS. The insight into the forces and energy balances during the simulated push-off augmented the experimental data from the drop test campaigns. Together they led to the conclusion that the observed touching contacts, albeit dissipating a significant fraction of the initial energy, were predictable and reproducible and could be accounted for in the total energy budget for the push-off.

Fig. 32

MASCOT LM body motion state in z-axis, velocity versus time (top) and eject distance (bottom). Velocity, discernible as “steps” in the graph, is lowered by gentle touches/bounces within the MESS frame

Fig. 33

Separation and push-off sequence between separation ($t = 0.00$ s) and $t = 5.00$ s into the flight. Intermediate images show occurrences of contacts between the LM body and the MESS frame

Flight data analysis

Flight activation of the preload release mechanism

The flight activation of the PRM was performed on September 17, 2015. Shortly before this activation, the functionality was tested with a health check in which the heater current and the PRM temperature were monitored. Both heaters of the PRM were activated for only 10 s with an interval of 5 s in between. The measured temperature increase was $25^\circ \,\hbox {C}$ which was well below the expected melting temperature of the two thermoplastic disks. The current, on the other hand, could not be measured directly since no measurement point was available at the heater lines. For this reason, the PRM current was estimated based on the current and voltage of the unregulated power bus (UPB) which was an indicator between the PRM on/off state. The estimated PRM current was 1.68 A, which was within the expected range of 1.64 –1.96 A.

However, even with the confirmed nominal operation, the time duration of the PRM activation had to be precisely defined to ensure sufficient heating of the disks but without overheating any other MASCOT components. Ground test results indicated that a suitable activation duration had to be selected based on the initial PRM temperature. Therefore, two command sequences with different activation durations were prepared. The selection criteria were defined as follows:

• If the PRM temperature is between $-10$ and $5^\circ \,\hbox {C}$, then a duration of 11.5 min shall be used.

• If the PRM temperature is between 5 and $20^\circ \,\hbox {C}$, then a duration of 10 min shall be used.

• For other cases, the activity shall be aborted.

Prior to the final activation, an initial temperature of $-2^\circ \,\hbox {C}$ was observed and a duration of 11.5 min was selected for the execution.

Figure 34 shows the PRM temperature behavior and contact closure timing during the flight activation. The observed temperature increase and profile was as expected based on the ground testing results (see again Fig. 15), and the closure of the PRM contacts indicated the successful reduction of the preload.

Fig. 34

Temperature profile of the MASCOT PRM flight activation

Release velocity a posteriori based on image analysis and flight dynamics

While the separation direction was known by the MESS mechanics well, a prediction of the separation velocity was constrained by the interplay of the four subunits explained above. Furthermore, the rotation behavior of the LM could have been arbitrary because it depended on the ultimate contact of the LM with the MESS during release. Therefore, an in-flight validation of the separation velocity and the LM’s attitude behavior was needed. One approach, applied by the MASCOT flight dynamics (FD) group, was the fitting of the LM’s attitude and its position vs. Ryugu by analyzing the onboard GNC solar sensors and images taken of MASCOT by the Optical Navigation Camera Wide (ONC-W2) from HY2 shortly after its release.

Initially, an ejection velocity of 4.9 ± 1.7 ($3\sigma$) cm/s, based on the drop tower test (Sect. 4), was used along the direction ($270^\circ$, $-15^\circ$) in the HY2 S/C frame. The angles are azimuth and elevation of the velocity vector. These values were of course theoretical and needed to be refined from the trajectory and attitudes analyses after the landing. The HY2 ONC-W2 camera obtained three pictures of the LM at 34 s, 44 s and 54 s after the commanded release [15, 16]. On the two first pictures, the LM was too dark to accurately determine its attitude, whereas it was totally visible in the field of view of the last picture. Thanks to this third image, it was possible to determine the LM’s attitude and the relative position of the LM/HY2 centers of mass at the epoch of the pictures. The LM and HY2 trajectories were first simulated from departure (i.e. when the LM was entirely out of the MESS) up to 54 s after the commanded release. Using the LM’s attitude derived from the last ONC-W2 picture, a “theoretical” picture based on the initial conditions given above was simulated. Figure 35 shows an overlay of the simulated and real picture. Within the overlay, the LM is obviously closer to HY2 than supposed. From this, a relative distance LM/HY2 was derived and an improved estimation of the release velocity was performed by the following fitting process:

• 1. Determination of the eject conditions: computation of the positions, velocities and attitudes of the LM and HY2 at the epoch of deployment based on image analyses from [16]. These data were expressed in the asteroid centered fixed frame. FD computed the HY2 position and velocity by taking into account the theoretical ejection velocity (direction and magnitude) and the geometry LM/HY2 before release.

• 2. Numerical propagation of both trajectories up to the epoch of the last ONC pictures (i.e. 54 s after the commanded release).

• 3. Computation of the relative geometry (i.e. simulation of ONC-W2 pictures by taking into account the two S/C positions, velocities and attitudes and the camera parameters) at the epoch of the last picture.

• 4. Iteration of the process 1–3 until an accuracy of 1 cm is reached in the relative distance between the center of mass of LM/HY2. At each loop, the ejection velocity was updated thanks to a numerical optimizer.

The analysis of ONC images yielded a separation velocity of 5.9 cm/s [16]. The FD optimization led to a slightly higher velocity, around 6.1 cm/s (Table 8). An uncertainty range was not given for both of these values. As the MESS has an internal length of $\sim$ 20 cm, the LM did probably leave the MESS in $\sim$ 3.1 s. This value is consistent with the theoretical separation velocity provided by the drop tower test and the MasMag measurements that indicated 3.2 s ± 1 s between the release command and the departure from the MESS.

Fig. 35

Comparison of the real MASCOT-LM position and the reconstructed position considering the theoretical ejection velocity

Table 8 Theoretical and estimated eject directions and release velocities in Hayabusa2 frame

Separation conditions as detected by the MASCOT magnetometer

Alternatively, the magnetic field decay measured by the MasMag experiment [17] due to the increasing distance to the intrinsic magnetic moment of HY2 after separation could be used for the reconstruction of the descent velocity.

The rotation period could be measured by analyzing the harmonic wave of a rotating magnetometer sensor in a constant ambient field and has been determined to 139 s (± 1 s) with high precision. Detailed results are presented in [18]. However, due to the short landing period (about 6 min, which corresponds to $\sim$ 2.5 full rotations only), the determination of the direction of the rotation axis was less precise. It could be done with the magnetometer data only under the assumption that the motion consists of a pure rotation. In contrast, the flight dynamics approach took also precession into account. Both results differed by about 30 degree. Thus, the uncertainty for the rotation axis was large.

After clearing the MESS ($\sim$ 3 ± 1 s after separation activation), the MasMag observed a rapid decrease in the magnetic field. The decay consisted of two parts with different slope characteristics. Both had different sources and both could have been used for estimating the separation speed. The measured magnetic field profile during the descent in MasMag internal coordinates is shown in Fig. 36. The decay soon after separation (3–10 s after release) was more steep and resulted most probably from the magnetic moment of the MESS environment, although other HY2 equipment in the vicinity may have contributed. A simple check was performed using just the assumed distance to the source before separation and knowing the decay of the magnetic field. As the field of the magnetic moment decreased inverse with the third power of the distance, the distance at a given time

$$\begin{aligned} r_t = \root 3 \of {\frac{B_0}{B_t}}\cdot r_0 \end{aligned}$$

(3)

could be computed. From the first seconds after separation, using this formula and assuming the source (before separation, $r_0$) to be between 30 and 60 cm away from MasMag, the resulting velocity would be in the range of about 4–7 cm/s.

Fig. 36

Magnetic field measured by MasMag after separation from HY2 during MASCOT’s descent. MOBT: MASCOT onboard time, $\hbox {MOBT-UTC}=450.4\,\hbox {s}$

The more distant part (measured between 10 and 100 s after release) was dominated by the magnetic moment of the HY2 spacecraft. This effect was expected, as the source of the magnetic field inside HY2 was dominated by the ion engine with its eight permanent magnets (four of them with a moment of 22 $\hbox {Am}^{2}$). Nevertheless, it was required to assume other unknown sources which contributed to the HY2 dipole as well, because the spacecraft was never subject to a magnetic screening. Thus, an assumed overall dipole moment and its position was prone to large error bars. For this reason, the analysis of the second part of the descent profile was based on the minimization of differences between the model field and the measured field. The model field was calculated as a magnetic field produced by a dipole moment at a given position from MasMag which changed with the separation velocity. Several assumptions had to be taken into account. The solution was not unique and the position and magnitude of the moment were linked parameters, so that a higher moment positioned further away would have given the same field values but with a different velocity. Another complexity, as mentioned already above, was the rotation of the LM during its descent. The measured field was not in the HY2 frame, where it would have been stable. It was rotating in the MASCOT reference frame and was needed to be despun for the purpose of the fit. An analysis of the data from the distant descent part close to the Ryugu’s surface, where the HY2 field was negligible, produced a stable rotation axis and provided MasMag internal offsets. A following sensitivity analysis showed that the direction of the rotational axis was well determined in the range of ± 15 degrees. Therefore, the estimation of the rotation period ($\sim$ 139 s) is robust and was supported by the flight dynamics analysis.

To validate the model results, it was necessary to limit the possible position and strength of the HY2 representative dipole moment. For this, the HY2 team provided (personal communication) design information about the ion engine, and in particular the location, strength and orientation of the permanent magnets. At first, an ideal ion engine model was assumed and it was tried to fit the magnetic field as produced by the ion engine model. The fit, however, was not satisfactory and gave a velocity of $\sim$ 7.5 cm/s. Apparently, in reality, there were other sources of magnetic fields modifying the total signature on HY2. Therefore, a different approach was adopted. We explored the parameter space, having the rotation axis fixed and fit only velocity and moment. The resulting set of results for different rotation axes in a given range could be used to compute the mean velocity as a best guess for the separation velocity giving also the error bar estimate. The range for the rotation axis direction was based on the best fit from the descent period shortly before touchdown, where the data were not influenced by the HY2 field. This gave a robust but rather flat-bottomed solution for the rotation axis $a=(1, -139^{\circ }$, $20^{\circ }$). The vector being in spherical coordinates in MasMag coordinate system: (radius, longitude, latitude). Table 9 shows the vector also in the transformed MASCOT LM coordinate system. The resulting velocity for the LM after ejection was therefore $\Vert v\Vert = 6.0\,\hbox {c/m}\pm 1.5\,\hbox {cm/s} (3\sigma)$.

Table 9 Rotation axis as derived by MasMag in spherical coordinates as well as in normalized axis components ($\left| a\right| =1$)

Final evaluation of test and flight data

A comparison of the values derived by MasMag, the flight dynamics group as well as by the initial separation tests in microgravity is presented in Table 10. Overall, the values for $v_\mathrm{rel}$ and $t_\mathrm{rel}$ are comparable since they are within the given error range. Comparing only the flight data, the mean values from FD and MasMag are compatible. The largest difference, $27^\circ$, is on the elevation of direction of the LM rotation axis. The components of $\omega _x$ and $\omega _y$ of the rotation vectors are also comparable, whereas for the component $\omega _z$, there is an offset of $1.2^\circ$. The accuracy of each determination method is not known. However, since the FD method takes precession into account, it is believed to be more accurate then the MasMag measurement.

The differences to the measured and predicted test values are larger. On the one hand, one can see that the release velocity during test is lower. But on the other, the angular velocity is higher. The test model rotated much faster and almost only about its x-axis. As it was mentioned above, the last contact with the MESS was not predictable neither in its location nor in its magnitude. For this reason, one explanation could be that the magnitude of the push energy is comparable. However, during tests, a slightly larger amount of the push energy was transferred into rotation as compared to the flight release event, where the push energy was mostly transferred into translation.

Table 10 Comparison of release velocity, release time, rotation axis and angular velocity as predicted by the initial separation tests in microgravity and as derived by the FD group and MasMag given in the MASCOT-LM frame

Conclusions

The first-ever landing of a European spacecraft on the surface of an asteroid was accomplished on October 03, 2018, by the Mobile Asteroid Surface Scout (MASCOT). The very compact lander, built by a German–French collaboration from DLR and CNES, was a prototype design of a new class of nano-size surface science packages for the exploration of small solar system bodies. Carried for almost 4 years by its Japanese mother spacecraft Hayabusa2 towards the Near-Earth Asteroid (162173) Ryugu, MASCOT was successfully deployed over the surface at a relative altitude of $\sim$ 41 m with the aid of a newly developed miniaturized separation mechanism. This new design was necessary due to the strict constraints of mass and volume and its unique operational microgravity environment. In this paper, we describe its system design, architecture and subunits and compare it to other currently available standardized and custom build deployment systems. Its functionality was verified by the combined efforts of numerical simulation, extensive subunit components testing as well as in system level tests in its expected microgravity environment. Necessary design improvements, which were the direct results of these investigations, are explained in detail. Finally, we compare the test measurements and final predictions of the mechanisms performance with the analysis of two independent methods using actual flight data taken during the flight separation event. One method applied by the MASCOT flight dynamics group used MASCOT’s onboard sensors and images taken by the optical navigation camera from Hayabusa2. The second method applied by the MasMag, one of MASCOT’s scientific instruments, used the magnetic field decay from the intrinsic magnetic moment of Hayabusa2 after separation. Both methods verified the predicted performance and reliability of the MASCOT Separation Mechanism. With its simple and robust design, this mechanism could be easily adapted to serve also other future carry-on units of similar size, constraints and/or mission scope.