Abstract
This paper reports the investigation of acoustic combustion instability experienced during repetitive ignition testing of a sub-scale LOX-methane rocket thrust chamber. The occurrence of resonant coupling between the LOX injectors and the combustion chamber acoustic modes was assessed from the experimental data recorded during the highly transient phase of operation from ignition up to around 2 s. A method was developed to model the evolution of acoustic properties in both the combustion chamber and the injectors during the transient period. For the LOX injectors, the Woods equation was used to estimate the speed of sound in the two-phase flow. The models were used to identify the corresponding mode frequencies in the unsteady pressure measurements, and show that the high-amplitude instability occurred when they intersected. Very close coupling of less than 3% frequency difference is required for high amplitudes to be observed. However, the condition was necessary but not sufficient for high amplitudes to be reached.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Combustion instability remains an important issue in liquid rocket engine development programs. The thermoacoustic kind, involving the coupling of unsteady heat release and acoustic modes of the combustion chamber volume, can damage hardware within an extremely short time period [1]. Recent examples include instabilities which arose in testing of the liquid oxygen (LOX)-methane powered ROMEO thrust chamber [2] in Germany, and the LOX-hydrogen fed LE-X thrust chamber in Japan [3].
In the case of the LE-X thrust chamber, coupling of acoustic resonance modes of the LOX injectors with those of the combustion chamber volume was identified as the cause of the instability [3]. This type of driving mechanism for instability, referred to as ‘injector coupling’, has been reported in the literature for both cryogenic engines [4, 5] and sub-scale experiments [6,7,8].
A recent case of injector-coupled instability in a sub-scale LOX-hydrogen combustor is well documented by Gröning et al. [9,10,11]. This experimental combustor has a chamber diameter of 80 mm and 42 shear coaxial injection elements, and experienced high amplitudes of the first tangential (1T) acoustic mode of the chamber volume when its frequency coincided with that of the LOX-post second longitudinal (2L) mode. The combined application of dynamic pressure and optical probe diagnostics allowed the frequencies of these two modes to be identified and tracked as they evolved with varying operating conditions and coupled for particular stationary load points.
The injector-coupling mechanism does not appear to have been explored for the start-up phase of rocket engines in the open literature—perhaps due to the challenge of defining the thermodynamic conditions within chamber and injector volumes during transients covering such wide ranges of temperature and pressure. Cases of combustion instability are reported to have occurred between ignition and steady-state operation, for example during the development of the HM7 thrust chamber [12]. Coupling with the feed system was blamed during periods of low injection pressure drop, but without further definition of the components involved or their dimensions. Combustion instability followed an anomalous ignition sequence during start-up of the upper stage engine in Ariane flight 510 [13]. Instabilities in the Morpheus LOX-methane engine during start-up were associated with two-phase flow effects in the LOX injectors [14]. In none of these cases, the role of injector acoustics was clarified.
Combustion instabilities were recently experienced during the start-up of a sub-scale, multi-element combustor with LOX-methane. In several tests, thermoacoustic instability arose after ignition and grew to high amplitudes. This work describes how the injector-coupling mechanism as presented by Gröning et al. [9, 10] can explain the observed instability.
Following Gröning, simplified models of combustion chamber and LOX injector acoustic modes are used to identify and trace the transient frequencies of modes in dynamic pressure data from the experiment. In this work, two-phase flow effects during start-up are additionally accounted for. Specifically, LOX injector modes are properly predicted only after the strong influence of two-phase flow on speed of sound is included in the model. This allows the coincidence of acoustic modes to be consolidated with the occurrence of instability in the combustor.
In this paper, the experimental combustor and the experienced cases of thermoacoustic instability are introduced. Then, a model for the two-phase flow condition within the LOX injectors is established and its sensitivity to assumed parameters is tested. The model is used to estimate the injector acoustic mode frequencies during the start-up transient. Transient combustion chamber mode frequencies are also estimated from measurements of propellant inlet conditions. Both are compared to the evolving spectrum of dynamic pressure in the combustion chamber and associated with their measured counterpart. Finally, the relationship between unstable mode amplitude and frequency matching of injector and chamber modes is established.
2 Experimental method
2.1 Combustor model ‘A’ (BKA)
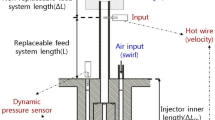
This work concerns the stability behavior of the sub-scale research combustor model ‘A’ (abbr. BKA), operated at the European Research and Technology Test Bench P8 at the DLR Institute of Space Propulsion near Lampoldshausen, Germany. A photograph of BKA during a test is shown in Fig. 1. The cylindrical, segmented combustion chamber has an inner diameter of 50 mm and is water-cooled. A dimensioned sketch of BKA is shown in Fig. 2 indicating the positions of the sensors relevant for this study. The chamber is equipped with static and dynamic pressure transducers as well as thermocouples. The dynamic pressure sensor is integrated radially with a recess of 10 mm with respect to the inner combustion chamber wall and a port of 3 mm diameter.
The dynamic pressure sensors were recorded at a sampling frequency of 100 kHz, whereas the thermocouples and static pressure sensors were recorded at 1 kHz. A band-pass filter in a range from 400 Hz to 50 kHz is used on the dynamic pressure sensors.
The injector head contains 15 coaxial shear injector elements and a central torch igniter. The LOX posts contain an orifice located 2.5 mm downstream from the inlet. The manifolds of the injector head are equipped with static and dynamic pressure transducers and thermocouples which are calibrated individually. The tip of the thermocouples end within the manifold volumes, whereas the static and dynamic pressure transducers are connected via a narrow tube from the manifold side wall. A laser ignition system is mounted radially near the injection plane to realize ignition. It generates a sequence of 20 individual laser pulses with individual pulse lengths of 2–3 ns and pulse energies of about 33 mJ at a wavelength of 1064 nm. The pulses are focused into the shear layer of one coaxial injector element to guarantee ignition during the transient injection phase. Further details on the combustor and the laser ignition system can be found in Ref. [15].
2.2 Test procedure
The combustor was operated with the propellant combination LOX-methane at varying ratios of oxidiser to fuel mass flow rate (ROF). The ignition tests had a duration of about 2 s of combustion time.
For cases A and B, the laser ignition system was activated before the propellant injection to ensure the earliest time of ignition possible and to reduce the risk of over-pressure levels by ignition of accumulated propellants in the combustion chamber. In case C, the laser igniter was activated at \(t = 1\) s to investigate the influence of a longer fuel and oxygen pre-injection duration on the ignition behavior.
The injection rates of the propellants were then increased during the ignition phase, resulting in the pressure evolution profiles shown in Fig. 3 for pressure in the combustion chamber (\(P_{\text {cc}}\)), the LOX manifold (\(P_{\text {O}}\)), and the fuel (methane) manifold (\(P_{\text {F}}\)).
2.3 Combustion instability
Three different cases were identified with respect to combustion stability during the ignition process:
- 1.
Case A is stable combustion with no apparent excitation of any acoustic modes.
- 2.
Case B is characterized by combustion instability leading to extinction of the combustion
- 3.
Case C tests contain periods of both stable and unstable combustion.
The cases are characterized by dynamic pressure measurements within the combustion chamber (\(p'_{\text {cc}}\)) in the following paragraphs. Spectrograms of \(p'_{\text {cc}}\) are presented to illustrate the evolution of acoustic modes over the course of the ignition test sequence.
Case A is characterized by stable combustion. A spectrogram and the raw \(p'_{\text {cc}}\) signal are shown in Fig. 4. A single pressure peak corresponding to the ignition event can be seen at \(t_{\text {ign}} = 0.19\) s, which corresponds to the first instance of methane arrival in the combustion chamber shortly after \(P_F\) begins to rise. For the duration of the test up to extinction of combustion at \(t_{\text {shutdown}}= 2.2\) s, a broadband excitement is visible around \(f = 11 \pm 2\) kHz, which corresponds to the combustion chamber 1T mode. The relative peak rms pressure amplitude (\(p'_{\text {rms}}/P_{\text {cc}}\)) is 15.8%, where \(p'_{\text {rms}}\) is calculated from \(p'_{\text {cc}}\) after band-pass filtering of 400 Hz to 50 kHz. From around 1.1 s, there are low-frequency oscillations at around 500 Hz.
Case B shows strong instabilities during combustion. The spectrogram and raw signal of \(p'_{\text {cc}}\) in Fig. 5 show multiple ignition peaks from 0.18 s corresponding to the laser pulse instances. These were ignition events which failed to result in sustained combustion. Successful ignition was achieved at \(t_{\text {ign}} = 0.31\) s, after which the laser pulses have no further influence on chamber pressure and no more peaks appear in \(p'_{\text {cc}}\). Immediately following ignition, strong lines are visible in the spectrogram at regular multiples of 2–2.5 kHz. These will be identified in Sect. 4 as the longitudinal modes of the combustion chamber. From around 0.9 s, additional lines appear at multiples of 830 Hz, and will be identified as modes of the LOX posts. Below the spectrogram, the peak-to-peak amplitude of \(p'_{\text {cc}}\) is seen to increase up to 25 bar before combustion ceases suddenly and prematurely at 1.01 s. The peak relative rms value is \(p'_{\text {rms}}/P_{\text {cc}} > 100\)%.
In case C, periods of unstable and stable combustion are separated by extinction and a re-ignition event. A pressure peak is recorded after \(t = 0.22\) s. The first ignition event is labeled in Fig. 6 at \(t_{\text {ign}} = 0.3\) s and was initiated by an external propane burner downstream of the nozzle. This ignition event was unintended. A very short time period of unstable combustion is observed. After this, the combustion is stable until 0.52 s, when the chamber longitudinal modes appear. Combustion is unstable, reaching a maximum of \(p'_{\text {rms}/P_{\text {cc}}} > 100\)%, and the spectral content resembles that of the unstable Case B. Extinction occurs at 0.95 s, and then at 1.12 s, the combustor is re-ignited by a laser spark. Re-ignition is accompanied by a 0.05-s period of unstable combustion with \(p'_{\text {rms}}/P_{\text {cc}} > 200\)%. Then, the combustor operates stably until the end of the test run at \(t_{\text {shutdown}} = 2.2\) s, during which time the spectral content resembles that of the stable Case A.
The differences in stability behavior of Cases A, B, and C could not be associated consistently with injection temperatures or pressures. Measured temperatures in the fuel (\(T_{\text {F}}\)) and oxygen (\(T_{\text {O}}\)) manifolds for all three cases are shown in Fig. 7. A slight rise of the fuel temperature \(T_F\) in case B is the only deviation in temperature. Injection pressures \(P_{\text {F}}\) and \(P_{\text {O}}\) are plotted in Fig. 8. Here, it can be seen that a slight oxygen lead was realized, since \(P_{\text {O}}\) rises rapidly followed by \(P_{\text {F}}\). In terms of pressure evolution for individual cases, \(P_\text {O}\) differs in Case A from the other two cases, and \(P_\text {F}\) differs in Case C from the other two.
Otherwise, there do not appear to be any features in the pressure and temperature traces which coincide with significant events in \(p'_{\text {cc}}\).
The evolution of ROF is shown in Fig. 9, using oxygen mass flow rate calculated as described later in Sect. 3.1. In all cases, its value peaks before \(t=0.5\) s due to oxygen lead. The highest ROF was reached in Case A, which had immediate ignition and stable combustion. This observation coincides with test observations from Melcher et al. [14], where an effective LOX lead and higher mixture ratio during start-up improved combustion stability behavior. However, consistency between ROF and the stability characteristics of cases B and C is not present since case C is stable before \(t=0.5\) s while case B is unstable with a higher ROF. Therefore, the stability behavior of BKA appears to be too complex to explain by injection parameters alone.
3 Acoustic model
The goal of this work is to determine if acoustic coupling of the combustion chamber with the LOX injectors can explain the stability behavior in BKA. To achieve this, accurate estimates of the acoustic eigenmodes of these components are required, so that they can be used to identify corresponding features in the experimental data.
3.1 Combustion chamber
To calculate the speed of sound in the combustion chamber, the software packages CEA [16] and Refprop [17] are used. In the first step, the enthalpies \(H_\text {O}\) and \(H_\text {F}\) of both fluids are obtained from Refprop. Since the enthalpy of the fluids just before injection is needed, the temperatures are taken from the injection manifolds (\(T_{\text {F}}\), \(T_{\text {O}}\)) and the pressure is taken from the combustion chamber (\(P_{\text {cc}}\)). With these enthalpies and the additionally required input values of ROF, the cross-sectional area of the combustion chamber \(A_{\text {cc}}\) and nozzle throat \(A_\text {t}\), temperatures \(T_\text {O}\) and \(T_\text {F}\), and the pressure \(P_{\text {cc}}\), the speed of sound in the combustion chamber \(c_{\text {cc}}\) is calculated using CEA.
The chamber eigenfrequencies (\(f_{\text {cc}}(n)\)) are then determined using the Helmholtz solution to the wave equation in a closed–closed cylinder. The result is, therefore, based on the following assumptions and simplifications:
The injection mass flow rate of oxygen (\({\dot{m}}_{\text {O,inj}}\)) is calculated via the manifold pressure \(P_\text {O}\) (see below).
There is no change in propellant temperature from the manifold to the point of injection.
The conversion of propellants to reaction products is instantaneous.
The reaction products are at chemical equilibrium throughout the chamber.
Of the model parameters, ROF has the greatest influence on \(c_{\text {cc}}\) and, therefore, on \(f_{\text {cc}}\). The time-resolved ROF is defined by the mass flow rates at the injector, which cannot be measured directly. The measurement of oxygen mass flow rate in the test bench supply system (\({\dot{m}}_{\text {O,FM}}\)) is inaccurate during start-up transients due to the reaction time of the turbine flow meter and two-phase flow effects. For the purposes of this work, the instantaneous oxygen mass flow rate (\({\dot{m}}_{\text {O,inj}}\)) was estimated using the fluid properties measured in the injection manifold according to:
with
Equation (1) can be derived using the Bernoulli equation. The mass flow is calculated using the pressure drop between the manifold pressure \(P_\text {O}\) and the pressure in the combustion chamber \(P_{\text {cc}}\). It is assumed that the turbine is correct in nearly stationary conditions (\(t = 2\) s); therefore, the flow coefficient is represented by the ratio \({\dot{m}}_{\text {O,FM}}(2s)/ {\dot{m}}_{\text {O,inj}}(2s)\). The density \(\rho _\text {O}\) is calculated by a linear approach using the void fraction \(\chi\) and the density at both sides of the phase boundary \(\rho _\text {g}\) (density, gaseous) and \(\rho _\text {l}\) (density, liquid) at \(P_\text {O}\).
The resulting \({\dot{m}}_{\text {O,inj}}\) from Eq. (1) and the raw \({\dot{m}}_{\text {O,FM}}\) signal is shown in Fig. 10 for the example of Case B. By comparing with Fig. 8, it can be seen that \(P_\text {O}\) rises before the mass flow measured at the flow meter \({\dot{m}}_{\text {O,FM}}\). Furthermore, \({\dot{m}}_{\text {O,FM}}\) is seen to overshoot \({\dot{m}}_{\text {O,inj}}\) at \(t=0.6\) s due to the dynamical behavior of the fluid at the flow meter, located many meters upstream of the combustor. After \(t=1.8\) s, the mass flow approaches steady conditions where \({\dot{m}}_{\text {O,FM}}\) is taken to be accurate. Thus, \({\dot{m}}_{\text {O,inj}}\) is considered to be more accurate to represent the instantaneous injected oxygen mass flow rate throughout the initial transient phase.
The measured mass flow rate of methane \({\dot{m}}_{\text {F,FM}}\), also shown in Fig. 10, does not require correction. It is also measured with a turbine flow meter but which is installed close to the combustor and which has a negligible reaction delay. In particular, the methane is in gaseous state, so the measurement is not affected by two-phase flow effects.
3.2 LOX injectors
To estimate the acoustic modes of the LOX injectors, the evolution of the speed of sound inside the LOX posts must be described. The start-up transient is characterized by rapidly increasing pressure and decreasing temperature. Therefore, it is expected that the injectors are filled initially with gaseous \(\hbox {O}_{2}\) with a later transition to full-flowing LOX conditions.
The evolution of speed of sound obtained from Refprop (\(c_{\text {O(refp)}}\)) using \(T_\text {O}\) and \(P_\text {O}\) is shown for Case B in Fig. 11. After ignition at \(t_{\text {ign}}=0.31\) s, \(c_{\text {O(refp)}}\) decreases due to the chilldown of the LOX manifold. From \(t_{\text {ign}}\) up to around 1.4 s, \(P_{\text {cc}}\) is around 4.5 bar. The rapid change at \(t=1.4\) s can be explained by crossing the saturation line. The values directly before and after \(t=1.4\) s correspond to the speed of sound of the gaseous (\(c_\text {g}\)) and liquid (\(c_\text {l}\)) phases of \(\hbox {O}_{2}\) at \(p=4.5\) bar, respectively.
However, the value of \(c_{\text {O(refp)}}\) is not believed to accurately describe the phase-transition process throughout the injector head. The values of \(T_\text {O}\) and \(P_\text {O}\) are only measured at one point in the LOX manifold, and their distributions within the volume are unknown. The injector head is supplied with LOX starting from the time which the run valve opens, at which time the structure is still warm. Since \(T_\text {O}\) decreases from an initial value of 230 K, the wall temperature in the manifold will follow this trend with some time lag. This leads to a region of warmer oxygen near the wall, which will be mixed throughout the manifold volume by the complex and highly turbulent flow field. The complex flow field will also result in local pressure values which differ from the measured value of \(P_\text {O}\) at the wall. Together, the continuous heating and mixing in the manifold is believed to result in a longer transition period of two-phase flow entering the LOX posts than is conveyed by the plot in Fig. 11. This effect was visualized and verified by some of the authors of this paper in [18].
3.2.1 Speed of sound in bubbly liquids
In proximity to the saturation line, Eq. (3) formulated by Wood [19] and experimentally validated by Wilson et al. [20] can be used to estimate the speed of sound in the presumably two-phase \(\hbox {O}_2\) flow. Input variables are the gaseous and liquid densities (\(\rho _\text {g}\), \(\rho _\text {l}\)), speed of sound (\(c_\text {g}\), \(c_\text {l}\)), and void fraction \({\mathcal {X}} = {\dot{V}}_\text {g}/{\dot{V}}_\text {m}\), where \({\dot{V}}_\text {g}\) is the volume flow of the gas phase and \({\dot{V}}_\text {m}\) is the total volume flow. The values of \(\rho\) and c are obtained from Refprop using \(P_\text {O}\) and \(T_\text {O}\). It is assumed that the pressure in the injector is closer to \(P_\text {O}\) than \(P_{\text {cc}}\):
For appropriate values of \(c_\text {g}\) and \(c_\text {l}\), we refer again to \(c_{\text {O(refp)}}\) in Fig. 11, where \(c_\text {g}\) and \(c_\text {l}\) are well defined near the beginning and end of the test, respectively. For \(c_\text {g}\), \(c_{\text {O}}(t_{\text {ign}})\) is used, because heat transfer between the LOX and methane flows through the LOX-post may influence \(T_\text {O}\) along the injector. For \(c_\text {l}\), the maximum value of \(c_{\text {O}}\) is used, because \(c_{\text {O(refp)}}\) is nearly constant after the phase change at \(t=1.4\) s.
The resulting \(c_{\text {mlf}}\) is displayed over \({\mathcal {X}}\) in Fig. 12, illustrating the strong influence of two-phase flow on c. The minimum \(c_{\text {mlf}}\) occurs for \({\mathcal {X}}=0.5\). It is a factor of 6 lower then the \(c_\text {l}\) and a factor of 2 lower than \(c_\text {g}\). Furthermore, \(c_{\text {mlf}}\) is nearly constant in the range \({\mathcal {X}} = 0.1-0.9\), where the maximum difference is about \(\varDelta c_{\text {mlf}} = 57\) m/s.
3.2.2 Evolution of void fraction
The conditions in the LOX injector itself are unknown, and so, the evolution of \({\mathcal {X}}(t)\) must be modeled. A sinusoidal profile of \({\mathcal {X}}(t)\) was assumed between beginning (\(t_{\text {b}}\)) and end times (\(t_{\text {e}}\)) of the model. The begin time \(t_b\) was chosen to be the start of the oxygen injection (see Fig. 10). The influence of the end time \(t_e\) is explained in Sect. 3.2.3. A sine was chosen, because it is a continuously differentiable function. Before and after the transition limits, constant values of \({\mathcal {X}}(t)\) are assumed, as summarized in Table 1.
The evolution of density \(\rho _\text {O} (t)\) is calculated with Eq. (2), taking \(\rho _\text {l}(t)\) and \(\rho _\text {g}(t)\) from Refprop along the phase boundary using \(P_\text {O}\). These traces are plotted in Fig. 13 for Case B.
Case B: Density of the liquid oxygen (red) and the gaseous oxygen (blue), and two-phase density using Eq. (2) (black)
The evolution of \({\mathcal {X}}(t)\) is shown for Case B in Fig. 14. The transient interval begins at \(t_b\) with \(O_2\) flow into the LOX manifold and ends \(\varDelta t =1.5\) s later. The start and end values are \({\mathcal {X}}(t_{\text {b}})=95\%\) and \({\mathcal {X}}(t_{\text {e}})=40\%\). These values were selected, because they showed the best match between the model and experimental frequencies for Case B. Because of the characteristic of the Wood equation (Fig. 12), these values have no great influence on \(c_{\text {mlf}}\) in the range \(5\%<{\mathcal {X}}<95\%\).
Case B: void fraction \({\mathcal {X}}(t)\), assuming the beginning of phase transition \(t_{\text {b}}=0.18\) s (begin of oxygen injection, see Fig. 10) and end of phase transition \(t_{\text {e}}=1.68\) s, \({\mathcal {X}}(t_{\text {b}})=95\%\),\({\mathcal {X}}(t_{\text {e}})=40\%\)
The speed of sound in the two-phase area \(c_{mlf(t)}\) can now be calculated using Eq. (3). Due to the limited amount of sensors in the injector head, the unknown wall temperature, and the highly complex flow, it is not possible to estimate the flow and acoustic behavior at the inlet of the injectors. Therefore, the injector is modeled as a pipe open at both ends. This choice of boundary conditions is also justified by the success of Gröning et al. [9] in its use to identify LOX-post modes in fully flowing injectors of similar scale. With the length of the LOX injector \(l_{\text {LOX,inj}}=70\) mm, the natural frequencies are given by Eq. (4), where \(n \in {\mathbb {N}}\) is the mode number [11]:
3.2.3 Sensitivity analysis
Due to the uncertainty in the four parameters defining the profile of \({\mathcal {X}}(t_{\text {e}})\), a sensitivity analysis was performed. A good robustness of the model is desirable as the conditions in the LOX injector are unknown.
The LOX frequency profiles f(t) for a constant \(t_{\text {b}}\), \({\mathcal {X}}(t_{\text {b}})\), \({\mathcal {X}}(t_{\text {e}})\), and several values of \(t_{\text {e}}\) are shown in Fig. 15. The start time of the transition \(t_{\text {b}}\) is set when the LOX injection begins, around 0.2 s. The time interval of interest is during the appearance of the \(f=n \cdot 800\) Hz longitudinal modes, in this example from \(t=0.8\) s to \(t=1\) s. The minimum range of frequency is \(\varDelta f\) around 100 Hz at \(t=0.8\) s. Thereafter, \(\varDelta f\) decreases to around 50 Hz at \(t=1\) s. Thus, the choice of \(t_e\), or the duration of the transition profile influences the frequencies approximately linearly, in this case most strongly in the period 0.3–1.2 s. This is, therefore, the parameter which must be adjusted most carefully to fit the experimental data.
The influence of varying \({\mathcal {X}}(t_{\text {b}})\) and \({\mathcal {X}}(t_{\text {e}})\) is shown in Fig. 16. The model is sensitive for \({\mathcal {X}}(t_{\text {b}})\) values approaching 0 and \({\mathcal {X}}(t_{\text {e}})\) approaching 1, where \(\varDelta f\) reaches around 3500 Hz. Fortunately, the model is least sensitive to the choice of start and end void fractions in the area of interest from \(t=0.8\) s to \(t=1\) s. In this period, \(\varDelta f\) ranges only from around 230 to 90 Hz. This is largely owing to the course of the Wood function (Eq. 3, Fig. 12), which is relatively flat for \(0.1<{\mathcal {X}}<0.9\) (\(\pm 75\) Hz), but has high gradients close to single phase limits.
4 Comparison with experiments
The acoustic mode frequencies estimated with the models will now be compared to the experimental data to identify the mode frequencies which appear in the spectrograms.
Combustion chamber modes will first be compared with the spectrograms. The calculation of modes with the model starts with the injection of oxygen. This is at \(t_{\text {b}}=0.18\) s for all three cases. The transient phase ends 1.5 s later at \(t_{\text {e}}=1.68\) s, defined by the time after which the value of \(c_{\text {O}}\) from REFPROP passes the saturation line (Fig. 11). The void fraction is set to \({\mathcal {X}}(t=t_{\text {b}})=0.95\) and drops to \({\mathcal {X}}(t=t_{\text {e}})=0.4\).
The calculated 1T mode is overlaid on the measured spectrogram of Case A in Fig. 17. The frequency does not fit to any feature in the spectrum, but lies closest to a broad peak with low spectral power density around 11 kHz. Being the closest calculated mode, and appears to follow the progression of the mode, the broad peak is presumed to be the 1T mode of the chamber. The 1T mode is thus excited by the broadband noise in the chamber during stable operation.
Figure 18 shows the same spectrogram as in Fig. 5 including the calculated L modes of the chamber. These frequencies coincide well with the strongest lines of the spectrogram. Some deviation becomes visible near the end of the combustion phase, especially at the fourth and higher overtones (\(n>3\)), where the cumulative error increases. However, the good match in frequencies and the transient course of the mode frequencies allow these features of the spectrogram to be identified as the chamber L modes with confidence.
In Fig. 19, the calculated LOX-post modes are overlaid on the Case B spectrogram. These frequencies coincide well with the first seven suspected LOX-modes in the spectrogram. Again, the deviation becomes evident for the higher order modes (\(n > 7\)) where small errors are multiplied by the mode order. Assessing the frequency matching of higher order modes thus represents a good accuracy benchmark for the model. However, the transient frequency evolution is considered just as important for the mode identification, which is captured well here also for the higher order modes.
The calculated L modes in Case C, shown in Fig. 20, match extremely well with the strong features in the experimental spectrogram. This applies for nearly the entire period of unstable combustion for the period \(t=0.5-1\) s. During stable combustion from ignition up to 0.5 s, only the first mode of the combustion chamber (1L) can be observed in the spectrogram.
The calculated LOX-modes for Case C are shown in Fig. 21. A good match is achieved for the first seven modes during unstable combustion before the extinction of the flame at \(t=0.95\) s. The calculated mode frequencies tend to overestimate those in the spectrogram slightly, especially at the beginning of unstable combustion. Following re-ignition, the calculated LOX-modes match the first four modes in the spectrogram.
The 1T mode of the combustion chamber in Case C does not match well with the experimental data (Fig. 22). As in case A, the estimated 1T frequency best matches the broad peak around 10–11 kHz most easily discerned during stable combustion (\(t>1.2\) s). The initial increase of the mode frequency following ignition appears to be captured by the model, allowing the mode to be identified.
5 Acoustic mode coupling
After the frequencies in the spectrograms have been associated with resonance modes of the combustion chamber or the LOX injectors, a connection between the rise of the instability amplitude and a matching of the LOX-post and the combustion chamber modes can be assessed.
For this purpose, the frequencies are measured from the \(p'_{\text {cc}}\) spectrograms. However, the LOX-post and chamber modes cannot be easily discerned from one another where they closely intersect. As seen in Figs. 18, 19, 20 and 21, the LOX-post modes appear three times as often as the chamber L modes. Thus, a multiple of the first mode can be used as a surrogate for the overtones. The first mode is also well defined, isolated, and thus easiest to measure from the spectrum. The frequency difference of coupled LOX and chamber modes is calculated as \({\varDelta f = f_{\text {cc},n}-3\cdot n \cdot f_{\text {LOX},1}}\) with \(n \in {\mathbb {N}}\).
The scheme for measuring the mode frequencies and amplitudes from the \(p'_{\text {cc}}\) signals is shown in Fig. 23. It shows the combustion chamber static pressure trace \(p_{\text {cc}}\), the dynamic pressure signal \(p'_{\text {cc}}\), and its gliding rms value \(p_{\text {rms}}\) with a time window of 121 data points (1.21 ms). An FFT is calculated for time steps of 0.001 s using a window of \(\pm 0.1\) s. The center of this window is marked in Fig. 23 at \(t=0.6\) s with \(t_{\text {FFT}}\). The window center runs with \(\varDelta t = 0.001\) s from \(t=0.5\) to \(t=1\) s.
To identify \(f_{\text {cc},1}\), the maximum amplitude of the FFT in the range \(2000<f<2800\) Hz is identified. In the same way, \(f_{LOX,1}\) is identified in the range \(400<f<1200\) Hz. The rms value of dynamic chamber pressure at the corresponding time \(p_{\text {rms}}(t_{\text {fft}})\), normalized by \(p_{\text {cc}}\), is taken to indicate the instability amplitude.
The dependence of amplitude on frequency difference from 11 tests (7 stable and 4 unstable), including Cases A, B, and C, is presented in Fig. 24, similar to Gröning et al. [9]. The stable runs show no significant increase in amplitude over a very wide range of \(\varDelta f\). Referring to the spectrogram of the stable Case A in Fig. 17, and the stable period after \(t = 1.2\) s in Fig. 22 of Case C, the very low amplitudes do not allow positive identification of the chamber or injector modes, and so the spread of values from \(-1200< \varDelta f < 500\) below \(p_{\text {rms}}/P_{\text {cc}}\) of around 0.2 simply represents noise from false detections. They do not imply that coupling takes place in stable runs.
High amplitudes are reached in unstable runs for \(\varDelta f \rightarrow 0\). This can be interpreted as a coupling of the LOX-post 3L mode and the chamber 1L mode. A frequency difference of \(\varDelta f < 3\%\) (FWHM) appears to be necessary for high amplitudes, which is in agreement with the observations of Gröning et al. [9]
Lower amplitude instabilities are also visible over a wide \(\varDelta f\) range in unstable runs, with a baseline around \(p_{\text {rms}}/P_{\text {cc}}=0.3\). Furthermore, the large range of amplitudes observed for \(\varDelta f\) around 0 in unstable cases leads to the conclusion that frequency matching was a necessary condition for high-amplitude instability in BKA, but not a sufficient one.
6 Conclusions
Ignition testing with LOX and methane has been performed in an experimental, multi-injector rocket combustor at the test bench P8 at DLR Lampoldshausen. The target test duration of 2 s is sufficient to confirm ignition and combustion for a portion of the start-up phase of a typical liquid rocket engine. In some of the tests, combustion instabilities of the first longitudinal mode of the chamber led to premature extinction of the flame. The current work shows how acoustic coupling of the chamber and injector was determined to play a role in the observed instabilities.
Three different test runs were presented in detail, representing stable, unstable, and partially unstable tests. Two dominant frequency systems were identified in unsteady pressure signals as belonging to the longitudinal eigenmodes of the combustion chamber and the LOX injector. The chamber eigenmodes could be identified through estimation of the evolution of acoustic properties over the course of the ignition transient. Estimation of the injector modes required the influence of two-phase flow on the speed of sound during the transient period to be taken into account. For this purpose, a model was developed based on the Woods equation with a time-dependent void fraction. A set of boundary conditions for the model satisfying all observed experimental cases could be found, and the model was demonstrated to be robust.
Following identification of the modes using the acoustic models, the frequency difference between the first chamber mode and the third LOX injector mode was correlated with the amplitude of the instability. Frequency difference of less than 3% between coupling modes was necessary for high-amplitude instabilities. However, peak amplitude values were not always reached when modes were coupled, so the coupling condition is necessary but not sufficient to cause the observed instabilities.
It has been shown that injector-coupled instabilities can occur during the ignition and start-up transient of thrust chambers, in addition to the main phases of operation as demonstrated, for example, by Gröning et al. [9]. Furthermore, two-phase flow effects must be taken into account to correctly capture injector acoustics. Since both two-phase flow and the intersection of chamber and injector eigenmodes can scarcely be avoided during engine start-up, the described mechanism for combustion instability is believed to be relevant for the designers and operators of engines of all scales and cryogenic propellant combinations.
Abbreviations
- \(\mathcal {X}\) :
-
Void fraction
- \(\rho\) :
-
density
- A :
-
Cross-section area
- c :
-
Speed of sound
- f :
-
Frequency
- P :
-
Static pressure
- \(p'\) :
-
Dynamic pressure
- T :
-
Temperature
- \(t_{\text {b}}\) :
-
Begin of phase transition
- \(t_{\text {e}}\) :
-
End of phase transition
- \(\cdot _F\) :
-
Fuel
- \(\cdot _g\) :
-
Gaseous phase
- \(\cdot _l\) :
-
Liquid phase
- \(\cdot _O\) :
-
Oxygen
- \(\cdot _{CC}\) :
-
Combustion chamber
- \(\cdot _{\text {FM}}\) :
-
Flow meter
- \(\cdot _{\text {mlf}}\) :
-
Two phase
- \(\cdot _{t}\) :
-
Throttle
References
Harrje, D.T.: Historical survey. In: Harrje, D.T., Reardon, F.H. (eds.) Liquid Propellant Rocket Combustion Instability, pp. 30–34. NASA, Washington, DC (1972)
Dutheil, J.-P., Bou, Y.: Highly reusable LOx/LCH4 ACE rocket engine designed for spaceplane: technical maturation progress via key system demonstrators results. In: 7th European Conference for Aeronautical and Space Sciences (2017)
Watanabe, D., Tamura, T., Onga, T., Manako, H., Negoro, N., Kurosu, A., Kobayashi, T., Okita, K.: Hot-fire testing of LE-X thrust chamber assembly. In: ISTS, Kobe, Japan. Mitsubishi, JSASS (2015)
Hulka, J., Hutt, J.J.: Instability phenomena in liquid oxygen/hydrogen propellant rocket engines, volume 169 of progress in astronautics and aeronautics. In: Yang, V., William, A. (eds.) Liquid Rocket Engine Combustion Instability, pp. 39–72. AIAA, Washington, DC (1995)
Jensen, R.J., Dodson, H.C., Claflin, S.E.: Lox/hydrocarbon combustion instability investigation. Technical Report NASA-CR-182249, Rocketdyne Division, Rockwell International (1989)
Kawashima, H., Kobayashi, K., Tomita, T.: A combustion instability phenomenon on a LOX/methane subscale combustor. In: 46th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, number July, pp. 1–10. AIAA, Nashville, Tennessee(2010)
Nunome, Y., Onodera, T., Sasaki, M., Tomita, T., Kobayashi, K., Daimon, Y..: Combustion instability phenomena observed during cryogenic hydrogen injection temperature ramping tests for single coaxial injector elements. In: 47th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, number August, pp. 1–7. AIAA, San Diego, California (2011)
Armbruster, W., Hardi, J.S., Suslov, D.I., Oschwald, M.: Experimental investigation of self-excited combustion instabilities with injection coupling in a cryogenic rocket combustor. Acta Astron. 151, 655–667 (2018)
Gröning, S., Hardi, J.S., Suslov, D.I., Oschwald, M.: Injector-driven combustion instabilities in a hydrogen/oxygen rocket combustor. J. Propuls. Power 32, 560–573 (2016)
Gröning, S., Hardi, J.S., Suslov, D., Oschwald, M.: Influence of hydrogen temperature on the stability of a rocket engine combustor operated with hydrogen and oxygen. CEAS Sp. J. 9, 59–76 (2017)
Gröning, S.: Investigation of Self-Excited Combustion Instabilities in a Rocket Combustor. PhD thesis, RWTH Aachen, Germany (2017)
Preclik, D., Spagna, P.: Low frequency and high frequency combustion oscillation phenomena inside a rocket combustion chamber fed by liquid or gaseous propellants. In: AGARD Conference Proceedings, volume 450, Neuilly Sur Seine, France, 1989. NATO Advisory Group for Aeronautical Research and Development (1989)
Dutheil, J.P., Langel, G.: Ariane 5 upper-stage ignition conditions improvement, and return to operation with “envisat” payload. Acta Astron. 53, 585–595 (2003)
Melcher, J.C., Morehead, R.L.: Combustion stability characteristics of the project morpheus liquid oxygen/liquid methane main engine. In: 50th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, AIAA Propulsion and Energy Forum. NASA, AIAA (2014)
Brner, M., Manfletti, C., Hardi, J., Suslov, D., Kroupa, G., Oschwald, M.: Laser ignition of a multi-injector LOX/methane combustor. CEAS Sp. J. 10(2), 273–286 (2018)
McBride, B.J., Gordon, S.: Computer Program for Calculation of Complex Chemical Equilibrium Compositions and Applications, Users Manual and Program Description. NASA, Office of Management, SCientific and Technical Information Program, Washington, D.C. (1996)
Lemmon, E.W., Huber, M.L., McLinden, M.O.: NIST Reference Fluid Thermodynamic and Transport Properties REFPROP, User’s Guide. U.S. Department of Commerce, Technology Administration, National Institute of Standards and Technology, Washington, DC (2007)
Börner, M., Manfletti, C., Kroupa, G., Oschwald, M.: Repetitive laser ignition by optical breakdown of a LOX/H2 rocket combustion chamber with multi-injector head configuration. CEAS Sp. J. 9(3), 289–297 (2017)
Wood, A.B., Lindsay, R.B.: A textbook of sound. Phys. Today 9, 37 (1956)
Wilson, P.S., Roy, R.A.: An audible demonstration of the speed of sound in bubbly liquids. Am. J. Phys. 76(10), 975–981 (2008)
Acknowledgements
The authors greatly acknowledge the support of the DLR P8 test facility team and Alex Grebe during the test campaign.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Klein, S., Börner, M., Hardi, J.S. et al. Injector-coupled thermoacoustic instabilities in an experimental LOX-methane rocket combustor during start-up. CEAS Space J 12, 267–279 (2020). https://doi.org/10.1007/s12567-019-00294-4
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12567-019-00294-4