Design of converging-diverging nozzles with constant-radius centerbody

Abstract

Several flow phenomena, such as recirculating wake flows or noise generation, occur in aerodynamic configurations with backward facing steps. In this context, subsonic nozzles with constant-radius centerbodies exist, which enable fundamental research of these phenomena for $M < 1$. For the supersonic regime, however, the existing database and knowledge are limited. Therefore, this work presents a design approach for a converging-diverging nozzle with constant-radius centerbody. For the nozzle throat, Sauer’s method is modified to include a centerbody. The method of characteristics is used for the subsequent supersonic portion. Comparing the analytical calculations to numerical simulations results in very good agreement and therefore underlines the feasibility of the chosen approach. Viscosity reduced the Mach number on the exit plane by 1.0–1.2% and therefore had little influence.

1 Introduction

In axisymmetric configurations with two flow paths, such as a dual-mode airbreathing propulsion system, there are usually backward facing steps at the trailing edges (Fig. 1). Another example is the flow around a rocket stage, and its hot gas exhaust plume generated at the rear. Near these backward facing steps, several flow phenomena occur. First, there is usually a recirculation region that can drastically affect the heat transfer into the structure. If the recirculation region, for example, interacts with an exhaust plume, hot gas could lead its way upstream and harm the structure. Second, if two air flows mix with each other at a backward facing step, the shear layer is usually a noise source. Understanding these mixing phenomena better could therefore reduce the noise level generated by the two jets.

When investigating configurations with backward facing step experimentally, problems frequently occur, when the length is relatively large compared to the investigated step size or base diameter. For axisymmetric configurations, such as the Ariane 5 or the Falcon 9 rockets, the ratio between length and base diameter is approximately 10 and 15, respectively. A downscaled version that could fit into a wind tunnel setup would automatically downgrade the field of view, capability for instrumentation or mechanical accessibility. The maximum model size, on the other hand, is limited by the wind tunnel dimensions and allowable blockage.

A setup which can overcome these challenges is displayed in Fig. 2 for a subsonic configuration. The key component is a centerbody which is axially aligned with the nozzle outer wall. The centerbody’s back plane could be further modified to contain, for example, an own miniaturized nozzle geometry. In addition, there are ducting lines which can contain different forms of instrumentation. The benefit of the setup is a relatively large base diameter and homogeneous flow around the backward facing step of the centerbody, which enables fundamental investigations on the flow phenomena listed above. Further information can be found in [8, 9].

Fig. 1

Schematic of dual-model rocket-ramjet configuration

Fig. 2

CAD image of subsonic nozzle with constant-radius centerbody

The present paper focuses on a nozzle configuration, which contains a constant-radius centerbody. The main focus is to extend the nozzle shape to a converging-diverging geometry, which has supersonic flow at its exit. A similar design is used in the extensive studies on supersonic wake flows by Dutton [3] and Herrin [6]. More detailed information about the design of the wind tunnel nozzle, however, is limited. The design method we present in this paper consists of the following: Sauer’s method is used in the throat region, while it was extended to include a centerbody. For the supersonic section, a classical method of characteristics (MOC) was used, which again considered a centerbody. In the design of hypersonic wind tunnel nozzles or air intakes [4], often times the boundary layer displacement is considered, as it additionally contracts the flow. In this manuscript, however, we did not consider viscosity during the design, as the investigated Mach numbers are well below the hypersonic range. The results generated with the analytical approach are compared to and validated with inviscid numerical simulations. Next, certain design boundary conditions are varied and general trends and limitations are discussed based on the analytical results. Finally, to determine the effect of viscosity, analytical results are compared to viscous simulations for various conditions. In all cases, the nozzle exit Mach number is only slightly affected and dropped by 1.0–1.2% compared to the design value. This justifies neglecting viscosity during the nozzle design process.

2 Methods and materials

Various literature about the design of converging-diverging nozzles exists [1, 2, 12,13,14]. Based on our experience, the books by Zucrow and Hoffman [13, 14] give an excellent overview of the design of the subsonic as well as the supersonic portion. In the following, our approach is presented in more detail.

2.1 Subsonic portion

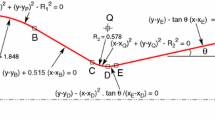
Sauer’s method [10] was used for the converging section near the throat, also labeled the subsonic portion. The method uses a perturbation technique [13, p. 555] to quantify the influence of the throat curvature onto the flow. Sauer’s classical equations, which provide an initial value line, are extended to include the center body ratio, $\mathrm{cbr} = r_{\mathrm {cb}}/r_{\mathrm {th}}$. The values $r_{\mathrm {cb}}$ and $r_{\mathrm {th}}$ are the centerbody and throat radii, respectively. A centerbody ratio approaching 1 corresponds to two-dimensional flow; a centerbody ratio equal to 0 corresponds to axisymmetric flow. For our approach, cbr can be chosen arbitrarily in between $\left\{ 0, \ldots , 1 \right\}$. The following set of equations describes the modified method:

$$\begin{aligned}&z_{\mathrm {iv}} \in \left\{ 0, \ldots , \varDelta _{\mathrm {th}} \right\} \end{aligned}$$

(1)

$$\begin{aligned}&\varDelta _{\mathrm {th}} = r_{\mathrm {th}} - r_{\mathrm {cb}} \end{aligned}$$

(2)

$$\begin{aligned}&\alpha = \sqrt{\frac{2 - \mathrm{cbr}}{(\gamma + 1) r_{\mathrm {sub}} \varDelta _{\mathrm {th}} }} \end{aligned}$$

(3)

$$\begin{aligned}&x_{\mathrm {iv}} = \frac{(\gamma + 1) \alpha }{2 (4 - \mathrm{cbr})} \left( \varDelta _{\mathrm {th}}^{2} - z_{\mathrm {iv}}^{2} \right) \end{aligned}$$

(4)

$$\begin{aligned}&u_{\mathrm {iv}} \left( x_{\mathrm {iv}}, z_{\mathrm {iv}} \right) = a^{*} \left( 1 + \alpha x_{\mathrm {iv}} + \frac{(\gamma +1)\alpha ^2 z_{\mathrm {iv}}^2}{2(2-\mathrm{cbr})} \right) . \end{aligned}$$

(5)

The values $a^{*}$ and $\gamma$ are the critical speed of sound and ratio of specific heats, respectively. The parameters $r_{\mathrm {sub}}$, $r_{\mathrm {th}}$, and cbr are defined as sketched in Fig. 3. For an equally spaced variable $z_{\mathrm {iv}}$, the axial coordinate of the initial value line $x_{\mathrm {iv}}$ can be calculated (Eq. (4)). Note that the value $x_{\mathrm {iv}} = 0$ corresponds to the throat location. The value $z_{\mathrm {iv}} = 0$ is on the centerbody surface. Subsequently, the axial velocity $u_{\mathrm {iv}}$ on the initial value line can be calculated (Eq. (5)). Note that by definition, the radial velocity $w_{\mathrm {iv}}$ on the initial value line is zero.

According to Eq. (1), the z-coordinate of the initial value line starts at 0. Therefore, for different cbr the initial value lines can be plotted above one another as done in Fig. 4a, which shows the initial value lines and Mach number plots for a constant $r_{\mathrm {sub}}/\varDelta _{\mathrm {th}}$. With decreasing cbr, the initial value lines extend more into the diverging section of the nozzle. The Mach numbers increase from 1 at $z_{\mathrm {iv}}=0$ to larger values on the outside. To properly start the MOC, the Mach number at $z_{\mathrm {iv}}=0$ was set to a value slightly greater than 1, usually $1.0 + 1\times 10^{-9}$. Therefore, with the Mach number on the initial value line being known and $> 1$, the method of characteristics can be started. Note that the initial value line is not a right running characteristic, but a direct outcome from Sauer’s method.

As the initial value lines do not yet contain the centerbody radius in the z-direction, they need to be shifted according to:

$$\begin{aligned} z_{\mathrm {shifted}} = z_{\mathrm {iv}} + r_{\mathrm {cb}}. \end{aligned}$$

(6)

This results in an initial value line that is fitted into the throat section of the nozzle (Fig. 4b). Note that if the throat would not be located in $x=0$, some offset would have to be included in the x-direction as well.

Fig. 3

Schematic of convergent-divergent nozzle with centerbody

Fig. 4

Treatment of subsonic portion

2.2 Supersonic portion

The supersonic portion is calculated with a method of characteristics (MOC) approach, as sketched in Fig. 3. It consists of three steps: first, the initial value data are calculated from the initial value line. This region solely depends on the initial value line, thus on the output of Sauer’s method. Second, the remaining kernel can be calculated. In this process, the supersonic curvature $r_{\mathrm {sup}}$ and the desired exit Mach number $M_{\mathrm {exit}}$ have to be specified. Along the supersonic curvature line, the flow direction is imposed as a boundary condition. Furthermore, along the symmetry axis or centerbody wall, the flow direction is horizontal. The most downstream point on the remaining kernel defines the exit Mach number of the flow. Once it reaches the desired value, the calculation of the remaining kernel is finished. Third, the transition region is calculated, which redirects the flow to create a uniform exit stream. The remaining nozzle contour, which is sometimes referred to as turning contour, is calculated by tracing a streamline from the most downstream wall point of the remaining kernel through the transition region. The exit radius $r_{\mathrm {exit}}$ and nozzle length $L_{\mathrm {sup}}$ directly depend on the previous parameters and cannot be defined a priori.

2.3 Numerical modeling

The converging-diverging geometries were investigated with the computational fluid dynamics (CFD) flow solver DLR-TAU [5, 7, 11]. DLR-TAU is a finite volume solver and the Runge–Kutta relaxation solver with explicit time stepping was used in this work. Furthermore, it was capable of parallelization to simultaneously run one simulation on multiple cores, thus absolute run times were reduced. To quickly damp out low-frequency oscillations during time integration, the solver could be set to multigrid mode. The numerical domain duplicated the internal portion of the converging-diverging nozzle (Fig. 5). For inviscid simulations, the wall condition was set to Euler wall, which allowed for a finite, but wall-parallel velocity. For viscous simulations, the wall condition was set to viscous wall, which enforced a no-slip boundary condition. A two-equation turbulence model was used, namely the $k-\omega$ shear-stress transport (SST) model. Temperature at the wall was assumed to be constant at 300 K.

Fig. 5

Numerical domain used for the inviscid simulations

3 Results

The present section discusses the four following topics. First, the modified Sauer’s method and MOC are validated with inviscid numerical simulations. Second, various design parameters are varied, and their influence on nozzle properties is discussed. Third, the impact of viscosity is investigated by comparing results from Reynolds-averaged Navier–Stokes (RANS) simulations to the results of the analytical approach. Finally, the impact of a centerbody misalignment is discussed by investigating a rotationally or translationally displaced centerbody.

3.1 Validation: MOC and CFD

To validate the MOC calculations, their results were compared to a numerical Euler simulation with an identical contour. As reference condition, a nozzle was designed for a Mach number of 3, and a centerbody ratio of 0.4. The contour plots of the numerical simulation and the MOC are shown in Fig. 6. As the MOC only contains the supersonic portion of the nozzle, there are no results for the subsonic downstream part. The display of the MOC contour is via a scattering plot of discrete points. In some areas, this causes the appearance of sharper edges. Regardless, overall the two contour plots very accurately match.

Fig. 6

Mach number contour extracted from CFD results (top) and from MOC algorithm (bottom)

A more quantitative result is given by the Mach number and pressure contours on the nozzle wall and centerbody (Fig. 7). The pressures, which are normalized to the stagnation pressure ($p_0 = 36 \mathrm {~bar}$), are practically identical. Note that upstream of the throat, the MOC values on the nozzle wall were complemented with quasi-one-dimensional values. The wall properties extracted from CFD and the quasi-one-dimensional values are slightly different for $M < 1$. This is due to slightly non-uniform flow. The values calculated with the MOC very nicely match the values extracted from CFD. Therefore, we conclude that the modified Sauer’s method and the MOC are properly suited to predict the inviscid flow through converging-diverging nozzles.

Fig. 7

Pressure ratio (top) and Mach number (bottom) on nozzle wall and centerbody plotted against axial coordinate

3.2 Analytical discussion

The present section summarizes results obtained with the analytical approach for various design Mach numbers and centerbody ratios. Frequently, a supersonic wind tunnel infrastructure is limited in size, for example, by having costly optical windows for Schlieren imaging. Therefore, in the present section, the exit radius $r_{\mathrm {exit}}$ is held constant at $1\mathrm {~m}$. The supersonic and subsonic radii varied with cbr and were set to:

$$\begin{aligned} r_{\mathrm {sup}} = r_{\mathrm {sub}} = 2 \times \left( r_{\mathrm {th}} - r_{\mathrm {cb}} \right) . \end{aligned}$$

(7)

Note that as the results are all for inviscid cases, the geometries could technically be scaled to any arbitrary size. Mach number was varied from 2 to 5 in steps of 0.5; the centerbody radius was varied from 0 to 0.99 in steps of 0.2.

Figure 8 shows the calculated geometries for a constant Mach number of 3 and it is evident that the nozzle size decreases with increasing centerbody ratio. Note that for all geometries, the symmetry line was located at $r=0$.

Fig. 8

Size comparison of Mach 3 nozzles for different centerbody ratios

The subsonic portion was designed for an inflow Mach number of 0.1. Therefore, the area ratio of the converging section is constant for all Mach numbers and centerbody ratios (Fig. 9a). Naturally, the area ratio of the diverging section is increasing with Mach number, as the flow is further expanded to larger velocities. The ratios are independent of centerbody ratio. Figure 9b shows the stagnation temperatures and pressures normalized with their corresponding exit values. Again the ratios increase with Mach number, as the flow is further expanded and therefore cooled down. Similar to the area ratio, the pressure and temperature ratios are independent of centerbody. Furthermore, they are equal to the quasi-one-dimensional values, which proves the correctness of the MOC.

Fig. 9

Nozzle parameters

Figure 10 shows the nozzle length $L_{\mathrm {sup}}$, which refers to the distance from the nozzle throat to the exit as sketched in Fig. 3. Figure 10a shows the length normalized with the exit radius. It is evident, that with increasing Mach number the nozzle length increases, as further expansion and therefore length is necessary to reach higher velocities. Adding a centerbody to a nozzle with constant exit radius results in shorter nozzle lengths.

If the configuration is mounted in a similar way to the subsonic nozzle, shown in Fig. 2, then there is a significant portion of the centerbody hanging freely in the supersonic portion of the nozzle. Manufacturing or design guidelines might impose certain thresholds on the maximum number of length over diameter. Therefore, in Fig. 10b the length is normalized with the diameter of the centerbody $D_{\mathrm {cb}}$. If, for example, there is a strict limit from the manufacturing department, that requires the L / D to be lower than 10, then for Mach 4, the centerbody ratio has to be $\mathrm{cbr} \ge 0.6$. Therefore, Fig. 10b can be regarded as a characteristic diagram that can be consulted during design.

Fig. 10

Nozzle length from throat to exit

The mass flow through an intake is dependent on its stagnation conditions. To give a unit-free discussion about how mass flow behaves, depending on the centerbody ratio, the mass flows were referenced to the value for $\mathrm{cbr} = 0$ (Fig. 11). For moderate centerbody ratios, the decrease in mass flow rate is not very large. For a centerbody ratio $< 0.4$, for example, and for Mach 2, the mass flow dropped by less than 10%. The decay in mass flow rate is larger for low Mach numbers.

Fig. 11

Normalized mass flow ratios

3.3 Influence of viscosity

In the present section, results for RANS simulations are discussed. The wall temperature was set to constant with $T_{\mathrm {wall}} = 300 \mathrm {~K}$ and the boundary layer was assumed to be turbulent. If not stated differently, the sizes of the geometries were all scaled to a constant exit radius of $r_{\mathrm {exit}} = 0.3 \mathrm {~m}$. Stagnation temperature was always assumed to be constant at 300 K. Stagnation pressure was adjusted to a value that resulted in a nozzle exit pressure of approximately 1 bar. Three aspects were investigated: first, the variation of the centerbody ratio; second, the influence of Mach number; and finally, the influence of Reynolds number.

3.3.1 CBR variation

The centerbody ratio was varied from 0.4 to 0.8 in steps of 0.2 and the design Mach number was constant at 3.0. As the exit radius was held constant, centerbody radius increased with increasing cbr. The geometries are shown in Fig. 12; Mach number profiles are plotted in Fig. 13.

For all cases, the Mach numbers were slightly below the design Mach number, which indicated that the boundary layer slightly decreased the effective contraction ratio of the nozzle. The deviation was on the order of $- 1\%$. In the core flow, near the centerbody, there was a small peak in Mach number, while nothing comparable was observed on the outer side of the nozzle exit. The Mach number in the nozzle slightly decreased with increasing cbr. The exit flow was more uniform for low cbr.

Fig. 12

Geometries designed for different cbrs; M was constant at 3.0

Fig. 13

Mach number on exit plane for different centerbody ratios

3.3.2 Mach number variation

The design Mach number was varied from 2.0 to 4.0 in steps of 0.5. The centerbody ratio was held constant at 0.4, and the exit radius was scaled to a constant value of $r_{\mathrm {exit}} = 0.3 \mathrm {~m}$. The geometries are plotted in Fig. 14. Nozzle length increased and throat area decreased with larger Mach numbers.

In Fig. 15a, the exit plane Mach numbers are plotted. As cbr and $r_{\mathrm {exit}}$ were held constant, the core flow area decreased with lower Mach number. To give a more comparable impression, the Mach numbers are subtracted with and divided by their corresponding design Mach numbers (Fig. 15b). The core flow Mach numbers were below the design value, due to the influence of viscosity. The deficit varied from $-0.8$ to $-1.2\%$ when increasing Mach number from 2 to 4, respectively. The peak in Mach number near the centerbody was also present for all cases.

Fig. 14

Geometries designed for different nozzle exit Mach numbers; cbr was constant at 0.4

Fig. 15

Mach number on exit plane

3.3.3 Reynolds number variation

The standard configuration for the Reynolds number variation was the Mach 3 contour with $\mathrm{cbr} = 0.4$ and $r_{\mathrm {exit}} = 0.3 \mathrm {~m}$. The geometry was scaled to $4 \times$ and $1/4 \times$ its size and thereby Reynolds number was varied. The inflow conditions were held constant at a temperature and pressure of 300 K and 36 bar, respectively.

Figure 16 shows Mach number on the exit plane, while the radial coordinate for each curve is normalized with its corresponding exit radius. For all Reynolds numbers, the Mach number in the core flow was slightly below the design value. The peak in Mach number near the centerbody was also present for all cases. Furthermore, Mach number deviated less from the design value with higher Reynolds number. This is due to decreasing boundary layer thicknesses for $\mathrm{Re} \rightarrow \infty$.

Fig. 16

Mach number on exit plane for different Reynolds numbers

3.4 Design and manufacturing aspects

To investigate the influence of a misalignment of the centerbody, one nozzle was designed and investigated in a three-dimensional configuration. An image of the regular nozzle without misalignment is shown in Fig. 17. Its scale was adjusted to match certain sizes that were already existing within our facility. The centerbody and nozzle exit diameter were 66 mm and 310 mm, respectively. This resulted in a cbr of 0.33. The design Mach number was 2.5. The lengths of the converging and diverging portions of the nozzle were 233 mm and 484 mm, respectively. Upstream of the converging section, the centerbody diameter increased to 136 mm. The diameter of the reservoir inflow channel duct was 460 mm.

Two different misalignment options were chosen: first, the centerbody was displaced in a translational direction. Second, the centerbody was rotated. Results are discussed in the following subsections.

Fig. 17

Sketch of the fully three-dimensional nozzle configuration

3.4.1 Translational displacement

Figure 18 shows the general movement of the displacement. The calculations were performed for $\mathrm{d}z = 0$ mm, 1 mm, 2 mm, 3 mm, and 4 mm.

Fig. 18

Translational displacement of centerbody

Similar to the previous subsections, properties on the nozzle exit plane (Fig. 19) are of interest. The small asymmetries for $\mathrm{d}z = 0 \mathrm {~mm}$ (left images) stem from the three-dimensional mesh, which is not symmetrical in z-direction. With increasing translational displacement, there is more space on one side of the nozzle exit for the flow to expand. In Fig. 19, this was above the centerbody. Therefore, the pressure decreased above and increased below the centerbody. Analogously, Mach number increases due to further expansion. Therefore, the Mach number behaves contrary to pressure and increased above and decreased below the centerbody.

Fig. 19

Influence of translational displacement on pressure (top) and Mach number (bottom) on nozzle exit plane

3.4.2 Angular displacement

Figure 20 shows the rotational movement of the displacement. The calculations were performed for $\mathrm{d}\varphi = 0^\circ$, $0.25^\circ$, $0.5^\circ$, $0.75^\circ$, and $1^\circ$.

Fig. 20

Angular displacement of centerbody

The case without displacement ($\mathrm{d} \varphi = 0^\circ$) is identical to the case with $\mathrm{d}z = 0 \mathrm {~mm}$ in the previous subsection. With increasing angular displacement, there is again more space on one side of the nozzle exit for the flow to expand. In Fig. 21 this was above the centerbody, while the scale of the color contour is identical to the previous subsection. Similar to the previous case, the pressure is decreased above and increased below the centerbody. Analogously, due to the further expansion, Mach number increases. Therefore, the Mach number behaves contrary to pressure and is increased above and decreased below the centerbody.

The changes in pressure and in Mach number were comparable for the $\mathrm{d}\varphi = 0.5^\circ$ and $\mathrm{d}y = 4\mathrm {~mm}$ cases. Therefore, we conclude that an angular displacement of $0.5^\circ$ has a similar impact on the nozzle exit flow, as a translational displacement of 4 mm into the same direction.

Fig. 21

Influence of angular displacement on pressure (top) and Mach number (bottom) on nozzle exit plane

4 Conclusion

The present paper outlines an analytical approach to calculate a converging-diverging nozzle with a constant-radius centerbody. Sauer’s method for the transition from subsonic to supersonic flow was extended to include a centerbody. It was combined with a MOC to calculate a nozzle contour and analytical solution. The results of the analytical approach were validated with inviscid numerical simulations. Finally, the numerical simulations were performed for viscous flow and compared to the analytical results. The main conclusions are:

• The analytical solution agreed with the results from the inviscid numerical simulations, which proves the correctness of the approach.

• When keeping the exit diameter and design Mach number of a nozzle constant, including a centerbody leads to shorter nozzle lengths.

• In all cases investigated, viscosity slightly reduced the nozzle exit Mach number by 1–1.2%. We consider this deviation to be negligible and therefore assume that no viscous treatment is necessary in the design approach.

• Displacing the centerbody in angular and translational direction led to higher pressure and lower Mach number on that side where the centerbody was moved to. An angular displacement of $0.5^\circ$ and a translational displacement of 4 mm were approximately equal in their impact.