Force limited random vibration testing: the computation of the semi-empirical constant $C^2$ for a real test article and unknown supporting structure

Abstract

To prevent over-testing of the test-item during random vibration testing Scharton proposed and discussed the force limited random vibration testing (FLVT) in a number of publications. Besides the random vibration specification, the total mass and the turn-over frequency of the test article (load), $C^2$ is a very important parameter for FLVT. A number of computational methods to estimate $C^2$ are described in the literature, i.e. the simple and the complex two degree of freedom system, STDFS and CTDFS, respectively. The motivation of this work is to evaluate the method for the computation of a realistic value of $C^2$ to perform a representative random vibration test based on force limitation, when the description of the supporting structure (source) is more or less unknown. Marchand discussed the formal description of obtaining $C^2$, using the maximum PSD of the acceleration and maximum PSD of the force, both at the interface between test article and supporting structure. Stevens presented the coupled systems modal approach (CSMA), where simplified asparagus patch models (parallel-oscillator representation) of load and source are connected. The asparagus patch model consists of modal effective masses and spring stiffnesses associated with the natural frequencies. When the random acceleration vibration specification is given the CSMA method is suitable to compute the value of the parameter $C^2$. When no mathematical model of the source can be made available, estimations of the value $C^2$ can be find in literature. In this paper a probabilistic mathematical representation of the unknown source is proposed, such that the asparagus patch model of the source can be approximated. The chosen probabilistic design parameters have a uniform distribution. The computation of the value $C^2$ can be done in conjunction with the CSMA method, knowing the apparent mass of the load and the random acceleration specification at the interface between load and source, respectively. Data of two cases available from literature has been analyzed and discussed to get more knowledge about the applicability of the probabilistic method.

1 Introduction

In spacecraft structure design force limits are established to prevent over-testing of the test-article (load), because its dynamic behavior on the shaker table is different from its dynamic behavior when placed on the actual supporting structure (source).

In [25] the history, the actual status and application guidelines of the force limited vibration testing (FLVT) are discussed and 41 interesting references regarding the FLVT are provided.

During the FLVT both the random acceleration as well as the random force limits are specified, however, the random acceleration specification may be overruled by the random force limits.

The well-known semi-empirical method (SEM) of the force-limit approach is a method to establish force-limits at the interface between the load and the shaker table, [10, 24, 25].

$$\begin{aligned} \begin{array}{ll} &{}W_{\mathrm{FF}}(f) = C^2 M_{\mathrm{o}}^2 W_{\mathrm{AA}}(f) \quad f\le f_0, \\ &{} W_{\mathrm{FF}}(f) = C^2 M_{\mathrm{o}}^2 W_{\mathrm{AA}}(f) \left( \frac{f_0}{f}\right) ^n \quad f > f_0, \end{array} \end{aligned}$$

(1)

where $W_\mathrm{FF}(f)$ is the random force spectral density, $W_\mathrm{AA}(f)$ is the specified random acceleration spectral density, $M_\mathrm{o}$ is the total mass of the test article and $C^2$ is a dimensionless semi-empirical constant which depends on the configuration. $f$(Hz) is the frequency and $f_0$ is the natural frequency of the primary mode with a significant modal effective mass of the load. The factor $n$ can be estimated from the apparent mass of the load, in general, $n=2$. $C^2$ should not be selected without adequate justification [22].

Scharton et al revisited the force limiting vibration testing in a presentation [22] and reviewed the methods of estimation of $C^2$ using the simple two degree of freedom system (STDFS).

Dharanipathi main conclusions in [8] are that the range of values of $C^2$ is between 2 and 5, however, there are several cases where $C^2=10\ldots 17$, and he stated that $C^2$ does not depend on the damping in the structure.

In [27] Soucy et al recommend values for $C^2$, however, based on limited number of measured (flight) data. It has been observed that in normal conditions $C^2=2$ might be chosen for complete spacecraft or strut mounted heavier equipment. $C^2=5$ might be considered for directly mounted lightweight test items.

Based on the frequency shift of a two degree of freedom system [23] Scharton developed two methods to establish the value $C^2$; the simple two degree of freedom system (STDFS) [24] and the complex two degree of freedom system (CTDFS) [6].

In [13] Gordon proposed a conservative analytical value of $C^2=9$, which is based on the STDFS when the load/source ratio is 0.16. This conservative estimation of $C^2$ will cover model uncertainties and the test configuration remain relatively simple because no force measurement devices are used during the random vibration test.

Salvignol reported in his paper [21] the use of $C^2=3$ during the random vibration test on the NIRspec (Near Infrared) instrument, part of the integrated science instrument (ISIM) on the James Webb telescope.

Stevens presented a paper [28], to compute the force limits, based on the coupled system modal approach (CSMA). The coupled asparagus patch models of both source and load are needed. These models can be extracted from finite element analysis models or apparent mass measurements. This CSMA method forms the core of this paper.

In general, the mathematical model (FEM, modal effective masses, $\ldots$) of the load is available, because the random vibration test will be conducted under the responsibility of contractor/subcontractor which is responsible for the design of the load as well. To apply the methods to obtain the value $C^2$ the dynamical properties of the source need to be known as well, however, if the mathematical description of the supporting structure (source) is lacking a probabilistic approach is necessary.

In this paper the replacement of the source by a probabilistic-source is discussed. The mathematical modeling of the probabilistic source will be an asparagus patch model, consisting of a number of parallel placed lightly damped SDOF systems, with the modal effective masses [12, 18] as the discrete mass and the spring stiffnesses representing the undamped natural frequencies. The CSMA method [28] is applied to compute maximum random accelerations and forces at the interface between load and source.

The Rosenblueth point estimated moments (PEM) will be applied [17, 20] to minimize the number of samples (analysis cases) describing the probabilistic design parameters. The probability density functions of the probabilistic design parameters is assumed to be uniform.

The proposed probabilistic method has been verified by investigating available data from literature [7, 10], to study the applicability of the probabilistic approach. In the second example [10] besides the Rosenblueth PEM method the Monte Carlo Simulation (MCS) method [1] is applied as well.

The mean value $\mu$, the $1\sigma$ value and the $\mu + 3 \sigma$ value of the semi-empirical constant $C^2$ are computed and compared with published data.

2 Force limits analysis method

The semi-empirical force-limit vibration test (FLVT) approach has been established to prevent over-testing of a flexible test item when placed on the shaker table with a very high impedance compared to the impedance of the supporting structure of the test item. This (FLVT) test philosophy or method is described in [25]. The simple equations to compute the PSD of the force limits $W_\mathrm{FF}$ from the PSD of the random acceleration test specification $W_\mathrm{AA}$ are already given in Eq. (1).

Marchand provides in [16] an equation to compute the value of $C^2$ in the interface between the source and the load, both consisting of MDOF systems. Considering that the maximum PSD of the interface force $W_{\mathrm{FF}_{\mathrm{max}}}$ and the maximum PSD of the interface acceleration $W_{\mathrm{AA}_{\mathrm{max}}}$, which need not to occur at the same frequency, the value of $C^2$ can be defined as

$$\begin{aligned} C^2=\frac{W_{FF_{{\rm max}}}}{M_\mathrm{o}^2 W_{AA_\mathrm{max}}}, \end{aligned}$$

(2)

where $M_\mathrm{o}$ is the total mass of the load. Later on the total mass of the load will be denoted by $M_\mathrm{l}$.

3 Coupled system modal approach method (CSMA)

The CSMA method, proposed by Stevens in [28], is the selected method to compute the force limits for the random vibration testing of the load. The dynamic or apparent mass of the load [9], as well as the random acceleration test specification are required.

Fig. 1

Coupled system in parallel-oscillator representation

The reduced asparagus patch models of both source and load are shown in Fig. 1. The spring stiffnesses and damper values are, respectively, given by $k_{il}=\omega _{il}^2 m_{il}$ and $c_{il}=2 \zeta _i \omega _{il}m_{il}$, where $\omega _{il},\, i=1,2,\ldots ,n$ are the natural frequency of the load. $\zeta _i$ is the modal damping ratio of mode $i$. The residual mass of the load is denoted by $m_{rl}$. The notations for the source are similar.

The random acceleration vibration specification $W_{\mathrm{AA}}(f)$ at the interface between the source and the load is provided (specified) by the customer and is a requirement for the design of the load. In general, this specification is an envelope that is based on data “smooths over” of peaks and valleys. The load is very responsive at the anti-resonance frequencies and acts as a dynamic absorber to reduce the input.

To compute the parameter $C^2$ in Eqs. (1) and (2) is applied. Therefore we need to compute a set of scaled random acceleration spectra at the interface between the load and the source. This set of scaled random acceleration spectra are multiplied by the absolute value squared of the apparent mass of the load to obtain the composite of the random force spectra at the interface. The mathematical models (parallel oscillators, Fig. 1) of the source and the load are represented by their modal effective masses and associated spring stiffness and damping and are coupled. The modal effective masses can be either calculated by a modal analysis with a fixed-free finite element model [30], or extracted from a measured apparent mass of the load, i.e. on a shaker table performing sinusoidal base-excitation [11, 26]. The boundary conditions of the asparagus model of the source are assumed to be fixed at the interface between load and source.

To calculate the maximum random force spectrum at the interface between source and load the following procedure is followed:

• Generate the mathematical models (asparagus patch models) of both the source and load (Fig. 1), to perform a coupled random response analysis as described later in the procedure.

• Compute the apparent mass (dynamic mass) of the load, rigidly fixed at the interface between source and load.

• Define the random load spectrum $W_F(f)$ to be applied subsequently at every oscillator of the source. This may be a unitary band-limited white noise spectrum.

• Perform for every subsequent loaded oscillator of the source a random acceleration response analysis and scale that response spectra at the interface such that the maximum acceleration at a certain excitation frequency is equal to the specified random acceleration spectrum $W_{\mathrm{AA}}(f)$ at that frequency (see Fig. 2). This random acceleration specification is given by the customer. Multiply these scaled random acceleration spectra by the squared absolute value of the apparent mass spectra of the load. The composite (envelope) random force spectrum $W_{\mathrm{FF}}(f)$ then represents the upper bound of the random force spectrum at the interface. Later on the following simple constant spectra are taken: $W_{\mathrm{AA}}(f)=0.01$ g$^2$/Hz and $W_{F}(f)=1$ N$^2$/Hz, both between 20–2000Hz as usual in spacecraft structures design.

• Apply Eq. (2) to compute the semi-empirical constant $C^2$. In that equation $M_\mathrm{o}$ is the rigid body mass of the load. Later on the the mass of the load $M_\mathrm{o}$ is denoted by $M_\mathrm{l}$.

Fig. 2

Scaled random response spectrum

One of the main tasks in the previous procedure is to establish the asparagus patch models of the source and the load followed by the random response analyses. The elements needed to perform the computations of $C^2$ are discussed in detail in subsequent sections.

4 Definition (availability) of source and load

To perform a random vibration test of the load the test conductor needs the availability of a hardware (H/W) model of the load, i.e. the item to be tested on a shaker table. When the FLVT [25] is planned the value of $C^2$ (1) shall be obtained either by experience (data base) [25] or applying the simple two degree of freedom (STDFS) system and or the complex two degree of freedom (CTDFS) system as described in [19]. When modal characteristics of both source and load can be made available from FEA/FEM or measurements Eq. (2) can be used [15]. Simplified computations may be done when the CSMA method will be applied as illustrated in Fig. 1.

4.1 Load

4.1.1 Mathematical model

We assume the availability of a mathematical description (finite element model) of the load. An estimation of the modal damping ratio shall be done, in general, based on past experiences or measurements. The finite element model degrees of freedom at the interface between the load and source shall be fixed. The following modal data of the load is needed to build the asparagus patch model for the CSMA method:

• The total mass of the load $M_{\mathrm{l}}$ (kg).

• The undamped natural frequencies $f_i, \,\, i=1,2,\ldots ,n$ (Hz) assuming clamped conditions at the interface load/source.

• The associated modal effective masses $m_{il}, \, i=1,2,\ldots ,n$ (kg) and the residual mass $m_{rl}$, in the three translational directions, respectively. The cross-coupling is not considered.

• The estimated or measured modal damping ratios $\zeta _i, \, i=1,2,\ldots ,n$.

• The apparent mass $M_{\mathrm{al}} (f)$ (kg) of the load in the three translational directions with respect to the interface.

4.2 Source

Coté [5] stated in his paper that the asparagus patch model of the source (common to the load); modal effective masses, natural frequencies, can be extracted from a finite element model, experiment or from experience. However, in this subsection we assume that the finite element model or experimental results cannot be made available, so the simplified model will be constructed using engineering design rules (i.e. ECSS ¹ standards and handbooks).

The dynamic characteristics (design parameters) of the source with respect to the interface between the load and the source are considered to be probabilistic related to the modal properties of the load.

The fuzzy design parameters are discussed in detail in [31] and are common to the modal data of the load. The fuzzy design parameters of the source are described in the following section.

5 Virtual building of asparagus patch model of the source

The design parameters of the source are related to the mass and modal properties of the load and are discussed in [31].

5.1 Total mass

The total rigid body mass of the source ${M}_\mathrm{s}$ shall be provided (i.e. by the prime contractor). If the $M_\mathrm{s}$ can’t be made available the following total mass variation is assumed:

$$\begin{aligned} M_\mathrm{s}=0.1 \cdots 10 {M}_\mathrm{l} \end{aligned}$$

(3)

5.2 Natural frequencies

When the lowest undamped natural frequency of the load is $f_{\mathrm{l}}$, the interface source/load fixed, the assumed undamped natural frequency of the source will vary between

$$\begin{aligned} f_{\mathrm{1s}}=\frac{f_\mathrm{l}}{2} \cdots \frac{f_\mathrm{l}}{\sqrt{2}}. \end{aligned}$$

(4)

This range is based on the design practice that the dynamic interference between load and source is minimized.

This undamped natural frequency of the source is associated with a high modal effective mass $m_{\mathrm{1s}}$.

The following (first guess) distribution of natural frequencies, with substantial modal effective mass, is defined by:

$$\begin{aligned} \begin{array}{ll} &{}f_{\mathrm{2s}}=2f_{\mathrm{1s}}, \\ &{}f_{\mathrm{3s}}=4f_{\mathrm{1s}}, \\ &{}f_{\mathrm{4s}}=6f_{\mathrm{1s}}. \end{array} \end{aligned}$$

(5)

Force limits typically cover only the first three modes [14]. Therefore, it is usually adequate to specify the force limits of the load only in the frequency regime encompassing a few modes for each axis, which might be up to approximately 100 Hz for a large spacecraft, 500 Hz for an instrument, or 2000 Hz for a small component [25].

5.3 Modal effective masses

The first undamped natural frequency $f_{\mathrm{1s}}$ will be associated with the first significant modal effective mass $m_{\mathrm{1s}}$. The fundamental modal effective masses of simple systems is assumed to be a first approximation of modal effective mass of the source. This modal effective mass will be assumed in the following mass range:

$$\begin{aligned} m_{\mathrm{1s}}=0.4\cdots 0.6M_{\rm s}. \end{aligned}$$

(6)

This range may be confirmed by the calculation of the modal effective mass of simple structures [31]. The residual mass is the sum of the modal effective masses excited outside the frequency range of interest and the residual mass $m_{\mathrm{rs}}$ will be assumed to be 5 % of the total mass of the source, such that

$$\begin{aligned} m_{\mathrm{rs}}=0.05M_\mathrm{s}. \end{aligned}$$

(7)

The summed modal effective masses of the computed modes shall be about 95 % of the total mass of the source $M_\mathrm{s}$.

Further $\Delta m$ is the sum of the missing modal effective masses that must be still distributed and is defined by

$$\begin{aligned} \Delta m= M_\mathrm{s}-(m_{\mathrm{1s}}+m_{\mathrm{rs}}). \end{aligned}$$

(8)

The deterministic distribution (best guess) of the modal effective $m_{\mathrm{ks}}(f_{\mathrm{ks}}),\,k=2,\ldots ,4$ will be descending and the effective masses of the remaining modes are distributed according to the following descending scheme:

$$\begin{aligned} \begin{array}{ll} &{}m_{\mathrm{2s}}=0.5 \Delta m, \\ &{}m_{\mathrm{3s}}=0.3 \Delta m, \\ &{}m_{\mathrm{4s}}=0.2 \Delta m.\\ \end{array} \end{aligned}$$

(9)

5.4 Modal damping ratio

We will assume a variation of the modal damping ratio in the interval $\zeta =0.01\cdots 0.1$. The modal damping ratio is constant and applies for all modes, both for load and source.

6 Probabilistic approach

6.1 Summary of mean and standard deviation of design variables

The probability density function of the stochastic design variables $M_\mathrm{s}, \, f_{\mathrm{1s}}, m_{\mathrm{1s}}$ and $\zeta$ are assumed to be uniform.

The summary of mean and standard deviation of the selected design variables, with a uniform distribution ² is presented in Table 1.

Table 1 Mean and standard deviation stochastic variables

6.2 Probabilistic analysis by the Rosenblueth 2k+1 PEM & CSMA

The Rosenblueth point estimates moment method (PEM) for probability moments [17, 20], computes the mean and the variance of the value $C^2$ in combination with the CSMA. If the number of design variables is $k$, $2k+1$ samples (analysis cases) have to be computed.

The $Y_0$ value of $C^2$ is computed by substituting the mean values $\mu$ for all $k$ design variables in the asparagus patch model of the source, $Y_{nm}$ value of $C^2$ is computed by substituting for the nth design variable the value $\mu _n-\sigma _n$ and for the other design variables the mean values and the $Y_{np}$ value of $C^2$ is computed by substituting for the nth design variable the value $\mu _n+\sigma _n$ and for the other design variables the mean values, respectively. Index $m$ indicates subtracting the standard deviation and index $p$ indicated adding the standard deviation.

The mean $Y_n$ of two point estimates $Y_{np}, Y_{nm}$ is given by

$$\begin{aligned} Y_n=\left| Y_{np}+Y_{nm}\right| /2, \,n=1,\ldots ,k, \end{aligned}$$

(10)

and the variance is $V_n$ can be obtained by

$$\begin{aligned} V_n=\left| \frac{Y_{np}-Y_{nm}}{Y_{np}+Y_{nm}}\right| , \,n=1,\ldots ,k. \end{aligned}$$

(11)

When we assume that all design variables are statistically independent the following approximation of the mean $\bar{Y}=\mu _Y$ and the variance $V_Y=\sigma _y/\mu _Y$ can be made [20]

$$\begin{aligned} \frac{\bar{Y}}{Y_0}=\prod _{n=1}^{2k+1} \frac{Y_n}{Y_0}, \end{aligned}$$

(12)

and

$$\begin{aligned} 1+V_Y^2=\prod _{n=1}^{2k+1} (1+V^2_n). \end{aligned}$$

(13)

7 Test cases

7.1 Introduction

The probabilistic description of the asparagus patch model of the source has been investigated using two cases taken from literature:

• ESA study: “IFLV-Improvement of Force Limites Vibration Testing Methods for Equipment Instrument Unit Mechanical Verification”, [7].

• The Linear Drive Unit (LDU), which is an Orbital Replacement Unit (ORU) of the International Space Station (ISS) program, [10].

7.2 ESA IFLV study

This real life example is taken from the ESA study: “IFLV-Improvement of Force Limited Vibration Testing Methods for Equipment Instrument Unit Mechanical Verification” presented by Destefanis in [7]. The IFLV study facilitated a full test campaign (both sine and random) on a test system composed of a honeycomb panel (source) which supported an optical unit (MIRI) (load) and an electronic box (EBOX) (not considered) (see Fig. 3). Force measurement devices (FMDs) were installed at the mechanical interfaces between units and honeycomb plate (1210 mm $\times$ 910 mm). The test runs were performed both on the system and on the units (MIRI, EBOX) standalone, therefore collecting experimental evidence of the difference (in terms of mechanical interface forces) between soft mounted and hard mounted configurations. However, the numerical data of the interface forces were difficult to assess.

Fig. 3

IFLV total and MIRI test setup on shaker slip table, courtesy [7]

7.2.1 Mass properties of IFLV system

The individual mass properties of the test setup are taken from [7]. These mass properties were extracted from the very detailed finite element models of the EBOX, MIRI, panel and FMD and are presented in Table 2, however, the EBOX is further not considered in this paper. The third column represents the mass properties of the hard-mounted MIRI and FMD’s (FMD’s between the MIRI and shaker slip table).

Table 2 Mass properties of individual items

7.2.2 Dynamic properties of IFLV system and individual parts

Numerical modal analyses were done on the total test setup (with and without FMD’s), the EBOX, the MIRI and the Honeycomb panel hard-mounted, respectively. The classical results are: the undamped natural frequencies and associated modal effective masses. The modal effective masses are associated to the Z axis, that is perpendicular to the sandwich panel. In the other directions no information about modal effective masses and associated natural frequencies were made available. The honeycomb panel had been supported along the edges. The results of the modal analyses are given in Table 3. The values of the natural frequency and the modal effective mass of the honeycomb panel are only given for information, because later on the dynamic properties of the honeycomb panel are estimated in a probabilistic manner and other boundary conditions are applied.

Table 3 Mass and modal properties [7]

7.2.3 $C^2$ interface MIRI/panel

The values of $C^2$ are applicable in the Z-direction, thus perpendicular to the panel, and in particular between the sandwich panel and het MIRI instrument. The $C^2$ values, computed by the STDFS method are taken from [7].

Applying the CSMA method the dynamic properties of the panel are computed with respect to the interface between panel and MIRI instrument. The natural frequency of the honeycomb panel supported at the midpoint, [3], is approximately 50 Hz. The corresponding modal effective mass varies between 1.50–3.0 kg. The CSMA method gives $C^2$ values in line with the other methods. The computational results of $C^2$ are presented in Table 4.

Table 4 Values of modal effective masses and $C^2$ (Z-dir), $Q=10$ [7]

7.2.4 Probabilistic computation of $C^2$

The deterministic asparagus patch model of the load (MIRI) is derived from the dynamic properties with respect to the interface between the load and the source (sandwich panel) taken from Table 3 and presented in Table 5. The residual mass is augmented with an artificial high natural frequency outside the frequency range of 20–2000 Hz. The sum of the modal effective and residual masses is equal to the total mass of the MIRI, $M_\mathrm{l}=27.945$ kg. The dynamic properties of the sandwich panel are assumed to be unknown.

Table 5 Asparagus patch model MIRI, Z-dir

The damping is probabilistic and applicable to both the load and the source.

To start the probabilistic computation of $C^2$, with the Rosenblueth $2k+1$ point estimation method, the uniform distributions of the design variables of the source; the total mass $M_\mathrm{s}$, the first fundamental natural frequency $f_{\mathrm{1s}}$, the first primary modal effective mass $m_{\mathrm{1s}}$ and modal damping $\zeta$, as presented in Table 1, are used.

The results of the probabilistic computations, the mean $\mu$, the standard deviation $\sigma$ and the $\mu +3\sigma$ of $C^2$ with additional variations of the distributions of the total $M_\mathrm{s}$, the modal effective mass $m_{\mathrm{1s}}$ and the fundamental natural frequency $f_{\mathrm{1s}}$ are presented in Table 6. The intervals of the design variables: $m_{\mathrm{1s}}$, $f_{\mathrm{1s}}$ and $\zeta$ are well chosen, however, the estimation of the mass of the source $M_\mathrm{s}$ shall be good as possible.

Table 6 Rosenblueth probabilistic computations of $C^2$, Z-dir, $M_\mathrm{l}=27.945$ kg (ref. means reference values)

In Table 7 the influence of the modal damping ratio has been numerically investigated. Except for very high damping the modal damping ratio $\zeta$ has less influence on $C^2$.

Table 7 Rosenblueth PEM computations of mean $\mu$, standard deviation $\sigma$ and $\mu +3 \sigma$ value of $C^2$, varying the modal damping ratio $\zeta$

Compared to the estimated values of $C^2$, given in Table 4, it can be concluded from the probabilistic computations that a good estimation of the total mass of the source $M_\mathrm{s}$ is of importance to obtain more reliable figures of $C^2_{\mu +3\sigma }$. The distributions of the other design parameters were well chosen, however, the values of $C^2_{\mu +3\sigma }$ are enveloping the STDFS calculations as given in Table 4. That means that the load is good dynamically uncoupled from the source. This is one of the major assumptions in the probabilistic approach.

A dynamically stiff source with a high interval of the natural frequency $f_{\mathrm{1s}}$ in conjunction with the proposed interval of the modal effective masses $m_{\mathrm{1s}}$ will increase the statistical estimation of $C^2$, in general, due to increasing dynamic coupling between load and source.

A low interval of natural frequency $f_{\mathrm{1s}}$ associated with a low interval of the modal effective mass $m_{\mathrm{1s}}$ of the source will lower the values of $C^2_{\mu +3\sigma }$. That means the load is supported by a flexible source with less dynamic interaction.

The selection of the interval of the modal effective mass $m_{\mathrm{1s}}$ has less influence on the values of $C^2$.

The clustering of the natural frequencies has less influence. In Table 7 it can be seen that the influence of the modal damping is not so sensitive as the estimation of the total mass of the source.

7.3 LDU/FSE/FRAM

The Linear Drive Unit (LDU) is an Orbital Replacement Unit (ORU) of the International Space Station (ISS) program. During the flight of the LDU to the ISS, it is connected to a Space Shuttle Orbiter by an adaptor plate and locking system. The LDU is connected to the adaptor plate by four points, which will be known as interface points. The configuration of the LDU, flight support equipment (FSE) adapter plate and active flight release attachment mechanism (FRAM) together forms the integrated model. The integrated model is attached to the Orbiter at seven points, which have various constraint directions. The models are shown in Fig. 4. The mass of the LDU (load) is $M_\mathrm{l}=113.85$ kg and the remaining FSE and FRAM parts (source) make up $M_\mathrm{s}=187.33$ kg. The modal effective masses of the significant modes and the $C^2$ of the semi-empirical force limits equations (1) are given in the next sections.

Fig. 4

LDU-FSE-FRAM FEM in launch configuration [10]

The dynamic properties of the FSE/FRAM (source) are not presented in [10], hence unknown.

7.3.1 Dynamic properties LDU and value $C^2$

The natural frequencies and associated modal effective masses of the first three dominant modes of the LDU, fixed at the interface between LDU and FSE (see Fig. 4), are taken from the paper of Fitzpatrick [10] and presented in Table 8. The Z-dir is perpendicular to the mounting plane

Table 8 Dynamic properties LDU, courtesy [10]

7.3.2 $C^2$ from literature

The value $C^2$ was derived from the STDFS equations and the scaled force power spectral density response at the interface between LDU/FSE and taken from [10] and given in Table 9. The scaled random interface force is computed from the enveloped random acceleration specification multiplied by the squared magnitude of the apparent mass of the LDU (load).

Fig. 5

Scaled random interface force procedure, courtesy [10]

The PSD acceleration at the four interface points between the LDU and FSE/FRAM are represented by the four dotted curves. The final random acceleration specification is the envelope of these four curves. This is illustrated in Fig. 5a. The drawn curve in Fig. 5b represents the PSD of the interface force and corresponds to the enveloped random acceleration. Applying Eq. (2) the value $C^2$ can be established.

Table 9 Values of $C^2$ and $n$, from STDFS and analytical data (FEA), courtesy [10]

7.3.3 Probabilistic computations of $C^2$

The asparagus patch model of the load (LDU) is derived from the dynamic properties with respect to the interface between the load and the source (FSE/FRAM) taken from Table 8 and presented in Table 10. The residual mass is augmented with an artificial high natural frequency outside the frequency range of 20–2000 Hz. The sum of the modal effective and residual masses is equal to the total mass of the LDU, $M_\mathrm{l}=133.85$ kg.

Table 10 Asparagus patch model LDU, X, Y and Z-dir, $M_\mathrm{l} = 113.85$ kg

Two probabilistic methods are applied to compute $C^2$:

• The Monte Carlo Simulation (MCS) method [1].

• The Point estimates for probability moments [20].

We start the probabilistic computations of $C^2$ with the Monte Carlo Simulation (MCS) approach with 2000 runs and in each run 4 uniform distributed random samples. Hence in total 8000 samples. The MCS method may be interpreted as an optimization method trying to find the maximum value of $C^2$ subjected to constraint functions (the intervals of the design variables) [29].

Most of the MCS computations are repeated applying the Rosenblueth point estimation method, which means 9 samples. Variations of the design variables; the total mass of the source $M_s$ and the modal viscous damping ratio $\zeta$ are investigated. The presented results of the computations are the mean $\mu$, the standard deviation $\sigma$ and the $\mu + 3 \sigma$ values of $C^2$.

The computations of $C^2$ applying the MCS method with 8000 samples are given in Table 11, and the computations of $C^2$, and applying the Rosenbleth PEM method the probabilistic results with 9 samples are provided in Tables 12, 13, 14, 15, 16 and 17.

Table 11 MCS results of mean $\mu$, standard deviation $\sigma$ and $\mu +3 \sigma$ value of $C^2$, 8000 samples

In Table 11 we present the mean $\mu$, the standard deviation $1\sigma$, the $\mu + 3 \sigma$ and maximum values of $C^2$ when the number of samples is 8000. The design variables $M_\mathrm{s}$ and $\zeta$ are varied. The total value of the source mass $M_\mathrm{s}$ is: (a) the standard interval and (b) tailored to the real value of $M_\mathrm{s}$. The value of the modal damping ratio $\zeta$ is varied too: (a) the standard interval and (b) a constant value. The computations of $C^2$ are done in X-, Y- and Z-direction. When the mass of the source is tailored to the real value the values of $C^2$ are lower compared to values of $C^2$ when applying the standard interval of $M_\mathrm{s}$. There is little influence of the modal damping ratio $\zeta$ on the $C^2$.

The distributions of $C^2$ are calculated with the MCS method and shown in Fig. 6. The standard intervals and uniform distributions of the design variables are taken (Table 1). The distribution are similar to the Lognormal distribution [1]. Assuming the Lognormal distribution for $C^2$ the probability $\text {Prob} (C^2 \le C^2_{\mu +3 \sigma }) =0.9915$. In general, the values $C^2_{\mu +3 \sigma }$ don’t cover the computed maximum values $C^2_{\mathrm{max}}$, however, the maximum values have a very low density.

Fig. 6

Distributions of $C^2$ in X-, Y-, Z-directions, with standard intervals and distributions of design variables (Table 1)

The computations of $C^2$ with the Rosenblueth PEM method are presented in Table 12. The number of samples is 9. The mean $\mu$, the standard deviation $1 \sigma$ and $\mu +3 \sigma$ values of $C^2$ are computed. No maximum values could be obtained. The results presented in Table 12 are comparable to those presented in Table 11. The accuracy achieved by the Rosenblueth PEM method is comparable to the MCS method with 8000 samples. The modal damping ratio $\zeta$ has a minor influence, but tailoring the total mass of the source $M_\mathrm{s}$ is very beneficial and will improve to computations of $C^2$.

Table 12 Rosenblueth PEM computations of mean $\mu$, standard deviation $\sigma$ and $\mu +3 \sigma$ value of $C^2$

In Table 13 the distribution of the source natural frequency $f_{\mathrm{2s}},f_{\mathrm{3s}},f_{\mathrm{4s}}$ has been altered compared to the standard proposed values given in Eq. (5). This leads to an increase of the values of $C^2$.

In the Tables 14 and 15 the effect of the variation of the interval of the dominant modal effective mass $m_{\mathrm{1s}}$ is investigated. Decreasing the interval has minor influence, however, increasing the interval compared to Eq. (6) has a major increasing impact on the values of $C^2$. A high modal effective mass will increase dynamic responses at the interface.

Table 13 Rosenblueth PEM computations of mean $\mu$, standard deviation $\sigma$ and $\mu +3 \sigma$ value of $C^2$, $f_{\mathrm{2s}}=1.5 f_{\mathrm{1s}} f_{\mathrm{3s}}=2 f_{\mathrm{1s}},f_{\mathrm{4s}}=2.5 f_{\mathrm{1s}}$

Table 14 Rosenblueth PEM computations of mean $\mu$, standard deviation $\sigma$ and $\mu +3 \sigma$ value of $C^2$, $m_{\mathrm{1s}}\in [0.2, 0.4 ] M_\mathrm{s}$

Table 15 Rosenblueth PEM computations of mean $\mu$, standard deviation $\sigma$ and $\mu +3 \sigma$ value of $C^2$, $m_{\mathrm{1s}}\in [0.6, 0.8 ] M_\mathrm{s}$

Table 16 Rosenblueth PEM computations of mean $\mu$, standard deviation $\sigma$ and $\mu +3 \sigma$ value of $C^2$, $f_{\mathrm{1s}}\in [0.3, 0.5 ] f_{\mathrm{1l}}$

Table 17 Rosenblueth PEM computations of mean $\mu$, standard deviation $\sigma$ and $\mu +3 \sigma$ value of $C^2$, $f_{\mathrm{1s}}\in [\frac{1}{2} \sqrt{2}, 0.9 ] f_{\mathrm{1l}}$

In the Tables 16 and 17 the intervals of the first natural frequency of the source $f_{\mathrm{s}}$ are varied. The effect of decreasing or increasing the interval, compared to Eq. (4) leads to increase of the computed values of $C^2$.

From previous Tables it turned out that the most important design variable is the total mass of the source $M_\mathrm{s}$. It is worthwhile to invest time to find a good approximation of $M_\mathrm{s}$.

8 General conclusions/recommendations

Two testcases from literature were investigated to confirm the basis for the probabilistic approach to estimate the value of $C^2$, which is the key variable in the semi-empirical method of the force limited random vibration testing (Eq. 1):

• ESA study: “IFLV-Improvement of Force Limited Vibration Testing Methods for Equipment Instrument Unit Mechanical Verification”, [7]. The ratio of the masses of the load and the source is $M_\mathrm{l}/M_\mathrm{s}=27.47/1.5=18.34$, which is a high value. The probabilistic analysis results are presented in the Tables 6 and 7.

• The Linear Drive Unit (LDU), which is an Orbital Replacement Unit (ORU) of the International Space Station (ISS) program, [10]. The ratio of the masses of the load and the source is $M_\mathrm{l}/M_\mathrm{s}=113.85/187.33=0.61$, which is a more reasonable ratio. The probabilistic analysis results are presented in the Tables 11 – 17.

In both examples the dynamic properties of the test-item (load) are known, while these properties are unknown for the supporting structure (source) The proposed probabilistic approach to estimate $C^2$ is performed, however, in combination with the CSMA method. The interface response analyses are done using the CSMA method.

The dynamic properties of the unknown source are described by four main design variables with a uniform probability distribution: the total mass of the source $M_\mathrm{s}$, the first dominant natural frequency $f_{\mathrm{1s}}$, the associated modal effective mass $m_{\mathrm{1s}}$ and the modal damping ratio $\zeta$, which is applicable to load too. The other design variables $f_{\mathrm{2s}}, f_{\mathrm{3s}}. f_{\mathrm{4s}}$ and $m_{\mathrm{2s}}, m_{\mathrm{3s}}.m_{\mathrm{4s}}$ and the residual mass $m_{\mathrm{rs}}$ are related to the main design variables.

After the probabilistic analyses of both examples the following general conclusions can be drawn:

• If the ratio $M_\mathrm{l}/M_\mathrm{s} \ge 1$ the probabilistic approach will overestimate $C^2$, hence $C^2 < C^2_{\mu +3 \sigma }$.

• If the ratio $M_\mathrm{l}/M_\mathrm{s} \approx 1$ the probabilistic approach will provide a realistic value of $C^2$, hence $C^2 \approx C^2_{\mu +3 \sigma }$.

• It is very helpful to estimate the mass $M_\mathrm{s}$ of the source as good as possible. This will improve the estimation of $C^2$ considerably.

• The Rosenblueth PEM method turned out to be a very efficient alternative for the MCS method.

When the dynamic properties of the test-item (load) are known and the dynamic properties of supporting structure (source) are unknown the recommended values for the design variables, intervals and associated uniform distributions, which are presented in Table 18, can be applied to perform the probabilistic computations of the semi-empirical constant $C^2$. That means that the dynamic characteristics of both the load and the source are properly separated and the dynamic coupling minimized.

If the mass of the source can’t be made available the recommended interval for the mass of the source is $M_\mathrm{s}=[0.1,10]M_\mathrm{l}$ (see Table 1), however, there may load/source combinations where $M_\mathrm{s}/M_\mathrm{l} > 10, M_\mathrm{l}/M_\mathrm{s} \ll 1$.

Table 18 Recommended distributions of probabilistic design variables

Only two cases, reported in the literature, were investigated applying the probabilistic approach, therefor there is still a need for further study.

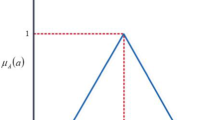
It is of great interest to consider situations where $M_\mathrm{l}/M_\mathrm{s} \ll 1$, and therefor recommended to be investigated with the probabilistic approach for comparison with real-life cases. From the STDFS method an increase of the value $C^2$ may be expected as shown in Fig. 7.

Fig. 7

Computation of $C^2$ with the STDFS method [23]