The Calibrated Bayesian Hypothesis Test for Directional Hypotheses of the Odds Ratio in $2\times 2$ Contingency Tables

Abstract

The $\chi ^{2}$ test is among the most widely used statistical hypothesis tests in medical research. Often, the statistical analysis deals with the test of row-column independence in a $2\times 2$ contingency table, and the statistical parameter of interest is the odds ratio. A novel Bayesian analogue to the frequentist $\chi ^{2}$ test is introduced. The test is based on a Dirichlet-multinomial model under a joint sampling scheme and works with balanced and unbalanced randomization. The test focusses on the quantity of interest in a variety of medical research, the odds ratio in a $2\times 2$ contingency table. A computational implementation of the test is developed and R code is provided to apply the test. To meet the demands of regulatory agencies, a calibration of the Bayesian test is introduced which allows to calibrate the false-positive rate and power. The latter provides a Bayes-frequentist compromise which ensures control over the long-term error rates of the test. Illustrative examples using clinical trial data and simulations show how to use the test in practice. In contrast to existing Bayesian tests for $2\times 2$ tables, calibration of the acceptance threshold for the hypothesis of interest allows to achieve a bound on the false-positive rate and minimum power for a prespecified odds ratio of interest. The novel Bayesian test provides an attractive choice for Bayesian biostatisticians who face the demands of regulatory agencies which usually require formal control over false-positive errors and power under the alternative. As such, it constitutes an easy-to-apply addition to the arsenal of already existing Bayesian tests.

1 Introduction

The analysis of $2\times 2$ contingency tables is among the most widely used statistical methods in medical research [1,2,3,4]. Traditional frequentist methods to test hypotheses in a $2\times 2$ contingency table include Fisher’s exact test and Pearson’s $\chi ^{2}$ test [5, 6], and the research hypothesis of interest is formulated in these tests as independence between rows and columns. The idea behind this approach is that whenever the null hypothesis can be rejected, an association between rows and columns is inferred. The latter can be interpreted as the effect of a treatment or drug given that an appropriate experimental design including randomization has been used [7].

While frequentist tests such as Fisher’s exact test or Pearson’s $\chi ^{2}$ test are well established, recent years have shown an increase in the use of Bayesian hypothesis tests in medical research [8,9,10,11,12,13]. The replication crisis in medical research has been discussed in an abundance of scientific publications [14,15,16] and isolated the reliance of traditional frequentist hypothesis tests on p-values and the concept of statistical significance as one problem contributing to the issue. As a consequence, recent research has brought the advent of various Bayesian counterparts to a broad palette of traditional frequentist hypothesis tests [17, 18].

Bayesian approaches to the analysis of $2\times 2$ contingency tables range back to Lindley [19], Gunel and Dickey [20, 21], see also Albert [22, 23], and various Bayesian hypothesis tests for contingency tables have been developed [24,25,26]. Most of these Bayesian tests are either based on the Bayes factor [20] or on posterior probability of the hypothesis of interest. Although each of the approaches has its merits, one often neglected aspect is that in practical research interest lies in directional testing of hypotheses which deal with the odds ratio. The odds ratio is usually computed alongside traditional frequentist hypothesis tests for $2\times 2$ contingency tables and quantifies the strength of the association between two events. In epidemiology, odds ratios are relevant in case–control and cohort studies [27]. In the context of clinical trials, the odds ratio is relevant in phase II trials which investigate the safety and efficacy of a treatment. There, the binary outcome often corresponds to an adverse reaction to treatment and a comparison between treatment and placebo group is conducted. Alternatively, the binary event of interest can also be the response to a (novel) treatment, death, complete remission, or another quantity of interest.

The majority of existing Bayesian hypothesis tests deals with the hypothesis of row-column independence, in close analogy to Fisher’s exact and Pearson’s $\chi ^{2}$ test. In terms of the odds ratio in a $2\times 2$ contingency table, this equals the test of

$${\text {H}}_{0}{\text {: OR}}= 1 {\text { versus }} {\text {H}}_{1}{\text {: OR}} \ne 1$$

(1)

because ${\text {OR}}=1$ if and only if X and Y are independent. In the above, ${\text {OR}}$ denotes the unknown true odds ratio of interest.

As mentioned in the introduction, we consider directional hypotheses of the form in Eq. (3) in this paper. The odds ratio in a $2\times 2$ contingency table as given in Table 1 is defined as

$${\text {OR}}({\varvec{p}}):=\frac{p_{01}/(1-p_{01})}{p_{11}/(1-p_{11})}=\frac{p_{01}p_{10}}{p_{00}p_{11}},$$

(2)

where ${\varvec{p}}:=(p_{00},p_{01},p_{10},p_{11})$ denotes the vector of success and failure probabilities [28].

When ${\text {H}}_{0}$ is rejected, a frequentist might then infer that the treatment and the event of interest are associated. However, in practice, the test of

$${\text {H}}_{0}{\text {: OR}}\le 1 {\text { versus }} {\text {H}}_{1}{\text {: OR}}>1$$

(3)

would often be more appropriate. When ${\text {H}}_{1}$ holds, the odds of the event of interest (e.g., complete remission, observation of an adverse event) are increased in the treatment group. Importantly, the conclusion can be drawn that the treatment increases the probability for the event of interest (e.g., for complete remission or the observation of an adverse event). The test in (1) requires additional estimation of the odds ratio to infer the same. Even when a point estimate of the odds ratio is provided, no formal test has been conducted as is the case in (3). Statistical inference about the underlying populations of the form to conclude a positive odds ratio is therefore not legitimate when rejecting ${\text {H}}_{0}$ in (1), even if the point estimate shows an effect in the desired direction.

1.1 Outline

In this paper, a novel Bayesian analogue to the frequentist $\chi ^{2}$ test for the odds ratio in $2\times 2$ contingency tables is introduced. In contrast to existing Bayesian tests for $2\times 2$ contingency tables, the focus is on directional hypotheses as given in (3). Furthermore, the developed test is based on a Bayes-frequentist compromise, which allows to calibrate the test’s operating characteristics, such as the false-positive rate and power.

The plan of the paper is as follows: The next section outlines the necessary notation for contingency tables. The section afterward outlines the theory of the Full Bayesian Evidence Test (FBET), which constitutes the decision criterion which is later used for the calibration. The following section then develops the novel Bayesian analogue to the $\chi ^{2}$ test based on a Dirichlet-multinomial model under a joint sampling scheme and based on the theory of the FBET. The subsequent section introduces a calibration of the Bayesian test which allows to calibrate the false-positive rate and power of the test. The latter provides a Bayes-frequentist compromise which ensures control over the long-term error rates and meets the demands of regulatory agencies. Illustrative examples using clinical trial data and simulations follow in the subsequent section and show how to use the test in a practical setting. The last section provides a discussion and concludes the article.

2 Notation

Table 1 shows the structure of a $2\times 2$ contingency table, where it is assumed that the random variable X measures the binary event of interest, for example, occurrence of an adverse event or response to a treatment. Thus, $X=1$ is interpreted as a success, and $X=0$ as a failure. The random variable Y is the treatment indicator where $Y=1$ means the patient has been randomized into the treatment group and $Y=0$ is interpreted as the patient not being randomized into the latter. The status $Y=0$ could be a placebo group or a standard of care group, depending on the context of a clinical trial. The probabilities $p_{00}$ to $p_{11}$ are unknown, but researchers often have a rough idea about the marginal row and column probabilities $M_{y}$ and $M_{x}$. The marginal row probability $M_{Y}$ has a direct connection to the randomization scheme that is applied: if patients are randomized into the groups $Y=0$ and $Y=1$ with equal randomization probabilities, then the marginal row probability $M_{Y}$ takes the value $M_{Y}=0.5$. Likewise, if the randomization scheme is 1/3 for group $Y=0$ and 2/3 for group $Y=1$, the marginal row probability takes the value $M_{Y}=2/3$.

Concerning the marginal column probability $M_{X}$ of success, there is more uncertainty in any estimate. However, as $M_{X}=p_{01}+p_{11}$ and $p_{01}$ constitutes the probability of the event of interest under either a placebo or standard of care treatment, there is at least a credible range of values for $M_{X}$. For example, suppose the response probability to the standard of care treatment is given by $\approx 0.2$. Assuming balanced randomization, $p_{00}+p_{01} \approx 0.5$ holds and as by assumption the success probability under standard of care is $\approx 0.2$, it follows that $p_{01}\approx 0.5 \cdot 0.2 = 0.1$ and $p_{00}\approx 0.5\cdot (1-0.2)=0.4$. As a consequence, substituting $p_{01}\approx 0.1$ in $M_{X}=p_{01}+p_{11}$ then shows that $M_{X}$ ranges from $\approx 0.1$ to $\approx 0.6$, as $p_{11}\le 0.5$ due to the assumption of balanced randomization. These considerations are relevant, in particular, when dealing with a Bayesian power analysis later, because it shows that under suitable assumptions on the success probability under placebo or standard of care (which often is known from the relevant literature) a realistic range of values $M_{X}$ is implied. We elaborate on these points in the section which deals with the calibration of the novel Bayesian analogue to the $\chi ^{2}$ test.

Table 1 A $2\times 2$ contingency table

3 The Full Bayesian Evidence Test (FBET)

In this section, the theory of the Full Bayesian Evidence Test (FBET) is outlined. The FBET was recently proposed by Kelter [29] as a unified theory for Bayesian parameter estimation and hypothesis testing. It generalizes the Full Bayesian Significance Test (FBST) of Pereira and Stern [30,31,32], which recovers frequentist p-values under suitable regularity conditions [33]. Details on the FBST can be found in [32] and [34,35,36].

The FBET measures the statistical evidence in favor or against a hypothesis by means of the Bayesian evidence value. The latter will constitute the decision criterion in the novel Bayesian analogue to the $\chi ^{2}$ test, which is developed in the subsequent section. The Bayesian evidence value is the key ingredient of the Full Bayesian Evidence Test (FBET), which is a generalization of the Full Bayesian Significance Test (FBST). The FBET can be used with any standard parametric statistical model, where $\theta \in \varTheta \subseteq {\mathbb {R}}^{\text {p}}$ is a (possibly vector-valued) parameter of interest, $\varTheta$ denotes the parameter space, $L(\theta | {\varvec{y}})$ is the likelihood and $p(\theta )$ is the density of the prior distribution $P_{\vartheta }$ for the parameter $\theta$, and ${\varvec{y}}\in {\mathcal {Y}}$ denotes the observed sample data, while ${\mathcal {Y}}$ being the sample space.

3.1 Statistical Information and the Bayesian Evidence Interval

A natural measure from a Bayesian perspective to quantify the information in the observed data $Y={\varvec{y}}$ is the Bayesian information function¹ which compares the posterior density and a suitable reference function at a given parameter value $\theta \in \varTheta$:

$$I(\theta ):=\frac{p(\theta | {\varvec{y}})}{r(\theta )}.$$

(4)

If $r(\theta ):\equiv 1$, the information provided by the maximum a posteriori value $\theta _{\text {MAP}}$ is largest. A common choice for the reference function $r(\theta )$ is the prior density $p(\theta )$ [32]. Then, the Bayesian information function quantifies the ratio between posterior and prior density. Importantly, the definition of information as given by $I(\theta )$ can be derived as the probabilistic explication of information from only few very general axioms, see Good [48], and is motivated by connections to information theory [49, 50]. Further information is provided in the Appendix. The Bayesian evidence interval is based on the information function I as follows:

Let $I(\theta ):=p(\theta | {\varvec{y}})/r(\theta )$ be the Bayesian information function for a given reference function $r:\varTheta \rightarrow [0,\infty )$, $\theta \mapsto r(\theta )$. The Bayesian evidence interval ${\text {EI}}_{r}(\nu )$ with reference function $r(\theta )$ to level $\nu$ is defined as

$${\text {EI}}_{r}(\nu ):=\left\{ \theta \in \varTheta \bigg | \frac{p(\theta | {\varvec{y}})}{r(\theta )}\ge \nu \right\}.$$

(5)

Kelter [29] showed that commonly used Bayesian interval estimates are special cases of the EI and that the EI provides an encompassing generalization of various Bayesian interval estimates. For $r(\theta ):=1$ and $\nu :=\nu _{\alpha \%}$, the ${\text {EI}}_{r}(\nu )$ evidence interval recovers the standard Bayesian $\alpha \%$-highest posterior density (HPD) interval as a special case if the posterior distribution is symmetric where $\nu _{\alpha \%}$ is the $\alpha \%$-quantile of the posterior distribution $P_{\vartheta | Y}$.² If the posterior distribution is asymmetric, the ${\text {EI}}_{r}(\nu )$ evidence interval still recovers the standard Bayesian HPD interval as a special case asymptotically for $n\rightarrow \infty$ when $\nu _{\alpha \%}$ is the $\alpha \%$-quantile of the posterior distribution $P_{\vartheta | Y}$.³

3.2 The Bayesian Evidence Value

The Bayesian evidence value incorporates the Bayesian evidence interval and provides a theory which unifies Bayesian hypothesis testing and parameter estimation.

Therefore, denote by ${\text {H}}_{0}:=\varTheta _{0}$ and ${\text {H}}_{1}:=\varTheta \setminus \varTheta _{0}$ a null and alternative hypothesis with $\varTheta _{0} \in \varTheta$. For a given Bayesian evidence interval ${\text {EI}}_{r}(\nu )$ with reference function $r(\theta )$ to level $\nu$, the Bayesian evidence value ${\text {Ev}}_{{\text {EI}}_{r}(\nu )}({\text {H}}_{0})$ for the null hypothesis ${\text {H}}_{0}$ is defined as follows:

$${\text {Ev}}_{{\text {EI}}_{r}(\nu )}({\text {H}}_{0}):=\int _{{\text {EI}}_{r}(\nu ) \cap \varTheta _{0}} p(\theta | {\varvec{y}}){\text {d}}\theta.$$

(6)

The corresponding BEV ${\text {Ev}}_{{\text {EI}}_{r}(\nu )}({\text {H}}_{1})$ for the alternative hypothesis ${\text {H}}_{1}$ is defined as follows:

$${\text {Ev}}_{{\text {EI}}_{r}(\nu )}({\text {H}}_{1}):=\int _{{\text {EI}}_{r}(\nu ) \cap \varTheta _{1}} p(\theta | {\varvec{y}}){\text {d}}\theta.$$

(7)

The evidence value ${\text {Ev}}_{{\text {EI}}_{r}(\nu )}$ is based on the approach to consider a (small) interval hypothesis instead of a point-null hypothesis, which was first proposed by Hodges and Lehmann [52]. It provides a generalization of the Full Bayesian Significance Test (FBST) which champions the e-value as a Bayesian version of frequentist p-values [32]. As shown by [33], e-values asymptotically recover frequentist p-values under Bernstein–von Mises regularity conditions. Kelter [29, Theorem 2] showed recently that the evidence value ${\text {Ev}}_{{\text {EI}}_{r}(\nu )}({\text {H}}_{0})$ includes the e-value of the FBST as a special case. Thus, Bayesian evidence values are, under certain regularity conditions, asymptotically, valid frequentist p-values.⁴

The test based on ${\text {Ev}}_{{\text {EI}}_{r}(\nu )}({\text {H}}_{0})$ is also called the Full Bayesian Evidence Test (FBET) or simply Bayesian evidence test.

The Bayesian evidence value depends on three quantities:

• (1) the choice of the hypothesis ${\text {H}}_{0} \subset \varTheta ,$

• (2) the reference function $r(\theta )$ which is used for calculation of the Bayesian evidence interval ${\text {EI}}_{r}(\nu ),$

• (3) and the evidence threshold $\nu$ that is used for deciding which values are included in the Bayesian evidence interval ${\text {EI}}_{r}(\nu ).$

The decision in favor or against ${\text {H}}_{0}$ is made based on the evidence value ${\text {Ev}}_{{\text {EI}}_{r}(\nu )}({\text {H}}_{0})$: If ${\text {Ev}}_{{\text {EI}}_{r}(\nu )}({\text {H}}_{0})>\lambda$ for a threshold $\lambda \in (0,1]$, then the statistical evidence for ${\text {H}}_{0}$ is considered convincing. Reasonable thresholds are $\lambda =0.90$ or $\lambda =0.95$, while a minimum threshold is given as $\lambda =0.5$.

From a fully Bayesian point of view, the choice of $\lambda$ might be based on the amount of posterior probability which is deemed convincing to accept a hypothesis. Another option is to take a hybrid Bayes-frequentist stance, in which the test is calibrated to attain a required false-positive rate (rejecting ${\text {H}}_{0}$ although it is true) and Bayesian power (which is discussed in detail later in this paper). In brief, calibrating a Bayesian test requires a Monte Carlo simulation to determine the resulting false-positive rate and Bayesian power of the test for specific sample sizes and under assumption of a certain statistical model. An overview is provided in Berry [9], see also Rosner [55] and Kelter [56]. Concerning the FBET, the threshold $\lambda$ can be calibrated to achieve the required frequentist operating characteristics. We will later follow this approach when calibrating the novel Bayesian analogue to the $\chi ^{2}$ test, which is developed in the following section below.

The FBET is implemented in the R package fbst, which is available on CRAN and detailed in [34].

4 The Novel Bayesian Analogue to the Frequentist $\chi ^{2}$ Test

The last section provided a brief introduction to the FBET. In this section, the novel Bayesian analogue to the $\chi ^{2}$ test is developed. First, the underlying Dirichlet-multinomial model is detailed. Then, based on this statistical model, the FBET for the directional hypotheses on the odds ratio in Eq. (3) is developed. We provide an illustrative example of the test before the next section discusses the important aspect of calibration.

4.1 Dirichlet-Multinomial Model

Suppose the data

$${\varvec{y}}:=\begin{pmatrix} y_{11} &{} y_{12} &{} \ldots &{} y_{1C}\\ y_{21} &{} \ldots &{} \ldots &{} \ldots \\ \ldots &{} \ldots &{} \ldots &{} \ldots \\ y_{R1} &{} y_{R2} &{} \ldots &{} y_{RC} \end{pmatrix}$$

are observed, which can be rewritten as the vector ${\varvec{y}}:=(y_{11},\ldots ,y_{RC})$. For the case of the $2\times 2$ contingency table, we have $R=C=2$. We assume that the data random variable Y which realizes as $Y={\varvec{y}}$ follows a multinomial distribution

$$Y \sim {\mathscr {M}}(R\cdot C, {\varvec{p}})$$

(8)

with $R\cdot C$ categories and a probability vector ${\varvec{p}}$ of dimension $R\cdot C$. Thus, ${\varvec{p}}:=(p_{11},\ldots ,p_{RC})$. A Dirichlet distribution is assigned as the prior distribution for ${\varvec{p}}$,

$${\varvec{p}}|{\varvec{\alpha }} \sim {\mathscr {D}}(R \cdot C,{\varvec{\alpha }}),$$

(9)

where ${\varvec{\alpha }}$ is a hyperparameter of the Dirichlet distribution. The parameter $\alpha$ takes the form

$${\varvec{\alpha }}:=\begin{pmatrix} a_{11} &{} a_{12} &{} \ldots &{} a_{1C}\\ a_{21} &{} \ldots &{} \ldots &{} \ldots \\ \ldots &{} \ldots &{} \ldots &{} \ldots \\ a_{R1} &{} a_{R2} &{} \ldots &{} a_{RC} \end{pmatrix}$$

and can be interpreted as the concentration of ${\varvec{p}}$. If the elements $a_{ij}$ for $i=1,\ldots ,R$ and $j=1,\ldots ,C$ have similar and large values, e.g., $a_{ij}=1000$ for all i, j, then the prior distribution is very informative where the probability of any $p_{l}$, $l=1,\ldots ,R\cdot C$ being large would be equal for all $p_{l}$ [57]. In contrast, if all $a_{ij}$ take similar and small values, e.g., $a_{ij}=0.1$ for all i and j, then the resulting distribution ${\varvec{p}}$ would be non-informative, and the resulting ${\varvec{p}}$ will resemble the uniform distribution of dimension $R\cdot P$.

The Dirichlet distribution in (9) is conjugate to the multinomial distribution in (8), and the resulting posterior distribution is again Dirichlet distributed with updated hyperparameter:

$${\varvec{p}}|Y,{\varvec{\alpha }} \sim {\mathscr {D}} \left( R\cdot C, {\varvec{\alpha }}+ {\varvec{y}} \right).$$

(10)

In the case of a $2\times 2$ contingency table, $R=C=2$ in the hyperparameter of the Dirichlet posterior in (10). The concentration parameter is thus updated in each entry depending on how many observations are made in the corresponding category.

4.2 FBET for the Odds Ratio in $2\times 2$ Contingency Tables

Building on the Dirichlet-multinomial model introduced in the previous subsection, the theory of the FBET is now employed to construct a Bayesian analogue to the $\chi ^{2}$ test for directional hypotheses on the odds ratio. Therefore, we make use of the posterior in (10) and suppose that

$${\varvec{p}}^{(1)},\ldots ,{\varvec{p}}^{(M)}$$

constitutes a Monte Carlo sample of the posterior of size M. For each ${\varvec{p}}^{(i)}$, $i=1,\ldots ,M$, we have

$${\varvec{p}}^{(i)}=(p_{11}^{(i)},\ldots ,p_{RC}^{(i)})$$

so each ${\varvec{p}}^{(i)}$ is a vector of size $R\cdot C$ which includes the probabilities for the $R\cdot C$ categories. In the case of the $2\times 2$ contingency table, $R=C=2$, so

$${\varvec{p}}^{(i)}=\left( p_{00}^{(i)},p_{01}^{(i)}, p_{10}^{(i)},p_{11}^{(i)}\right)$$

is a vector for the four categories, compare Table 1. Now, based on the definition of the odds ratio in (2), Monte Carlo theory [58] asserts that for large M the posterior density of the odds ratio ${\text {OR}}({\varvec{p}})$ can be approximated as follows:

$\blacktriangleright$:

Draw M samples ${\varvec{p}}^{(i)}=(p_{00}^{(i)},p_{01}^{(i)},p_{10}^{(i)},p_{11}^{(i)})$.

$\blacktriangleright$:

Compute ${\text {OR}}^{(i)}=\frac{p_{01}^{(i)}p_{10}^{(i)}}{p_{00}^{(i)}p_{11}^{(i)}}$ for $i=1,\ldots ,M$.

$\blacktriangleright$:

Use nonparametric Gaussian kernel density approximation to construct the posterior density

$$p({\text {OR}}({\varvec{p}})|Y,{\varvec{\alpha }}).$$

For large M, the approximation error will be negligible [58] and the novel Bayesian analogue to the $\chi ^{2}$ test can test ${\text {H}}_{0}{\text {: OR}}({\varvec{p}})\le 1$ against ${\text {H}}_{1}{\text {: OR}}({\varvec{p}})> 1$ as follows:

• (A) Fix ${\varvec{\alpha }}$, $R=C=2$, and let ${\varvec{y}}$ be the observed data.

• (B) Compute $p(\text {OR}({\varvec{p}})|Y,{\varvec{\alpha }})$ based on large M, e.g., $M:=10,000$ according to the above procedure.

• (C) Fix $\varTheta :=(0,\infty )$ as the parameter space of the odds ratio $\text {OR}({\varvec{p}})$, fix a reference function $r(\text {OR}({\varvec{p}}))$ and an evidence threshold $\nu$, and compute

  $${\text {Ev}}_{{\text {EI}}_{r}(\nu )}({\text {H}}_{1})$$

  for ${\text {H}}_{1}{\text {: OR}}({\varvec{p}})> 1$.

• (D) Fix a $\lambda \in (0,1)$ and reject ${\text {H}}_{0}$ and accept ${\text {H}}_{1}$, if

  $${\text {Ev}}_{{\text {EI}}_{r}(\nu )}({\text {H}}_{1})> \lambda.$$

  (11)

The above steps (A) to (D) perform the FBET on the odds ratio in a $2\times 2$ contingency table based on the Dirichlet-multinomial posterior in Eq. (10). Three comments are in order: first, the choice of ${\varvec{\alpha }}$ is important as is the case for any prior hyperparameter in a Bayesian analysis. Secondly, the choice of M is relatively unimportant due to standard Monte Carlo theory, and $M:=10,000$ should suffice as the posterior $p(\text {OR}({\varvec{p}})|Y,{\varvec{\alpha }})$ is unidimensional [58]. Thirdly, the choice of reference function $r({\text {OR}}({\varvec{p}}))$ and evidence threshold $\nu$ are important and are considered in detail below. Importantly, there are two default choices which simplify application of the novel Bayesian analogue to the $\chi ^{2}$ test significantly. Lastly, the threshold $\lambda$ is the rejection threshold for ${\text {H}}_{0}$ (or acceptance threshold for ${\text {H}}_{1}$). As a consequence, the calibration of $\lambda$ will become important in the next section, as its selection has immediate impact on the resulting operating characteristics of the Bayesian test. In particular, the false-positive rate under ${\text {H}}_{0}$ and the Bayesian power under ${\text {H}}_{1}$ are influenced by the choice of $\lambda$. Appropriate concepts of Bayesian power are discussed separately in the subsequent section.

From an informal perspective, the steps (A) to (D) produce a single number ${\text {Ev}}_{{\text {EI}}_{r}(\nu )}({\text {H}}_{1})$ which is used to reject ${\text {H}}_{0}$ and accept ${\text {H}}_{1}$ if (11) holds. If ${\text {H}}_{0}$ is rejected, ${\text {OR}}({\varvec{p}})>1$ can be inferred. The conclusion reached is thus that the odds in the treatment group are larger than in the control for the event of interest.

Before turning to an illustrative example, the next two subsections provide default choices for the reference function $r({\text {OR}}({\varvec{p}}))$ and the evidence threshold $\nu$. These default choices simplify the calibration of the Bayesian analogue to the $\chi ^{2}$ test in the next section.

4.3 Choice of the Reference Function

There is a variety of options to select the reference function $r({\text {OR}}({\varvec{p}}))$, and details are provided in [29]. Here, we opt for the most intuitive choice, that is, a flat reference function

$$r({\text {OR}}({\varvec{p}})):=1.$$

(12)

This choice has the benefit that the evidence interval in (5) reduces to

$$\begin{aligned} {\text {EI}}_{r}(\nu ):&=\left\{ {\text {OR}}({\varvec{p}}) \in {\mathbb {R}} \bigg | \frac{p({\text {OR}}({\varvec{p}}) | {\varvec{y}})}{r({\text {OR}}({\varvec{p}}))}\ge \nu \right\} \\&=\left\{ {\text {OR}}({\varvec{p}}) \in {\mathbb {R}} | p({\text {OR}}({\varvec{p}}) | {\varvec{y}}) \ge \nu \right\} . \end{aligned}.$$

The above shows that the evidence interval reduces to a highest posterior density set in terms of the posterior density $p({\text {OR}}({\varvec{p}}) | {\varvec{y}})$ of the odds ratio ${\text {OR}}({\varvec{p}})$. The larger the evidence threshold $\nu$ is chosen, the smaller the resulting highest posterior density set will be. Further options for the reference function are given by the prior density—which amounts to measuring the point-wise Kullback–Leibler divergence between prior and posterior distribution as the information gained through observing data y—and by a density which incorporates historical data similar to a power prior [29]. However, we do not explore these options in detail here, to calibrate the novel Bayesian analogue to the $\chi ^{2}$ test. This is due to the fact that the interpretation of highest posterior density sets will be uncontroversial for most Bayesians. Henceforth, the flat reference function (12) is used. Still, to clarify the relevance of calibrating the test, we provide results and simulations also under a non-flat reference function, where the latter is chosen as an informative Dirichlet density. Details are provided in the examples and simulations.

4.4 Choice of the Evidence Threshold

The choice of the evidence threshold $\nu$ is similarly simple: one option would consist in increasing $\nu =0$ to positive values $\nu >0$ until a desired false-positive control is reached. The latter amounts to interpreting statistical evidence as a certain highest posterior density set to attain a prespecified false-positive control and power. On the other side, this renders the threshold $\lambda$ superfluous in this setting, compare Eq. (11), and therefore, we opt to pick the threshold $\nu =0$ by default. The latter choice implies that the full posterior probability mass of the posterior density $p({\text {OR}}({\varvec{p}}) | {\varvec{y}})$ is interpreted as statistical evidence.

We emphasize that an alternative way to calibrate the $\chi ^{2}$ test is given by fixing a value for $\lambda$, say $\lambda =0.9$, so that $90\%$ of the posterior probability mass are interpreted as convincing enough to accept ${\text {H}}_{1}$. Calibration of the test could then proceed by selecting a $\nu >0$ large enough to that the corresponding false-positive rate and Bayesian power attain their desired thresholds. However, we leave this alternative for future research and select $\nu :=0$ henceforth.

4.5 Illustrative Example: Salt Intake, Stroke, and Cardiovascular Disease

In this section, we provide an illustrative example using real data and show how to apply and interpret the results of the novel Bayesian analogue to the $\chi ^{2}$ test.

4.5.1 The TOHP I and II Trials

The evidence from a variety of sources suggests that diets high in salt are associated with risks to human health. The relationship between salt intake and stroke was investigated by Strazzullo et al. [59], and information from 14 studies was combined in a meta-analysis. The subjects were classified based on the amount of salt in their normal diet and were followed for several years and classified according to whether or not they had developed cardiovascular disease (CVD). A total of 104,933 subjects were studied, and 5161 of them developed CVD. The data from one of the 14 studies published by Cook et al. [60] are shown in Table 2.

Table 2 Long-term effects of dietary sodium reduction on cardiovascular disease outcomes: observational follow-up of the trials of hypertension prevention (TOHP) published by Cook et al. [60]

In TOHP I and TOHP II, 744 and 2382 participants were randomized to a sodium reduction intervention or control. Net sodium reductions in the intervention groups were 44 mmol/24 h and 33 mmol/24 h, respectively. The vital status was obtained for all participants and follow-up information on morbidity was obtained from 2415 (77%), with 200 reporting a cardiovascular event as shown in Table 2.

In this example, due to balanced randomization, the row-column probabilities for the sodium reduction interventions and control are equal to 0.5, so $M_{Y} = 0.5$ in the terms of Table 1.

A traditional Pearson’s $\chi ^{2}$ test yields $\chi _{1}^{2} = 1.5079$ with a p-value of $p=0.2195$, so the null hypothesis of row-column independence cannot be rejected.

For the novel Bayesian analogue to the $\chi ^{2}$ test using the flat reference function, evidence threshold $\nu :=0$ as outlined in the previous section and an non-informative ${\mathscr {D}}(1,1,1,1)$ Dirichlet prior, we arrive at

$${\text {Ev}}_{{\text {EI}}_{r}(\nu )}({\text {H}}_{1})=0.8995,$$

where ${\text {H}}_{1}{\text {: OR}}({\varvec{p}})>1$. On the other hand, the evidence for ${\text {H}}_{0}{\text {: OR}}({\varvec{p}}) \le 1$ results in

$${\text {Ev}}_{{\text {EI}}_{r}(\nu )}({\text {H}}_{0})=0.1005$$

so there is substantial evidence in favor of the alternative hypothesis. The question arises how to pick the threshold $\lambda$ for deciding between ${\text {H}}_{0}$ and ${\text {H}}_{1}$ based on the above data. While a fully Bayesian perspective can proceed with using a subjectively chosen threshold which is deemed convincing (e.g., $\lambda = 0.89$), we follow a hybrid Bayes-frequentist compromise and will determine the threshold $\lambda$ to calibrate the Bayesian test in the next section.

5 Calibration

The last section introduced the Dirichlet-multinomial model and developed the FBET for the odds ratio in $2\times 2$ contingency tables. Together, these considerations present a Bayesian version of a $\chi ^{2}$ test which considers directional hypotheses on the odds ratio as given in Eq. (3).

In this section, we turn to the important task of calibrating the developed Bayesian test.

5.1 Calibration of Frequentist Operating Characteristics

Regulatory agencies usually require (1) control on the false-positive rate under the null and (2) a minimum power under the alternative hypothesis [7, 9]. Bayesian trial design thus in practice faces the challenge of being calibrated to attain certain frequentist operating characteristics such as (1) and (2), compare Berry [9], Rosner [55], and Kelter [56]. The same holds when applying a Bayesian hypothesis test for a primary or secondary trial endpoint [7].

We proceed as follows: next, the distinction between Bayesian and frequentist power is discussed and a suitable definition of Bayesian power for the developed $\chi ^{2}$ test is isolated. Then, the choice of the calibration parameter $\lambda$ is discussed. A calibration procedure is developed which allows to calibrate the Bayesian test in an algorithmic fashion. This simplifies application of the test and provides a selection of $\lambda$ based on a Bayes-frequentist compromise. Henceforth, we assume for simplicity that our test targets a false-positive rate of $\alpha :=0.05$ and a Bayesian power of 0.8. The calibration works, however, for any values of $\alpha$ and $\beta$. The false-positive rate for a Bayesian is defined here as

$$\begin{aligned}&\sup \limits _{{\text {OR}}({\varvec{p}})\in {\text {H}}_{0}}P_{Y}\left( {\text {Ev}}_{{\text {EI}}_{r}(\nu )}({\text {H}}_{1})>\lambda |{\text {OR}}({\varvec{p}})\right) =P_{Y}\left( {\text {Ev}}_{{\text {EI}}_{r}(\nu )}({\text {H}}_{1})>\lambda |{\text {OR}}({\varvec{p}})=1\right) , \end{aligned},$$

(13)

where the equality uses that the probability is largest for ${\text {OR}}({\varvec{p}})=1$. Thus, an upper bound on the false-positive rate is the probability to accept ${\text {H}}_{1}$ when the true odds ratio equals one.

Regarding power, for a frequentist, power is a well-known concept in the Neyman–Pearson theory [61, 62]. In contrast, the concept of Bayesian power for sample size calculations is more ambiguous. A concise overview about Bayesian concepts of power (and sample size calculation) is given by Kunzmann et al. [63] and a monograph-length treatment can be found in Grieve [64]. In this paper, we follow a hybrid Bayes-frequentist position [64] where we are interested in

$\blacktriangleright$:

Strict control of the false-positive rate at a prespecified level $\alpha$, that is, accepting ${\text {H}}_{1}{\text {: OR}}({\varvec{p}})>1$ when ${\text {H}}_{0}{\text {: OR}}({\varvec{p}}) \le 1$ holds and the true odds ratio is smaller or equal to one, compare (13).

$\blacktriangleright$:

A minimum power to accept ${\text {H}}_{1}{\text {: OR}}({\varvec{p}})>1$ for a prespecified odds ratio O larger than one, where it is detailed below how to define Bayesian power precisely.

5.2 Bayesian Power

A fully Bayesian approach to power would be based on the (possibly subjective) prior distribution. In the context of the Bayesian analogue to the $\chi ^{2}$ test for $2\times 2$ contingency tables, a Bayesian power analysis would proceed by simulating $M_{1}$ Dirichlet-distributed probability vectors ${\varvec{p}}^{(1)},\ldots ,{\varvec{p}}^{(M_{1})}$ with a true odds ratio $\text {OR}({\varvec{p}}^{(i)})$ for $i=1,\ldots ,M_{1}$. For each of these $M_{1}$ odds ratios, a Bayesian could then simulate $M_{2}$ datasets $y^{(1)},\ldots ,y^{(M_{2})}$ according to the multinomial model

$$y^{(j)}|p^{(i)} \sim {\mathscr {M}}(R\cdot C, {\varvec{p}}^{(i)})$$

for $j=1,\ldots ,M_{2}$, compare Eq. (8). Based on these $M_{2}$ datasets, we define the Bayesian local power at this odds ratio $\text {OR}({\varvec{p}}^{(i)})$ as follows:

$${\text {BLP}}({\text {OR}}({\varvec{p}}^{(i)}),M_{2}, \lambda ):=\frac{1}{M_{2}}\sum _{i=1}^{M_{2}} {\mathbbm {1}}_{{\text {Ev}}_{{\text {EI}}_{r}(\nu )}^{y^{(j)}}({\text {H}}_{1})>\lambda }.$$

(14)

The idea behind Bayesian local power is that it provides a percentage with which the alternative hypothesis ${\text {H}}_{1}$ is accepted based on the threshold $\lambda$, that is, when the statistical evidence in favor of ${\text {H}}_{1}$ passes the value $\lambda$. Note that ${\mathbbm {1}}_{{\text {Ev}}_{{\text {EI}}_{r}(\nu )}^{y^{(j)}}({\text {H}}_{1})>\lambda }=1$ when ${\text {Ev}}_{{\text {EI}}_{r}(\nu )}^{y^{(j)}}({\text {H}}_{1})>\lambda$ and else ${\mathbbm {1}}_{{\text {Ev}}_{{\text {EI}}_{r}(\nu )}^{y^{(j)}}({\text {H}}_{1})>\lambda }=0$. Furthermore, the superscript $y^{(j)}$ in ${\text {Ev}}_{{\text {EI}}_{r}(\nu )}^{y^{(j)}}({\text {H}}_{1})$ indicates that the evidence value ${\text {Ev}}_{{\text {EI}}_{r}(\nu )}({\text {H}}_{1})$ depends on the dataset $y^{(j)}$, which serves for notational clarity only.

In sum, Bayesian local power provides an estimate of the power to accept ${\text {H}}_{1}$ based on $M_{2}$ simulated datasets if the true odds ratio is equal to ${\text {OR}}({\varvec{p}}^{(i)})$.

A problem with the concept of local power is the dependence on the true odds ratio ${\text {OR}}({\varvec{p}}^{(i)})$. In reality, it is unknown which value the true odds ratio takes, so the uncertainty about this state of nature should be incorporated in the power analysis.⁵ As a consequence, a more natural measure for a Bayesian is given by averaging the Bayesian local power under the $M_{1}$ different odds ratios ${\text {OR}}({\varvec{p}}^{(i)})$ for $i=1,\ldots ,M_{1}$. We define the resulting Bayesian average power as

$$\begin{aligned} {\text {BAP}}(\lambda ,M_{1}, M_{2}):=\frac{1}{M_{1}}\sum _{i=1}^{M_{1}} {\text {BLP}}({\text {OR}}({\varvec{p}}^{(i)}),M_{2},\lambda ).{} & {} \end{aligned}.$$

(15)

The Bayesian average power is the average power to reject ${\text {H}}_{1}$ when the true odds ratio indeed follows the prior distribution. Importantly, ${\text {BAP}}(\lambda ,M_{1}, M_{2})$ depends only on the threshold $\lambda$, and the number of Monte Carlo repetitions $M_{1}$ and $M_{2}$. It does not depend on one specific probability vector ${\varvec{p}}^{(i)}$ like ${\text {BLP}}(\text {OR}({\varvec{p}}^{(i)}),M_{2}, \lambda )$. Importantly, for large $M_{1}$ and $M_{2}$, the dependence reduces to a dependence of ${\text {BAP}}(\lambda ,M_{1}, M_{2})$ on $\lambda$ only because of Monte Carlo theory. Details are provided in the “Appendix.”

From a fully Bayesian perspective, the Bayesian average power seems like a reasonable concept. However, there is substantial uncertainty about the truth of the selected prior distribution in reality, so Bayesian average power is only useful if there are strong reasons to believe in the prior distribution or interpret it as reasonably close to the true parameter-generating process. This holds, even if the prior is only weakly informative.

5.3 Hybrid Bayes-Frequentist Power

A possible solution to the subjectiveness inherent in ${\text {BAP}}(\lambda ,M_{1}, M_{2})$ defined above is to take a hybrid Bayes-frequentist point of view. Such an approach is often taken in Bayesian power analyses and sample size calculations [9, 63, 64], and here we follow this approach and focus on the most relevant question for power analysis in the context of a $2\times 2$ contingency table:

Given a prespecified true odds ratio ${\text {OR}}({\varvec{p}})>1$, how large is the probability to accept ${\text {H}}_{1}{\text {: OR}}({\varvec{p}})>1$ for a specific sample size $n\in {\mathbb {N}}$?

From a different angle, this question can be rephrased as follows:

Which sample size $n\in {\mathbb {N}}$ is required to accept ${\text {H}}_{1}$ with at least $80\%$ probability when the true odds ratio is larger than one?

The answer to these questions can be provided if (1) the Bayesian average power is modified accordingly and (2) two additional assumptions are made.

Regarding (1), Eq. (15) depends on the prior distribution, as $M_{1}$ Dirichlet-distributed probability vectors ${\varvec{p}}^{(1)},\ldots ,{\varvec{p}}^{(M_{1})}$ are generated according to the Dirichlet prior, and results in a vector of true odds ratios ${\text {OR}}({\varvec{p}}^{(1)}),\ldots ,{\text {OR}}({\varvec{p}}^{(M_{1})})$. Based on the Dirichlet-distributed probability vectors ${\varvec{p}}^{(1)},\ldots ,{\varvec{p}}^{(M_{1})}$, $M_{2}$ contingency table datasets are then simulated according to Eq. (8) for each ${\varvec{p}}^{(i)}$, $i=1,\ldots ,M_{1}$ to arrive at Bayesian average power in (15).

In contrast, if an odds ratio ${\text {OR}}({\varvec{p}})>1$ is prespecified as $O\in {\mathbb {R}}_{+}$ for which a minimum power to accept ${\text {H}}_{1}{\text {: OR}}({\varvec{p}})>1$ is desired (e.g., 80%), one only requires a mapping from the prespecified true odds ratio O to the true probabilities ${\varvec{p}}$ according to which table data are generated in (8).

This leads to point (2), because under two additional assumptions such a mapping exists and is bijective. As shown in the Appendix, there is a one-to-one mapping

$$\{p_{11},p_{01},p_{10}\} \mapsto \{O,M_{X},M_{Y}\},$$

(16)

where $M_{X}:=p_{01}+p_{11}$ and $M_{Y}:=p_{10}+p_{11}$ are the true marginal column and row probabilities and $p_{00}$ can be recovered from the remaining three table entries as $p_{00}=1-p_{11}-p_{01}-p_{10}$.

Thus, if the true marginal column and row probabilities $M_{X}$ and $M_{Y}$ are specified together with a true odds ratio $O>1$ (under which at least $80\%$ power is desired), the true probability vector ${\varvec{p}}:=(p_{00},p_{01},p_{10},p_{11})$ can be recovered by inverting the mapping (16). Based on this true probability vector ${\varvec{p}}$, one can then simulate $M_{2}$ datasets according to Eq. (8) and compute the Bayesian local power at this odds ratio O as given in Eq. (14).

The threshold $\lambda$ and sample size $n\in {\mathbb {N}}$ [of the data ${\varvec{y}}$, generated according to (8)] can then be chosen to achieve e.g., $80\%$ power under the alternative.

From a fully Bayesian point of view, the disadvantage of such a hybrid Bayes-frequentist compromise is that the uncertainty about the true odds ratio is ignored. From a frequentist perspective, however, the advantage is that no unrealistic assumptions about the parameter-generating distribution, that is, the prior are incorporated into the power calculations.

It should be stressed that such a power analysis can still be used in conjunction with a highly subjective prior distribution. The prior would then be subjective, but the power analysis would be based on the prespecified minimum odds ratio $O>1$ of interest (and the randomization probability $M_{Y}$ and estimate for $M_{X}$).

A position which places itself between the Bayesian and frequentist arguments is that the above procedure ensures that for a prespecified minimum odds ratio of interest $O>1$, a minimum power can be ensured for a fixed threshold $\lambda$ and sample size $n\in {\mathbb {N}}$. Thus, the two questions formulated at the start of this subsection can be answered.

Henceforth, we use the hybrid Bayes-frequentist position and require that

$${\text {BLP}}(O,M_{2},\lambda )\ge P$$

(17)

for a prespecified odds ratio $O>1$ holds, where P denotes the desired power (e.g., $P=0.80$). The latter depends on (1) the value of $\lambda$ and (2) the sample size $n\in {\mathbb {N}}$ of the observed data ${\varvec{y}}$.⁶

Importantly, the false-positive rate in (13) can be estimated through Bayesian local power, too. This follows easily from the relationship

$${\text {BLP}}(1,M_{2},\lambda )\xrightarrow [M_{2} \rightarrow \infty ] {\text {a.s.}}P_Y({\text {Ev}}_{{\text {EI}}_{r}(\nu )}({\text {H}}_{1})> \lambda |{\text {OR}}({\varvec{p}})=1)$$

which is an immediate consequence of the strong law of large numbers. Thus, for a large enough number $M_{2}$ of Monte Carlo repetitions, the false-positive rate (13) is controlled if

$${\text {BLP}}(1,M_{2},\lambda )\le \alpha$$

(18)

for a prespecified upper bound $\alpha$ on the false-positive rate.

5.4 Calibration Parameters

The above line of thought requires to carefully think about the values of $M_{X}$ and $M_{Y}$, as these are an additional researcher degree of freedom in the hybrid power analysis outlined above. However, if a trial is performed with balanced randomization, it was already mentioned in the introduction that $M_{Y}=0.5$ holds. Thus, whenever a randomized controlled trial is carried out the value of $M_{Y}$ can be specified. For example, if unbalanced randomization is applied one could have $M_{Y}=0.7$ if $70\%$ of the patients are randomized into the treatment group.

The choice of $M_{X}$ is more subtle, as $M_{X}$ is the marginal probability of the event of interest (e.g., occurrence of an adverse event, response to treatment). The latter is the sum of the response probabilities $p_{01}$ in the placebo and $p_{11}$ in the treatment group, and while there might be knowledge on the response probability under placebo, the response to the (novel) treatment is possibly unknown. There are cases where two well-investigated treatments may be compared, but even then there is uncertainty about $M_{X}$. As a consequence, we propose to vary $M_{X}$ and report the resulting power curves of the test for increasing sample size $n\in {\mathbb {N}}$ separately. If, for example, the power for $M_{X}=0.3$ is substantially different from the power for $M_{X}=0.7$ for the same sample size, researchers can then still transparently report either the minimum power (which is the recommended conservative choice) or the assumed power under the value of $M_{X}$ which is backed up by available knowledge (which is a more subjective and liberal choice).

5.5 Calibration Procedure

Based on the above considerations we propose the following calibration procedure: first, the acceptance threshold $\lambda$ is calibrated so that the false-positive rate is controlled at a prespecified level $\alpha$. Secondly, the sample size $n\in {\mathbb {N}}$ under a minimum odds ratio $O>1$ under the alternative ${\text {H}}_{1}$ is calibrated so that Eq. (17) holds.

The calibration of the false-positive rate under ${\text {H}}_{0}$ proceeds as follows:

$\blacktriangleright$:

Fix $O=1$, fix a boundary $\alpha$ on the false-positive rate, fix $M_{Y}$ according to the randomization scheme, and select a credible range of values for $M_{X} \in (0,1)$.

$\blacktriangleright$:

Fix a threshold $\lambda \in (0,1]$ (e.g., $\lambda =0.90$) and a Monte Carlo repetition size $M_{2}$.

$\blacktriangleright$:

Invert the one-to-one mapping (16) to recover ${\varvec{p}}=(p_{00},p_{01},p_{10},p_{11})$ and simulate $M_{2}$ datasets according to

$$y^{(j)}|{\varvec{p}} \sim {\mathscr {M}}(R\cdot C,{\varvec{p}})$$

for $j=1,\ldots ,M_{2}$ for a range of attainable sample sizes $n\in {\mathbb {N}}$, compare the multinomial model in Eq. (8).

$\blacktriangleright$:

Compute the Bayesian local power

$${\text {BLP}}(1,M_{2}, \lambda )$$

at ${\varvec{p}}$, compare Eq. (14).

$\blacktriangleright$:

If ${\text {BLP}}(1,M_{2}, \lambda )>\alpha$ for the range of values of $n\in {\mathbb {N}}$, increase $\lambda$ until (18) holds.

The above procedure calibrates the $\chi ^{2}$ test so that the false-positive rate in (13) is controlled at the nominal level $\alpha$.

Calibration of the power under ${\text {H}}_{1}$ then proceeds similarly:

$\blacktriangleright$:

Fix a minimum odds ratio $O>1$ of interest, fix a boundary P (e.g., $P = 0.80$) for the Bayesian local power under ${\text {H}}_{1}{\text {: OR}}({\varvec{p}})>1$, fix $M_{Y}$ according to the randomization scheme, and select a credible range of values for $M_{X} \in (0,1)$.

$\blacktriangleright$:

Fix the threshold $\lambda$ obtained through the calibration of the false-positive rate of the test.

$\blacktriangleright$:

Invert the one-to-one mapping (16) to recover ${\varvec{p}}=(p_{00},p_{01},p_{10},p_{11})$ and simulate $M_{2}$ datasets according to

$$y^{(j)}|{\varvec{p}} \sim {\mathscr {M}}(R\cdot C,{\varvec{p}})$$

for $j=1,\ldots ,M_{2}$ for a range of attainable sample sizes $n\in {\mathbb {N}}$, compare the multinomial model in Eq. (8).

$\blacktriangleright$:

Compute the Bayesian local power

$${\text {BLP}}({\text {OR}}({\varvec{p}}),M_{2}, \lambda )$$

at ${\varvec{p}}$, compare Eq. (14).

$\blacktriangleright$:

Increase $n\in {\mathbb {N}}$ until ${\text {BLP}}({\text {OR}}({\varvec{p}}),M_{2}, \lambda )>P$ holds, compare (17).

In summary, we propose to calibrate $\lambda$ to control the false-positive rate as specified in (18) under ${\text {H}}_{0}$ in a first step and then proceed identically for a minimum $O>1$ of interest under ${\text {H}}_{1}$ and isolate the required $n\in {\mathbb {N}}$ so that (17) holds. We illustrate this calibration routine in the following subsection.

5.6 Revisiting the Illustrative Example

We revisit the illustrative example on the long-term effect of dietary sodium reduction on cardiovascular disease outcomes, compare Table 2, where we arrived at

$${\text {Ev}}_{{\text {EI}}_{r}(\nu )}({\text {H}}_{1})=0.8995$$

(19)

and the question arose whether this evidence is large enough to accept ${\text {H}}_{1}{\text {: OR}}> 1$. The key question thus boils down to whether it is legible to accept ${\text {H}}_{1}$ based on this magnitude of statistical evidence, given the requirement that a calibrated Bayesian test is warranted. Therefore, we suppose the usual $\alpha :=0.05$ level for false-positive errors and a minimum power of $P:=0.80$ under the alternative, if the odds ratio is at least 3.47. As shown by Chen et al. [66], these odds ratios are equivalent to a small, medium, and large effect size d of Cohen [67].⁷

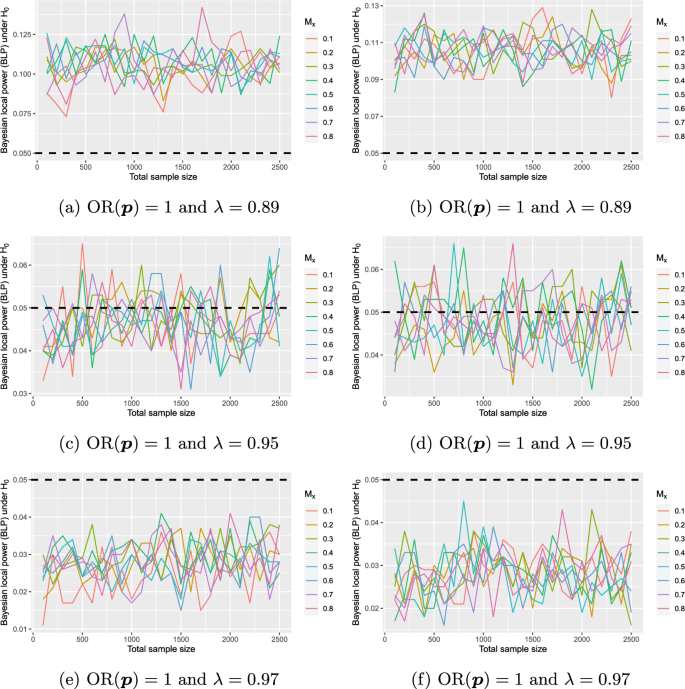
Figure 1a shows the resulting false-positive rate under ${\text {H}}_{0}{\text {: OR}}\le 1$ when the threshold $\lambda =0.89$ is used and the simulation according to the above procedure uses a true odds ratio of one and balanced randomization, so $M_{X}=0.5$. The estimates for $M_{Y}$ vary from 0.1 to 0.8.

A justification to vary $M_{Y}$ in this range is given as follows: note that $p_{11}\le M_{Y}=0.5$ and thus for $M_{X}=0.8$, it could happen that the response $p_{01}$ under placebo or standard of care is 0.3, which is quite large. To see this, note that $p_{01}=0.3$ implies due to balanced randomization $p_{00}=0.2$, and this means that $60\%$ of the patients who get the placebo or standard of care respond to the treatment, which is quite unlikely. For $M_{Y}\ge 0.9$, we could arrive at $p_{11} = 0.4$, which becomes already unrealistic as the corresponding implication is that at least $80\%$ of the patients receiving placebo or standard of care respond to the treatment.

Fig. 1

Bayesian local power (BLP) for true odds ratio of ${\text {OR}}({\varvec{p}})=1$ and varying marginal response probabilities $M_{X}$, for thresholds $\lambda =0.89$ (top), $\lambda =0.95$ (middle), and $\lambda =0.97$ (bottom); dashed black line shows the usual $5\%$ threshold for false positives; left plots show results under a flat reference function $r({\text {OR}}({\varvec{p}}))=1$, right plots show the same results under an informative reference function, chosen as the density of the ${\mathscr {D}}(4,{\varvec{\alpha }})$ distribution with $\alpha _{11}=500$, $\alpha _{12}=200$, $\alpha _{21}=800$, and $\alpha _{22}=100$

Fig. 2

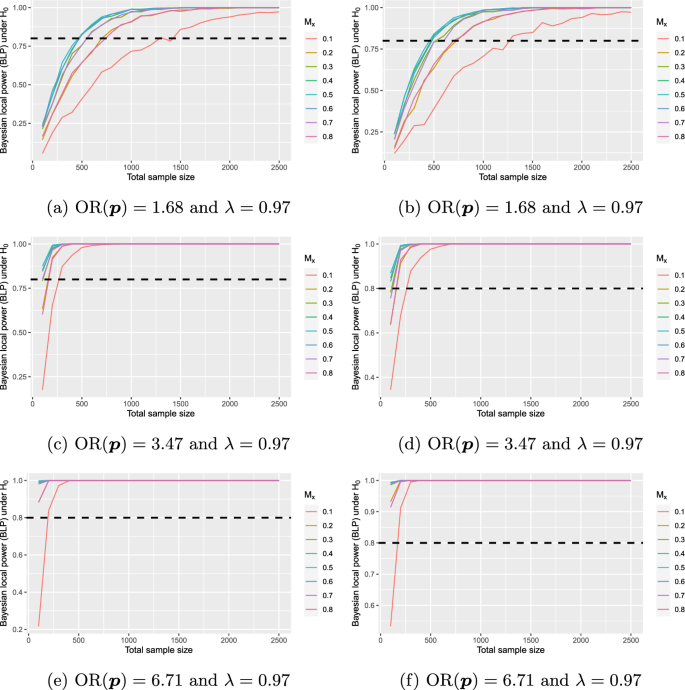
Bayesian local power (BLP) for $\lambda =0.97$ and true odds ratios of ${\text {OR}}({\varvec{p}})=1.68$ (top), ${\text {OR}}({\varvec{p}})=3.47$ (middle), and ${\text {OR}}({\varvec{p}})=6.71$ (bottom) for varying marginal response probabilities $M_{X}$; dashed black line shows the usual $80\%$ threshold for power to reject ${\text {H}}_{0}$; left plots show results under a flat reference function $r({\text {OR}}({\varvec{p}}))=1$; right plots show the same results under an informative reference function, chosen as the density of the ${\mathscr {D}}(4,{\varvec{\alpha }})$ distribution with $\alpha _{11}=500$, $\alpha _{12}=200$, $\alpha _{21}=800$, and $\alpha _{22}=100$

Now, Fig. 1a is based on 1000 simulated datasets under a true odds ratio of one and shows that the false-positive rate is above the usual level of 0.05 for all values of $M_{X}$ and sample sizes in the range of $n=100$ up to $n=2500$ (the trial’s sample size was 2415, compare Table 2). As a consequence, a larger threshold for $\lambda$ is required to decrease the false-positive rate below the desired $5\%$ level.

Figure 1c shows the results for $\lambda =0.95$, and while there is a shift in the resulting false-positive rate, Fig. 1e shows that a further increase of $\lambda$ to $\lambda =0.97$ suffices to attain a false-positive rate which is bounded by 0.05.

Now, Fig. 2 shows the associated Bayesian local power at true odds ratios of $\text {OR}({\varvec{p}})=1.68$, ${\text {OR}}({\varvec{p}})=3.47$, and ${\text {OR}}({\varvec{p}})=6.71$, when the threshold $\lambda = 0.97$ is used.

Figures 1e and 2c show that when $\lambda$ is increased to $\lambda =0.97$, false-positive errors are controlled at the nominal level of 0.05, and the power is sufficient under ${\text {OR}}({\varvec{p}})=3.47$. Still, as

$${\text {Ev}}_{{\text {EI}}_{r}(\nu )}({\text {H}}_{1})=0.8995<0.97$$

one cannot accept ${\text {H}}_{1}$ and reject ${\text {H}}_{0}$ given these requirements.

In summary, the power analysis shows that a calibrated Bayesian analogue to the $\chi ^{2}$ test for the data of Cook et al. [60] must pick a threshold of $\lambda =0.97$ to provide false-positive control and a guaranteed minimum power under ${\text {OR}}({\varvec{p}})=3.47$. As the evidence does not pass this threshold, the calibrated Bayesian analogue to the $\chi ^{2}$ test reaches a similar conclusion that the p-value based $\chi ^{2}$ test of Pearson arrives at the null hypothesis cannot be rejected.

Note, however, that the two tests use entirely different hypotheses: While Pearson’s $\chi ^{2}$ test investigates row-column independence, the novel Bayesian analogue to the $\chi ^{2}$ test compares ${\text {H}}_{0}{\text {: OR}}({\varvec{p}})\le 1$ and ${\text {H}}_{0}{\text {: OR}}({\varvec{p}})> 1$.

Note further that a fully Bayesian perspective may be convinced of the magnitude of evidence and accept ${\text {H}}_{1}$, because long-term error guarantees can be ignored. If this position is sensible in the context of a randomized controlled trial, it is however questionable. Furthermore, regulatory agencies usually require control of these errors [7, 9], and the calibration provides a threshold which ensures that prespecified requirements on the false-positive rate and power are met.

The right plots in Fig. 1 show the same results when shifting to an informative reference function, chosen as the density of the ${\mathscr {D}}(4,{\varvec{\alpha }})$ distribution with $\alpha _{11}=500$, $\alpha _{12}=200$, $\alpha _{21}=800$, and $\alpha _{22}=100$. This can be interpreted as using historical data of a study which yielded the corresponding numbers in a $2\times 2$ contingency table, thus, a study which comprises $500+200+800+100=1600$ individuals. The comparison of Fig. 1a with 1b shows that under the informative reference function the false-positive rate is slightly larger. This phenomenon is, however, not substantial as shown by the comparison of Fig. 1c and d and Fig. 1e and f. However, investigation of the BLP under ${\text {H}}_{1}$ in Fig. 2 shows that in certain settings reaching $80\%$ BLP is achieved a few hundred samples earlier ($M_{X}=0.1$).

Figure 1 also shows that as a rule of thumb, the false-positive rate is approximately given by $1-\lambda$. However, we refrain from recommending this instead of running the calibration algorithm, because, e.g., Fig. 1f shows that the false-positive rate can range up to $\approx 0.045$ in some settings, for quite large sample sizes, which is about $50\%$ excess over the rule-of-thumb false-positive rate $1-\lambda =1-0.97=0.03$.

5.7 Influence of Unbalanced Randomization

A further topic of interest is the robustness of the developed Bayesian analogue to the $\chi ^{2}$ test for $2\times 2$ contingency tables to unbalanced randomization. In general, balanced randomization schemes require the smallest number of patients to reach a required minimum power under the alternative, compare Matthews [7]. A simulation study was carried out to investigate the false-positive rate and power of the developed test under different randomization probabilities.

Fig. 3

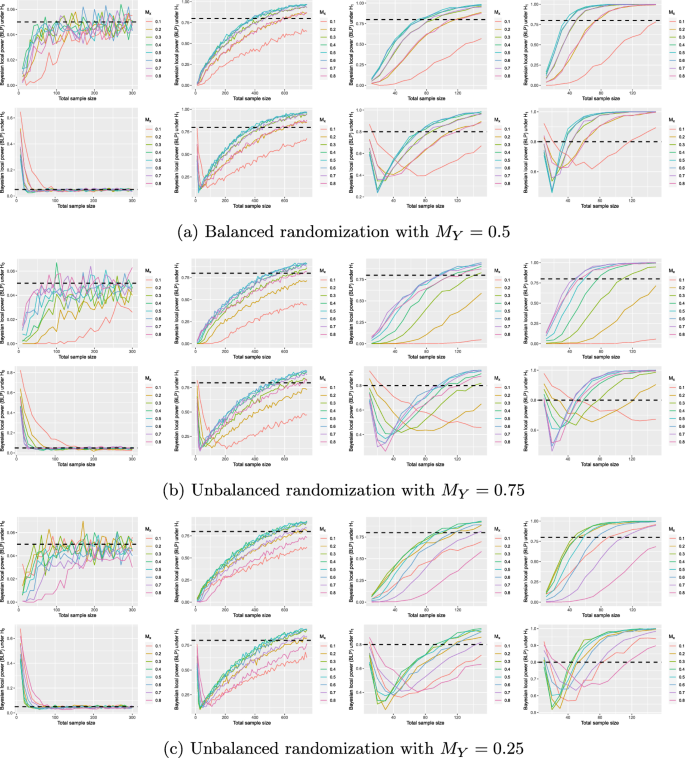
Bayesian local power (BLP) for true odds ratio of ${\text {OR}}({\varvec{p}})=1$, ${\text {OR}}({\varvec{p}})=1.68$, ${\text {OR}}({\varvec{p}})=3.47$, and ${\text {OR}}({\varvec{p}})=6.71$ (left to right plots), varying randomization probability $M_{Y}$ and varying marginal response probabilities $M_{X}$, using $\lambda =0.95$; dashed black line shows the usual $5\%$ threshold for false positives, respectively, $80\%$ threshold for power under ${\text {H}}_{1}{\text {: OR}}({\varvec{p}})>1$; top rows in each panel show results under a flat reference function, bottom rows show the results under an informative reference function, chosen as the density of the ${\mathscr {D}}(4,{\varvec{\alpha }})$ distribution with $\alpha _{11}=500$, $\alpha _{12}=200$, $\alpha _{21}=800$, and $\alpha _{22}=100$

Figure 3 shows the effect of unbalanced randomization when applying the Bayesian $\chi ^{2}$ test. Therefore, $\lambda =0.95$ was fixed, a flat Dirichlet prior ${\mathscr {D}}(1,1,1,1)$ was used and $M_{X}$ was varied between 0.1 and 0.8 for each setting. In the first setting, $M_{Y}=0.5$ is the balanced randomization scenario, shown in Fig. 3a. In the second setting, an unbalanced randomization scheme was applied with $M_{Y}=0.75$, the results of which are shown in Fig. 3b. The third setting involves an unbalanced randomization scheme with $M_{Y}=0.25$ shown in Fig. 3c. All three settings were repeated for an informative informative reference function, chosen as the density of the ${\mathscr {D}}(4,{\varvec{\alpha }})$ distribution with $\alpha _{11}=500$, $\alpha _{12}=200$, $\alpha _{21}=800$, and $\alpha _{22}=100$. Top rows in Fig. 3 thus show results under a flat reference function, and bottom rows show the results under the informative Dirichlet reference function.

First, the left plots in Fig. 3 show that the false-positive rate is slightly decreased when unbalanced randomization probabilities are used, no matter whether the treatment or control group has a larger randomization probability. More importantly, however, the results of the power shown in the second to fourth columns are provided in Fig. 3 (again under the three odds ratios ${\text {OR}}({\varvec{p}})=1$, ${\text {OR}}({\varvec{p}})=1.68$, ${\text {OR}}({\varvec{p}})=3.47$, and ${\text {OR}}({\varvec{p}})=6.71$). For example, when ${\text {OR}}({\varvec{p}})=1.68$, the second column in Fig. 3 shows that when balanced randomization is used with $M_{Y}=0.5$, the desired power of 0.80 is attained for all values of $M_{X}$ except $M_{X}=0.1$ when the sample size reaches $n=600$ participants. In the unbalanced randomization settings in the second and third row, second column, nearly half of the scenarios for $M_{X}$ have not attained the desired power. Thus, the novel Bayesian analogue to the $\chi ^{2}$ test behaves similar to existing tests which reach their largest power under balanced randomization schemes [7]. The same effect can be observed for larger odds ratios, compare the third and fourth columns in Fig. 3.

Comparing the top and bottom rows in Fig. 3, it becomes apparent that the reference function can strongly influence the results. In particular, for small to moderate sample sizes, the false-positive rate is substantially influenced, even under balanced randomization with $M_{Y}=0.5$. This phenomenon worsens under unbalanced randomization even further. The power is also substantially affected, in particular, for sample sizes below $n\approx 200$. Thus, a Monte Carlo analysis to calibrate the test—under balanced or unbalanced randomization—schemes is highly recommended. Figure 3 also shows that when using an informative reference function, the test is less robust to unbalanced randomization than when using a flat reference function.

6 Discussion

We close this paper with a discussion of applying the novel Bayesian analogue to the $\chi ^{2}$ test in clinical versus epidemiological studies, a comparison with existing approaches, and a possible extension to general $R\times C$ contingency tables. Also, we discuss the benefits and limitations of the proposed test and provide a conclusion of the results.

6.1 Comparison with the Frequentist $\chi ^{2}$ Test

The developed Bayesian test is not intended to replace the traditional $\chi ^{2}$ test. The frequentist $\chi ^{2}$ test tests whether the rows and columns in the $2\times 2$ table are independent. If this null hypothesis is rejected, an estimate of the odds ratio may provide insights into how much better, e.g., a novel treatment is compared to the standard of care. In contrast, the developed Bayesian test directly tests a hypothesis of the odds ratio, that is ${\text {H}}_{0}{\text {: OR}} \le 1$ vs. ${\text {H}}_{1}{\text {: OR}} > 1$. Thus, the result of the test immediately provides information about the relevant quantity of interest. Furthermore, an associated Bayesian point estimate (e.g., posterior mean of the odds ratio) can accompany the test result and provide the values of the OR which are most probable after observation of the trial data. The frequentist confidence interval cannot be interpreted in such a way [68, 69], so the only information then is that in 95 out of 100 repetitions of the trial, the true parameter will be located inside the 95% confidence interval. The developed Bayesian test thus focusses on different aspects: the odds ratio and quantification of the uncertainty in terms of posterior probability. Furthermore, it does not make use of asymptotic arguments, such as the $\chi ^{2}$ test’s test statistic distribution. The test is thus a Bayesian alternative to the $\chi ^{2}$ test—with all epistemological benefits and limitations of Bayesian methods [36, 68, 70].

6.2 Clinical Versus Epidemiological Studies

An important aspect to consider is whether the novel Bayesian analogue to the $\chi ^{2}$ test is used in a clinical or an epidemiological study. In a clinical study, it is almost always the case that patients are randomized into treatment and control group(s). In epidemiological cohort studies, a group of patients who are exposed (e.g., to a drug or pollutant or who undergo a certain medical procedure) are compared to a group of nonexposed patients, and no randomization takes place. The same holds for case–control studies which compare a cohort of patients with a particular disease and healthy individuals and search retrospectively for reasons of the disease.

If no randomization takes place, the marginal row probability $M_{Y}$ cannot be fixed to the randomization probability (e.g., $M_{Y} = 0.5$ when balanced randomization is used). For example, suppose the long-term effect of dietary sodium reduction reported by Cook et al. [60] used in the illustrative example above was not studied using randomization of participants into sodium reduction intervention and control. Then, the marginal row probability $M_{Y}$ could only be estimated based on available literature on how many people live on a high. respectively, low-salt diet. Although this is possible and a credible range of values for $M_{Y}$ could be based on estimates published in the relevant literature, there is additional uncertainty compared to when a randomized controlled trial is performed. As a consequence, the calibration of the novel Bayesian analogue to the $\chi ^{2}$ test depends further on the uncertainty about $M_{Y}$ in epidemiological settings. A separate analysis of the Bayesian local power under ${\text {H}}_{0}$ and ${\text {H}}_{1}$ is then required for the different values which are deemed credible for $M_{Y}$.

Future research could also develop a novel model where no joint multinomial sampling is used, but each row in the table is itself multinomial distributed with appropriate sample sizes. This would be an alternative for nonrandomized trials.

6.3 Comparison with Existing Approaches

Compared to existing Bayesian alternatives to the $\chi ^{2}$ tests for contingency tables, the difference of the developed test is the focus on directional hypotheses of the odds ratio as specified in (3). Existing tests such as the ones of Albert [22, 23], Gunel and Dickey [21, 71], Smith [24], Nandram et al. [25], and Goméz-Villegas and Pérez [26] mostly deal with the null hypothesis of row–column independence, respectively, equal probabilities in all groups. Although some of these tests are applicable to general $R\times C$ contingency tables, they do not perform a hypothesis test on the odds ratio which was the approach taken in this paper.

The latter allows for a simple interpretation which is more suitable for inference: if ${\text {H}}_{0}{\text {: OR}}({\varvec{p}})\le 1$ is rejected, the odds ratio between the underlying populations of the trial arms is positive. Also, an important advantage to existing solutions is the calibration of the developed Bayesian test, which guarantees false-positive control at a prespecified level $\alpha$ and a minimum power under a specified odds ratio of interest. The price paid for these properties is that the test is only applicable to $2\times 2$ tables, but see the subsequent section.

Importantly, we close this subsection by noting that directional tests on the table probabilities themselves are possible via the Gunel–Dickey Bayes factors detailed in [20], for an accessible introduction see Jamil et al. [71], but these tests do not deal directly with the odds ratio. Also, there is no calibration available to achieve certain operating characteristics for these Bayes factor tests.

6.4 Extension for $R\times C$ Contingency Tables

The derivation of the Bayesian test was based on a general Dirichlet-multinomial model. Therefore, as the resulting Dirichlet posterior in (10) has dimension $R\times C$, application of the test to general contingency tables is possible. However, there are differences compared to other Bayesian tests such as the Bayes factors reported by Gunel and Dickey [20], because no global test of row–column independence is possible. In this paper, we considered directional hypotheses on the odds ratio as given in (3). An $R\times C$ table where R groups are analyzed with a multinomial variable that has C categories and can be splitted into ${R\atopwithdelims ()2} \cdot {C\atopwithdelims ()2}$ tables of dimension $2\times 2$ [because there are ${R\atopwithdelims ()2}$ combinations of groups which can be drawn without ordering and replacement from the R groups, and there are ${C\atopwithdelims ()2}$ categories which can be drawn without ordering and replacement from the C categories]. For example, for $R=C=3$, there are already 9 subtables each of dimension $2\times 2$. For each of these tables, the Bayesian analogue to the $\chi ^{2}$ test for $2\times 2$ tables can be applied. However, as the latter introduces a multiple testing problem, calibration of the test is inherently more difficult.

Also, it is questionable whether shifting to other measures than the odds ratio is not more appropriate for general $R\times C$ tables. For example, a Bayesian test based on the FBET could handle general $R\times C$ tables when shifting to Cramér’s

$$V:=\sqrt{\frac{\chi ^{2}}{N(k-1)}}$$

or the contingency coefficient

$$C:=\sqrt{\frac{\chi ^{2}}{N+\chi ^{2}}},$$

where N is the total number of observations in the $R\times C$ table and $\chi ^{2}$ is Pearson’s $\chi ^{2}$-statistic. For example, based on the Dirichlet posterior in (9) one could simulate the posterior probabilities ${\varvec{p}}:=(p_{11},\ldots ,p_{RC})$ and then generate M datasets of $R\times C$ tables $Y^{(1)},\ldots ,Y^{(M)}$ according to the multinomial model in (8) conditional on these posterior probabilities. Based on the M contingency table datasets, one would then compute Pearson’s $\chi ^{2}$ statistics $T^{(1)},\ldots ,T^{(M)}$ for each of the M datasets and obtain the posterior predictive distribution of Pearson’s $\chi ^{2}$-statistic based on the Dirichlet-multinomial model. Finally, a distribution of C and V which is based on the Dirichlet posterior in (10) and the posterior predictive of Pearson’s $\chi ^{2}$-statistic is easily obtained. A test analogue to the one on the odds ratio considered for the $2\times 2$ case considered in this paper can then be carried out on Cramér’s V or the contingency coefficient C. Note, however, that the use of the posterior predictive of the $\chi ^{2}$-statistic renders this approach not fully Bayesian, because inference is not based solely on the posterior distribution of C or V itself. Nevertheless, the above method could provide a reasonable Bayes-frequentist compromise which attains attractive operating characteristics, but any further analysis is outside the scope of this paper. Such a posterior predictive based calibrated Bayesian analogue to the $\chi ^{2}$ test for Cramér’s V or the contingency coefficient in general $R\times C$ contingency tables could be a direction for future research.

Appendix

This “Appendix” includes three sections:

• Relationship of the Bayesian evidence value to statistical evidence: here, the relationship of the evidence value to statistical evidence from a Bayesian point of view is outlined.

• Mapping between odds ratio and table probabilities: the mapping to recover table probabilities from odds ratios and marginal column and row probabilities is specified.

• Dependence of Bayesian average power on $\lambda$ for large numbers $M_{1}$ and $M_{2}$ of Monte Carlo repetitions: based on the strong law of large numbers, we show that the dependence of Bayesian average power on the number of Monte Carlo draws vanishes asymptotically.

1.1 Relationship of the Bayesian Evidence Value to Statistical Evidence

The relationship to statistical information was outlined above. Note that the notion of evidence associated with the Bayesian evidence interval ${\text {EI}}_{r}(\nu )$ stems from the relationship to the Bayes factor [72, 73], which constitutes the best explicatum for weight of evidence for a Bayesian according to [44]. Parameter values ${\tilde{\theta }} \in {\text {EI}}_{r}(\nu )$ fulfill the condition $I({\tilde{\theta }})\ge \nu$, which is equivalent to $p({\tilde{\theta }}| y)/r({\tilde{\theta }})\ge \nu$. Whenever the reference function $r(\theta )$ is chosen as the model’s prior distribution $p(\theta )$ for the parameter $\theta$, for the values ${\tilde{\theta }}$ the ratio $p(\theta | y)/p(\theta )$ can be identified as the Savage–Dickey density ratio which is equal to the Bayes factor ${\text {BF}}_{01}$ for the precise null hypothesis ${\text {H}}_{0}{\text {: }}\theta ={\tilde{\theta }}$ when Dickey’s continuity condition holds [74,75,76]. Thus, the evidence for ${\text {H}}_{0}{\text {: }}\theta ={\tilde{\theta }}$ obtained through a traditional Bayes factor hypothesis test is at least $\nu$ for all values inside the Bayesian evidence interval ${\text {EI}}_{r}(\nu )$.

1.2 Mapping Between Odds Ratio and Table Probabilities

In this “Appendix,” we show that the mapping in Eq. (16) is indeed one to one and that based on fixed row and column marginal probabilities $M_{Y}$ and $M_{X}$ and a specified odds ratio O, the original table probabilities $p_{11},p_{01},p_{10}$ and $p_{00}$ can be recovered. It suffices to recover the former three since $p_{00}=1-p_{11}-p_{10}-p_{01}$.

The map

$$\{p_{11},p_{01},p_{10}\} \mapsto \{O,M_{X},M_{Y}\}$$

is straightforward since for each combination of $p_{11},p_{01}$ and $p_{10}$ there exists one triple $\{O,M_{X},M_{Y}\}$ (note that when e.g., $p_{10}$ and $p_{11}$ are swapped, yielding the same $M_{Y}=p_{10}+p_{11}$, the column marginal probability $M_{X}=p_{01}+p_{11}$ changes, yielding a different triple $\{O,M_{X},M_{Y}\}$).

Inverting the map

$$\{p_{11},p_{01},p_{10}\} \mapsto \{O,M_{X},M_{Y}\}$$

is more complicated, and we use that for fixed marginal column and row probabilities $M_{X}$ and $M_{Y}$

$$\begin{aligned} \log ({\text {OR}}({\varvec{p}})&=\log (p_{11})-\log (M_{Y}-p_{11})\\&\quad -\log (M_{X}-p_{11})\\&\quad +\log (-M_{X}-M_{Y}+p_{11}). \end{aligned}.$$

Now, the inequalities

$$\begin{aligned}&p_{01}+p_{10}+p_{11}\le 1\\&\Leftrightarrow p_{01}+p_{11}+p_{10}+p_{11}\le 1+p_{11}\\&\Leftrightarrow M_{X}+M_{Y}\le 1+p_{11}\\&\Leftrightarrow M_{X}+M_{Y}-1\le p_{11}\\ \end{aligned}$$

and

$$p_{11}\le \min (M_{X},M_{Y})$$

together imply that

$$\max (0,M_{X}+M_{Y}-1)\le p_{11}\le \min (M_{X},M_{Y}).$$

Now, inside this range the odds ratio increases monotonically as a function of $p_{11}$ and thus there is unique root of

$$\begin{aligned}&\log (p_{11})-\log (M_{Y}-p_{11})\\&\quad -\log (M_{X}-p_{11})\\&\quad +\log (-M_{X}-M_{Y}+p_{11})-\log (\text {OR}({\varvec{p}}) \end{aligned}$$

as a function of $p_{11}$. Once this root is found, the remaining probabilities $p_{10}=M_{X}-p_{11}$ and $p_{01}=M_{Y}-p_{11}$ can be found based on the fixed values of $M_{X}$ and $M_{Y}$ and $p_{00}$ is recovered from the three probabilities $p_{11}$, $p_{10}$, and $p_{01}$.

1.3 Dependence of Bayesian Average Power on $\lambda$ for Large Numbers $M_{1}$ and $M_{2}$ of Monte Carlo Repetitions

It suffices to note that for increasing $M_{2} \rightarrow \infty$,

$$\underbrace{\frac{1}{M_{2}}\sum _{j=1}^{M_{2}} {\mathbbm {1}}_{{\text {Ev}}_{{\text {EI}}_{r}(\nu )}^{y^{(j)}}({\text {H}}_{1})>\lambda }}_ {=:{\text {BLP}}({\text {OR}}({\varvec{p}}^{(i)}),M_{2},\lambda )}$$

converges against

$$P({\text {Ev}}_{{\text {EI}}_{r}(\nu )}^{y^{(j)}}({\text {H}}_{1})>\lambda |{\text {OR}} ({\varvec{p}})={\text {OR}}({\varvec{p}}^{(i)}))$$

due to the strong law of large numbers. Therefore,

$${\text {BAP}}(\lambda ,M_{1},M_{2}):=\frac{1}{M_{1}}\sum _{i=1}^{M_{1}} {\text {BLP}}({\text {OR}}({\varvec{p}}^{(i)}),M_{2},\lambda )$$

converges almost surely for $M_{1} \rightarrow \infty$ against

$$\frac{1}{M_{1}}\sum _{i=1}^{M_{1}} P({\text {Ev}}_{{\text {EI}}_{r}(\nu )}({\text {H}}_{1})>\lambda |{\text {OR}} ({\varvec{p}}={\text {OR}}({\varvec{p}}^{(i)})),$$

where the latter converges for $M_{1} \rightarrow \infty$ almost surely against

$$\int P({\text {Ev}}_{{\text {EI}}_{r}(\nu )}({\text {H}}_{1})>\lambda | {\text {OR}}({\varvec{p}}={\text {OR}}({\varvec{p}})) {\text {d}}p$$

due to the strong law of large numbers. The above integral is equal to

$$P({\text {Ev}}_{{\text {EI}}_{r}(\nu )}({\text {H}}_{1})>\lambda )$$

which shows that the dependence of Bayesian average power on $M_{1}$ and $M_{2}$ vanishes for large $M_{1}$ and $M_{2}$. The BAP then depends solely on $\lambda$ as shown by the last equation.