Skip to main content
SpringerLink
Log in

Gradient-based Parameter Estimation for a Nonlinear Exponential Autoregressive Time-series Model by Using the Multi-innovation

  • Regular Papers
  • Control Theory and Applications
  • Published:
International Journal of Control, Automation and Systems Aims and scope Submit manuscript

Abstract

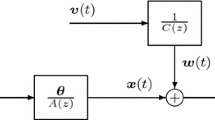
The parameter estimation methods for the nonlinear exponential autoregressive model are investigated in this paper. We develop a forgetting factor gradient parameter estimation algorithm for improving the estimation accuracy. For the purpose of improving the identification accuracy further, a forgetting factor multi-innovation stochastic gradient algorithm is derived by using the multi-innovation theory. The effectiveness of the proposed algorithms is proved by a simulation example.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Y. Ji, C. Zhang, Z. Kang, and T. Yu, “Parameter estimation for block-oriented nonlinear systems using the key term separation,” International Journal of Robust and Nonlinear Control, vol. 30, no. 9, pp. 3727–3752, June 2020.

    Article  MathSciNet  MATH  Google Scholar 

  2. P. Ma and L. Wang, “Filtering-based recursive least squares estimation approaches for multivariate equation-error systems by using the multiinnovation theory,” International Journal of Adaptive Control and Signal Processing, vol. 35, no. 9, pp. 1898–1915, September 2021.

    Article  MathSciNet  Google Scholar 

  3. M. Li and X. Liu, “Particle filtering-based iterative identification methods for a class of nonlinear systems with interval-varying measurements,” International Journal of Control, Automation, and Systems, vol. 20, no. 7, pp. 2239–2248, 2022.

    Article  Google Scholar 

  4. Y. Ji, Z. Kang, and C. Zhang, “Two-stage gradient-based recursive estimation for nonlinear models by using the data filtering,” International Journal of Control, Automation, and Systems, vol. 19, no. 8, pp. 2706–2715, August 2021.

    Article  Google Scholar 

  5. Y. Ji, X. Jiang, and L. Wan, “Hierarchical least squares parameter estimation algorithm for two-input Hammerstein finite impulse response systems,” Journal of the Franklin Institute, vol. 357, no. 8, pp. 5019–5032, May 2020.

    Article  MathSciNet  MATH  Google Scholar 

  6. J. Wang, Y. Ji, and C. Zhang, “Iterative parameter and order identification for fractional-order nonlinear finite impulse response systems using the key term separation,” International Journal of Adaptive Control and Signal Processing, vol. 35, no. 8, pp. 1562–1577, August 2021.

    Article  MathSciNet  Google Scholar 

  7. Y. Ji, Z. Kang, and X. Liu, “The data filtering based multiple-stage Levenberg-Marquardt algorithm for Hammerstein nonlinear systems,” International Journal of Robust and Nonlinear Control, vol. 31, no. 15, pp. 7007–7025, October 2021.

    Article  MathSciNet  Google Scholar 

  8. M. Li and X. Liu, “Maximum likelihood least squares based iterative estimation for a class of bilinear systems using the data filtering technique,” International Journal of Control, Automation, and Systems, vol. 18, no. 6, pp. 1581–1592, June 2020.

    Article  Google Scholar 

  9. M. Li and X. Liu, “Maximum likelihood hierarchical least squares-based iterative identification for dual-rate stochastic systems,” International Journal of Adaptive Control and Signal Processing, vol. 35, no. 2, pp. 240–261, February 2021.

    Article  MathSciNet  Google Scholar 

  10. M. Li and X. Liu, “Iterative identification methods for a class of bilinear systems by using the particle filtering technique,” International Journal of Adaptive Control and Signal Processing, vol. 35, no. 10, pp. 2056–2074, October 2021.

    Article  MathSciNet  Google Scholar 

  11. G. Chen, M. Gan, C. Chen, and H. Li, “A regularized variable projection algorithm for separable nonlinear least-squares problems,” IEEE Transactions on Automatic Control, vol. 64, no. 2, pp. 526–537, February 2019.

    MathSciNet  MATH  Google Scholar 

  12. L. Xu and G. Song, “A recursive parameter estimation algorithm for modeling signals with multi-frequencies,” Circuits Systems and Signal Processing, vol. 39, no. 8, pp. 4198–4224, August 2020.

    Article  MATH  Google Scholar 

  13. L. Xu, “Separable multi-innovation Newton iterative modeling algorithm for multi-frequency signals based on the sliding measurement window,” Circuits Systems and Signal Processing, vol. 41, no. 2, pp. 805–830, February 2022.

    Article  Google Scholar 

  14. Y. Fan and X. Liu, “Two-stage auxiliary model gradient-based iterative algorithm for the input nonlinear controlled autoregressive system with variable-gain nonlinearity,” International Journal of Robust and Nonlinear Control, vol. 30, no. 14, pp. 5492–5509, September 2020.

    Article  MathSciNet  MATH  Google Scholar 

  15. X. Liu and Y. Fan, “Maximum likelihood extended gradient-based estimation algorithms for the input nonlinear controlled autoregressive moving average system with variable-gain nonlinearity,” International Journal of Robust and Nonlinear Control, vol. 31, no. 9, pp. 4017–4036, June 2021.

    Article  MathSciNet  Google Scholar 

  16. T. Ozaki, “Non-linear time series models for non-linear random vibrations,” Journal of Applied Probability, vol. 17, no. 1, pp. 84–93, 1980.

    Article  MathSciNet  MATH  Google Scholar 

  17. S. Dong, T. Liu, and Q. Wang, “Identification of Hammerstein systems with time delay under load disturbance,” IET Control Theory and Applications, vol. 12, no. 7, pp. 942–952, April 2018.

    Article  MathSciNet  Google Scholar 

  18. W. Tang and A. Rollin, “Model identification for ARMA time series through convolutional neural networks,” Decision Support Systems, vol. 146, Article Number: 113544, July 2021.

  19. T. Liu, W. Zhang, L. Ye, M. Ueland, S. Forbes, and S.W. Su, “A novel multi-odour identification by electronic nose using non-parametric modelling-based feature extraction and time-series classification,” Sensors and Actuators B-Chemical, vol. 298, Article Number: 126690, November 2019.

  20. S. Ahmed and F. Kopsaftopoulos, “Stochastic identification of guided wave propagation under ambient temperature via non-stationary time series models,” Sensors, vol. 21, no. 16, Article Number: 5672, January 2021.

  21. D. Jones and D. Cox, “Nonlinear autoregressive processes,” Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences, vol. 360, no. 1700, pp. 71–95, March 1978.

    Article  MathSciNet  MATH  Google Scholar 

  22. T. Ozaki, “Non-linear threshold autoregressive models for non-linear random vibrations,” Journal of Applied Probability, vol. 18, no. 2, pp. 443–451, June 1981.

    Article  MATH  Google Scholar 

  23. M. Al-Qassam and J. Lane, “Forecasting exponential autoregressive models of order 1,” Journal of Time Series Analysis, vol. 10, no. 2, pp. 95–113, March 1989.

    Article  MathSciNet  Google Scholar 

  24. M. Merzougui, H. Dridi, and A. Chadli, “Test for periodicity in restrictive EXPAR models,” Communications in Statistics-Theory and Methods, vol. 45, no. 9, pp. 2770–2783, May 2016.

    Article  MathSciNet  MATH  Google Scholar 

  25. J. Sanchez, J. Torvisco, and M. Arias, “TAC method for fitting exponential autoregressive models and others: Applications in economy and finance,” Mathematics, vol. 9, no. 8, Article Number: 862, January 2021.

  26. T. Ozaki, “The statistical analysis of perturbed limit cycle processes using nonlinear time series models,” Journal of Time Series Analysis, vol. 3, no. 1, pp. 29–41, January 1982.

    Article  MathSciNet  MATH  Google Scholar 

  27. T. Ozaki, “2 Non-linear time series models and dynamical systems,” Handbook of Statistics, vol. 5, no. 5, pp. 25–83, 1985.

    Article  Google Scholar 

  28. K. Chan and H. Tong, “On the use of the deterministic Lyapunov function for the ergodicity of stochastic difference equations,” Advances in Applied Probability, vol. 17, no. 3, pp. 666–678, September 1985.

    Article  MathSciNet  MATH  Google Scholar 

  29. H. Koul and A. Schick, “Efficient estimation in nonlinear autoregressive time series models,” Bernoulli, vol. 3, no. 3, pp. 247–277, September 1997.

    Article  MathSciNet  MATH  Google Scholar 

  30. G. Chen, M. Gan, and G. Chen, “Generalized exponential autoregressive models for nonlinear time series: Stationarity, estimation and applications,” Information Sciences, pp. 46–57, Article Number: 438, April 2018.

  31. F. Ding, H. Ma, J. Pan, and E. F. Yang, “Hierarchical gradient- and least squares-based iterative algorithms for input nonlinear output-error systems using the key term separation,” Journal of the Franklin Institute, vol. 358, no. 9, pp. 5113–5135, June 2021.

    Article  MathSciNet  MATH  Google Scholar 

  32. M. H. Li and X. M. Liu, “The least squares based iterative algorithms for parameter estimation of a bilinear system with autoregressive noise using the data filtering technique,” Signal Processing, vol. 147, pp. 23–34, June 2018.

    Article  Google Scholar 

  33. Y. Ji and Z. Kang, “Model recovery for multi-input signal-output nonlinear systems based on the compressed sensing recovery theory,” Journal of the Franklin Institute, vol. 359, no. 5, pp. 2317–2339, 2022.

    Article  MathSciNet  MATH  Google Scholar 

  34. L. Xu, F. Chen, and T. Hayat, “Hierarchical recursive signal modeling for multi-frequency signals based on discrete measured data,” International Journal of Adaptive Control and Signal Processing, vol. 35, no. 5, pp. 676–693, May 2021.

    Article  MathSciNet  Google Scholar 

  35. J. Chen and Y. Liu, “Modified Kalman filtering based multi-step-length gradient iterative algorithm for ARX models with random missing outputs,” Automatica, vol. 118, Article Number: 109034, August 2020.

  36. J. Chen and C. Chen, “A novel reduced-order algorithm for rational models based on Arnoldi process and Krylov subspace,” Automatica, vol. 129, Article Number: 109663, July 2021.

  37. C. Wei, X. Zhang, and E. Yang, “Overall recursive least squares and overall stochastic gradient algorithms and their convergence for feedback nonlinear controlled autoregressive systems,” International Journal of Robust and Nonlinear Control, vol. 32, no. 9, pp. 5534–5554, 2022.

    Article  MathSciNet  Google Scholar 

  38. J. Pan, X. Jiang, and W. Ding, “A filtering based multi-innovation extended stochastic gradient algorithm for multivariable control systems,” International Journal of Control, Automation, and Systems, vol. 15, no. 3, pp. 1189–1197, June 2017.

    Article  Google Scholar 

  39. H. Ma, J. Pan, and W. Ding, “Partially-coupled least squares based iterative parameter estimation for multivariable output-error-like autoregressive moving average systems,” IET Control Theory and Applications, vol. 13, no. 18, pp. 3040–3051, December 2019.

    Article  MathSciNet  Google Scholar 

  40. L. J. Wan, “Decomposition- and gradient-based iterative identification algorithms for multivariable systems using the multi-innovation theory,” Circuits Systems and Signal Processing, vol. 38, no. 7, pp. 2971–2991, July 2019.

    Article  Google Scholar 

  41. Y. Wang and M. Wu, “Recursive parameter estimation algorithm for multivariate output-error systems,” Journal of the Franklin Institute, vol. 355, no. 12, pp. 5163–5181, August 2018.

    Article  MathSciNet  MATH  Google Scholar 

  42. T. Ozaki and H. Oda, “Non-linear time series model identification by Akaike’s information criterion,” IFAC Proceedings Volumes, vol. 10, no. 12, pp. 83–91, January 1977.

    Article  Google Scholar 

  43. R. Stine, “Non-linear time series: A dynamical system approach,” Journal of the American Statistical Association, vol. 87, no. 419, pp. 903–905, September 1992.

    Article  Google Scholar 

  44. H. Xu, L. Wan, and T. Hayat, “Fitting the exponential autoregressive model through recursive search,” Journal of the Franklin Institute, vol. 356, no. 11, pp. 5801–5818, July 2019.

    Article  MathSciNet  MATH  Google Scholar 

  45. Y. Ji and Z. Kang, “Three-stage forgetting factor stochastic gradient parameter estimation methods for a class of nonlinear systems,” International Journal of Robust and Nonlinear Control, vol. 31, no. 3, pp. 871–987, February 2021.

    Article  MathSciNet  Google Scholar 

  46. L. Xu, “Separable Newton recursive estimation method through system responses based on dynamically discrete measurements with increasing data length,” International Journal of Control, Automation, and Systems, vol. 20, no. 2, pp. 432–443, February 2022.

    Article  Google Scholar 

  47. L. Xu and E. Yang, “Auxiliary model multiinnovation stochastic gradient parameter estimation methods for nonlinear sandwich systems,” International Journal of Robust and Nonlinear Control, vol. 31, no. 1, pp. 148–165, January 2021.

    Article  MathSciNet  Google Scholar 

  48. X. Zhang and E. Yang, “Highly computationally efficient state filter based on the delta operator,” International Journal of Adaptive Control and Signal Processing, vol. 33, no. 6, pp. 875–889, June 2019.

    Article  MathSciNet  MATH  Google Scholar 

  49. X. Zhang and E. Yang, “State estimation for bilinear systems through minimizing the covariance matrix of the state estimation errors,” International Journal of Adaptive Control and Signal Processing, vol. 33, no. 7, pp. 1157–1173, July 2019.

    Article  MathSciNet  MATH  Google Scholar 

  50. L. Xu and E. Yang, “Separable recursive gradient algorithm for dynamical systems based on the impulse response signals,” International Journal of Control, Automation, and Systems, vol. 18, no. 12, pp. 3167–3177, December 2020.

    Article  Google Scholar 

  51. L. Xu and Q. Zhu, “Decomposition strategy-based hierarchical least mean square algorithm for control systems from the impulse responses,” International Journal of Systems Science, vol. 52, no. 9, pp. 1806–1821, 2021.

    Article  MathSciNet  MATH  Google Scholar 

  52. Y. J. Wang, S. H. Tang, and X. B. Gu, “Parameter estimation for nonlinear Volterra systems by using the multiinnovation identification theory and tensor decomposition,” Journal of the Franklin Institute, vol. 359, no. 2, pp. 1782–1802, January 2022.

    Article  MathSciNet  MATH  Google Scholar 

  53. Y. J. Wang, and L. Yang, “An efficient recursive identification algorithm for multilinear systems based on tensor decomposition,” International Journal of Robust and Nonlinear Control, vol. 31, no. 16, pp. 7920–7936, November 2021.

    Article  MathSciNet  Google Scholar 

  54. X. Zhang, “Optimal adaptive filtering algorithm by using the fractional-order derivative,” IEEE Signal Processing Letters, vol. 29, pp. 399–403, 2022.

    Article  Google Scholar 

  55. J. Hou, F. Chen, and Z. Zhu, “Gray-box parsimonious subspace identification of Hammerstein-type systems,” IEEE Transactions on Industrial Electronics, vol. 68, no. 10, pp. 9941–9951, October 2021.

    Article  Google Scholar 

  56. N. Zhao, A. Wu, Y. Pei, and D. Niyato, “Spatial-temporal aggregation graph convolution network for efficient mobile cellular traffic prediction,” IEEE Communications Letters, vol. 26, no. 3, pp. 587–591, 2022.

    Article  Google Scholar 

  57. Y. Chen, C. Zhang, C. Liu, Y. Wang, and X. Wan, “Atrial fibrillation detection using feedforward neural network,” Journal of Medical and Biological Engineering, vol. 42, pp. 63–73, 2022.

    Article  Google Scholar 

  58. Y. Zhou, “Partially-coupled nonlinear parameter optimization algorithm for a class of multivariate hybrid models,” Applied Mathematics and Computation, vol. 414, p. 126663, Februray 2022.

    Article  MathSciNet  MATH  Google Scholar 

  59. S. Su, T. Tang, J. Xun, F. Cao, and Y. Wang, “Design of running grades for energy-efficient train regulation: A case study for Beijing Yizhuang line,” IEEE Intelligent Transportation Systems Magazine, vol. 13, no. 2, pp. 189–200, February 2021.

    Article  Google Scholar 

  60. Y. Cao, Z. Wang, and G. Xie, “Bio-inspired speed curve optimization and sliding mode tracking control for subway trains,” IEEE Transactions on Vehicular Technology, vol. 68, no. 7, pp. 6331–6342, July 2019.

    Article  Google Scholar 

  61. Y. Cao, Y. Sun, and T. Wen, “Fault diagnosis of train plug door based on a hybrid criterion for IMFs selection and fractional wavelet package energy entropy,” IEEE Transactions on Vehicular Technology, vol. 68, no. 8, pp. 7544–7551, August 2019.

    Article  Google Scholar 

  62. Y. Cao, L. Ma, S. Xiao, and W. Xu, “Standard analysis for transfer delay in CTCS-3,” Chinese Journal of Electronics, vol. 26, no. 5, pp. 1057–1063, September 2017.

    Article  Google Scholar 

  63. Y. Cao, J. Wen, and L. Ma, “Tracking and collision avoidance of virtual coupling train control system,” Alexandria Engineering Journal, vol. 60, no. 2, pp. 2115–2125, April 2021.

    Article  Google Scholar 

  64. S. Su, X. Wang, Y. Cao, and J. Yin, “An energy-efficient train operation approach by integrating the metro timetabling and eco-driving,” IEEE Transactions on Intelligent Transportation Systems, vol. 21, no. 10, pp. 4252–4268, October 2020.

    Article  Google Scholar 

  65. Y. H. Zhou and X. Zhang, “Hierarchical estimation approach for RBF-AR models with regression weights based on the increasing data length,” IEEE Transactions on Circuits and Systems-II: Express Briefs, vol. 68, no, 12, pp. 3597–3601, December 2021.

    Article  Google Scholar 

  66. Z. Kang, Y. Ji, and X. Liu, “Hierarchical recursive least squares algorithms for Hammerstein nonlinear autoregressive output-error systems,” International Journal of Adaptive Control and Signal Processing, vol. 35, no. 11, pp. 2276–2295, November 2021.

    Article  Google Scholar 

  67. Y. Zhou, “Modeling nonlinear processes using the radial basis function-based state-dependent autoregressive models,” IEEE Signal Processing Letters, vol. 27, pp. 1600–1604, 2020.

    Article  Google Scholar 

  68. J. Ding and W. Zhang, “Finite-time adaptive control for nonlinear systems with uncertain parameters based on the command filters,” International Journal of Adaptive Control and Signal Processing, vol. 35, no. 9, pp. 1754–1767, September 2021.

    Article  MathSciNet  Google Scholar 

  69. X. Wang, “Modified particle filtering-based robust estimation for a networked control system corrupted by impulsive noise,” International Journal of Robust and Nonlinear Control, vol. 32, no. 2, pp. 830–850, January 2022.

    Article  MathSciNet  Google Scholar 

  70. J. Pan, W. Li, and H. Zhang, “Control algorithms of magnetic suspension systems based on the improved double exponential reaching law of sliding mode control,” International Journal of Control, Automation, and Systems, vol. 16, no. 6, pp. 2878–2887, December 2018.

    Article  Google Scholar 

  71. X. Zhang, “Hierarchical parameter and state estimation for bilinear systems,” International Journal of Systems Science, vol. 51, no. 2, pp. 275–290, 2020.

    Article  MathSciNet  MATH  Google Scholar 

  72. Y. Cao, Y. K. Sun, and P. Li, “A sound-based fault diagnosis method for railway point machines based on two-stage feature selection strategy and ensemble classifier,” IEEE Transactions on Intelligent Transportation Systems, vol. 23, no. 8, pp. 12074–12083, 2022.

    Article  Google Scholar 

  73. Y. Cao, J. K. Wen, and T. Wen, “Parameter-varying artificial potential field control of virtual coupling system with nonlinear dynamics,” Fractals, vol. 30, no. 2, 2240099, 2022.

    Article  MathSciNet  MATH  Google Scholar 

  74. S. Su, J. F. She, and Y. Zhou, “A nonlinear safety equilibrium spacing based model predictive control for virtually coupled train set over gradient terrains,” IEEE Transactions on Transportation Electrification, vol. 8, no. 2, pp. 2810–2824, 2022.

    Article  Google Scholar 

  75. J. M. Li, “A novel nonlinear optimization method for fitting a noisy Gaussian activation function,” International Journal of Adaptive Control and Signal Processing, vol. 36, no. 3, pp. 690–707, 2022.

    Article  Google Scholar 

  76. Y. An, Y. J. Zhang, W. J. Cao, and Z. Q. He, “A lightweight and practical anonymous authentication protocol based on bit-self-test PUF,” Electronics, vol. 11, no. 5, 772, 2022.

    Article  Google Scholar 

  77. J. Wang, C. Ding, M. Wu, Y. Liu, and G. Chen, “Lightweight multiple scale-patch dehazing network for real-world hazy image,” KSII Transactions on Internet and Information Systems, vol. 15, no. 12, pp. 4420–4438, December 2022.

    Google Scholar 

  78. M. Li and X. Liu, “The filtering-based maximum likelihood iterative estimation algorithms for a special class of nonlinear systems with autoregressive moving average noise using the hierarchical identification principle,” International Journal of Adaptive Control and Signal Processing, vol. 33, no. 7, pp. 1189–1211, 2019.

    Article  MathSciNet  MATH  Google Scholar 

  79. C. Zhang, H. Liu, and Y. Ji, “Gradient parameter estimation of a class of nonlinear systems based on the maximum likelihood principle,” International Journal of Control, Automation, and Systems, vol. 20, no. 5, pp. 1393–1404, 2022.

    Article  Google Scholar 

  80. T. Cui, “Moving data window-based partially-coupled estimation approach for modeling a dynamical system involving unmeasurable states,” ISA Transactions, vol. 128, Part B, pp. 437–452, 2022.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Electrical and Electronic Engineering, Hubei University of Technology, Wuhan, 430068, China

    Jian Pan, Yuqing Liu & Jun Shu

Authors
  1. Jian Pan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yuqing Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jun Shu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jian Pan.

Additional information

Jian Pan was born in Wuhan, China. He received his B.Sc. degree from Hubei University of Technology, Wuhan, China in 1984. He has been a Professor in the School of Electrical and Electronic Engineering, Hubei University of Technology. His research interests include control science and engineering, computer control systems, and power electronics.

Yuqing Liu was born in Xiangtan, Hunan Province, China. She received her B.Sc. degree from the Hunan Institute of Science and Technology (Yueyang, China) in 2019. She is now a master student at the Huibei University of Technology, Wuhan, China. Her research interests include nonlinear system identification and control theory.

Jun Shu was born in Wuhan, China. He received his B.Sc. degree in 2009 and an M.Sc. degree from Hubei University of Technology, Wuhan, China. He has been an Associate Professor at Hubei University of Technology. His research interests include intelligent control and process control.

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This work was supported by the National Natural Science Foundation of China (No. 61571182, 61273192).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Pan, J., Liu, Y. & Shu, J. Gradient-based Parameter Estimation for a Nonlinear Exponential Autoregressive Time-series Model by Using the Multi-innovation. Int. J. Control Autom. Syst. 21, 140–150 (2023). https://doi.org/10.1007/s12555-021-1018-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12555-021-1018-8

Keywords

Search

Navigation