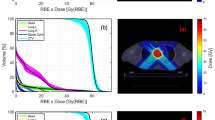
Abstract
Background
Due to the advantageous depth dose profile of carbon ion beams, carbon ion therapy is commonly applied in the form of intensity modulated particle therapy (IMPT) with few treatment fields. Carbon ion arc therapy (C-Arc) has recently been proposed to improve dose conformity and increase the dose-averaged linear energy transfer (LETd) inside the target to levels relevant for overcoming tumor radioresistance. In this work, we investigate different energy selection approaches for C-Arc, including a novel greedy energy layer refinement strategy.
Methods
Robust biologically optimized C-Arc plans were generated for six head &neck cancer patient previously treated at the Shanghai Proton and Heavy Ion Center (SPHIC). Different heuristic approaches for mono- and dual-energy C-Arc were implemented, and compared to carbon IMPT pans. A novel greedy energy layer refinement was developed, acting directly on the dose influence matrix, rather than on an iterative plan optimization. A key challenge in C-Arc with few energy layers per angle is the sharpness of the carbon ion Bragg peak, which is challenging for plan robustness. To improve robustness and plan quality, we propose the use of a 6 mm ripple filter instead of the typical 3 mm ripple filter used for carbon IMPT.
Results
Most mono-energetic C-Arc plans were able to meet the established clinical goals, but some of the heuristic energy selection schemes were not universally applicable with low plan quality in some patients. The developed energy layer refinement strategy delivered high quality plans even for complex cases. Mono-energetic C-Arc plans presented an average increase between 10% and 33% in the maximum LETd in the target, with similar or up to 19% improved average target LETd\(_{50\%}\) compared to the IMPT carbon ion plans. C-Arc plans with 2 energies per treatment angle, for the employed energy selection heuristic, improved dosimetric quality compared to mono-energetic C-Arc plans, but did not provide the same natural improvement in LETd compared to IMPT.
Conclusions
For small, centrally located targets C-Arc demonstrates the greatest potential, but feasible plans could also be achieved for more complex cases in this work. Further development is necessary for improving C-Arc delivery efficiency and plan quality toward possible clinical application.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
For many years, the ability of particle therapy to produce highly conformal target doses with just few treatment fields has been pointed out as a key advantage over conventional photon therapy [1]. This approach, denoted intensity modulated particle therapy (IMPT), is currently the most common practice among particle therapy treatment centres [2]. Following the development of spot-scanning proton arc plan optimization [3], interest has grown also in particle arc therapy as means to further reduce mean healthy tissue dose, mitigate range uncertainties and focus the high dose-averaged linear energy transfer (LETd) inside the tumor [4, 5]. Regions of high LET outside the target have been associated with adverse effects [6], such that particle arc therapy could lead to better patient outcomes. A recent treatment planning study comparing the normal tissue control probability between photon volumetric modulated arc therapy, intensity modulated proton therapy, and proton arc therapy found that proton arc therapy can reduce toxicity for patients suffering from oropharyngeal cancer [7].
Most studies so far have focused on proton arc therapy due to the more wide-spread availability of proton therapy (119 centres) and proton gantries compared to heavy ion therapy (14 centres) and gantries (4) [2]. A first demonstration of proton arc delivery with continuous gantry rotation was achieved by Li et al. [8]. They observed a reduced treatment delivery time for proton arc compared to proton IMPT. Since then, several works have focused on the further improvement of plan quality and treatment delivery efficiency by means of a smart selection of energy layers for each angular control point. A key objective is to reduce the overall number of energy changes in the treatment plan delivery to keep delays associated with energy layer switching to a minimum. Aside from direct heuristic approaches [5], iterative optimizations [3, 9], and more sophisticated approaches, including the energy layer switching directly into the plan optimization cost function, have been proposed [10, 11]. Recently, high quality, robustly optimized proton arc plans, with delivery times in the order of a minute at modern proton beam lines were achieved [12]. Fast proton arc delivery may also be achieved without a gantry, using static arc devices, such as proposed by Nesteruk et al. [13].
Compared to protons, heavy ion beams feature a higher LET and biological effectiveness [14]. Heavy ion arcs therefore have the potential for highly increased LETd inside the target reaching levels relevant for overcoming hypoxia-induced tumor radioresistance [15, 16]. To further exploit this feature, even multi-ion arc strategies have been proposed [17]. Since heavy ion therapy is currently exclusively available at synchrotron facilities, energy changes during the arc delivery are even more of an efficiency hurdle than for proton arc therapy. Due to the synchrotron spill structure with alternating extraction and acceleration phases, each of few seconds duration, any energy change is associated with considerable delay. This necessitates the use of only one or two energy layers per angular control point. In order to make most use of the spill and to enable gantry/patient rotation during the beam delivery, the energy would ideally also remain constant over a range of adjacent arc angular control points. Energy layer optimization, as used for proton arc therapy, [3, 10, 11] addresses these challenges at the treatment planning stage. However, the necessity to consider the variable radiobiological effectiveness (RBE) for heavy ion plan optimization makes including a large number of energy layers for each arc angle in a direct or iterative optimization strategy computationally expensive or even impractical in some cases. More straightforward, heuristic energy selection approaches have thus been applied in previous works [15, 16], following the mono-energetic proton arc strategy presented by Bertolet and Carabe [5].
At the same time, robust optimization is a must for particle therapy in general [18,19,20,21], and heavy ion arc therapy in particular. Due to range uncertainties and the variable RBE, dose errors cannot be avoided by simply introducing margins to the target, as is the case in photon therapy. Rather, already at the optimization stage, the possible uncertainties need to be accounted for to ensure an acceptable dose coverage. For heavy ion arc, the expected high LETd gradients inside the target could pose a challenge for robustness, such that this needs to be carefully considered.
The purpose of this work was to expand on previous literature by exploring carbon ion arc therapy (C-Arc) optimization schemes for a cohort of head &neck patients treated at the Shanghai Proton and Heavy Ion Center (SPHIC). Different heuristic energy selection schemes for C-Arc were compared, as well as a novel greedy energy layer refinement algorithm that acts on the dose influence matrix directly. Further, the use of a broader ripple filter setup compared to the common clinical setup was investigated as means to improve C-Arc treatment planning.
2 Methods
2.1 Patient data
The patient cohort featured one nasopharyngeal carcinoma (NPC) case, three recurrent NPC (R-NPC) cases, one glioblastoma (GBM) case, and one chordoma (Chor) case. These patients were treated at SPHIC with protons, carbon ions or a combined treatment of both modalities [22,23,24]. The patient specifications, as well as the clinically applied treatment fields, are indicated in Table 1. The target volumes ranged between 27 cm\(^3\) and 365 cm\(^3\). The patients represented geometrically complex scenarios, which posed challenges for the arc optimization.
2.2 Treatment planning
Treatment plans were generated using the TRiP98 [25, 26] treatment planning software, that was originally developed for the pilot carbon ion therapy project at GSI and has since then been extensively extended and experimentally validated toward robust and 4D optimized dose calculations [27,28,29,30]. In this work, a new framework for spot-scanning particle arc therapy was added to TRiP98. It was extensively expanded to enable generating robust, biologically optimized C-Arc plans for single or even multiple target lesions, considering different energy layer selection strategies for mono- or multi-energy C-arc plans, as explained in Section 3.2. In detail, the framework performs the setup of control points including ray-tracing for energy selection, setup of robust scenarios, and spot-reduction strategies. For the heuristic mono-energetic C-arcs, plan optimization, including the setup of arc control points with robust scenarios and dose-influence matrix calculation, took \(\sim\)10 minutes for P1 (smallest target) and \(\sim\)35 minutes for P3 (largest target) when running on a Linux server with 40 parallel threads.
2.2.1 Carbon ion beam base data
As carbon ion beam base data underlying the plan optimization, we used the beam characteristics of the Shanghai Proton and Heavy Ion Therapy Center (SPHIC; Shanghai, China). Aside from the typical 3 mm ripple filter (RiFi) used at most contemporary carbon ion therapy facilities to broaden the carbon Bragg peak, a 6 mm RiFi setup is available at SPHIC. This broader RiFi setup is used for larger targets in order to enable wider steps between iso-energy layers, and speed up the irradiation. Depth-dose profiles for a central beam energy with the 6 mm and 3 mm RiFi are shown in Fig. 1. A broader RiFi typically also reduces the dose conformity for IMPT plans. However, this may not be the case for C-Arc, where the beam is aimed at the center of the target, as the conformity in this case is not dominated by the distal dose fall-off. To determine the impact of the RiFi setup on C-Arc plan quality, a comparison for C-Arc plans with a 3 mm and 6 mm RiFi is provided.
2.2.2 Heuristic energy selection
Heuristic a-priori energy selection strategies for piece-wise mono-energetic C-Arc plans were investigated similar as proposed for proton arc [5]. During the field setup, the target voxels’ water equivalent depth (WED) was determined via ray tracing. This yielded a band of possible carbon ion ranges from which the beam energy was chosen (see Fig. 2). For example, one may select the energy such that the beam range always corresponds to the center of the target (cWED), defined as the geometric mid point between the minimum and maximum WED. A possibly more sophisticated approach is to select the energy such that the beam range corresponds to the WED of the maximum number of target voxels (peak, pWED), or to the mean WED over all target voxels (mWED).
While above schemes fulfill the requirement that only a single energy is used per beam arc control point, they still result in a large number of energy changes between adjacent fields. Exploiting that much fewer particles are delivered per arc control point than available from a single synchrotron spill, irradiating multiple control points in a single spill may be possible if these are assigned the same energy. In the study by Bertolet et al. on proton arc, the longest mono-energetic arc segments for which the beam range was still within \(\pm 5\,\%\) of the central tumor WED were selected. Similar to Bertolet et al. we investigated sticking to the same energy as long as the range is not further than 5% from the central WED of the target (lWED).
In addition to the mono-energetic approaches, a dual-energy setup, i.e., with 2 energies per angular control point was investigated. The first energy was set the same as the lWED, the second energy was chosen as the midpoint between the central and maximum WED. The rationale behind this approach was to provide good coverage also in case of partial arc scenarios. To reduce the amount of energy changes, the higher energy was also kept the same between adjacent angular control points if the deviation from the midpoint between central and maximum WED was not exceeding 5%.
2.2.3 Energy layer refinement
A novel a-piori energy layer re-optimization was introduced in the TRiP98 treatment planning platform, which was based on the a-priori estimated target coverage provided by a candidate energy set. First, the cWED beam energy selection strategy outlined above was used to select an initial sequence of energies. Then, the dose influence matrix \(D_{i,j}\) for this initial set of energies was computed, and the target coverage was evaluated by calculating the sum over the contribution of all pencil beams (\(N_{PB}\)) to each voxel \(v_i,\, i\in N_{voxel}\)
Voxels with low \(d_i\) compared to the mean and/or a strongly varying \(d_i\) in the target already indicate a low final plan optimization quality. Hence, we chose the variance of \(d_i\) and the minimum of \(d_i\) over all voxels as measure of the dose coverage. A greedy algorithm was implemented, which assigned each arc angular control point the same energy as one of its direct neighboring control points, if that reduced the variance of \(d_i\), while keeping or increasing the minimum of \(d_i\). This only requires to recalculate the dose influence matrix for the contribution of the specific angle. While a full iterative plan optimization would be a more complete measure of the quality of a candidate set [9], this would also be more time consuming for carbon ion therapy.
The algorithm circled 10 times over all angular control points. By design, this resulted in mono-energetic arc segments, similar to the lWED approach, with the advantage that the choice of segments already includes information about the achievable target coverage. This approach was denoted optWED. An example result for P1 can be seen in Fig. 2 as the green line.
2.2.4 Treatment planning and evaluation parameters
For C-Arc, patients were assumed to be placed supine with a 90\(^\circ\) couch position with a gantry moving around the patient. This setup is equivalent to positioning the patient in a seated position with straight back, and rotating them in front of a fixed horizontal beam, as would be the case for arc therapy on the chair positioning system at SPHIC [31]. The prescription dose was set to 3 Gy(RBE) for all patients. It is important to note that this differs from the original plans delivered for these patients. Some patients received boost doses, or were planned for proton instead of carbon, which made it impractical to follow the original prescription. Full arcs were considered, comprising 180 angular control points spaced at 2\(^\circ\). The lateral spot spacing was set to 2 mm. During the control point setup, spot positions outside a small margin around the target contour were disregarded. The RBE-weighted dose was computed using the local effect model (LEM I) [32]. A global \(\alpha /\beta\) ratio of 2 Gy was assumed. A minimum particle number of 15800 particles per beam spot was enforced. Robust optimization with a voxel-wise worst-case scenario approach with 9 scenarios [20, 21] was performed. The position uncertainty was set to 2 mm and the range uncertainty to 1.7 mm, assuming the availability of dual-energy X-ray CTs [33]. With the idea of carbon arc being to increase LETd in the target, dose homogeneity may no longer be important to judge plan quality, and permitting overdose can aid in LETd improvement [34]. We factored in the maximum dose to the target with a relatively low weight (20% to 50% of the target dose weight) to control overdose and keep the plan comparable to the reference carbon IMPT. The brainstem, optical nerves and the chiasm were considered organs at risk (OARs) during the optimization. In addition, we used an isotropic extension of the target (between 1 mm and 10 mm distance) as additional low-weighted avoidance volume to improve the dose fall-off.
All generated treatment plans were evaluated based on dose coverage measures in the target (D95%), as well as the homogeneity index (HI) computed as
and conformity number here computed as [35]:
For the brainstem, as a relevant OAR close to the target for all patients, the maximum dose (here calculated as D1%) is reported. In addition, the LETd distribution was computed for all plans, and LETd-volume histograms were evaluated. In particular, for the target, the median LETd, LETd50%, and maximum LETd, LETd1%, are reported. For Brain and brainstem, the maximum LETd, LETd1%, is reported.
For all metrics, a Wilcoxon signed-rank test was performed. Statistical significance was assumed at a p-value of 0.05.
2.3 Beam delivery time estimation
The beam delivery time for the reference and arc plans was estimated with an in-house developed beam delivery simulator [36]. The simulator was originally developed for emulating the beam delivery characteristics of the GSI accelerator complex as well as the Heidelberg Ion-Beam Therapy Center (HIT), including dynamic intensity control [37], beam scanning with realistic magnet speed and beam monitoring feedback. Due to the similarities between HIT and SPHIC, this model was applied in this work.
The simulator was extended to enable arc plan simulation with gantry or patient rotation during the synchrotron spills. In this framework, adjacent arc angular control points with the same energy were delivered within the same spill in a step-and-shoot fashion. If the rotation happened during the spill, a short beam gate of 0.29s for the \(2^\circ\) patient/gantry rotation was added, according to the maximum rotation speed of medical equipment set to \(7^\circ /\)s stated by the International Electronics Commission (IEC) norm IEC60601. Spill pauses occurred when the energy needed to be changed between control points or when the maximum spill delivery time of \(4\,\)s was reached, or when no more particles were available within the spill. The spill pause was set to \(4\,\)s and the maximum spill hold time to 8 s as per the specifications at SPHIC.
3 Results
3.1 Comparison of energy layer selection approach
Figure 2 provides an example comparison of different energy layer selection strategies for patient P1, including information on the distribution of the target voxels’ WED.
a Distribution of the water equivalent depth (WED) of the target voxels as function of the arc angular control point. The radial axis shows the WED, the azimuth axis the gantry angle. b Example depiction of a-priori energy selection strategies for P1. The WED of the target voxels is determined via ray tracing, from which the minimum (dashed light gray) and maximum (dashed dark gray) WED are determined. Different energy selection strategies were investigated in this work: shown are the central WED (determined as (minWED+maxWED)/2.) as black line (noted cWED), and the piece-wise mono-energetic approach (lWED) as green line. The second energy layer of the dual-energy C-Arc approach as orange line, the first layer is identical to lWED. The peak WED approch (pWED) is depicted as blue line, while the mean WED (mWED) approach is shown in purple line. The greedy refined energy layers (optWED) is shown as red line
3.2 Comparison of ripple filter setup
Figure 3 shows a the target coverage when using a 3 mm ripple filter compared to using a 6 mm ripple filter. In both cases, the optWED approach was used for energy selection. The setup with a 3 mm ripple filter resulted in significantly lower target coverage and significantly reduced dose homogeneity compared to the 6 mm ripple filter setup. The C-Arc plans optimized with 3 mm ripple filter setup increased the maximum LETd (LETd\(_{1\%}\)) by 7% on average compared to the approach with the 6 mm ripple filter, which was statistically significant. No significant difference in median LETd (LETd\(_{50\%}\)) was observed.
Comparison of a 3 mm and 6 mm ripple filter for carbon ion arc plan quality. Top: target DVH metrics. Shown is the mean and standard deviation of the robust evaluation for each patient. On the right, the average over all patients is shown, with error bars depicting the average standard deviation of the robustness evaluation. Bottom: LETd evaluated on the nominal scenario for each patient, and the average over all patients
3.3 RBE-weighted dose distribution
In Fig. 4, the dose distribution achieved with the optWED approach is compared against the reference treatment fields. The dose distributions highlight the complex dose shaping capabilities of the C-Arc plans. Despite the large tumor volumes, a single energy was enough to provide a homogeneous dose to most of the target.
Figure 5 presents the DVH metrics for the target achieved for the different energy selection methods in comparison to the reference IMPT plan, averaged over the six patients to better distinguish methods. Detailed DVH plots for each patient are given in Fig. 7.
Most plans passed D\(_{95\%}>\)95% and V\(_{95\%}>\)95% criteria, with the exception of the mWED approach. The reference IMPT was significantly better than all C-Arc approaches in target D\(_{95\%}\) and HI. optWED, cWED and lWED showed no statistically significant difference between each other when looking at target D\(_{95\%}\) and HI, resulting from the similarity of these energy selection approaches. mWED and pWED performed significantly worse regarding HI, and mWED also in terms of target D\(_{95\%}\) compared to the other mono-energetic approaches. The 2WED approach was significantly better in D\(_{95\%}\) and HI compared to the mono-energetic approaches.
optWED enabled better healthy tissue sparing with significantly improved conformity compared to lWED and cWED. It also led to reduced dose to the brainstem on average, although this was only significant compared to mWED and pWED. All mono-energetic C-arc plans showed worse HI in the target compared to the reference and dual-energy C-Arc approach. In addition, the mono-energetic C-Arc approaches had increased overdose in the target, which can be understood from the increased HI. The dual-energy C-Arc approach, 2WED, yielded significantly better CN than the mono-energetic C-Arc approaches.
3.4 Dose averaged LET
Figure 6 shows example slices through the LETd distribution obtained for the reference plans compared to the optWED C-Arc plans. Table 2 shows the average metrics from analyzing the nominal LETd-volume histograms for the six patients. Detailed plots for each of the six patients are provided in the appendix.
The median LETd (LETd\(_{50\%}\)) was similar for IMPT and C-Arc plans, when the optWED, lWED or cWED energy selection was applied. Except for patient P6, all mono-energy C-Arc plans show superior maximum LETd (evaluated as LETd\(_{1\%}\)) inside the target compared to the reference plans with an average increase between 10% and 33%. When neglecting P6, the increase was statistically significant for all mono-energetic C-Arcs. For patient P6, who had a very shallow tumor volume, the reference plan yielded a higher LETd\(_{50\%}\) and LETd\(_{1\%}\) compared to most C-Arc approaches, except for the pWED approach (see Appendix Fig. 8). The pWED and mWED approaches yielded the on average highest LETd focus inside the target, with improved average LETd\(_{50\%}\) by 19% (significant) and 11% compared to the reference, respectively. The dual-energy C-Arc approach showed the lowest LETd focus in the target, similar to that of the reference plans.
For the brain, C-Arc plans produced a similar LETd\(_{1\%}\) compared to the reference IMPT plans, except for patient P5, where a considerable increase in LETd\(_{1\%}\) was observed for the C-Arc plans compared to the reference plan. For the brainstem, the C-Arc approaches yielded on average a reduced LETd\(_{1\%}\) compared to the reference plans. For patient P3 the LETd\(_{1\%}\) to the brainstem was greatly increased for most C-Arcs.
3.5 Beam delivery and treatment time
In Table 3, the delivery time estimated with our in-house beam simulator is listed. The time needed for setup changes between the individual fields for the reference IMPT plans was not accounted for. For the arc plans, if possible, adjacent angular control points with the same energy were irradiated in the same spill. For the 2WED approach, the delivery was assumed to consist of 2 arcs, irradiated back to back.
Approaches that feature multiple neighboring angles with the same energy achieve better spill use. Compared to the cWED approach, for optWED the maximum decrease in delivery time was 45% for P1, and for the lWED approach, an improvement by 48% was observed for P2. The 2WED approach, having two energy layers per control point, resulted in the longest delivery times on average, but was still close to the pWED approach, the slowest of the mono-energetic strategies.
4 Discussion
This work investigated different energy selection schemes for robust biological optimization of C-Arc plans for head &neck cancer patients. This work built on previous literature for proton mono-energetic arc therapy [5] and complements previous literature in the field investigating the feasibility of heavy ion arc therapy [15, 16]. Beside heuristic approaches, a new greedy optimization based directly on the dose influence matrix has been implemented.
Mono-energetic C-Arc plans in general showed reduced target coverage and increased overdose compared to the reference plans. The use of just a single-energy layer per angular control point is challenging due to the non-linearity of biological doses. This makes it in general more difficult to find a solution robust against range and position changes, and typically this is overcome by overdose in the target and reduced homogeneity. Penalizing overdose inside the target in the robust optimization objective function mitigates this issue to a certain degree. Nevertheless, with the same optimization parameters, the reference plans showed practically no overdose inside the target, while overdose in the order of several percent was observed for arcs. For the non-robust optimizations performed in preparation of this work, generally better optimization convergence, with improved dose metric and greater LETd focus in the target was observed. It is, however, unclear whether the here observed overdose for robustly optimized C-Arcs is meaningful in the clinical context, considering the overall goal of C-Arc to increase the LETd and tackle hypoxia. Tumor heterogeneity, including hypoxic regions and the tumor micro-environment, results in different tumor regions being more or less sensitive to irradiation, which depends on LETd [38]. Moreover, increased target heterogeneity can be advantageous, as long as it does not affect healthy tissue doses, and may even be used to improve on OAR constraints [39]. For example, a recent work indicated improved local control for inhomogeneous target doses applied in brain metastases [40]. Whether C-Arc will present a clinically meaningful dosimetric benefit will depend on the specific patient and OAR constraints. For example, reducing skin dose with C-Arcs for shallow targets could be a measurable benefit for the patient. The greatest benefit likely comes for spherical, centrally located tumors, where the geometry fosters a conformity and LETd advantage.
Between the heuristic energy selection strategies, the pWED and mWED strategies were the least reliable, and failed to produce acceptable target coverage in some cases. For intracranial tumors, the convex patient surface and relatively homogeneous geometry results in convex iso-range lines inside the target. For a certain beam direction, the peak and mean WED of the target voxels will therefore be slightly lower than the central WED, as seen for example in Fig. 2. Choosing this WED to select the beam energy results in in a central volume lacking coverage, which is compensated by overdosing the surrounding tissue. The pWED and mWED approaches thus yield more overdose in the target and suffer reduced homogeneity, as evidenced in Fig. 5. On the other hand, they also led to the highest LETd inside the target, since most of the dose comes from the high LET region of the carbon ion depth dose profile. If the goal is purely LETd increase, and overdose is of no concern, these strategies are preferential.
This work suggests that of the purely heuristic energy selection strategies, cWED or lWED should be favored for C-Arc, when the goal is a IMPT-like homogeneous target coverage. Still, the geometric central WED, which is the basis for cWED and lWED approaches, may not work well for more complex tumor shapes, e.g., toroidal targets. The new energy layer refinement strategy helps to overcome this challenge. Even for the difficult target geometries represented by the patient cohort, high quality plans could be produced. Especially when using a 3 mm ripple filter or for partial arcs, the optWED approach performed favorable compared to the other mono-energetic C-Arc approaches.
The optWED approach reduced dose to healthy tissue, as evident from the improved average conformity and lower dose to the brainstem. The optWED approach also was slightly more robust on average compared to the heuristic approaches. Still, the benefit of optWED compared to the simpler lWED approach is relatively small, indicating that the lWED approach first proposed in the context of proton arcs [5] is indeed a viable planning option also for C-Arc. One key limitation of our optWED approach was using cWED (or any other heuristic energy selection) as starting point, which inherently limits the achievable solutions. With the setbacks in mind, lWED is the preferred option for energy selection in most cases.
Dosimetrically, the best strategy was one with two energies per control point, when the goal is to reproduce IMPT-like homogeneous doses. In this work, the two energies were selected to provide a constant energy for a long angular segment, which reduces the overall amount of energy changes considerably, and hence, could still be a viable option for C-Arc delivery. Further optimization with energy layer reordering into several arcs can further increase efficiency. However, the dual-energy C-arc did not achieve an increased LETd inside the target compared to the IMPT approach. This may well be related to the employed heuristic: The second beam energy was set higher than the central range for the target, which was chosen with future partial arcs in mind, and may be not ideal with respect to LETd improvement, for which choosing a lower second energy may be better.
It has been pointed out in previous works that carbon ion arc plans greatly improve the LETd inside the target [15, 16]. A perhaps unsurprising result from this work is that not all patients and C-Arc energy selection methods showed the same natural LETd improvement. While for patient P1 and patient P2, the LETd was generally increased in the target with C-Arc, and similar or decreased in the OARs, patients P3 through P6 showed a less clear picture. For patient P6 the reference plan did even provide a higher maximum LETd in the target than reached with most of the arc plans. Nevertheless, this is not a patient necessarily recommended for the application of C-Arc, as the shallow location of the target already works really well for an IMPT approach with 2 fields. The most straightforward LETd benefit appears for patients with small, centrally located tumors. Here the mono-energetic C-Arc approaches resulted in a very high LETd focus in the target even without an explicit LETd optimization. An explicit LETd optimization [4, 34] would also be useful for C-Arc to maximize its potential for increasing LETd in the target. The trade-off between target homogeneity, robustness and LETd focus observed for LETd optimization in carbon IMPT[34] was also apparent for C-Arc in this work. What is worth mentioning is that TRiP98 assumes a monochrome beam model, i.e., one where the particle spectra and LET distribution is laterally isotropic. For fully accurate LETd estimation, more advanced beam models, like the trichromatic model by Inaniwa et al. [41], or a Monte Carlo simulation would be needed. This was, however, beyond the scope of this work and is subject for further investigations.
All plans in this work assumed the LEM I model to estimate biological doses [42]. LEM I has known deficiencies regarding the entrance dose of the carbon ion beam, where it shows an overestimation. More recent versions, like the LEM IV model [43], predict lower entrance doses, which would be particularly favorable for C-Arc therapy. Future works should investigate a comparison of different RBE models for C-Arc therapy.
For the energy selection schemes that resulted in longer mono-energetic arc segments, the delivery time was shorter by \(\sim\)32% (lWED) and \(\sim\)34% (optWED) compared to the cWED approach on average, if the gantry/patient rotation was assumed to be possible during the spill. A major cause of delay is the duration of the spill pause. The delivery time may be reduced, if a shorter spill-pause and longer spill was available. Dedicated C-Arc delivery strategies may therefore be beneficial. Further gain in efficiency would be possible with continuous rotation of the patient or gantry during the delivery, which would save about 1 min compared to the reported duration in Table 3, as it would eliminate the need for the 0.29 s beam gate to move between control points. While the beam delivery under continuous rotation was found by Li et al. [8] to yield sufficient dosimetric accuracy for proton arc, the variable RBE of carbon ions complicates the situation. It remains to be proven, whether arc delivery under continuous rotation also presents a feasible option for carbon ion arc plans.
In this work, no attention was given to the direction of the energy changes. For some carbon facilities, changing the direction of energy changes may not be possible during the delivery of a single plan, or at least would result in a considerable delay. Since rotation of the gantry (1rpm) or patient (up to 2rpm [44]) can be much faster than the overall delivery duration, sorting the delivery sequence into multiple arcs with energy changes according to the facility specifications could be feasible.
All C-Arc plans had comparatively sparse raster scanning positions for each control points, featuring several jumps of up to few centimeters. Many small spots with relatively large distances cause delays in the treatment time due to the time required for the scanner magnets to make large steps (>5 mm), which was associated with a 0.3 s delay in our study. The path optimization algorithms implemented into TRiP98 reduce this issue by minimizing the number of large jumps needed, but jumps were still frequently present in the C-Arc plans. Jumps therefore contributed a non-negligible portion of the overall treatment duration for the patients. Future work should include scan path and spot sparsity optimization algorithms, such as recently proposed in the context of proton arc therapy [45].
The 6 mm ripple filter setup currently available at SPHIC was preferential for mono-energetic C-Arc plans compared to a 3 mm ripple filter setup. The 6 mm setup enables a single energy layer to cover more of the overall target area, improving dose homogeneity and robustness. Small loss in LETd advantage was present, but this may be a tolerable setback for the greater optimization flexibility. It would be interesting to further explore this direction, for example by using dynamic ripple filter setups as recently proposed by Maradia et al. [46].
5 Conclusion
This work presented robust, biologically optimized C-Arc treatment plans for six patients originally treated at SPHIC. The work corroborates previous studies indicating the feasibility of C-Arc to deliver IMPT-like biological doses to the target. Different heuristic energy selection strategies were investigated and a new energy layer refinement technique was presented. Among heuristic strategies previously applied in the context of heavy ion arc therapy, none could be identified as generally superior. The specifically developed energy layer refinement method yielded consistently good plan quality with little setback in LETd. It therefore has great potential for further developments. C-Arc presents an interesting option for increasing conformity and raising the LETd in the target for some patients and may be achieved within clinically tolerable delivery duration. However, these benefits were not naturally present for all patients. To make most of the potential of C-Arc for target LETd increase while keeping plan robustness, an explicit LETd optimization may still be needed. Ultimately, the decision on whether C-Arc or regular two/three field plans are to be applied depends on the specific case and needs to be carefully evaluated.
Availability of data and material
Restrictions apply to the availability of the data analyzed within this research. Anonymized patient CT data was provided by the Shanghai Proton and Heavy Ion Center (SPHIC), Shanghai, China, and data sharing is subject to the permission through SPHIC and the SPHIC Institutional Review Board.
Code availability
The work relied on the TRiP98 treatment planning system (http://bio.gsi.de/DOCS/TRiP98/NEW/DOCS/trip98.html), including recent updates for motion handling and efficiency, and extensive extensions for heavy ion arc therapy. An executable binary of the software can be made available upon reasonable request to the corresponding author. Data analysis software was custom developed for this work, and will be made available upon reasonable request.
References
Graeff C, Volz L, Durante M. Emerging technologies for cancer therapy using accelerated particles. Prog Part Nucl Phys. 2023;131: 104046.
PTCOG, Facilities in operation. Data Collected by the Particle Therapy Co-Operative Group. 2024. Last Accessed 10 Apr 2024.
Ding X, Li X, Zhang JM, Kabolizadeh P, Stevens C, Yan D. Spot-Scanning Proton Arc (SPArc) Therapy: The First Robust and Delivery-Efficient Spot-Scanning Proton Arc Therapy. Int J Radiat Oncol Biol Phys. 2016;96:1107–16.
Li X, Ding X, Zheng W, Liu G, Janssens G, Souris K, Barragán-Montero AM, Yan D, Stevens C, Kabolizadeh P. Linear Energy Transfer Incorporated Spot-Scanning Proton Arc Therapy Optimization: A Feasibility Study. Front Oncol. 2021;11.
Bertolet A, Carabe A. Proton monoenergetic arc therapy (PMAT) to enhance LETd within the target. Phys Med Biol. 2020;65:165006.
Harrabi SB, von Nettelbladt B, Gudden C, Adeberg S, Seidensaal K, Bauer J, Bahn E, Mairani A, Alber M, Haberer T, Debus J, Herfarth K. Radiation induced contrast enhancement after proton beam therapy in patients with low grade glioma - How safe are protons? Radiother Oncol. 2021;167:211–8.
de Jong BA, Battinelli C, Free J, Wagenaar D, Engwall E, Janssens G, Langendijk JA, Korevaar EW, Both S. Spot scanning proton arc therapy reduces toxicity in oropharyngeal cancer patients. Med Phys. 2023;50(3):1305–17.
Li X, Liu G, Janssens G, De Wilde O, Bossier V, Lerot X, Pouppez A, Yan D, Stevens C, Kabolizadeh P, Ding X. The first prototype of spot-scanning proton arc treatment delivery. Radiother Oncol. 2019;137:130–6.
Engwall E, Battinelli C, Wase V, Marthin O, Glimelius L, Bokrantz R, Andersson B, Fredriksson A. Fast robust optimization of proton PBS arc therapy plans using early energy layer selection and spot assignment. Phys Med Biol. 2022;67:065010.
Gu W, Ruan D, Lyu Q, Zou W, Dong L, Sheng K. A novel energy layer optimization framework for spot-scanning proton arc therapy. Med Phys. 2020;47:2072–84.
Wuyckens S, Saint-Guillain M, Janssens G, Zhao L, Li X, Ding X, Sterpin E, Lee JA, Souris K. Treatment planning in arc proton therapy: Comparison of several optimization problem statements and their corresponding solvers. Comput Biol Med. 2022;148:105609.
Zhao L, Liu G, Li X, Ding X. An evolutionary optimization algorithm for proton arc therapy. Phys Med Biol. 2022;67:16NT01.
Nesteruk KP, Bolsi A, Lomax AJ, Meer D, van de Water S, Schippers JM. A static beam delivery device for fast scanning proton arc-therapy. Phys Med Biol. 2021;66:055018.
Tinganelli W, Durante M. Carbon Ion Radiobiology. Cancers. 2020;12.
Mein S, Tessonnier T, Kopp B, Harrabi S, Abdollahi A, Debus J, Haberer T, Mairani A. Spot-Scanning Hadron Arc (SHArc) Therapy: A Study With Light and Heavy Ions. Adv Radiat Oncol. 2021;6.
S. Mein, T. Tessonnier, B. Kopp, C. Schömers, S. Harrabi, A. Abdollahi, J. Debus, T. Haberer, and A. Mairani, Biological Dose Optimization for Particle Arc Therapy using Helium and Carbon Ions, International Journal of Radiation Oncology*Biology*Physics (2022).
Mein S, Kopp B, Tessonnier T, Liermann J, Abdollahi A, Debus J, Haberer T, Mairani A. Spot-scanning hadron arc (SHArc) therapy: A proof of concept using single- and multi-ion strategies with helium, carbon, oxygen, and neon ions. Med Phys. 2022;49:6082–97.
Liu W, Mohan R, Park P, Liu Z, Li H, Li X, Li Y, Wu R, Sahoo N, Dong L, Zhu XR, Grosshans DR. Dosimetric benefits of robust treatment planning for intensity modulated proton therapy for base-of-skull cancers. Pract Radiat Oncol. 2014;4:384–91.
Cubillos-Mesías M, Baumann M, Troost EGC, Lohaus F, Löck S, Richter C, Stützer K. Impact of robust treatment planning on single- and multi-field optimized plans for proton beam therapy of unilateral head and neck target volumes. Radiat Oncol. 2017;12:190.
Wolf ME. Robust optimization in 4D treatment planning for carbon ion therapy of lung tumors, PhD thesis, Technische Universität, Darmstadt, 2018.
Wolf M, Anderle K, Durante M, Graeff C. Robust treatment planning with 4D intensity modulated carbon ion therapy for multiple targets in stage IV non-small cell lung cancer. Phys Med Biol. 2020;65:215012.
Hu W, Hu J, Huang Q, Gao J, Yang J, Qiu X, Kong L, Lu JJ. Particle Beam Radiation Therapy for Adenoid Cystic Carcinoma of the Nasal Cavity and Paranasal Sinuses. Front Oncol. 2020;10.
Kong L, Gao J, Hu J, Lu R, Yang J, Qiu X, Hu W, Lu JJ. Carbon ion radiotherapy boost in the treatment of glioblastoma: a randomized phase I/III clinical trial. Cancer Commun. 2019;39:5.
Guan X, Gao J, Hu J, Hu W, Yang J, Qiu X, Hu C, Kong L, Lu JJ. The preliminary results of proton and carbon ion therapy for chordoma and chondrosarcoma of the skull base and cervical spine. Radiat Oncol. 2019;14:206.
Krämer M, Jäkel O, Haberer T, Kraft G, Schardt D, Weber U. Treatment planning for heavy-ion radiotherapy: Physical beam model and dose optimization. Phys Med Biol. 2000;45:3299–317.
Hild S, Graeff C, Trautmann J, Kraemer M, Zink K, Durante M, Bert C. Fast optimization and dose calculation in scanned ion beam therapy. Med Phys. 2014;41: 071703.
Anderle K, Stroom J, Vieira S, Pimentel N, Greco C, Durante M, Graeff C. Treatment planning with intensity modulated particle therapy for multiple targets in stage IV non-small cell lung cancer. Phys Med Biol. 2018;63:025034.
Lis M, Newhauser W, Donetti M, Wolf M, Steinsberger T, Paz A, Graeff C. Preliminary tests of dosimetric quality and projected therapeutic outcomes of multi-phase 4D radiotherapy with proton and carbon ion beams. Phys Med Biol. 2021;66:235004.
Steinsberger T, Alliger C, Donetti M, Krämer M, Lis M, Paz A, Wolf M, Graeff C. Extension of RBE-weighted 4D particle dose calculation for non-periodic motion. Phys Med Eur J Med Phys. 2021;91:62–72.
Lis M, Newhauser W, Donetti M, Wolf M, Steinsberger T, Paz A, Graeff C. Dosimetric Validation of a System to Treat Moving Tumors Using Scanned Ion Beams That Are Synchronized With Anatomical Motion. Front Oncol. 2021;11:.
Sheng Y, Sun J, Wang W, Stuart B, Kong L, Gao J, You D, Wu X. Performance of a 6D Treatment Chair for Patient Positioning in an Upright Posture for Fixed Ion Beam Lines. Front Oncol. 2020;10:122.
Krämer M, Scholz M. Rapid calculation of biological effects in ion radiotherapy. Phys Med Biol. 2006;51:1959.
Peters N, Wohlfahrt P, Hofmann C, Möhler C, Menkel S, Tschiche M, Krause M, Troost EG, Enghardt W, Richter C. Reduction of clinical safety margins in proton therapy enabled by the clinical implementation of dual-energy CT for direct stopping-power prediction. Radiother Oncol. 2022;166:71–8.
Fredriksson A, Glimelius L, Bokrantz R. The LET trilemma: Conflicts between robust target coverage, uniform dose, and dose-averaged LET in carbon therapy. Med Phys. 2023;50:7338–48.
Application to the prostate. A. v. Riet, A. C. Mak, M. A. Moerland, L. H. Elders, and W. van der Zee, A conformation number to quantify the degree of conformality in brachytherapy and external beam irradiation. Int J Radiat Oncol Biol Phys. 1997;37:731–6.
Richter D. Treatment planning for tumors with residual motion in scanned ion beam therapy, PhD thesis, Technische Universität, Darmstadt, 2012.
Schoemers C, Feldmeier E, Naumann J, Panse R, Peters A, Haberer T. The intensity feedback system at Heidelberg Ion-Beam Therapy Centre, Nuclear Instruments and Methods in Physics Research Section A, Accelerators, Spectrometers, Detectors and Associated Equipment , 2015; p 92–99.
Tinganelli W, Durante M, Hirayama R, Krämer M, Maier A, Kraft-Weyrather W, Furusawa Y, Friedrich T, Scifoni E. Kill-painting of hypoxic tumours in charged particle therapy. Sci Rep. 2015;5:17016.
Benedict SH, et al. Stereotactic body radiation therapy: The report of AAPM Task Group 101. Med Phys. 2010;37:4078–101.
Lucia F, Key S, Dissaux G, Goasduff G, Lucia A-S, Ollivier L, Pradier O, Schick U. Inhomogeneous tumor dose distribution provides better local control than homogeneous distribution in stereotactic radiotherapy for brain metastases. Radiother Oncol. 2019;130:132–8.
Inaniwa T, Kanematsu N. A trichrome beam model for biological dose calculation in scanned carbon-ion radiotherapy treatment planning. Phys Med Biol. 2014;60:437.
Scholz M, Kellerer AM, Kraft-Weyrather W, Kraft G. Computation of cell survival in heavy ion beams for therapy. Radiat Environ Biophys. 1997;36:59–66.
Pfuhl T, Friedrich T, Scholz M. Comprehensive comparison of local effect model IV predictions with the particle irradiation data ensemble. Med Phys. 2022;49:714–26.
Whelan B, Welgampola M, McGarvie L, Makhija K, Turner RM, Holloway L, Feain I, Jackson M, Barton M, Keall P. Patient reported outcomes of slow, single arc rotation: Do we need rotating gantries? J Med Imaging Radiat Oncol. 2018;62:553–61.
Zhao L, You J, Liu G, Wuyckens S, Lu X, Ding X. The first direct method of spot sparsity optimization for proton arc therapy. Acta Oncol. 2023;62:48–52. PMID: 36729848.
Maradia V, Colizzi I, Meer D, Weber DC, Lomax AJ, Actis O, Psoroulas S. Universal and dynamic ridge filter for pencil beam scanning particle therapy: a novel concept for ultra-fast treatment delivery. Phys Med Biol. 2022;67:225005.
Acknowledgements
The publication is funded by the Open Access Publishing Fund of GSI Helmholtzzentrum fuer Schwerionenforschung.
Funding
Open Access funding enabled and organized by Projekt DEAL. This project has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 101008548 (HITRIplus). LK has received funding from the National Key Research and Development Program of China (No. 2022YFC20401505).
Author information
Authors and Affiliations
Contributions
LV: conceptualization, literature review, software development, data generation, data analysis, manuscript writing (original draft), manuscript writing (revision); YS: conceptualization, material preparation, manuscript writing (revision); LK: manuscript writing (revision), material preparation, funding acquisition; MD: supervision, funding acquisition, manuscript writing (revision); CG: conceptualization, literature review, software development, manuscript writing (original draft), manuscript writing (revision), supervision, funding acquisition.
Corresponding author
Ethics declarations
Ethics statement
The study was approved by the Institutional Review Board of Shanghai Proton and Heavy Ion Center (approval number SPHIC-MP-2022-02, RS).
Consent to participate
Not applicable.
Consent for publication
Not applicable.
Conflict of interests
The authors have no relevant financial or non-financial interests to disclose.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix
1.1 Detailed DVH metrics
Figure 7 shows the DVH specific to each patient. The nominal scenarios are depicted for the IMPT reference plan, as well as each of the C-Arc energy selection methods.
Detailed LETd metrics
Figure 8 shows the LETd volume histograms for the different methods for each of the six patients. The nominal scenario is depicted for the IMPT reference plan, as well as each of the C-Arc energy selection methods.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Volz, L., Sheng, Y., Kong, L. et al. Exploring energy selection methods for robust biologically optimized carbon ion arc for head&neck cancer patients. Health Technol. (2024). https://doi.org/10.1007/s12553-024-00877-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12553-024-00877-0