Abstract
In this paper, we study Malthusian pressures in a frontier economy. Using the empirical data on real prices and demographic variables from 1688 to 1860 for Quebec and Montreal, we test for the existence of Malthusian pressures. Bearing in mind the particularities of frontier economies and the development of the Canadian economy, we conduct a Granger-causality analysis for the time-series of real wheat prices, birth and death rates with the help of VARs in order to identify positive and preventive checks. Using the Bai–Perron test we find a structural break in 1767 and divide the sample into pre- and post-conquest periods. We find that the positive checks were operating in the years prior to the conquest but that they faded during the nineteenth century. It follows that an increase in the wheat prices Granger-causes an increase in death rates in the pre-conquest period. Additional tests and a robustness check of the detrending methods are performed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
For most of human history, wages fluctuated at the edge of subsistence level, sometimes slightly above and sometimes slightly below it. Although technological innovations were not absent, most movements in living standards were determined by changes in population sizes. This reality has been labelled “Malthusian” in reference to Thomas Malthus and his work on population. The key features of this model are that the supply of land is fixed and that this supply is small relative to the population. This applied very well to countries in Europe where these conditions were met, but what about New World economies from the seventeenth to nineteenth centuries which had only recently been settled?
Quebec, the modern-day French-speaking province of Canada, is a good candidate to answer that question. Known as New France from 1608 to 1760 before it was taken from the French crown by the British and then known interchangeably as Quebec, Lower Canada and Canada East up to 1867, historians of this society have often portrayed it as a society rife with Malthusian pressures. The eminent Fernand Ouellet (1966) asserted that the colony lived through an “economic crisis” from 1802 to 1850 mainly because of soil erosion and overpopulation of the colony. According to Ouellet, grain price fluctuations were symptomatic of the underlying performance of the agricultural economy whose surplus fed into the other sectors of the economy.
This view is still commonly portrayed by popular historians (Bédard 2012). This a surprising argument given that numerous authors have found that the land supply was still very large at the time specified by Ouellet (see Altman 1983; McInnis 1982). Moreover, the data from mortality rates and crude birth rates do not fit the Malthusian framework. The steepest increases in the mortality rate (indicative of the positive check) are found in the period of French rule since less than 10 % of the attributed estates of the colony were cleared for agricultural production in 1739. In the 1831 census, this proportion stood at 34 %. But even by the mid-nineteenth century, that claim is dubious since the 1851 census reveals that only 44 % of the total lands owned were improved.
The literature on Malthusian pressures in Canada and the United States is constrained by the absence of continuous data series. We try to fill in the gap. Thanks to the existence of numerous economics papers that detail operational procedures to test the existence of Malthusian pressures in economic history, filling this gap is made easier. It is possible that this lack of testing for Lower Canada and Quebec was the result of limited statistics with regard to economic indicators. Recent work by one of the current authors Geloso (2014a, b) has generated large databases of prices in the colony from 1688 to 1858. Combined with the exhaustive data already available with regard to vital statistics (crude mortality rate, crude birth rate, nuptiality rate), it is possible to run statistical tests. We find that Malthusian pressures in the Quebec economy post-conquest were non-existent—at a time when the land supply was growing scarcer. In fact, we find evidence of Malthusian pressures in the pre-conquest period—at a time when land was more easily available.
The Malthusian economy
Under Malthusian theory, real wages are not determined by the marginal product of labour but rather by the population size relative to the pool of available resources in a technologically stagnant environment (see Wrigley and Schofield 1981). Under the constraint of slow technological improvements, the first equation of the Malthusian model sets wages as a function of population. However, in the short run, population is endogenous to real wages. Births (the rate of population increase) are respondent to wages. Deaths also respond to wages. When real wages increase (decrease), births increase (decrease) while deaths decrease (increase). In the long run, the equilibrium rate of population is equal to zero. In the short run, an increase in real wages (reflected by a one-time technological shock) that increases productivity brings demographic behaviour out of equilibrium and population increases. However, the marginal product of labour will decline as more individuals compete for a fixed stock of capital, leading to lower real wages (mostly through higher prices). Two forces will act to restore equilibrium: preventive check and positive check. The preventive check refers to households delaying family formation. This may be expressed through later marriage ages, planned sexual activities, contraception, longer stays in the parental household and greater spacing between births. The positive check refers to the impact of mortality increasing to force the population back to equilibrium level (Guinnane and Ogilvie 2008).
It is these two checks that have been the topic of discussion amongst economic historians. More precisely, the discussion has centered on when the two checks disappeared. In England, Nicolini (2007) and Craft and Mills (2009) have argued that the two checks disappeared somewhere between the sixteenth and eighteenth century with the positive check disappearing earlier than the preventive check. However, in eighteenth century Germany, Fertig and Pfister (2012) found that the positive check was stronger and weakened slightly past 1815 and that the preventive check was equally strong throughout the period. According to these two authors, the weakening of the positive check was caused by greater market integration. Most of the research has concentrated on economies that were already densely populated.
Malthusian framework in the New World and Quebec
This theoretical framework works differently if there are large quantities of unused inputs. The concept behind Malthusian equilibrium is that inputs are being used more intensively for diminishing marginal returns. However, if there are unused resources to be introduced cheaply into production, an increase in population will not have these effects. In fact, in the short run, the larger population would increase prospects for specialization and would increase output very rapidly relative to inputs. One example of this is provided by Alvarez-Nogal and Prados De La Escosura (2013) in the case of Spain after the Black Death. Since Spain was at that time a frontier economy with more abundant land, the Black Death did not reduce pressures on scarce land resources; it merely eradicated commercial networks, isolated scarce populations and led to a decline in specialization.
This Spanish case shares similarities with North America prior to the first half of the nineteenth century. These were economies where land was a cheap input that could easily be introduced into production and an increase in population would not lead to falling real wages. Quebec qualifies as such an economy in our opinion. Yet numerous are the authors who would disagree (Ouellet 1972, 1980; Russell 2012; Greer 1985). These authors have tended to attribute the poor economic performance of Quebec up to the 1850s in great part to Malthusian pressure. Ouellet has made this claim in a different manner, pointing out that overpopulation was caused by a “shortage of fertile, easily accessible land” (see Ouellet 1980, p. 144). Ouellet argued that this shortage was localized in some long-settled areas and individuals resettled in other parishes and townships in the colony (ibid, p. 156). These new parishes would have been on marginally less productive lands. Along these lines, and although he never uses the term, Ouellet is arguing for the existence of a preventive check. According to this framework, the pressures materialized thanks to inputs that were costly to introduce into production and whose productivity was marginally lower than previously settled lands. Haines (2000, pp. 168–169) defended his claim that there existed evidence of a preventive check in New England in the form of high costs of household formation. More broadly, the claim of economic distress in Quebec is attributed to the rapid increase in the rural population whose effects were amplified by exogenous shocks like the Hessian fly and the wheat midge as well as a supposed innate conservatism amongst the French-Canadians that made them less efficient than English-Canadian households (Le Goff 1974). However, this approach by Ouellet is at odds with another of his claims. Arguing that French-Canadian farmers were conservative towards new farming practices, Ouellet then added that this cultural conservatism expanded to fertility patterns. If these patterns were culturally determined, the preventive check would have been weaker because of their cultural component and the positive check stronger. Moreover, claims of culturally determined fertility patterns are often exaggerated (also hard to prove) as shown by Zhongwei (2006, pp. 10, 13 and 27) for the case of China where similar claims have been made.
Paquet and Wallot (2007) countered this line of argument by denying that the economy was performing poorly. In doing so, they negated the existence of any significant pressures along the lines proposed by Malthus. They pointed out that the economy of Lower Canada was diversifying into products like timber, potash and pearl ash. Bédard and Geloso (2014) have advanced evidence supporting this view that economic growth was positive in the first half of the nineteenth century. McInnis (1982) also feeds this line of argument by pointing out that colonists in Quebec exported timber to England and imported wheat from Upper Canada, which places the performance of the agricultural economy (whose decline is central to the claim of Malthusian pressure) in a more positive light. Serge Courville also noted a distinct trend in favour of diversification in the form of new villages and small towns appearing in the countryside (1990, 1995, 2008). Increased urbanization is contradictory to the Malthusian model as Becker and Murphy (1999) pointed out. Greater population density promotes specialization and greater investment in human capital. These “increasing returns from specialization would raise per capita incomes as population grew and are likely to be far more important than diminishing returns in resource-constrained sectors” (Becker and Murphy 1999, p. 146). However, this is a question of degree. It is possible, under the Malthusian model, for both population and economic growth to be positive if there are improvements in productivity and technological settings. Hence, observing positive growth, as Paquet and Wallot do, does not invalidate the existence of Malthusian pressures. Haines (2000) makes the claim that the United States did manage to generate fast economic growth on a per capita basis in the antebellum era while there was a preventive check operating. All of the facts highlighted above suggest that the literature is at an impasse, which can only be settled through empirical testing.
Data
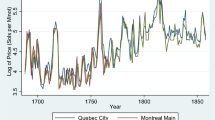
Wheat prices were selected because of their importance to the diets of the French Canadians. According to Fyson (1992, p. 74), 56 % of the diets of workers in Lower Canada came from starches. But this is a conservative estimate since Vallieres and Desloges (2008) put this proportion above 60 % in urban areas during the New France era and close to 70 % in rural areas during the same era. Given this great importance of wheat, it should be seen as a good measure of the variation in the standard of living. “From one year to the next, fluctuations in the price of grain were the primary determinants of variations in the real wage” (Galloway 1988, p. 276), since nominal wages were relatively stable from year to year (see Geloso 2014b for New France). The prices collected for wheat stem in part from Geloso (2014a) for the pre-conquest era and from Ouellet et al. (1982) for the post-conquest era. Both these price series should be seen as wholesale prices collected from the account books of religious congregations. Market exchanges were thus always an option for the habitant farmer. Even if he chose not to trade his labour on the market, he could always do so at the prevailing price. Most peasants in Quebec produced for themselves, but they always tried to sell part of their crop to the fifth of the population in urban areas in exchange for money that would allow them to acquire imported goods like cloth, sugar, pepper and salt. For the Montreal area prior to the conquest, we have used the price series produced by Dechêne (1994), which is also illustrative of wholesale prices. Prices were deflated over the broad price index produced by Geloso (2014a), which was a combination of his own price index for the pre-conquest era with that of Paquet and Wallot (2007).
The vital statistics we have used have been drawn from multiple sources. The raw numbers of births and deaths have been drawn from the work of Langlois (1935) and concern only the Catholic population. In order to provide births and deaths relative to population, we have relied on the Catholic population estimates from Henripin and Péron (2000). We do not believe that the focus on the Catholic population is problematic. The Catholic population of Quebec was predominantly French while the non-Catholic population tended to be English-speaking. By 1861, the vast majority of the population (85 %) was Catholic, making our concentration on Catholics warranted (see Pelletier et al. 1997, p. 93). According to the 1851 census of Canada East (as Quebec was then known), the mortality rate observed in predominantly English-settled areas was equal to those of French-settled areas (see Public Archives of Canada 1873). Some differences emerge in closer studies. For example, studies concerned with the late nineteenth century show that Catholics had a higher rate of infant mortality (see Gauvreau and Gossage 2001). Catholics also tended to marry earlier than Protestants in the city of Montreal in the 1860s and their mortality rate was higher (see Olson and Thornton 2011, pp. 154 and 62). Differences were also observed in the average family size. Yet this fact could be used to support our conclusions. As we will see later, we find the absence of the preventive check and positive check after 1760. If the Protestants were doing better than the poorer Catholics who exhibited greater birth rates and mortality rates while the two Malthusian checks operating upon the Catholics were disappearing, this means that the case we are making in this paper is quite conservative. Any attempt at including time series from the Protestant minority would reinforce the strength of our results. Moreover, the focus on Catholics is justified in order to solve the impasse discussed above. Those who hold the position that there were population pressures have largely focused on the Catholic population, which was believed to be poorer than the Protestant population. Since poorer populations tend to be more susceptible to Malthusian pressures (through poorer nutrition, poor diets and a lesser ability to withstand shocks), the focus on the Catholic population is warranted. If they did not experience Malthusian pressures, it is quite unlikely that Protestants experienced them as well.
Normally, we would opt for the inclusion of a variable for infant mortality. If there were a positive check with regard to the population through higher mortality, it would have been felt more strongly for younger individuals whose immune systems were not fully developed—namely children. The problem is that the dataset we use does not differentiate mortality on the basis of age; it is merely the crude mortality rate. However, there is a mortality quotient provided by Gentil (2009). Gentil estimates infant mortality in Quebec up to 1779 and even has regional breakdowns (Quebec city, Montreal, Trois-Rivières and rural areas). While it is tempting to use the above-mentioned estimates to refine ours, Gentil’s data is not suited to any such attempts. Her mortality quotients do not cover the full population and concentrate on the mortality of legitimate children whose mortality rate was considerably below that of illegitimate children. Hence, using these data could lead to some bias. However, papers like those of Nicolini (2007) and Craft and Mills (2009) have relied on the broader crude mortality and crude birth rates with sufficiently robust results.
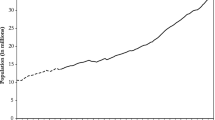
Wars and climate in this economy would have been very problematic and could potentially disrupt any statistical analysis if no control is attempted. Consequently, we have included a war dummy variable throughout the sample, which we combined with the climate dataset provided by Mann et al. (1998). The war dummy is straightforward and includes also the rebellions of 1837–1838 in Lower Canada as well as the international wars the colony was brought into from 1688 to 1860. The climate variable is expressed in deviation from the average temperature observed between 1961 and 1990. Although other climate datasets exists (McIntyre and McKitrick 2003), we have opted for the more often cited dataset by Mann et al. (1998). Other factors (technology, public health, urbanization) that could influence our tests were negligible. There was very little technological innovation during our period of study. The predominant sector of agriculture would not benefit from new technologies like the mechanical reapers until the 1850s (which is the last decade of our study). Other innovations like refrigeration (which would eventually allow the boom in dairy production in Quebec) would also arrive later in the century. Railways could have contributed, but by the 1830s, few miles had been constructed and a truly inter-colonial network of railways only emerged after Confederation in 1867. With regard to advances in health care, most of the public health infrastructure began to emerge in the 1840s onwards (see Vallieres and Charbonneau 2008, p. 833). There had been some health institutions prior to the 1840s like that established by the Augustine congregation of Quebec City, but they had always been confined to urban areas and were modest in terms of mission relative to the public health efforts deployed in the years preceding Confederation. The importance of public health improvements would tend to appear mostly after our period of interest. At this point, we can also rule out urbanization. Up to the 1851 census, the share of the population living in the three large urban centers of Quebec (Quebec City, Trois-Rivières and Montreal) declined progressively. Table 1 shows that individuals were leaving for the countryside from 1688 to 1851. However, this trend should be divided in two. Prior to the 1780s, individuals were leaving for the countryside and no new urban centres appeared. After that point, urbanization was driven mostly by the formation of villages and small towns in the countryside, not by the growth of large cities (Courville 1990). Hence, the share of all inhabitants living in all cities, towns and villages increased from the 1810s onwards. In those villages and small towns, mortality rates were very much in line with those generally experienced in the countryside. Had we expanded our period of interest beyond the 1850s, this would have been a problem. However, it does not represent a problem before that point in time. Moreover, when we compare our data with that of Vallieres and Charbonneau (2008), we find that they share similar trends (Fig. 1).
Empirical strategy, methods and results
We begin with testing the key variables, real wheat prices, birth and death rates on stationarity. We apply the Augmented Dickey–Fuller test with Generalized Least Squares (ADF GLS) estimation as in Elliott et al. (1996) which performs better in small samples compared to the original version of the test using the Order of the Least Squares (OLS) estimation. The optimal lag length of the test is selected according to the Akaike Information Criteria (AIC) as in Akaike (1974).Footnote 1 Thus, we report the test statistics at the optimal lagFootnote 2 in Table 2. As it follows from the test, all of the levels of the three key variables are not stationary and need to be transformed. This test result implies that prices and population in Canada from 1688 to 1860 were unstable. The subsequent step is to choose an appropriate specification: a vector error correction model (VECM) or a vector autoregression (VAR). To do so, we require a cointegration test, since if the series are cointegrated we need to include a cointegrating vector in the specification; otherwise, a VAR framework would be appropriate.
One has to note that the cointegration test is merely a tool in selecting an appropriate specification for causal inference of the relation between real wheat prices, birth and death rates. We have given preference to the Johansen cointegration test (Johansen 1988; Hamilton 1994, see Ch. 14) due to its multivariate framework and a good performance on finite samples, as stated in Dhrymes and Dimitrios (1997). The optimal number of lagsFootnote 3 is determined by the AIC, as in the ADF GLS test. As we observe from Table 3, the trace statistic exceeds the critical value dramatically and therefore we reject the null hypothesis of the presence of a cointegrating vectorFootnote 4 in a system of prices, birth and death rates. The implication of these results is the rejection of the VECM in favour of the VAR specification.
Further we investigate the interaction between the cyclical fluctuations. The time frames of our analysis are 1688–1860. As we have noted before, a number of historical events took place during this period and the economy of Canada and its structure changed dramatically. Therefore, we would like to test our data on structural breaks for which we apply the package from Zeileis et al. (2002). The first step is to determine the potential number of the structural breaks with the help of the Bayesian Information Criterion (BIC) resembling the tests applied in Hall et al. (2013). As it follows from Fig. 2, the minimum values of the BIC point out a single break. Therefore we proceed with an F test as in Bai and Perron (2003) to identify the time point. The results of the structural break test considering wheat pricesFootnote 5 are depicted on Fig. 3. The F statistics suggest that the break point occurred in 1767, which is roughly 7 years after the British conquest.Footnote 6 This allows us to divide the sample into two periods for the analysis according to historical events: we treat the data according to two periods, pre-conquest 1688–1767 and post-conquest 1768–1860.
First of all, let us examine the descriptive statistics of our key variables: real wheat prices, birth and death rates. According to the results from Table 2, we required a transformation to achieve stationarity. In order to perform detrending and obtain cyclical fluctuations \((y_{t} - \tau_{t} )\) we apply filtering with the Hodrick–Prescott filter (further HP) to remove the trend \((\tau_{t} )\) and achieve stationarity. Below is the minimization problem of the HP filter. For demonstration we choose 6.25 for λ as in Ravn and Uhlig (2002, p. 374). The HP filter (see Hodrick and Prescott 1997, p. 3) penalizes the series up to the second order and all of our series are I(1), which should not cause any distortions.
We obtain detrended data that represent cyclical fluctuations in prices and in birth and death rates. Further we use the detrended cyclical data for the descriptive statistics and for the time series Granger-causality analysis. Let us first examine the descriptive statistics of the filtered cycles.
Let us consider descriptive statistics from Table 4 for the main variables of interest. It appears that in the second period prices and birth and death rates have become less volatile: the standard deviation of prices decreased by 20.3 %, of birth rates by 62.5 % and of death rates by 41.5 %. We observe narrower cyclical price fluctuations that imply a decrease in volatility of all variables. Indeed, the period after 1767 appears to be less volatile in terms of demographics; however, one has to question whether this was a smooth change or a discontinuous change. Figure 4 depicts rolling standard deviations of birth and death rates. From Fig. 3 we can tell that there was a structural break in wheat prices after 1767; however, the demographic variables did not display such obvious structural breaks and therefore we depict rolling standard deviationsFootnote 7 of the related series in Fig. 4. There are two important points to highlight: firstly, the standard deviation of birth and death rates gradually decreased after 1740–1760, exhibiting occasional humps. Secondly, the decrease in demographic volatility was gradual; however, we should note that most of this decrease took place in the post-conquest period (1768–1860). The latter fact is confirmed by the descriptive statistics from Table 4.
Descriptive methods allowed us to capture decreasing volatility in the fundamental time-series characteristics. This decrease of volatility in real wheat prices and in birth and death rates in the post-conquest period of our analysis requires a thorough investigation of the causal interaction between these variables. In order to perform such an analysis, we have selected the well-established VAR framework, as in Hamilton (1994, Ch. 11) and the Granger-causality test, as in Granger (1969). The cyclical fluctuations, obtained with the help of the HP filter, are stationary and can be used for the VAR analysis and Granger-causality testing with the help of the following modelFootnote 8:
where y 1,t denotes cyclical fluctuations in real wheat prices; y 2,t denotes cyclical fluctuations in birth rates, y 3,t denotes cyclical fluctuations in death rates; C denotes a constant, whereas \(\pi\) denotes coefficients; e is an error. In addition, we include exogenous controls into the model: dummies for war periods and temperature change. Let us investigate the results in Table 5 for the pre-conquest period (1688–1767). Using temperature change and war dummies for periods of war clashes as exogenous controls, we have obtained the following result: the first lag of the change of the real wheat prices has a positive impact on the death rates of 0.286 %. This effect of a positive check is significant at the 5 % level. Naturally, this is confirmed by the Granger-causality test in Table 7 for specifications 1, 2 and 3. From the test it follows that cyclical fluctuations in real wheat prices Granger-cause cyclical fluctuations in death rates. For the pre-conquest period this effect is valid at the 5 % level. The second effect is related to lagged birth rates Granger-causing death rates. This effect is also positive and significant at the 5 % level. We associate this effect with infant mortality and note that in the post-conquest period it vanishes. The preventive check was not discovered. One should note that in the pre-conquest period the climate control was significant in the equation for real wheat prices, whereas in the post-conquest period it was significant in the equation for the birth rates.
Post-conquest period results from Table 6 seem to be different: the lags of the cyclical fluctuations in the wheat prices are insignificant for the death rates. The causal effect vanishes, which is confirmed by the Granger-causality test in Table 8. The results suggest no preventive or positive check in this period. However, we note significant impact of wars and temperature change, as exogenous controls, on birth rates (see Table 6). Therefore, we can conclude that the causal effect of real wheat prices on demographic variables vanishes in the post-conquest period, after 1767. This is consistent with the decreases in demographic volatility after 1740–1760, depicted in Fig. 4.
Additionally we perform a robustness check of our estimations using simple growth rates of the original series, as an alternative to detrending with the HP filter. This would ensure that the Granger-causality test results are not sensitive to the detrending methodology. The Granger-causalities with growth rates are presented in Tables 7 and 8. The test results confirm the ones obtained from the filtered series: in the pre-conquest period at the 5 % level we observe Granger-causality from the growth rates of wheat prices to the growth of death rates and from the growth rates of birth rates to the growth of death rates as well. In the post-conquest period none of the Granger-causalities are detected. Therefore, the presence of the positive check is robust to the detrending methodology. Finally, we verify that the residuals of our models pass the Portmanteau Q test for white noise at the 5 % level as in Ljung and Box (1978).
Discussion and conclusion
In this paper we focused on the causal inference of the relationship between real wheat prices, birth and death rates. We found that when it was under French rule, Quebec did seem to exhibit signs of population pressures in the form of the positive check. We found that fluctuations in wheat prices Granger-cause fluctuations in death rates in the pre-conquest period. However, after the conquest of Quebec by the British, the positive check disappeared. These are surprising results given that the literature that argues for population pressures locates them in the era of British rule.
We believe that our results can be explained through two possible channels: migration and market efficiency. Throughout our studied period, migration was mostly possible past the conquest. It is quite possible that French-Canadians mitigated demographic pressures through migration to the United States. Paquet and Smith (1983) provide evidence for such an argument, pointing out that there was a large migration flux of French-Canadians. Unfortunately, their data is not annualized and we only possess conjectural estimates that, on average, roughly 9000 French-Canadians left Lower Canada for other colonies between 1831 and 1851 (see Paquet and Smith 1983, p. 440). However, their own analysis suggests that the bulk of the migration occurred in the 1830s—a decade of poor economic performance. Indeed, those years were marked by political rebellion and the effects of the wheat midge. Yet, the 1840s exports and imports data (Vallieres and Desloges 2008) suggest a recovery of economic activity which compensated for the unfortunate decade of the 1830s. Furthermore, the rate of population growth did not seem to have decelerated considerably between population estimates. While the compound rate of population growth was 1.8 % between 1831 and 1844, it bounced back to 3.56 % between 1844 and 1851 and to 2.76 % between 1851 and 1861. Moreover, there was a positive flow of British settlers to Canada and Quebec, which also went through a lull in the 1830s before picking up in the 1840s and 1850s (see McInnis 2000, p. 386). Anyhow, the reversal of population movements away from Canada is more relevant in the second half of the nineteenth century—a period beyond the focus of this paper (see McInnis 2000, p. 416). As a result, we are not convinced that emigration—although a relevant factor—was sufficient to distort the impact of Malthusian pressures in the latter period.
The other explanation that we find more convincing is that of institutions which made markets more efficient. At this point, the logic presented by Boserup (2005) can be useful. Instead of population growth slowing down to equilibrium level associated with the given technologies, population growth leads to the adoption of new methods of production. Cultivators have a wide set of production possibilities via different mixtures of capital and labour inputs. They choose the mixture that reflects best the relative scarcities of these inputs. As population increases, they shift to new techniques that prevent output from falling. According to Boserup, this implies a decline in productivity. However, her model is concerned only with a one-sector economy (agriculture). If productivity increases in agriculture, households could decide to shift labour inputs to other non-agricultural sectors. Moreover, if productivity increased in other sectors, households could be tempted to sacrifice on leisure and use the freed labour inputs on other markets. These latter two forms of development would still appear to be close to the Malthusian ceiling of production and yet there would still be an increase in living standards if they occurred. Such developments are well illustrated in the work of De Vries (2008) regarding the “industrious revolution”. Reduction in transaction costs allowed the labour market to better coordinate employers and employees, leading to greater allocative efficiency and to greater incentives to intensification.
This logic of greater market efficiency explains the absence of the Malthusian checks after the conquest. First of all, the larger population of Quebec allowed for thicker markets to be formed which means more trade opportunities. As trade opportunities become more easily available, arbitrage opportunities also become exploitable. This implies that local supply shocks are eased thanks to the ability of merchants to ship grain around leading to some price equalization in the colony. In our case, the data supports the idea that markets grew increasingly integrated after the conquest and they began to move closely together after 1790 as can be seen with the diminishing price gap between the different cities of the colony (see Figs. 6, 7). This is a first channel by which increased population might not have led to the operation of either the preventive or the positive check. Second, households would have shifted inputs away from agriculture as they could now rely on providers outside their local markets (or even outside the household). In this case, they could work in other areas in order to acquire a monetized income and then complement this income with a small sized farm. Such a channel could have easily materialized through the emergence of the timber trade. Households in Quebec would have allocated inputs to the timber trade (or even the winter ship-yards on the banks of the St. Lawrence River (Dufour 1981), sold the timber on British markets and bought wheat from the neighbouring colony of Upper Canada. Up to the early nineteenth century, furs had been the main exports of Quebec, but this trade occupied only a small share of the population. However, once the timber trade progressively replaced the fur trade, it occupied a much larger share of the population. Households would have shifted inputs away from agriculture to harvest wood, which they could sell to merchants who would then resell it in England. Figure 5 illustrates the importance—on a per person basis—of the increase in the timber trade throughout the nineteenth century. This specialization would have allowed households to better tolerate higher wheat prices because incomes were substantially higher. This argument is strengthened by the fact that throughout the early nineteenth century, trade with the United States was also progressively liberalized. This is well exemplified by the 1831 Colonial Trade Act, which allowed American grains and flour to enter freely into Canada and allowed Canadians to sell timber to Britain and buy wheat from the Americans.
This greater level of market efficiency is well supported by many forms of secondary evidence. First of all, as Bédard and Geloso (2014) underlined, the rise of banking in Quebec which was permitted by the local legislatures allowed the emergence of a network of private bank notes which eased denominational shortages of small currency. Secondly, the British domination over the seas allowed for safer trade and hence allowed the timber trade to expand in the colony to previously unseen levels. Thirdly, trade policy with the United States and other areas was progressively eased allowing for trade to become relatively freer than it had been under French rule. Combined with greater populations within the colony (allowing trade networks to form), this would have also played in favour of increased specialization and hence in favour of the diminution of the preventive and positive checks. Finally, the British also allowed land settlement past 1791 to be outside the realms of seigniorial tenure—whereby the person who farmed the land never owned it—and rather under the British law whereby one owned his farm plot. This would have allowed greater investments in agricultural techniques. Taken together, these factors would have mitigated Malthusian pressures. One important sign in our results that support this claim is the disappearance of the relation between birth rates and death rates during the post-conquest era. The disappearance of this link means that some form of demographic transition had been initiated in Lower Canada through lower mortality. Although it is beyond the scope of this paper to study the demographic transition, we believe that the presence of early signs of its beginning support our claim that population pressures were disappearing. This is because demographic transition is associated with industrialization—something that runs against Malthusian theory. These explanations we propose are merely suggestions at the present time. However, they are plausible and will be easily tested in future papers. We hope at the very least that this new presentation of Malthusian pressures will lead to further research by historians and economists.
Notes
In order to preserve methodological consistency we will apply the AIC lag selection method for further estimations in the paper. We check the lag length with the Wald lag-exclusion test.
In the ADF GLS test for wheat prices the AIC-determined optimal lag is 8; for birth rates it is 2 and for death rates the optimal lag length is 10.
In the Johansen cointegration the AIC-determined optimal lag length is 2.
Malthusian pressures are usually analyzed in the short run (see Nicolini 2007); however, the methodology requires us to avoid specification errors and thus in the presence of a cointegrating vector we would have to include one in our model. Since we do not find cointegration, we apply the VAR framework, which appears to be the appropriate specification in this case.
The Bai–Perron test applied to birth and death rates yields different results: structural breaks at the end and beginning of our time frames, which would not allow us to divide the time-series into sub-samples.
Given the risk of spurious structural breaks, mentioned in Hall et al. (2013, p. 61), we validate the result obtained with the F test by applying the Cumulative Sum test (CUSUM) as in Ploberger and Kramer (1992). The latter test is capable of detecting multiple breaks; however in our case the only extreme point is located at 1767, which validates the result of the F test.
In order to obtain smooth results we use a window of 20 observations and set the smallest step of 1.
For the simplicity a one-lag model is described. The number of lags to be included is determined by the AIC and the Wald lag-exclusion test. We have tested specifications up to the 10th lag and the Wald lag-exclusion test showed no substantial benefits from including lags further than 6. The latter specification with 6 lags outperformed specifications with fewer lags according to the Likelihood Ratio test and the AIC. Therefore, the optimal specification used for our estimations includes 6 lags.
References
Akaike, H. (1974). A new look at the statistical model identification. IEEE Transactions on Automatic Control, 19(6), 716–723.
Altman, M. (1983). Seignorial tenure in New France, 1688–1739: An essay on income distribution and retarded economic development. Historical Reflections/Réflexions historiques, 10(3), 335–375.
Alvarez-Nogal, C., & Prados De La Escosura, L. (2013). The rise and fall of Spain (1270–1850). Economic History Review, 66(1), 1–37.
Bai, J., & Perron, P. (2003). Computation and analysis of multiple structural change models. Journal of Applied Econometrics, 18(1), 1–22.
Becker, G. E., & Murphy, K. (1999). Population and economic growth. American Economic Review, 89(2), 145–149.
Bédard, E. (2012). Histoire du Québec pour les nuls. Montréal: First Editions.
Bédard, M., & Geloso, V. (2014). Free banking and economic growth in Lower Canada, 1817 to 1851. Conference paper presented at Lund University during the Free Banking Conference.
Boserup, E. (1965 [2005]). The conditions of agricultural growth: The economics of agrarian change under population pressure. New Brunswick, NJ: Transaction.
Courville, S. (1990). Entre ville et campagne: l’essor du village dans les seigneuries du Bas-Canada. Québec: Les Presses de l’Université Laval.
Craft, N., & Mills, T. (2009). From Malthus to Solow: How did the Malthusian economy really evolve? Journal of Macroeconomics, 31(1), 68–93.
De Vries, J. (2008). The industrious revolution: Consumer behavior and the household economy, 1650 to the present. Cambridge: Cambridge University Press.
Dechêne, L. (1994). Le partage des subsistances au Canada sous le régime Français. Montréal: Éditions Boréal.
Dhrymes, P. J., & Dimitrios, T. D. (1997). Small sample properties of certain cointegration test statistics: A Monte Carlo study. Columbia University Economics Department discussion paper no. 9798-08.
Dufour, P. (1981). La construction navale à Québec 1760–1825: sources inexplorées et nouvelles perspectives de recherches. Revue d’histoire de l’Amérique française, 35(1), 231–251.
Elliott, G., Rothenberg, T. J., & Stock, J. H. (1996). Efficient tests for an autoregressive unit root. Econometrica, 64(4), 813–836.
Fertig, G., & Pfister, U. (2012). When did Germany cease to be Malthusian? The evolution of the preventive and positive checks, 1730–1870. Paper presented to the BETA-Workshop in Historical Economics at the University of Strasbourg, May, 2012.
Fyson, D. (1992). Du pain au madére: L’alimentation à Montréal au début du XIXe siècle. Revue d’histoire de l’Amérique française, 46(1), 67–90.
Galloway, P. (1988). Basic patterns in annual variations in fertility, nuptiality, mortality, and prices in pre-industrial Europe. Population Studies, 42(2), 275–303.
Gauvreau, D., & Gossage, P. (2001). Canadian fertility transitions: Quebec and Ontario at the turn of the twentieth century. Journal of Family History, 26(2), 162–188.
Geloso, V. (2014a). A history of prices in New France, 1688 to 1760. Economic and Business History Society conference paper.
Geloso, V. (2014b). The seeds of divergence: The economy of French America, 1688 to 1760. Doctoral thesis in progress, Department of Economic History, London School of Economics.
Gentil, M. (2009). Les niveaux et les facteurs déterminants de la mortalité infantile en Nouvelle-France et au début du régime Anglais (1621–1779). Ph.D. thesis, Department of Demography, Université de Montréal.
Government of the Province of Canada. (1853). Census of the Canadas, 1851–1852 (Vol. I). Quebec: John Lowell Printer.
Granger, C. W. J. (1969). Investigating causal relations by econometric models and cross-spectral methods. Econometrica, 37(3), 424–438.
Greer, A. (1985). Peasant, lord and merchant: Rural society in three Quebec parishes, 1740–1840. Toronto: University of Toronto Press.
Guinnane, T. W., & Ogilvie, S. (2008). Institutions and demographic responses to shocks: Wuerttemberg, 1634–1870. Yale University Economic Growth Center discussion paper no. 962.
Haines, M. (2000). Malthus and North America: Was the United States subject to economic-demographic crises? In T. Bengtsson & O. Saito (Eds.), Population and economy: From hunger to modern economic growth (pp. 165–182). Oxford: Oxford University Press.
Hall, A. R., Osborn, D. R., & Sakkas, N. (2013). Inference on structural breaks using information criteria. Manchester School, 81, 54–81.
Hamilton, J. (1994). Time series analysis. Princeton, NJ: Princeton University Press.
Henripin, J., & Péron, Y. (2000). Évolution démographique récente du Québec. In H. Charbonneau (Ed.), La population du Québec: Études rétrospectives (pp. 45–72). Montréal: Éditions du Boréal Express.
Hodrick, R. J., & Prescott, E. C. (1997). Postwar U.S. business cycles: An empirical investigation. Journal of Money, Credit and Banking, 29(1), 1–16.
Johansen, S. (1988). Statistical analysis of cointegration vectors. Journal of Economic Dynamics and Control, 12(2–3), 231–254.
Langlois, G. (1935). Histoire de la population Canadienne-Française. Montréal: Éditions Albert Lévesque.
Le Goff, T. (1974). The agricultural crisis in Lower Canada, 1802–1812: A review of a controversy. Canadian Historical Review, 55(1), 1–31.
Ljung, G. M., & Box, G. E. P. (1978). On a measure of lack of fit in time series models. Biometrika, 65(2), 297–303.
Mann, M. E., Bradley, R. S., & Hughes, M. K. (1998). Global-scale temperature patterns and climate forcing over the past six centuries. Nature, 392(6678), 779–787.
McInnis, M. (1982). A reconsideration of the state of agriculture in Lower Canada in the first half of the nineteenth century. Canadian Papers in Rural History, 3, 9–49.
McInnis, M. (2000). The population of Canada in the nineteenth century. In M. Haines & R. Steckel (Eds.), A population history of North America (pp. 371–432). Cambridge: Cambridge University Press.
McIntyre, S., & McKitrick, R. (2003). Corrections to the Mann et. al. (1998) proxy data base and northern hemispheric average temperature series. Energy & Environment, 14(6), 751–771.
Nicolini, E. (2007). Was Malthus right? A VAR analysis of economic and demographic interactions in pre-industrial England. European Review of Economic History, 11(1), 99–121.
Olson, S., & Thornton, P. (2011). Peopling the North American city: Montreal, 1840–1900 (Vol. 222). Montreal, QC: McGill-Queen’s University Press.
Ouellet, F. (1966). Histoire économique et sociale du Québec, 1760–1850. Montréal: Éditions Fides.
Ouellet, F. (1972). Élements d’histoire sociale du Bas-Canada. Montréal: Huburtise HMH.
Ouellet, F. (1980). Lower Canada, 1791–1840: Social change and nationalism. Toronto: McClelland and Stewart.
Ouellet, F., Hamelin, J., & Chabot, R. (1982). Les prix agricoles dans les villes et les campagnes du Québec avant 1850: aperçus quantitatifs. Histoire Sociale/Social History, 15(29), 83–128.
Paquet, G., & Smith, W. R. (1983). L’émigration des canadiens-français vers les États-Unis, 1790–1940: Problématique et coups de sonde. L’Actualité économique, 59(3), 423–453.
Paquet, G., & Wallot, J.-P. (2007). Un Québec moderne, 1760–1840: Essai d’histoire économique et social. Montréal: Éditions Huburtise HMH.
Pelletier, F., Légaré, J., & Bourbeau, R. (1997). Mortality in Quebec during the nineteenth century: From the state to the cities. Population Studies, 51(1), 93–103.
Ploberger, W., & Kramer, W. (1992). The CUSUM Test with OLS residuals. Econometrica, 60(2), 271–285.
Public Archives of Canada. (1873). Volume IV of the 1871 census of Canada. Ottawa: Department of Agriculture.
Ravn, M. O., & Uhlig, H. (2002). On adjusting the Hodrick–Prescott filter for the frequency of observations. The Review of Economics and Statistics, 84(2), 371–375.
Russell, P. (2012). How agriculture made Canada: Farming in the nineteenth century. Montréal: McGill-Queen’s University Press.
Vallieres, M., & Charbonneau, A. (2008). Histoire de Québec et de sa région (Vol. II). Quebec: Presses de l’Université Laval.
Vallieres, M., & Desloges, Y. (2008). Les échanges commerciaux de la colonie laurentienne avec la Grande-Bretagne, 1760–1850: l’exemple des importations de produits textiles et métallurgiques. Revue d’histoire de l’Amérique française, 61(3–4), 425–467.
Wrigley, E., & Schofield, R. (1981). The population history of England, 1541–1871. Cambridge: Cambridge University Press.
Zeileis, A., Leisch, F., Hornik, K., & Kleiber, C. (2002). strucchange: An r package for testing for structural change in linear regression models. Journal of Statistical Software, 7(2), 1–38.
Zhongwei, Z. (2006). Towards a better understanding of past fertility regimes: The ideas and practice of controlling family size in Chinese history. Continuity and Change, 21(1), 9–35.
Acknowledgments
The authors would like to thank Harald Hagemann for his suggestions and guidance and Daniel Aichinger, Germain Belzile, Christine Clement and participants at the HEC Montréal research seminar for useful comments.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Geloso, V., Kufenko, V. Malthusian pressures: empirical evidence from a frontier economy. J Pop Research 32, 263–283 (2015). https://doi.org/10.1007/s12546-015-9153-9
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12546-015-9153-9