Abstract
Purpose
The accessibility of a certain place can evolve either as the direct result of transport changes or as a consequence of the spatial redistribution of economic activities. These two factors are often indistinguishable—especially at regional level—since improved infrastructure stimulates relocation of activities. Moreover, infrastructure investment choices tend to follow population and economic activity patterns, distorting the cause and effect relationship between infrastructure and accessibility even further. The methodology and results presented here decompose the impact of both factors in terms of accessibility using Spanish data between 1960 and 2010. During this period, Spain experienced profound changes in transport infrastructure and economic activity.
Methods
We use the potential accessibility indicator and resort to index number theory to disentangle the contribution of transport infrastructure from that of land-use changes. Detailed historical data on road infrastructure and population is used to represent the transport and land-use components of accessibility.
Results
Our results show that changes in transport infrastructure had a relevant impact on accessibility, as expected, but changes in the spatial distribution of population had an even greater effect. This outcome may be used as an argument for sustainable accessibility, a concept that advocates integration of transport and land use planning.
Similar content being viewed by others
1 Introduction
There is a growing trend in the literature on transport planning that advocates a change of paradigm from mobility to accessibility planning ([1–5]). Mobility-based measures that have dominated many transport policies include delay per capita, monetary cost of congestion, and highway level of service. Behind the mobility approach, travel speed is considered to be a fundamental key to transport policy success. However, many of those arguing for a paradigm change recall that mobility is rarely an end in itself, but rather a means to increase accessibility [6]. People move towards opportunities and thus the ultimate objective of transport policies should be maximising accessibility instead of speed.
The accessibility concept may be defined as ease of access to markets and it is usually related with lower transport costs, higher levels of competitiveness and better quality of life. This concept has the advantage of simultaneously showing the quality of transport systems (infrastructure) and the location of activities (land-use). An improvement in transport infrastructure, such as constructing a new highway, will reduce travel time and increase accessibility. While, (re)location of economic activities, will change job opportunities for residents in the surrounding areas.
However, in the long run, the effects of transport infrastructure and land uses on accessibility may merge. New economic geography literature suggests that the relationship between transport investments and changes in activity patterns does not always favour economic cohesion but may result in core-periphery distributions [7]. Decreasing returns of transport investments have been measured by several authors ([8, 9]). This is also true for accessibility, since accessibility impacts decrease with network density.
In addition, increased transport capacity may induce spatial dispersion of economic activities, resulting in longer and costlier trips. Spence and Linneker [10] studied the relationship between regional employment and accessibility changes due to new motorways. Their results showed that employment growth was higher in areas with low accessibility, suggesting a decentralization process of economic activities.
Conversely, the agglomeration of economic activities usually entails higher congestion levels which negatively affect accessibility, through increasing transport costs. Nonetheless, most of the more accessible regions also have the highest congestion levels.
It is clear that accessibility is a function of transport infrastructure and the location of economic activities, but which of the two conjoint effects will have a higher impact on accessibility changes? And how does the weight of these two factors evolve over time?
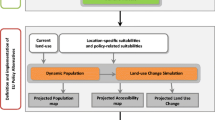
The present study attempts to answer these questions by proposing a new methodology and analysing accessibility change in Spain at the NUTS-3 level, over a 50 year period between 1960 and 2010. During this period a significant transformation of transport infrastructure and economic activity took place. We do so by applying index number theory, which allows us to aggregate (i.e. summarize into a single scalar) the bilateral relation between a given location (origin) and its surrounding destinations (e.g. commercial partners), considering infrastructure as the main input yielding accessibility to economic opportunities. Infrastructure, in the form of travel time, is considered as the input producing accessibility to markets as output, resulting in a productivity index that is defined as the ratio of potential economic opportunities to infrastructure. Furthermore, resorting to the product rule of index numbers, we can consistently decompose accessibility change across locations and over time, enabling us to disentangle the contribution of transport infrastructure from the land-use dimension.
The next section reviews previous studies devoted to the effects of transport infrastructure and land-use on accessibility change, and discusses the advantages of index number theory when pursuing this objective. The following sections present the data and statistical sources used for this analysis (section 3) and the methodology employed to measure accessibility change and decompose it into suitable infrastructure and land use components (section 4). Section 5 reports the results for the Spanish case, while section 6 draws the main conclusions.
2 Accessibility dimensions and their decomposition
In the literature, there are several indicators that can be used to measure accessibility, each one capable of showing one or several of the following dimensions [11]:
-
Land-use: represents the amount and spatial distribution of opportunities at destinations. Opportunities can be measured as population, jobs or other socio-economic variables that may characterize the economic importance of places;
-
Transport: describes the transport system as a facilitator of movements (both passenger and freight flows) between an origin and destination. This is commonly represented by time or cost variables reflecting the quality of the transport system;
-
Time: captures the potential to access a certain location, depending on factors such as time budgets or opening hours of available opportunities;
-
Individual: accessibility is a characteristic of individuals and varies according to their socio-economic status (i.e. income, age, education level).
Given the aggregate national scope of our analysis we will focus on the contribution of the first two dimensions, while time and individual aspects of accessibility are better looked at using micro-level approaches.
Table 1 presents several studies that have used accessibility measures to evaluate changes in transport infrastructure and land-use dimensions. Many accessibility studies have analysed the effect of these two components, either separately or looking at the combined effect of transport and land-use. The common procedure to “isolate” the dynamics of a certain accessibility dimension is to compare the accessibility levels of two periods of time, allowing only the selected dimension to change. This approach has been extensively used to appraise transport infrastructure, such as evaluating the impacts of new transport infrastructure. In Spain, several studies use this approach to analyse road network improvements, generally concluding that road investments bring positive benefits to accessibility changes ([12–15]). Similarly, in Finland, improvements in road and rail networks between 1970 and 2007 were associated with positive accessibility changes and population growth [16]. Other applications can be found in the field of charging policies, [17], or in the field of congestion impacts, [18]; both generally entailing a negative impact on accessibility due to an increase in transport costs. Also, regarding the transport dimension, some studies found spatial spillover effects, defined as accessibility impacts related with transport infrastructure changes in neighbouring regions ([19, 20]).
Only a few studies evaluate both the contribution of transport and land use dimensions to accessibility levels. Spence and Linneker provide one of the first attempts to analyse the evolution of motorways and changing levels of employment on accessibility in Great Britain [10]. Using a standard market potential indicator, these authors show a positive effect of motorways on accessibility levels and some negative impacts due to decentralization of employment, mainly in London and the cities surrounding it.
For the Netherlands, Geurs and Ritsema van Eck, study the effect of transport infrastructure (further subdivided into changes in infrastructure and changes in congestion) and the land use component (measured as the number of jobs), as well as impacts from the interaction of both components [18]. Authors found a higher overall accessibility increase due to changes in employment levels, a lower positive contribution of infrastructure expansion and a negative contribution of the congestion and interaction components.
At a metropolitan level, an interesting study decomposes accessibility into speed and proximity effects for several pairs of US metropolitan regions, [6]. In overall terms, authors show a positive relationship between area density and accessibility, given the greater weight of origin-destination proximity. They have also shown that increasing urban density improves the number of jobs and services 10 times more than a proportional change in travel speed.
Some studies look at longer periods of time, individualizing the contribution of population and/or transport infrastructure change to accessibility ([21, 22]). However, depending on the study’s objective, the separate contribution from accessibility components is omitted.
Despite attempts in the literature to draw conclusions on the contribution of different accessibility dimensions to the overall variation of accessibility levels, the use of different methodologies and case studies make them difficult to compare. In this study we use index number theory to define and decompose accessibility variation into mutually exclusive transport infrastructure and land-use components ([23, 24]). Specifically, we define a productivity index that relates the infrastructure component to land-use, where the latter can be consistently used to recover the former by means of the product rule (and vice versa).
One of the main advantages of analysing accessibility levels and its determinants using index number theory is that this type of approach allows comparability with other studies that may use the same methodology in other places and times. In addition, we improve the methodology to accurately measure the change in accessibility and provide a consistent decomposition of these changes, which allows us to draw conclusions on the precise effects of transport infrastructure and population determinants.
Zofío, J. L. et al. have applied this methodology to study the drivers of generalized transport cost evolution, basically economic costs and infrastructure [25] although as far as we know, this is the first time basic index number theory has been used to estimate the relative contribution of different accessibility components, namely, transport infrastructure and land use dimensions.
Another contribution from this study is the use of historical data to measure the contribution from these two components to accessibility change, covering a long time period (50 years) and providing outcomes for every decade within this period.
3 Data
To calculate accessibility changes in Spain, we use Eurostat population data for the 47 Spanish NUTS 3 regions (islands are excluded), representing 1960, 1970, 1980, 1990, 2000 and 2010. NUTS 3 regions are represented by their centroids (the regional central point) for distance matrix calculations, while NUTS 3 boundaries are used to represent accessibility changes in maps. NUTS 3 regions seemed the most appropriate level of analysis given the relatively low spatial detail of the road network (presented below), while the use of more disaggregated units (i.e., NUTS 5) would require a set of assumptions on how those regional units connect with road links.
Figure 1 shows the overall variation of population for 1960–2010 (upper left map) and the annual variation for the decades within this period. One of the most striking conclusions when analysing these figures is the fact that some Spanish regions have been losing population continuously during these five decades. These are the regions close to the Portuguese border, located in the Autonomous Communities of Galicia, Castilla y León and Extremadura. Other regions in Castilla La-Mancha and Aragón have also suffered from demographic losses, especially in the first decades due to a strong internal migration towards large urban agglomerations such as Madrid and Barcelona. In fact, the Madrid and Barcelona regions, together with some regions in the Mediterranean arch, such as Valencia, Alicante, Murcia or Malaga, have experienced the highest population increase throughout the whole period. In the last analysed decade, the population decline seems to be reversed in many Spanish provinces, but in some cases not so much as to compensate for the loss when compared with their 1960 levels.
The road network is the most extensive transport infrastructure and also the most used transport mode (90% modal share for passenger transport in 2012 and 84% of freight transport, [26]).
A set of digital road networks, covering 1960, 1970, 1980, 1990, 2000 and 2010 is used to calculate accessibility (Fig. 2). These roads were selected from a European database [27] which includes separate datasets for each year. We have combined these separate files into a single network in order to preserve the same network characteristics (i.e. level of detail, geometry of arcs and enable the comparability of networks along the analysed period). Additionally we have defined three different speed profiles, one for each road category (see Table 2).
Despite the potential drawbacks of the aforementioned networks, including the low level of detail mentioned at the beginning of this section, this is the only dataset that covers such a long period of time. The Spanish highways started during the 60s around Madrid, Barcelona and Galicia. In the following decade, the corridors linking Catalonia with the Basque Country and the Mediterranean corridor, connecting Catalonia with Valencia were built. In 1990, many radial highways linking Madrid with the remaining provincial capitals were already in place, and this radial system of highways was fully completed by 2000. In the following decade, there was an attempt to connect provincial capitals, resulting in a more meshed configuration of high capacity roads.
Table 2 shows the evolution of the Spanish road network between 1960 and 2010, according to our set of digital networks. Highways evolved from 0 km in 1960 to almost 5700 km in 2010, while main and secondary roads have declined in terms of length. The decrease in length of these types of roads is mainly due to a common assumption considering that they are upgraded to highways when new lanes run parallel to existing roads.
4 Methods
4.1 Measuring accessibility
For this exercise, we use the potential accessibility indicator that has proven its usefulness to correctly represent travellers’ negative perception of distance, as well as the weight of economic activities within a territory [28]. This indicator is particularly useful for the purpose of our study, since it is sensitive to changes in both land-use and transport infrastructure. Considering j = 1,...,i, …,n, locations, the potential accessibility indicator of a particular location i has the following general form:
where:
- \( {M}_j^t \) :
-
represents the economic opportunity (mass) of each j = 1,...n locations in period t;
- \( f\left({t}_{ij}^t\right) \) :
-
is a function reflecting the distance decay (travel time) between locations in period t; and finally,
- \( {A}_i^{t, t} \) :
-
is the indicator of accessibility of location i to all its n counterparts—including itself, defined as the sum of the ratios of the two previous expressions, and where time superscripts refer to the reference periods of the economic opportunities and access costs.Footnote 1
The accessibility indicator measures access to opportunities at destinations in which smaller and more distant (costly) opportunities provide diminishing influence. In this sense, it correctly replicates some aspects of accessibility valued by individuals such as distance and the socio-economic importance of destinations.
This ratio can be understood as an efficiency or productivity index where infrastructure (in this case through travel time) yields access to markets, defined in terms of socio-economic potential. Indeed, according to Eq. 1, for a population living in location i, the importance of access to each destination j is represented by a function that is directly related to j’s economic weight (mass, M) and is inversely related to the access time through f(t) between i and j. In this study the economic weight (M) is represented by population, and the origin and destination locations are represented by the centroids of the NUTS 3 regions.
Access cost between origin and destination regions is measured in terms of the minimum travel time through the (uncongested) road network, plus an access and egress time that is a function of the area of NUTS 3 regions (Eq. 2). In our case, we do not calibrate the distance decay factor, since historical data for all analysed years would be needed to reflect the evolution of travel behaviour. Travel time between i and j is formulated as:
where:
- RT t ij :
-
represents the fastest travel time between i and j;
- IT t i and IT t j :
-
represent half the estimated internal travel time of i and j NUTS 3 regions, which is calculated as a function of their area; e.g., for location i (Eq. 3, [29]):
and D t ii is the internal distance of NUTS 3 region, in squared kilometres, X is a transformation of the regional radius equal to 0.33. Internal tavel time is obtained, assuming an internal travel speed of 50 km/h. Internal travel distances are important in accessibility analysis that use the potential indicator, since they determine the contribution of self-potential that is the weight of internal market in the overall accessibility level. Equation 3 has the advantage of requiring very little data and it is easy to calculate. This explains why it is used throughout the accessibility analysis, especially when there is a lack of data on mobility patterns or in the level of network detail [30] as in our case. This measurement estimates internal travel time comparing the region to a circle of equivalent area and assuming that population is concentrated towards the regional centre.
4.2 Decomposing the accessibility variation: productivity indices
As in Konüs, A.A., 1924 and Maroto, A. and J.L. Zofío [31, 32], we rely on suitable productivity measures to analyse the variation in accessibility (ΔA i t,t+1) between a base period t = 0 and the current period t + 1 = 1 (see also [24, 31, 33] for general references). Specifically:
where ΔA i 0,1 measures the variation in accessibility as the ratio of the indicators corresponding to the reference period\( \kern0.5em {A}_i^{1,1} \) \( ={\sum}_{j=1}^n{M}_j^1/{t}_{ij}^1 \) to that of the base period \( {\ A}_i^{0,0} \)=\( {\sum}_{j=1}^n{M}_j^0/{t}_{ij}^0 \) . This index contains information relating to the change in both accessibility components: land-use (population) and infrastructure (time), referred to alternative time periods t according to the superscripts. In order to disentangle the individual contribution of these components to the overall accessibility change, we make use of a productivity index that consider the change in population M t j , and its counterpart index representing the change in optimal travel time t t ij .
To this end, it is possible to determine the contribution made by the variation in population to accessibility by explicitly defining the change in the “output” side of the index, which allows the comparison in accessibility considering the existing population in the base and current periods, while taking the base period t = 0 as the benchmark yielding market accessibility:
where the denominator corresponds to Eq. 4, but the numerator reflects a hypothetical accessibility value \( {A}_i^{1,0} \) that considers current period population and the base year road network—with the superscript 0 in \( {PA}_i^0 \) referring to the constant base (time) benchmark. If \( {PA}_i^0 \) > 1 it means increasing accessibility change due to population variation, while the opposite is true for \( {PA}_i^0 \) < 1.
Once \( {PA}_i^0 \) has been defined and calculated, it can be effectively separated from the infrastructure index underlying accessibility change; i.e. it is possible to recover its “input” (infrastructure) counterpart capturing the change in the cost measure of accessibility: \( {IA}_i^{1\ } \). From an operational perspective \( {IA}_i^{1\ } \) is completely determined by means of the product rule.Footnote 2 In particular, it can be solved for in the following way:
and therefore:
Equation 7 renders the infrastructure index explicit but on this occasion considering the current period population as the reference constant:\( {A}_i^{1,1} \) and \( {A}_i^{1,0} \)—hence the superscript in \( {IA}_i^1 \), and updating the road network for consecutive periods. \( {IA}_i^{1\ } \) reflects the aggregate increase of accessibility brought about by changes in transport infrastructure, and therefore it is normally expected that \( {IA}_i^1 \) > 1, showing that improvements in transport networks will lead to an increase of accessibility levels by reducing travelling times.Footnote 3
We now define analogous indices to Eqs. 5 and 7 reversing the reference current and base periods for the network infrastructure and population levels, respectively. In this case, we define \( {PA}_i^1={A}_i^{1,1}/{A}_i^{0,1}=\left({\sum}_{j=1}^n{M}_j^1/{t}_{i j}^1\right)/\left({\sum}_{j=1}^n{M}_j^0/{t}_{i j}^1\right) \), with the same interpretation as Eq. 5, but on this occasion the optimal (minimum time) itineraries remain constant in the current period. Similarly the counterpart decomposition to Eq. 6 is \( {\Delta A}_i^{0,1}={A}_i^{1,1}/{A}_i^{0,0}={PA}_i^1\bullet {IA}_i^0=\left({A}_i^{1,1}/{A}_i^{0,1}\right)\cdotp {IA}_i^0 \), allowing us to recover the corresponding implicit input infrastructure index that uses the population levels observed in the reference period, thereby obtaining \( {IA}_i^0={\Delta A}_i^{0,1}/{PA}_i^1=\left({A}_i^{1,1}/{A}_i^{0,0}\right)/\left({A}_i^{1,1}/{A}_i^{0,1}\right)={A}_i^{0,1}/{A}_i^{0,0}=\left({\sum}_{j=1}^n{M}_j^0/{t}_{i j}^1\right)/\left({\sum}_{j=1}^n{M}_j^0/{t}_{i j}^0\right) \).
Thus there are two equivalent ways of decomposing the variation in accessibility, depending on the choice of reference periods for the counterpart reference period t of the output population and input infrastructure indices: \( {PA}_i^t \) and \( {IA}_i^t \), t = 0, 1. Indeed, depending on the selected reference period, we would generally obtain alternative values for the different accessibility terms of the population and infrastructure measures. This suggests the following geometric mean decomposition taking both periods into account symmetrically:
We can also decompose the time variation from an initial period to a final period into consecutive subperiods (corresponding to the transitivity property of index numbers, see [24]). This allows analysing periods where there have been significant investments in transport infrastructure or identifying periods with greater demographic changes. Therefore, given a sequence of periods, e.g., t = 0, 1, 2, it is verified that \( {\Delta A}_i^{0,2}={\Delta A}_i^{0,1}\cdotp \Delta {A}_i^{1,2} \). Focusing on the initial definition in Eq. 4 and the decomposition presented in Eq. 8, we see that for a general sequence of T periods, t = 0,…T, it is possible to decompose the variation in accessibility between the first and last periods into any subperiods using any of the available alternatives:
From this expression, we can recover any accessibility change between an intermediate period t and the final year T by dividing the fixed base indices corresponding to those periods; i.e.
where \( \Delta {A}_i^{t, T} \) corresponds to a chain component of the variation in accessibility for the whole period: \( \Delta {A}_i^{0, T}=\Delta {A}_i^{0, t}\bullet \Delta {A}_i^{t, T} \). Moreover, as this expression can be generalized to any two particular subperiods, we can also calculate the cumulative variation—chained components—of the accessibility levels between periods t and t + k, whose particular definition is (k = 1 would yield year by year variations):
5 Results
This section shows the variation of accessibility levels for the 1960–2010 period and it presents the results of decomposing the accessibility variation into population and infrastructure contributions.
Table 3 shows cumulated changes in accessibility using 1960 as the reference period (\( \Delta {A}_i^{60, t}\Big) \), together with the relative contribution made by changes in population (ΔPA i 0,t) and infrastructure (ΔIA i 0,t). Values are expressed as the arithmetic mean of all provinces (47 NUTS-3). For the overall period between 1960 and 2010, about two thirds of the accessibility increase is due to population change (50.0% out of 78.1%).Footnote 4 The remainder is due to changes in transport infrastructure. Regarding the accumulated change in accessibility and its population and infrastructure components in ten year periods, we can see that the increase in accessibility driven by population and infrastructure is monotonic, as it increases constantly in a cumulative way.
Figure 3 illustrates the cumulative accessibility change as well as the contribution brought about by the population and infrastructure components for the 2010/1960 period. Comparing the three maps, it is possible to come to a conclusion regarding the positive effect that demographic changes and the improvement of transport infrastructure have had on the accessibility of Spanish regions. Regarding the component that is driving the accessibility change, demographic change has a higher weight for all regions in the overall period. This is particularly true for the largest urban regions such as Madrid and Barcelona, where population has constantly increased through immigration flows during this period (Fig. 1), as well as for their surroundings provinces, which have benefited from increased accessibility to more dynamic regions.
It is worth noting that some regions register a positive contribution of population in their accessibility levels, despite the decline of their population. This happens because regional accessibility levels take into account not only the population within the regional boundaries but also the population of all other regions. Thus, a region that experiences population decline in a specific period can still benefit from positive population changes occurring elsewhere, especially if these changes are registered in nearby places (given the gravity formulation of Eq. 1).
Table 4 shows the change that takes place as the base period is updated every 10 years. The highest overall accessibility increase (18.8%), considering both population and transport infrastructure changes, occurred between 2000 and 2010. This decade also registered the highest contribution of population to the accessibility improvement (14.7%) which is in line with population changes shown in Fig. 1. Population contribution was particularly important for Madrid and its surroundings as well as for most Mediterranean provinces. In addition, the first two decades (1960–1970; 1970–1980) experienced a relatively high accessibility improvement (11.8% and 15.8%, respectively), particularly driven by the population change registered in regions such as Madrid, Catalonia or the Basque Country.
For the period between 1980 and 1990 and 1990–2000, accessibility changes were lower due to a modest population increase, especially in most accessible Spanish provinces. On the other hand, during this period the contribution from transport infrastructure outweighs the contribution from population and partly compensates the negative population growth in provinces such as Orense and Vizcaya. If we compare the interannual infrastructure contribution with the number of kilometres constructed in every decade (Table 2), we can conclude that the highest contributions do not fully correspond with the highest investment periods. Instead, transport infrastructure has had the highest impacts in years of network structural changes, such as 1970–1980 when the radial system of highways started to emerge, and during 1990–2000 when this radial structure led to a denser configuration of highways.
6 Conclusions
Historical data on population and transport infrastructure enables the analysis of accessibility change over time, while the computation of its separate infrastructure and land use components offers a much richer explanation concerning the drivers of accessibility improvements. Index number theory has proven very useful to consistently disentangle these components of accessibility change at a regional level.
When applying this methodology for Spain, our results show that changes in transport infrastructure have helped to increase accessibility, although to a lesser degree than demographic changes. In practical terms, this is the result of transport infrastructure developments following the actual needs of land use and economic activity during most of the period being analysed, as opposed to being used as an instrument to stimulate growth in less developed zones. The findings for Spain are generally consistent with the results reported in the literature, summarized in section 2.
The results suggest that while transport infrastructure can have a long term regional development dimension, policy makers give priority to short-term maximisation of the positive impacts of increasing accessibility. Transport networks linking the main centres of population and economic activity—mainly Madrid and Barcelona in the case of Spain—usually follow radial patterns, which are normally the most efficient solutions in terms of return on investment. The alternative strategy of improving access for areas that lack opportunities would lead to a more equitable evolution of accessibility, but would be far less efficient in economic terms, at least in the short term. For most countries that are in an important spatial redistribution phase (like Spain during the period), the temptation to concentrate on the short term effects is difficult to avoid. Such investment decisions, however, also lead to a vicious circle: improving the accessibility of the central zones draws new activities to these zones, reinforcing their central role, their attractiveness for additional future investments, and resulting in core-periphery patterns.
It is also clear that priorities, choices and impacts change over time, depending on the level of development already achieved. The returns on improving transport infrastructure in the most accessible regions begin to diminish after reaching a certain point of development. For Spain, given the already high connectivity of Madrid and Barcelona with other locations, increasing their accessibility even more would come at a high cost. The political pressure to invest in less developed regions also increases over time, changing the balance between economic and equity considerations in investment decisions.
Our results show that the highest impact of transport infrastructure on accessibility changes does not correspond to the years of greatest network extension, but with years when the network changes structurally. This is particularly due to the development of a radial system of highways, with Madrid as the central point and subsequently, due to the construction of a denser, better connected highway system.
As a general conclusion, the approach and results presented here add to the discussion on the need to integrate transport and land use planning. Our results suggest that the goal to improve accessibility can be better achieved by combining social-economic policies with transport investment decisions.
They also provide evidence on the impacts of improving transport networks and their relative weight compared to the impacts of population change for a 50 year period. This allows an ex-post evaluation of the impact of transport infrastructure policies and the quantification of the role of infrastructure and land-use changes in the evolution of accessibility. While the approach can certainly be useful for transport policy in different contexts, it should be kept in mind that the results refer to a specific country (Spain) and a single mode of transport (road). Second order effects, such as congestion, have not been taken into account but may be relevant for other geographic areas.
Notes
As distance is actually measured in terms of network travel time, we have decided to adopt t to denote distance, which should not be confused with the time superscripts referring to the year in which variables are referred.
While the proposed decomposition of accessibility change is multiplicative in nature and only differentiates between the land-use and infrastructure components, other studies adopt an additive decomposition that results in a third term capturing the interaction or combination effect between the two [18]. This latter component represents the change in accessibility that cannot be solely ascribed to the land use or infrastructure components. This interaction does not emerge in our approach as it allocates accessibility change into the land use (population) and travel time change (infrastructure) components; i.e., the index number methodology results in an exact decomposition that fully exhausts accessibility change into these two mutually exclusive terms.
Indeed, \( {IA}_i^1 \) corresponds to the inverse of the change in time access, thereby contributing to productivity increases with values greater than 1. This can be shown by resorting to the single bilateral relationship between origin i and a specific destination j (hence the ij subscript notation). In this case\( {IA}_i^1={\varDelta A}_i^{0,1}/{PA}_i^0=\frac{A_i^{1,1}}{A_i^{0,0}}/\frac{A_i^{1,0}}{A_i^{0,0}} = \frac{M_j^1/{t}_{i j}^1}{M_j^0/{t}_{i j}^0}/\frac{M_j^1/{t}_{i j}^0}{M_j^0/{t}_{i j}^0}=\frac{A_i^{1,1}}{A_i^{1,0}} = \frac{M_j^1/{t}_{i j}^1}{M_j^1/{t}_{i j}^0}=\frac{1}{{t_{i j}^1/ t}_{i j}^0} \), i = 1,…, n, j = 1,…, n.
A similar outcome is achieved using municipalities (LAU regions instead of NUTS3), where for the overall period between 1960 and 2010 we have registered \( \varDelta {A}_i \) 60,t = 86.3%; \( \varDelta {PA}_i \) 60,t = 52.4%; \( \varDelta {IA}_i \) 60,t = 22.2. Additionally, we have performed a sensitivity analysis on the role of distance decay parameter and internal distances definition. It was found that accessibility variations slightly decrease with higher distance decay parameters and smaller internal travel distance specifications. However, differences are small and similar patterns are observed regarding the contribution of transport infrastructure and population change. Summary results of this sensitivity analysis can be seen in the Appendix.
References
Levine J, Garb Y (2002) Congestion pricing’s conditional promise: promotion of accessibility or mobility? Transp Policy 9:179–188
Department for Transport (2004) Guidance on accessibility planning in local transport plans. DfT, London
Litman T (2016) Evaluating accessibility for transportation planning. Victoria Transport Policy Institute, Victoria
Litman T (2013) The new transportation planning paradigm. ITE J 83(6):20–28
Bertolini L, le Clercq F, Kapoen L (2005/5) Sustainable accessibility: a conceptual framework to integrate transport and land use plan-making. Two test-applications in the Netherlands and a reflection on the way forward. Transp Policy 12:207–220. doi: 10.1016/j.tranpol.2005.01.006
Levine J, Grengs J, Shen Q, Shen Q (2012) Does accessibility require density or speed? J Am Plan Assoc 78(2):157–172
Fujita M, Krugman P, Venables AJ (1999) The spatial economy. Cities, regions and international trade. MIT Press, Cambridge
Fernald JG (1999) “Roads to prosperity” assessing the link between public capital and productivity. Am Econ Rev 89:619–638
Moreno R, Artís M, López-Baso E, Suriñach J (1997) Evidence on the complex link between infrastructure and regional growth. Int J Dev Plan Lit 12(1&2):81–108
Spence N, Linneker B (1994) Evolution of the motorway network and changing levels of accessibility in Great Britain. J Transp Geogr 2:247–264. doi:10.1016/0966-6923(94)90049-3
Geurs KT, van Wee B (2004) Accessibility evaluation of land-use and transport strategies: review and research directions. J Transp Geogr 12:127–140. doi:10.1016/j.jtrangeo.2003.10.005
Gutiérrez J, Gómez G (1999) The impact of orbital motorways on intra-metropolitan accessibility: the case of Madrid's M-40. J Transp Geogr 30:1–15
Holl A (2007) Twenty years of accessibility improvements. The case of the Spanish motorway building programme. J Transp Geogr 15(4):286–297
López E, Gutiérrez J, Gómez G (2008) Measuring regional cohesion effects of large-scale transport infrastructure investments: an accessibility approach. Eur Plan Stud 16:277–301
Monzón A, Ortega E, López E (2013) Efficiency and spatial equity impacts of high-speed rail extensions in urban areas. Cities 30:18–30. doi:10.1016/j.cities.2011.11.002
Kotavaara O, Antikainen H, Rusanen J (2011) Population change and accessibility by road and rail networks: GIS and statistical approach to Finland 1970-2007. J Transp Geogr 19:926–935
Condeço-Melhorado A, Gutiérrez J, García-Palomares JC (2011) Spatial impacts of road pricing: accessibility, regional spillovers and territorial cohesion. Transp Res A Policy Pract 45:185–203. doi:10.1016/j.tra.2010.12.003
Geurs K, van Ritsema Eck JR (2003) Evaluation of accessibility impacts of land-use scenarios: the implications of job competition, land-use, and infrastructure developments for the Netherlands. Environ Plann B Plann Des 30:69–87. doi:10.1068/b12940
Gutiérrez J, Condeço-Melhorado A, Martín JC (2010) Using accessibility indicators and GIS to assess spatial spillovers of transport infrastructure investment. J Transp Geogr 18:141–152. doi:10.1016/j.jtrangeo.2008.12.003
López E, Monzón A, Ortega E, Mancebo S (2009) Assessment of cross-border spillover effects of national transport infrastructure plans: an accessibility approach. Transp Rev 29:515–536
Koopmans C, Rietveld P, Huijg A (2012) An accessibility approach to railways and municipal population growth, 1840–1930. J Transp Geogr 25:98–104. doi:10.1016/j.jtrangeo.2012.01.031
Axhausen KW, Froelich P, Tschopp M (2011) Changes in Swiss accessibility since 1850. Res Transp Econ 31(1):72–80
Fisher I (1922) The making of index numbers. Houghton-Mifflin, Boston
Diewert EW (1992) Fisher ideal output, input, and productivity indices revisited. J Prod Anal 3:211–248. doi:10.1007/bf00158354
Zofío JL, Condeço-Melhorado A, Maroto-Sánchez A, Gutiérrez J (2014) Generalized transport costs and index numbers: a geographical analysis of economic and infrastructure fundamentals. Transp Res A Policy Pract 67:141–157. doi:10.1016/j.tra.2014.06.009
MFOM (2014) Los transportes, las infraestructuras y los servicios postales en España: Informe Anual 2013. Ministerio de Fomento, Madrid
Stelder D, Groote P, de Bakker M (2013) Changes in road infrastructure and accessibility in Europe since 1960. Tender reference nr 20112 CE.16.BAT.040. Final Report
Hansen WG (1959) How accessibility shapes land-use. J Am Inst Plann 25:73–76. doi:10.1080/01944365908978307
Rich D (1980) Potential models in human geography. Norwich, Report Number, 26
Condeço-Melhorado AM, Demirel H, Kompil M, Navajas E, Christidis P (2016) The impact of measuring internal travel distances on self-potentials and accessibility. Eur J Transp Infrastruct Res 16(2):300–318
Konüs AA (1924) The problem of the true index of the cost of living. Transp Econ 7(1939):10–29
Maroto A, Zofío JL (2016) Accessibility gains and transport infrastructure in Spain: a productivity approach based on the Malmquist index. J Transp Geogr 52:43–152. doi:10.1016/j.jtrangeo.2016.03.008
Balk B (1998) Industrial price, quantity, and productivity indices. Springer, New York
Author information
Authors and Affiliations
Corresponding author
Additional information
Disclaimer: The views expressed are purely those of the authors and may not in any circumstances be regarded as stating an official position from the European Commission
This article is part of the Topical Collection on Accessibility and Policy Making
Appendix
Appendix
Table 5 shows a sensitivity analysis to distance decay values (\( f\left({t}_{ij}^t\right) \) in Eq. 1) and internal distance specifications (X in Eq. 3), as well as on the interaction between these two factors. Results are expressed in terms of overall accessibility variation as well as changes due to the evolution of population and transport infrastructure.
The impact of distance decay values was tested by using a power distance decay function and comparing two values of distance decay (α): 1 and 2. Looking at the results for X = 0.33 (which are the ones used in the paper) we conclude that using a distance decay parameter of 2, slightly decreases the accessibility variation from 78 to 70% at the aggregated level, from 50 to 45% regarding the population component, and from 19 to 12% for the infrastructure component. However, the general patterns remain unchanged, since the greater amount of variation in accessibility is due to population change.
Regarding the effect of using different values for X in Eq. 3 and the interaction with different distance decay values, we observe a small variation when α = 1 and slightly higher differences for α = 2.
In general terms, accessibility changes are lower with smaller internal travel distances, as in X = 0.25. This occur because of two joint factors:
-
Variations of internal relations in the OD matrix (when I andj are the same) between to subsequent periods are low, because these are only determined by population changes, since internal distances remain unchanged in the overall period.
-
The weight of self-potential is higher using smaller internal travel distances.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Condeço-Melhorado, A., Zofío, J.L. & Christidis, P. Drivers of changes in Spanish accessibility for the 1960–2010 period. Eur. Transp. Res. Rev. 9, 19 (2017). https://doi.org/10.1007/s12544-017-0229-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12544-017-0229-9