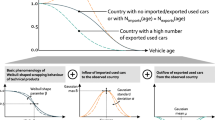
Abstract
Purpose
Various regulatory and fiscal policy instruments are in force to reduce the amount of greenhouse gases and local pollutants emitted by private cars. The incentives operate primarily—or exclusively—on the newest generation of cars. But how fast will technological developments affecting new vehicle models penetrate into the car fleet? The speed at which the adverse effects of private car use will be mitigated through the normal vehicle renewal process, or through an accelerated one, carries considerable interest. Suitable modelling tools are needed. This paper aims to demonstrate the usefulness and flexibility of a bottom-up stock-flow modelling approach to private car fleet forecasting and policy analysis.
Methods
In the BIG model of the Norwegian automobile fleet, the annual stocks and flows characterising the car fleet are specified as matrices of 682 mutually exclusive and exhaustive cells, formed by cross-tabulations between 22 vehicle segments and 31 age classes. New car registrations follow from a disaggregate generic discrete choice model based on two decades of complete sales data for individual passenger car models.
Results
Example projections are presented onto the 2050 horizon under a low carbon fiscal policy scenario as well as a business-as-usual scenario. The fiscal policy is seen to make a large difference in terms of long term fuel consumption and CO2 emissions.
Conclusions
Stock-flow cohort modelling of the automobile fleet is a powerful and handy tool for policy analysis. Even quite simple and straightforward accounting relations may provide important insights into the dynamics of fleet development. It is possible to incorporate, into the stock-flow modelling framework, interesting and useful behavioural relations, explaining aggregate automobile ownership and travel demand, scrapping and survival rates, or consumer choice in the market for new cars.
Similar content being viewed by others
1 Introduction and rationale
The prospect of having two billion private cars roaming the planet’s streets and roads, while emitting greenhouse gases as well as local pollutants, is discomforting [1]. Responsible governments worldwide are contemplating how to prevent the motor vehicle stock from reaching unsustainable levels and/or to decouple income and travel demand growth from environmental degradation and climate change [2]. In most OECD countries, passenger cars constitute the primary source of greenhouse gas (GHG) emissions from transport.
The European Commission has mandated maximum CO2 emission targets for new passenger cars sold in 2015 and 2021, respectively. The targets are 130 g of CO2 per km in 2015 and 95 g/km in 2021, as measured by the NEDC laboratory test cycle. To meet the targets, automobile manufacturers are working to reduce the type approval fuel consumption of conventional vehicles equipped with internal combustion engines (ICE), while also introducing a widening range of zero and low emission vehicles, such as battery electric (BEV) and plug-in hybrid electric vehicles (PHEV).
Similarly, the Euro 1–6 standard for light duty vehicles and the Euro I–VI standard for heavy duty engines oblige manufacturers to fulfil steadily more demanding requirements in terms of nitrogen oxide (NOX), particulate matter (PM), hydrocarbon (HC) and carbon monoxide (CO) emissions.
A common feature of the approaches taken in OECD countries is that the regulatory and fiscal policy instruments operate primarily—or exclusively—on the newest generation of cars. If one can make sure that the next generation of vehicles is consistently more eco-friendly than the previous one, the car fleet will be steadily improving in terms of its environmental footprint.
But how fast will this improvement take place? The need to reduce the annual amount of GHG emitted into the atmosphere is an urgent one [3]. Hence the speed at which the adverse effects of private car use will be mitigated through the normal vehicle renewal process, or through an accelerated one, carries considerable interest. How long will it take for a new technology to penetrate (almost) the entire car fleet? How fast can we lower the fleet’s mean CO2 emission rate? If certain technologies, such as combustion engines, were to be banned from new cars, or subjected to stiff taxes, how long would it take before emissions from the car fleet had dropped by, say, 50 or 90 %? What kind of modelling apparatus is needed to resolve such questions? The aim of this paper is to provide some answers to these questions.
In Norway, the government has set a CO2 target of maximally 85 g/km emitted, according to the NEDC type approval tests, from new cars sold in 2020 on average. While there is no domestic car manufacturing, the purchase, ownership and use of zero emission vehicles—BEVs and fuel cell electric vehicles (FCEV)—enjoy substantial fiscal and regulatory incentives. These vehicles are exempt of value added tax (VAT), vehicle purchase tax, road tolls and public parking charges. They benefit from strongly reduced annual circulation tax and ferry fares. Moreover, they are generally allowed to travel in the bus lane and may be parked and recharged for free in many public parking lots.
Also, the vehicle purchase tax payable upon first registration in Norway strongly penalises conventional cars with high CO2 emission rates, be they petrol or diesel driven, while low emission vehicles, such as PHEVs, may in the best of cases come out with almost no purchase tax.Footnote 1
The stock of vehicles, be it at the global, national, local or company level, is the result of several flows operating over time: new registrations, scrapping, and second hand import and export. To keep track of how fast technological developments and other changes in the attributes of new vehicles penetrate into the vehicle fleet, a stock-flow cohort model approach is an obvious methodological choice. We have therefore set out to develop a detailed, comprehensive and coherent vehicle turnover model for the Norwegian passenger car fleet.
While ours is not the first stock-flow model of the passenger car fleet,Footnote 2 few—if any—of these modelling efforts have been exhaustively described in the scientific literature. Our paper should help fill this gap. It aims to illustrate the fruitfulness of the stock-flow vehicle cohort approach, while also demonstrating the wealth of relevant information accessible through a rigorous and detailed bottom-up accounting system for passenger car segments and their respective attributes. Relying almost exclusively on administrative records available from government or corporate agencies, our approach does not depend on costly household data collection or on any other type of stated or revealed choice survey.
In Section 2, we describe the general structure and segmentation used in our BIGFootnote 3 model of the Norwegian passenger car fleet, while also presenting a first picture of the car stock, by segments and age, as of our base year 2012. In Section 3, we show how the systematic information put into the model can be used to derive a host of intermediate results, such as mileage patterns, CO2 emission developments, vehicle survival rates and life expectancy. In Section 4, a we present a simulation exercise demonstrating the usefulness of the discrete choice model of automobile purchase. Another BIG model application is presented in Section 5, where a set of scenario projections illustrate the long-term impact of a low carbon fiscal policy. Certain strengths, weaknesses and opportunities to our approach are discussed in Section 6. Conclusions are drawn in Section 7.
2 Model structure and empirical foundation
2.1 Segmentation
The BIG model splits the car stock into 22 segments and 31 age classes. There are nine segments for petrol driven cars and nine for diesel driven ones, each fuel class being subdivided into weight classes. In addition, there is one segment for hybrid vehicles (HEVs, including PHEVs), one for BEVs, one for FCEVs, and one for vehicles using other energy carriers (compressed natural gas, ethanol, etc.).
The segmentation is based on objective criteria only. We have chosen to avoid the commonly accepted segmentation into ‘compact’ cars, ‘mid-sized’ cars, ‘luxury’ cars, etc., for the simple reason that these labels are to some extent subjective and hence elusive. Relying on objective measurements, we will always be able to know how to classify a given vehicle, and even a hypothetical one, as long as its engine type and curb weight are declared.
The composition of the Norwegian automobile fleet as of 31 December 2012 is shown in Fig. 1.
One notes that, while older vehicle generations are made up predominantly by petrol driven cars, diesel driven vehicles have become more frequent from the 2007 cohort onwards. In later years BEVs and HEVs have acquired noticeable market shares (Fridstrøm L and Østli V, 2016, under review for Transportation Research A).
Vintage cars older than 30 years are fairly numerous in Norway. These are exempt of the purchase tax otherwise payable upon first registration or import, and subject to a strongly reduced annual circulation tax.
2.2 Accounting relations
The recursive structure of the BIG forecasting algorithm is shown in Fig. 2. To each cell in the 22 × 31 matrix of the car fleet, various attributes are assigned, such as mean type approval fuel consumption per km, mean annual distance driven, annual rate of scrapping, and an annual rate of second hand (used car) import. There is also a residual outflow of vehicles defined, with its own annual rate, covering second hand vehicle export and net temporary or permanent deregistration.Footnote 4
Let A n i,j , (i = 1, 2,...., 22; j = 1, 2, …, 31) denote the number of vehicles in segment i and age class j at the end of year n. Also, let b n i,j , s n i,j and d n i,j denote, respectively, the used car import, the scrapping, and the net deregistration of vehicles in segment i and age class j during year n.
For notational clarity, we use capital letter symbols for stocks, while lower case letters denote flows. For coefficients, we shall use lower case Greek letters.
Now, the following accounting identities apply:
where we have defined the used car import, scrapping and net deregistration rates
Most cars survive until the next year. The j’th youngest cohort in year n becomes the j + 1 youngest cohort in year n + 1. In addition, second hand vehicle import augments the stock of vehicles within segment i and each age class j by a fraction β i,j of the stock at New Year. Similarly, scrapping and deregistration mean that each year there is some attrition. Here, for notational simplicity, we have assumed that the used car import, scrapping and deregistration rates are temporally stable, i. e. they do not depend on the year n. In practical model applications, this default option may or may not be adhered to.
From the Norwegian motor vehicle registry we extracted the following vehicle stock, used car import and scrapping data for 2010, 2011 and 2012:
From these data we estimated the following used car import and scrapping rates:
i. e., by taking the average empirical rates as observed over the 2 years 2011 and 2012.
The residual net deregistration rate was determined—how else?—residually, by taking
i. e. by solving Eq. (1) for \( {\widehat{\delta}}_{i,j} \) and computing the average over the years 2011 and 2012.
For hybrid and battery electric vehicles, the empirical basis for the assessment of survival rates and mileage is scant, to say the least. As of 2012, few of these vehicles were old enough to have made their first odometer reading at periodic vehicle inspection, and too few were old enough to provide reliable statistical information on annual survival rates up to the end of the vehicles’ lifespan. Moreover, since early BEV and HEV models are uncharacteristic—typically smaller and simpler—compared to later generations, it would be quite misleading to base long-term projections on the scrapping rates and mileage observed for these early varieties. Instead, provisional ad hoc survival rates and mileage parameters for BEVs, HEVs and FCEVs have been set similar to those of mid-size petrol driven cars, or somewhat lower. Information released by Nissan on their battery electric model LEAFFootnote 5 suggests an average annual mileage of 16 500 km, comparable to that of new ICE cars. Figenbaum et al. [7] confirm that modern BEVs in Norway are driven 14–15,000 km per year—just about as much as the average, new petrol driven car.
2.3 A discrete choice model for new cars
For j = 1, i. e. for the youngest cohort of cars, shown in Fig. 2 as the blue, left-most column of the vehicle stock matrix A n = [A n i,j ], one cannot start from cohort data taken from the previous year. A different source of information is needed. To this purpose, a nested logit model of new car purchases was developed by Østli V et al. (2016, under review, European Transport Research Review).
Drawing on the software and data organising facilities of the Norwegian Road Federation (www.ofv.no), complete and detailed new car sales data were extracted for the period from January 1992 through July 2011. A total of 44,087 different passenger car models enter this data set.
For reasons of completeness, only the period 1996–2011 was used for estimation, including 1.6 million transactions involving 38,468 different automobile models. Obviously, few—if any—of these models are available on the market throughout the period. Only a certain subset of car models enter the choice set in a given year.
In the logit model every single car sale is regarded as a separate discrete choice where, in principle, every car model available in the market at that time is included in the buyers’ set of alternatives. For each vehicle model, the data set includes information such as the vehicle’s make, list price, purchase tax amount, type of fuel, calculated per kilometre cost of fuel, curb weight, engine power, drivetrain (rear, front or 4-wheel drive), utility load, width, length, and number of seats and doors, as well as the number of units sold each year. The nested logit model uses these individual vehicle characteristics as explanatory variables, i. e. as arguments in the buyers’ indirect utility function.
Since the model is supposed to predict the market share of potential new car models with known or assumed attributes, care was taken to specify the model as a generic one. There are no alternative specific coefficients, other than the dummies capturing the vehicle’s make. Model coefficients have the expected sign, almost all of them being highly significant by the robust t-test. The per kilometre fuel cost coefficient is compatible with car buyers taking full account of future energy cost savings, while also not applying a discount rate much higher than zero (Table 1).
Extensive testing was done in order to find the appropriate nest structure. It was found that the only permissible nest structure is one that assigns all cars of a given make to one nest. There are 21 such nests in the model, the last one being a residual nest assembling ‘all other makes’.
The model does not predict automobile sales at the level of the individual vehicle model with any degree of precision. Nor is this the intention. Some vehicle models are very similar—indeed, in some cases deciding whether two cars represent two different models or two versions of the same model may seem like a matter of fine judgment. Hence the prediction of demand at the level of the individual vehicle model carries less political interest than forecasting at the somewhat more aggregate level, whereby cars are grouped according to, e. g., their make, size, fuel economy or exhaust emissions. At this level, the model appears to discriminate well between various policy scenarios, as demonstrated by the simulation exercise described in Section 4 below.
In using the model for such purposes, one is greatly helped by the fact that the model includes, in addition to the retail price, an explanatory variable defined as the share of the retail price which is not made up by tax. One may interpret this variable as a proxy for all those quality attributes which are not captured by other explanatory variables. With this specification we may have avoided, and at worst reversed, one type of omitted variable bias commonly found in econometric studies of demand for heterogeneous products—that of ignoring that the price variable reflects quality differences between the products, something which results in a numerically underestimated price elasticity.
According to our model, price changes due to taxation have larger demand effects than those originating from the manufacturing or marketing side. Example price elasticities, calculated under two distinct assumptions are exhibited in Fig. 3. On the horizontal axis, we measure arc elasticities resulting from uniform 10 % increases in tax and pre-tax price. These are typically between −3 and −1. On the vertical axis, elasticities resulting from a tax increase alone are shown. Most of these are between −5 and −4.
Elasticities depend crucially on the level of aggregation. Since the assumption in Fig. 3 is that the price changes only for one particular model at a time, the elasticities shown are numerically large. Much smaller elasticities result if one assumes that all models of a given make have their prices changed by the same percentage (red dots in Fig. 4). In such a case, some less expensive cars may actually experience higher sales, i. e. a positive price elasticity, as buyers flock to cheaper models.
One notes that the more expensive models come out as consistently more price elastic. This follows from the structure of the generic multinomial logit model, whereby the price elasticity of demand for a certain alternative is proportional to its initial price and to the estimated price coefficient [8: 111].
Further details on our discrete choice model of automobile purchase can be found in the companion paper by Østli V et al. (2016, under review European Transport Research Review). Our model differs from most vehicle choice models reported in the literature in that it contains no information on the vehicle owners or their households. Hence the model cannot predict the effect of changes occurring to the car owners rather than to the vehicles themselves. Yet the buyers’ preferences are implicit in the utility functions estimated. The model coefficients are interpretable as the vehicle attributes’ (relative) marginal utility, as judged by the average buyer.
The benefit of disregarding buyer characteristics is one of considerable simplification, leaving room for a maximally detailed, exhaustive and disaggregate representation of the automobiles themselves. Also, it means that no input is required on such variables as household structure, population and income growth, or transport infrastructure and prices, in order for the model to produce a forecast.
By aggregating the predicted, model specific market shares into the segments shown in Fig. 1, and multiplying by an exogenously given aggregate number of new cars registered, we obtain, for each forecasting year n, the 22 × 1 vector of new car purchases forming the left-most column of the stock matrix A n.
2.4 Mileage, fuel consumption and exhaust emissions
Denote by f n i,j the aggregate fuel consumption of vehicles in segment i and age class j during year n, and by m i,j the kilometrage of segment i cars in their jth life year. Also, denote by ϕ i,j the mean real-world per kilometre fuel consumption within segment i and cohort j, by \( {\tilde{\phi}}_{i,j} \) the corresponding laboratory measured, type approval fuel consumption rate, and by \( {\eta}_{\ast j}={\phi}_{i,j}/{\tilde{\phi}}_{i,j} \) the cohort specific ratio of real-world to type approval rates of fuel use, as established by Mock et al. [9, 10]. For lack of better information, we assume this ratio to be uniform across vehicle segments. Also, we assume that the fuel efficiency of a cohort of passenger cars does not change with the vehicles’ age. Here, again, we rely on Mock et al. [9].
The total fuel consumption of the car fleet in year n is then calculable as
where we have weighted the fuel consumption of each cohort by the average size of the car stockFootnote 6 through year n.
Letting \( {\varepsilon}_{\begin{array}{l}i\\ {}\end{array}} \) denote the kilogram amount of CO2 emitted per litre of fuel consumed by cars in segment i, we compute the total amount of CO2 emissions from the car fleet in year n by the formula
The ratio of CO2 emissions to fuel combustion is, with small variations, a physical constant specific to each type of fuel. In the BIG algorithm, we have set ε i = 2.316 gCO2/l for hybrid (i = 1) and petrol driven cars (i = 5, 6,…,13) and ε i = 2.663 gCO2/l for diesel driven ones (i = 14, 15,…, 22).
To obtain data on the annual mileage of cars in their jth life year (m i,j ), we have extracted odometer readings from the registry of periodic vehicle inspection. Under EU regulations, passenger cars are generally inspected at 2-year intervals, the first inspection taking place about 4 years after the vehicle’s first registration. Certain interpolations and adjustments were made in order to convert these 4-year and 2-year readings into consistent annual mileage estimates (see Section 3.2).
3 Intermediate results
Using the above framework, programmed as a set of Excel spreadsheets, we are able to simulate several paths of development, differing primarily in terms of new car entries, until the 2050 horizon. Interesting pieces of information can be distilled from the stock-flow modelling framework even before making the first model projection.
3.1 Survival rates and vehicle life expectancy
The sum of the scrapping and net deregistration rates translate into age and segment specific survival rates given by
and cumulative survival probabilities
The life expectancy of a car within a given segment is calculable as
where k ∗ is the average age of vintage cars older than 30 years. We have set this constant to 35 years.
The survival probabilities and life expectancies are exhibited in Figs. 5 and 6, in which the colour codes are roughly the same as in Fig. 1.
Note that in the BIG stock-flow model, life expectancy measurements exceed the vehicles’ real life span, as reckoned in calendar months, by a little more than 1 year. This is so because, in the stock-flow model, age is counted from January 1 in the year of first registration to December 31 in the scrapping year. But on the average new vehicle enters the stock at mid-year, while scrapping is concentrated between 1 January and 20 March, since the annual circulation tax is due at the latter date.
Larger cars live longer than smaller cars. While nearly half of the largest petrol cars last as long as 25 years, the smallest diesel cars have an average life span in Norway of only 14–16 years. The overall life expectancy of Norwegian registered passenger cars is 17.8 years, as reckoned in the BIG model, or roughly 16.5 years as counted from the date of first registration to the date of scrapping, export or final deregistration.
3.2 Annual vehicle kilometres travelled
The annual vehicle kilometres travelled, as distilled from the odometer readings taken during periodic vehicle inspection, are shown in Fig. 7.
Diesel driven cars travel considerably farther than petrol cars, and younger vehicles are used a lot more than older ones.
Behind the latter phenomenon there are probably three mechanisms at work. Newer cars are perceived as safer, more comfortable, more fuel efficient, and generally more attractive as a travel mode, than older cars. Put otherwise, the same person would have a higher probability of choosing her own car over travelling by bus or coach, if this car is new and technologically up-to-date, than if it is old and tattered. Also, the overall trip frequency may be positively influenced by having access to a nice new car.
Secondly, since purchase decisions are made, not by the vehicles themselves, but by people, there is a selection process going on, whereby car owners with a large road travel demand tend to invest in newer and more expensive cars.
Thirdly, somewhere between 40 and 50 % of all new passenger cars are registered to a company,Footnote 7 in many cases to a leasing, car rental or taxi company. These cars are typically driven longer than average distances, until they are traded in the second hand market after a few years.
Some vehicle segments, such as the smallest diesel cars and the biggest petrol cars, exhibit seemingly erratic mileage patterns at high age. This is simply because the number of vehicles in these categories is quite small, which gives rise to pronounced random variation. We have chosen not to smooth out the empirical curves and replace them by artificial rates, since, on account precisely of the small number of vehicles affected, the potential aggregate forecasting error is quite limited.
3.3 CO2 emission rates
The mean type approval rates of per kilometre CO2 emissions characterising different cohorts of vehicles within each segment are shown in Fig. 8. The trend is clearly downwards in all segments. Note, however, that the growing discrepancy between type approval and real-world emission rates serves to neutralise a large part of the improvement.Footnote 8
4 Short-term policy simulations
The consumers’ choice of cars being sensitive to retail prices, and to the share of the price which is not made up by tax, the logit model of vehicle choice can be used to predict changes in the different car models’ market share under changes in the vehicle purchase tax regime. The Norwegian automobile purchase tax, payable upon first registration of a vehicle, is a sum of four independent components, calculated on the basis of curb weight, ICE power, and type approval CO2 and NOX emission rates, respectively (Fig. 9). All but the NOX component are convex, exhibiting increasing marginal tax rates. The CO2 component is negative (as of 2014) for vehicles emitting less than 105 gCO2/km by the type approval test. For PHEVs, the electric motor does not count towards the tax on engine power, only the combustion engine does, and the weight component is reduced by a benchmark 15 % (as of 2014), so as to leave the weight of the battery pack out of the calculation. As noted above, BEVs and FCEVs are altogether exempt of purchase tax, as well as of the standard 25 % value added tax (VAT).
Vehicle purchase tax as a function of curb weight, combustion engine power, and type approval CO2 and NOX emission rates, in Norway 2014 (NOK = Norwegian kroner. As of 1 July 2014, € 1 = NOK 8.43). Source: Fridstrøm et al. [12]
In Figs. 10 and 11, we show the results of a simulation exercise, in which the effects of certain hypothetical changes to the VAT and vehicle purchase tax rates are simulated.
The fiscal policy changes simulated are the following:
-
A.
Ten per cent higher total purchase tax for all vehicle models
-
B.
Ten per cent increase in the CO2 component of the purchase tax
-
C.
Introduction of VAT and purchase tax on BEVs, according to same rules as for PHEVs.
Figure 10 depicts relative changes in market shares, under each of the above three assumptions, for the 20 most important segments of the BIG model (confer Fig. 1). By assumption, any tax increase is passed on entirely to the buyers, in the form a higher retail price.
According to the model, a generally 10 % higher purchase tax (alt. A) will boost the market for BEVs by almost 10 %, since these vehicles are exempt of the tax. Hybrid cars also gain market shares. The larger petrol and diesel driven cars will, however, lose up to 14 % of their sales.
More moderate effects in the same direction are predicted under a 10 % increase in the CO2 component only (alt. B).
If and when the tax rules applicable to PHEVs are brought to bear even on BEVs (alt. C), a 24 % drop in BEV sales can, according to the model, be expected. All other vehicle segments will see their market shares increase.
The corresponding changes in average type approval CO2 emissions are shown in Fig. 11. A 10 % stiffer overall purchase tax is consistent with a 2.41 gCO2/km lower average type approval emission rate from all new passenger cars. Abolishing the tax exemptions for BEVs will, on the other hand, boost the mean emission rate by 3.85 gCO2/km, through changes in the mix of cars sold.
The left-most and right-most policy options shown in Fig. 11 differ by 6.3 gCO2 per km. This difference corresponds to roughly 2.5–3 ml/km lesser fuel consumption by the type approval test. For a car running 200,000 km before scrapping, the total fuel savings are 7–800 l over the vehicle’s lifetime, when considering that the real-world, on-the-road fuel consumption of the 2014 cohort of cars is about 40 % higher than according to the EU type approval test [11]. For the entire 2014 cohort of Norwegian registered cars, the lifetime CO2 emissions difference between the two policy options is around 250,000 tonnes. Today’s policy choice affects GHG emissions for decades to come.
5 Long-term scenario projections
The main objective of the BIG stock-flow model is to provide a tool for long-term policy analysis. A few applications are presented below.
In Fig. 12, we show the stock of vehicles at year-end 2030 according to a reference path developed by Fridstrøm et al. [12]. In this scenario, no changes are made to the design of the vehicle purchase tax as applicable in 2014, but the tax and toll exemptions for BEVs are gradually abolished between 2018 and 2022.
Regarding technology development, the following assumptions were made. The manufacturing cost differential between BEVs and petrol driven cars will decrease gradually and disappear around 2022. Energy efficiency improvements will take place for all ICE and hybrid vehicles. The mean type approval rate of fuel consumption of new petrol and diesel driven cars is assumed to drop by 1 % per year throughout the period 2014–2050. For hybrid vehicles, the rate is set at 3 % per year, reflecting an assumption than an increasing share of these vehicles will be plug-in hybrids.
On top of the improvements in fuel economy and manufacturing costs, BEVs are also assumed to undergo gradual quality improvements (e. g., extended range), valued at NOK 100 000 (= € 11 862) per vehicle by 2022 and another NOK 60,000 by 2050. For hybrid vehicles, half as large an improvement is assumed.
One notes that even under the ‘business-as-usual’ scenario, hybrid and battery electric vehicles are projected to become considerably more numerous.
The 2- to 10-year old cohorts are seen to be more numerous than the youngest one. This has nothing to do with changes in the total number of new cars registered, which is assumed constant throughout our projection period. The explanation is second hand car import, which typically adds 20–25 % more vehicle registrations on top of the new car sales. The great majority of second hand cars imported are between 2 and 5 years of age.
In Fig. 13, we show a corresponding picture from the alternative ‘low carbon’ policy scenario, in which the purchase tax incentives to buy low and zero emission vehicles are strengthened considerably. Here, hybrid and battery electric vehicles are seen to make up more than 50 % of the youngest cohort, but still only 21 % of the total car fleet in 2030.
A car fleet is, in other words, an inert matter. This becomes even more visible when we plot average CO2 emission rates, as in Fig. 14. The red curve, representing the car fleet’s mean type approval rate of CO2 emissions, lags 10–15 years behind the green curve, which represents the newest generation of cars. Moreover, the real-world CO2 emissions, shown in blue, are considerably higher than the type approval rates. This gap is widening, since the discrepancy between laboratory and on-the-road emissions has been growing with later generations of cars [9–11].
Passenger cars’ average CO2 emission rates under business-as-usual (a) and low carbon fiscal policy (b) scenarios 2013–2050. Source: [12]
Figure 15 shows the development of the automobile stock 2012–2050, as segmented by energy carrier or propulsion technology, under the low carbon scenario. One notes that in this particular projection, the aggregate car fleet increases slightly between 2012 and 2030, before levelling out. In the BIG model, aggregate car ownership is endogenous, following from new car acquisitions and from the second hand import, scrapping and net deregistration rates. By adjusting these rates, the user may, however, steer the size of the car fleet towards a given target, if desired.
6 Discussion
The BIG stock-flow cohort model constitutes a bottom-up approach to vehicle fleet forecasting. New car registrations follow from a disaggregate discrete choice model based on sales data for individual passenger car models. The flows and stocks characterising the car fleet are specified at a somewhat coarser, yet relatively detailed level, describing each year’s stocks and flows of vehicles as the aggregation of 22 × 31 = 682 mutually exclusive and exhaustive cells. This accurate bottom level accounting guards against gross errors of aggregation, without, of course, preventing the model user from producing and presenting results at a much less detailed level.
In the interest of tractability, it has been necessary to make certain simplifying assumptions. As a default option, age and segment specific scrapping, deregistration and second hand car import rates have been assumed temporally stable, calibrated in accordance with the empirical means observed over the 2-year period 2010–2012. Also, for lack of better information, certain default parameters have been assumed invariant across vehicle segments or cohorts. The model user may, of course, deviate from these default values whenever suitable.
Also, since annual mileage factors are set exogenously for each cell in the 22 × 31 vehicle stock matrix, and—as a default—do not vary over time, the model does not take account of rebound effects, such as when aggregate road travel demand increases in response to a lower average per km energy cost. Moreover, since there is no behavioural relation explaining aggregate car ownership or acquisition, there is also a possible rebound effect—not accounted for—in terms of a larger (or smaller) car fleet. As demonstrated by D’Haultfoeuille et al. [13] in the context of the French feebate system for car purchases, such effects could be quite important.
With the present version of the BIG algorithm, rebound effects must be calculated outside the model, by combining BIG model runs with travel demand modelling. Fridstrøm et al. [12] used the national and regional travel demand systems for Norway to assess the effect of a 50 % lower average per km fuel cost, brought about by fiscal incentives bearing on new car purchases. Car travel demand is then projected to increase by 15 %, as measured in vehicle kilometres on short-haul (urban) trips, and by 48 % on long-haul (interurban) trips. As measured in terms of overall CO2 emissions, however, the rebound effect is more important in the urban than in the interurban setting. This is so because, while short urban car trips compete with generally more climate friendly public transport, long-haul interurban car trips in Norway compete primarily with the air mode.
The BIG stock-flow model is primarily a coherent accounting framework, into which economic, behavioural or technological relations can be built. Apart from the discrete choice model of new car purchases, the framework itself is almost void of behavioural content. But the accounting identities allow for several useful deductions, such as when we estimate the time lag between changes occurring to, respectively, the flow of new cars registered and the stock of cars, or when the survival rates of different vehicle segments are derived from a few years’ data on the stock of cars and the flow of vehicles scrapped.
Potential extensions and improvements of the stock-flow model include (i) the integration, into the framework, of behavioural relations endogenising, e. g., scrapping rates, aggregate vehicle miles travelled, or aggregate car purchases, including second hand import, (ii) the extension to a wider set of knock-on effects covered, so as to include, e. g., particulate matter, NOX emissions, or accidents, and (iii) the extension to other types of vehicles, such as buses, vans and heavy freight vehicles.
7 Conclusions
Stock-flow vehicle cohort models exploit the accounting relations inherent in the processes of fleet development, new car acquisition, scrapping, import, export and deregistration, in a way very similar to how, in a demographic forecasting model, the flows of births, deaths, immigrants and emigrants would influence and depend on the stock of individuals, i. e. the human population.
Stock-flow cohort modelling of the car fleet is a powerful and handy tool for policy analysis. Even quite simple and straightforward accounting relations may provide important insights into the dynamics of fleet development. A particularly useful piece of information concerns the amount of inertia involved, as characterised, e. g., by the time lag between technological improvements affecting new vehicles and their penetration into the car fleet.
It is possible to incorporate, into the stock-flow modelling framework, interesting and useful behavioural relations, explaining aggregate passenger car ownership and travel demand, scrapping and survival rates, or consumer choice in the market for new cars. Even without such behavioural relations, the framework is useful for analysing and predicting policy dependent developments in terms of energy use, GHG emissions, local pollution, accident rates, fiscal impact and economic costs.
Far from presupposing sophisticated computer programming, the recursive stock-flow cohort model can be implemented by means of standard spreadsheet software.
Notes
See companion paper by Fridstrøm L and Østli V (2016, under review, Transportation Research A).
BIG is an acronym for ‘bilgenerasjonsmodell’ – meaning ‘car generation model’ in Norwegian.
By ‘scrapping’, we mean turning the car in to an authorised vehicle recycling facility, whereby the scrap deposit payable upon the vehicle’s first registration is reimbursed. Residual net deregistration covers all those cases where the vehicle is removed from (Norwegian) roads, however without the owner collecting the scrap deposit. Net deregistration could be negative, if more vehicles are reregistered than deregistered. It is not uncommon for owners to temporarily hand in the vehicle’s license plates, i. e. to deregister the car, so as to avoid paying the annual circulation tax.
By convention, we set A n i,0 ≡0 ∀ i, n. Since, on the average, last year’s cohort of cars enter the stock around mid-year, they travel only half a normal annual mileage.
Source: www.ofv.no
References
Sperling D, Gordon D (2009) Two billion cars. Driving towards sustainability. Oxford University Press, Oxford
OECD (2002) Indicators to measure decoupling of environmental pressure from economic growth. OECD, Paris
IPCC (2013) The physical science basis. Contribution of working group I to the fifth assessment report of the Intergovernmental Panel on Climate Change. Cambridge University Press, Cambridge
Meurs H, Haaijer R, Smit R, Geurs K (2006) DYNAMO: dynamic automobile market model for the Netherlands. Paper presented at the European Transport Conference, Strasbourg 2006
Meurs H, Haaijer R, Geurs KT (2013) Modeling the effects of environmentally differentiated distance-based car-use charges in the Netherlands. Transp Res D 22:1–9
Hugosson MB, Algers S, Habibi S, Sundbergh P (2014) The Swedish car fleet model. Evaluation of recent applications. CTS Working Paper 2014:18, KTH Royal Institute of Technology, Stockholm
Figenbaum E, Kolbenstvedt M, Elvebakk B (2014) Electric vehicles – environmental, economic and practical aspects. TØI Report 1329, Institute of Transport Economics, Oslo
Ben-Akiva M, Lerman SR (1985) Discrete choice analysis. Theory and application to travel demand. MIT Press, Cambridge
Mock P, German J, Bandivadekar A, Riemersma I, Ligterink N (2013) From laboratory to road: a comparison of official and ‘real-world’ fuel consumption and CO2 values for cars in Europe and the United States. ICCT, Berlin
Mock P, Tietge U, Franco V, German J, Bandivadekar A, Ligterink N, Lambrecht U, Kühlwein J, Riemersma I (2014) From laboratory to road: a 2014 update of official and ‘real-world’ fuel consumption and CO2 values for passenger cars in Europe. ICCT, Berlin
Tietge U, Zacharof N, Mock P, Franco V, German J, Bandivadekar A, Ligterink N, Lambrecht U (2015) From laboratory to road: a 2015 update of official and ‘real-world’ fuel consumption and CO2 values for passenger cars in Europe. ICCT, Berlin
Fridstrøm L, Steinsland C, Østli V (2014) Engangsavgift på personbiler. In: Fridstrøm L, Alfsen KH (eds) Vegen mot klimavennlig transport. TØI report 1321. Institute of Transport Economics, Oslo, pp 92–106
D’Haultfoeuille X, Givord P, Boutin X (2013) The environmental effect of green taxation: the case of the French Bonus/Malus. Econ J 124:F444–F480
Acknowledgments
The basic research underlying this paper was made possible through the TEMPO project funded by the Research Council of Norway (grant number 195191) and supported by 12 stakeholder partners, viz. the Norwegian Public Roads Administration, the Ministry of the Environment, the National Rail Administration, the Norwegian State Railways (NSB), Akershus County Council, Ruter AS, the Norwegian Automobile Association (NAF), NHO Transport, NOR-WAY Bussekspress, DB Schenker, Norsk Scania AS, and Vestregionen. Some of the policy analyses reported here were made possible through a grant from the Swedish-Norwegian BISEK programme. The last mile funding for the analysis presented herein came from the Institute of Transport Economics (TØI). All contributions are gratefully acknowledged. Thanks are also due to Ragnvald Reed of the Norwegian Public Roads Administration for his help in extracting data from the central motor vehicle registry, and to the Norwegian Road Federation (OFV) for providing disaggregate automobile sales data.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Fridstrøm, L., Østli, V. & Johansen, K.W. A stock-flow cohort model of the national car fleet. Eur. Transp. Res. Rev. 8, 22 (2016). https://doi.org/10.1007/s12544-016-0210-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12544-016-0210-z