Abstract
Purpose
Aeronautic transport has an effective necessity of reducing fuel consumption and emissions to deliver efficiency and competitiveness driven by today commercial and legislative requirements. Actual aircraft configurations scenario allows envisaging the signs of a diffused technological maturity and they seem very near their limits. This scenario clearly shows the necessity of radical innovations with particular reference to propulsion systems and to aircraftarchitecture consequently.
Methods
This paper presents analyses and discusses a promising propulsive architecture based on an innovative nozzle, which allows realizing the selective adhesion of two impinging streams to two facing jets to two facing Coanda surfaces. This propulsion system is known with the acronym ACHEON (Aerial Coanda High Efficiency Orienting Nozzle). This paper investigates how the application of an all-electric ACHEONs propulsion system to a very traditional commuter aircraft can improve its relevant performances. This paper considers the constraints imposed by current state-of-the-art electric motors, drives, storage and conversion systems in terms of both power/energy density and performance and considers two different aircraft configurations: one using battery only and one adopting a more sophisticated hybrid cogeneration. The necessity of producing a very solid analysis has forced to limit the deflection of the jet in a very conservative range (±15°) with respect to the horizontal. This range can be surely produced also by not optimal configurations and allow minimizing the use of DBD. From the study of general flight dynamics equations of the aircraft in two-dimensional form it has been possible to determine with a high level of accuracy the advantages that ACHEON brings in terms of reduced stall speed and of reduced take-off and landing distances. Additionally, it includes an effective energy analysis focusing on the efficiency and environmental advantages of the electric ACHEON based propulsion by assuming the today industrial grade high capacity batteries with a power density of 207 Wh/kg.
Results
It has been clearly demonstrated that a short flight could be possible adopting battery energy storage, and longer duration could be possible by adopting a more sophisticated cogeneration system, which is based on cogeneration from a well-known turboprop, which is mostly used in helicopter propulsion. This electric generation system can be empowered by recovering the heat and using it to increase the temperature of the jet. It is possible to transfer this considerable amount of heat to the jet by convection and direct fluid mixing. In this way, it is possible to increase the energy of the jets of an amount that allows more than recover the pressure losses in the straitening section. In this case, it is then possible to demonstrate an adequate autonomy of flight and operative range of the aircraft. The proposed architecture, which is within the limits of the most conservative results obtained, demonstrates significant additional benefits for aircraft manoeuvrability. In conclusion, this paper has presented the implantation of ACHEON on well-known traditional aircraft, verifying the suitability and effectiveness of the proposed system both in terms of endurance with a cogeneration architecture and in terms of manoeuvrability. It has demonstrated the potential of the system in terms of both takeoff and landing space requirements.
Conclusions
This innovation opens interesting perspectives for the future implementation of this new vector and thrust propulsion system, especially in the area of greening the aeronautic sector. It has also demonstrated that ACHEON has the potential of renovating completely a classic old aircraft configuration such as the one of Cessna 402.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.1 Introduction
1.1 Generalities
The future of the aeronautic domain is predicated on the necessity to meet public and legislative demand in terms of increased safety and capacity, reduced emissions and noise, higher manoeuvrability and increased flexibility of use, reduced time for travel and take off, and reduced landing space requirements. For example, NASA has launched the ‘Revolutionize Aviation’ program, demonstrating that ‘game-changing’ novel propulsion systems are necessary to enable the design of revolutionary aircraft that could meet future and greener needs [1].
The ACHEON (Aerial Coanda High Efficiency Orienting-jet Nozzle) [2] is a new propulsive architecture that aims to fulfil most of these goals. It defines a novel class of aerial vehicles, which are green, all electric, with improved manoeuvrability, reduced takeoff, and landing spaces. Cen et al. [3] have verified that this system has the potential of increasing the manoeuvrability of a high performance jet with a significant increase in performance.
This paper considers a more conservative domain. It aims to verify how ACHEON can be implemented inside the architecture of a traditional twin-engine transport aircraft and analyzes the benefits and the feasibility of the system. A novel class of transport aircraft, which is designed to benefit of ACHEON nozzle, is subsequently defined inside this paper.
1.2 ACHEON nozzle architecture
ACHEON nozzle has been defined by Trancossi [4] as a two-stream nozzle, which has the ability of deflecting the resulting synthetic jet by means of the Coanda Effect. This result has produced a patent by Università di Modena e Reggio Emilia [5, 6]. The patent has been initially presented by Trancossi and Dumas [7, 8]. This preliminary investigation has evidenced the main advantage of the system, which is the extraordinary reactivity and velocity of response, and the main constraint of the system that relates to its intrinsic instability. In particular, subsequent to investigating the stability problem, the project has integrated the Coanda effect nozzle with a dielectric barrier discharge (DBD) to increase the stability of the system, as defined by Cattafesta [9] and improved by Xisto [10].
The architecture of the nozzle as originally defined by the patent is represented in Fig. 1.
The ACHEON nozzle (1) is capable of mixing two primitive fluid jets (2) and (2') and producing a selective and controllable angular deviation of the synthetic jet (7) without any moving mechanical part. The nozzle (1) is also capable of changing the direction of this jet in a continuous and dynamic manner to allow the jet to sweep a preset and arbitrary angle. The nozzle (1) is constituted, in a first part thereof, by a conduit (8) divided into two channels by a central baffle (9) and, in a second part thereof, by a convergence zone and an outflow mouth (5) whose walls have a curvilinear profile and are connected seamlessly to the walls of the conduit. Dragan [11] has independently validated the preliminary Coanda effect model by Trancossi and Trancossi and Dumas.
A general overview has been produced by Dumas et al. [12]
1.3 Coanda effect modelling
Significant research activity has been conducted on Coanda effect modelling and analysis. In particular, Trancossi, Dumas et al. [13] produced a theoretical model of Coanda attachment mechanisms and the laws of the Coanda effect. The proposed model has been realized by integration of Navier Stokes equations starting from the Dragan [14] model. The authors consider a very conventional setup in order to define by a theoretical analysis a mathematical model of the Coanda adhesion and define a preliminary model, which could be suitable for simple engineering calculations and preliminary comprehension of the model by elementary equations. A parametric model has defined as a function of the main cinematic and geometric parameters. The final model relates to three fundamental parameters: outlet section, Coanda surfaces radius and inlet velocities. Turbulent and laminar models have been defined. Validation through a large CDF development programme has been produced in a regime of stream velocities from 5 to 40 m/s with good correlation results.
This activity has been improved by Subhash and Dumas [15], who have produced a large set of numerical computations with different turbulence models on an air jet flowing tangentially over the curved surface. In particular, they have obtained that without resolution of the viscous sub-layer, since it is not possible to determine the computationally independent angle of jet deflection and boundary layer thickness. The boundary layer analysis has been performed at different radius of curvatures and at jet Reynolds numbers ranging from approximately about 2400–10,000. The skin-friction coefficient has been also studied at the separation in relation to the surface radius and jet Reynolds number. In this research work, the inter-relation between flow and geometric parameters has been identified for the further design of the Coanda nozzle flow.
Dumas, Subhash at al. [16] have analysed the effect of the temperature of the surface on the Coanda effect adhesion. This activity has led to the identification of a negative effect of heated Coanda surfaces on the adhesion phenomena.
Das at al. [17] have carried out numerical simulations to investigate Coanda flow over a curved surface and analysed the application to the ACHEON system. He has observed the effect of Dielectric barrier discharge (DBD) plasma actuators, concluding that it has an effective capacity both of stabilizing the behaviour of the system and of increasing the angle of adhesion. CFD computations were performed under subsonic condition by Reynolds averaged Navier stokes equations (RANS).
1.4 Coanda nozzle modelling
After preliminary analysis by Trancossi and Dumas, a more focused activity has been performed on the nozzle. Trancossi, Subhash et al. [18] has analysed the ACHEON Coanda effect based propulsion nozzle for aircraft propulsion considering the dynamic equilibrium of two jet streams and explain how the Constructal Optimization process allowed the preliminary definition of the nozzle. The model has been produced by assuming an inviscid model. A preliminary mathematical model of a 2D case of the system has been developed, focusing on the combined effect of the mixing effect of the two streams and the Coanda Effect Adhesion over a convex surface. Trancossi et al. [19] have specifically modelled the ACHEON Coanda effect two streams nozzle. The paper tries to produce an effective design guideline, which can be adopted for design activities of the nozzle for aeronautic propulsion. The presented model allows the definition of a governing method for this innovative two-stream synthetic jet nozzle. The uncertainness levels of the model are discussed and novel aircraft architectures based on it are presented. A CFD validation programme is presented focusing on validating the model and the designs produced. Pascoa et al. [20] have produced an effective bibliographic analysis on thrust deflection systems producing an effective comparison with other thrust and vector system.
1.5 Dielectric barrier discharge
The Dielectric barrier concept and architecture, which are used in the ACHEON nozzle, are derived directly from the one defined by Pascoa et al. [21] in 2009, and is presented in Fig. 2. Abdollahzadeh and Pascoa [22] introduced a generic analytical approach that can be used to predict analytically the momentum transfer in DBDs, allowing a better analytical analysis of the dynamic behaviour of the ACHEON nozzle.
Abdollahzadeh et al. [23] have explored the use of thermal DBDs. Until the moment, only non-thermal DBDs have been used for ACHEON, due to the lower flow speeds involved. This is a general paper dealing with the numerical modelling of nanosecond pulse micro-shock wave plasma actuators. As verified by Subhash et al. thermal effects are negative at low Reynolds number, but becomes an effective solution at high Mach numbers, including transonic or supersonic conditions.
2 Definition of the problem
2.1 Generalities
Sunol and Vucinic [24] have started a preliminary analysis of integration of the ACHEON nozzle into an aerial Vehicle. Building upon this preliminary result, this paper aims to analyze how the ACHEON nozzle can be further integrated into aircraft architecture, and in particular will focus on the definition of a specific aircraft model taking maximum advantage of this nozzle.
Current S-VTOL aircraft are generally not optimized designs because they are based on very traditional aircraft architectures not specifically designed for this kind of operation. The design optimization will focus on a simplified 2D plane of motion considering initially only the advantage during take off, climbing and landing operations.
Four forces act on an aircraft in flight: lift, weight, thrust, and drag. For an aircraft in cruise, the four forces are balanced, and the aircraft moves at a constant velocity and altitude. Any altitude change makes them diverge from equilibrium. Vertical and horizontal axes of the aircraft have their origin in the center of gravity. Two flight paths are designed as red and blue lines inclined to the horizontal at angle c as in Fig. 3. Take off and landing operation will be evaluated.
The results obtained allow the definition of a configuration that allows the installation of ACHEON on a very conservative classical airplane design.
This paper will analyze flight mechanics problems starting from a rigorous Newtonian approach, considering basic equations derived from Newton’s second law. to enable analysis and understanding of the benefits of the ACHEON nozzle under different conditions.
Preliminary calculations will be performed assuming the effects of the pitch as included in the Drag and Lift aerodynamic coefficient.
2.2 Final Remarks about methodology
Because of the methodological analysis performed, some theoretical benefits have clearly been shown. This analysis and FAR regulations enables the production of an effective mission analysis based on a real plane model.
The characteristics of flight related to the considered potential ACHEON applications inside the project are restricted to subsonic airplanes. A significant class of vehicles which has been identified is a twin-engine commuter aircrafts, which are suitable for Corporate transport and airliner up to 9/12 passengers. Cessna 402 and Piper PA 31 Navajo have been considered also because of their constitutive characteristics and design, even if they are not recent designs.
3 Methodology
3.1 Airplane data
The availability of accessible data makes the Cessna 402 (Fig. 3) the preferred airframe for analysis, also having a wing structure, which simplifies the adoption of ACHEON ducted fan system to replace traditional propulsion. The Cessna 402 with ACHEON propulsion is represented in Fig. 4. Each aircraft is designed in order to satisfy the needs of potential users. Aircraft performance depends mainly on the structural and aerodynamic characteristics, and the features of the system propulsion. Assuming Cessna 402 data, which have been obtained from several sources [25–30], it will be possible to compare a traditional twin-engine aircraft with one propelled by this new propulsion system. .
3.2 Propulsion and thrust
Thrust is a mechanical force generated by propulsion, as explained by Newton's third law of motion: if a working fluid is accelerated in rear direction, the aircraft is accelerated in the opposite direction. From Newton's second law of motion, we can define a force F to be the change in momentum of an object with a change in time. The thrust is equal to
considering an inlet section 0 and an exit section e, the force is given by:
Considering the additional effect due to the pressure difference between inlet and outlet, an additional force term equal to the exit area Ae times the exit pressure minus the free stream pressure must be considered. The general thrust equation is then given by:
Assuming propeller disk model it can be modelled as Substituting the values given by Bernoulli's equation into the thrust equation and results:
It is then clear that the relation between propulsive power and thrust is
where η P is the propulsive efficiency.
Characteristic and performance table is reported in Appendix 1, while power propulsion system is evaluated in Table 1. The propeller is schematized in Fig. 5. Main dimensional parameters, which are calculated according to Trancossi et al. [31, 32], are reported in Table 2 and considering a different diameter of the fan. Installing four ducted fan units with a pressure ratio 1.1, turbofan characteristics can be evaluated according to Mingtai [33] who suggest the relation
where k t is the static thrust coefficient and n is the speed of rotation of the fan.
The advantage supporting the adoption of the Cessna 402 model is the relative high number of aircraft in operation both produced by Cessna and by Sukhoi. It is an aged project, but displays good flight performance and behaviour, which is appreciated by pilots, and the very traditional distribution of weight in the airplane, which fits very well with the use of such propulsion also because of the construction of wings, which could allow a good integration of ACHEON derived propulsion nozzles instead of traditional propulsion.
The ducted fan units have the dimensions specified in Table 1 and performance specified in Table 2. In particular, a turbo machine with a pressure jump Δp = 0.3 P atm has been adopted.
The Cessna 402 has a thrust to weight ratio about 0.37, and a total thrust of approximately 11000 N. The proposed compressor units, to achieve 30 % pressure jump, require multiple stages, typical of turbo machinery. The typical compressor unit has a max thrust about 3000 N, thus there will be 4 compressor units to propel the aircraft with a max thrust about 12000 N.
On this basis, it is possible to evaluate the system. The deflected thrust by Coanda effect is evaluated according to Keen [34], who has verified that it is almost negligible because of very reduced frictional effects, and because a very low lift is produced, in a boxed architecture of the ACHEON nozzle (Fig. 6). Starting from those preliminary evaluations the aircraft system will be evaluated.
3.3 Wing characteristics
The wing planform area (S) is shaded in Fig. 6. The wing taper ratio is assumed to be the ratio of tip chord (c t ) to root chord (c r ),
The mean aerodynamic chord can be found by integrating the individual section chords across the span.
In case of wings with simple linear taper. In this case, the mean aerodynamic chord will roughly equal the mean geometric chord,
The aspect ratio of the external wing parts will be,
moreover, for the central rectangular planform this simplifies to,
In the case of Cessna 402, wing area is about 21 m 2. Aspect ratio of Cessna 402 is 8.61.
3.4 Lift and lift coefficient
To simplify the problem, lift is typically measured as a non-dimensional coefficient.
In the normal range of operations, the variation of lift coefficient with angle of attack of the vehicle will be approximately linear,
until a maximum lift coefficient value at which point the wing flow stalls and lift reduces.
A simple approximation for straight, moderate to high aspect ratio wings is to assume an elliptical spanwise load distribution, which gives the following result,
where it is assumed that the ideal two-dimensional result for the section used is 2π.
Calculation of zero angle lift coefficient or zero lift angle can be done by crudely assuming that the zero lift angle for the aircraft equals the combination of zero lift angle of the aerofoil section and wing incidence setting. Calculation of maximum lift coefficient can be approximately equal to the two dimensional section data minus 5 % due to the negative lift needed at the tailplane to maintain moment equilibrium. These approximations works properly for the Cessna 402 because of it has almost rectangular wings.
3.5 Drag coefficient
In theory the drag can be predicted by using a simple parabolic drag assumption,
If the offset due to camber is neglected, the following simplified equation can be obtained
According to (15) and (15'), the drag is assumed with a reasonable precision as a quadratic function of lift.
The effect of compressibility can be predicted by the use of a correction factor for speeds ranging from M = 0.4 up to transonic, but in this case it can be not considered.
The lift dependant component can be approximated as
where e is the efficiency factor of planform wing. It is indicated in Appendix 1 for the specific kind of aircraft.
In case of takeoff and landing, drag can be evaluated by considering that the landing gears are fully extended, increase the CD0 and there is a reduction in the induced drag due to the close proximity of the wings to the ground. The following expression is used to calculate the increase in CD0:
and the drag is consequently (8'')
where:
-
W/S is the wing loading in unit of Newton per square meter intended primarily for use in incompressible flow conditions
-
m is the maximum mass of the airplane in kilograms
-
K uc is a factor that depends of the amount of flap deflection. For maximum flap deflection, K uc = 3,16 10 −5.
3.6 Flight mechanics
3.6.1 Flight analysis in a vertical plane
The lift and drag are aerodynamic forces that are defined relative to the flight path. The lift is perpendicular to the flight path and the drag is along the flight path. The thrust of the aircraft is also usually aligned with the flight path. We initially assume and investigate the ideal positioning of the ACHEON nozzle to take the max advantage during take off and landing operations, assuming that it changes the angle of the thrust only during take off and landing operations.
Elementary equations of flight become (Fig. 7):
where lift is
and drag is
The resulting equations of motion are:
For small climb angles (<6°), the cos γ is nearly 1 and the sin(γ) is nearly zero. The system of Eq. (1') then reduces to
Assuming that thrust can assume different angles than the trajectory of motion (Fig. 8), the angle of the variable thrust respect the trajectory is defined with t. The thrust can be expressed as a function of the angle t + c, which is the sum of the climbing angle with the angle of the thrust with the trajectory:
where T x and T y are expressed as follows:
The system of Eq. (23) can be expressed by assuming the internal trigonometric relations and becomes:
As before, for small climb angles (<6°), the term cos (c) is nearly one and the term sin (c) is null. The system of Eq. (24) then reduces to Eq. (25):
Showing clearly the contribution of the terms due to the variable direction thrust, which is positive, when thrust is directed upward, and negative, when thrust is directed downward the climbing trajectory.
3.6.2 Stall analysis
The calculated the stall speeds are respectively:
It is evident that the stall speed with upward directed thrust is lower than the stall speed in a traditional airplane, higher when thrust is directed downward.
It can be obtained that u stall = 0 if
3.6.3 Stability analysis
Stability analysis will allow the definition of the optimal positioning of the ACHEON propulsion to achieve different goals and satisfy different mission profiles. Stability analysis is fundamental for defining optimal aircraft architecture. In flight, any aircraft will rotate about its center of gravity, a point, which is the average location of the mass of the aircraft. We can define a three dimensional coordinate system through the center of gravity with each axis of this coordinate system perpendicular to the other two axes (Fig. 9).
In Fig. 9, two coordinate systems have been defined: x, y, z (with x parallel to the horizontal and z vertical), x',y,z' (with x' parallel to the trajectory and z' axis orthogonal to the trajectory) and x'', y, z'' with (x'' parallel to the aircraft fuselage axis and z'' perpendicular to this axis). The angle α is the angle of attach that the fuselage forms with the trajectory. The orientation of the aircraft by the amount of rotation of the x'',y,z'' coordinate system on x,y,z in the point G.
3.6.4 Pitch motion
The pitch axis is the y axis, perpendicular to the aircraft centreline and lies in the plane of the wings. Pitch motion is an up or down rotation around the centre of gravity.
The pitching motion is being caused by the deflection of the elevator of the aircraft. but also influenced by position where thrust is applied.
The pitch equilibrium is presented in Fig. 10.
The equilibrium of torques of the aircraft is calculated around one of the significant points. Usually it is defined as the center of aerodynamic forces, but in this case due to its variation as a function of different parameters such as speed it is preferred to define the centre of mass as being nearly constant.
It can be demonstrated that the case when the thrust application point is almost coincident with the centre of gravity the action of the thrust direction change is neutral in terms of effects on the pitch. It can be also easily demonstrated that, if it is not coincident, the directional change of the thrust can be used instead of ailerons for stabilizing the aircraft.
3.6.5 Roll motion
In flight, any aircraft will rotate about its center of gravity. The roll axis lies along the aircraft centreline. The deflection of the ailerons of the aircraft causes the rolling motion. The aileron is a hinged section at the rear of each wing. The ailerons work in opposition; when the right aileron goes up, the left aileron goes down.
Changing the angle of deflection at the rear of an airfoil will change the amount of lift generated by the foil. With greater downward deflection, the lift will increase in the upward direction; with greater upward deflection, the lift will decrease in the upward direction. Since the ailerons work in pairs, the lift on one wing increases as the lift on the opposite wing decreases. Because the forces are not equal, there is a net twist, or torque about the center of gravity and the aircraft rotates about the roll axis. The pilot can use this ability to bank the aircraft, which, causes the airplane to turn. it is clear that, if variable direction propulsion, such as ACHEON, are installed, benefits could immediately arise on the roll motion control assuming that the distance of the propeller could be long enough.
Figures 11 and 12 shows the roll rotation with upward directed thrust and Fig. 8 with downward directed thrust. Both configurations can be achieved during different flight operations.
3.7 Pull up and push over manoeuvres
Considering at this level only manoeuvres on the vertical plane, two types of flight manoeuvres are a symmetric: pull up and push over. In either case further terms are added to define the dynamic equilibrium of flight.
For a symmetric pitch up, we conventionally assume that the vehicle is moving in a large vertical circle, even if the trajectory can present some differences. When the manoeuvre starts, the forces, in an airplane with thrust aligned with the x-axis in the vertical direction are:
The forces in horizontal direction are:
In the case of an inclined thrust, the equilibrium of the forces is:
and
It is the clear that by deflection of the thrust lower pitch up radius can be assumed with upward directed thrust and higher with downward directed thrust.
3.8 Take off and landing operations
3.8.1 Takeoff run dynamics
Figure 13 represents take off operation with a directional thrust.
A well working set of equation that allows modelling takeoff operations is provided by Phase [25]. It is also necessary to consider in this part the Federal Aviation Regulations that defines acceptable procedures for take off operations, FAR 25.103, 105, 107, 109, 111, 113 [35–40].. If thrust is horizontal and the weight W = m g the equations of takeoff run are:
where
and
If the thrust is directed in a direction, which is different from the horizontal, it can be obtained:
which becomes
where
and
The equal condition in Eq. (39) is satisfied at the takeoff point.
The take off condition results:
the equilibrium in vertical direction expressed by Eq. (38) results
that allows calculating the take off speed, which results in the case of t = 0,
and in the case of directional thrust it becomes
Equation (43) demonstrates clearly that the take off speed is lower than the one with t = 0 in the case that t > 0, or thrust is oriented upward, and higher in the case that thrust is oriented downward.
Usually the takeoff speed is higher than stall speed at ground level. It is usually assumed that:
it can be then verified that
which gives
An effective analysis of the detachment phase can be performed after the analysis of the ground-based run after take off.
3.8.2 Detachment from the ground
After the preliminary ground run the most critical phase of the plane behaviour is the detachment phase, which is regulated by FAR standards (Fig. 14). Take off is concluded only when an airplane has reached an height of 10 m. Assuming the hypothesis that during this phase the velocity does not change significantly and remains almost constant .
The radius of curvature can be calculated by Eqs. (33) and (34). In the case of assuming u takeoff constant, they becomes respectively:
it can be demonstrated that the most interesting condition is
After this operation, the motion continues with a climb.
3.8.3 Landing operations
Landing operations can be modelled in a similar way and are almost symmetrical (Fig. 15). In this case FAR 25.119 - Landing climb all engines [41], and FAR 25.125 - Landing [42] applies. Landing operations can be described assuming an initial push over manoeuvre, which starts at cruise speed u cruise and can be modelled in both cases respectively:
In the case of Eq. (49) with directional thrust, it is evident that the same radius can be obtained in two modes: a low lift configuration with higher vertical thrust component, or a higher lift configuration and lower vertical thrust component, but also with a downward directed thrust, without changing the aircraft configuration.
The following manoeuvre is the climb down, with deceleration to a velocity, which is about touch down speed u landing . It is in the range
Usually a value of 1.23 ustall is adopted.
In this case, a much lower landing horizontal speed can be ensured:
where γ is the climbing angle.
In particular, it assumes vertical configuration when
The final manoeuvre before touching the ground is a further rotation with centre higher than the trajectory starting at 50 ft (15.24 m) with radius:
In addition, in this case operations could be performed by different combinations of vertical thrust and lift force, including fixed aerodynamic configurations governed simply by jet.
It can be then possible to model the final part. If the thrust is directed in horizontal direction or in a direction, which is different from the horizontal, it can be obtained:
where μ brake is the friction coefficient during braking phase.
In this case, some thrust directed vertically can be interesting. Braking space can be easily evaluated as in the case of the takeoff run.
3.9 Aircraft configuration
The aircraft configuration has been studied subject to the aircraft performance and required power for different operations. A complete analysis of the performances of the modified Cessna 402 plane will be performed against the traditional plane with propellers [43]. In particular, Fig. 16 shows the airplane configuration with a section on the ACHEON propeller illustrating the main positioning of the system.
Figure 17 shows the detail of the ACHEON nozzle section and its configuration so to allow a better comprehension of its behaviour. In particular, the proposed model presents a limitation in angular terms of the jet, to allow an effective prediction of the maximum angle, which could be reached.
To simplify the model controls and to ensure a better integration with the airplane configuration a positioning of the geometric centre of thrust coincident with the centre of gravity will be considered. Otherwise, it is evident that torque components could be introduced with negative consequences on the aircraft behaviour. The application of the centre of thrust rotation in the centre of gravity could is also considered to increase the safety of the system and allowing an adequate system behaviour in case of technical problems.
In particular, there will be assumed three limiting positions:
-
an angle = 0 ensured by top jet (horizontal flight);
-
an angle = t ensured by both jets (take off);
-
an angle = 2 t ensured by bottom jet (landing).
Different angles t could apply, as demonstrated by the project activities. they space in a range 12 ÷ 25° . The effects will be evaluated for some specific angles, while jet velocity and regimes will be defined according to specific conditions.
Energetic and environmental evaluations will be also performed.
3.10 Mission profile
To describe the results a specific mission will be considered. The typical mission profile is defined according to the FAR standards for commercial vehicles.
In some operations, different operative methods will be taken into account and will be compared. The analysis will also consider FAR standards to verify the suitability of the system for future application into aviation. Further considerations will regard the possible modifications, which could be necessary to the FAR to allow ACHEON integration. ACHEON will be also preliminarily evaluated against EC Reg. No. 216/2008 [25], identifying future certification needs for flying in Europe. A typical mission profile is illustrated in Fig. 18.
4 Results
The results will be compared to the effective performance of a Cessna 402 identifying improved and degraded operation. Energy and performance related considerations would be performed focusing on the specific effects of the all-electric ACHEON propulsion system.
Further consideration will regard the necessity of further improvements, which could be necessary for implementing in ACHEON. It is assumed to use the same aerodynamic configuration, which is used for the traditional version and equal thrust condition.
The main parameters of the aircraft have been preliminarily calculated [27–30, 44]. The propulsion model is shown in Fig. 19. The lift and drag data are calculated and reported in Table 2 and the engine data in Annex, will be used as models of the aircraft and engine.
A concrete/asphalt runoff is assumed with a friction coefficient 0.02 for takeoff and landing operations.
4.1 Take off evaluation
The following data can be assumed by FAR Part 25 (Table 3).
Simplified takeoff profile is assumed Main data have been reported in Tables 4 and 5.
The values in Table 6 have been calculated during takeoff, considering that the average speeds during these operations has been evaluated at 0.71 u takeoff [45]. It is the first part of the takeoff it relates to the following phases transition a screen up to 35 ft (10 m) has been considered, as specified by FAR Part 25. Maximum initial vertical speed of 7.6 m/s is assumed for the CESSNA 402 and it results after take off. It means that the initial average horizontal speed is 52.7 m.
Energy requirements for take off includes also taxi time, wait and run, according to FAR Part 25. Ten minutes operation time has been estimated. .
Advantages in terms of energy saving are evident at each angle of the takeoff length. It can be verified that if a well defined load factor has been assumed during operations that could not exceed 1, adequate comfort of the passengers is ensured,
which becomes for ACHEON propelled airplanes
that constitutes a precise limit to aerodynamic loading in function of the thrust.
It shows clearly that the flight assist can be ensured in two ways:
-
1.
by changing lift maintaining directional thrust;
-
2.
by changing thrust direction maintaining aerodynamic lift.
The other evident result is that the same take off performance could be also obtained with a much-reduced aerodynamic lift and then a lower drag.
4.2 Climb
It is assumed that the plane at the end of takeoff segments up to 10,000 ft (3048 m) reaches the cruise speed (109 m/s).
After the transition phase there is a slow transition from the dual jet configuration to allow the jet to adhere to the upper surface, as shown in Fig. 19, but also a climb with inclined Thrust can be performed. An angle of attach of 7 ͦ has been considered.
The difference in terms of accelerations between the two solutions is evident by subtracting the system of Eqs. (13) and (15).
It is clear the difference of accelerations along x-axis is reduced, while the one along y-axis is increased.
Average speed during climb can be evaluated in different configurations:
An average climb rate of 6.7 m/s has been assumed. About 40 kWh (144000 kJ) are necessary in all the configurations. Expected energy consumption is about 140 kWh (504000 kJ) for traditionally propelled aircraft and about 53 kWh (191000 kJ) for electric ones.
4.3 Horizontal Flight
Flight will is estimated considering the above model and standard atmospheric data at 1000 m. An average angle of attachment of 3° has been assumed, even if a twin engine aircraft in cruise could also fly with horizontal axis. Consumption for 1 h flight at 1000 m and cruise velocity is expected to be 1060 kWh (3816000 kJ) for traditional propulsion and about 360 kWh (1296000 kJ) for the electrical one only because of increased efficiency of electric propulsion. In the case of horizontal flight electric propelled airplane there is no mass reduction and this aspect must be considered during landing operations.
4.4 Landing
Landing energy needs can be evaluated according to usual twin-engine general aviation aircraft. Typical angle and airspeed during landing are presented in Table 6.
Landing modes have been presented in Fig. 20 assuming a traditional 3° glideslope. Figure 20 shows instead the complete landing manoeuvre considered. It is clear that gliding takeoff requires low energy consumption. A 3° degree glideslope for a traditional Cessna 402 will require a landing space, which can be calculated and against the value of 757 m (declared by the producer). Calculations give a worst result of about 763 m, which is acceptable because of the necessary approximations in calculations.
Data between the descent phase and landing using ACHEON can be assumed adopting a different profile (Table 7).
Different profiles of climbing have been considered for ACHEON propelled aircraft. They can be ensured by hybrid combination of vertical component of the thrust, when adhering to the lower surface and aerodynamic lift. In this case the thrust in vertical direction could be almost equal to the one during takeoff, while the horizontal one is much reduced. Angle of attack is considered the same as above. Considering different stall speeds and maximum deceleration about 3 m/s both spaces and times for landing operations have been calculated. Results are presented in Table 8.
It is now evident that ACHEON can also perform better performances in case of landing.
4.5 Further ACHEON system improvements
The ACHEON propulsion system can be improved by optimizing the inlet by an effective improvement of the inlet section, as verified by Trancossi and Madonia [46]. By optimizing the air intake design it can be possible to increase the propulsive efficiency especially at high altitude. But this level of optimization it is not performed at this level because it requires a more effective design activity.
4.6 Energy analysis
This analysis focuses on the energy analysis of the electrical ACHEON propelled Cessna 402 against the model on the market [47, 48]. This analysis produces some interesting results.
In particular, the energy comparison are presented in Table 9. An emergency reserve higher than 15 % is assumed to ensure some minutes flight for the electric ACHEON Propelled aircraft then the time for flight at cruise condition could not exceed 20 min for electric ACHEON propelled plane.
It can be verified that the original configuration is not adequately performing in terms of autonomy and energy storage. A better energy efficiency and cruise performance of the ACHEON propelled aircraft can be obtained by decreasing cruise speed to about 324 km/h (90 m/s). Data in this case indicates increase to 40 min cruise speed.
Assuming average European electric production efficiency [49], which has been estimated about 50 % in 2010, the effective energy demand will be about double than declared consumptions, but much lower than the one for the conventional engine.
4.7 Improving the airplane configuration
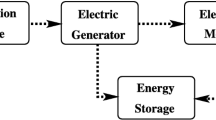
Improved performance can be ensured by equipping the plane by an electric lightweight cogeneration system coupled to heat recovery system. Assum Rolls Royce-Allison Model 250 C20R turboprop [49] with a max nominal power of about 190 kW and continuous power about 170 kW (602.5 MJ) is considered [50]. It has a weight of 62 kg dry (0.32 kg/kW). Considering all the necessary accessories a weight about 1.2 kg/kW can be conservatively assumed, including the heat recovery system. Assuming the hypothesis of recovering heat from the turboprop and converting it by heating the fluid flow, preliminarily conceived by Trancossi [31], patented by Dumas et al. [51] and studied by Trancossi et al. [32]. Using the same calculation methodology used by Trancossi et al., thermal emission can be calculated by considering consumption about 0.48 kg/kWh and a conservative global thermal exchange efficiency about 0.4. The amount of recovered heat per hour is then 338.65 kWh (1220 MJ).
It means an increase in terms of thrust about 30 % that means a reduction of required electrical power about 54 kW.
This new condition enables flight with a partial system redefinition and general improve, with overall energy efficiency about three times the one of the traditional airplane.
In this case, it can be assumed the following configuration 250 kg of fuel, 250 kg cogeneration system and 1050 kg batteries.
This configuration could allow flight endurance about 6 h with a sufficient reserve,
This result is also interesting because the heat exchanger produces some losses but can be also used as a stator for straightening the jet as demonstrated by Shyam and Trancossi, which increases the adhesion, but also a positive thermal difference is a benefit because of an increased adhesion capability as demonstrated by Subhash in his thermal analysis.
The resulting configuration is summarized in Table 10.
The operational reduction of payload, which has been assumed in previous all electric architecture is maintained.
5 Conclusions
This paper has clearly demonstrated the benefits of the ACHEON nozzle applied to the propulsion of a commuter class transport twin-engine aircraft. The choice has been focused on the Cessna 402 aircraft because its geometric conformation, which could easily allow a positioning of the ACHEON nozzle with centre of thrust almost coincident with centre of mass. The paper produces the basic control equations of an aircraft with this singularity showing the benefits of variable direction thrust applied in this position.
For simplicity only three positions have been considered, because they seems the state that can be easily produced at this level of research activity. They are full thrust (two fans on) with an angle t of inclination (with t comprised between 0° and 15 °. A nozzle with opening equal to t so that two extreme positions could be stabile:
-
0° for horizontal flight, with higher jet near 100 % ant the other below 50 %.
-
2 t for takeoff operations to sustain the airplane during operations with lower jet about 100 % and lower below 50 %.
Kinematic and dynamic main parameters have been estimated during critical operations such as take off and landing verifying the benefits produced by the ACHEON nozzle in different flight condition. It appears fundamental, even if not directly presented in the paper, the importance of DBD to ensure an effective governable transition between the positions to avoid both too fast modifications of the airplane behaviour with potential stability problems and the actual considered capacity of producing thrust in three well-defined directions.
In particular, further application could benefit from the preliminary definition of a possible single jet architecture, which aims to reduce the problems derived from high frontal section required by the dual jet configuration.
A preliminary airplane configuration equipped by high performance batteries is presented.
Energetic evaluations have been performed demonstrating clearly the advantages of the proposed all electric system because of much higher energy conversion efficiency and because of the possibility, which has been presented to define a cogeneration airplane architecture equipped by a Rolls-Royce Model 250 turboprop based cogeneration unit. The large disposability in terms of heat to be dispersed could ensure the possibility of producing a more effective propulsion effect by using them to heat the jets produced by the ducted fans.
The clear advantages of the cogeneration based solution against the battery only one is evident demonstrating the possibility of an effective applicability of ACHEON all electric propulsion in the future, with a cogeneration based propulsion architecture.
In conclusion, this paper demonstrates the benefits of ACHEON based architecture to civil aircrafts ensuring enhanced performance. Even if it is not still sufficient for future ACHEON equipped aircrafts it is a preliminary basis for continuing the studies on ACEHON through a novel class of all electrical high performance aircraft, which could not been conceived before this revolutionary project.
Abbreviations
- α :
-
Angle of attach (rad, deg)
- γ:
-
Climb angle (rad, deg)
- λ:
-
Wing taper ratio (−)
- μ :
-
Friction coefficient (−)
- a :
-
Acceleration (m/s2)
- a L :
-
Variation of lift coefficient with angle of attack (−)
- A x,y :
-
Planform Area (m2)
- A x,z :
-
Frontal section (m2)
- AR :
-
Aspect ratio (1/m)
- b :
-
Wing length (m)
- C D :
-
Drag coefficient (−)
- C D0 :
-
Drag coefficient with lift at null angle of attach (−)
- C L :
-
Lift coefficient (−)
- C L0 :
-
Lift coefficient at null angle of attack (−)
- c r :
-
Wing root chord (m)
- c t :
-
Wing tip chord (m)
- \( \overline{c} \) :
-
Average wing chord (m)
- D :
-
Drag force (N)
- e :
-
Wing planform efficiency factor (−)
- K :
-
Drag increase coefficient with Lift (−)
- k t :
-
Static thrust coefficient (−)
- K uc :
-
Factor of flap deflection (−)
- L :
-
Lift force (N)
- m :
-
Mass of the airplane (kg)
- M :
-
Mach number (−)
- n :
-
Speed of rotation of the fan (RPM)
- P :
-
Power of the engine motor (kW)
- R in :
-
Inlet radius of the ducted fan unit (m)
- R m :
-
Radius of the motor (m)
- R out :
-
Outlet radius of the ducted fan unit (m)
- R f :
-
Fan radius of the ducted fan unit (m)
- S :
-
Wing planform area (m2)
- t :
-
Angle of thrust (rad)
- T :
-
Thrust (N)
- u :
-
Aircraft speed (m/s)
- u stall :
-
Aircraft stall speed (m/s)
- V exit :
-
Air speed at the outlet of the ducted fan unit
- W :
-
Weight (kg)
- W/S :
-
Wing loading (N/m2)
References
Sehra AK (2003) Novel propulsion and power concepts for 21st century aviation. AVT Spring 2003 Symposium and Panel Business Week, Brussels
Trancossi M, Dumas A (2011) ACHEON: Aerial Coanda high efficiency orienting-jet nozzle. Sae Technical Papers N. 2011-01-2737, ISSN 0148–7191
Cen Z, Smith T, Stewart P, and Stewart J. Integrated flight/thrust vectoring control for jet-powered unmanned aerial vehicles with ACHEON propulsion. Proc Inst Mech Eng Part G: J Aerospace Eng 0954410014544179, first published on July 29, 2014 doi:10.1177/0954410014544179
Trancossi M (2011) An overview of scientific and technical literature on coanda effect applied to nozzles. SAE Technical Papers N. 2011-01-2591, ISSN 0148–7191
Baffigi F, Dumas A, Giuliani I, Madonia M, Trancossi M (2014) Ugello capace di deviare in modo dinamico e controllabile un getto sintetico senza parti meccaniche in movimento e relativo sistema di controllo. Patent IT 0001406404, Deposito RE2011A000049, Filling date July 01, 2011, Publication date September 30, 2011, approved on February 21, 2014
Baffigi F, Dumas A, Giuliani I, Madonia M, Trancossi M (2014) Nozzle capable of deviating a synthetic jet in a dynamic and controllable manner with no moving mechanical parts and a control system thereof. PTC Patent WO2013005132 A1, Publication date Jan 10, 2013, Filing date Jun 25, 2012, Priority date Jul 1, 2011, Published also as EP2726213A1, US20140191059
Trancossi M, Dumas A (2011) Coanda syntetic jet deflection apparatus and control. SAE Technical Papers N. 2011-01-2590
Trancossi M, Dumas A (2011) ACHEON: Aerial Coanda High Efficiency Orienting-Jet Nozzle. Sae Technical Papers N. 2011-01-2737
Cattafesta LN, Sheplak M (2011) Actuators for active flow control. 43(1): 247–272
Xisto C, Páscoa J, and Oliveira P (2013) Modelling plasma flow on a self-field MPD thruster using a PISO based method. 44th AIAA Plasmadynamics and Lasers Conference, San Diego, USA
Dragan V (2014) Reynolds number calculation and applications for curved wall jets. INCAS Bull 6(3):35–41
Dumas A, Pascoa J, Trancossi M, Tacchini A, Ilieva G, Madonia M (2012) Acheon project: A novel vectoring jet concept. Proc. ASME. 45172; Volume 1: Advances in Aerospace Technology: 499–508, IMECE2012-87638
Trancossi M, Dumas A, Vucinic D (2013) Mathematical modelling of coanda effect. SAE Technical Paper 2013-01-2195, doi:10.4271/2013-01-2195
Drăgan V (2012) A New mathematical model for Coandă effect velocity approximation. INCAS Bull 4:85–92
Subhash M, Dumas A (2013) Computational study of Coanda adhesion over curved surface. SAE Int J Aerosp 6(1):260–272. doi:10.4271/2013-01-2302
Dumas A, Subhash M, Trancossi M, Marques JP (2014) The influence of surface temperature on Coanda effect. Energy Proc 45:626–634
Das SS, Abdollahzadeh M, Pascoa JC, Dumas A, Trancossi M (2014) Numerical modelling of Coanda effect in a novel propulsive system. Int J Multiphys 8(2):181–201
Trancossi M, Subhash M, Angeli D (2013) Mathematical modelling of a two streams Coanda effect nozzle. ASME Int. Mech. Engg. Conf. and Exhibition, paper no. IMECE2013-63459
Trancossi M, Dumas A, Das SS, Páscoa JC (2014) Design methods of Coanda nozzle with two streams. INCAS Bull 6 (1); 83–95, ISSN 2066–8201, doi: 10.13111/2066-8201.2014.6.1.8
Pascoa JC, Dumas A, Trancossi M, Stewart P, Vucinic D (2013) A review of thrust-vectoring in support of a V/STOL non-moving mechanical propulsion system. Cent Eur J Eng 3(3):374–388
Páscoa JC, Brójo FMP, Monteiro JMM (2009) Numerical simulation of magneto-plasma thrusters for aerospace propulsion using and MHD formulation. Paper O-7.2, Proc. 14th International Conference on Emerging Nuclear Energy Systems, Instituto Tecnológico e Nuclear, 6 pgs
Abdollahzadeh M, Pascoa J (2014) Modified split-potential model for modelling the effect of DBD plasma actuators in high altitude flow. Control Current Applied Physics
Abdollahzadeh M, Páscoa JC, Oliveira PJ (2014) Two-dimensional numerical modelling of interaction of micro-shock wave generated by nanosecond plasma actuators and transonic flow. J Comput Appl Math 270:401–416
Suñol A, Vucinic D (2014) Numerical analysis and UAV application of the ACHEON vectorial thrust nozzle. 32nd AIAA Applied Aerodynamics Conference. June 2014. doi: 10.2514/6.2014-2046
European Parliament and European Council (2008), Reg. (EC) No 216/2008 of the on common rules in the field of civil aviation and establishing a European Aviation Safety Agency, and repealing Council Directive 91/670/EEC, Regulation (EC) No 1592/2002 and Directive 2004/36/EC, Eurlex, European Union
Wolowiczc CH (1972) Longitudinal aerodynamic characteristics of light, twin-engine, propeller-driven airplanes. Nasa Technical Notes 6800, June 1972, NASA
Nicolosi F, Della Vecchia P, Corcione S (2012) Aerodynamic analysis and design of a twin engine commuter aircraft. Procedings of ICAS 2012, International Council of the Aeronautical Sciences, Brisbane, Australia
Roskam J (2000) Airplane design, part VI: preliminary calculation of aerodynamic, thrust and power characteristics, 2nd edn. DARcoporation, Lawrence
Frlschtak CR (2000) Learning, technical progress and competitiveness in the commuter aircraft industry: an analysis of embrarer. The World Bank, June, 1992
Williams JP (1983) Small transport aircraft technology. NASA SP-460, 1983
Trancossi M, Pascoa J (2013) Thermojet: an old idea can define a novel family of jets. SAE Technical Paper 2013-01-2205, doi:10.4271/2013-01-2205
Trancossi M, Dumas A, Stewart P, Vucinic D (2014) Increasing aeronautic electric propulsion performances by cogeneration and heat recovery. SAE Technical Paper 2014-01-2106, doi:10.4271/2014-01-2106
Mingtai C (2012) Static thrust measurement for propeller-driven light aircraft, the 2nd international conference on computer application and system modelling. Taiyuan Institute of Science and Technology, Taiyuan. ISBN 978-94-91216-00-8
Keen EB (2004) A conceptual design methodology for predicting the aerodynamics of upper surface blowing on airfoils and wings. MS. Thesys, Virginia Polytechnic Institute & State University
FAR 25.105 - Takeoff, FAA, Doc. No. 5066, 29 FR 18291, Dec. 24, 1964, as amended by Amdt. 25–92, 63 FR 8318, Feb. 18, 1998; Amdt. 25–121, 72 FR 44665, Aug. 8, 2007
FAR 25.107 - Takeoff Speeds, FAA, Doc. No. 5066, 29 FR 18291, Dec. 24, 1964, as amended by Amdt. 25–38, 41 FR 55466, Dec. 20, 1976; Amdt. 25–42, 43 FR 2320, Jan. 16, 1978; Amdt. 25–92, 63 FR 8318, Feb. 18, 1998; Amdt. 25–94, 63 FR 8848, Feb. 23, 1998; Amdt. 25–108, 67 FR 70826, Nov. 26, 2002; Amdt. 25–121, 72 FR 44665, Aug. 8, 2007; Amdt. 25–135, 76 FR 74654, Dec. 1, 2011
FAR 25.109 - Accelerate-stop distance, FAA, Doc. No. 5066, 29 FR 18291, Dec. 24, 1964, as amended by Amdt. 25–42, 43 FR 2321, Jan. 16, 1978; Amdt. 25–92, 63 FR 8318, Feb. 18, 1998
FAR 25.111 - Takeoff path, FAA, Doc. No. 5066, 29 FR 18291, Dec. 24, 1964, as amended by Amdt. 25–6, 30 FR 8468, July 2, 1965; Amdt. 25–42, 43 FR 2321, Jan. 16, 1978; Amdt. 25–54, 45 FR 60172, Sept. 11, 1980; Amdt. 25–72, 55 FR 29774, July 20, 1990; Amdt. 25–94, 63 FR 8848, Feb. 23, 1998; Amdt. 25–108, 67 FR 70826, Nov. 26, 2002; Amdt. 25–115, 69 FR 40527, July 2, 2004; Amdt. 25–121, 72 FR 44666; Aug. 8, 2007
FAR 25.113 - Takeoff distance and takeoff run, FAA, Doc. No. 5066, 29 FR 18291, Dec. 24, 1964, as amended by Amdt. 25–23, 35 FR 5671, Apr. 8, 1970; Amdt. 25–92, 63 FR 8320, Feb. 18, 1998
FAR 25.115 - Takeoff flight path, FAA, Doc. No. 5066, 29 FR 18291, Dec. 24, 1964, as amended by Amdt. 25–92, 63 FR 8320, Feb. 18, 1998
FAR 25.119 - Landing climb: all-engines-operating, FAA, Amdt. 25–121, 72 FR 44666; Aug. 8, 2007
FAR 25.125 - Landing, FAA, Amdt. 25–121, 72 FR 44666; Aug. 8, 2007; 72 FR 50467, Aug. 31, 2007
Anderson JD (2000) Introduction to flight, 4th edn. McGraw-Hill, Boston, 766 p
VV AA (xxxx) Cessna 402 User manual, Cessna Corporation
Phase P (1993) Take off & landing performance. USAF Test Pilot School, Edwards AFB, California, www.dtic.mil/dtic/tr/fulltext/u2/a320210.pdf
Trancossi M, Madonia M (2012) The efficiency of an electric turbofan vs. inlet area: a simple mathematical model and CFD simulations. SAE Technical Paper 2012-01-2217
Taylor M (1989) Jane's encyclopedia of aviation. Studio Editions, London
Cessna (2007) Type Certificate data sheet no. A7CE, FAA, Wichita Certification Office, Revision 47, CESSNA, March 27, 2007
VV AA (2008) Energy efficiency indicators for public electricity production from fossil fuels. International Energy Agency, Paris
Pegors D (1987) Advanced Allison small turboprop engines. SAE Technical Paper 871055. doi:10.4271/871055
Dumas A, Niccolai G, Trancossi M, Vucinic D. Aeromobile con prestazioni incrementate mediante sistema di propulsione cogenerativo, IT Patent request n. RE2014A000022
Acknowledgments
The present work has been performed as part of ACHEON Project | ACHEON Project - Aerial Coanda High Efficiency Orienting-jet Nozzle project, with ref. 309041 supported by European Union through the 7th Framework Programme (www.acheon.eu).
Author information
Authors and Affiliations
Corresponding author
Annex
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Trancossi, M., Madonia, M., Dumas, A. et al. A new aircraft architecture based on the ACHEON Coanda effect nozzle: flight model and energy evaluation. Eur. Transp. Res. Rev. 8, 11 (2016). https://doi.org/10.1007/s12544-016-0198-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12544-016-0198-4