1 Introduction

Due to the excellent capability of position accuracy and loading, ball screws are widely applied in precise CNC machining equipment to transmit force or movement [1]. With the rotational speed increasing, the temperature of the ball screw mechanism rises obviously. This phenomenon results in a thermal elongation and decreases the position accuracy of ball screws. It is reported in Ramesh’s research paper [2] the thermal error takes 40–70% of the total position accuracy error. Thus, the temperature rise prediction is necessary for the application of ball screws.

In recent years, plenty of studies have been conducted on the thermal behavior, temperature distribution, and thermal error analysis of ball screws. Xia et al. [3] put forward a dynamics characteristic thermal deformation model of the ball screw according to the least square system identification theory and proved the correctness and validity of the model by simulation data. Min et al. [4] developed a thermal model by the finite element method to investigate the temperature distribution in a ball screw feed drive system. In order to decrease the thermal errors and achieve thermal equilibrium faster, Xu et al. [5] established a thermal behaviour model based on the finite element method to estimate the function of an air-cooling system. Based on multiple linear regression methods, Huang et al. [6] considered the front bearings, back bearings, and cover nut of ball screws as independent variables and predicted thermal deformation of ball screws well under different rotational speeds. Nevertheless, the studies on thermodynamics analysis of ball screws mentioned above pay much attention to the distribution of the temperature rise by the finite element method. The method to calculate the temperature rise at different positions in a ball screw mechanism under various rotational speeds is neglected.

As the rotational speeds and positions influence the temperature rise of the ball screw directly, it is necessary to investigate the relationship between these three variables. Thus, a model is built to calculate the temperature rise based on the rotational speed and positions, and the thermal elongation of the ball screw is predicted in this paper.

2 Theoretical Analysis

In a ball screw mechanism, the heat is generated from the cutting process and friction. Generally speaking, the heat generated from the cutting process is taken away by the swarf and coolant [5]. So, three heat sources of the ball screw in operation are considered in this study: the friction between the balls and the bearings [7], the friction between balls and nut grooves, and the friction between the balls and screw grooves. Besides the heat generation, the heat keeps spreading into the air at the surface of the ball screw by convection. When the heat generation is equal to the heat loss, the ball screw mechanism will be in thermal equilibrium, and the temperature of every position will be stable.

2.1 Heat Transmission Analysis

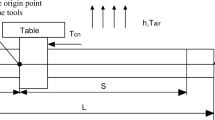
The heat transmission of ball screws in thermal equilibrium is shown in Fig. 1. \({H}_{b}\) is the heat generated from the supporting bearings. \({H}_{A}\) is the heat lost to the air at the surface of the ball screw by thermal convection. \({H}_{BS}\) is the heat generated from the friction of ball screws. \({L}_{0}\) is the total length of the ball screw. \({L}_{1}\) is the running distance of the ball screw. \(L\) is the distance between plane B and plane D. Plane A, B, and C are three adjacent planes. Plane D is at the center of the running area with the highest temperature.

Fig. 1
figure 1

Heat transmission of a ball screw mechanism

Full size image

2.2 Heat Transmission Calculation

In terms of a ball screw, the major heat source is the friction force at the contact area between the balls and the raceway. As the ball screw is structurally similar to the ball bearing, the heat generation in a ball screw mechanism can be defined as [8]

$$H_{{{\text{BS}}}} = 0.12\pi f_{{{\text{BS}}}} v_{{{\text{BS}}}} nM_{{{\text{BS}}}}$$
(1)

where \(H_{{{\text{BS}}}}\) is the heat generated by the ball screw, \(f_{{{\text{BS}}}}\) is a factor related to the lubricant condition and types of the ball screw, \(v_{{{\text{BS}}}}\) is the kinematic viscosity, \(n\) is the rotational velocity of the ball screw, and \(M_{{{\text{BS}}}}\) is the friction torque caused by the preload and dynamic load of the ball screw. The friction torque of the ball screw can be described as [9]

$$M_{BS} = = \frac{{2f \cdot F \cdot \left( {r_{m} + r_{b} \cdot \cos \alpha } \right)}}{\sin \alpha }$$
(2)

where \(f\) is the friction coefficient of the ball screw, \(F\) is the applied axial load of the ball screw (the preload in this study), \(r_{m}\) is the radius of the ball screw, \(r_{b}\) is the radius of the ball, \(\alpha\) is the contact angle of the ball screw.

In a ball screw mechanism, the heat lost in the air for convection can be defined as [10], 11

$$H_{A} = h_{v} \cdot A \cdot \Delta T$$
(3)
$$h_{v} = N_{u} \cdot k_{f} /d$$
(4)

where \(H_{A}\) is the heat loss from the ball screw to the ambient air, \({h}_{v}\) is the heat transfer coefficient, \(\Delta T\) is the temperature rise value of the ball screw,\(N_{u}\) is Nusselt number, and it can be computed by Eq. (5), \(k_{f}\) is the thermal conductivity of the surrounding air and \(d\) is the diameter of the surface where the heat convection occurs.

$$N_{u} = 0.133{\text{Re}}^{2/3} \Pr^{1/3}$$
(5)
$${\text{Re}} = u_{f} d/v_{f}$$
(6)
$$\Pr = c_{f} \mu_{f} /k_{f}$$
(7)

where \({\text{Re}}\) is the Reynolds number, \(\Pr\) is the Prandtl number, \(u_{f}\) is the airflow velocity, \(v_{f}\) is the kinematic viscosity of the air, \(c_{f}\) and \(\mu_{f}\) are the heat capacitance and dynamic viscosity of the air. Thus, by substituting Eq. (4)-(6) and Eq. (7) into Eq. (3), we can define \(H_{A}\) as

$$H_{A} = 0.133(u_{f} d/v_{f} )^{2/3} \Pr^{1/3} \cdot k_{f} /d \cdot A \cdot \Delta T$$
(8)

2.3 The Thermal Elongation of the Ball Screw

Figure 2 shows the heat transmission between planes A, B, and C. \({T}_{A}\), \({T}_{B}\), and \({T}_{C}\) are the temperature of planes A, B, C correspondingly when the ball screw is in the thermal equilibrium state. The distance between the planes is \(\Delta L\). In order to analyze the heat transmission of the three planes, it is assumed that the temperature of every point of each plane is the same. \(\Delta {T}_{AB}\) is the temperature difference between plane A and Plane B. \(\Delta {T}_{BC}\) is the temperature difference between plane B and plane C.

Fig. 2
figure 2

Heat transmission between plane (a, b and c)

Full size image

When plane A, B, and C are in the running area, according to Fig. 2, the temperature difference between plane A, B, and C can be written as

$$\Delta T_{{{\text{AB}}}} = T_{A} - T_{B} = T_{L - \Delta L} - T_{L}$$
(9)
$$\Delta T_{{{\text{BC}}}} = T_{B} - T_{C} = T_{L} - T_{L + \Delta L}$$
(10)

The heat conduction between the planes can be described as (\(\left( {h_{T} \cdot s \cdot \Delta T_{AB} /\Delta L} \right)\)) and (\(h_{T} \cdot s \cdot \Delta T_{BC} /\Delta L\)). In terms of plane B, the heat absorption includes the heat from plane A and the friction of ball screws. At the same time, the heat of plane B is lost to plane C and the air. So, the heat transmission of plane B can be described as

$$\frac{{h_{T} \cdot s \cdot \Delta T_{AB} }}{\Delta L} + \frac{{H_{BS} \cdot \Delta L}}{{L_{1} }} = h_{v} \cdot c \cdot \Delta L \cdot (T_{L} - T_{a} ) + \frac{{h_{T} \cdot s \cdot \Delta T_{BC} }}{\Delta L}$$
(11)
$$\frac{{h_{T} \cdot s \cdot \Delta T_{AB} }}{\Delta L} - \frac{{h_{T} \cdot s \cdot \Delta T_{BC} }}{\Delta L} = \frac{{(h_{v} \cdot c \cdot L_{1} \cdot (T_{L} - T_{a} ) - H_{BS} ) \cdot \Delta L}}{{L_{1} }}$$
(12)

By substituting Eq. (1), (3) into Eq. (12), Eq. (12) can be written as

$$\frac{{h_{T} \cdot s \cdot (T_{L - \Delta L} - T_{L} ) - h_{T} \cdot s \cdot (T_{L} - T_{L + \Delta L} )}}{{\Delta L^{2} }} = \frac{{(h{}_{v} \cdot c \cdot (T_{L} - T_{a} ) \cdot L_{1} - H_{BS} )}}{{L_{1} }}$$
(13)
$$h_{T} \cdot s \cdot \frac{{\partial^{2} T_{L} }}{{\partial L^{2} }} = \frac{{(h_{v} \cdot c \cdot (T_{L} - T_{a} ) \cdot L_{1} - H_{BS} )}}{{L_{1} }}$$
(14)

The solution for Eq. (14) can be written as

$$T_{L} = ke^{nL} + m$$
(15)

where \({T}_{L}\) is the temperature for each position, k, n, and m can be described as

$$k = T_{D} - m$$
(16)
$$n = \sqrt {\frac{{h_{v} \cdot c}}{{h_{T} \cdot s}}}$$
(17)
$$m = T_{a} + \frac{{H_{BS} }}{{h_{v} \cdot c \cdot L_{1} }}$$
(18)

where \({T}_{D}\) is the realistic temperature of plane D, \({T}_{a}\) is the temperature of the air, \({h}_{T}\) is the thermal conductivity, \({h}_{v}\) is the heat transfer coefficient, s is the sectional area of each plane, c is the perimeter of each plane.

Thus, the correlation between temperature and position within the running area can be written as

$$T_{L} = (T_{D} - (T_{a} + \frac{{H_{BS} }}{{h_{v} \cdot c \cdot L_{1} }})) \cdot e^{{\sqrt {\frac{{h_{v} \cdot c}}{{h_{T} \cdot s}}} \cdot L}} + (T_{a} + \frac{{H_{BS} }}{{h_{v} \cdot c \cdot L_{1} }})$$
(19)

When plane A, B, and C are outside the running area, the heat transmission of plane B can be described as

$$\frac{{h_{T} \cdot s \cdot \Delta T_{AB} }}{\Delta L} = h_{v} \cdot c \cdot \Delta L \cdot (T_{L} - T_{a} ) + \frac{{h_{T} \cdot s \cdot \Delta T_{BC} }}{\Delta L}$$
(20)
$$\frac{{h_{T} \cdot s \cdot \Delta T_{AB} }}{\Delta L} - \frac{{h_{T} \cdot s \cdot \Delta T_{BC} }}{\Delta L} = h_{v} \cdot c \cdot \Delta L \cdot (T_{L} - T_{a} )$$
(21)
$$h_{T} \cdot s \cdot \frac{{\partial^{2} T_{L} }}{{\partial L^{2} }} = h_{v} \cdot c \cdot (T_{L} - T_{a} )$$
(22)

Thus, the correlation between temperature and position outside the running area can be written as

$$T_{L} = \left( {T_{{\tfrac{{L_{1} }}{2}}} - T_{a} } \right) \cdot e^{{ - \sqrt {\frac{{h_{v} \cdot c}}{{h_{T} \cdot s}}} \cdot \left( {L - \frac{{L_{1} }}{2}} \right)}} + T_{a}$$
(23)

The correlation between temperature and position in ball screws can be written as

$$T_{L} = \left\{ {\begin{array}{*{20}c} {\left( {T_{D} - \left( {T_{a} + \frac{{H_{BS} }}{{h_{v} \cdot c \cdot L_{1} }}} \right)} \right) \cdot e^{{\sqrt {\frac{{h_{v} \cdot c}}{{h_{T} \cdot s}}} \cdot \left| L \right|}} + \left( {T_{a} + \frac{{H_{BS} }}{{h_{v} \cdot c \cdot L_{1} }}} \right)} \\ {\left( {T_{{\tfrac{{L_{1} }}{2}}} - T_{a} } \right) \cdot e^{{ - \sqrt {\frac{{h_{v} \cdot c}}{{h_{T} \cdot s}}} \cdot (\left| L \right| - \frac{{L_{1} }}{2})}} + T} \\ \end{array} \;\begin{array}{*{20}c} {\left| L \right| \le 0.5L_{1} } \\ {\left| L \right| > 0.5L_{1} } \\ \end{array} } \right.$$
(24)

Thus, the thermal elongation of the ball screw can be described as

$$E_{T} = \int {\alpha \cdot (T_{L} - T_{a} )} \cdot \partial L$$
(25)

where \({E}_{T}\) is the thermal elongation of the ball screw, \(\alpha\) is the linear expansion coefficient of the material.

2.4 Theoretical Temperature Values of Plane D

According to Z. Z. Xu’s study [5], the heat generated by the bearing is less than 8% of the ball screw, and it only transmits in a small range. So, at the center of the ball screw, the effect of the heat generated by the bearing on temperature rise can be ignored.

When plane D is in thermal equilibrium, the heat conduction and temperature change rate can be considered as zero according to the thermal laws. So, the temperature balance equation of a ball screw in plane D in thermal equilibrium can be written as

$$H_{BS} - H_{A} \cdot (T_{D} - T_{a} ) = H_{3}$$
(26)

where \(T_{D}\) is the temperature of plane D of ball screws, \({H}_{3}\) is the temperature rise coefficient and can be written as

$$H_{3} = M \cdot C$$
(27)

where \(M\) is the mass of the ball screw, \(C\) is the specific heat capacity of steel.

By substituting Eq. (1) and (3) to Eq. (26), Eq. (28) is obtained

$$0.12\pi f_{BS} v_{BS} nM_{BS} = 0.133(u_{f} d/v_{f} )^{2/3} \Pr^{1/3} \cdot k_{f} /d \cdot A \cdot \Delta T_{D}$$
(28)

Thus, \(\Delta T_{D}\) and \({T}_{D}\) can be described as

$$\Delta T_{D} = T_{D} - T_{a} = \frac{{0.9\pi f_{BS} v_{BS} nM_{BS} \cdot d}}{{(u_{f} d/v_{f} )^{2/3} \Pr^{1/3} \cdot k_{f} \cdot A}}$$
(29)
$$T_{D} = \frac{{0.9\pi f_{BS} v_{BS} nM_{BS} \cdot d}}{{(u_{f} d/v_{f} )^{2/3} \Pr^{1/3} \cdot k_{f} \cdot A}} + T_{a}$$
(30)

In fact, although the heat conduction and temperature change rate of plane D are very small, it cannot be zero. Thus, the theoretical temperature values of plane D are bigger than the realistic temperature values.

3 Experiment Details

In order to obtain the temperature rise phenomenon, a test bench was constructed shown in Figs. 3 and 4. The servo motor, roller linear guides, roller bearings, and working tables are designed to supply rotational speed and movement for the ball screw. The axial load applied to the ball screw in this study is caused by the preload. In order to decline the effect of the extra force, the worktable is supported by the roller liner guides. The total length of the tested ball screw is 2200 mm, and the running distance of the sample is 400, 600, 800, 1000, and 1200 mm. The preload of the ball screw is adjusted to investigate the effect of the load. The temperature of the ball screw is detected by a temperature sensor. When the ball screw is running, the friction torque will be detected by a torque sensor at the same time, and the thermal elongation of the ball screw is measured by a displacement sensor.

Fig. 3
figure 3

Schematic diagram of the experimental temperature rise test bench for ball screws

Full size image
Fig. 4
figure 4

Temperature rise test bench for ball screws

Full size image

In this running experiment, the main component parameters are shown in Table. 1. Before each experiment of different rotational speeds starts, the sample will be placed on the test bench until the temperature of the sample is the same as the air. Through the whole process of every experiment, the revolution of the ball screw is a constant value. For the temperature rise of every position, the temperature detection starts when the running process is conducted for 2.5 h, then the detection is conducted every 30 min. The temperature is confirmed until the detected values deviate less than 0.2℃. When the experiment is over, the ball screw makes its natural cooling without disassembly before the next experiment.

Table 1 Parameters of the sample and running test
Full size table

4 Results and Discussion

Through a series of detection experiments, we obtained the temperature rise at different positions and the thermal elongation of the ball screw under various rotational speeds and loads. The experimental results and theoretical results of the temperature rise at various positions are shown in Fig. 5 at 500 rpm and 1000 rpm when the applied load is 2895 N. Figure 6 shows the experimental results and theoretical results of the temperature rise at 1500 rpm, 2000 rpm, and 2500 rpm when the applied load is 2895 N.

Fig. 5
figure 5

Temperature of different positions under 500 and 1000 rpm

Full size image
Fig. 6
figure 6

Temperature of different positions under 1500, 2000 and 2500 rpm

Full size image

Based on Figs. 5 and 6, it can be seen clearly that the temperature descends from the middle to both sides in the ball screw mechanism. When the position is inside the running area, the temperature rise decreases slowly. When the position is outside the running area, the temperature rise decreases quickly. There is a quick change in the edge position. This is because heat absorption plays an important role in the running area. However, heat loss plays an important role outside the running area. With the rotational speed increasing, the temperature rise of the total length increases. This is due to the heat generation increases with the increasing rotational speed. The experimental temperature is smaller than the theoretical temperature in the running area. In terms of the positions outside the running area, although the experimental temperature and the theoretical temperature show the same tendency, the experimental value could bigger than the theoretical value. This is due to the installation condition of the ball screw.

Figure 7 shows the experimental and theoretical temperature rise values at the center of the ball screw under different rotational speeds. There is an approximate linear correlation between the temperature rising and the revolution. Figure 8 shows the temperature rise difference of the center when the rotational speed changes from 400 to 2500 rpm. It shows that the temperature rise difference values increase when the rotational speed increase. This is because when the temperature gets higher, the heat convection gets higher, which leads to a higher temperature change. The experimental temperature is smaller than the theoretical temperature in the running area. This is because the heat conduction and temperature change rate cannot be zero.

Fig. 7
figure 7

Experimental and theoretical temperature rise values of the center point

Full size image
Fig. 8
figure 8

Difference between the theoretical and experimental temperature rise of the center point

Full size image

Figure 9 shows the temperature of center point under the different applied loads when the rotational speed is 1000 rpm. The temperature of the center point increases with the applied axial load, and there is an approximate linear correlation between the temperature rising and the applied load. This is because the friction torque increases linearly with the axial load as described in Eq. (2). When the temperature of the center point increases linearly with axial load, the temperature of each point, shown in Fig. 10, increases with the axial load as well.

Fig. 9
figure 9

Experimental and theoretical temperature values of the center point under different loads

Full size image
Fig. 10
figure 10

Experimental temperature of different positions under different loads

Full size image

The thermal elongation of the ball screw is shown in Fig. 11. The thermal elongation of the ball screw increase when the rotational speed increase, and the theoretical curve and the experimental curve show the same tendency. When the rotational speed is low, the difference between the theoretical values and the experimental values is small. When the rotational speed gets higher, the difference between the theoretical values and the experimental values increases. This is because the headstock and the tailstock provide a drag force to limit the thermal elongation. The bigger the thermal elongation is, the bigger the drag force is. The relative error between the theoretical and experimental elongation is within 17% when the rotational speed is smaller than 2500 rpm.

Fig. 11
figure 11

The thermal elongation of the ball screw when the running distance is 800 mm

Full size image

Figure 12 shows the temperature rising of the ball screw under different running distances. The temperature rising of the running area decreases when the running distance increase. This is because heat absorption increases in the running area when the running distance decreases. However, the temperature rising outside the running area increase when the running distance increase. Because the temperature rising outside the running area is determined by the temperature at the boundary of the running area. Corresponds to temperature rising, the thermal elongation of the ball screw under different running distances is shown in Fig. 13. The thermal elongation of the ball screw increases at first and then decreases. This is because the thermal elongation of the ball screw is determined by the temperature rising and the length at the same time. When the running distance increase, the temperature rising decreases while the area of the temperature rising increases. Thus, there is a maximum point in the thermal elongation.

Fig. 12
figure 12

The temperature rising of the ball screw under different running distances

Full size image
Fig. 13
figure 13

The thermal elongation of different running distances at 400 rpm

Full size image

5 Conclusions

The temperature rise and thermal elongation influence the reliability and positioning accuracy of ball screws. The prediction of temperature rise is necessary for the thermal error control and selection of lubrication methods. In this paper, a new model to predict the thermal elongation of the ball screw at different rotational speeds is proposed based on the temperature rise. The experimental results of different rotational speeds agree well with the theoretical results calculated by this method. The main conclusions are as follows.

  1. (1)

    The realistic temperature change range of every position within the running area increases slowly when the rotational speed and load get higher. The value of temperature change is less than 5 degrees when the rotational speed is within 2500 rpm.

  2. (2)

    The theoretical thermal elongation and experimental thermal elongation show the same tendency. The deviation of theoretical values and experimental values is within 17% when the rotational speed of ball screws is within 2500 rpm.

  3. (3)

    The experimental temperature rise is smaller than the theoretical values by this method, as the boundary conditions of heat transmission at the center position cannot be realized. This leads to the difference between the theoretical thermal elongation and experimental thermal elongation.

  4. (4)

    The temperature rising of the running area decreases when the running distance increase. While the temperature rising outside the running area increase when the running distance increase.