Multi-objective Optimization of Machine Tool Spindle-Bearing System

Abstract

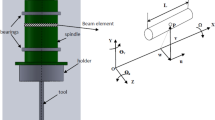
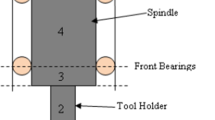
In this study, a multi-objective optimization is performed for the design of a spindle-bearing system based on particle swarm optimization (PSO). Multiple objectives, such as natural frequencies, static stiffness, and total friction torque are considered in this design optimization. Bearing preload and bearing locations are selected as the design variables. Pareto-optimal solutions are used to support the selection of optimal values of the design parameters. A finite element model is established for the analysis and design of the spindle system with four angular contact ball bearings. Two optimization processes are performed with the PSO technique. The first process involves the first two natural frequencies and friction torque of the spindle, whereas the second process focuses on the spindle’s static stiffness and friction torque. The simulation results show noticeable improvement in the objectives compared with those of the primitive spindle. The experiments conducted on an actual spindle system fabricated with the optimal design demonstrate the benefits of the optimal design. The proposed design method is expected to be very useful in the design optimization of machine tool spindle systems subjected to various customer-oriented objectives.

Appendix: Computation of Objective Functions

1.1 A1. Bearing Friction Torque

The friction torque model proposed by SKF is used [33]. The total friction torque of an angular contact ball bearing (ACBB) is the sum of four different sources as follows:

$$ M = M_{rr} + M_{sl} + M_{drag} + M_{seal} $$

(17)

where $M_{rr} ,M_{sl} ,M_{drag}$, and $M_{seal}$ represent the rolling, sliding, drag, and seal friction torque components, respectively. As the seal friction torque $M_{seal}$ is not affected by either the bearing position or the preload, it is ignored. The details of the remaining friction torque components are briefly described below.

1.2 A1.1 Rolling Friction Torque

The rolling friction torque can be calculated by:

$$ M_{rr} = \phi_{ish} \phi_{rs} \left[ {R_{1} d_{m}^{1.97} \left( {F_{r} + R_{3} d_{m}^{4} n^{2} + R_{2} F_{a} } \right)^{0.54} \left( {n\upsilon } \right)^{0.6} } \right] $$

(18)

where $\phi_{ish}$ and $\phi_{rs}$ are the inlet shear heating factor and the kinematic replenishment factor, respectively:

$$ \phi_{ish} = \left[ {1 + 1.84 \times 10^{ - 9} \left( {nd_{m} } \right)^{1.28} \upsilon^{0.64} } \right]^{ - 1} $$

(19)

$$ \phi_{rs} = \left[ {e^{{K_{rs} \upsilon n\left( {d/D} \right)}} \sqrt {\frac{{K_{z} }}{{2\left( {D - d} \right)}}} } \right]^{ - 1} $$

(20)

where R₁, R₂, and R₃ are the geometry constants for the rolling friction torque; R₁ = 5.03 × 10⁻⁷, R₂ = 1.97, and R₃ = 1.9 × 10⁻¹². D and d denote the outer and inner diameters of the bearing, respectively. The bearing mean diameter d_m is calculated by:

$$ d_{m} = 0.5\left( {d + D} \right) $$

(21)

F_r and F_a represent the external radial and axial load of the bearing, respectively. n and υ indicate the bearing rotating speed and kinematic viscosity of lubricant at the operating temperature, respectively. K_rs and K_z are the replenishment/starvation constant and the bearing type related geometry constant, respectively. For the current ACBBs and spindle system, K_rs = 3 × 10⁻⁸ and K_z = − 4.4.

1.3 A1.2 Sliding Friction Torque

The sliding friction torque can be calculated by:

$$ M_{sl} = \mu_{sl} S_{1} d_{m}^{0.26} \left[ {\left( {F_{r} + S_{3} d_{m}^{4} n^{2} } \right)^{4/3} + S_{2} F_{a}^{4/3} } \right] $$

(22)

where S₁, S₂, and S₃ are the geometry constants for the sliding friction torque; S₁ = 1.3 × 10⁻², S₂ = 0.68, and S₃ = 1.9 × 10⁻¹². μ_sl is the sliding friction coefficient, which is calculated by:

$$ \mu_{sl} = \phi_{bl} \mu_{bl} + \left( {1 - \phi_{bl} } \right)\mu_{EHL} $$

(23)

where μ_bl is the sliding friction coefficient; μ_bl = 0.15. μ_EHL is the friction coefficient in the full film conditions; μ_EHL = 0.04. The weighting factor for the sliding friction torque ϕ_bl is estimated by:

$$ \phi_{bl} = \left[ {e^{{2.6 \times 10^{ - 8} \left( {n\upsilon } \right)^{1.4} d_{m} }} } \right]^{ - 1} $$

(24)

1.4 A1.3 Drag Friction Torque

The drag friction torque of an ACBB with the oil bath lubrication method can be calculated by:

$$ M_{drag} = V_{M} K_{ball} d_{m}^{5} n^{2} $$

(25)

where V_M is the parameter depending on oil level. K_ball is a ball bearing constant, calculated by:

$$ K_{ball} = \frac{{i_{rw} K_{z} \left( {d + D} \right)}}{D - d} \times 10^{ - 12} $$

(26)

where i_rw indicates the number of ball rows of bearing; i_rw = 1. For the ACBB lubricated with oil jet lubrication, the drag loss with above-mentioned oil bath method can be used with the oil level equal to half of the ball diameter, and multiplying the obtained M_drag by a factor of two [33].

1.5 A2. Spindle System Natural Frequency

The spindle shaft is modelled by Timoshenko beam method, which considers bending and shearing effects [32]. The shaft is divided into a number of finite elements and the supported ACBBs are supposed to be located at the nodes (Fig. 14). The equation of motion for a shaft element can be written, by neglecting the internal damping of shaft, as follows:

$$ \left[ {\begin{array}{*{20}c} {m^{s} } & 0 \\ 0 & {m^{s} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\ddot{y}^{s} } \\ {\ddot{z}^{s} } \\ \end{array} } \right\} + \varOmega \left[ {\begin{array}{*{20}c} 0 & {g^{s} } \\ { - g^{s} } & 0 \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\dot{y}^{s} } \\ {\dot{z}^{s} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {k^{s} } & 0 \\ 0 & {k^{s} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {y^{s} } \\ {z^{s} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {f_{y}^{s} } \\ {f_{z}^{s} } \\ \end{array} } \right\} $$

(27)

where $m^{s}$ and $g^{s}$ represent the [4 × 4] mass and gyroscopic matrices of the shaft element, respectively. $\left\{ {y^{s} } \right\}$ and $\left\{ {z^{s} } \right\}$ indicate the [4 × 1] displacement vectors in xOy and xOz planes. The equation of motion for an ACBB is represented as:

$$ \left[ {\begin{array}{*{20}c} {k_{yy}^{b} } & {k_{yz}^{b} } \\ {k_{zy}^{b} } & {k_{zz}^{b} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {y^{b} } \\ {z^{b} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {f_{y}^{b} } \\ {f_{z}^{b} } \\ \end{array} } \right\} $$

(28)

where $\left\{ {\begin{array}{*{20}c} {f_{y}^{b} } & {f_{z}^{b} } \\ \end{array} } \right\}^{T}$ is the force vector of the ACBB. $k_{yy}^{b}$, $k_{yz}^{b}$, $k_{zy}^{b}$, and $k_{zz}^{b}$ are the [2 × 2] stiffness matrix of the bearing [32]. By combining the equations of all the shaft elements and the ACBBs, the equation of motion for the whole spindle system is derived as

$$ \left[ M \right]\left\{ {\ddot{q}} \right\} + \varOmega \left[ G \right]\left\{ {\dot{q}} \right\} + \left[ K \right]\left\{ q \right\} = \left\{ f \right\} $$

(29)

Fig. 14

FE model of spindle-ACBB system

Equation (29) can be described, in a state-space form, as:

$$ \left[ A \right]\left\{ {\dot{h}} \right\} + \left[ B \right]\left\{ h \right\} = \left\{ P \right\} $$

(30)

where

$$ \left[ A \right] = \left[ {\begin{array}{*{20}c} M & 0 \\ 0 & M \\ \end{array} } \right] $$

(31)

$$ \left[ B \right] = \left[ {\begin{array}{*{20}c} 0 & { - M} \\ K & {\varOmega G} \\ \end{array} } \right] $$

(32)

$$ \left\{ h \right\} = \left\{ {\begin{array}{*{20}c} q \\ {\dot{q}} \\ \end{array} } \right\} $$

(33)

$$ \left\{ P \right\} = \left\{ {\begin{array}{*{20}c} 0 \\ f \\ \end{array} } \right\} $$

(34)

The eigenvalue problem associated with the state-space form equation can be written as

$$ \left( {\alpha \left[ A \right] + \left[ B \right]} \right)\left\{ h \right\} = \left\{ 0 \right\} $$

(35)

where α and {h} represent the eigenvalue and the corresponding eigenvector, respectively. From Eq. (35), the natural frequencies are determined from the imaginary parts of the eigenvalues.

1.6 A3. Spindle Static Stiffness

For the static condition of the spindle system, the first two terms in Eq. (29) are vanished. Therefore, the displacement vector of all the nodes {q} can be calculated using the following static relationship:

$$ \left[ K \right]\left\{ q \right\} = \left\{ f \right\} $$

(36)

where {f} is the load vector of the spindle-bearing system. In this study, because the static stiffness at the spindle nose position is considered, only a vertical radial load P is applied at the spindle nose (Fig. 14). Accordingly, the load vector {f} contains only one non-zero element of P at the nose node, whereas the other elements of {f} are all zeros. Having obtained the displacement vector {q} for all the nodes, the displacement of the spindle nose can be easily extracted and denoted as q_n. The spindle static stiffness, estimated at the spindle nose is finally calculated, as follows:

$$ K = \frac{P}{{q_{n} }} $$

(37)