1 Introduction

Various welding technologies are applied in constructing large structures such as nuclear power plants. During welding, especially multi-pass welding, cyclic heat input and cooling affect the material unevenly depending on distance from the heat source, so that phase transformations occur differently in different locations and microstructures with low toughness may develop around the heat-affected zone (HAZ) [1, 2]. At the same time, in general, tensile residual stress may be generated around the weld and HAZ due to uneven expansion and contraction of the material during heating and cooling process [3].

The welding residual stress is an important factor in determining structural integrity, since it can cause unexpected fracture and strongly influences stress corrosion cracking (SCC) and fatigue life as well [4,5,6,7]. To overcome these issues, post-weld heat treatment (PWHT), a process of reheating below the material’s critical transformation temperature, has been widely applied to welds; PWHT reduces tensile residual stress by tempering the HAZ and weld metal [8,9,10], improves microstructural homogeneity and toughness, and decreases the corrosion rate [11]. For this reason, standards and codes related to manufacturing or construction by welding generally require or recommend PWHT after welding. The American Society for Mechanical Engineers (ASME) Boiler & Pressure Vessel (BPV) Code Section III, a code for the design, manufacturing, and construction of nuclear power plants, has also presented PWHT requirements for many decades by taking into account the mechanical properties, microstructure, and residual stress. The ASME BPV Code, Section III gives mandatory specifications for preheat and PWHT depending on material group, thickness and preheat temperature [12, 13].

However, PWHT for large, thick-walled steel components such as pressure vessels is expensive and time-consuming process. Additionally, since the fracture toughness of steels has been substantially enhanced as steel-making technology improves, many technical studies now support the relaxation of current mandatory PWHT [14, 15]. Furthermore, deterioration in mechanical properties has been reported for a number of steels during PWHT: some quenched and tempered steels show severe degradation in impact-test fracture toughness and crack-tip-opening displacement (CTOD) fracture toughness after PWHT [16, 17], and improper heat treatment may degrade tensile properties and ductility [18, 19]. The PWHT exemption ranges therefore have been extended by the revision of ASME BPV Code, Code Cases, such as N-71 and N-763 [20]. Although there are many supportive aspects for PWHT exemption, it requires a thorough review of weld quality that takes into account the possible drawbacks of omitting the heat treatment.

As part of a proposal for a new PWHT exemption criterion for ferritic steel welds, this study evaluated the structural integrity of SA508 Gr.1a welds used in the steam generator of Korean Standard Nuclear Plants (KSNP) and examined the appropriateness of its PWHT exemption in terms of microstructure, mechanical properties and residual stress. Five welding coupons were fabricated with different welding methods and heat treatment conditions. Mechanical properties and microstructures were evaluated according to the welding procedure qualification test in the ASME BPV Code. In order to check the effects of residual stress, nonductile fracture evaluation was performed by considering the geometric dimensions and operating conditions of the KSNP steam generator and assuming high tensile residual stresses. The test and evaluation results argue for a new PWHT exemption criterion applicable to the ferritic steel welds in nuclear power plants.

2 Experimental Evaluation: Mechanical Testing and Microstructural Analysis

2.1 Materials and Welding

The base and weld materials were provided by Doosan Heavy Industries & Construction and are the same as that used in steam generators of nuclear power plants. Table 1 describes the chemical composition of base and weld. Five weld coupons of SA508 Gr.1a with a single V-groove configuration were fabricated to identify the effects of PWHT and welding method on the mechanical and microstructural characteristics of the weldment (Table 2). The actual thickness of the SA508 Gr.1a weld used in the KSNP steam generator we are interested in is 120 mm. However, since the welding procedure qualification test for a 40-mm-thick welded coupon can guarantee up to 200-mm-thick welding specimens with the same Welding Procedure Specification (WPS) [21], we produced the coupons with 40-mm-thick base metal for three welding methods: submerged-arc welding (SAW), gas-tungsten arc welding (GTAW), and shielded-metal arc welding (SMAW). Since SAW is the most widely used of the three, a heat treated coupon (610 °C for 40 h) was prepared using SAW as a reference for checking the effect of PWHT. In addition, a coupon of thickness 120 mm was prepared using the SAW to check for thickness effects. The welding parameters for each welding method are summarized in Table 3.

Table 1 Chemical composition of base and weld materials
Full size table
Table 2 Coupon details and specification
Full size table
Table 3 Welding parameters for SAW, GTAW and SMAW
Full size table

2.2 Experimental Methods

2.2.1 Microstructure Analysis and Hardness Testing

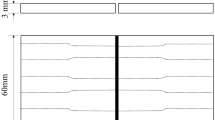
Microstructure analysis and hardness testing were performed in a cross-section perpendicular to the welding direction on a 120 mm thick welding coupon (coupon #5) as shown in Fig. 1a. Five 30 × 20 mm samples were taken at depth intervals of 5 mm from top to bottom through the coupon thickness; the positions were determined so as to place the welding fusion lines at the center of each sample (Fig. 1b). Prior to optical observation, sample surfaces were polished with 1 \({\mu m}\) diamond suspension and etched in a 50–50 mixture of picric acid solution (100 mL ethanol with 4 g trinitrophenol and 1 mL HCL) and sodium thiosulfate solution (100 mL distilled water with 1 g sodium thiosulfate). After microstructure analysis by optical microscope, the five samples were polished using 0.25 \({\mu m}\) colloidal silica suspension and electropolished in 90% ethanol (C2H5OH) and 10% perchloric acid (HCLO4) mixture at 15 V for 60 s to minimize the damage from mechanical polishing. Electron back-scatter diffraction (EBSD, TSL) analysis was performed in a field-emission scanning electron microscope (FE-SEM, JEOL, JSM-7600F) with tilting angle 70°, acceleration voltage 10 kV, beam intensity 13 and step size 0.5 \({\mu m}\). Locations 200 \({\mu m}\) from the fusion line toward the base were analyzed at the center of each sample.

Fig. 1
figure 1

a Schematic diagram of coupon #5, b schematic diagram of samples for microstructure analysis from A (top) to E (bottom)

Full size image

Vickers hardness testing was carried out on the same five samples using a Micro-AIS (Frontics, Inc., Seoul, Republic of Korea) with maximum indentation load 0.98 N (0.1 kgf); tests were performed at 14 points spaced 0.5 mm apart, starting from the base metal to welding region. After testing, the residual imprint areas were evaluated by optical microscope.

2.2.2 Mechanical Testing

Tension tests, transverse side bend tests, Charpy V-notch impact tests and drop weight tests were performed to assess the mechanical properties of the welds. Specimens for tension testing were of two kinds, weld material and HAZ, and were tested at room temperature. For Charpy V-notch testing, three specimens were prepared: weld material, base material and HAZ. Tests were performed at 30 °F. In addition, specimens for drop weight and transverse side bend testing also included the weld materials and HAZ. The side bend tests were done at room temperature and the drop weight tests at -20°F, following the technical basis. All specimen preparation and test procedures for the above mechanical tests were performed according to the technical basis in Table 4.

Table 4 Mechanical testing codes
Full size table

2.3 Experimental Results and Discussion

2.3.1 Microstructure Analysis and Hardness Testing

After welding, coupon #5 has heat-affected zone (HAZ) of which width is approximately 2 mm. The microstructure transition in HAZ from the weld fusion line toward base metal is shown in Fig. 2b–d. In the region adjacent to the weld metal, within 500 \({\mu m}\) from fusion line (Fig. 2b), a lath bainite microstructure was developed. As seen in Fig. 2c, the greater the distance from the fusion line, the finer the bainite microstructure at the middle of the HAZ. Figure 2d, at the end of the HAZ, shows partial grain refinement. The base metal microstructure (Fig. 2e) is composed of coarse ferrite and pearlite.

Fig. 2
figure 2

Optical micrographs of microstructure of the sample A (top) in coupon #5: a overall morphology of HAZ, b 0.5 mm, c 1 mm, d 1.5 mm from fusion line, e base metal

Full size image

Since coupon #5 is a thick weldment, its HAZ microstructure will vary from depth to depth due to uneven heat distribution. Figure 3 shows the microstructure of the HAZ about 500 µm away from the fusion line toward the base metal, through the coupon thickness at 25-mm intervals. The average grain size decreases with increasing distance from the top surface, because the lower-pass regions are reheated to a temperature above the recrystallization temperature by upper welding passes [22]. Therefore, the transformed microstructure in the upper-pass region is coarser than in the lower-pass region.

Fig. 3
figure 3

Microstructure of HAZ from a sample B, b sample C, c sample D, d sample E in Coupon #5

Full size image

Quantitative analysis of microstructure was conducted by electron back-scatter diffraction (EBSD) analysis. As shown in Fig. 4a–e, the IPF map results, the grain size decreases as the distance from the top surface increases, as seen in the microstructural analysis by optical microscope. The average grain size for the samples decreases to 28.7, 18.3, 11.5, 10.2, 6.6 µm from sample A (top) to sample E (bottom), as shown in Table 5 because of the recrystallization by reheating from the upper welding passes [22]. Figure 4f–j show a GOS map analyzing the area fraction of ferrite microstructure using grain of 5° and an orientation difference condition of 2°. The fraction of residual ferrite microstructure increases with distance from the surface. The length of the high-angle grain boundary, which is the boundary of the ferrite microstructure, increases from first to fifth, as is consistent with the area fraction of ferrite.

Fig. 4
figure 4

EBSD maps of HAZ: inverse pole figure (IPF) colored orientation maps from a sample A, b sample B, c sample C, d sample D, e sample E in Coupon #5 specified in Fig. 1b; grain orientation spread (GOS) maps from f sample A, g sample B, h sample C, i sample D, j sample E in Coupon #5 specified in Fig. 1b. Red and blue are ranges of 2° to 5° and 15° to 180° respectively. (Color figure online)

Full size image
Table 5 Results of EBSD analysis
Full size table

Figure 5 shows hardness distributions for samples extracted from locations from the top to bottom region in coupon #5. The hardness increases about 10% in the HAZ over the base metal region, which is the effect of microstructural transformation. The maximum hardness value was 254 HV 0.1 in sample C, which is located at the middle depth in coupon #5.

Fig. 5
figure 5

Hardness test results for five samples from top (A) to bottom (E) of coupon #5

Full size image

After welding, the HAZ generally becomes brittle due to carbide precipitation, martensite/bainite formation, and grain coarsening, and this is considered the weakest part of the weld [23]. In the 120 mm thick SA508 Gr.1a weldments, coarse grains developed near the fusion line and microstructures containing bainite formed, identifying typical SA508 welds. For hardness results, when compared with those of the SA508 steels in the previous study [23], it can be expected that coupon #5 has a small volume fraction of martensite and has tempering effect. Coupon #5 did not undergo PWHT, but was expected to become tempered during the welding process, it was fabricated using multi-pass welding [23, 24]. However, since analysis by microstructure and hardness can only indirectly evaluate a weldment’s structural integrity, a more quantitative mechanical characterization should be performed.

2.3.2 Mechanical Properties

For mechanical testing of coupon #5, we fabricated the specimens near the top surface of the coupon. As shown in Table 5, the grain size is larger near the top surface, and in general, the coarser the grain, the lower the toughness. We fabricated the specimens of coupon #5 near the top surface for a conservative approach.

Figure 6a shows the results of tension tests; the dotted red line indicates the minimum required tensile strength value of 70 ksi for SA508 Gr.1a material by ASME BPV Code, and it is seen that the results for all coupons satisfy the acceptance criterion. Of these, coupons #1, 3, and 4 were made using SAW, GTAW, and SMAW, respectively. These values are generally similar regardless of welding method. However, it can be seen that SMAW, which had the largest heat input during welding, has a relatively small value. The influence of PWHT can be confirmed in coupons #1 and 2, and it is noteworthy that the strength decreased after PWHT. This is consistent with what has been recently reported for quenched and tempered steel [18, 19, 23]. Another notable point is the influence of coupon thickness. Comparison of coupons #1 and 5 shows that the yield strength increases by more than 10% as the thickness is tripled from 40 to 120 mm.

Fig. 6
figure 6

Results of a tension tests and b Charpy V-notch tests

Full size image

The impact energy values in Fig. 6b all satisfy the minimum required value of 50 ft lbf specified in the ASME BPV Code (red dotted line). Comparing coupons #1 and 2 confirms that no significant change occurs due to PWHT, and it can also be seen that though the welding methods change the impact energy values slightly, there is no dramatic drop in values (coupons #1, 3 and 4). The results of the transverse side bend test and drop weight test shown in Table 6 confirm that all coupons met the acceptance criterion, which means that the structural integrity of the weldment is acceptable in terms of toughness: even with a change in welding method, the thickness increases up to 120 mm, and post-heat treatment is exempted.

Table 6 Results of the transverse side bend test and drop weight test
Full size table

Thus the results of tension testing, Charpy V-notch impact testing, transverse side bend testing and drop weight testing on the five coupons all met the criteria of the welding procedure qualification test. This means that PWHT does not significantly affect the mechanical properties of SA508 Gr.1a welds. In addition, for the SAW, SMAW and GTAW welding methods, this strongly suggests that, with respect to mechanical properties, PWHT may be eliminated from the welding procedure for the actual structure.

3 Analytical Evaluation: Nonductile Fracture Assessment

3.1 Effect of Residual Stress on Nonductile Fracture Evaluation

Relaxing residual stress is one of the main purposes of PWHT. If PWHT is not performed, high tensile welding residual stresses may remain in the weld. In thick-walled welded components, welding residual stresses may occur with a triaxial stress state that suppresses plastic deformation and promotes nonductile fracture even in ductile materials. In addition, tensile residual stress is a crack-driving forces that can induce nonductile fracture. Hence welding residual stress is critical to nonductile fracture of thick-walled welds. For these reasons, welding residual stress must be considered in determining exemption from PWHT.

Nonductile fracture occurs when the maximum stress intensity factor corresponding to the maximum tensile principal stress reaches the fracture toughness; in welding, the tensile residual stress at the surface generally has the maximum value [25]. The present study suggests a methodological approach to consider the residual stress effect using an analytical evaluation for nonductile fracture to guarantee weldment integrity in terms of residual stress by assuming that the maximum surface tensile stress is uniformly distributed along the specimen thickness.

The ASME BPV Code presents procedures for evaluating nonductile fracture of pressure vessels in nuclear power plants that require considering the welding residual stresses. Based on the nonductile fracture assessment procedures of the ASME BPV Code, Section III & Section XI [26, 27], in this study, the effect of the residual stress on the nonductile fracture was considered in the non-ductile fracture assessment as follows:

$$K_{Iall} = 2 \cdot K_{{\text{Im}}} + K_{It} + K_{Ir} \le K_{Ic}$$
(1)

where \(K_{Iall}\) is a total applied stress intensity factor, \(K_{Im}\) is a stress intensity factor due to primary membrane stress, \(K_{It}\) is a stress intensity factor due to thermal stress, and \(K_{Ir}\) is a stress intensity factor due to residual stress. These stress intensity factors were calculated based on the design conditions and the residual stress state of the target weld. \(K_{Ic}\) is the fracture toughness of the ferritic steel SA-508 Gr.1a. If the sum of the stress intensity factors, \(K_{Iall}\), is greater than \(K_{Ic}\), nonductile fracture would occur; if the sum is less than \(K_{Ic}\), nonductile fracture would not occur.

To calculate the stress intensity factors, a surface elliptical flaw with an aspect ratio (a/l) of 0.1667 was assumed, where a and l are the mean depth and width of the flaw, respectively. According to the allowable flaw sizes in the ASME BPV Code, Section XI, Subsec.IWB, Article IWB-3510.1 [21], the allowable flaw depth for our assumed flaw shape is 2.6% of the nominal wall thickness. For a more conservative approach, a safety factor was introduced in the flaw depth. Since it is highly improbable that a flaw four times larger than what is allowed by the Code will escape detection during in-service inspection (ISI) [28], the safety factor was taken as 5, and thus the flaw depth was determined as 13% of the nominal wall thickness in the nonductile fracture assessment.

The stress intensity factor for primary membrane stress (\(K_{Im}\)) is calculated according to the ASME BPV Code, Section XI, Nonmandatory Appendices, Appendix A [26]. Design practices should satisfy the following acceptable criteria for primary membrane stresses as presented in the ASME Code Section III NB-3221 [29]:

$$P_{m} \le S_{m} ,\quad P_{L} \le 1.5S_{m} ,\quad P_{L} + P_{b} \le 1.5S_{m}$$
(2)

where \(P_{m}\) and \(P_{L}\) are general primary membrane stress intensity and local primary membrane stress intensity, respectively. \(P_{b}\) is primary bending-stress intensity, and \(S_{m}\) is design-stress intensity presented in the ASME Code Section III, Div. 1, Appendices. In order to be sufficiently conservative, the primary membrane stress for calculating the \(K_{Im}\) is taken as 1.5 \(S_{m}\).

The stress intensity factor for thermal stress (\(K_{It}\)) is also calculated according to the ASME Code, Section XI, Nonmandatory Appendices, Appendix A. For pressure vessel shell components, design practices should generally satisfy the following acceptance criterion for secondary stresses in the ASME BPV Code section III NB-3222:

$$P_{e} \le 3S_{m} \quad P_{L} + P_{b} + P_{e} + Q \le 3S_{m}$$
(3)

where \(P_{e}\) is a secondary expansion stress intensity that results from the constraint of free end displacement and Q is secondary stress intensity. For a conservative assessment, values of \(P_{e}\) and \(P_{b}\) are assumed to be zero so as to maximize the value of Q. In addition, we took \(S_{m}\) as the average of the values at room temperature and operating temperature, and assumed that \(P_{L}\) is the same as \(P_{m}\) due to operating pressure. Finally, the secondary stress intensity Q for calculating the \(K_{It}\) is determined using the following equation: \(Q = 3S_{m} - P_{L} = 3S_{m} - 1.5S_{m} = 1.5S_{m}\). In addition, it is assumed that the thermal stress distribution is a linear function of first order having maximum and minimum values on the inner and outer surfaces.

In calculating the stress intensity factor for residual stress (\(K_{Ir}\)), a conservative approach was proposed by which the surface residual stress value evaluated in the field is considered as a membrane stress that is uniformly distributed along the thickness. This approach is conservative because the surface residual stress is generally the maximum or near-maximum tensile stress value, as presented in the residual stress distributions in the API 579-1/ASME FFS-1 Code [25]. The surface residual stress is evaluated in both the outside and inside surface. Among the residual stress values evaluated in the field, the maximum residual stress value is considered as a membrane stress and used for the calculation of \(K_{Ir}\). Because the welding residual stress is considered a membrane stress, \(K_{Ir}\) is calculated in the same way as \(K_{Im}\).

Fracture toughness (\(K_{Ic}\)) is obtained based on the fracture toughness master curve specified in the ASME BPV Code, Section III, Nonmandatory Appendices, Appendix G [23]. Though the stress values used to calculate \(K_{Im}\) and \(K_{It}\) are the stress limits at high pressure and high temperature, \(K_{Ic}\) is set as around 195 \({\text{MPa}}\sqrt {{\text{m}},}\) which is the fracture toughness value when \({\text{T}} - {\text{RT}}_{{{\text{NDT}}}}\) is about 53.9 °C. This is based on the assumption that T is room temperature and \({\text{RT}}_{{{\text{NDT}}}}\) is about − 28.9 °C (− 20.0°F), which is obtained based on the results and testing temperatures of drop weight testing and Charpy V-notch impact testing [29].

The parameter values, \(K_{Im}\), \(K_{It} ,\) and \(K_{Ic}\), calculated by the method presented above are substituted in Eq. (1). Because the parameters are calculated using the stress limit and design specification values, they are constants and only \(K_{Ir}\) is a variable depending on the residual stress value. For \(K_{Ir}\), the residual stress value is taken as a constant times the specified minimum yield strength of SA-508 Gr.1a specified in the ASME BPV Code, Section II, SA-508 Gr.1a [30]. To find the maximum residual stress value that makes the sum of the stress intensity factors, \(K_{Iall}\), equal to the fracture toughness, various residual stress values are substituted in the equation. As shown in Table 7, when the ratio of residual stress to yield strength is 1.5, the ratio of \(K_{Iall}\) and \(K_{Ic}\) is almost 1, which means that the sum of the stress intensity factors is almost equal to the fracture toughness. If the surface residual stress is greater than 1.5 times the specified minimum yield strength, the sum of the stress intensity factors would be greater than the fracture toughness, and there is risk that nonductile fracture would occur. Hence, 1.5 times the specified minimum yield strength is proposed as a residual stress acceptance criterion for weldment integrity as follows:

$$\frac{{\sigma_{res} }}{{\sigma_{ys} }} \le \frac{3}{2}$$
(4)
Table 7 Computational result of residual stress acceptance criterion
Full size table

In the case of SA-508 Gr.1a, the specified minimum yield strength is 250 MPa, so the maximum allowable residual stress will be 375 MPa.

3.2 Nonductile Fracture Evaluation for KSNP Steam Generator

To identify the applicability of the proposed criterion, stress intensity factors of the girth weld on the KSNP steam generator for primary membrane stress and thermal stress are calculated using the design stress report of KSNP. Table 8 presents the design parameters and operating conditions of the KSNP steam generator. Table 9 shows that, under these operating conditions of KSNP, even larger residual stress would be allowed. The acceptance criterion equal to 1.5 times the specified minimum yield strength suggested above is thus reasonably conservative. In other words, the proposed acceptance criterion can be conservatively applied as an exemption requirement for PWHT of ferritic steel welds of SA-508 Gr.1a.

Table 8 Design parameters and operating conditions of KSNP
Full size table
Table 9 Design parameters and operating conditions of KSNP: (a) Level A condition (b) Test condition
Full size table

4 Conclusions

This study investigated the appropriateness of PWHT exemption for thick welds of SA-508 Gr.1a, a ferritic steel widely used in nuclear power plants, by analyzing its nonductile fracture mechanism considering mechanical properties, microstructure and residual stress. As a result of the investigation, the following findings are derived:

  1. 1.

    For a 120-mm-thick SA508 Gr.1a weldment, bainite and ferrite developed in the heat-affected zone. The farther from the fusion line and from the top surface, the finer the grain size. Microstructure and hardness results indicate that its martensite/bainite volume fraction is small and that it underwent a tempering effect.

  2. 2.

    PWHT does not significantly affect the mechanical properties of SA508 Gr.1a welds and all results satisfied the acceptance criteria specified in ASME BPV Code. This strongly suggests that, with respect to mechanical properties, PWHT may be eliminated from the welding procedure for SA508 Gr.1a welds of thickness up to 120 mm.

  3. 3.

    A new acceptance criterion for PWHT exemption of thick welds was proposed using a welding residual stress value based on nonductile fracture evaluation. The residual stress value in the acceptance criterion is equal to 1.5 times the specified minimum yield strength. In other words, welding residual stress below this criterion does not cause nonductile fracture of the welds, and this acceptance criterion can be applied as an exemption requirement for PWHT of ferritic steel welds consisting of SA-508 Gr.1a. Its conservatism was verified using the design parameters and operation conditions of KSNP.