Existence of Partially Degenerate Electrical Transport in Intermetallic Cu₂SnSe₃ Thermoelectric System Sintered at Different Temperatures

Abstract

A detailed investigation on the temperature dependent electrical properties of Cu₂SnSe₃ system, synthesized via conventional solid-state reaction at different sintering temperatures are presented in this communication. All the samples exhibit degenerate semiconducting nature at low temperatures. The existence of small polarons and hence electron–phonon interactions are confirmed at temperatures below 400 K. A transition was observed from degenerate to non-degenerate semiconducting behaviour at high temperatures (T > 400 K). The study confirms the unusual transition in electrical resistivity as well as thermopower at high temperatures in all the compounds, demonstrating the existence of minority carrier excitation along with temperature-triggered ionisation of the defects. The transport behaviour is further supported by an upward movement of Fermi level away from the valence band. Highest weighted mobility of 8.2 cm² V⁻¹ s⁻¹ at 673 K was obtained for the sample sintered at 1073 K. A considerable decrease in electrical resistivity with increase in temperature (T > 400 K) has driven the power factor to increase exponentially, thereby achieving highest value of 188 µV/mK² (at 673 K) for the sample sintered at 673 K.

Graphic abstract

1 Introduction

Popularity of thermoelectric (TE) materials which enable the reversible and direct conversion of heat into electricity, has driven the materials research community to work on various thermoelectric materials and explore recovery of waste heat from various sources [1]. ‘Figure of merit’ ZT, is a decisive factor which portrays the efficiency of a material. It is an interconnect of thermopower (S), electrical conductivity (σ) and thermal conductivities (κ) and is given by, ZT = (S²σ/κ) T. The numerator of the equation is referred as power factor, which is the contribution from the charge transport to the thermoelectric performance. Here, optimization of carrier density (n) and mobility (µ) turns out to be a major task to keep up the good electrical transport and hence the higher power factor. Thermoelectric quality factor (β) which is proportional to ZT, is also one of the parameters that determines the TE performance of a semiconductor without spanning the entire range of carrier concentrations [2]. Expression for β is given by,

$$\beta = \frac{{8\pi \left( {2m_{e} } \right)^{{3/2}} k_{B} ^{{7/2}} }}{{3eh^{3} }}.\frac{{\mu _{w} T^{{5/2}} }}{{\kappa _{L} ~}}$$

(1)

where $h$ is Planck’s constant, $~k_{B} ~$ is Boltzmann constant, m_e and e are respectively the mass and charge of an electron and T is the absolute temperature. μ_w is the weighted mobility of the carriers which is related to carrier mobility (µ) and effective mass (m*) and is given by,

$$\mu _{w} = ~\mu ~\left( {\frac{{m^{*} }}{{m_{e} }}} \right)^{{3/2}}$$

(2)

Weighted mobility is the mobility weighted by the density of electronic states, which is effective in explaining the charge transport without the help of band structure calculations. μ_w can help to assess the carrier scattering mechanism, differences in the level of doping and electronic band structures [3]. Hence analysing and engineering the weighted mobility could be a strategy for higher thermoelectric performance.

Among several classes of thermoelectric materials, Cu₂SnSe₃ has drawn sufficient attention among researchers. Cu₂SnSe₃, a diamond structured semiconductor derived from the binary zinc blende structure, where the hole transport is governed by the network of Cu-Se bonding. Sn atoms residing inside this framework, contributes charge carriers to the hole transport. Hence it has larger flexibility in modifying the electronic and other physical properties. Cu₂SnSe₃ exists in different allotropic forms, viz. cubic, monoclinic, and orthorhombic [4, 5] depending on the changes in arrangement of atoms caused by the synthesis methods. Previous studies on the band structure calculations have revealed that they have narrow band gap in the range 0.1–1.7 eV [4,5,6]. Various attempts have been done to enhance the TE performance via modifying electron and phonon transports through doping, non-stoichiometry and composites [1, 7,8,9]. Different methods like conventional solid-state reaction [8], fast combustion synthesis [10], liquid phase reactive sintering [6], spark plasma sintering [11], direct fusion of precursors [12], melt quenching [4] have been tried for synthesis of good quality bulk Cu₂SnSe₃ polycrystalline materials. Siyar et al. [4] has analysed the effect of annealing on high temperature thermoelectric properties (300–600 K) of Cu₂SnSe₃ synthesized using melt quenching method. They observed the changes in structure with the different annealing temperatures. Compounds belonging to the diamond structured family like Cu₃SbSe₄ have been synthesized by Li et al. [13] at different hot pressing temperatures and they observed a transition in the electrical conductivity (degenerate to non-degenerate) at high temperatures thereby indicating the partial degeneracy in the samples. Similar results were observed in Cu₂SnSe₃ bulk materials [5] and its isostructural materials like Cu₂GeSe₃ [14] and Cu₂SnSe₄ [15] which is explained on the basis of excitation of minority carriers.

In the present report we have synthesized Cu₂SnSe₃ via a simple, cost effective conventional solid-state reaction route in which the consolidation consists of two different steps viz. pelletizing at high pressures and sintering at appropriate temperatures. The sintering temperatures were varied in the step of 200 K. Most of the previous reports on the electrical transport were focused on the transport properties at either high or low temperature regimes, this motivated us to investigate the temperature dependent electrical transport at both low and high temperature regime with an aim to explain the transport mechanism and to optimize the synthesis conditions for higher power factor.

2 Experimental

Bulk samples of polycrystalline Cu₂SnSe₃ were synthesized via conventional solid-state reaction of elemental powders. Highly pure precursors of elemental Cu (99.7% Loba chemie), Sn (99.999% Alfa Aesar) and Se (99.999% Alfa Aesar) were weighed according to the chemical stoichiometry and thoroughly mixed in an agate mortar for 2 h. Powder mixture was consolidated in to rectangular pellets using a hydraulic press applying a pressure of 6 tons. The pellets were sealed in quartz tubes under high vacuum of about 10^–5 mbar and sintered at three different temperatures viz. 673 K, 873 K, and 1073 K for 72 h followed by natural cooling. The metallurgical process is further repeated to get homogenised samples. Information regarding the phase formation of the samples are derived using powder X-ray diffraction at room temperature (Rigaku miniflex 600; Cu Kα). Morphological and compositional features were investigated using SEM EVO MA-18 equipped with oxford EDAX system. Temperature dependent electrical resistivity was measured in the temperature range 13–300 K using four-point probe resistivity set up with closed cycle refrigeration. Hall measurement was done employing Van der Pauw technique using Ecopia HMS-5500 Hall measurement system. High temperature electrical resistivity and Seebeck coefficient were measured simultaneously in the temperature range 323–673 K, using Linseis LSR-3 system.

3 Results and Discussions

3.1 Phase Formation and Microstructure

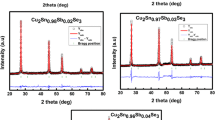
Figure 1a–c shows the room temperature XRD profile of all the samples, where the major peaks were indexed to JCPDS card # 04-002-6015. This corresponds to the cubic sphalerite type structure with space group F$\bar{4}$3 m. Unlike the samples sintered at 673 K and 873 K, the one sintered at 1073 K shows a minor monoclinic phase along with major cubic phase. This could be attributed to the slight non-stoichiometry present in the samples formed during the consolidation process [16]. The XRD profile was refined using the Rietveld analysis using Fullprof suite to derive the crystallographic details which is listed in Table 1. Microstructural parameters were examined using three different methods viz. modified Scherrer equation, Williamson-Hall analysis (W–H) and size-strain plot method (S–S). The three methods are quantitatively described by the following equations [17, 18],

$$\ln \beta = \ln \frac{{K\lambda }}{D} + \ln \frac{1}{{cos\theta }}$$

(3)

$$\beta = ~\left( {\frac{{K\lambda }}{D}} \right) + 4\varepsilon ~sin\theta$$

(4)

$$(d\beta cos\theta )^{2} = ~\frac{K}{D}~\left( {d^{2} \beta cos\theta } \right) + ~\left( {\frac{\varepsilon }{2}} \right)^{2}$$

(5)

Fig. 1

Rietveld refined XRD profiles of Cu₂SnSe₃ samples sintered at a 673 K, b 873 K, and c 1073 K

Table 1 Crystallographic parameters obtained by Rietveld analysis

The Eqs. (3), (4) and (5) correspond to modified Scherrer, W–H and S–S methods respectively, where D and ε are crystallite size and strain respectively, β is full width at half maximum (FWHM), and θ is the diffraction angle, and the plots are shown in Fig. 2. The various parameters listed along with estimated errors in Table 2. Values of the crystallite size estimated by modified Scherrer equation are found to be in the range of 30 nm which in fact is smaller than the values found out using the statistical methods (W–H and S–S). The discrepancy in the crystallite size can be related to the applicability of the Scherrer equation which doesn’t consider the strain induced peak broadening and well suitable in the case of nano-crystalline materials. The crystallite size estimated from S–S plot method is found to lie in the midway of the values calculated by Scherrer equation and W–H analysis. In both the statistical methods, decrease in the crystallite size was found with increase in sintering temperature which is expected for the bulk systems in which higher sintering temperatures cause agglomeration of the grains thereby increasing the number of crystallites per unit volume (Table 2).

Table 2 Microstructural parameters derived using Scherrer equation, W–H and S–S plot methods

Fig. 2

a Modified Scherrer, b Williamson–Hall and c size-strain plots of Cu₂SnSe₃ samples sintered at different temperatures

The densities of the samples sintered at 673 K, 873 K and 1073 K were estimated and it is seen that the density increases with sintering temperature. The densities of the samples are given in Table 2. The estimated porosities are 34%, 33% and 32% which slight decreases with increase in sintering temperature. The SEM images of the samples sintered at three different temperatures are compared in Fig. 3. It is observed that all the samples have fairly dense surfaces with fewer visible porosities which is observed to decrease in the samples synthesised at higher sintering temperatures. EDX results show the purity of the sample within experimental limits which is depicted in Fig. 4b. X-ray elemental mapping suggests the homogeneous distribution of all the elements in the samples.

Fig. 3

SEM images of Cu₂SnSe₃ samples sintered at a 673 K, b 873 K, c 1073 K

Fig. 4

a X-ray elemental mapping of Cu₂SnSe₃ samples sintered at 873 K and b EDS spectra with inset showing the composition of Cu₂SnSe₃ samples sintered at different temperatures

3.2 Low Temperature Electrical Resistivity (10–300 K)

Temperature dependency of resistivity of all the samples, measured in the range 10–300 K is shown in Fig. 5a. It can be seen that the electrical resistivity of all the samples increases with increasing temperature thereby demonstrating a heavily doped semiconducting behaviour. The sample sintered at lower temperature i.e. 673 K has lowest electrical resistivity. The resistivity is found to increase with increase in sintering temperature. This can be accounted by the decreased size of the crystallites and hence lowest resistivity observed in the compound sintered at 673 K. This can also be clarified by the small spaces or voids created between the grain boundaries due to the lack of sufficient energy for ions to diffuse there by creating the dislocation sites [19].

Fig. 5

a Temperature dependent resistivity at low and near room temperature regime with solid line showing the fit to Eq. (6), b graph consists of ln (ρ/T) versus 1/T with inset showing the linear fit for Eq. (7), the SPH model for Cu₂SnSe₃ samples sintered at different temperatures

The temperature dependency of the electrical transport of all the samples was analysed using the power law, [13]

$$\rho = \rho _{0} + aT^{\gamma }$$

(6)

Temperature dependency is found to follow the quadratic variation (γ⁓2) thereby indicating the existence of strong electron–phonon interaction. Hence, we adopted phonon assisted hopping to explain the transport based on small polaron hopping model (SPH) given by,

$$\rho = \rho _{0} T\exp \left( {\frac{W}{{k_{B} T}}} \right)~~~~$$

(7)

where $\rho _{0}$ is a temperature-independent parameter, k_B is the Boltzmann constant and W is the activation energy. A linear variation is seen in the graph consisting of 1/T versus ln (ρ/T) (see Fig. 5b) in the temperature range 120-300 K, which clearly reveals the formation of hole like polarons mediating the electrical transport. Activation energy (W) of the hopping is calculated by the linear fit as shown in the Fig. 5b and the values are listed in the Table 3. The increase in W with increase in sintering temperature can be related to the lowered density of carriers.

Table 3 Electrical transport parameters at near room temperature (323 K)

3.3 High Temperature Electrical Resistivity (323–673 K)

Electrical resistivity ρ(T) was measured in the high temperature regime 323–673 K (Fig. 6a). High temperature resistivity data shows that resistivity for all samples, initially increases with increase in temperature thereafter it is observed to decrease with further increase in temperature. The downturn in the resistivity seen in all the samples indicates the non-degenerate behaviour. We suspect the existence of small polarons at high temperatures where there is a possibility of rise in phonon hopping rate in an Arrhenius manner. Hence, to explain the intrinsic behaviour of ρ(T) we assume the thermal activation of the carriers given by the expression,

$$\rho = \rho _{{0~~}} \left( {\frac{{E_{a} }}{{2k_{B} T}}} \right)$$

(8)

where the E_a, the activation energy which was deduced from the linear fit of ln ρ versus 1/T plot. A linear relationship is perceived between ln ρ and 1/T beyond 500 K which clearly reflects the semiconducting behaviour. The E_a values are found to be 0.4 eV, 0.82 eV and 0.86 eV for the samples sintered at 673 K, 873 K and 1073 K respectively. Increased activation energy could be the main reason for the increased resistivity. The E_a values are found to be of the order of the possible energy band gap of Cu₂SnSe₃ material which confirms the non-degenerate behaviour of all the samples. Hall measurements were done at 323 K to have an insight into the electrical transport. Positive Hall coefficient of all the samples has proclaimed the p-type conductivity in the samples. A decrement in the carrier density was observed with increased sintering temperature, following the same trend as that of electrical conductivity. The electrical resistivity values are comparable with earlier reported values [12].

Fig. 6

a Temperature dependent resistivity at high temperature regime (323–673 K) with inset showing the relationship between resistivity and carrier density, b linear fit for thermal activation at high temperature, c temperature dependency of Seebeck coefficient at high temperature regime (323–673 K) for Cu₂SnSe₃ samples sintered at different temperatures

3.4 High Temperature Seebeck Coefficient (323–673 K)

Variation of Seebeck coefficient with temperature was measured in the temperature range, 323–673 K which is shown in Fig. 6c. Increase in thermopower with temperature up to an optimum temperature (T at S_max) and a declination beyond that, clearly describes the partial degenerate behaviour in all the samples which is reported previously in Cu₂SnSe₃ and isostructural materials [5, 14, 15]. The electron–phonon interactions corresponds to the linear increase of thermopower with temperature. The downturn in S(T) can be explained as the possibility of the excitation of minority carriers and also the defect ionisation, triggered due to high temperature which may become the source for higher density of carriers leading to the higher conductivity. Considering the degeneracy of the samples at near room temperature, density of states effective mass m^* was calculated using Mott’s equation for diffusion thermopower,

$$S~\left( {T > \theta _{D} } \right) = \frac{{\pi ^{2} k_{B}^{2} 2m^{*} }}{{e{\hbar}\left( {3n\pi ^{2} } \right)^{{2/3}} }}T$$

(9)

where n is the carrier density, m* is the effective mass and e, ħ, and k_B are electronic charge, Planck’s constant and Boltzmann constant respectively. Increase in m* values could be seen with conductivity. To support the variation in the thermopower, temperature dependent Fermi energy and Lorenz number were derived using the algorithm called SPBcal developed by Chang et al. [20] under Java SE runtime environment 1.8.0_131. The formula used for Fermi energy is given by,

$$S = ~ \pm \frac{{k_{B} }}{e}\left( {\frac{{2F_{1} \left( \eta \right)}}{{F_{0} \left( \eta \right)}} - ~\eta } \right)$$

(10)

where η is the reduced Fermi energy which is related to Fermi energy E_F as E_F/k_BT. F₀ (η) and F₁ (η) are Fermi integrals of order n = 0 and 1respectievely. Values of Fermi energy (see Fig. 7b) found to be in the range 0.1–0.2 eV, which is much lesser than the activation energy obtained by thermal activation, confirming extrinsic p-type nature of the material. For a nondegenerate semiconductor, one could anticipate the Fermi level to be situated in the energy band gap region. We observe an increase in fermi energy above 500 K, demonstrating the movement of the Fermi level away from the valence band. This variations in the E_F signifies the possibility of the modification of the band structure near Fermi level, hence the variations in the Seebeck coefficient values.

Fig. 7

a Temperature dependent Lorenz numbed deduced from Eq. (11) plotted in dotted lines and from Eq. (12) is in solid lines with data points, b temperature dependent Fermi energy at high temperature regime for Cu₂SnSe₃ samples sintered at different temperatures

The Lorenz number (L₀) was further evaluated to support the partial degenerate behaviour in the materials using two different methodologies [20, 20],

$$L_{0} = \frac{{k_{B}^{2} }}{{e^{2} }}~\frac{{\left( {3F_{0} (\eta } \right)F_{2} \left( \eta \right) - 4F_{1}^{2} \left( \eta \right))}}{{F_{0}^{2} \left( \eta \right)}}$$

(11)

$$L_{0} = 1.5 + exp\left[ { - \frac{{\left| S \right|}}{{116}}} \right]$$

(12)

where the unit of L₀ is in 10^–8 WΩK⁻², and S is in µVK⁻¹. Obtained values of L₀ are depicted in Fig. 7a. Both the relations are based on the single parabolic band approximation The values of L₀ deduced from both the methods are found to be nearby within the error limits. L₀ values are found to lie above 1.8 × 10^–8 WΩK⁻² indicating the partial degenerate behaviour of the samples.

To assess the total electrical transport, weighted mobility ($\mu _{{w~}} )$ which is independent of carrier density was evaluated using the methodology suggested by Snyder et al. [22] which is given by,

$$\mu _{{w~}} = ~\frac{{3h^{3} \sigma }}{{8\pi e~\left( {2m_{e} k_{B} T} \right)^{{3/2}} }}\left( {\frac{{\exp \left[ {\frac{{\left| S \right|}}{{k_{B} /e}}~ - ~2} \right]}}{{1 + \exp \left[ { - 5\left( {\frac{{\left| S \right|}}{{k_{B} /e}}~ - 1} \right)} \right]}} + \frac{{\frac{3}{{\pi ^{2} }}~\frac{{\left| s \right|}}{{k_{B} /e}}}}{{1 + \exp \left[ {5\left( {\frac{{\left| S \right|}}{{k_{B} /e}}~ - 1} \right)} \right]}}} \right)$$

(13)

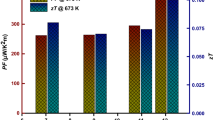
where σ is electrical conductivity at absolute temperature T. The values calculated using Eq. (2) are found to be almost same to the values as computed by Eq. (13). A decrease in $\mu _{{w~}} ~$ was seen with temperature signifying the heavily doped nature of the materials up to the temperature T at S_max. Beyond this an increase is observed with temperature which may be caused by the rapid enhancement in number of carriers and hence the DOS effective mass m^*. Highest $\mu _{{w~}}$ value achieved is 8.2 cm² V⁻¹ s⁻¹ at 673 K, for the sample sintered at 1073 K. The upturn in the weighted mobility at high temperatures can be correlated to the partial degeneracy of Cu₂SnSe₃ samples. Power factor (S²σ) is calculated from the electrical properties are found to increase with temperature which depicted in the Fig. 8b. Since the power factor is a combination of reciprocally dependent S and σ, it is the collective contribution from the charge carriers to the transport. The sample sintered at 673 K exhibits the highest power factor of 188 µV/mK² at 673 K which is comparable with the values obtained in previous reports [1, 7]. The results also suggest that samples with higher m* found to show higher power factor values.

Fig. 8

a Temperature dependent weighted mobility, b temperature dependent power factor at high temperature regime for Cu₂SnSe₃ samples sintered at different temperatures

4 Conclusion

Cu₂SnSe₃ samples were synthesized via conventional solid state rection carried out at three different sintering temperatures viz. 673 K, 873 K and 1073 K. The samples are found to crystallize into cubic sphalerite type structure with minor monoclinic phase found in the samples sintered at 1073 K. All samples found to be degenerate at low temperatures and the existence of small polarons and hence electron—phonon interactions are confirmed temperatures below 400 K. A transition was observed from degenerate to non-degenerate semiconducting behaviour at high temperatures (T > 400 K) hence the material can be referred as partially degenerate [23,24,25]. The studies confirm the unusual transition in electrical resistivity and the thermopower at high temperatures in all the compounds signifying the existence of minority carrier excitation along with temperature-triggered ionisation of the defects as seen in the case of Cu₂GeSe₃ [14]. This transport behaviour is supported by the upward movement of Fermi level away from the valence band. Highest weighted mobility of 8.2 cm² V⁻¹ s⁻¹ at 673 K was obtained for the sample sintered at 1073 K. The considerable decrease in electrical resistivity with increase in temperature (T > 400 K) has driven the power factor to increase exponentially, achieving a highest value of 188 µV/mK² (at 673 K) for the sample sintered at 673 K.