Abstract
This study investigates and compares the effects of different shot peening treatments including conventional and severe shot peening on microstructure, mechanical properties, fatigue behavior, and residual stress relaxation of AISI 1060 steel. Shot peening treatments were applied with two Almen intensities of 17 and 21 A and a wide ranges of coverage (100%–1500%). Various microstructural observations were carried out to analyze the evolution of microstructure. Microhardness, residual stress and surface roughness measurements and also axial fatigue test were performed. Moreover, the extent of the residual stress relaxation during cyclic loading was investigated by means of XRD measurements. Furthermore, numerical simulation of residual stress relaxation due to fatigue loading was carried out and validated against experimental investigations. The comparison indicated a good agreement for the surface residual stress relaxation up to 100 cycles. The experimental results indicated the efficiency of severe shot peening processes in obtaining nanostructured surface layer and achieving superior mechanical properties and fatigue behavior. Also, residual stress measurements revealed that stress relaxation started with a high rate at the initial stages of loading and gradually increased at higher number of cycles which was lower in the case of severely shot peened samples compared to the conventionally treated ones.
Graphic Abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Most failures and fractures in engineering components initiate from the surface, and the mechanical and metallurgical properties of the components’ surface play an important role in their service lifetime [1]. Therefore, improving the surface layer properties has attracted considerable scientific interest for many years. One of the known approaches to improve the surface properties especially in the metallic materials is refinement of the surface layer grains [2, 3]. Most of the metals produce through thermo-mechanical processing and their grain sizes vary typically in the range of few tenths of micron. In practice, it is generally not possible to use thermo-mechanical processing to produce metallic materials with grains sizes smaller than 1 µm [4]. Generally, by accomplishing grain refinement, the size of the grain (coarse grain) reduces to submicron (< 1000 nm) scale. The grains with size of 1–100 nm and 100–500 nm call nanostructured (NS) and ultrafine-grained (UFG), respectively [5]. NS and UFG materials contain in their microstructure a very high density of grain boundaries which play a significant role in the development and exhibition of novel properties. The attractive properties of NS metals and alloys are the high yield and fracture strength, the improve wear resistance. NS metals also exhibit high strain rate sensitivity as compared to UFG and MS materials [6, 7].
Shot peening (SP) based processes are known as common severe plastic deformation (SPD) techniques to obtain surface grain refinement. SP is a cold working process in which the surface of a component is bombarded with spherical media known as shot under controlled velocity. A single shot mechanically deforms the target material creating a dimple when it strikes the surface [8, 9]. The surrounding elastic material induces a compressive residual stress field within the cold-work hardened layers on attempting to return the yielded layer to its initial shape. SP effects on the surfaces and sub-surface layers can be classified into mechanical, metallurgical and micro-geometrical imperfections [10]. Generally, the improvement in surface properties of the material is a consequence of the strain hardening of surface layers that enhances the yield stress of the material, the induced compressive residual stresses in the sub-surface layers and the microstructural alterations [11]. Beneficial residual stresses provide retardation or prevention of crack initiation and propagation, thus extending the service life of mechanical components [12].
The capability of a metallic material to deform plastically depends on the ability of dislocations to move. Restricting dislocation motion makes the material stronger. Ordinarily, strengthening reduces ductility of the material. The reason for work hardening is the increase of dislocation density with plastic deformation. Microscopical observations of metallic materials treated by various SP-based processes have revealed a rearrangement of dislocations during the process. The dislocations move from the grain interiors to the region close to the grain boundaries [13, 14]. The increased density of microstructural defects, their annihilation and rearrangement, result in formation of finer grain structure. In summary, these changes can be made by two types of SP treatment including conventional shot peening (CSP) and severe shot peening (SSP) that depend on the main parameters of the SP process (i.e., Almen intensity and coverage). The effects of CSP on the improvement of the components surface properties have been the subject of considerable researches in the past, investigating the influence of process parameters on mechanical properties [15,16,17]. SSP process, on the other hand, using unconventional high Almen intensities and coverage, has been employed to introduce more compressive residual stresses and to refine the grains of the treated material surface layer [18]. SSP is generally used for nanocrystallizaion of the surface layer of material [19]. The effect of SSP has been investigated in the past few years on different materials including 39NiCrMo3 low-alloy steel, nodular cast iron with ferrite-pearlite matrix, 316 L stainless steel, AZ31 Magnesium alloy, AISI 1017 mild steel and pure titanium and Al alloys [20,21,22,23,24]. Moreover, researchers have investigated the residual stress relaxation of conventionally shot peened materials and its effects on fatigue behavior at different time steps up to fatigue failure on AISI 4140 steel, S30432 austenite steel, JIS S45C medium carbon steel and 2024-T351 aluminum alloy [25,26,27,28]. However, there are no studies on the evolution of residual stresses induced by SSP treatment under fatigue loading, considering the higher extent of the field commonly induced by SSP compare to CSP treatments.
In the present study, the influence of SSP process on a high carbon steel is presented. AISI 1060 steel is widely used in a variety of structural parts such as shafts, bushings, connecting rods, agricultural hand tools, springs, cold rolled strips, and railway wheels [29, 30]. Six different treatments, with different Almen intensity (17 and 21 A) and coverage (100%–1500%), including CSP and SSP were performed. Treated specimens were characterized using hardness, residual stress and roughness measurements, scanning electron microscopy (SEM), field emission scanning electron microscopy (FESEM), and high resolution transmission electron microscope (HRTEM) observations. The fatigue behavior of the specimens was investigated under axial fatigue loading and the residual stress relaxations of the both CSP and, SSP were studied and compared in the surface and depth.
In order to investigate the efficiency of the numerical method as an alternative approach, a novel finite element (FE) simulation was developed to study the residual stress relaxation in shot peened specimens under cyclic loading.
2 Experimental Procedure
2.1 Material and Specimens
The studied material is hot rolled sheet of a high carbon steel, AISI 1060. Table 1 illustrates the chemical composition of AISI 1060. The specimens were quenched at 850 °C in oil, then tempered for 1 h at 300 °C. Mechanical properties of the material are presented in Table 2.
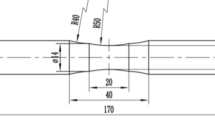
Fatigue test specimens were fabricated according to ASTM E466 standard [31]. The shape and dimensions of the specimens are shown in Fig. 1.
2.2 Shot Peening Processes
The SP treatments were applied to the specimens using an air blast shot peening (ABSP) device under controlled air pressure and peening time. Standard steel shots S280 were used. Table 3 shows the effective parameters of shot peening treatment.
Almen intensity and coverage are the main parameters of the SP process [32, 33]. Herein, we investigated the effects of these parameters on structural integrity of the AISI 1060 high carbon steel. Therefore, six SP treatments with different intensity and coverage were carried out. Almen intensity was determined according to SAE J443 standard by using the “A” Almen strips [34]. Table 4 shows the applied shot peening parameters for each different SP treatments.
S17-100 and S21-100 specimens were shot peened with the coverage of 100% (CSP) and the other series were treated with higher surface coverage and higher kinetic energy (SSP).
2.3 Microstructural Investigations
Microstructures of the specimens were characterized through SEM and FESEM observations using VEGA\\TESCAN-XMU and Mira 3-XMU respectively.
In order to obtain the grain size of the treated specimens, X-ray diffraction (XRD) measurements and high resolution transmission electron microscope (HRTEM) were applied. X’Pert PRO MPD (PANalytical) XRD system was employed with Cu-Kα radiation (λK1 = 1.54060 Å). Width of the diffraction peak at half the maximum intensity (FWHM) and crystallite size were evaluated on the surface. Specimens’ grain structure was evaluated via a JEOL JEM 2100 High Resolution Transmission Electron Microscope operated at 200 kV.
2.4 Microhardness Measurements
In order to study the effects of different SP treatments on the hardness of the specimens, microhardness measurements were performed on cross sections of treated specimens. Qness GmbH Q30A microhardness tester at a load of 10 gf with duration of 7 s using Vickers indenter was employed to obtain the in-depth profile (up to 800 µm).
2.5 Residual Stress Measurements
To study the state of residual stresses on the surface of the specimens, XRD analysis was applied using Xstress 3000 G2/G2R X-ray Stress Analyzer (radiation Cr-Kα, irradiated area of 4 mm diameter, sin2ψ method and diffraction angle (2θ) ~ 156 scanned between 45 and − 45). Measurements were carried out in depth step by step by removing a very thin layer of material (~ 20 µm) through electro-polishing with a solution of acetic acid (94%) and Perchloric acid (6%).
2.6 Surface Roughness Measurements
Surface roughness of the specimens as a well-known side effect of SP process with significant influence on fatigue behavior was measured using SURFCORDER SE500. The roughness parameters are presented based on the definition of ISO 4287 [35].
2.7 Fatigue Test
Fatigue behavior of the specimens were studied via SANTAM SAF-250 axial fatigue test machine under frequency of 30 Hz with the stress ratio, (R), equal to − 1. 14–18 fatigue test samples were employed to create the S–N diagram for each treatment and SP conditions. The fatigue test was performed at 9 different stress levels. Therefore, the average fatigue life of the two specimens is treated as the fatigue life at the respective cyclic load level. The endurance fatigue limit was obtained using JSME S 002 standard [36] and applying staircase method.
3 Numerical Simulation
The geometry of the model studied in the finite element (FE) simulations is the same of the high cycle fatigue specimen as shown in Fig. 1. However, the focus of the FE model presented in this study is on the gauge length of the specimen which is apt to fail (Fig. 2).
To be able to use the XRD residual stress experimental data as initial stress in the FE model and match the depths, 300 elements were considered through the thickness of the modeled specimen with a height of 20 µm, according to the step size in material removal phase of experimental residual stress measurements. Mesh convergence analysis was performed to define the optimum edge size for the elements and reduce computational cost of the simulation by using stress analysis under static loading of 1KN. Mesh sensitivity analysis results are reported in Table 5. Also, the detailed guidance for the mesh process is shown in Fig. 3a. The results indicate that the maximum Von- Mises stress did not change significantly (less than 1%), when the number of elements exceeded 28,800. However, in order to compromise between the accuracy and time saving, case number 3 was selected to perform further analysis. Contour of equivalent Von Misses stress as a result of static analysis is illustrated in Fig. 3b. It is clear that the maximum value of stress is related to the gauge length area which is apt to fail under cyclic loading. The final FE model with partition details is shown in Fig. 3c.
The experimental data of residual stress was used and defined as an initial stress to all the nodes at the corresponding depth of the specimen. In the SP process, the values of residual stress in the X and Y direction are assumed as equal because the effects of the process are considered to be homogeneous. Therefore, in mapping of the experimental data to each layer, the stress components of X and Y are applied as in-plane biaxial initial stress values. Moreover, because of some experimental limitations, other components of stress tensor were ignored and no initial strain was defined for the current model. SP is performed on the four faces of the sample. Since the sample color is completely blue (maximum compressive residual stress), the initial stresses are just illustrated on the top and bottom surfaces to show changes of residual stress profile in depth (Fig. 4). From this figure, it is clearly obvious that the initial residual stress is symmetric on the two sides of component. In addition, based on the experiments, mean residual stress of approximately − 3 MPa was assigned to the virgin material and eventually, for simulation value of zero for the layers with thickness of more than 700 μm was considered.
Transient analysis was performed under cyclic loading. Sine wave with maximum value of 350 MPa and stress ratio of − 1 was applied to the specimen. Loading frequency was set to 30 Hz in accordance with experimental procedure (i.e., one cycle duration was set to 0.033 s). Considering the high computational costs of the analysis and limited resources, FE of residual stress relaxation was carried out only for CSP series.
Stress component in sample’s longitudinal direction (\(\sigma_{xx}\)) was extracted for each node of the shoulder area at different time points. Mean stresses of nodes in each layer is reported as residual stress corresponding to its cycle.
where i and j are the layer number and node number, respectively.
4 Results and Discussion
4.1 Experimental Results
4.1.1 Microscopic Observations and XRD Measurements
SEM observations (cross section close to the surface) of as-received, CSP, and SSP specimens are presented in Fig. 5. The SEM micrographs clearly show the grain refinement induced by shot peening compared to the as received material.
FESEM analysis were employed to observe the plastically deformed surface layers of the treated specimens in more detail (Fig. 6). Cross-sectional FESEM observations of the as-received and shot peened specimens with different treatments indicate that the depth of the highly deformed layer that corresponds to the grain refined level is increasing by enhancing of kinetic energy of the SP treatment.
HRTEM analysis and XRD measurements were performed to investigate the grain size of the treated specimens. The XRD patterns of the treated specimens are presented in Fig. 7.
The crystallite sizes of the specimens were determined using Scherer’s equation which has acceptable accuracy for Nano-scale particles; for particles size larger than 100 nm HRTEM can provide more precise grain size distributions [37]. Therefore, crystallite size of the specimens treated with SSP processes were calculated using XRD measurements and the grain size of the specimens treated with CSP processes were obtained via HRTEM observations.
FWHM can be used as an index of hardening of the material [38]. The FWHM parameter and average size of crystallites of the SSP treated specimens, both extracted from XRD analysis are shown in Table 6.
XRD analysis indicated the crystallite size of all SSP samples to be under 82.3 nm, thus confirming the capacity OF SSP treatment in surface nanocrystallizaion. The analysis also demonstrates that the crystallite size reduces with increasing the Almen intensity and coverage. Increasing the kinetic energy of the SSP treatment and consequently the extent of plastic deformation via the combined effect of higher Almen intensity and coverage, leads to further reduction of the grains down to 45 nm.
Figure 8 presents the HRTEM observations of surface layer of the shot peened specimens with CSP treatments. Ultrafine grain structure is observed at the top surface of the CSP treated specimens: Almen intensities of 17 and 21A, both at full coverage. The average grain sizes measured by HRTEM at the surfaces were approximately 515 and 460 nm for S17-100 and S21-100 specimens respectively. The total counts for each grain size measurement using HRTEM observations was at least above 75 for both conventionally and severely peened samples (See “Appendix”). HRTEM micrographs indicated that the higher the Almen intensity results in smaller the grain size.
To have better understanding about the grain refinements in the CSP and SSP processes, Fig. 9 shows the microstructure of the shot peened specimens at higher magnifications. The generated nanostructured (NS) surface layer, sharp boundary, UFG layer, refined grain layer (refined grain: 500–1000 nm) and the work-hardened layer can be observed.
For clarity, based on the microscopic observations, the schematic microstructures of the CSP and SSP treated AISI 1060 are presented in Fig. 10.
The microstructural observations revealed that SSP treatment can produce NS layer on the surface by increasing the kinetic energy of the process, which can be achieved by increasing the surface coverage; increase exposure time will consequently enhance plastic strain, dislocation density that will promote the grain refinement process.
4.1.2 Hardness, Residual Stress and Surface Roughness Measurements
Figure 11, depicts the variations of the microhardness through the thickness (Fig. 11a) and residual stress distributions (Fig. 11b) of the treated specimens. Hardness trend that increased with the severity of SP treatment, is in good agreement with the microstructural confirmed by microscopical observations. The depth of plastically deformed layer showing high microhardness values compared to the as received material was measured to be higher than 250 µm for all shot peened series. As it is shown in Fig. 11b, SP treatments induced compressive residual stress in the top surface layer and the magnitude of on-surface, maximum in-depth and the depth of the profile depended on the severity of the parameters used for the SP process. As it can be observed by increasing both Almen intensity and coverage, the compressive residual stress field was extended.
SEM observations of surface morphology of the shot peened specimens are displayed in Fig. 12. Main roughness parameters, Ra (arithmetic mean), Rq (root mean square) and Rt (total height) measured on each specimen are presented in Table 7. The surface roughness raised with increasing coverage and also with Almen intensity until reaching a stable value at higher coverages.
4.1.3 Fatigue Behavior
Figure 13a illustrates the achieved S–N curves of the as-received and shot peened specimens and Fig. 13b compares the fatigue strength of the as-received and shot peened series. The fatigue test results revealed that the applied SP treatments on specimens S17-100, S17-700, S17-1500, S21-100, S21-700 and S21-1500 improved their fatigue strength up to 9, 15, 17, 12, 20 and 30% respectively in comparison with the as-received specimens. In these cases, the positive effects of microstructure refinement in the surface layer, hardness improvement and inducing compressive residual stresses are found to overcome the adverse influence of surface roughness alteration.
It is well-known that increasing of roughness is a side effect of shot peening process. Substantial changes in the surface features can have detrimental effects for the functionality of the treated component and can make it more vulnerable to unexpected failure, depending on in-service condition. However, the effect of induced compressive residual stresses is more pronounced and can compensate the adverse effect of surface roughness leading to enhanced fatigue strength.
4.1.4 Fractography
Fractrography was performed using SEM observations to compare and investigate the fractured surface of conventionally and severely treated specimens to assess the effects of SP severity on fatigue crack initiation and propagation. Figures 14 and 15 illustrate the fractured surface of shot peened specimens with S17-100 and S21-1500 treatments in details with specified different sections of the fracture surfaces. It can be seen that in the both conventionally and severely shot peened specimens, the fatigue crack initiated from the subsurface layer. However, the crack initiation site in the severely shot peened specimen is placed more interior from the surface compared to the conventionally treated specimen. In Figs. 14a and 15a, besides the crack initiation and propagations sites, transcrystalline fatigue fracture and closer sites to final rupture and also the transcrystalline ductile fracture with dimple morphology can be seen clearly from left to right. Also, higher increasing of the spacing between striations closer to the final rupture in the CSP treated specimen compared to the SSP treated one can be seen.
SEM images of a fracture surface of conventionally shot peened specimen S17-100, σa = 350 MPa, Nf = 706,000cycles, specifying details of different stages of crack initiation and propagation sites, b crack initiation site under the surface layer, c crack initiation in higher magnification and d transcrystalline fatigue fracture and closer sites to final rupture
SEM images of a fracture surface of severely shot peened specimen S21-1500, σa = 415 MPa, Nf = 2,960,000cycles, specifying details of different stages of crack initiation and propagation sites, b crack initiation site under the surface layer, c crack initiation in higher magnification and d transcrystalline fatigue fracture and closer sites to final rupture
4.1.5 Residual Stress Relaxation
In order to investigate the extent of residual stress relaxation, two sets of specimens including S17-100 and S21-1500, which demonstrated the lowest and the highest fatigue strength improvement respectively, were selected. The surface residual stress at different cycles of 1, 10, 50, 102, 103, 105, 5 × 105, 106 and 2 × 106 with different stress amplitudes were measured on these specimens (the cycles of 106 and 2 × 106 were only considered for severely shot peened set). For selection of stress amplitude, relevant stresses corresponding to their obtained fatigue strength as well as two other higher stress levels were considered (see Table 8).
Figure 16 presents the surface residual stress measurements at different cycles and the applied stress amplitudes of the considered specimens for each measurement. The results indicated a not significant initial stress relaxation with a more notable one at later stages that were found to depend on both number of cycles and the applied stress.
Before applying loads for relaxation, the compressive residual stress values were -221 and -314 MPa at the surface for S17-100 and S21-1500 respectively. By increasing the cycling number, the compressive residual stress relaxation took place at a fast rate in the initial stage for all three applied loadings for both specimens. This trend is reported also in previous studies [39,40,41,42]. After the first few cycles, the surface compressive residual stress decreased and then became stable till another strong relaxation occurred at higher cycles respectively between 104 ≤ N < l06 and 104 ≤ N ≤ 2 × l06 for conventionally and severely treated specimens, leading to complete residual stress relaxation which similar results were reported by Menig et al. [43] previously.
To investigate the state of residual stress relaxation in depth, residual stress distributions for the specimens S17-100 and S21-1500 at stress amplitudes of 350 and 415 MPa were achieved as shown in Fig. 17. The obtains results indicate that shot peening induced residual stresses in AISI 1060 tended to relax by more than 50% at about 0.7 Nf (Nf = number of cycles to failure) and then complete relaxation occurred by increasing the number of cycles in both CSP and SSP specimens (Fig. 17a, b).
4.2 Numerical Simulation Results
The contour of the residual stress on the specimen’s surface at various load cycles is demonstrated in Fig. 18.
As shown in longitudinal residual stress distribution, compressive residual stresses around the fillet radius are released and became positive earlier than other regions. Similarly, the finite element results demonstrated that there is a little difference in the distribution of surface residual stresses at 50 and 100 cycles. This indicated that the relaxation rate was high in the first few cycles and reduced by increasing the number of loading cycles. Moreover, the highest compressive residual stress was found on the middle reduced section that is the critical area prone to fatigue failure. The finite element results estimating the variations of residual stress distributions for S17-100 specimen at different loading cycles, as well as comparison with the experimental data for loading cycle 1 are presented in Fig. 19.
In addition, the comparison of surface residual stresses measured at different number of loading cycles based on the experiments and the FEM results are presented in Table 9. Finite element results demonstrate a good compatibility with the experiments. Data reported in Table 9 indicate that the greatest difference between numerical and experimental results occurs at the first loading cycle, and the finite element estimation shows a higher accuracy at higher loading cycles. This could be due to the more notable reduction of residual stress distribution at higher number of cycles; On the other hand, if as-received specimen (stress-free) is subjected to cyclic loading, we have the best simulation accuracy. Moreover, solving compatibility equations to obtain un-known conditions including strain tensor components is one of the reasons for causing a large error in the first loading cycle. But, for the subsequent loading cycles, to conditions obtained in the previous loading cycle are used by the software.
5 Conclusion
In the present study, AISI 1060 carbon steel specimens were shot peened using different sets of parameters to improve their mechanical properties and fatigue behavior. Six different shot peening treatments including 17A and 21A Almen intensities with surface coverages of 100, 700, 1500, 2000 and 3000% were performed. The properties of the treated specimens were investigated through various experimental approaches to identify the role of peening process parameters. Based on the obtained results, the following conclusions can be drawn:
-
Increasing both Almen intensity and surface coverage affect the microstructure of the material; however, Almen intensity was found to have a more pronounced effect compared to surface coverage.
-
The SEM micrographs indicated clear reduction of grain size in comparison with the as-received for specimens S17-100 and S21-1500.
-
The XRD analysis indicated that enhanced plastic deformation caused by combined increase of Almen intensity and surface coverage, led to significant grain size refinement down to 40 nm range.
-
The trend of surface hardness variation by increasing the severity of the shot peening parameters is in good agreement with the extent plastic deformation and the grain size gradient following the Hall–Petch equation.
-
The highest fatigue life was obtained for treatments with the highest kinetic energy of the process, obtained from the highest applied Almen intensity at the highest applied surface coverage.
-
Residual stress measurements indicated that stress relaxation started with a high rate at the initial stages of loading and gradually increased at higher number of cycles. After the high relaxation at the first cycles, the residual stresses gradually decreased at a lower rate remaining almost stable up to higher number of cycles closer to the fatigue life.
-
In case of the severe shot peened specimens less residual stress relaxation was observed. This can be attributed to the surface grain refinement, higher compressive residual stresses. The enhanced fatigue strength of the SSP series compared to the CSP ones can be justified by this observation.
-
Numerical simulation of residual stress relaxation up to 100 cycles, validated with experimental data, showed a good agreement for the surface residual stress relaxation confirming the trend observed for the experimental on-surface measurements.
References
G.H. Farrahi, J.L. Lebrun, D. Courtain, Fatigue Fract. Eng. M. 18, 211 (1995)
R. Karimbaev, Y.S. Pyun, E. Maleki, O. Unal, A. Amanov, Mater. Sci. Eng. A 791, 139752 (2020)
E. Maleki, O. Unal, Surf. Interfaces 11, 82 (2018)
Y. Huang, T.G. Langdon, Mater. Today 16, 85 (2013)
C. Koch, Nanostructured materials: an overview, in Bulk Nanostructured Materials, ed. by M.J. Zehetbauer, Y.T. Zhu (Wiley, Weinheim, 2009), pp. 1–20
H. Gleiter, Acta Mater. 48, 1 (2000)
E. Maleki, O. Unal, Optimization of shot peening effective parameters on surface hardness improvement. Met. Mater. Int. (2020). https://doi.org/10.1007/s12540-020-00758-x
E. Maleki, O. Unal, Shot peening process effects on metallurgical and mechanical properties of 316 L steel via: experimental and neural network modeling. Met. Mater. Int. (2019). https://doi.org/10.1007/s12540-019-00448-3
E. Maleki, O. Unal, Fatigue limit prediction and analysis of nano-structured AISI 304 steel by severe shot peening via ANN. Eng. Comput. (2020). https://doi.org/10.1007/s00366-020-00964-6
E. Maleki, O. Unal, K. Reza Kashyzadeh, Met. Mater. Int. 25, 1436 (2019)
Y. Efe, I. Karademir, F. Husem, E. Maleki, R. Karimbaev, A. Amanov, O. Unal, Appl. Surf. Sci. 528, 146922 (2020)
Y. Harada, K. Mori, J. Mater. Process. Tech. 162–163, 498 (2005)
R. Valiev, Nat. Mater. 3, 511 (2004)
Y. Estrin, A. Vinogradov, Acta Mater. 61, 782 (2013)
O. Unal, E. Maleki, Measurement 125, 133 (2018)
E. Maleki, O. Unal, K. Reza Kashyzadeh, Mater. Charact. 157, 109877 (2019)
K. Dai, L. Shaw, Mater. Sci. Eng. A 463, 46 (2007)
E. Maleki, G.H. Farrahi, K. Sherafatnia, Machining, Joining and Modifications of Advanced Materials, ed. by A. Öchsner, H. Altenbach. (Springer, Singapore, 2016), pp. 45–60
A. Amanov, R. Karimbaev, E. Maleki, O. Unal, Y.S. Pyun, T. Amanov, Surf. Coat. Tech. 358, 695 (2019)
S. Bagherifard, M. Guagliano, Eng. Fract. Mech. 81, 56 (2012)
S. Bagherifard, I. Fernandez-Pariente, R. Ghelichi, M. Guagliano, Int. J. Fatigue 65, 64 (2013)
S. Bagherifard, S. Slawik, I. Fernández-Pariente, C. Pauly, F. Mücklich, M. Guagliano, Mater. Des. 102, 68 (2016)
S. Bagherifard, M.F. Molla, D. Kajanek, R. Donnini, B. Hadzima, M. Guagliano, Acta Biomater. 98, 88 (2020)
O. Unal, A. Cahit Karaoglanli, R. Varol, A. Kobayashi, Vacuum 110, 202 (2014)
I. Altenberger, B. Scholtes, U. Martin, H. Oettel, Mater. Sci. Eng. A 264, 1 (1999)
M. Benedetti, V. Fontanari, P. Scardi, C.L.A. Ricarmalekido, M. Bandini, Int. J. Fatigue 31, 1225 (2009)
E. Capello, P. Davoli, M. Filippini, S. Foletti, J. Strain Anal. Eng. 39, 285 (2004)
T. Kim, J.H. Lee, H. Lee, S.-K. Cheong, Mater. Des. 31, 50 (2010)
J.F. Velez, G.W. Powell, Wear 66, 367 (1981)
H. Roy, N. Parida, S. Sivaprasad, S. Tarafder, K.K. Ray, Mater. Sci. Eng. A 486, 562 (2008)
ASTM E466-15, Standard Practice for Conducting Force Controlled Constant Amplitude Axial Fatigue Tests of Metallic Materials, ASTM International, West Conshohocken, PA (2015)
E. Maleki, G.H. Farrahi, IJE Trans. B: Appl. 31, 382 (2018)
E. Maleki, O. Unal, K.R. Kashyzadeh, Int. J. Fatigue 116, 48 (2018)
SAE J443, Procedures for Using Standard Shot Peening Almen Test Strip, SAE International, Warrendale, PA (2017)
ISO 4287, Geometrical product specifications (GPS)—surface texture: profile method—terms, definitions and surface texture parameters, International Organization for Standardization, London (1997)
JSME S 002, Standard Method of Statistical Fatigue Testing, Japan Society of Mechanical Engineers, Tokyo (1981)
Y.M. Wang, E. Ma, Acta Mater. 52, 1699 (2004)
G.H. Farrahi, J.L. Lebrun, Int. J. Eng. 8, 159 (1995)
K. Zhan, C.H. Jiang, V. Ji, Mater. Trans. 53, 1578 (2012)
J.-C. Kim, S.-K. Cheong, H. Noguchi, Int. J. Fatigue 55, 147 (2013)
O.S. Zaroog, A. Ali, B.B. Sahari, R. Zahari, Int. J. Fatigue 33, 279 (2011)
K.S. Chin, S. Idapalapati, D.T. Ardi, J. Mater. Sci. Technol. 59, 100 (2020)
R.M. Menig, V. Schulze, O. Vöhringer, in Shot Peening, ed. by L. Wagner. 8th International Conference on Shot Peening (ICSP-8), Garmisch-Partenkirchen, Germany, September 16-20, 2002. Residual stress relaxation and fatigue strength of AISI4140 under torsional loading after conventional shot peening, stress peening and warm peening (Wiley-VCH, Weinheim, 2003), pp. 311–316
Funding
Open access funding provided by Politecnico di Milano within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
Details of the grain size measurments using HRTEM observations. Firtsly as shown in Fig. 20, the grains boundaries were specified then avarage size of at least 75 grains were calculated and reported.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Maleki, E., Farrahi, G.H., Reza Kashyzadeh, K. et al. Effects of Conventional and Severe Shot Peening on Residual Stress and Fatigue Strength of Steel AISI 1060 and Residual Stress Relaxation Due to Fatigue Loading: Experimental and Numerical Simulation. Met. Mater. Int. 27, 2575–2591 (2021). https://doi.org/10.1007/s12540-020-00890-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12540-020-00890-8