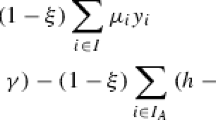Benders decomposition with adaptive oracles for large scale optimization

Abstract

This paper proposes an algorithm to efficiently solve large optimization problems which exhibit a column bounded block-diagonal structure, where subproblems differ in right-hand side and cost coefficients. Similar problems are often tackled using cutting-plane algorithms, which allow for an iterative and decomposed solution of the problem. When solving subproblems is computationally expensive and the set of subproblems is large, cutting-plane algorithms may slow down severely. In this context we propose two novel adaptive oracles that yield inexact information, potentially much faster than solving the subproblem. The first adaptive oracle is used to generate inexact but valid cutting planes, and the second adaptive oracle gives a valid upper bound of the true optimal objective. These two oracles progressively “adapt” towards the true exact oracle if provided with an increasing number of exact solutions, stored throughout the iterations. These adaptive oracles are embedded within a Benders-type algorithm able to handle inexact information. We compare the Benders with adaptive oracles against a standard Benders algorithm on a stochastic investment planning problem. The proposed algorithm shows the capability to substantially reduce the computational effort to obtain an $\epsilon$-optimal solution: an illustrative case is 31.9 times faster for a $1.00\%$ convergence tolerance and 15.4 times faster for a $0.01\%$ tolerance.

1 Introduction

In this paper we consider problems that can be expressed in the form

$$\begin{aligned} \begin{aligned}&\underset{{\mathbf {x}} \in {\mathcal {X}}}{\text {min}}&f({\mathbf {x}}) + \sum _{i \in {\mathcal {I}}} \pi _i g(x_i,c_i), \end{aligned} \end{aligned}$$

(1)

where $g(x_i,c_i)$ is the optimal solution of the LP subproblem

$$\begin{aligned} {{\mathbf {S}}}{{\mathbf {P}}} : g(x_i,c_i) := \underset{y_i \in {\mathcal {Y}}}{\text {min}}\{ c_i^\top C y_i | A y_i \le B x_i \}. \end{aligned}$$

(2)

The set of problems ${\mathcal {I}}$ is finite, the $x_i$ are (possibly overlapping) subvectors of ${\mathbf {x}}$, ${\mathcal {Y}}$ is a convex polyhedron, and the $\pi _i$ are non-negative constants. The coefficient matrices A, B, and C are the same in every subproblem so the subproblems differ only through the value of their parameters, $x_i$ and $c_i$. The $c_i$ are vectors of coefficients and the $x_i$ are vectors of variables for (1) and parameters for (2). However, elements of $x_i$ may be set to fixed values in ${\mathbf {x}} \in {\mathcal {X}}$, so become equivalent to parameters specific to subproblem i. The inclusion of the matrices B and C allow the dimensions of $x_i$ and $c_i$ to differ from (and in the case we shall present be much smaller than) the number of explicit constraints and variables $y_i$ in each subproblem.

The function $g(x_i,c_i)$ has properties that can be exploited in the solution procedure. It is a saddle function, convex w.r.t. $x_i$, and concave w.r.t. $c_i$. Moreover, we focus on problems where $g(x_i,c_i)$ is also a decreasing function of $x_i$ and an increasing function of $c_i$. Monotonicity can be a natural property of the problem, e.g. when $C \ge 0$, $y \ge 0$, and $B \ge 0$, or the problem can be usually rearranged to have this property.

An example of a problem with the above structure is an investment planning problem. Here the ${\mathbf {x}}$ represents investment decisions with corresponding investment cost $f({\mathbf {x}})$. The investments affect a set ${\mathcal {I}}$ of situations, and $x_i$ is the subvector of ${\mathbf {x}}$ that represents the investments that affect the situation i, $c_i$ specifies the operational costs, $y_i$ defines the operational decisions, and $g(x_i,c_i)$ gives the optimal operating cost. The test case we present in this paper is a stochastic problem, where the situations are the different possible scenarios that might occur in the future, each of which is weighted by the probability $\pi _i$ of that situation occurring. Note that in a multistage planning problem the sum of the $\pi _i$ at each stage is equal to 1, so $\sum _{i\in {\mathcal {I}}} \pi _i \ge 1$.

1.1 Literature review

In the standard Benders decomposition algorithms [2, 16] for problem (1) a sequence of relaxations is solved. At each iteration j the relaxed master problem is

$$\begin{aligned} \mathbf {RMP}:&\underset{{\mathbf {x}} \in {\mathcal {X}},\beta }{\text {min}} f({\mathbf {x}})+\sum _{i\in {\mathcal {I}}}\pi _i\beta _{i}\nonumber \\&\text {s.t.} \ \beta _{i}\ge \theta +\lambda ^{\top }(x_i-x), \qquad \forall (x,\theta ,\lambda ) \in \Theta ^{(j-1)}_i,\;\forall i \in {\mathcal {I}}, \end{aligned}$$

(3)

where $\Theta ^{(j-1)}_i$ is the set of cutting planes associated with subproblem i built up to iteration $j-1$. To generate a new cutting plane at iteration j, we first solve the $\mathbf {RMP}$ and obtain the optimal solution ${\mathbf {x}}^{(j)}$. Then, for each $i\in {\mathcal {I}}$ we call an oracle that, for given $x^{(j)}_i$, returns the optimal objective value $\theta ^{(j)}_i=g(x^{(j)}_i,c_i)$ of ${{\mathbf {S}}}{{\mathbf {P}}}$ and a subgradient $\lambda ^{(j)}_{i}$ w.r.t. $x^{(j)}_i$. Such an oracle that generates an exact value of g and its subgradient will be referred to as exact. The newly generated cutting plane is added to $\Theta ^{(j-1)}_i$ yielding $\Theta ^{(j)}_i := \Theta ^{(j-1)}_i \cup \{(x^{(j)}_i,\theta ^{(j)}_i,\lambda ^{(j)}_i)\}$.

The standard Benders algorithm requires calling the exact oracle $|{\mathcal {I}}|$ times at each iteration j. Consequently, when the number of subproblems is large and the exact oracle is hard to solve (e.g., the problem (2) is very large), the computational efficiency of these methods is badly affected. This motivates the investigation of Benders-type algorithms able to exploit the information of inexact oracles. An inexact oracle only provides an estimate of $\theta ^{(j)}_i$ and $\lambda ^{(j)}_{i}$, but possibly much faster than an exact oracle.

Inexact oracles can have different characteristics. They may or may not guarantee to generate valid bounds and cutting planes. Additionally it may or may not be possible to control the accuracy of the oracle, and bounds on the approximation error may or may not be known. An example of an inexact oracle is the one proposed in [11]. The authors suggest solving only a subset ${\mathcal {I}}_{ex} \subset {\mathcal {I}}$ of subproblems and using fast techniques to evaluate approximate values of $\theta ^{(j)}_i$ and $\lambda ^{(j)}_i$ for subproblems $i \in {\mathcal {I}} {\setminus } {\mathcal {I}}_{ex}$. Using a concept of collinearity the authors group similar subproblems, solve one subproblem per group, and derive an approximate solution for the remaining subproblems of each group. Similar inexact oracles that do not provide a guaranteed bound can be found in [6,7,8, 14]. Zakeri et al. [18] propose solving each subproblem $i \in {\mathcal {I}}$ up to a predefined tolerance which is then tightened over time to ensure convergence. The generated cutting planes are all valid and asymptotically exact. Similar inexact but always valid oracles are proposed by [4, 5]. The use of any of the above types of oracles leads to algorithms that are fast at the early iterations but are potentially almost as slow as exact oracles towards the end of the iterative procedure. As a matter of fact, in order to obtain high accuracy, the approach of [11] would need to solve almost all the set of subproblems (i.e., ${\mathcal {I}}_{ex} \approx {\mathcal {I}}$), and the inexact oracle of [18] would solve the subproblems up to a very tight tolerance.

An alternative approach to constructing inexact oracles is to exploit some known properties of the subproblems that allow valid cuts to be generated for subproblems from solution of different problems. This approach has been used in stochastic dual dynamic programming (Pereira et al. [12]), for example by exploiting convexity of the recourse function w.r.t. the uncertain parameters. Stochastic dual dynamic programming is also used to solve minimax problems, which can arise from the inclusion of risk-aversion within the model. This leads to saddle functions similar to $g(x_i,c_i)$, i.e., convex in some directions ($x_i$) and concave in others ($c_i$). Philpott et al. [13] exploit this property and construct an upper bound on the recourse function using an inner approximation. However, an inner approximation is infeasible if the point of interest is not in the convex hull of known points, so the authors propose to initially compute a solution for every extreme point of the uncertainty set. Work [1] proposes using penalties to deal with infeasibility and obtains valid lower and upper bounds to saddle functions without sampling all the vertices of the uncertainty set.

1.2 Approach and contributions

This paper proposes two new inexact oracles, which we refer to as adaptive oracles. The first adaptive oracle approximates $g(x_i,c_i)$ from below and it is called to generate inexact but valid cuts of those subproblems that are not solved at an iteration j. The second adaptive oracle approximates $g(x_i,c_i)$ from above and it is called to obtain a valid upper bound when a subproblem is not solved. The adaptive oracles exploit properties of $g(x_i,c_i)$ such as convexity w.r.t. $x_i$ and concavity w.r.t. $c_i$. In addition, they require $g(x_i,c_i)$ to be a monotonic function of both $x_i$ and $c_i$. The adaptive oracles use the knowledge of m solutions of $g(x_i,c_i)$, known by having solved some subproblems in the previous iterations. Increasing the number m of known solutions, makes both oracles progressively “adapt” towards the true function $g(x_i,c_i)$.

The proposed adaptive oracles are asymptotically exact oracles, since they provide valid upper and lower bounds of $g(x_i,c_i)$, a valid subgradient, and both bounds tend toward $g(x_i,c_i)$ as the number of iterations grows. However, they have properties that, combined, distinguish them from the inexact oracles available in the literature [5,6,7,8, 10, 11, 14, 15, 17, 18]. First, the computational effort required to solve the adaptive oracles is independent of the size and complexity of the exact oracle (2), and only depends on the number m of known solutions. Second, a Benders-type algorithm that uses the adaptive oracles converges to an $\epsilon$-optimal solution ($\epsilon \ge 0$) in a finite number of iterations even when only a single subproblem is solved at each iteration. As a consequence, when subproblems are expensive to solve and the set ${\mathcal {I}}$ of subproblems is large, each iteration is much faster than methods that solve every subproblem at each iteration, and we show this can lead to a significant reduction in total solution time. We test our new method on stochastic LP investment planning problems with up to $1.06\times 10^8$ variables and $3.11 \times 10^8$ constraints against a standard Benders algorithm and the Benders algorithm with inexact cuts of [18] (used as a benchmark). Compared to the standard Benders decomposition, the decomposition algorithm of [18] is 1.6, 1.7, and 1.9 times faster at reaching an optimality tolerance $\epsilon$ of $1.00\%$, $0.10\%$, and $0.01\%$, while our proposed algorithm is 31.9, 28.5, and 15.4 times faster than standard Benders and 19.5, 16.5, and 8.1 times faster than the Benders algorithm of [18] to reach the same $\epsilon$.

1.3 Paper structure

The remainder of the paper is organized as follows. Section 2 introduces assumptions on problems (1) and (2), needed to apply our adaptive oracles. Section 3 briefly presents a standard formulation of the Benders decomposition algorithm. Section 4 illustrates the intuitions behind the proposed adaptive oracles and derives the associated mathematical formulation. The adaptive oracles are embedded within a Benders decomposition algorithm in Sect. 5. Section 6 tests the proposed Benders with adaptive oracles against a standard Benders algorithm on a stochastic investment planning problem. Finally, conclusions are drawn in Sect. 7.

2 Assumptions

We consider solving problems of the form of (1). The subproblem ${{\mathbf {S}}}{{\mathbf {P}}}$ in (2) is assumed to be always feasible (any possible infeasibility having been dealt with by reformulating the subproblem using infeasibility penalties) and bounded for each decision ${\mathbf {x}}$ that belongs to ${\mathcal {X}}$ and for all $c_i$. Accordingly, we say that the function g(x, c) can be computed for all $x \in {\mathcal {K}}^x$ and $c \in {\mathcal {K}}^c$, where the region ${\mathcal {K}}^x$ is obtained by collecting all the possible $x_i$ such that ${\mathbf {x}} \in {\mathcal {X}}$, and the region ${\mathcal {K}}^c$ collecting all $c_i$ for all $i \in {\mathcal {I}}$. Then, we assume that there exist two vectors ${\underline{x}}$ and ${\underline{c}}$ such that ${\underline{x}} \le x, \; \forall x \in {\mathcal {K}}^x$, and ${\underline{c}} \le c, \; \forall c \in {\mathcal {K}}^c$, and that subproblem ${{\mathbf {S}}}{{\mathbf {P}}}$ is feasible and bounded at the special point $({\underline{x}},{\underline{c}})$.

Function g(x, c) is a convex function of x and a concave function of c (e.g., see [3]). In addition, we assume that g(x, c) is a non-increasing function of x, and a non-decreasing function of c. If the property of monotonicity does not hold naturally, problem (1) can be modified so that the rearranged subproblem is a monotonic function of both x and c (see “Appendix A”).

3 Standard benders

This section briefly describes how a Benders algorithm can exploit the block structure of problem (1) allowing it to be solved in a decomposed fashion.

3.1 Algorithm

In a standard Benders algorithm applied to problem (1), we iteratively approximate the subproblem cost function through a set of cutting planes. The formulation of the relaxed master problem $\mathbf {RMP}$ is given in (3) and the standard Benders decomposition is summarized in Algorithm 1.

3.2 Convergence of Algorithm 1

Definition 1

Let ${\mathcal {L}}_i$ be the set of cutting planes $\{(x^{(\ell )}_i,\theta ^{(\ell )}_i,\lambda ^{(\ell )}_i), \forall \ell \in {\mathcal {L}}_i\}$ associated with subproblem i already added to the relaxed master problem. We say that a new exact cut $(x,\theta ,\lambda )$ is locally-improving if and only if

$$\begin{aligned} \theta > \underset{\ell \in {\mathcal {L}}_i}{\max } \left\{ \theta ^{(\ell )}_i + \lambda ^{(\ell )\top }_i \left( x - x^{(\ell )}_i \right) \right\} . \end{aligned}$$

Lemma 1

At each iteration, either Algorithm terminates with an $\epsilon$-optimal solution, or the algorithm adds at least one locally-improving exact cut to the reduced master problem.

Proof

If none of the exact cuts $(x^{(j)}_i,\theta ^{(j)}_i,\lambda ^{(j)}_i)$ generated at iteration j is locally-improving, it follows that

$$\begin{aligned} \theta ^{(j)}_i \le \underset{\ell < j}{\max } \left\{ \theta ^{(\ell )}_i + \lambda ^{(\ell )\top }_i \left( x^{(j)}_i - x^{(\ell )}_i \right) \right\} , \quad \forall i \in {\mathcal {I}}, \end{aligned}$$

(4)

and given that the right side of (4) is equal to $\beta ^{(j)}_i$, it follows that the lower bound and the upper bound have converged exactly. $\square$

Lemma 2

There exists a finite number of locally-improving exact cutting planes that can be added to the relaxed master problem.

Proof

Since each subproblem $g(x_i,c_i)$ is an LP, there exist a finite number of faces (of all dimensions from 0, i.e. vertices, edges, ..., facets), and each exact cutting plane gives an exact representation of (at least) one of these faces. A new exact cut can be locally-improving if and only if it is associated with a face that has not been exactly represented yet. Then, given that the number $|{\mathcal {I}}|$ of subproblems is finite, it follows that there exists a finite number of locally-improving exact cuts that can be added to the relaxed master problem. $\square$

Theorem 1

For any $\epsilon \ge 0$, Algorithm 1 finds an $\epsilon$-optimal solution to problem (1) in a finite number of iterations.

Proof

Lemma 2 proves that there exists a finite number of locally-improving exact cuts that can be added to the reduced master problem, and Lemma 1 proves that Algorithm 1 adds at least one locally-improving exact cut at each iteration (or it has converged). It follows that Algorithm 1 finds an $\epsilon$-optimal solution to problem (1) in a finite number of iterations. $\square$

Remark 1

Convergence proofs for Benders decomposition (e.g., see [18]) usually rely on the existence of a finite number of basis matrices for each subproblem. In contrast, Theorem 1 relies on the existence of a finite number of faces and does not require that each exact cut corresponds to a basis matrix.

4 Adaptive oracles

This section presents the adaptive oracles used within the proposed novel Benders-type decomposition algorithm. Figure 1 illustrates a saddle function g(x, c), convex and non-increasing w.r.t x, and concave and non-decreasing w.r.t. c. This function is used to illustrate the intuition behind the proposed adaptive oracles.

Fig. 1

Illustration of the saddle function g(x, c), convex and non-increasing w.r.t x and concave and non-decreasing w.r.t. c

4.1 Graphical interpretation of the adaptive oracles

For a subproblem i that is not solved at iteration j, we call two adaptive oracles to retrieve the information needed to perform a Benders-type iteration. The first adaptive oracle provides ${\underline{\theta }}^{(j)}_i$ and ${\underline{\lambda }}^{(j)}_i$ such that $(x^{(j)}_i,{\underline{\theta }}^{(j)}_i,{\underline{\lambda }}^{(j)}_i)$ generates a valid cutting plane. The second adaptive oracle yields an upper bound ${\overline{\theta }}^{(j)}_i$ on $g(x^{(j)}_i,c_i)$, which is then used to compute a valid upper bound on the optimal solution of the relaxed master problem at ${\mathbf {x}}^{(j)}$.

Fig. 2

Illustrative example of how to obtain a valid lower and upper bound ${\underline{\theta }}_r$ on $\theta _r=g(x_r,c_r)$

Before presenting the mathematical formulation of the two adaptive oracles, we give a graphic and explanatory example using the saddle function g(x, c) shown in Fig. 1. Figure 2 illustrates how to obtain a valid lower bound on g(x, c), and Fig. 2 shows how to obtain a valid upper bound on g(x, c). Assume that we know the exact value $\theta _s = g(x_s,c_s)$ at points $\{(x_s,c_s),s=1,\ldots ,m\}$, shown with blue filled dots in Figs. 2a and d, and we want to obtain valid lower and upper bounds on g(x, c) at a new point $(x_r,c_r)$, shown with a blue empty dot. Note that Figs. 2a and d also include the special point $({\underline{x}},{\underline{c}})$, marked with a blue filled star, which is needed at the end of the examples.

Each red dashed line in Fig. 2a shows the tangent at a blue point $(x_s,c_s)$ w.r.t. x (i.e., for fixed $c_s$). Since $g(x,c_s)$ is convex w.r.t. x, the tangent lies below $g(x,c_s)$. The red squares are the points $({\underline{\theta }}'_s,x_r,c_s)$ on the tangent where $x=x_r$. If the gradients are $\lambda _s$, then ${\underline{\theta }}'_s = \theta _s + \lambda ^{\top }_s \left( x_r-x_s \right)$. Since $g(x_r,c)$ is concave w.r.t. c and all the red square points lie in $x=x_r$ plane and below $g(x_r,c)$, the convex hull of these points also lies below $g(x_r,c)$. Figure 2b illustrates this convex hull as a red shaded area, and the gray shaded areas indicate values of c where a convex combination can not be found. Figure 2c shows that if the special point $({\underline{x}},{\underline{c}})$ is included among the known points $(x_s,c_s)$, the non-decreasing property of g(x, c) w.r.t. c can be exploited to extend the convex hull and obtain a valid lower bound for all $c \ge {\underline{c}}$. In particular, the upper envelope of the convex hull gives the tightest lower bound on $g(x_r,c)$.

The green dashed lines in Fig. 2d are the tangents (with gradient $\phi _s$) at each blue point $(x_s,c_s)$ w.r.t. c, which lie above $g(x_s,c)$ since $g(x_s,c)$ is concave w.r.t. c. The green squares $(\overline{\theta _s^{'}},x_s,c_r)$ are the points on the tangents where $c=c_r$, i.e., $\overline{\theta _s^{'}} = \theta _s + \phi ^{\top }_s \left( c_r-c_s \right)$. The convex hull of these points lies above $g(x,c_r)$, given that $g(x,c_r)$ is convex w.r.t. x and the green square points lie above $g(x,c_r)$. Figure 2e shows this convex hull as a green shaded area, likewise two gray shaded areas where a convex combination can not be found. If the special point $({\underline{x}},{\underline{c}})$ is included we extend the convex hull and obtain a valid upper bound for all $x\ge {\underline{x}}$ by exploiting the non-increasing property of g(x, c) w.r.t. x (see Fig. 2f). Here, the lower envelope of the convex hull gives the tightest upper bound on $g(x,c_r)$.

Note that the methodology for obtaining a valid upper bound is the counterpart of the methodology for obtaining a valid lower bound. As an example, one could use the lower bounding oracle to get a valid lower bound on g(x, c) and the same oracle to also obtain a valid upper bound. To do that, one can compute a valid lower bound on ${\hat{g}}(c,x)=-g(x,c)$ and use it (with a change in sign) as a valid upper bound on g(x, c).

4.2 Adaptive oracles

This section gives a mathematical formulation of the intuitions illustrated in Sect. 4.1. Consider the saddle function g(x, c), and suppose we have already found m optimal solutions at $\{(x_s,c_s), s = 1,..,m\}$. At each point s, we know the true value $\theta _s$, a subgradient $\lambda _s$ w.r.t. x, and a subgradient $\phi _s$ w.r.t. c. We are interested in building a valid cutting plane and obtaining a valid upper bound at a new point (x, c), without solving the associated subproblem.

4.2.1 Adaptive oracle for valid cutting plane

Let ${\mathcal {A}}^{\mathrm {LB}}_{m}(x,c)$ be defined as

$$\begin{aligned} {\mathcal {A}}^{\mathrm {LB}}_{m}(x,c): \quad {\underline{\theta }}(x,c)= & {} \underset{\mu \ge 0}{\text {max}} \ \theta (x,c) = \sum _{s = 1}^{m} \mu _s \left( \theta _s + \lambda ^{\top }_s \left( x-x_s \right) \right) \nonumber \\&\text {s.t.} \sum _{s = 1}^{m} \mu _s c_s \le c, \quad \sum _{s = 1}^{m} \mu _s = 1. \end{aligned}$$

(5)

Lemma 3

Assume that the set of known points $\{(x_s,c_s), s = 1,\ldots ,m\}$ includes the special point $({\underline{x}},{\underline{c}})$, and let $\mu (x,c)$ be a feasible solution of (5) and $\lambda (x,c)=\sum _{s = 1}^{m} \mu _s(x,c) \lambda _s$. Then,

(a):

${\mathcal {A}}^{\mathrm {LB}}_{m}(x,c)$ is feasible for all $x \in {\mathcal {K}}^x$, $c \in {\mathcal {K}}^c$,

(b):

$\theta (x,c) \le {\underline{\theta }}(x,c) \le g(x,c)$, for all $x \in {\mathcal {K}}^x$, $c \in {\mathcal {K}}^c$,

(c):

${\underline{\theta }}(x_r,c_r) = g(x_r,c_r)$, for all $r=1,..,m$,

(d):

$\theta (x,c) + \lambda (x,c)^{\top } \left( {\hat{x}} - x \right) \le g({\hat{x}},c)$, for all ${\hat{x}} \in {\mathcal {K}}^x$, $x \in {\mathcal {K}}^x$, $c \in {\mathcal {K}}^c$.

Proof

(a):

Set the variable $\mu _s$ associated with $({\underline{x}},{\underline{c}})$ equal to 1, and all the others to 0. The first constraint of (5) becomes ${\underline{c}} \le c$, which is true by definition, and the other constraints also hold.

(b):

The definition of $\theta (x,c)$ leads to

$$\begin{aligned} \begin{aligned} \theta (x,c)&= \sum _{s = 1}^{m} \mu _s(x,c) (\theta _s + \lambda ^{\top }_s \left( x-x_s\right) ) \le \sum _{s = 1}^{m} \mu _s(x,c) g(x,c_s)\\&\le g(x,\sum _{s = 1}^{m}\mu _s(x,c) c_s)\\&\le g(x,c). \end{aligned} \end{aligned}$$

The first inequality holds since $\theta _s + \lambda ^{\top }_s \left( x-x_s\right)$ is an underestimator of the convex function $g(x,c_s)$ and $\mu (x,c)\ge 0$, the second inequality holds since the $\mu (x,c)$ define a convex combination and g(x, c) is concave w.r.t. c, and the third holds since $\sum _{s=1}^m \mu _s(x,c) c_s \le c$ and g(x, c) is non-decreasing w.r.t. c.

(c):

Setting $\mu _r=1$ gives a feasible solution with objective value $\theta _r + \lambda ^{\top }_r \left( x_r - x_r \right) = \theta _r$. Since $\mu _r$ is feasible for ${\mathcal {A}}^{\mathrm {LB}}_m(x_r,c_r)$, it follows that ${\underline{\theta }}(x_r,c_r) \ge \theta _r = g(x_r,c_r)$. This and b) imply ${\underline{\theta }}(x_r,c_r)=g(x_r,c_r)$.

(d):

Since the weights $\mu (x,c)$ are feasible for ${\mathcal {A}}^{\mathrm {LB}}_m(x,c)$, they are also feasible for ${\mathcal {A}}^{\mathrm {LB}}_m({\hat{x}},c)$. Hence,

$$\begin{aligned} \begin{aligned} g({\hat{x}},c)&\ge \sum _{s=1}^{m} \mu _s (x,c) ( \theta _s + \lambda ^{\top }_s \left( {\hat{x}}-x_s \right) ) \\&= \sum _{s=1}^{m} \mu _s (x,c) ( \theta _s + \lambda ^{\top }_s \left( x -x_s \right) ) + \sum _{s=1}^{m} \mu _s (x,c) (\lambda ^{\top }_s \left( {\hat{x}}-x \right) ) \\&= \theta (x,c) + \lambda (x,c)^{\top } \left( {\hat{x}}-x \right) . \\ \end{aligned} \end{aligned}$$

The first equality follows since

$$\begin{aligned} \lambda ^{\top }_s \left( {\hat{x}}-x_s \right) = \lambda ^{\top }_s \left( x -x_s \right) + \lambda ^{\top }_s \left( {\hat{x}}-x \right) , \end{aligned}$$

and the second from the definition of $\theta (x,c)$ and $\lambda (x,c)$. $\square$

4.2.2 Adaptive oracle for valid upper bound

Let ${\mathcal {A}}^{\mathrm {UB}}_{m}(x,c)$ be defined as

$$\begin{aligned} {\mathcal {A}}^{\mathrm {UB}}_{m}(x,c): \quad {\overline{\theta }}(x,c)= & {} \underset{\nu \ge 0}{\text {min}}\ \theta (x,c) = \sum _{s = 1}^{m} \nu _s \left( \theta _s + \phi ^{\top }_s \left( c-c_s \right) \right) \nonumber \\&\text {s.t.} \sum _{s = 1}^{m} \nu _s x_s \le x, \quad \sum _{s = 1}^{m} \nu _s = 1. \end{aligned}$$

(6)

Lemma 4

Assume that the set of known points $\{(x_s,c_s), s = 1,\ldots ,m\}$ includes the special point $({\underline{x}},{\underline{c}})$. Then,

(a):

${\mathcal {A}}^{\mathrm {UB}}_{m}(x,c)$ is feasible for all $x \in {\mathcal {K}}^x$, $c \in {\mathcal {K}}^c$,

(b):

$\theta (x,c) \ge {\overline{\theta }}(x,c) \ge g(x,c)$, for all $x \in {\mathcal {K}}^x$, $c \in {\mathcal {K}}^c$,

(c):

${\overline{\theta }}(x_r,c_r) = g(x_r,c_r)$, for all $r=1,..,m$.

Proof

Lemma 4 can be proved similarly to Lemma 3 (parts a, b, and c) since obtaining a valid upper bound is the exact counterpart than obtaining a valid lower bound. $\square$

4.2.3 Notes on adaptive oracles

Note that every feasible solution $\mu$ of ${\mathcal {A}}^{\mathrm {LB}}_m(x,c)$ gives a valid cutting plane $(x,\theta ,\lambda )$. Of these possible cuts, the one corresponding to the optimal solution, i.e., $(x,{\underline{\theta }},{\underline{\lambda }})$, is the tightest at x. If ${\mathcal {A}}^{\mathrm {LB}}_m(x,c)$ and/or ${\mathcal {A}}^{\mathrm {UB}}_m(x,c)$ are solved to a feasible but not optimal solution, the generated cutting plane and upper bound are still valid.

A graphical interpretation of ${\underline{\theta }}$ and $\theta$ of ${\mathcal {A}}^{\mathrm {LB}}_m(x,c)$ is shown in Fig. 2c, where the set $({\underline{\theta }},c)$ is the red continuous curve, and the set $(\theta ,c)$ is the red shaded area. Figure 2f gives an interpretation of ${\overline{\theta }}$ and $\theta$ of ${\mathcal {A}}^{\mathrm {UB}}_m(x,c)$, where the set $({\overline{\theta }},c)$ is the green continuous curve, and the set $(\theta ,c)$ is the green shaded area.

5 Benders decomposition with adaptive oracles

This section presents the Benders-type algorithm incorporating the inexact information of the adaptive oracles of Sect. 4.

5.1 Convergence of Algorithm 2

Lemma 5

At each iteration, either Algorithm 2 finds an $\epsilon$-optimal solution, or the algorithm adds at least one locally-improving exact cut to the reduced master problem.

Proof

At iteration j Algorithm 2 adds at least one locally-improving exact cut to the reduced master problem ($\xi ^{(j)}=1$) or all the subproblems are solved for the current solution (${\mathcal {E}}^{(j)}=\varnothing$). If none of the exact cuts $(x^{(j)}_i,\theta ^{(j)}_i,\lambda ^{(j)}_i)$ generated at iteration j is locally-improving ($\xi ^{(j)}=0$), it follows that

$$\begin{aligned} \theta ^{(j)}_i \le \underset{\ell < j}{\max } \left\{ {\underline{\theta }}^{(\ell )}_i + {\underline{\lambda }}^{(\ell )\top }_i \left( x^{(j)}_i - x^{(\ell )}_i \right) \right\} , \quad \forall i \in {\mathcal {I}}, \end{aligned}$$

(7)

and given that the left- and right-hand sides of (7) are equal to ${\overline{\theta }}^{(j)}_i$ and $\beta ^{(j)}_i$, respectively, it follows that the lower bound and the upper bound have converged exactly. $\square$

Theorem 2

For any $\epsilon \ge 0$, Algorithm 2 finds an $\epsilon$-optimal solution to problem (1) in a finite number of iterations.

Proof

Lemma 2 proves that there exists a finite number of locally-improving exact cuts that can be added to the reduced master problem, and Lemma 5 proves that Algorithm 2 adds at least one locally-improving exact cut at each iteration (or it has converged). It follows that Algorithm 2 finds an $\epsilon$-optimal solution to problem (1) in a finite number of iterations. $\square$

6 Case Study

We test the proposed Benders algorithm with adaptive oracles on power system stochastic investment planning problems. Serial and parallel versions of the algorithms are implemented in Julia 1.4. Two Linux Desktop computers Intel i7 6-core processor clocking at 2.40 GHz and 16 GB of RAM are used for running the code. The serial implementation is run on a single machine, and the parallel implementation uses both machines simultaneously. The optimization models are implemented in JuMP (Julia package) and solved with Gurobi 9.0. The Julia code implementing Algorithms 1 (Stand_Bend) and 2 (Adapt_Bend) for the proposed case study is provided at https://github.com/nimazzi/Stand_and_Adapt_Bend [9].

6.1 Investment planning model

We consider a power system investment planning problem with a time horizon of 15 years. The deterministic version of the problem has 3 decision nodes: one refers to decisions to be taken in the first stage, one to decisions in 5 years time, and one to decision in 10 years time. The stochastic version is obtained by modeling different possible scenarios for the future of the system in 5 and 10 years. At each node we also compute the cost of operating the system for the following 5 years for given installed capacity. We consider a construction time of 5 years, so new assets installed in the first stage will only be available in 5 and 10 years, and new capacity installed in 5 years will only be available in 10 years. We model a set ${\mathcal {P}}$ of technologies: 6 thermal units, 3 storage units, and 3 renewable generation units. The cost for operating the system is computed by solving an hourly economic dispatch for 5 years.

We formulate the stochastic investment planning problem as

$$\begin{aligned} \underset{{\mathbf {x}} \in {\mathcal {X}}}{\text {min}} \; f({\mathbf {x}}) + \sum _{i \in {\mathcal {I}}} \pi _i g(x_i,c_i), \end{aligned}$$

(8)

where ${\mathcal {I}}$ is the set of stochastic decision nodes, each associated with a probability $\pi _i$. The function

$$\begin{aligned} g(x_i,c_i) = \underset{y_i \in {\mathcal {Y}}}{\text {min}}\{ c_i^\top C y_i | A y_i \le B x_i \}, \quad \forall i \in {\mathcal {I}}, \end{aligned}$$

(9)

gives the cost of operating the system over 5 years. The vector of parameters $x_i$ is given by

$$\begin{aligned} x_i = \left( \left\{ x^{acc}_{pi}, \forall p \in {\mathcal {P}}\right\} ,-\nu ^{D}_i,\nu ^{E}_i\right) , \quad \forall i \in {\mathcal {I}}, \end{aligned}$$

where $x^{acc}_{pi}$ is the accumulated capacity of technology p at node i. Parameters $\nu ^{D}_i$ and $\nu ^{E}_i$ are the relative level of energy demand and the yearly $\hbox {CO}_2$ emission limit, respectively. Note that $g(x_i,c_i)$ is non-increasing w.r.t. $x^{acc}_i$ and $\nu ^{E}_i$, and non-decreasing w.r.t. $\nu ^{D}_i$, so using $-\nu ^{D}_i$ instead satisfies the non-increasing requirement. The vector of uncertain cost coefficients $c_i$ is

$$\begin{aligned} c_i = (c^{nucl}_i,c^{\mathrm {co}_2}_i), \quad \forall i \in {\mathcal {I}}, \end{aligned}$$

where $c^{nucl}_i$ is the uranium fuel price and $c^{\mathrm {co}_2}_i$ the $\hbox {CO}_2$ emission price, and $g(x_i,c_i)$ is non-decreasing w.r.t. both $c^{nucl}_i$ and $c^{\mathrm {co}_2}_i$. All the remaining parameters, e.g., A, B, and C, are the same for every node $i \in {\mathcal {I}}$. Finally, the function $f({\mathbf {x}})$ yields the expected total investment and fixed cost, and it is computed as

$$\begin{aligned} f({\mathbf {x}}) = \sum _{i \in {\mathcal {I}}} \pi _{i} \sum _{p \in {\mathcal {P}}} \left( c^{inv}_{pi} x^{inst}_{pi} + c^{fix}_{pi} x^{acc}_{pi}\right) , \end{aligned}$$

where the variable $x^{inst}_{pi}$ is the newly installed capacity of technology p at node i. Parameters $c^{inv}_{pi}$ and $c^{fix}_{pi}$ are the unitary investment and fixed costs of technology p at node i. The accumulated capacity $x^{acc}_{pi}$ at node i is computed as the sum of the historical capacity $x^{hist}_{pi}$ and the newly installed capacity $x^{inst}_{pi'}$ at nodes $i'$ ancestors to i. Finally, the initial special point $({\underline{x}},{\underline{c}})$ is set to

$$\begin{aligned} {\underline{x}},{\underline{c}} = \left( \left\{ \text {min}_i x^{hist}_{pi}, \forall p \in {\mathcal {P}}\right\} , -\text {max}_i \nu ^{D}_i, \text {min}_i \nu ^{E}_i \right) ,\left( \text {min}_i c^{nucl}_i,\text {min}_i c^{\mathrm {co}_2}_i\right) \end{aligned}$$

We consider three possible sources of uncertainty, i.e., $\nu ^{E}_i$, $c^{\mathrm {co}_2}_i$, and $c^{nucl}_i$. Each uncertain parameter has 3 possible outcomes in 5 years, each of which is linked to 3 additional possible outcomes in 10 years. The result is 9 possible trajectories for each source of uncertainty, all with the same probability. We consider 4 different cases of the investment problem. Case 0 is the deterministic version, where $\nu ^{E}_i$, $c^{\mathrm {co}_2}_i$, and $c^{nucl}_i$ are deterministic parameters (weighted average of the scenarios). Then, case 1 has 1 uncertain parameter ($\nu ^E_i$), case 2 has 2 uncertain parameters ($\nu ^E_i$ and $c^{\mathrm {co}_2}_i$), and case 3 has 3 uncertain parameters ($\nu ^E_i$, $c^{\mathrm {co}_2}_i$, and $c^{nucl}_i$). The number of decision nodes and the size of the deterministic equivalent for the 4 versions of the problem is summarized in Table 1. As a benchmark, we try to solve the deterministic equivalent problem for cases 0, 1, 2, and 3 on our Linux Desktop computer. Case 0 is successfully solved in 4 minutes, and case 1 in 58 minutes. The deterministic equivalent of cases 2 and 3 is not solved since the Julia instance is killed due to a memory overload.

Table 1 Decision nodes ${\mathcal {I}}$ and size of the deterministic equivalent problem for different cases of the study

6.2 Results

We use Algorithms 1 (Stand_Bend) and 2 (Adapt_Bend) to solve the stochastic investment planning problem (8), whose operational subproblems (9) are LP problems with $4.11 \times 10^5$ constraints and $1.40 \times 10^5$ variables. All the subproblems are solved with Gurobi barrier method (“Method”=2), while we do not impose a predefined solution method for the $\mathbf {RMP}$ and the oracles (“Method”=-1). In the serial implentation of the algorithms we set “Threads”=0 for the $\mathbf {RMP}$, the subproblems, and the oracles, i.e., Gurobi decides the amount of threads to use. In the parallel implementation of the algorithms we impose “Threads”=1 for the subproblems and the oracles.

For Algorithm 2 at each iteration j we choose the set ${\mathcal {I}}_{ex}=\{i_k, \; k=1,..,w \}$ of w subproblems that are solved exactly. Each element $i_k$ is the (or one of the) $i \in {\mathcal {E}}_k^{(j)}$ for which the difference $\pi _i {\overline{\theta }}^{(j-1)}_i - \pi _i {\underline{\theta }}^{(j-1)}_i$ is maximum, where the ${\mathcal {E}}^{(j)}_k$ form a partition of ${\mathcal {E}}^{(j)}$. The idea is to group in each subset ${\mathcal {E}}^{(j)}_k$ subproblems that are potentially similar to each others, to diversify the exact solutions that are added to the oracles. To select the w subsets of ${\mathcal {E}}^{(j)}$ we use the kmeans function of the Clustering package with $(\nu ^{D}_i,\nu ^{E}_i, c^{nucl}_i,c^{\mathrm {co}_2}_i)$ as the input parameters.

As a benchmark, we also implement the Benders algorithm with inexact cuts as presented in [18], and we refer to it as Algorithm 3 or Zaker_Bend. The core idea is to solve subproblems up to primal-dual feasible solution with an optimality gap lower than $\delta ^{(j)}$ which is large for early iterations and progressively tightened ($\delta ^{(j)} \rightarrow 0$ for $j \rightarrow \infty$) as the algorithm approaches the optimal solution. The dual solution and dual objective are used to build valid cutting planes, and the primal objective is used to build a valid upper bound. To obtain such primal-dual feasible solution, we solve subproblems with barrier method, we disable crossover (“Crossover”=0), and we impose the optimality gap to $\delta ^{(j)}$ (“BarConvTol”=$\delta ^{(j)}$), in accordance with [18]. The optimality gap is set to 1 (maximum value of “BarConvTol”) for the first iteration, i.e., $\delta ^{(1)}=1$, then we use the update rule $\delta ^{(j)}:=\tfrac{1}{10}\delta ^{(j-1)}$ suggested by [18]. We set a minimum threshold for $\delta ^{(j)}$ to $10^{-8}$ which is the default value for “BarConvTol”.

Table 2 gives the optimal investment decisions to be taken in the first investment stage for cases 0–3. The solutions are obtained solving (8) with Algorithm 1 up to an $0.01\%$-optimal solution. Including a more accurate description of the stochastic processes involved in the decision-making process progressively modifies the optimal decisions of the system planner. Using the full stochastic model (case 3) the planner takes considerably different decisions compared to the ones yielded by its deterministic counterpart (case 0). In case 0 the system planner builds 13.7 GW of CCGT, 1.4 GW of diesel, and 19.0 GW of onshore wind. In case 3 the investment in CCGT (11.4 GW) is less and there is a slight increase in the amount of diesel (2.0 GW). In addition, the planner invests in 1.2 GW of coal with CCS which is not used at all in case 0.

Note that other technologies (e.g., nuclear and off-shore wind) are chosen in many scenarios of the second investment stage (in 5 years) and that varying amounts of most of the technologies are explored during the iterative solution procedure, even if these are not used in the optimal solution.

Table 2 Optimal investments in the first investment stage for cases 0–3

6.2.1 Serial implementation

This section discusses the results of the serial implementation of the algorithms, where only one Julia instance is launched. For Algorithm 2 we set $w=1$ so one single subproblem is solved exactly at each iteration.

Table 3 shows the effort in terms of iterations and computation time (the timer starts after the Julia code has been precompiled) to reach an $\epsilon$-optimal solution using Algorithms 1 (Stand_Bend), 2 (Adapt_Bend), and 3 (Zaker_Bend) for case studies 0–3. We report the results for values of the optimality tolerance $\epsilon$ of $1.00\%$, $0.10\%$, and $0.01\%$. For case 0 the computation efficiencies of Algorithms 1, 2, and 3 are similar. In this small case study Algorithms 1 and 3 solve 2 subproblems each iteration and Algorithm 2 solves 1 subproblem. However, Algorithm 2 needs more iterations to reach the target tolerance. As an example, to obtain a tolerance lower than $0.01\%$ Algorithm 1 requires 26 iterations and Algorithm 2 needs 50. Increasing the size of the problem makes the comparison more interesting. For example, for case 2 Algorithm 1 needs 13 and 24 iterations to reach tolerance of $1.00\%$ and $0.01\%$, respectively. To reach the same tolerances Algorithm 3 performs 12 and 21 iterations, respectively, and Algorithm 2 performs 67 and 190 iterations. However, an iteration of Algorithms 1 and 3 solves 90 subproblems while Algorithm 2 solves only 1. The results show that Algorithm 1 takes 64 minutes to yield an $0.01\%$-optimal solution compared to 38 minutes for Algorithm 3, i.e., 1.7 times faster. To reach the same tolerance Algorithm 2 needs less than 8 minutes, i.e., 8.1 and 4.8 times faster than Algorithm 1 and 3, respectively. For case 3 this difference is even larger as Algorithms 1 and 3 solve the subproblem 756 times at each iteration. Accordingly, even if they reach a $1.00\%$ tolerance in only 12 iterations, this requires 4 hours and 15 minutes, and 2 hours and 36 minutes, respectively. On the other hand, Algorithm 2 reaches the same tolerance in 8 minutes, 31.9 times faster than Algorithm 1 and 19.5 times faster than Algorithm 3. If a tighter tolerance is needed the difference of performances progressively reduces but it is still significant for $\epsilon =0.01\%$. Indeed, Algorithm 1 requires around 9 hours and 18 minutes, Algorithm 3 takes 4 hours and 53 minutes (1.9 times faster than Algorithm 1), and Algorithm 2 needs 36 minutes (15.4 and 8.1 times faster than Algorithm 1 and 3, respectively).

Table 3 Comparative results for Algorithm 1 (Stand_Bend), Algorithm 2 (Adapt_Bend), and Algorithm 3 (Zaker_Bend)

Table 4 shows the (relative) computation time of the main steps of Algorithm 2, i.e., solving the relaxed master problem, solving the subproblems, and solving the adaptive oracles, to reach an $\epsilon$-optimal solution for case studies 0–3. We report the results for value of the optimality tolerance $\epsilon$ of $1.00\%$, $0.10\%$, and $0.01\%$. In cases 0, 1, and 2 almost all the computation time is spent solving subproblems (one each iteration). However, in case 3 more than 10% of the computation time to obtain an $0.01\%$-optimal solution is spent solving the master problem, 27% solving the adaptive oracles, and only 65% solving subproblems. These results suggest that the proposed rule of solving one subproblem at each iteration may not be the best when the number $|{\mathcal {I}}|$ of subproblems grows significantly and that a selection rule that dynamically decides the number of subproblems to solve at each iteration may then achieve a better balance.

Table 4 Analysis of Algorithm 2 (Adapt_Bend) computation time

6.2.2 Parallel implementation

This section discusses the results of the parallel implementation of Algorithms 1 and 2, where together with the main Julia instance we also start up a pool of workers via function addprocs of the Distributed package. The $\mathrm {RMP}$ is solved in the main Julia instance, while the subproblems and the oracles are solved by the pool of workers via the function pmap. For Algorithm 2 we set w equal to the number of workers in the pool, so one single subproblem is solved exactly by each worker at each iteration.

Table 5 compares the time and the number of iterations to reach an $0.01\%$-optimal solution of case 3 using Algorithms 1 and 2 as a function of the size of the workers pool. Algorithm 1 takes 23 iterations and 10 hours and 57 minutes with one worker in the pool, whereas Algorithm 2 takes 537 iterations and 1 hour, i.e., 10.8 times faster than Algorithm 1. The number of iterations for Algorithm 2 is slightly different from the values shown in Table 3, even though when the pool contains one worker only it should be equivalent to the serial implementation. The only difference from the serial implementation is the number of threads used to solve subproblems and oracles. Changing that value can make Gurobi converge to slightly different solutions (within optimality and feasibility tolerances) and alter the way the Benders algorithm finds an $\epsilon$-optimal solution. Increasing the number of workers in the pool slightly changes the relative speed-up obtained with Algorithm 2, mainly due to some load balancing issues when solving subproblems. When there are 4 workers in the pool Algorithm 1 needs 3 hours and 17 minutes, while Algorithm 2 takes 20 minutes, 9.5 times faster.

Table 5 Comparative results of the parallel implementation for Algorithm 1 (Stand_Bend) and Algorithm 2 (Adapt_Bend) to solve case 3 up to $\epsilon =0.01\%$

It is worth highlighting that running the parallel code on a single Linux Desktop machine with more than two workers in the pool showed some severe slow down, probably due to cache issues given the large size of the subproblems to solve.

7 Conclusions

This paper presents a novel concept of inexact oracles that can be used to speed up the computational time of Benders-type decomposition algorithms for a class of large scale optimization problems. We propose two adaptive oracles that yield inexact and progressively more accurate information when subproblems are not solved. The first adaptive oracle builds valid cutting planes, and the second adaptive oracle provides a valid upper bound of the objective function. The two oracles exploit properties of the Benders subproblem such as convexity w.r.t. right-hand side coefficients and concavity w.r.t. cost coefficients, as well as monotonicity w.r.t. to both coefficients.

We use the novel adaptive oracles within a Benders-type decomposition algorithm to solve a stochastic investment planning problem. The results show substantial improvements in terms of computational efficiency (w.r.t. a standard Benders algorithm), especially if a large optimality gap is allowed. The largest problem we solve has 756 subproblems, each of which has $4.11 \times 10^5$ linear constraints and $1.40 \times 10^5$ linear variables. Our algorithm is 31.9 times faster than the standard Benders algorithm to reach a $1.00\%$ optimal solution and 15.4 times faster if the optimality tolerance is tightened to $0.01\%$.

Reformulation to achieve monotonicity w.r.t. x and c.

We consider the case when $g(x,c):=\underset{y \in {\mathcal {Y}}}{\text {min}}\{ c^\top C y | A y \le B x \}$ is not a monotonic function of x and c. First, we formulate a modified version of g(x, c) as

$$\begin{aligned} \begin{aligned} {\tilde{g}}(x,c)&= \underset{y \in {\mathcal {Y}}}{\text {min}}\quad c^\top C y + \gamma ^\top x\\&\quad \, \text {s.t.} \quad A y \le B x \end{aligned} \end{aligned}$$

(10)

and choose a value of $\gamma$ that makes the objective function $c^\top C y + \gamma ^{T} x$ monotonic w.r.t. x. The master function objective is changed to $f({\mathbf {x}}) - \sum _{i \in {\mathcal {I}}} \gamma ^{T} x_i$ to cancel out this additional term. Then, we formulate a relaxed version of ${\tilde{g}}(x,c)$ as follows

$$\begin{aligned} \begin{aligned} {\tilde{g}}_{\mathrm {c}}(x,c^{\alpha },c^{\beta }) =&\underset{y \in {\mathcal {Y}},z^\alpha ,z^\beta }{\text {min}} \quad c^{\alpha \top } z^\alpha + c^{\beta \top } z^\beta + \gamma ^\top x\\&\text {s.t.} \qquad z^\alpha -z^\beta = Cy, \quad A y \le B x \\&\qquad 0\le z^\alpha \le Z^\alpha , \quad 0 \le z^\beta \le Z^\beta \end{aligned} \end{aligned}$$

(11)

where parameters $Z^\alpha$ and $Z^\beta$ ensure that the relaxed subproblem is not unbounded. The value of $Z^\alpha$ and $Z^\beta$ is to be chosen so that they do not restrict the feasible region w.r.t. (10). Note that ${\tilde{g}}_{\mathrm {c}}(x,c^\alpha ,c^\beta )$ is a concave and increasing function of both $c^\alpha$ and $c^\beta$, and that ${\tilde{g}}_{\mathrm {c}}(x,c^\alpha ,c^\beta ) = {\tilde{g}}(x,c)$ if $c^\alpha =c$ and $c^\beta =-c$. Computing ${\tilde{g}}_{\mathrm {c}}({\underline{x}},{\underline{c}},-{\underline{c}})$ gives a solution that can be used in the adaptive oracle for obtaining a valid lower bound on ${\tilde{g}}(x,c), \; \forall x \in {\mathcal {K}}^x, \forall c \in {\mathcal {K}}^c$.