Introduction

Adolescent obesity has reached an epidemic level in developed countries [1, 2]. Nisbett's set point theory [3] and Herman and Polivy's boundary theory [4] proposed that dieting may mediate the association between externality and obesity. Therefore, understanding the restrained eating behaviors may help better understand the risk factors of obesity problems. Building upon these theories, the Restraint Scale (RS) was developed to measure dietary restraint and identify restrained eaters. The ten-item Revised Restraint Scale (RRS) [5] is as an improvement of the original RS [6]. A two-factor structure of RRS including domains of concern for dieting and weight fluctuations has been proposed in normal-weight subjects [7, 8]. Nevertheless, robustness of results generated from the traditional principal component analysis (PCA) is subjective to the variations of rotation and extraction methods. In addition, simultaneous loadings of items on factors of RRS are not uncommon. Most studies of the psychometric properties of RRS [9, 10] and its comparisons with other restrained eating measures [11] are conducted in the western populations. Applications of the RRS for the assessment of restrained eating in certain subgroups such as obese subjects are also prone to factorial structure [12, 13] and validity [14, 15] concerns.

There are increasing trends of body dissatisfaction, dieting [16], as well as eating disorders [16–20] in Chinese adolescents. Therefore, a well-validated instrument for restrained eating screenings in Chinese adolescents is urged. Prospective studies found that adolescent girls with elevated RRS scores are at a higher risk of onsets of binge eating [21, 22], eating disorders [23–25], and negative affects [26, 27]. Klem et al. suggested that white, female, and overweight college students obtained higher RRS scores than others [14]. However, such comparisons may be inappropriate without a prior validation of RRS in the subgroups. Therefore, this study aims to investigate the psychometric properties of the RRS in Hong Kong adolescents and its validity in different subgroups.

Methods

Study Design

A total of 909 Hong Kong students (55.3% boys) aged 12–18 years (mean age=15.7 years) from a secondary school completed a health survey in 2007. In addition, their standing height was measured with a tape fixed on a vertical wall and taken to the nearest 0.1 cm and body weight was measured to nearest 0.1 kg using electronic scales. All measurements were conducted barefoot and with light clothes. Ethical approval was obtained from the Survey and Behavioral Research Ethics Committee of the Chinese University of Hong Kong.

Measures

The RRS is a ten-item measure used for identifying restrained eaters. Items of RRS are rated on a four- to five-point scale, with a maximum total score of 35. RRS consists of two subscales (a) weight fluctuation (WF) with four items for assessing history of weight fluctuation and (b) concern with dieting (CD) with six items for assessing the attitudes towards dieting.

Moreover, the Eating Attitudes Test (EAT-26) [28], a 26-item measure of disordered eating attitudes and behaviors was also included in the questionnaire. EAT-26 was scored based on the factor structure obtained from a previous study in Chinese population [29]. The first factor dieting (EAT-diet) consists of 11 items (items 1, 2, 6, 7, 11, 12, 14, 16, 22, 23, 24), examining fat phobia and correlates of weight control behaviors. Moreover, the second factor Bulimia (EAT-bulimia) consists of five items (items 3, 4, 10, 18, 21), examining the inclinations of food preoccupation and binge eating. The third factor Social Pressure (EAT-pressure) consists of seven items (items 5, 8, 9, 13, 15, 20, 26), examining the social pressure to increase food intake. Options for the responses are in four-point Likert-scales (3=always, 2=usually, 1=often, 0=sometimes/rarely/never), where higher scores indicating a higher likelihood of maladaptive eating attitudes and behaviors. A score of 20 or above is regarded as at risk of eating disorders and diagnostic follow-ups are required.

In addition to RRS and EAT-26, the Motivation for Eating Scale (MFES)-physical with seven items was extracted from the physical eating subscale of the MFES, which are commonly used to assess motivations for initiating food consumption [30]. Options of the responses are on a five-point scale (1=almost never to 5=almost always). Higher scores indicate a higher likelihood of eating on the basis of physical needs.

Data Analysis

Students aged below 16 years are regarded as the younger group and 16 years or above as the older group. Moreover, body mass index (BMI) was computed and used to classify students into normal weight and overweight/obese groups based on the International Obesity Task Force standard [31].

In the factor analysis, the whole sample was randomly split into training (sample 1: N=454) and validation (sample 2: N=455) sets for exploratory and confirmatory factor analyses, respectively. Comparisons of the distributions of sex, age, and BMI between these two subsamples were performed to ensure independent grouping. To examine the latent structure of the construct of RRS, an exploratory factor analysis (EFA) with PCA was conducted among all of ten items of RRS for the training set (sample 1). Only factors that had eigenvalues greater than 1 were retained for interpretation. PCA with a Varimax rotation method was then used to detect the factor structure of the RRS items. The factor structure of the RRS was further investigated using the confirmatory factor analysis (CFA) on the validation set (sample 2). In addition, a series of other plausible models identified in the previous study were compared with the EFA model obtained. According to the result of van Strien et al's study [10], excluding items 1, “How often are you dieting?”, item 6, “Do you eat sensibly before others and splurge alone?”, and item 10, “How many kilograms over your desired weight were you at your maximum weight?” may improve the construct of the model. Item 1 was retained in our analysis in face of the observed conceptual centrality for the factor CD. However, items 6 and 10 were removed from the model. By submitting the remaining eight items to a maximum likelihood PCA, a 2-factor model with the factors CD including items 1, 5, 7, 8, and 9, as well as WF including items 2, 3, and 4 was found to be the best-fitting parsimonious model. Hence, models included in the CFA were: model A, a one-factor model including all ten items; model B, the two-factor model proposed by Herman and Polivy, with the factors CD including items 1, 5, 6, 7, 8, and 9, as well as WF including items 2, 3, 4, and 10 [5]; model C, the three-factor model obtained from the EFA; and model D, the two-factor model proposed by van Strien et al., with items 6 and 10 excluded [10].

Since the assumption of multivariate normality was not fulfilled by the sample, the robust maximum likelihood method of estimation with the Satorra–Bentler scaled χ 2 (SB χ 2) correction was used [32]. By convention, a value of 0.90 or more for the comparative fit index (CFI) [33], the normed fit index (NFI) and the non-normed fit index (NNFI) [34], and a value less than 0.08 for the root mean square error of approximation (RMSEA) [35] indicate a well-fitted model. Corrected scaled difference χ 2 (SDCS) test resembling the normal likelihood ratio test was conducted to detect any significant differences in the goodness-of-fit between nested models [32, 36], whereas Akaike's Information Criterion (AIC) and consistent AIC (CAIC) were used for comparisons between non-nested models. Smaller values of AIC and CAIC indicate a better fit to the hypothesized model. As no prior hypothesized structure of the RRS for non-western population is available, a two-step EFA-CFA approach was used. Furthermore, hierarchical multi-sample CFAs in sex, age (below 16 years vs. 16 years or above), and weight status (normal vs. overweight/obese) subgroups were performed to ensure the configural and measurement invariance of the best-fit RRS model between subgroups. The configural invariance of the selected model was tested by imposing the best-fit RRS model separately on each subgroup. To evaluate the measurement invariance of the model, equality constraints were imposed on the factor loadings and subsequent error variances of each RRS item across the subgroups. When the full forms of invariance could not be established, the poorest fit constraint indicated by the Lagrange multiplier (LM) test was set free to obtain partial configural, metric, or factorial invariance.

The internal consistency reliability of RRS was tested using the Cronbach's alpha coefficients and item-total correlations of RRS subscales and items [37]. The inter-item correlations of the scales were examined by the Pearson's Correlation Coefficients. Since RRS results are associated with bulimic pathology [9], we hypothesized that RRS would correlate with EAT-diet and EAT-bulimia, but not MFES-physical which is mainly a measure of physical needs of eating.

Based on the final model established in our sample, a series of analysis of variance (ANOVA) was conducted to investigate the main and interaction effects of sex, age, and weight status on the RRS composite and subscale sores. Comparisons of invariance across sex, age, and weight status were also made [38]. The SPSS 16.0 and EQS 6.1 programs were used in the analyses.

Results

Basic Characteristics

Of the 909 subjects included, all of them were Chinese, 55.3% were boys, and 74.6% were aged below 16 years of age. The mean BMI was 20.8 (SD=3.9) in boys and 20.6 (SD=3.6) in girls. Based on their BMI values, 21.0% of them were classified as overweight or obese. The mean BMI for the normal and overweight/obese groups was 19.2 (SD=2.1) and 26.2 (SD=3.4), respectively.

Exploratory Factor Analysis

In Table 1, the preliminary EFA yielded three components with eigenvalues greater than 1.0 in sample 1, which account for 54.55% of total variance. The three components each accounted for 21.47%, 19.42%, and 13.66% of the total variance. After omitting items with factor loadings lower than 0.30, only item 10 was found to load on more than one factor. The first factor (factor 1) was loaded with items 2, 3, 4, and 10; following the original factor loading pattern proposed by Herman and Polivy and labeled as weight fluctuation (RRS-WF) [5]. In addition, the original factor CD was split into two factors. The first half (factor 2) was loaded with items 1, 5, 6, and 8, and still labeled as concern with dieting (RRS-CD). Another half (factor 3) was loaded with item 7 and 9 only and was given a new label, food consciousness (RRS-FC). The inter-factor correlations between RRS-CD and RRS-WF, RRS-WF and RRS-FC, and RRS-CD and RRS-FC were 0.30, 0.19, and 0.30 (all p<0.001), respectively. The individual factor loadings and communalities, and inter-factor correlations are shown in Tables 1 and 2.

Table 1 Summary of factor loadings and communalities from exploratory factor analysis of RRS for the training set (sample 1) (N = 454)
Full size table
Table 2 Inter-correlations of RRS with EAT-26 and MFES-physical
Full size table

Confirmatory Factor Analysis

Table 3 reports the results of CFAs on the four competing models (model A to D) in sample 2. The SDCS test results suggested that the data covariance matrix of model C was not significantly different from the implied one with SB χ 2 =47.85, df=32, p=0.35. The fit indices also indicated a satisfactory level of goodness-of-fit for model C (NFI=0.90, NNFI=0.95, CFI=0.96, RMSEA (90% CI)=0.03(0.009, 0.051)). An acceptable level of goodness-of-fit was not found in other models (i.e. models A, B, and D) and multi-dimensional structure for RRS was suggested for model A.

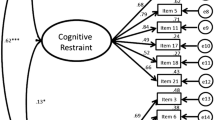
Table 3 Summary of fit indices of competing models of Revised Restraint Scale for the validation set (sample 2) (N = 455)
Full size table

Consistent with the results of fit indices, SDCS test indicated significant differences between models A and C with corrected ΔSB χ 2=161.11, df=3, p<0.001; and models B and C with corrected ΔSB χ 2=52.20, df=2, p<0.001 (data not shown in tables). Moreover, smallest values of AIC and CAIC were found in model C (Table 3). The standardized statistics of all factor loadings and factor correlations of model C are presented in Fig. 1. Moderate to strong factor loadings, ranging from 0.48 to 0.70 were observed in model C with p for Wald test<0.05 (Fig. 1). In summary, these convergent test results suggested that the construct of RRS is multi-dimensional and model C is the best-fitting model for RRS in our sample.

Fig. 1
figure 1

Standardized path coefficients for the final three-factor correlated model (model C) of the Revised Restraint Scale for the validation data set (sample 2) (N = 455). SB χ2 = 50.82, p = 0.35; df = 32; CFI = 0.90; RMSEA (90% CI) = 0.03 (0.01, 0.05). Standardized factor loadings are indicated by single-headed arrows. Correlations between factors are indicated by double-headed arrows. SBχ 2 Satorra–Bentler scaled χ 2, CFI Comparative Fit Index, RMSEA Root Mean Square Error of Approximation, 90% CI 90% Confidence Interval

Full size image

Measurement Equivalence of Revised Restraint Scale

In Table 4, an unconstrained model without any equality constraints was fitted respectively to all testing subgroups. The configural results indicated that the structure of model C is valid to be used as the baseline model for further comparisons of models with a higher level of measurement equivalence (sex: RMSEA (90% CI)=0.03 (0.018, 0.046), CFI=0.92; age group: RMSEA (90% CI)=0.03 (0.007, 0.041), CFI=0.92; weight status: RMSEA (90% CI)=0.02 (0.001, 0.0038), CFI=0.96). In addition, metric invariance was not rejected for all of the three multigroup comparisons according to the non-significant differences from the SDCS test (sex: corrected ΔSB χ 2=5.97, df=7, p=0.54; age group: corrected ΔSB χ 2=2.62, df=7, p=0.92; weight status: corrected ΔSB χ 2=6.92, df=7, p=0.44). In addition, strong factorial invariance indicating equality of error variances among all items of model C was found between age groups with corrected ΔSB χ 2=17.44, df=10, p=0.07 and between weight status with corrected ΔSB χ 2=9.57, df=10, p=0.48. However, such invariance was not found in sexes with corrected ΔSB χ 2=18.81, df=10, p=0.04.

Table 4 Test of invariance of Revised Restraint Scale factorial structures among subgroups
Full size table

In view of the lack of error variance equivalence between sexes, the LM test results were further examined. The LM results indicated that the cross-group equality constraints on the intercept for item 8 “Do you have feelings of guilt after overeating?” of the RRS are the major contributor to the lack of fitness of the model. After the removal of the equality constraint of equality error variances of item 8, the corrected ΔSB χ 2 became 12.03 (df=9, p=0.21) which indicated a partial strong factorial invariance of RRS between sexes. Summary of the statistics of fit indexes of tests of configural, metric, and strong invariance are presented in Table 4.

Internal Consistency

Item analyses were conducted based on models A and C for the RRS. Model A is a unitary factor model with good overall internal consistency reliability. The Cronbach's alpha was 0.71 and removal of items did not improve the overall reliability of model A. On the other hand, model C is a multifactor model with acceptable level of internal consistency reliability. The Cronbach's alpha for the factor RRS-CD, RRS-WF, and RRS-FC was 0.63, 0.69, and 0.53, respectively (Table 5). Although all subscale alphas were lower than the cutoff point of 0.70, removal of items from model C did not improve the overall reliability. In addition, the item-total correlations were all beyond the acceptable value of 0.30, ranging from 0.35 to 0.46 for RRS-CD, 0.40 to 0.56 for RRS-WF, and 0.36 to 0.36 for RRS-FC (data not shown in tables). Nevertheless, with only two to four items for each scale, the obtained Cronbach's alpha are still of acceptable values, and thus the internal consistency of the RRS of model C [39].

Table 5 Means, standard deviations, and internal consistency estimates of the composite and subscales of the RRS for different sex, age, and weight status subgroups
Full size table

Concurrent Validity

The Cronbach's alpha for EAT-26 items is 0.88 and that for MFES-physical is 0.79. Table 2 presents the correlation coefficients of composite and subscale scores of RRS with EAT-26 and MFES-physical. The composite RRS score associated moderately with EAT-diet (r=0.48, p<0.001) and EAT-bulimia (r=0.36, p<0.001); and weakly with EAT-pressures (r=0.16, p<0.001) and MFES-physical (r=0.13, p<0.001). For the RRS subscales, strong correlations were found between RRS-CD and EAT-diet (r=0.50, p<0.001) and between RRS-FC and EAT-bulimia (r=0.31, p<0.001). Moreover, weak correlations were found between RRS-CD and MFES-physical (r=0.07, p=0.04), and between RRS-WF and EAT-pressures (r=0.08, p=0.02).

Subgroup Differences

In Table 5, the mean RRS score for the whole sample was 7.11 (SD=4.20). Subjects being female (F(1, N=899)=18.65, p<0.001) and overweight/obese (F(1, N=899)=8.09, p=0.005) scored significantly higher RRS composite scores than others. As in another study [6], the median RRS score (7 in our sample) was used as a cutoff for restrained eating. A total of 41.7% of boys and 62.1% of girls were classified as restrained eaters. The prevalence of restrained eaters was significantly higher in girls (χ 2=37.17, df=1, p<0.001) and in overweight/obese group (χ 2=9.50, df=1, p=0.002) than others. No significant difference of RRS scores and prevalence of restrained eaters was found between the age groups. Furthermore, ANOVA results indicated significant sex differences in RRS-CD, weight status differences in RRS-WF, and sex and age differences in RRS-FC. No significant interaction effect was found for all subscales.

Discussion

Construct Validity of the Revised Restraint Scale

This study has examined the factor structure of the RRS and its invariance among Hong Kong boys and girls with different weight status using the two-step EFA-CFA framework. EFA preliminarily suggested a three-factor structure of the RRS. The first factor identified was identical to the factor WF obtained in previous studies [7, 15]. Two new factors were generated from the original factor CD. Similar to the previous studies, item 10 loaded on both factors CD and WF [12, 40]. The resulting three-factor model was different from the two-factor model proposed by van Strien et al. [41]. Moreover, elimination of items 6 and 10 from the RRS was not supported by our results, although they were suggested to confound the criterion of restrictive eating in young adults [9].

Using the multigroup analysis of measurement invariance, the three-factor structure proposed in this study was found to be applicable to different age and weight status groups. It is also different from the conclusions of van Strien et al., suggesting a two-factor model for both normal-weight and overweight females [10]. Nevertheless, differential factorial structure of RRS was found in our male and female samples with unequal intercepts found in item 8 “Do you have feelings of guilt after overeating?”. This probably suggests boys and girls have different acquiescence response styles to this question.

The Cronbach's alpha values for internal consistency of RRS in our adolescents are relatively lower when compared to those among normal-weight college students [8, 14, 42] and general public [13]. In addition, the external validity of RRS was supported by its convergence with EAT-26 (measuring dieting and bulimia) and discrimination with Motivation for Eating Scale (MFES)-physical (measuring perceived social pressures for food intake and physical eating). It is consistent with the existing literature that disinhibited eating is an important component of dietary restraint [43] and RRS scores are correlated with both dieting and bulimia [11]. Moreover, eating based on physiological hunger and satiety cues are found to be conceptually antagonistic to the construct of dietary restraint which is cognitive inhibition over desires to eat [3]. The non-significant correlation between RRS and perceived social pressures scores indicated that overeating or weight fluctuation may not attribute to external pressures to eat, but intrinsic disinhibition of eating. In general, RRS is a reliable and valid measurement of restrained eating for Hong Kong adolescents.

Restrained Eating in Hong Kong Adolescents

A mean composite RRS score of 7.11 was obtained in our sample. Consistent with the findings in college students [14], main effects of sex and weight status, but not age on restrained eating were found. Since only Chinese subjects are included in the present study, testing the ethnic variable was not feasible. When compared with the previous studies, our RRS scores are relatively lower than those reported in university students [44] or adults [11, 13, 45]. Without a standard clinical threshold, different arbitrary cutoffs are also used for the classification of restrained eaters in these studies.

Based on our proposed construct, sex differences were found in concerns about dieting and food consciousness, but not in perceived weight fluctuation. Similar results were reported in university students [44]. Although our normal-weight subjects reported to have less weight fluctuation than their overweight counterparts, they reported similar concerns about dieting and foods. This may imply that overweight/obese subjects obtained higher RRS scores due to their greater extent of absolute weight fluctuations, rather than their intentions to diet [46, 47]. Furthermore, the RRS subscales correlated more strongly with EAT-diet and EAT-bulimia, than with EAT-pressures and MFES-physical. These correlations demonstrated the good convergent and divergent validity of the RRS.

Strengths and Limitations

To our knowledge, it is the first study investigating the construct validity of the RRS in non-western population. Measured anthropometric data have reduced biases in self-reports that are common in adolescents [48]. This study has also provided a comprehensive psychometric evaluation of the RRS in different sex, age, and weight status subgroups using a two-step EFA–CFA approach. Nevertheless, information on the behavioral measures of dietary restraint such as actual weight fluctuation or caloric intake of the subjects was not available. This limited our further investigation of the predictive validity of the RRS for discriminating successful from unsuccessful dieters. Establishment of the invariance of the RRS using second-order sub-grouping, such as measurement equivalence between sexes within a weight status group was also limited by the sample size. In addition, sociocultural influence from peers, family, and mass media on weight concerns and eating behaviors are also relevant to adolescents [49] and should be assessed in future studies.

Conclusions

The present study proposes a three-factor structure including concern for dieting, weight fluctuation, and food consciousness as the best RRS construct for Hong Kong adolescents. In general, RRS is a valid instrument to assess retrained eating behaviors in adolescents, regardless of sex, age, and weight status.