Abstract
Chemical compositional data sets of archaeological artefacts are often analysed using standard statistical procedures. Adopting a different approach, we examine the major element oxides found in Parthian and Sasanian glazed pottery by identifying statistically important ratios of oxides in conjunction with the expert knowledge of the archaeological scientist during, rather than after, the identification process. This results in meaningful ratios, both statistically and archaeologically, which help identify the recipes and production practices used by Mesopotamian glass and glaze producers. The application of logratio analysis to interrogate the chronological groups suggests that the silica sources used for glazes were significantly purer in later periods and exhibited less variation. Comparing the expert-assisted selection of ratios derived from a legacy data set to the ratios from compositional data of Parthian glazed pottery recovered at the early 3rd century CE Roman military outpost of Ain Sinu in northern Iraq supports the hypothesis that there was a shift to more standardised recipes in the production of glass used for glazes. If this translates to a centralised glass-making industry, it would suggest that there are, as yet, undiscovered glass production centres, potentially in areas associated with increased urbanisation in southern Mesopotamia around the time of the Parthian–Sasanian transition.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Chemical compositional analyses suggest that glaze technology in Mesopotamia did not change significantly between the first use of alkaline glazes on clay-based ceramics (ca. 1500 BCE) and the transition to lead-based glazes in the early Islamic period (Hedges and Moorey 1975; Peltenburg 1971; Vandiver 1983; McCarthy et al. 1995). Although this assessment recognises the establishment of a tradition of making glass and glazes with plant ash, evidence of increased urbanisation, especially in the late first millennium BCE by the Parthians (ca. 247 BCE-224 CE) and in the early first millennium CE by the Sasanians (224 CE−mid-7th century CE) (Daryaee 2009), could suggest that this interpretation reflects how compositional data have been collected and analysed rather than indicating that glass and glaze technology had not developed for over 2000 years. Here, we present a workflow (and the associated R code - see supplementary material) of a recently developed statistical procedure, which is applicable to many compositional data systems in archaeology, in order to investigate Mesopotamian glass and glaze technology.
Freestone (2013) neatly describes the need for compositional ‘anchors’ from which to examine the variation within a production assemblage to determine the significance of the differences between assemblages. Although compositional analyses have had some success for medieval European glass making, where raw materials were obtained locally, with each glasshouse producing vessels of a distinctive composition (Freestone 2005), they have often had limited success with glasses and glazes with relatively homogenous compositions (e.g. Roman glass) until production assemblages were discovered, such as late antiquity (ca. 6th-8th century CE) glass-making sites on the Levantine coast (Freestone and Gorin-Rosen 1999). Furthermore, as highlighted by Baxter et al. (1995), even the most carefully formulated analytical programmes have failed to produce clear compositional groupings corresponding to typology. This presents a problem for Parthian and Sasanian glasses and glazes which, coupled with low numbers of sherds available for analysis (Brill 2005), have only been recovered from consumption assemblages, as production sites in Mesopotamia have not been reported.
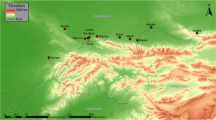
It was shown recently that glazes on Parthian pottery recovered at the early 3rd century CE Roman military outpost of Ain Sinu in northern Iraq (Fig. 1) had compositions similar to Roman glass, suggesting that Roman glass was recycled and reapplied as a glaze by Parthian potters (Wood and Hsu 2020). More significantly, this practice indicates that glass and glazes were regarded as the same material in Mesopotamia and that the presence of Roman glass reapplied as a glaze on Parthian pottery reflects the practice of using a glass precursor in the form of crushed glass frit to glaze pottery rather than applying a fluxing mineral to react directly with the silica-rich clay surface during firing. This could suggest that there are, as yet, undiscovered glass production sites in Mesopotamia.
a Map showing Ain Sinu and other sites in the Parthian and Sasanian empires. b Aerial photograph of Ain Sinu from the British Academy, Sir M. Aurel Stein Collection (item: ASA/3/35; Obverse: 15098). Use of photograph permitted by British Academy. c Parthian blue-glazed pottery jar (second–third century CE) recovered in North Syria (item: 1915, 1218.1). d Glazed sherd from Ain Sinu held at the British Museum (item: 1988, 0410.126) showing the diagnostic Parthian diamond-stamp pattern. Use of photographs permitted by British Museum
The current article recognises that there are plenty of compositional data in archaeological site reports, academic theses and research articles which are ready for re-analysis. Although ‘standard’ techniques using the original compositional values are often considered sufficient in archaeology (Baxter and Freestone 2006), we advocate the approach to compositional data which involves logarithmically transformed ratios or logratios (Aitchison 1986, 2005; Aitchison and Greenacre 2002; Baxter 1989; Buxeda i Garrigós 1999, 2008; Pawlowsky-Glahn and Buccianti 2011; Greenacre 2018, 2021), as we consider this approach to be more mathematically rigorous than traditional ones. Against this backdrop, we examine legacy data from Parthian and Sasanian glazed pottery by applying statistical procedures based on logratio analysis (LRA) which utilise the expert knowledge (Greenacre 2019; Graeve and Greenacre 2020) of the archaeological scientist during, rather than after, their application to identify patterns which reflect changes in recipes and production practices. We use the logratios that emerge from the legacy data to interrogate compositional data derived from glazed pottery recovered at the 3rd century CE Roman military outpost at Ain Sinu (also known as Zagurae), a contested area in northern Mesopotamia (northern Iraq), excavated by Professor David and Dr. Joan Oates in the 1950s.
Analysing glass and glazes
One of the main problems in comparing percentages of each chemical component which makes up glass or a glaze (or any multicomponent system) is that compositions are fundamentally multivariate in nature, and their components are necessarily interdependent. That is, even if one part of a composition is reported, it is implicitly related to the other components. Moreover, compositional measurements conducted on glass and glazed pottery use techniques such as X-ray fluorescence (XRF), which cannot generally detect many of the lighter elements found in glass, glazes and pottery (Hedges and Moorey 1975). In other words, the amounts that are measured do not add up to the real total. For example, in Hedges and Moorey’s (1975) paper, the percentages of silica present in the Sasanian glazes were not measured directly but calculated by subtracting the sum of the other components from 100%. Although this provides a useful approximation of the amount of silica expected in these glazes, it is clearly difficult to compare accurately with other studies which have measured additional (or fewer) components. In fact, the whole data set is rarely (if ever) measured, as different instruments focus on different parts of the composition. This means that the total amount varies due to missing data, and since the total cannot be determined, the percentage of nonmissing variables cannot be calculated.
More recently, trace element and isotopic data have been used in glass provenance studies (Shortland et al. 2007; Walton et al. 2009; Degryse et al. 2010). These types of data, however, are not routinely collected and, more significantly, are difficult to relate to recipes used by ancient glass and glaze producers. In effect, although trace element and isotopic data can be used to determine compositional groups (e.g. traces of Ti, Cr, Zr and La and Sr and Nd isotopes have been used to discriminate between Egyptian and Near Eastern glasses), such signatures can also result in the emergence of abstract compositional typologies which are difficult to relate to any changes in glass- and glaze-making practice. In fact, the analysis of major element oxides is perhaps preferable when trying to study ancient technological practices as they are more closely related to the recipes of ancient glass and glaze producers and allow the application of statistical procedures based on logratios since generally all components are present in measurable amounts.
The problem with dealing with the major element oxides, however, is that there are fewer components to provide the compositional variation that may be required to identify statistically significant groups in data sets. We address this problem by incorporating the expert knowledge of the archaeological scientist into the statistical investigation. In effect, the approach proposed in this paper is to replace the original compositional data with a set of carefully selected ratios, with the following requirements: (1) the ratios are easily interpretable by the practitioner, i.e. the archaeological scientist; (2) the set of ratios, after log-transformation, explains either all or a very high percentage of the variability contained in the original data set and defines a geometry that comes measurably close to that of the original data set and so preserves its essential multivariate structure (Greenacre 2019); and (3) the ratios can be validly reported as univariate statistics, with conventional summary measures and plots, which can be compared with the same ratios in similar studies.
Legacy data set
The following criteria were used to select glazes in the archaeological record to determine representative Parthian and Sasanian compositional signatures:
-
Samples classified as Parthian, Sasanian or Parthian–Sasanian were included in the analyses. Those classified as Sasanian/Early Islamic or similar were not included.
-
Gravimetric methods, e.g. Matson (1943), or semi-quantitative techniques which could not measure the full suite of major element oxides, e.g. portable X-ray fluorescence (pXRF), were excluded. The glaze compositions reanalysed were generated from two analytical techniques: energy dispersive spectroscopy (EDS) and wavelength dispersive spectroscopy (WDS).
-
Glazes of all colours were included on the assumption that additives that modified the glaze colour were added to the same base glaze and reflected variations in oxidising conditions in the kiln rather than variations in the base compositional ‘recipes’ of the glazes.
Reliable chronology is clearly essential to interpret the significance of these glazes, but unfortunately, it is not always available with the desired precision. We are therefore using the most generally accepted chronological attributions but appreciate that some may be revisited in the future. Moreover, terms such as Parthian–Sasanian and Partho-Sasanian are not always well-defined in the archaeological literature and could be interpreted as a glaze produced in either the Parthian or Sasanian period or around the time of the Parthian–Sasanian transition, i.e. ca. 224 CE. For the current article, we have included a Parthian–Sasanian chronological group for these indeterminate samples (and would therefore anticipate a greater spread in data compared to the other groups) where we have placed samples such as the 1st–3rd century AD samples from Seleucia in Iraq (Pace et al. 2008) (see Table 1).
The main components of Mesopotamian glazes derive from silica and plant ash (Brill 2005; Freestone 2013; Hedges and Moorey 1975; Simpson 1997) and contain oxides of silicon, aluminium, iron, magnesium, calcium, potassium and sodium (SiO2, Al2O3, FeO, MgO, CaO, K2O and Na2O, respectively). These components can also be found in pottery body fabrics that could influence the composition of the glazes during firing. However, McCarthy (1996) measured the compositional profile across Parthian glazes, showing that there was very little change from the outer surface of the glaze to the glaze-body interface for all measured oxides, suggesting that levels in the glaze do not change significantly. Similar experiments have found that any influence of the body fabric on the composition of the glaze is confined to a narrow layer (< 150 μm from the fabric) immediately adjacent to the body (Wood and Hsu 2020). It has therefore been assumed that compositions of the glazes predominantly reflect the recipes used to make the glass applied to the body.
A second data set (Table 2), from the early 3rd century CE site of Ain Sinu in northern Iraq (Wood and Hsu 2020), was investigated independently of the legacy data presented in Table 1. Ain Sinu was a contested territory for both the Parthian and Sasanian empires, being occupied by the Romans between 197 and 364 CE (Oates and Oates 1959). Three glazes analysed from this Roman military outpost were found to have chemical compositions which were consistent with Roman glass (Wood and Hsu 2020), thereby suggesting strongly that Roman glass had been recycled and reapplied as a glaze on local pottery, that is, Roman glazes were lead based, with alkaline natron glass only being used for objects of glass (Hatcher et al. 1994; Walton and Tite 2010). Five glazed sherds were found to have typical glaze compositions for the Parthian and Sasanian periods. Table 2 shows the normalised mean glaze compositions of oxides, with samples in italics being those made from recycled Roman glass (i.e. glazes with lower concentrations of MgO and measurable levels of the decolouriser Sb2O5).
Methods
Although multivariate statistical applications in the archaeological literature are almost exclusively based on means and correlation (or covariance) matrices determined directly from raw percentage data (e.g. Foy et al. 2003; Maltoni et al. 2015), the approach followed here treats the system as a series of subcompositional components or parts, realising that the oxides being analysed are a subset of a potentially larger set, which affects their percentage values. The main idea is to analyse oxide ratios, which are unchanged whether observed in subcompositions or extended compositions, and to logarithmically transform the ratios to put them on an additive (interval) scale, resulting in logratios. This method was first proposed by Aitchison (1986) who defined a relative geometry where only the pairwise logratios of the different components were considered (see Aitchison 2005).
Apart from the simple pairwise logratios of parts, other logratio transformations are possible; the most useful being the centred logratios (CLR), the logarithm of each component (oxide) xj relative to the geometric mean of all the parts:
It has been shown that the principal component analysis (PCA) of the D CLRs is equivalent to the PCA of all ½D(D - 1) pairwise logratios (Aitchison and Greenacre 2002). This method of dimension reduction is called logratio analysis (LRA), and its interpretation differs from that of regular PCA in that it is not the parts themselves that are interpreted in the solution but rather the directions linking pairs of parts, which represent the logratios (for a practical introduction, see Greenacre 2018).
Basing the analysis of compositions on logratios is subcompositionally coherent as it removes the effects of the constant sum constraint (which compels the data to lie between 0% and 100%) in order to eliminate any ‘spurious correlations’ (Chayes 1949). In essence, the logratio approach considers from the outset that the interest lies in the relative magnitudes and variations of components instead of in their absolute values, thereby retaining the proper covariance structure of any compositional data set. The transformation to logratios then allows the full range of standard statistical methods, both exploratory and inferential, to be available for identifying and confirming groups or patterns in the data.
Further development of the logratio approach was introduced by Greenacre (2019) who showed that a careful stepwise selection of a small set of simple pairwise logratios could explain essentially all the variance in the total set of logratios and that this selection could be enhanced by expert knowledge of the data context (Graeve and Greenacre 2020). This is the approach adopted here, namely, identify a small set of pairwise logratios, which have both a substantive interpretation and as high as possible statistical explanation of the total logratio variance.
The procedure adopted here also makes use of bootstrapping methods in order to determine univariate or multivariate confidence limits. Bootstrapping involves taking a large number (in our application, 1000) of samples of the original sample, with replacement, computing the group means on each one, giving an approximate empirical distribution of the mean. Greenacre (2016) defines a univariate confidence plot, where the bootstrapping method is used to construct the confidence interval, with ‘whiskers’ extending from the mean (shown as a dot) to the upper 97.5th and lower 2.5th percentiles, thus giving an estimated 95% confidence interval for the mean (e.g. see Fig. 4). To enhance the interval in a style similar to the boxplot, a box has been added to show the boundaries of the 75th and 25th percentiles, thus enclosing 50% of the mean’s distribution (Greenacre 2016). Thus, there is a 50:50 chance that the box covers the true mean and a 95% chance that the range of the extended interval includes the true mean. Notice that these confidence plots show the variability in the mean rather than the variability in individual values.
As a rule of thumb, if two confidence intervals do not overlap, then there will be a significant difference between the respective groups (Krzywinski and Altman 2013); whereas if they do overlap, then it depends by how much, and a formal test is required to make a decision. In every case, a p value of group difference should be computed, and this is conveniently done using a distribution-free permutation test (Good 2005); we used the function oneway_test in the coin package in R (Hothorn et al. 2008), i.e. the asymptotic Fisher–Pitman test.
Similarly, in multivariate space, bootstrapping allows the computation of a region enclosing a multivariate mean with prescribed confidence, usually 95%. In reduced-dimension plots such as Figs. 2 and 3 and regular bivariate plots such as Fig. 5, these regions are represented by confidence ellipses (see Greenacre 2016 and associated R function CIplot_biv in supplementary material).
Logratio analysis (LRA) of the data in Table 1, where the additional samples in Table 2 are displayed as supplementary points (Roman samples 171, 163 and 156 in italic on the right). A 95% confidence ellipses around the group means (large symbols: P, P–S and S) of the three groups, clearly demonstrating that S (Sasanian) is separate from P (Parthian), with P–S (Parthian–Sasanian) overlapping with both S and P. Around 74.0% of the variance is explained by the two principal dimensions
PCA of the four logratios selected, which account for 93.1% of the total logratio variance. Since 50.4 + 29.7 = 80.1% of the variance is explained by these two dimensions, this means that 0.801 × 93.1 = 74.6% of the total logratio variance is explained by this two-dimensional solution. The samples in Table 2 are added as supplementary points (Roman samples 171, 163 and 156 in italics on the right)
Results
Figure 2 shows the results of the LRA, explaining 74% of the logratio variance using the first two principal components of the logratios. This biplot is interpreted in terms of the directions linking the tips of the arrows rather than the arrows themselves. These connecting links represent the ratios between parts (on a logarithmic scale) so that large distances between pairs of oxides represent high variances of logratios, for example, those of FeO/Na2O and FeO/Al2O3. In effect, every pairwise logratio is a direction between two oxides, and inverting the ratio just inverts the direction.
When two oxides such as MgO and CaO are at the same position, this indicates highly correlated logratios with the other oxides. For example, FeO/MgO and FeO/CaO are indeed highly correlated (r = 0.9541), and there is similarly a high degree of correlation between Al2O3/MgO and Al2O3/CaO (r = 0.9539). This suggests that MgO and CaO can be amalgamated with minimal loss of variance (Greenacre 2020), i.e. summing (MgO + CaO), and thus simplifying the analysis. From an archaeological science perspective, this suggests strongly that MgO and the CaO in these glazes derive from the same source. More specifically, since MgO is associated with the plant ash flux (Barkoudah and Henderson 2006; Tite et al. 2008), this suggests that CaO enters the system inadvertently with the plant ash rather than being deliberately added in the form of limestone or shell.
The shaded regions show 95% confidence ellipses around the means of the three groups, clearly demonstrating that S (Sasanian) is separate from P (Parthian), with P–S (Parthian–Sasanian) overlapping with both S and P. Furthermore, the variances for each group show that the Parthian group has the most variance (0.1072), and Sasanian has the least variance (0.0440), with the nebulous Parthian–Sasanian group falling between these two groups (0.0773). Multivariate permutation tests for group differences using the vegan package in R (Oksanen et al. 2015) confirm that Parthian and Sasanian are significantly different in their compositions (p = 0.002), whereas Parthian–Sasanian is not significantly different to Parthian (p = 0.209) or to Sasanian (p = 0.187).
Figure 2 represents the analysis of all pairwise logratios (numbering 21 if MgO and CaO are separated but 15 when they are amalgamated), but we also recognise that a smaller set can be determined, which explains almost of the variance while approximating closely the geometric structure of the compositional data. Since several logratios compete for being chosen at similar levels of explained variance, it is preferable that selection is assisted by expert knowledge in order to explain as much variability as required to reveal the underlying structure of the data using logratios that are meaningful to the archaeological scientist. In our stepwise selection, for the formation of logratios, MgO and CaO were amalgamated (summed), and the individual oxide values of MgO and CaO are then removed, but the logratio variance to be explained remained that of the original data set of seven oxides.
The following stepwise process was followed (details of the steps are given in Table 3):
Step 1: The automatic procedure produced a list of candidate logratios in descending order of explained variance. Table 3 presents the top five ratios in terms of the percentage of variance that each explains. The first logratio (SiO2/FeO) in the list for the first step explains the most variance (38.5%) and was also the preferred choice. From an archaeological science perspective, this ratio could relate to the purity of the silica source since iron impurities in the silica source can affect the colour of a glaze. For example, glazes can turn yellow, red or brown when iron oxide within a glaze is oxidised (Vandiver 1990), with the colour depending on the amount present. Under reducing conditions, it turns the glaze green (Matson 1971). A silica source with low iron could produce glass or glaze which is closer to being colourless than a glaze with high levels of FeO. This could have been desirable for the ancient glass/glaze producer especially if other additives were to be introduced to colour the base glaze, e.g. copper compounds. This suggests that certain silica sources may have been deliberately sought out. By this rationale, log(SiO2/FeO) was selected, explaining 38.5% of the variance, and the procedure continued to the second step.
Step 2: The second column in Table 3 shows the list of candidates after log(SiO2/FeO) has been forced in, after which the same stepwise procedure was performed on all the remaining ratios. The percentages are now the cumulative ones, in addition to that of the log(SiO2/FeO) chosen previously. The first logratio in the list, Al2O3/(MgO+CaO), explains the most additional variance (33.3%), bringing the explained variance to 71.8%. However, log(SiO2/Al2O3) was selected despite being slightly below (1.1%) the statistically optimal logratio. This ratio is coherent from an archaeological science perspective: glass with low levels of alumina is considered to reflect the use of quartz sand or quartz pebbles as the silica source (Freestone and Gorin-Rosen 1999; Paynter and Tite 2001). Consequently, the logratio of (SiO2/Al2O3) was selected from this second step because, like log(SiO2/FeO), it could relate to the purity of the silica source used.
Step 3: Now that log(SiO2/FeO) and log(SiO2/Al2O3) have been forced in, the top of the list of ratios became dominated by the amalgamation of MgO and CaO. When ratioed with this amalgamation, K2O brings the explained variance up to 84.0%, while any of the three parts already in the two previous logratios, i.e. FeO, Al2O3 or SiO2, similarly ratioed with this amalgamation, would bring the explained variance up to 83.5%. The logratio of (SiO2/(MgO + CaO)) was selected despite being 0.5% below the statistically optimal logratio as it reflects the variation in the silica source to the plant ash source, i.e. the silica-flux recipe used by glass and glaze producers. Furthermore, K2O potentially derives not only from the plant ash but also from the fuel used during firing (Paynter 2009; Wood and Hsu 2020), making any ratios which include K2O more difficult to interpret.
Step 4: After forcing in log(SiO2/(MgO + CaO)) along with the two previously selected logratios, several ratios that include Na2O bring the explained variance to 93.1%. Although soda (Na2O) should come in with the plant ash (i.e. it is a flux in these soda–lime–silicate glazes), it is a problematic indicator since Na2O can leach out during deposition (i.e. weathering). Nevertheless, archaeological scientists tend to sample select the least weathered samples for analysis and avoid weathered regions of the sample when measuring compositions (McCarthy 1996; Tite et al. 1998; Paynter 2009; Wood and Hsu 2020), so variation in the logratio (Na2O/(MgO + CaO)) could reflect variations in the types of plant ash used. This is the final logratio selected, with 93.1% of the total logratio variance in the data set accounted for.
The four logratios identified from the stepwise procedure described above (i.e. logs of SiO2/FeO, SiO2/Al2O3, SiO2/(MgO + CaO) and Na2O/(MgO + CaO)), representing 93.1% of the variance of the data set, are both high statistically and meaningful to the archaeological scientist. It should be noted that if the stepwise algorithm made its own optimal choice, it would explain 94.9% of the variance. However, this modest gain includes ratios with K2O which, as mentioned above, are more difficult to interpret. Figure 3 shows the PCA using only the selected logratios. As with Fig. 2, 95% confidence ellipses around the means of the three groups clearly demonstrate that S is separate from P, with P–S overlapping with both S and P.
From Fig. 3, it appears that the logratios of SiO2/FeO and SiO2/Al2O3 separate the groups along dimension 1, whereas those of SiO2/(MgO+CaO) and Na2O/(MgO+CaO) are accounting chiefly for differences amongst the samples along dimension 2. To demonstrate this one variable at a time and to implement a statistical test, Fig. 4 shows 95% confidence plots for the logratio means of the groups, using bootstrapping (see Greenacre 2016 and the associated R function CIplot_uni in supplementary material).
95% confidence plots for means of the four selected logratios based on 1000 bootstrap samples. The mean is indicated by a dot (as opposed to a line for the median in a boxplot). The box encloses a 50% confidence interval for the mean and the whiskers a 95% confidence interval. In each case, confidence plots are shown for the three chronological groups in Table 1: Parthian, Parthian–Sasanian (P–S) and Sasanian, as well as for the group of the early 3rd century CE glaze samples from Ain Sinu in Table 2, denoted as AS. The three Roman samples (171, 163 and 156) are highlighted with triangles
As suggested by the overlapping confidence plots, Fig. 4a (upper left) highlights that log(SiO2/(MgO + CaO)) is relatively invariant across all three chronologies. The p value (p = 0.295) for testing differences between the groups suggests strongly that the null hypothesis cannot be rejected, i.e. there is no difference. This could suggest that the silica source and the plant ash were added together in similar proportions over these periods. In effect, the analysis supports that the recipe of adding plant ash to the silica source was relatively constant.
Figure 4b (upper right) shows that log(Na2O/(MgO + CaO)) is also relatively invariant between the Parthian and Sasanian chronological groups (p = 0.315). This would suggest that the flux used was either similar across groups (i.e. plant ash flux) or that any changes in recipe (e.g. types of plant used) cannot be differentiated using the major element oxides.
In Fig. 4c (lower left), the confidence intervals for P, P–S and S overlap, and we have to rely on the statistical test to decide on between-group significance. The p value is 0.025, showing that log(SiO2/FeO) is statistically different across the three chronological groups (Note: The p value is even lower if only Parthian and Sasanian groups were compared: p = 0.009). This could suggest that either the raw materials and/or the practice changed. As the ratio is higher in the Sasanian than the Parthian period, this would indicate that either the concentration of silica was higher or that the concentration of iron oxide was lower in the Sasanian compared to the Parthian period. In Fig. 4d (lower right), there is no overlap between the confidence intervals of P and S for the logratio log(SiO2/Al2O3), and the groups are statistically different (p = 0.002), suggesting that either the concentration of silica was higher or that the concentration of alumina in the Sasanian period was generally lower compared to the Parthian period.
A cursory examination of the raw data (Table 1) shows that the silica levels are similar for the Parthian, Parthian–Sasanian and Sasanian periods, suggesting that the main variation is within the iron oxide and alumina concentrations. Furthermore, Fig. 5 presents these two logratios on one plot, which shows that there is an increasing trend between the Parthian period and Sasanian period for both these ratios (with the Parthian–Sasanian data falling between the means of P and S). This indicates that log(SiO2/FeO) and log(SiO2/Al2O3) are correlated. In fact, the plot is similar to the LRA plot (Fig. 3), thereby demonstrating that most of the between-group variance can be explained by these two logratios. Essentially, the increasing trend on this logratio plot indicates that the silica source became increasingly pure in later periods (i.e. concomitant decreasing levels of iron oxides and alumina), suggesting the increasing application of quartz sand/pebbles as the silica source in the production of glazed pottery.
Figures 2, 3, 4 and 5 also present data from glazes recovered at Ain Sinu (AS). As expected, the samples identified as Roman glazes (in italics) appear to separate on all these plots. The remaining glazes from Ain Sinu generally lie within either the Parthian or Sasanian ellipses or between them in Figs. 2, 3 and 5. Similarly, this separation is reflected in Fig. 4. Applying the exact Fisher–Pitman oneway_test for the non-Roman Ain Sinu samples and Parthian legacy data groups (Hothorn et al. 2008) shows that log(SiO2/(MgO + CaO)) (p = 0.35), log(Na2O/(MgO + CaO)) (p = 0.40) and log(SiO2/FeO) (p = 0.48) ratios for the five Ain Sinu samples are not significantly higher than the Parthian group. However, log(SiO2/Al2O3) ratios are much closer to significance (p = 0.07). In fact, samples 1988-410-157 and 1988-410-169 have lower levels of alumina than the other Ain Sinu samples (Table 2) which could suggest that the glazed pottery recovered at Ain Sinu followed more than one tradition. This would be consistent with a region which was using recycled Roman glass to glaze pottery and with their early 3rd century CE chronology, i.e. the Parthian–Sasanian transition.
Discussion
The motivation for an archaeologist to use a method based on ratios of components is that this makes compositional data, and thus the results of the statistical analysis, invariant to the particular choice of components. This choice depends on the availability of data. In this study, there were seven components in the form of oxides. Extending or reducing the number of components (if greater or fewer oxides had been available) changes the compositional data, which are normalised to sum to 1, but the ratios between components remain unchanged. As we have shown, it is possible to select a few ratios (always on a logarithmic scale) to adequately account for the variance in the compositional data set and provide sound archaeological interpretation by incorporating the expert knowledge of the archaeological scientist during, rather than after, the selection process.
Restricting the logratio analysis (LRA) of the glaze compositional legacy data set (Table 1) to three chronological periods shows that glazes from Parthian and Sasanian periods lie in statistically different groups, with the more nebulous Parthian–Sasanian group falling between the means of these groups (Fig. 2). As expected, the confidence ellipse for Sasanian glazes is smaller than that of the nebulous Parthian–Sasanian group. It is, however, also smaller than the Parthian group. This is due to both the lower inherent variance of the Sasanian sample and its higher sample size. In effect, the lower variation for the Sasanian glazes suggests strongly that recipes or practices were becoming more standardised in the later periods.
This patterning is perhaps not so surprising as technological processes would be expected to improve over time. However, interrogating the LRA shows that a change in the silica source used could reflect standardisation through the deliberate selection of higher purity sources (Fig. 4c, d). The expert-assisted selection of the logratios (Fig. 3) shows that four meaningful logratios can explain a high proportion of the variance of the legacy data set. Although the ratios which relate to plant ash (i.e. SiO2/(MgO + CaO) and Na2O/(MgO + CaO) ) do not exhibit any statistically significant differences over the time periods under investigation, the logratios of (SiO2/Al2O3) and (SiO2/FeO) could suggest that later glaze producers deliberately sought quartz sand or quartz pebbles. This would be in line with glazes from Seleucia and Veh Ardasir which suggest that different types of sand may have been used for glazes during the Parthian and Sasanian periods (Mirti et al. 2008).
The data we have reanalysed appear to show that changes in sources of silica occurred around the time of the Parthian–Sasanian transition. We are not claiming, however, that Parthian potters never sought out purer silica sources or that change in practice was abrupt. In fact, the early 3rd century CE glazes from Ain Sinu suggest that purer silica sources were already being used in the late Parthian period. Nonetheless, it appears that the practice of seeking out purer silica sources for glazes was much more prevalent under the Sasanians.
The acquisition and application of purer silica sources in later periods could suggest that during Parthian times, individual potters made their own glazes (thereby explaining the higher variation in the silica sources), whereas in Sasanian times, glass-making became more centralised, perhaps producing glass ingots (similar to the sixth–eighth century CE primary glass production sites in the Levant) which were subsequently broken up into cullet, procured by potters and used for making glazed wares. Since potters at Ain Sinu were making use of local glass (in their case, recycled Roman glass), it would appear that there was sufficient know-how to glaze pottery but insufficient glass to carry it out. Glazed pottery, however, is common at Ain Sinu in contrast to the ornate but unglazed wares generally recovered in northern Mesopotamia (Oates 1968). The fact that northern Mesopotamia does not appear to have a tradition of producing glazed wares could suggest a southern Mesopotamian provenance for the non-Roman glass glazed sherds at Ain Sinu or the movement of glass into this contested region to glaze pottery (Table 2).
This would suggest that people travelled from the south to the contested area of this Roman frontier post in northern Mesopotamia around the time of the Parthian–Sasanian transition, perhaps bringing glass or glazed wares with them — a movement which included those with the skills to glaze pottery using acquired glass frit such as recycled Roman glass. Essentially, it is proposed that standardisation potentially began in the south from the late Parthian period or earlier, which is consistent with the notion of centralised glass production in a region where most glazed wares from these periods have been recovered.
Concluding remarks
The aim of compositional analyses in archaeology is to find patterns in compositional data which can be used to understand the behaviour of people in the past. These analyses, however, often solely focus on explaining variance, which can lead to the archaeological scientific practice of group finding becoming too abstract to investigate the recipes and practices conducted to produce ancient artefacts. Here, were have shown that the application of statistical operations based on logratios to a compositional data set comprising the major element oxides of Parthian and Sasanian glazes can provide useful archaeological information, particularly when the analyses utilise the knowledge of the archaeological scientist during their application. The workflow (and the associated R code) assists in the identification and interrogation of meaningful patterns in compositional data. We consider that it is applicable to many areas of archaeology in addition to the case study on Mesopotamian glass and glaze technology investigated here.
To some extent, the findings of this study are not controversial: there appears to have been standardisation in the practice of producing glazes. However, better control over the purity of the components to produce these glazes also suggests centralisation of production in later periods. This may also not seem to be a controversial claim, as there was increased urbanisation throughout the Parthian and Sasanian periods (Daryaee 2009). This glass seems to be of a typical type for the region: soda–lime–silicate glass fluxed using plant ash but with less compositional variation and significantly lower levels of alumina and iron oxides in later periods. This suggests purer silica sources were deliberately sought after (i.e. quartz sand or pebbles), especially in the Sasanian period, which in turn suggests that glass began to be made independently of craft workers who glazed the pottery. In fact, since it is known that potters from the early 3rd century CE utilised recycled glass at Ain Sinu in northern Mesopotamia, this could suggest that indigenous glass was generally acquired by potters to glaze their wares at this time rather than the potters making glass themselves. Furthermore, since it is unlikely that Parthian or Sasanian glass production would have been instigated in contested territory, the know-how to glaze pottery using glass and the glass itself potentially moved from southern to northern Mesopotamia into this contested region. The mechanism of this movement is unclear. Nonetheless, this could suggest that there are, as yet, undiscovered glass production sites in southern Mesopotamia from around the time of the Parthian–Sasanian transition.
Change history
16 July 2021
A Correction to this paper has been published: https://doi.org/10.1007/s12520-021-01379-0
References
Aitchison J (1986) The statistical analysis of compositional data. Chapman and Hall, London
Aitchison J (2005) A concise guide to compositional data analysis. 2nd compositional data analysis workshop – CoDaWork’05. Girona: Universitat de Girona. Available at: http://www.leg.ufpr.br/lib/exe/fetch.php/pessoais:abtmartins:a_concise_guide_to_compositional_data_analysis.pdf (accessed 26 October 2020).
Aitchison J, Greenacre M (2002) Biplots for compositional data. J R Stat Soc: Ser C: Appl Stat 51:375–392
Barkoudah Y, Henderson J (2006) Plant ashes from Syria and the manufacture of ancient glass: ethnographic and scientific aspects. J Glass Stud 48:297–321
Baxter MJ (1989) Multivariate analysis of data on glass compositions: a methodological note. Archaeometry 31:45–53
Baxter MJ, Freestone IC (2006) Log-ratio compositional data analysis in archaeometry. Archaeometry 48:511–531
Baxter MJ, Cool HEM, Heyworth MP, Jackson CM (1995) Variation in Roman colourless vessel glass. Archaeometry 37:129–141
Brill RH (2005) Chemical analyses of some Sasanian glasses from Iraq: Appendix 2. In: Whitehouse D (ed) Sasanian and post-Sasanian glass in the Corning Museum of Glass. Corning Museum of Glass, London
Buxeda i Garrigós J (1999) Alteration and contamination of archaeological ceramics: the perturbation problem. J Archaeol Sci 26:295–313
Buxeda i Garrigós J (2008) Revisiting the compositional data: some fundamental questions and new prospects in archaeometry and archaeology. Proc CODAWORK 8:27–30
Chayes F (1949) On correlation in petrography. J Geol 57:239–254
Collinet A, Rante R (2013) Nishapur revisited: stratigraphy and ceramics of the Qohandez. Oxbow Books, Oxford
Daryaee T (2009) Sasanian Persia: the rise and fall of an empire. I B, Tauris
Degryse P, Boyce A, Erb-Satullo N, Eremin K, Kirk S, Scott R, Shortland AJ, Schneider J, Walton M (2010) Isotopic discriminants between Late Bronze age glasses from Egypt and the Near East. Archaeometry 52:380–388
Foy D, Picon M, Vichy M (2003) Verres Omeyyades et Abbasides d’origine Egyptienne: Les temoignages de l’archéologie et de l’archéometrie. Annales 15e Congrès de l’Association Internationale pour l’Histoire du Verre 138-143.
Freestone IC (2005) The provenance of ancient glass through compositional analysis. Mater Res Soc Symp Proc 852:1–14
Freestone IC (2013) Parthian, Sasanian and early Islamic pottery: dating, definition and distribution. In: Priestman S., Simpson S-J (eds.) A specialist workshop at The British Museum. http://www.britishmuseum.org/pdf/Pottery%20seminar.pdf
Freestone IC, Gorin-Rosen Y (1999) The great glass slab at Beth She’arim: an early Islamic glass-making experiment? J. Glass Stud 41:105–116
Good P (2005) Permutation, parametric and bootstrap tests of hypotheses, 3rd edn. Springer, New York
Graeve M, Greenacre M (2020) The selection and analysis of fatty acid ratios: a new approach for the univariate and multivariate analysis of fatty acid trophic markers in marine pelagic organisms. Limnol Oceanogr Methods 18:196–210. https://doi.org/10.1002/lom3.10360
Greenacre M (2016) Data reporting and visualization in ecology. Polar Biol 39:2189–2205. https://doi.org/10.1007/s00300-016-2047-2
Greenacre M (2018). Compositional data analysis in practice. Chapman & Hall / CRC Press, Boca Raton
Greenacre M (2019) Variable selection in compositional data analysis using pairwise logratios. Math Geosci 51:649–682. https://doi.org/10.1007/s11004-018-9754-x
Greenacre M (2020) Amalgamations are valid in compositional data analysis, can be used in agglomerative clustering, and their logratios have an inverse transformation. Appl Comput Geosci 5. https://doi.org/10.1016/j.acags.2019.100017
Greenacre M (2021) Compositional data analysis. Ann Rev Stat Appl 8:21.1–21.29
Hatcher H, Kaczmarczyk A, Scherer A, Symonds RP (1994) Chemical classification and provenance of some Roman glazed ceramics. Am J Archaeol 98:431–456
Hedges REM, Moorey PRS (1975) Pre-Islamic ceramic glazes at Kish and Nineveh in Iraq. Archaeometry 17:25–43
Hill DV (2006) The materials and technology of glazed ceramics from the Deh Luran Plain, Southwestern Iran: a study in innovation. BAR International Series.
Hothorn T, Hornik K, van de Wiel MA, Zeileis A (2008) Implementing a class of permutation tests: the coin package. J Stat Softw 28(8):1–23 http://www.jstatsoft.org/v28/i08/
Krzywinski M, Altman N (2013) Error bars. Nat Methods 10:921–922
Maltoni S, Chinni T, Vandini M, Cirelli E, Silvestri A, Molin G (2015) Archaeological and archaeometric study of the glass finds from the ancient harbour of Classe (Ravenna- Italy): new evidence. Herit Sci 3:13–21. https://doi.org/10.1186/s40494-015-0034-5
Mason RB (2004) Shine like the sun. Lustre-painted and associated pottery from the medieval Middle East. Mazda Publishers, Costa Mesa (USA)
Mason RB, Tite MS (1997) The beginnings of tin-opacification of pottery glazes. Archaeometry 39:41–58
Matson FR (1943) Technological notes on the pottery. In: Toll N (ed) The excavations at Dura-Europus: final report IV – Pt. I Fascicle I – The green glazed pottery. Yale University Press, New Haven, pp 81–95
Matson FR (1971) A study of temperatures used in firing ancient Mesopotamian pottery. In: Brill RH (ed.) Science and Archaeology. MIT Press, Cambridge
McCarthy BE (1996) Microstructural and compositional studies of the technology and durability of ceramic glazes from Nippur, Iraq, ca. 250BC - 1450 AD. PhD Thesis, The John Hopkins University.
McCarthy B, Vandiver PB, Gibson M (1995) Innovation and continuity in the technology of Southwest Asian monochrome blue glazes. In: Vincenzini P (ed) The ceramics cultural heritage. Techna Srl, Faenza
Mirti P, Pace M, Negro Ponzi MM, Aceto M (2008) ICP-MS Analysis of glass fragments of Parthian and Sasanian epoch from Seleucia and Veh Ardasir (Central Iraq). Archaeometry 50:429–450
Oates D (1968) Studies in the ancient history of Northern Iraq. Oxford University Press for the British Academy, London
Oates D, Oates J (1959) Ain Sinu: a Roman frontier post in Northern Iraq. Iraq 21:207–242
Oksanen J, Blanchet FG, Kindt R, Legendre P, Minchin PR, O’Hara RB, Simpson GL, Solymos P, Stevens MHH, Wagner H (2015). vegan: community ecology package. R package version 2.3-2. https://CRAN.R-project.org/package=vegan (last accessed 24 December 2020)
Pace M, Bianco Prevot A, Mirti P, Venco Ricciardi R (2008) The technology of production of Sasanian glazed pottery from Veh Ardasir (Central Iraq). Archaeometry 50(4):591–605. https://doi.org/10.1111/j.1475-4754.2007.00344.x
Pawlowsky-Glahn V, Buccianti A (eds) (2011) Compositional Data Analysis: Theory and Applications. Wiley, Chichester
Paynter S (2009) Links between glazes and glass in mid-2nd millennium BC Mesopotamia and Egypt. In: Shortland AJ, Freestone I, Rehren T (eds) From mine to microscope: advances in the study of ancient technology. Oxbow Books, Oxford
Paynter S, Tite M (2001) The evolution of glazing technologies in the ancient Near East and Egypt. In: Shortland A (ed) The Social context of Technological Change, Egypt and the Near East, 1650-1550BC. Oxbow Books, Oxford
Peltenburg E (1971) Some early developments of vitreous materials. World Archaeol 3:6–12
R Core Team (2020) R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria https://www.R-project.org
Shortland AJ, Rogers N, Eremin K (2007) Trace element discriminants between Egyptian and Mesopotamian Late Bronze age glasses. J Archaeol Sci 34:781–789
Simpson S-J (1997) Early urban ceramic industries in Mesopotamia. In: Freestone I, Gaimster D (eds) Pottery in the making: world ceramic traditions. British Museum Press, London, pp 50–55
Tite MS, Freestone I, Mason R, Molera J, Vendrell-Saz M, Wood N (1998) Lead glazes in antiquity—methods of production and reasons for use. Archaeometry 40:241–260
Tite MS, McCarthy B, Paynter S (2008) Production of glazed pottery and brickwork in the Near East. In: Tite MS and Shortland AJ (eds) Production technology of faience and related early vitreous materials Oxford University School of Archaeology – Monograph 72:187-198.
Vandiver P (1983) Glass technology at the mid-second-millennium BC Hurrian site of Nuzi. JGlass Stud 25:239–247
Vandiver P (1990) Ancient glazes. Sci Am:80–87
Walton MS, Tite MS (2010) Production technology of Roman lead-glazed pottery and its continuance into Late Antiquity. Archaeometry 52:733–759
Walton MS, Shortland A, Kirk S, Degryse P (2009) Evidence for the trade of Mesopotamian and Egyptian glass to Mycenaean Greece. J Archaeol Sci 36:1496–1503
Wood JR, Hsu Y-T (2020) Recycling Roman glass to glaze Parthian pottery. Iraq 82:259–270. https://doi.org/10.1017/irq.2020.9
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of Interest
Both authors contributed equally to the study and read and approved the final manuscript. The R code and data can be found in the supplementary material and are available for use.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The original online version of this article was revised: An administrative error resulted in the original version of this paper being published with incorrect supplementary file. The correct file has now been added.
Supplementary Information
A script is provided in order to reproduce the analyses and figures in this paper in R (R Core Team 2020). The data files (.csv), the script (.R) and the functions associated with the script (.R) can be found with this paper. Instructions are given to guide the user through each part of the script.
The same data files and R script, as well as additional scripts, data files and other material can be found at the GitHub repository:
Several R packages are used, including the easyCODA package for logratio analysis (Greenacre 2018). Apart from the usual package installation in R (presently version 0.34.3 is available), the very latest version of easyCODA can be downloaded from R-Forge as follows:
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wood, J.R., Greenacre, M. Making the most of expert knowledge to analyse archaeological data: a case study on Parthian and Sasanian glazed pottery. Archaeol Anthropol Sci 13, 110 (2021). https://doi.org/10.1007/s12520-021-01341-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12520-021-01341-0