Introduction

Adult stature is one of the most prominent physical characteristics of human individuals. As a highly complex trait, it is thought to be determined by genetic factors by up to 90% (Silventoinen 2003; Lango Allen et al. 2010; Dubois et al. 2012; Wood et al. 2014), and the responsible genes are not distributed equally between populations (Turchin et al. 2012). In addition, heterosis effects are discussed based on the observation that genetically remote individuals have larger offspring (Kozieł et al. 2011), and molecular epigenetics suggest that prenatal exposure to adverse conditions can have lasting consequences for the life course (Heijmans et al. 2008; Tobi et al. 2014), while it even appears possible that poor health can be passed on to later generations (Gowland 2015). Moreover, stature can also be modified on the phenotypic level, since detrimental natural and sociocultural conditions during the growth period can cause adult stature to stay behind the genetic potential. Here, under- and malnutrition must be considered not only in respect to the qualitative lack of essential nutrients but also as net nutrition in relation to the demands of the climate and disease environment (Waterlow 1994; Silventoinen 2003). Moreover, stature is recently discussed as a biologically expressed signal on social status (Bogin et al. 2015; Hermanussen and Scheffler 2016). Not only modern but also past stature as a proxy for health and living conditions (Steckel 2008; Steckel et al. 2018) therefore represents a highly interesting field of research.

Unlike modern stature data that can be assessed from written records of stature measurements or directly from living individuals, stature in prehistory and early history must be derived from skeletal remains. Here, regarding preservation and recording quality, the number of skeletal finds allowing for direct corpse length measurement or reconstruction using the forensic Fully (Fully 1956; modified by Raxter et al. 2006) method is small beyond applicability (Formicola 1993; Ruff et al. 2012). Hence, long bone lengths or body heights estimated from them—a procedure for which a variety of formulas is available (for overviews, see, e.g., Rösing 1988; Moore and Ross 2013; Zeman et al. 2014)—are the only universally available proxies for stature. Several studies have so far used long bone lengths or stature estimations to address early body height development for various regions, especially in Old World Archaeology (e.g., Angel 1984; Bennike 1985; Jaeger et al. 1998; Koca Özer et al. 2011; Siegmund 2010; Piontek and Vančata 2012; MacIntosh et al. 2016). One first broader study on Central, Western, and Northern Europe has only appeared very recently (Ruff 2018), but leaves aside Southeastern Europe, the Mediterranean, and the Near East, which are key areas for many prehistoric socioeconomic developments.

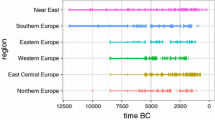
This lacuna in research hampers our understanding of the diverse effects of post-glacial developments on the stature of populations in the different regions of the Old World. Previous studies have yielded an ambiguous picture of stagnating, declining, or even rising stature during the Holocene of the Near East, the Mediterranean, Southeastern, Central, and Northern Europe (e.g., Cohen and Armelagos 1984; Larsen 1995, 2014; Mummert et al. 2011; Pinhasi and Stock 2011). Here, a supra-regional perspective can account for the individual effects in various points in time and regions in space in Old World prehistory. Moreover, it can enlighten us about the past and origins of the recent gradient in body height between NW Europe and SE Europe and the Near East (e.g., Grasgruber et al. 2014; Robinson et al. 2015; Rosenstock et al. 2015, Fig. 4 based on data by Baten and Blum 2014). While researchers in economic history have embraced this issue and have found evidence for the existence of this gradient in the early modern era, the medieval period, and antiquity using skeletal data (Köpke and Baten 2005), its very origins still remain hidden in prehistory.

The present study traces stature in Europe and the Near East further down in time to the beginning of the Holocene. Besides this content-related objective, i.e., to provide the prequel to studies into historic and modern body height variation in Europe and the Near East, the paper also has three methodological aims. It sets out to assess whether body heights estimated by one formula can at all represent a suitable means of aggregating long bone lengths into a proxy for supra-regional comparisons given reservations regarding, for instance, possible limb proportion differences between populations (Ruff et al. 2012). Moreover, it tests the potential of Bayesian errors-in-variables modeling (Konigsberg and Frankenberg 2013; Groß 2016) as a new approach to overcome problems associated with the patchy distribution of data in space and time, as well as the often-inexact and fragmentary archaeological skeletal data. In many regions, only very few sites and individuals document certain periods: the skeletons from the Iron Gates region, for instance, represent the only Mesolithic dataset for the entire area of Southeastern Europe (Supplement 1) and consequently have a disproportionate influence on every study in this region (e.g., Macintosh et al. 2016; Rosenstock and Scheibner 2018). Such effects can be alleviated by allowing preceding and subsequent data to contribute information on a certain region and period in a Bayesian approach. Moreover, especially in archaeological datasets including material excavated and published many decades ago, dating intervals and poorly sexed individuals frequently force conventional unmodeled analyses to make questionable classifications and even omissions. While a radiocarbon date range of 6100–5900 cal BC, for instance, would require a skeleton to be quite arbitrarily sorted into either a late 7th or an early 6th millennium time slot (Nakoinz 2012), missing pelvis and skull bones would cause it to be dropped from analyses entirely. Here, we present how treating date and sex as well as the occasional bone mismeasurement as errors-in-variables can provide a possible solution to make use of all existing data.

Material and methods

Skeletal data

Skeletal data for this study is based on two major older anthropometric data collections, the “Mainzer Lochkartenarchiv für postkraniales Skelettmaterial” (Perscheid 1974) and the ADAM data bank hosted in Geneva (Bertato et al. 2003), which were integrated into a larger database as well as corrected and supplemented by additions from recent literature (Ebert et al.  forthcoming) . From this collection, two samples A and B were extracted from the new database, and sample A serves as the source for four long bone and three stature models, whereas sample B serves as the source for four stature models with several variants (Fig. 1). Both samples A and B (Supplement 1; see also Rosenstock et al., forthcoming) were drawn according to the following criteria:

  1. 1.

    individual age group according to Szilvássy (1988) must be adult, mature or senile to ensure the closure of epiphyseal gaps and therefore accomplishment of adult stature

  2. 2.

    geographical location coordinates of the entry are checked and updated to a precision of two digits after decimal point (decimal World Geodetic System 1984 (WGS84) coordinates) provided by tools such as Google Maps and Google Earth

  3. 3.

    archaeological and/or absolute date of the entries is checked and updated according to current state of knowledge

  4. 4.

    archaeological dating span of the entry starts after the last glacial maximum, i.e., at 22000 BC (Clark et al. 2009), and ends before 1 BC to allow for enough data to “buffer” the modeling before 10,000 BC and 1000 BC as the start and end dates of this study.

Fig. 1
figure 1

Samples and estimation methods underlying the ten models including variants run for this paper. Models discussed and illustrated in the text are highlighted; all others can be found in Supplement 5

Full size image

Among the alternative long bone length measurements defined by Martin (1928) given in the literature (Table 1), F1, T1, H1, and R1 were the most frequent lengths for the femur, tibia, humerus, and radius, respectively. Hence, sample A requires as criterion

  1. 5.

    that at least one of these long bone lengths, i.e., F1, T1, H1, or R1, is available per entry

Table 1 Alternative long bone lengths measurements and their abbreviations according to Martin (1928) and Siegmund (2010) as well as -- in the case of Tx—Pearson (1899) and Raxter et al. (2006)
Full size table

Consisting of 2107 F1 and 1358 T1 measurements for the lower limbs as well as 1622 H1 and 1281 R1 measurements for the upper limbs from 454 sites, sample A is small but very strict concerning data quality. The data is derived from a total of 3228 individuals aggregated into 2828 entries, as for a number of sites not individual, but mean long bone lengths were published. For sample B, criterion

  1. 5.

    is broader, also including the alternative long bone measurements F2, T1b, T1a, H2, and R1b as well as entries where only stature estimates are available.

Based on 6098 individuals in 4466 datasets from 715 locations, B is a maximum sample; however, several interpolations were necessary to operationalize this data for modeling (see below for details). It is also important to note that stature estimates from sample A are significantly lower than stature estimates from sample B (Fig. 2). As this is irrespective of the estimation method (for details, see below) we used, it is likely the result of more data from times and regions with taller stature, as simple t tests revealed highly significant differences between the two samples (average differences B-A: 8.1° longitude, − 2.6° latitude, 453 years). Additionally, published ready-made stature estimations might be biased towards taller estimations in sample B.

Fig. 2
figure 2

Estimated density of F1 and T1 (upper row) as well as stature from skeletal sample A and stature from skeletal sample B, according to our own OLS method based on the Ruff 2018 dataset (lower row)

Full size image

Keeping in mind that the archaeological record is always only a fraction of the past facts, the spatiotemporal distribution of sample B (Figs. 3 and 4) shows a general preponderance of skeletal data in Southeastern and Central Europe. The sparsity of data from Northern Europe is in the first place a result of unfavorable environmental preservation conditions with acidic soils often causing bone to disintegrate at a fast pace (Nielsen-Marsh et al. 2007). The remaining patterning, however, is most likely rooted in either cultural habits of the past populations or recent research bias. Collective burial customs in the 5th and 4th millennia in Western and Northern Europe led to the disruption of anatomical articulation and mixing of bones so that they could not be assigned to individuals. As another example, cremation in the Urnfield Culture around 1000 BC caused bone distortion and fragmentation beyond any possibility of obtaining a long bone measurement. In, e.g., the Copper and Bronze Ages of the Near East, however, skeletal remains were not routinely studied for bone metrics, as anthropological research has focused more on pathological aspects (Rosenstock 2015, p. 39).

Fig. 3
figure 3

Spatial distribution and dates of the skeletal data sample B used in this paper

Full size image
Fig. 4
figure 4

Spatial distribution and frequency of skeletal data sample B used in this paper

Full size image

Operationalization of long bone lengths and stature estimations

We operationalized long bone lengths and stature data in a three-stage approach: first, unmodified bone lengths from sample A (models A_F, A_T, A_H, and A_R); then, stature derived from these lengths (models A_Pearson, A_Ruff_RMA_46, A_Ruff_OLS_N, A_Ruff_OLS_S, A_Ruff_OLS_46) and finally, stature derived from alternative lengths and estimated stature based on sample B (models B_Pearson, B_Ruff_RMA_46, B_Ruff_OLS_N, B_Ruff_OLS_S, B_Ruff_OLS_46; for an overview of models, see Fig. 1). This is advisable, as correction factors as well as stature estimation formulas are all based on samples with their own allometric traits that may not be the same as those of the prehistoric populations which, in turn, very likely exhibited their own specific variance (Rösing 1988; Ruff et al. 2012).

Although the definitional conventions codified by Rudolf Martin (1928) generally make for a well-comparable sample of long bone lengths, occasional mismeasurements are to be expected. These, however, likely do not create problems given the small differences of a few mm (Rösing 1988, p. 595, Tab. 81) between the alternative measurements (Siegmund 2010, p. 27–33). The same is true of differences between left and right side of the body, which were deemed too small, insignificant, and unsystematic to be accounted for (Trotter and Gleser 1952, p. 512; Rösing 1988, p. 589; Auerbach and Ruff 2006; Siegmund 2012, p. 28; cf. Pearson 1899). Rather, the mean value from left- and right-side measurements was used if available or calculable. If only left- or right-side measurements or no information on the side was available, these were used unmodified.

Various methods have been proposed for stature estimation from long bones, including linear (ordinary) least squares (OLS) regression (e.g., Pearson 1899), (reduced) major axis regression (RMA) (e.g., Sjøvold 1990; Ruff et al. 2012), calibration (Konigsberg et al. 1998), or piecewise linear regression (Duyar and Pelin 2003). Whether OLS and RMA is preferable for stature estimation is yet an unsettled issue (e.g., Warton et al. 2006; Smith 2009), and, moreover, only some formula sets include at least four long bones as well as female and male formulas. Here, we therefore apply three basic methods to our two samples (Fig. 1): the OLS formulas developed by Pearson (1899), the RMA formulas developed by Ruff et al. (2012), and newly developed OLS formulas we derived from the dataset underlying the Ruff et al. 2012 formulas. For the Pearson method (Table 2), we approximated the non-standard measurement Tx used by Pearson (Pearson 1899; see also Trotter and Gleser 1952 and Supplement 2) by T1 (Siegmund 2010). To follow Pearson as strictly as possible (Pearson 1899; Siegmund 2010, p. 7; Siegmund 2012; but cf. Moore and Ross 2013, p. 158), all available bones for each individual were used for calculation with their respective formulas, and from these intermediate estimations, the arithmetic mean was calculated as the final estimation. As the sample underlying Pearson (1899) is a modern Western European one, whereas that underlying Ruff et al. 2012 is prehistoric and covers a larger region, the RMA formulas developed by Ruff et al. 2012 (Table 3) were also used. For this, we approximated T1a by T1 using  the constants published by Pearson (1899, p. 197) for the conversion of T1a into Tx (Table 4). However, since we agree with Smith (2009) that OLS, not RMA, is the method of choice for stature estimation from long bone lengths, we generated new OLS formulas from the dataset underlying the Ruff et al. 2012 formula (published online as a supplement to Ruff 2018 on https://www.hopkinsmedicine.org/fae/CBR.html) and used them accordingly (Table 5).

Table 2 Formulas by Pearson (1899) for the estimation of stature from dry long bones
Full size table
Table 3 RMA regression formulas for the estimation of stature (S) from femur, tibia, humerus, and radius published by Ruff et al. 2012
Full size table
Table 4 Correction constants for conversion of long bone length measurements used for this study according to Pearson (1899, 196f) and Rösing (1988, p. 589, 595 Tab. 81)
Full size table
Table 5 OLS regression formulas for the estimation of stature (S) from femur, tibia, humerus, and radius derived from the Ruff 2018 dataset (available as an Excel file on https://www.hopkinsmedicine.org/fae/CBR.html) as an alternative to the Ruff et al. 2012 formula set. Numbers of underlying skeletons are given in parentheses
Full size table

For models A_F, A_T, A_H and A_R, F1, T1, H1, and R1 from sample A were used unmodified to separately model the spatiotemporal development of each long bone length. Comparing the resulting models opens the possibility to identify eventual discordant trends among the individual long bones as an indicator for proportion changes that might disrupt comparisons of estimated stature through space and time (Piontek and Vančata 2012; Ruff et al. 2012).

Models A_Pearson and A_Ruff_RMA_46 as well as A_Ruff_OLS_N, A_Ruff_OLS_S, and A_Ruff_OLS_46 are based on stature estimates derived from these long bone lengths. For model A_Pearson on stature estimated according to the Pearson (1899) method, we used all maximum bone lengths unmodified. For models A_Ruff_RMA_46 as well as A_Ruff_OLS_N, A_Ruff_OLS_S, and A_Ruff_OLS_46 on stature estimated according to the Ruff et al. (2012) RMA method and our OLS method based on the Ruff (2018) dataset, we used F1, H1, and R1 unmodified and converted T1 into T1a according to Pearson (1899, 196f) (Table 3). As Ruff et al. (2012) found evidence that the length ratio of femur and tibia differs between populations from northern and southern latitudes, they developed specific N and S formulas for the femur and tibia in combination and tibia alone. We interpreted the cutoff between the two sets, i.e., roughly the alps according to Ruff et al. (2012), as a 46° N latitude cutoff for our model A_Ruff_RMA_46. As the latitude of the alps is maybe not a criterion applicable to the Eastern European populations covered by our study, we ran three model variants for our own OLS regressions, using 46° N latitude as the cutoff as well as using exclusively the N and S formulas, respectively. Following Niskanen and Ruff (2018), we preferred the combined femur and tibia formulas where both bones were available and prioritized single bones in the following order: femur, tibia, humerus, and radius. On the one hand, the respective performance of these three models can be compared to the trends from models A_F, A_T, A_H, and A_R, and on the other hand, they serve as crosschecks for the more daring models based on stature estimated also on alternative long bone lengths and estimated body heights from sample B.

For models B_Pearson and B_Ruff_RMA_46 as well as B_Ruff_OLS_N, B_Ruff_OLS_S, and B_Ruff_OLS_46, the additional alternative measurements F2, T1a, T1b, H2, and R1b were converted into F1, T1, H1, and R1 using conversion constants (Table 3) published by Pearson (1899, 196f) and Rösing (1988, p. 589, 595 Tab. 81). Additionally, entries with estimated statures only according to various methods (see Supplement 3 for details) were also considered. If stature had been calculated with the Pearson (1899) method or derived from Manouvrier’s (1892) tables, the unmodified figure was used (597 cases) for model B_Pearson on the Pearson (1899) method. For cases where estimates based on another estimation formula set containing femur-based formulas were available (4575 cases), we converted these estimates into Pearson estimates following Köpke (Köpke 2008; Köpke and Baten 2005): as the best predictor of stature, “virtual” femur length was calculated by rearranging the respective femur formula (Table 6). If the formula entailed F2, the result was converted into F1 using conversion constants (Table 3). The resulting virtual F1 was then entered into the Pearson F1 formulas. For model B_Ruff_RMA_46 based on the Ruff et al. (2012) regressions, estimates according to this formula were used unmodified (140 cases), and the remaining 5961 cases were converted via the virtual femur length. For models B_Ruff_OLS_N, B_Ruff_OLS_S, and B_Ruff_OLS_46 based on our own OLS regressions on the Ruff 2018 data, all estimates were transformed accordingly. In the altogether 1477 cases where the formula set used did not contain a femur formula (e.g., Duyar and Pelin 2003 for tibia only) or the formula was unknown or where stature was measured from in situ or skeletal length, unmodified stature information was used but given minimal weight in the models.

  1. 1.

    F1 or T1 present (n = 2555): To weigh the resulting body heights in the models A_Pearson and A_Ruff_RMA_46 as well as A_Ruff_OLS_N, A_Ruff_OLS_S, and A_Ruff_OLS_46, two reliability categories were defined according to the presence of lower limb bones as better predictors of height (number of individuals in parentheses)

  2. 2.

    Only R1 or H1 present (n = 1974)

Table 6 Formulas used for obtaining a “virtual” femur from calculated stature information
Full size table

For models B_Pearson and B_Ruff_RMA_46 as well as B_Ruff_OLS_N, B_Ruff_OLS_S, and B_Ruff_OLS_46, data was weighted according to the error variance of the residuals

  1. 1.

    F1 or T1 present (n = 2555)

  2. 2.

    R1 or H1 present (n = 1974)

  3. 3.

    Alternative long bone measures present (n = 1051)

  4. 4.

    Only stature  is known, but derived from known formula (n = 2860)

  5. 5.

    Only stature is known, derived from unknown formula, in situ or skeletal length (n = 432)

For each of these five reliability categories, a different error term is estimated by our Bayesian regression model and the inverse error variance is used as the statistical weight, resulting in considerably lower weighting for categories 4 and 5 (see below for details).

The application of the formulas for females or males, respectively, demands knowledge of the sex of the skeleton. However, depending on the preservation of the skeletons, sex can often only be assessed with some degree of uncertainty and is therefore usually expressed in a five-part scale (“female,” “likely female,” “uncertain,” “likely male,” “male”: Sjøvold 1988). Similar “fuzziness” is inherent to other attributes of our sample, such as the archaeological dating spans of the skeletons that are caused by the circulation times of artifacts used for relative dating or by the probabilistic nature of absolute dating methods. Hence, from a statistical point of view, sex and date are not available directly, but only with measurement error and are therefore implemented as variables in a Bayesian errors-in-variables model.

Spatiotemporal Bayesian errors-in variables modeling

So far, “fuzzyness” in archaeological data has usually been dealt with during data entry rather than by analytical calculations. Koepke and Baten (Köpke and Baten 2005), for instance, have reduced the usual five-part sexing scale (Sjøvold 1988) to a two-part scale, controlled for insecure determinations and excluded individuals with undetermined sex. Nakoinz (2012) has proposed entering probability information to archaeological dating slots in databanks, and Siegmund (2010) and Ruff et al. (2018) resorted to assigning their data to very broad chronological units such as Mesolithic, Neolithic, and Bronze Age. These span several millennia and prevent proper integration of the results with our knowledge on prehistoric processes, which are often datable with much higher resolution. Our study, in contrast, treats such insecurities as errors-in-variables, since the underlying measurement error processes are known. Moreover, archaeological data is typically distributed unequally in space and time, a situation that can be counteracted by Bayesian modeling, as it is able to complement missing data by extrapolating from prior information (Konigsberg and Frankenberg 2013).

Here, a Bayesian additive mixed model with errors-in variables is used (Fig. 5; see also Groß 2016 for more details). The dependent variable body height is assumed to follow a normal distribution and is modeled using the spatial  variables longitude and latitude, the dating interval given as upper (Time +) and lower (Time −) date limits, the sex category (Sex C.),  the   reliability category (Rel. C.) as well as site_id. The mean of stature is represented by a three-dimensional smooth function g(), depending on space (latitude and longitude), date as well as the sex of the considered individual, and a site location effect, whereas the variance is different for each reliability category. The site location effect γ is included as a so-called random effect (therefore the term “mixed model”) into the model to control for dependencies in the data within archaeological sites, such as similar genetic makeup of their population. It is modeled by a normal distribution with mean zero and variance τ, which follows an inverse gamma distribution with parameters aτ and bτ given weakly informative priors (Groß 2016). As both dating and sex are measured with uncertainty (“errors-in variables”), these must be treated as additional variables in the model as well. The true dating is a priori assumed to follow a uniform distribution with upper and lower date limits (Time+, Time−). The true sex is a variable modeled by a Bernoulli (0/1) distribution, where the parameter pC is the probability of being male and is unique for each sex category. In turn, these probabilities are modeled by a beta distribution with parameters a_Sex and b_Sex which are given informative priors with means of 0.25 (likely female), 0.50 (uncertain), and 0.75 (likely male) for the probability of being male (cf. Groß 2016 for discussion). The parameter vector β follows a normal distribution with mean zero and variance λ, whereas λ again follows an inverse gamma distribution with parameters aλ and bλ, which are given weakly informative priors (Groß 2016). Similarly, the variance of the body height also follows an inverse gamma distribution with parameters aRel. and bRel. (with weakly informative priors, again) separated by each reliability category. The computation is realized via Markov Chain-Monte Carlo (MCMC) method with a Metropolis-Hastings algorithm. To control for autocorrelation effects, four MCMCs are employed with 20,000 iterations each whereby the first 7500 samples were discarded as “burn-in” iterations. On the remaining samples, every 10th sample was used (“thinning”). To check for convergence, the Gelman-Rubin diagnostics was computed which was well below the value of 1.1 for each parameter.

Fig. 5
figure 5

Graphical representation of the spatiotemporal Bayesian errors-in-variables model based on stature, sex, and reliability category as well as space (longitude, latitude) and date (time −, time +) as variables. For details, see text and Groß 2016

Full size image

Within the resulting tempo-spatial model, we can calculate body height for every location and point in time within the study area and time, i.e. even make predictions for regions and periods poorly attested by skeletal finds by borrowing strength from adjacent areas and times. For visualization and evaluation of the results for long bone lengths and estimated body heights, two cross-sections of the spatiotemporal models were chosen:

  1. 1.

    isoline maps (or “staturescapes” in the style of “isoscapes” coined for similar approaches to isotopic data by West et al. 2008) of long bone lengths or body heights covering the entire study area for both females and males and sliced at 10000, 7500, 6000, 5000, 4000, 3000, 2000, and 1000 cal BC

  2. 2.

    long bone lengths or body heights plotted against archaeological date as line charts showing the trends for selected points in the study area. In accordance with the broad progress of Neolithization, here, we have chosen (Fig. 6) a trajectory from points in the Northern Fertile Crescent (A) and Central Anatolia (B) through the Aegean (C) (Rosenstock in press). From here, the Central Balkan Peninsula (D) and Central Europe (E) cover the Danubian branch of Neolithization, while the Italian (H) and Iberian (I) peninsulas as well as Central France (J) constitute the Mediterranean branch. Additionally, Southern Scandinavia (F), the South of the British Isles (G), and the Pontic Steppes (K) were included as regions of later Neolithization (Guilaine 2001; Schier 2009; Rasse 2014).

Fig. 6
figure 6

Exemplary points in the study area selected for the visualization of regional time trends of the models

Full size image

Results and discussion

Tempo-spatial modeling of unprocessed long bone lengths and estimated stature

By borrowing strengths from nearby times or regions where- and whenever data coverage is insufficient, the Bayesian errors-in-variables approach taken is able to produce continuous staturescapes for all ten models (Figs. 7a, b, 8a, b, 9a, b, and 10a, b), hence providing the first consistent phase maps published so far for long bone lengths and stature in the prehistory of the Old World. While unmodeled results for the respective regions (such as Angel 1984; Bennike 1985; Jaeger et al. 1998; Koca Özer et al. 2011; Siegmund 2010; Piontek and Vančata 2012; MacIntosh et al. 2016) have to either create large and hence often too general geographical and chronological categories or suffer from insufficient data in smaller classes, the alternative visualizations for selected points (Figs. 7c, 8c, 9c, and 10c) show that the models provide values with a much finer spatial and temporal resolution by finding the best trade-off between class size and data density and attenuating the effects of more distant data. The reduction of relative importance of the Iron Gates data in our model for the Central Balkans (D), for instance, leads to a significantly lower impact of the Neolithic on stature than the unmodeled data (Rosenstock and Scheibner 2018) suggests.

Fig. 7
figure 7figure 7figure 7figure 7

Model A_F: tempo-spatial variance of F1 (sample A): a females sliced by time, b males sliced by time, c females (lower red curve) and males (upper blue curve) with 90% pointwise credible intervals for the points shown in Fig. 6

Full size image
Fig. 8
figure 8figure 8figure 8figure 8

Model A_T: a tempo-spatial variance of T1 (sample A): females sliced by time, b males sliced by time, c females (lower red curve) and males (upper blue curve) with 90% pointwise credible intervals for the points shown in Fig. 6

Full size image
Fig. 9
figure 9figure 9figure 9figure 9

Model A_Ruff_OLS_46: tempo-spatial variance of stature estimated from long bones (sample A) using OLS formulas based on the Ruff 2018 dataset: a females sliced by time, b males sliced by time, c females (lower red curve) and males (upper blue curve) with 90% pointwise credible intervals for the points shown in Fig. 6

Full size image
Fig. 10
figure 10figure 10figure 10figure 10

Model B_Ruff_OLS_46: tempo-spatial variance of stature estimated from long bones and recalculated stature estimates (sample B) using OLS formulas based on the Ruff 2018 dataset: a females sliced by time, b males sliced by time, c females (lower red curve) and males (upper blue curve) with 90% pointwise credible intervals for the points shown in Fig. 6

Full size image

All ten models (Figs. 1, 7, 8, 9, and 10; Supplement 4) show that regions in the center of the study area, such as the Central Balkans (D), Central Europe (E), and Italy (H), have reasonably small uncertainty intervals, because they are “surrounded” by data. In contrast, the Fertile Crescent (A) and the Pontic Steppes (K) as well as Northern (F, G) and Western (I, J) Europe are on the fringe of the modeled area and therefore have larger uncertainty intervals. While the Atlantic forms a natural edge of data, this situation could theoretically be alleviated for the East and South of the study area by adding more data from further East and South, but for Northern Europe, not much more data is to be expected due to preservation issues. Moreover, in reading the models, it must be kept in mind that geographical boundaries such as seas, rivers, and mountain ranges and cultural thresholds, e.g., “farming frontiers” between Mesolithic and Neolithic (Guilaine 2001; Schier 2009; Rosenstock in press), are smoothed spatially. There are some approaches for hard, insurmountable frontiers (e.g., Wood et al. 2008), but modeling softer frontiers, which can be crossed albeit with some effort, gets very complicated and relies on additional researcher assumptions and was not implemented here.

Sample A consists of 2107 F1 (model A_F) and 1358 T1 (model A_T) measurements for the lower limbs (Figs. 7 and 8) as well as 1622 H1 (model A_H) and 1281 R1 (model A_R) measurements for the upper limbs (Supplement 5). In general, all four bone lengths appear to follow an East-West gradient for both sexes with longer bones in a zone stretching from Eurasia into the Eastern part of the Fertile Crescent and shorter bones towards the West of the modeled area. F1 (Fig. 7), for instance, is around 45 cm for males and 43 cm for females in the Pontic Steppes (K) throughout the whole period, but only approx. 43 cm (males) and 41 cm (females) in the mid-Holocene of the Iberian Peninsula (I). Likewise, T1 (Fig. 8) is approx. 37 cm and 34 cm in the Pontic Steppes (K) and only approx. 36 cm and 33 cm in the Iberian Peninsula (I). Bone lengths develop concordantly in almost all regions except the Fertile Crescent (A). Here, F1 declines from approx. 46 to 44 cm in males and from approx. 43 to 42 cm in females between 10,000 and 6000 BC (Fig. 7), whereas tibia length T1 remains stable at around 36 cm (males) and 34 cm (females) (Fig. 8). Humerus and radius not only behave in opposite patterns for males and females but are also at odds with the lower limb bones (Supplement 4). These inconsistencies in the Near East (A) might only be a fringe effect of lacking data further East and South (s. a.). That Western, Northern, and Eastern Europe (A, B, C, L, and K) are also likely to be subject to fringe effects in the data and do not show such inconsistencies, however, makes it more likely that the model either suffers from the low number of observations in the Near East (Figs. 3 and 4) or actually grasps a physical reality here. Through the early Holocene, bone lengths in Anatolia (B), Southern (C, H), and Southeastern Europe (D) as well as the Pontic Steppes (K) show a slight trend towards a decline. Interestingly, femur and humerus lengths stagnate in Eastern Europe, whereas tibia and humerus lengths decline. In the Iberian Peninsula (I), the overall decline in bone lengths is quite marked. In Central Europe (E), bone lengths stagnate and in Western and Northern Europe (F, G, J), they show a slight trend towards an increase. The later Holocene in most regions except the Pontic Steppes (K) is characterized by a slight increase of bone lengths.

Modeling of stature from the bone lengths of sample A yielded 2828 datasets underlying models A_Pearson and A_Ruff_RMA_46 as well as A_Ruff_OLS_N, A_Ruff_OLS_S, and A_Ruff_OLS_46. In sample B, the alternative long bone measurements account for only 72 additional stature estimates, whereas 2798 published stature estimates increase sample B significantly to 6098 individuals in 4471 datasets in models B_Pearson and B_Ruff_RMA_46 as well as B_Ruff_OLS_N, B_Ruff_OLS_S, and B_Ruff_OLS_46. For the most part, comparison of the ten generated models (Figs. 1, 6, 7, 8, 9; Supplement 4) reveals that trend differences are more profound between the two different samples A and B than between the three different estimation methods. Also, a model run on a sample taken with the same strategy as sample B and using the Pearson 1899 method, albeit with considerably less data representing the database status of some years ago (Groß 2016; Rosenstock et al. 2015, Fig. 2), the overall trends have remained the same. Despite the low statistical weight given to them, trends in the model for estimated stature data from sample B are considerably more pronounced in comparison to sample A. This effect is particularly visible in Southeastern (D), Central (D), Northern (F), and Northwestern Europe (G). Apparently, quality of the underlying data must be traded off against the quantity of the underlying data.

To implement a N and a S formula set, as in models A_Ruff_RMA_46 and B_Ruff_RMA_46 and model variants A_Ruff_OLS_46 and B_Ruff_OLS_46, or not, as in models A_Pearson and B_Pearson as well as in model variants A_Ruff_OLS_N, A_Ruff_OLS_S, B_Ruff_OLS_N, and B_Ruff_OLS_S, has some influence on the absolute values of the estimations. For instance, within sample A, the Pearson 1899 method (model A_Pearson) reveals average statures of approx. 167 cm for males and 154 cm for females in early Holocene southern Scandinavia (F), whereas the RMA (Ruff et al. 2012) and OLS variants based on the Ruff 2018 data give 165–167 cm and between 155 and 158 cm, respectively (models A_Ruff_RMA_46 vs. A_Ruff_OLS_N, A_Ruff_OLS_S, and A_Ruff_OLS_46). General trends, which we were aiming to detect with our model, however, remain robust irrespective of the method chosen. While all other models can be found in Supplement 5, we have chosen the model variants A_Ruff_OLS_46 (Fig. 9) and B_Ruff_OLS_46 (Fig. 10) on samples A and B, respectively, to base our descriptions and interpretations on. After all, our preferred stature estimation method is our modification of the Ruff et al. 2012 method with a 46° N latitude cutoff between the N and S formulas, based on OLS formulas developed from the Ruff 2018 dataset.

The general East-West gradient already visible in the individual bone data is corroborated in the stature models. In the Pontic Steppes (K), males and females were very tall throughout, whereas towards the South and West, stature was significantly shorter. In almost the entire study area, early Holocene stature stagnates or declines only slightly. In the Fertile Crescent (A) and Anatolia (B), a decrease is only visible from the 8th millennium onwards and reversed in the 5th millennium. The discordant trends for the Fertile Crescent between the individual long bones (models A_F, A_T, A_H, and A_R), however, should serve as a warning that stature estimates may not be reliable in this region. While the Aegean (C) shows stable stature, stature declines in the Balkans (D) in the 8th to 6th millennium. In Central Europe (E), stature remains stable until later prehistory brings about an increase which is especially marked in sample B, mirroring a trend also visible in the rest of Europe, which is particularly strong in Northern Europe after ca. 4000 BC (F, G). Large credible intervals indicate that the increasing stature in the early Holocene of Northern and Western Europe (F, G, J) might only be an artifact of the small sample size, but still these regions stand in contrast to Southern (H, I) Europe characterized by a decline in stature in the early Holocene. Judging from the time-slice maps of models A_Ruff_OLS_46 and B_Ruff_OLS_46 (Figs. 9a, b and 10a, b), taller heights expand from the eastern part of the studied area into the Near East as well as into Northern and Western Europe after ca. 4000 BC.

Stature variation in the context of current anthropometric, archaeogenetic, and archaeological knowledge

The tempo-spatial picture of stature variation in the Near East and Europe ca. 10,000–1000 cal BC according to our models is broadly consistent with current archaeogenetic and archaeological evidence. The existence of an East-West gradient in body height at the onset of the Holocene corresponds with evidence for several genetically distinct populations brought about by the last glacial with its severe climatic conditions (Haak et al. 2015). Longest bone lengths and tallest stature in the Pontic Steppes and the declining trend in the Iberian Peninsula already noted by Lalueza-Fox (1998) not only confirm expectations derived from a genetic study on potential body height in these regions (Mathieson et al. 2015), but also supply evidence for the validity of the Bergmann rule of larger bodies in colder climates also for humans. While the open landscapes of Eurasia might have had a greater carrying capacity for large game enabling the continuation of taller stature similar to the Paleolithic, stagnating proximal and declining distal bone lengths in Eurasia could be related to climate directly via Allen’s rule, stating that colder climates demand shorter distal limbs (Ruff et al. 2012; Niskanen et al. 2018). Formicola and Giannecchini (1999) already observed stagnating to slightly declining stature in the early Holocene of the rest of the study area, but it is unclear whether this decline is caused by selection towards smaller bodies or a stunting effect by poorer nutrition. Still, it can support the idea that the diminishing of large game resources during the post-glacial reforestation (Jochin 1980) was not sufficiently counteracted by the dietary widening towards aquatic resources within the “Broad Spectrum Revolution” (BSR; Flannery 1969; Zeder 2012; Crombé and Robinson 2014). Rising stature around what is today the Channel, as well as the southern Baltic Sea area (F, G) well fit such an explanation, as rapid land loss during the early Holocene increased access to marine resources (Gaffney et al. 2007; Harff and Lüth, 2009).

In the Near East, the BSR is further expressed as primary Neolithization during the Pre-Pottery Neolithic (PPN) ca. 10,000 to 7000 cal BC. In the Fertile Crescent, this period is characterized by stagnating stature in both models A_Ruff_OLS_46  and B_Ruff_OLS_46. This is not surprising given the broad spectrum of exploitable food resources (Scheibner 2016) and the gradual development from foraging of wild local species to tending and domestication (Zohary et al. 2012; Larson and Burger 2013). The diverging long bone length trends may point to a more complex population history than the current idea of the Fertile Crescent as core region of origin for outward dispersals suggests and puts a general caveat to stature estimates in this region, as a decline in stature is only visible after ca. 7500 BC. This pushes the onset of the long-suspected negative effects on health and stature by way of nutrition and disease load brought about by a sedentary lifestyle formerly associated with the primary Neolithization in the Near East (e.g., Cohen and Armelagos 1984; Mummert et al. 2011; Larsen 1995, 2014; cf. Hershkovitz and Gopher 2008) into a second phase foreseen by Flannery (1969, 74) and now termed “Second Neolithic Revolution.” Roughly coinciding with the onset of the Pottery Neolithic (ca. 7000–5000 BC), the Second Neolithic Revolution witnessed the development of intensive mixed farming, i.e., an intensive garden-based cultivation with full integration of animal husbandry (Bogaard 2005), ceramic vessels, and increased inter-household competition within settlements (Düring 2011, p. 122–125; Gopher 2012).

It is probably no coincidence that the “Farming Threshold” that kept the Neolithic within the Near East was breached right after the Second Neolithic Revolution (Rosenstock in press), and Secondary Neolithization carried plant cultivation and livestock keeping from its Near Eastern homeland into Southeastern and Central Europe as well as the Central and Western Mediterranean (Guilaine 2001; Schier 2009). It entailed not only the introduction of completely new foodstuffs such as cereals and pulses as well as milk products (Craig et al. 2005; Evershed et al. 2008; Salque et al. 2013; Hendy et al. 2018), but also a considerable degree of migration of early farmers (Hofmanová et al. 2016) into these regions. Nevertheless, no reflection in stature during and after the Pre- and Protosesklo cultures ca. 6500 cal BC (Perlès 2001; Reingruber 2015) is visible in the Aegean, hence contradicting an earlier (Angel 1984) and supporting a recent study (Rosenstock and Scheibner 2018) on this region using unmodeled data. Likewise, further sea-bound Neolithization across the Mediterranean into the Adriatic and Western Mediterranean instigated by the Impresso-related cultures ca. 6000 cal BC (Müller 1994; Forenbaher and Miracle 2005) did not leave a significant stature footprint. This supports that at least in coastal areas Neolithization did not lead to substantial changes in the nutritional composition of the diet (for isotopic evidence in the Aegean see Rosenstock and Scheibner 2018). Admixture of Near Eastern stature genes by means of a migration-transmitted Neolithization (Fernández et al. 2014) would probably go undetected, as at ca. 6500 BC, male and female stature in the Near East is roughly the same as in the Aegean as well as the Central and Western Mediterranean.

In the Balkans, previous studies have focused on the skeletal material from the Iron Gates region as virtually the only anthropological source for the Mesolithic in the region. As the effect of this data is moderated in the models presented here, it appears questionable if the negative impact of Secondary Neolithization in Southeastern Europe on stature at ca. 6000 BC was indeed as sharp as signaled by unmodeled data (e.g., Macintosh et al. 2016; Rosenstock and Scheibner 2018). Rather, some stature decrease already starts around ca. 7000 BC in the models, i.e., almost a millennium before the advent of the first Neolithic with the Starčevo culture. Also, the land-bound expansion of the Neolithic entailed migration (Hofmanová et al. 2016), and Near Eastern statures are shorter than those in Southeastern Europe. Moreover, a dietary shift towards lower trophic levels is observable in the isotopic record of the region at the transition of the 7th and the 6th millennia (Rosenstock and Scheibner 2018). Hence, the subtleness of impact on stature in Southeastern Europe is remarkable. Around 5500 BC, the Neolithic reaches Central Europe with the Linear Pottery Culture (Schier 2015), which has no apparent effect on stature in the models. This contradicts previous studies (e.g., Piontek and Vančata 2012; Sládek et al. 2018) which saw a decline in stature with the Neolithic. However, their findings may largely be the result of comparing mainly western Mesolithic skeletons with mainly eastern Neolithic skeletons, an effect which is alleviated in our models.

After the 4th millennium, a general trend of increasing stature is observable in almost the entire study area (Lalueza-Fox 1998; Bennike 1985; Jaeger et al. 1998; Roberts and Cox 2007; Giannecchini and Moggi-Cecchi 2008; Siegmund 2010; Koca Özer et al. 2011; Piontek and Vančata 2012; Niskanen et al. 2018), albeit very weak in the Aegean (cf. Angel 1984) and the Balkans (MacIntosh et al. 2016; Rosenstock and Scheibner 2018) and missing in Eurasia. Especially in the light of evidence for negative impacts of urbanization on biological welfare in historical periods due to the easier spread of infectious disease in densely populated communities (e.g., Köpke/Baten 2005), the rise of stature in the late Copper and Bronze Age Near East and Eastern Mediterranean is remarkable.

It must be kept in mind that the development of more stratified societies might have led to a bias towards taller individuals in the skeletal database due to social screening effects favoring taller people (Teschler-Nicola 1989). Furthermore, possible reasons for a generally increasing stature could be increasing “globalization” in later prehistory, leading to increased spatial and social mobility (Kristiansen and Larsson 2005; Vandkilde et al. 2015). Increased spatial mobility is likely to have resulted in increasingly mixed gene pools in the populations of the Old World. In such populations, heterosis effects, i.e., the observation that genetically remote individuals have larger offspring (Kozieł et al. 2011), might not only have increased stature variability but also average stature. Moreover, increased social mobility as a by-effect of social stratification is thought to be associated with stature increase due to the so-called community effect that views stature as a biologically expressed signal on social status (Bogin et al. 2015; Hermanussen and Scheffler 2016). Additionally, another change in subsistence in the Copper and Bronze Ages has recently been noted as the “Third Food Revolution” (Taylor et al. 2015). It encompassed new foods, i.e., secondary crops such as oats, rye, and broad bean and the introduction of millet and sesame from Eastern Eurasia. Dairying probably intensified (Greenfield 2015 based on ideas by Sherratt 1981), and wine, olive, and other arboriculture developed (Myles et al. 2011; Diez et al. 2015), while new methods of intensification and extensification such as ard (Mischka 2014; Kerig 2013) and swidden agriculture (Schier 2009, 2017) were established. The resulting better nutrient supply and lower workload might also have generally increased stature in the Copper and Bronze Ages (Rosenstock et al. 2015; Niskanen et al. 2018).

This general trend to increasing stature in later prehistory is superseded by a simultaneous even stronger increase in stature in Northern Europe noted earlier (Bennike 1985; Roberts and Cox 2007; Niskanen et al. 2018). After another threshold-like arrest of the Neolithic in Central Europe, the Funnel Beaker culture represents the first Neolithic farmers in Northern Europe after ca. 4000/3500 cal BC. This breaching of another major “Farming Threshold” has been termed “Tertiary Neolithization” by Wolfram Schier (2009), as it occurred only after the adoption of agricultural innovations such as the ard or swidden cultivation. Additionally, the subsequent Corded Ware culture is closely related to the Yamnaya culture of the Pontic Steppes according to archaeological (Kaiser 2010) and archaeogenetic (Haak et al. 2015) evidence and might have introduced genes for larger stature into European populations (Heyd 2017; Niskanen et al. 2018). The lack of any signal for the immigration of smaller stature from Iberia into Western and Central Europe sheds significant doubt onto the commonly held view that the Bell Beaker culture originated in the Iberian Peninsula. Rather, it is well in line with a Corded Ware-based origin in NW Europe advocated earlier for archaeological (van der Waals 1984; Jeunesse 2014) and most recently for archaeogenetic reasons (Olalde et al. 2018; Valdiosera et al. 2018). Moreover, given the somatotrophic and probably growth hormone–related effect of unfermented milk (Wiley 2012) or an assumed direct relationship between genes determining tall stature and lactase persistence (Grasgruber et al. 2014), the ability to consume raw milk beyond childhood could be another reason for increasing stature in Northern Europe. This assumes that the current prevalence of this genetically determined trait, for which first evidence is found in the Bell Beaker culture of Central Europe (Mathieson et al. 2015), can be projected back into prehistory (Gerbault 2014). The model seeking the appearance of lactose tolerance in the Starčevo culture of 6th millennium Southeastern Europe (Itan et al. 2009) lost ground as, so far, no Linear Ceramic Culture (LBK) skeleton has been tested positive for this gene (Burger et al. 2007). Consequently, the 4th to 3rd millennia have come into focus, either by postulating Northern European cultures as a possible origin of the trait (Grasgruber et al. 2014, p. 98–99) or by connecting earlier ideas locating its origin in Eastern Europe (Enattah et al. 2007) with the Yamnaya-Corded Ware migration (Vuorisalo et al. 2012). Irrespective of its exact reasons, the increase of stature in Northern Europe in the 3rd millennium cal BC appears to establish the Northwest-Southeast gradient traced down to the 1st millennium cal BC in previous studies on Iron Age and later skeletal material (Köpke and Baten 2005) and is still visible until today (e.g., Grasgruber et al. 2014; Robinson et al. 2015; Rosenstock et al. 2015, Fig. 4 based on data by Baten and Blum 2014).

Conclusions

The comparison between the models on long bone lengths (models A_F, A_T, A_H and A_R) and all models on stature estimated from them (models A_Pearson, A_Ruff_RMA_46, A_Ruff_OLS_46 ) shows broadly similar trends. This confirms that Bayesian error-in-variables modeling of stature estimated using the Pearson (1899), Ruff et al. (2012), and our own OLS estimation formulas based on the Ruff 2018 dataset, all weighted for lower vs. upper limbs, is a viable approach to aggregating long bone data into an upper-level proxy. Moreover, comparison with models derived from additionally using alternative long bone measurements and readily estimated body heights (models B_Pearson, B_Ruff_RMA_46, B_Ruff_OLS_46) shows no major inconsistencies with the other models and can hence be considered a feasible way to obtain a maximum dataset. Moreover, comparison with a picture derived earlier from a considerably smaller database (Groß 2016; see also Rosenstock et al. 2015, Fig. 2) attests to the robusticity of the picture derived by our modeling technique. One of its advantages is that it not only allows for the inclusion of larger cemeteries but can also bring data on single individuals to meaningful use. In weighing all available data according to temporal and spatial distance, it counteracts over-interpretation of larger datasets on otherwise ill-attested times and regions and allows for more dating precision than previous studies. Overall, the modeling method appears to smoothen regional and temporal variance to a degree that only robust trends become manifest, making them a rather conservative approximation to the underlying facts. While the timewise slicing of the models yields vivid “staturescapes” and facilitates the detection of possible spatial trends within a model, pointwise slicing is often more helpful to identify regional trends and differences between models.

Long-term post-glacial and environmentally driven selection for taller stature in Eurasia and shorter stature in Iberia predicted by archaeogenetics is confirmed by the actual phenotypic data. Moreover, regional stature trends might also reflect regional subsistence differences within the Broad Spectrum adaption. Here, especially previous notions about declining stature during the Primary Neolithization in the Near East have to be re-visited. The stagnation of stature during the PPN and the decline only with the Pottery Neolithic around 7500/7000 cal BC observed in the models is well in line with recent views of the Neolithic Revolution as a gradual process that only gained momentum during the late 8th and 7th millennium. Discrepancies between the long bone models presented here, however, underline the fact that the Near East is still an under-researched region in terms of both morphology and genetics of prehistoric populations. While secondary Neolithization by means of migration and acculturation might have led to some stature decline in the Balkans with the advent of the Neolithic at ca. 6000 cal BC, no effects are visible in the rest of Europe. This calls for revision of studies that identified a clearly negative impact usually based on very divergent Mesolithic vs. Neolithic datasets with an insufficient temporal resolution and rethinking of archaeological ideas about Secondary and Tertiary Neolithization as processes rather than a point in time.

From the 4th millennium onwards, increasing heights are visible in almost the entire study area. Coinciding with increasing globalization during the Copper and Bronze Ages, this phase of acceleration might be related to heterosis and community effects or an improved nutritional situation in the wake of the broadening of subsistence spectra during a possible “Third Food Revolution.” Additionally, around 3000 cal BC, Northern Europe experiences a marked increase in stature, which might reflect the immigration of genes determining taller stature from the Pontic Steppes via the Corded Ware culture. However, also other factors such as the Tertiary Neolithization of Northern Europe characterized by changing modes of production during the 4th millennium or the onset of the consumption of unfermented milk beyond childhood not earlier than the 3rd millennium cal BC must be considered. In any case, the stature increase in Later Prehistory was marked enough to establish the Northwest-Southeast gradient in European and Near Eastern stature that can be traced through Antiquity and the Medieval and Modern Period until today.