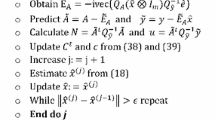Point-wise weighted solution for the similarity transformation parameters

Abstract

In the paper, we consider solutions to the similarity transformation under different adjustment scenarios. We consider asymmetric cases, i.e., random errors included either in a target system (Gauss–Markov model, the most common case) or in a source system and a symmetric case when both systems are considered to be contaminated by random errors (Gauss–Helmert or errors-in-variables model). The presented solutions are based on Procrustes approach and all cases use point-wise weighting scheme. The asymmetric cases have closed-form solutions but the symmetric one, in the most general case considered herein, does not. In the latter case, weight matrices for a source and target systems are combined into one equivalent weight matrix which depends on a scale factor. This case is solved through a simple iterative process but there are some special instances which lead to closed-form solutions. The paper discusses the behavior of transformation parameters (rotations, translations, and a scale) under different adjustment scenarios.

Introduction

Similarity transformation known also as Helmert transformation or 7-parameter transformation (4 parameters in 2D) is among the most frequently used operation in geodesy, surveying, photogrammetry, and GIS. Coordinates of source and target systems are related by a single-scale factor, three rotation angles (one rotation angle in 2D), and three translations (two translations in 2D). Usually, the problem of finding transformation parameters, in the least squares sense, is carried out by means of linearization and iterative refinement of successive approximations. In some instances, this nonlinear problem may be simplified and solved as a linear one (at least within the Gauss–Markov framework), e.g., 2D case when it may be solved through a simple substitution or 3D case (Bursa–Wolf or Molodensky–Badekas transformations) when it is simplified by the use of small rotation angles and assumption on a scale factor not much different from unity (Deakin 2006; Li et al. 2012). In this contribution, we use the Procrustes approach to solve for similarity transformation parameters in the least squares framework under Gauss–Markov and Gauss–Helmert (errors-in-variables) models. The Procrustes analysis matches one configuration of points to another configuration by using only a central (isotropic) dilation (a scale factor), rotations, and translations, i.e., the same operations as in its geodetic counterpart. The term Procrustes analysis itself first appeared in the paper by Hurley and Cattell (1962). To the best of the author’s knowledge, the first closed-form solution to the “similarity transformation” comes from Procrustean framework, from the field of Psychometrics (Schönemann 1966; Schönemann and Carroll 1970). The problem was solved as a matrix fitting algorithm (unweighted case) using the multivariate least squares framework under the Gauss–Markov model. The Procrustes analysis becomes more and more popular within the geodetic community due to Crosilla (2003) and Awange and Grafarend (2005). This contribution gives a complete solution for the similarity transformation parameters accessible within the Procrustean framework with a row-wise weighting scheme, i.e., all possibilities of error-contamination. In asymmetric cases, the error-contamination concerns either a source system or a target system, on the other hand, in symmetric case, both systems are considered to be the subject of random errors. Within asymmetric cases framework, the most often approach assumes a target system to be the source of random errors (Soler 1998; Shen et al. 2006; Sjöberg 2013). On the other hand, a less crowded path is to consider a source system to be erroneous. This instance is demonstrated in Li et al. (2013a) for the affine transformation model. Here, we also cover this case for the similarity transformation. The most general model, i.e., symmetric one, the term attributed to Teunissen (1988), solved in least squares framework and very often called a total least squares solution due to Golub and van Loan (1980) has been attracting attention for the last decades in the geodetic community. The model and its solution has been applied to geodetic problems (mainly coordinate transformations) under different assumptions by Teunissen (1988), Schaffrin and Wieser (2008), Schaffrin and Felus (2008a, 2008b), Mercan et al. (2018), Chang (2016), Neitzel (2010), and Li et al. (2013b) to mention only a few. Interesting studies on error analysis in the similarity transformation may be found in Chang et al. (2017a, 2017b). Procrustes-based approach presented herein yields attractive closed-form solutions in asymmetric cases and in certain instances of symmetric one. The derived algorithms use a modification to ensure the resulting orthogonal matrix to be a rotation one. This modification is adapted from Markley (1988), see also Umeyama (1991) and Sjöberg (2013) or for a broader exposition of the problem Myronenko and Song (2009). Markley and Mortari (1999) present a review of rotation matrix recovery algorithms in Wahba’s problem (Wahba 1965) or equivalently in orthogonal Procrustes problem (Schönemann 1966) with constraint on resulting orthogonal matrix to have determinant equal to unity (a rotation matrix not a reflection one). The solution for the symmetric case does not require linearization but it does require iteration. In the derivation process, the weight matrices in source and target systems are combined into one equivalent weight matrix—dependent on a scale factor (unfortunately). There are some special cases when it has closed-form solution. It also extends the discussion on the behavior of a rotation matrix under different adjustment scenarios.

Asymmetric cases

The first, as far as the author’s knowledge goes, closed-form solution of Helmert’s transformation parameters in unweighted case was presented by Schönemann and Carroll (1970) in the field of Psychometrics (the reason it remained unknown to geodetic society for some time). Here, we present a point-wise weighted solution of the Helmert’s transformation parameters when random errors are included either in a target system (1a) or in a source system (1b):

$$ \mathbf{P}-{\mathbf{E}}_P=s\mathbf{QR}+{\mathbf{ut}}^T $$

(1a)

$$ \mathbf{P}=s\left(\mathbf{Q}-{\mathbf{E}}_Q\right)\mathbf{R}+{\mathbf{ut}}^T $$

(1b)

where P is a matrix of coordinates in a target system (m × 2 or m × 3), Q is a matrix of coordinates in a source system (m × 2 or m × 3), E_P and E_Q are matrices of disturbances (m × 2 or m × 3), R is a proper orthogonal matrix (2 × 2 or 3 × 3), i.e., R^TR = RR^T = I and det(R) = 1, t is a translation vector (2 × 1 or 3 × 1), s is a scale factor (scalar), u is a vector of ones (m × 1), m is the number of corresponding points for both systems.

Error-affected P (target system) model

In this section, a target system is considered to be contaminated with random errors (the most usual case used in geodetic/surveying practice). As a loss function, a squared weighted Frobenius norm is used, i.e.:

$$ {}_{{\mathbf{W}}_P}{\left\Vert {\mathbf{E}}_P\right\Vert}_F^2= tr\left({\mathbf{E}}_P^T{\mathbf{W}}_P{\mathbf{E}}_P\right) $$

(2)

where W_P (m × m) is a point-wise weight matrix (a positive-definite matrix).

Inserting E_P, obtained from (1a), into (2) one obtains:

$$ {\displaystyle \begin{array}{l}\kern6.25em tr\left[{\left(\mathbf{P}-s\mathbf{QR}-{\mathbf{ut}}^T\right)}^T{\mathbf{W}}_P\left(\mathbf{P}-s\mathbf{QR}-{\mathbf{ut}}^T\right)\right]=\\ {}= tr\left(\begin{array}{l}{\mathbf{P}}^T{\mathbf{W}}_P\mathbf{P}-s{\mathbf{P}}^T{\mathbf{W}}_P\mathbf{QR}-{\mathbf{P}}^T{\mathbf{W}}_P{\mathbf{ut}}^T-s{\mathbf{R}}^T{\mathbf{Q}}^T{\mathbf{W}}_P\mathbf{P}+{s}^2{\mathbf{R}}^T{\mathbf{Q}}^T{\mathbf{W}}_P\mathbf{QR}+\\ {}+s{\mathbf{R}}^T{\mathbf{Q}}^T{\mathbf{W}}_P{\mathbf{ut}}^T-{\mathbf{tu}}^T{\mathbf{W}}_P\mathbf{P}+s{\mathbf{tu}}^T{\mathbf{W}}_P\mathbf{QR}+{\mathbf{tu}}^T{\mathbf{W}}_P{\mathbf{ut}}^T\end{array}\right)\end{array}} $$

(3)

Using properties of trace operator and taking into account that R^TR = RR^T = I, the above relation may be rewritten in the following, simpler form:

$$ {\displaystyle \begin{array}{l} tr\left({\mathbf{E}}_P^T{\mathbf{W}}_P{\mathbf{E}}_P\right)=\\ {}= tr\left({\mathbf{P}}^T{\mathbf{W}}_P\mathbf{P}-2s{\mathbf{P}}^T{\mathbf{W}}_P\mathbf{Q}\mathbf{R}-2{\mathbf{P}}^T{\mathbf{W}}_P{\mathbf{ut}}^T+2s{\mathbf{R}}^T{\mathbf{Q}}^T{\mathbf{W}}_P{\mathbf{ut}}^T+{s}^2{\mathbf{Q}}^T{\mathbf{W}}_P\mathbf{Q}+{\alpha \mathbf{tt}}^T\right)\end{array}} $$

(4)

where α = u^TW_Pu; which is minimized subject to the constraints

$$ {\mathbf{RR}}^T=\mathbf{I},\left|\mathbf{R}\right|=1 $$

(5)

By combining (4) with (5) in a Lagrange function, one obtains the following expression:

$$ {\displaystyle \begin{array}{l}\ell \left(\mathbf{R},\mathbf{t},s\right)= tr\left({\mathbf{P}}^T{\mathbf{W}}_P\mathbf{P}-2s{\mathbf{P}}^T{\mathbf{W}}_P\mathbf{Q}\mathbf{R}-2{\mathbf{P}}^T{\mathbf{W}}_P{\mathbf{ut}}^T+2s{\mathbf{R}}^T{\mathbf{Q}}^T{\mathbf{W}}_P{\mathbf{ut}}^T+{s}^2{\mathbf{Q}}^T{\mathbf{W}}_P\mathbf{Q}+{\alpha \mathbf{tt}}^T\right)+\\ {}+ tr\left[2\boldsymbol{\Lambda} \left({\mathbf{R}\mathbf{R}}^T-\mathbf{I}\right)\right]+2\lambda \left(\left|\mathbf{R}\right|-1\ \right)\end{array}} $$

(6)

where Λ and λ are Lagrange multipliers, a matrix and a scalar, respectively.

Taking partial derivatives of (6) with respect to the transformation parameters R, t, s and equating them to zero the following formulas emerge (suitable expressions for derivatives of traces and determinants may be found in, e.g., Petersen and Pedersen 2012):

$$ \frac{\partial \ell \left(\mathbf{R},\mathbf{t},s\right)}{\partial \mathbf{R}}=-2s{\mathbf{Q}}^T{\mathbf{W}}_P\mathbf{P}+2s{\mathbf{Q}}^T{\mathbf{W}}_P{\mathbf{ut}}^T+2\left({\boldsymbol{\Lambda}}^T+\boldsymbol{\Lambda} \right)\mathbf{R}+2\lambda \left|\mathbf{R}\right|\mathbf{R}=\mathbf{0} $$

(7a)

$$ \frac{\partial \ell \left(\mathbf{R},\mathbf{t},s\right)}{\partial \mathbf{t}}=2\alpha \mathbf{t}-2{\mathbf{P}}^T{\mathbf{W}}_P\mathbf{u}+2s{\mathbf{R}}^T{\mathbf{Q}}^T{\mathbf{W}}_P\mathbf{u}=\mathbf{0} $$

(7b)

$$ \frac{\partial \ell \left(\mathbf{R},\mathbf{t},s\right)}{\partial s}= tr\left(-2{\mathbf{P}}^T{\mathbf{W}}_P\mathbf{Q}\mathbf{R}+2{\mathbf{R}}^T{\mathbf{Q}}^T{\mathbf{W}}_P{\mathbf{ut}}^T+2\mathrm{s}{\mathbf{Q}}^T{\mathbf{W}}_P\mathbf{Q}\right)=0 $$

(7c)

Equation (7a) gives:

$$ {\mathrm{s}\mathbf{Q}}^T{\mathbf{W}}_P\mathbf{P}={s\mathbf{Q}}^T{\mathbf{W}}_P{\mathbf{ut}}^T+\mathbf{SR}+\lambda \mathbf{R} $$

(8)

where S = (Λ^T + Λ) is a symmetric matrix and det(R) was set to unity in (7a).

Eq. (7b) yields:

$$ \mathbf{t}=\frac{{\mathbf{P}}^T{\mathbf{W}}_P\mathbf{u}-s{\mathbf{R}}^T{\mathbf{Q}}^T{\mathbf{W}}_P\mathbf{u}}{\alpha }=\frac{{\left(\mathbf{P}-s\mathbf{QR}\right)}^T{\mathbf{W}}_P\mathbf{u}}{\alpha } $$

(9)

Inserting (9) to (7c) and rearranging terms, the scale factor may be expressed as:

$$ s=\frac{tr\left({\mathbf{R}}^T{\mathbf{Q}}^T{\mathbf{W}}_P\left(\mathbf{I}-\frac{{\mathbf{uu}}^T{\mathbf{W}}_P}{\alpha}\right)\mathbf{P}\right)}{tr\left({\mathbf{Q}}^T{\mathbf{W}}_P\left(\mathbf{I}-\frac{{\mathbf{uu}}^T{\mathbf{W}}_P}{\alpha}\right)\mathbf{Q}\right)} $$

(10)

By inserting expression for t into (8), the following formula emerges:

$$ {s\mathbf{Q}}^T{\mathbf{W}}_P\left(\mathbf{I}-\frac{1}{\alpha }{\mathbf{uu}}^T{\mathbf{W}}_P\right)\mathbf{P}=\left(\mathbf{S}+\lambda \mathbf{I}-\frac{s^2{\mathbf{Q}}^T{\mathbf{W}}_P{\mathbf{uu}}^T{\mathbf{W}}_P\mathbf{Q}}{\alpha}\right)\mathbf{R}=\mathbf{MR} $$

(11)

where the right hand side of (11) may be perceived as a polar decomposition of ${s\mathbf{Q}}^T{\mathbf{W}}_P\left(\mathbf{I}-\frac{1}{\alpha }{\mathbf{uu}}^T{\mathbf{W}}_P\right)\mathbf{P}$. This formula includes unknown scale factor s (in fact on both sides) but this does not pose a problem since uniform scaling does not change the orthogonal polar factor R (e.g., Gander 1989, 1990); hence, it is enough to find the orthogonal polar factor (restricted to det(R) = 1) of ${\mathbf{Q}}^T{\mathbf{W}}_P\left(\mathbf{I}-\frac{1}{\alpha }{\mathbf{uu}}^T{\mathbf{W}}_P\right)\mathbf{P}$ in order to obtain the solution. The polar decomposition of a matrix may be obtained, e.g., by means of singular value decomposition (SVD) which is in fact the basic tool in errors-in-variables literature. A firm review of the polar decomposition algorithms and its properties may be found in, e.g., Gander (1989, 1990), Markley and Mortari (1999), Higham (1986), and Shoemake and Duff (1992). A contribution by Higham and Noferini (2015) is especially interesting in this respect because it is dedicated to computing polar decomposition of 3 × 3 matrices (in references therein one may also find an effective algorithm for 2 × 2 matrices). Below, we summarize the derivation in a step-by-step computational algorithm.

Algorithm I

Weighted solution of Helmert transformation parameters in error-affected target system model

• 1. Prepare coordinate matrices P, Q, and a weight matrix for a target system W_P

• 2. Compute the weighted centering matrix C = W_P − W_Puu^TW_P/α, where α = u^TW_Pu and u^T = [1 1 … 1]

• 3. Compute singular value decomposition (SVD) of Q^TCP=UΣV^T and restore the rotation matrix as R = Udiag[1 1 det(U)det(V)]V^T see, e.g., Markley (1988), Umeyama (1991)

• 4. Compute the scale factor as $s=\frac{tr\left({\mathbf{R}}^T{\mathbf{Q}}^T\mathbf{CP}\right)}{tr\left({\mathbf{Q}}^T\mathbf{CQ}\right)}$

• 5. Compute the translation vector $\mathbf{t}=\frac{{\left(\mathbf{P}-s\mathbf{QR}\right)}^T{\mathbf{W}}_P\mathbf{u}}{\alpha }$

For W_P = I, one obtains the solution presented in Schönemann and Carroll (1970).

Error-affected Q (source system) model

A corresponding derivation for the error-affected source system (Q) model will be presented in a similar manner. The general form of the cost function reads:

$$ {}_{{\mathbf{W}}_Q}{\left\Vert {\mathbf{E}}_Q\right\Vert}_{\boldsymbol{F}}^{\mathbf{2}}= tr\left({\mathbf{E}}_Q^T{\mathbf{W}}_Q{\mathbf{E}}_Q\right) $$

(12)

and takes the explicit form (after inserting the expression for E_Q obtained from (1b) and some manipulations):

$$ {\displaystyle \begin{array}{c} tr\left[{\left(\mathbf{Q}+\frac{1}{s}{\mathbf{ut}}^T{\mathbf{R}}^T-\frac{1}{s}{\mathbf{PR}}^T\right)}^T{\mathbf{W}}_Q\left(\mathbf{Q}+\frac{1}{s}{\mathbf{ut}}^T{\mathbf{R}}^T-\frac{1}{s}{\mathbf{PR}}^T\right)\right]=\\ {}= tr\left(\begin{array}{l}{\mathbf{Q}}^T{\mathbf{W}}_Q\mathbf{Q}+\frac{1}{s}{\mathbf{Q}}^T{\mathbf{W}}_Q{\mathbf{ut}}^T{\mathbf{R}}^T-\frac{1}{s}{\mathbf{Q}}^T{\mathbf{W}}_Q{\mathbf{PR}}^T+\frac{1}{s}\kern0.5em \mathbf{R}{\mathbf{tu}}^T{\mathbf{W}}_Q\mathbf{Q}+\frac{1}{s^2}\mathbf{R}{\mathbf{tu}}^T{\mathbf{W}}_Q{\mathbf{ut}}^T{\mathbf{R}}^T-\\ {}-\frac{1}{s^2}\mathbf{R}{\mathbf{tu}}^T{\mathbf{W}}_Q\mathbf{P}{\mathbf{R}}^T-\frac{1}{s}{\mathbf{R}\mathbf{P}}^T{\mathbf{W}}_Q\mathbf{Q}-\frac{1}{s^2}{\mathbf{R}\mathbf{P}}^T{\mathbf{W}}_Q{\mathbf{ut}}^T{\mathbf{R}}^T+\frac{1}{s^2}{\mathbf{R}\mathbf{P}}^T{\mathbf{W}}_Q{\mathbf{PR}}^T\end{array}\right)\end{array}} $$

(13)

where W_Q (m × m) is a point-wise weight matrix. The above expression may be rewritten in a form (by using properties of a trace operator and taking into account R^TR = RR^T = I):

$$ {\displaystyle \begin{array}{l} tr\left({\mathbf{E}}_Q^T{\mathbf{W}}_Q{\mathbf{E}}_Q\right)=\\ {}= tr\left({\mathbf{Q}}^T{\mathbf{W}}_Q\mathbf{Q}+2\frac{1}{s}{\mathbf{Q}}^T{\mathbf{W}}_Q{\mathbf{ut}}^T{\mathbf{R}}^T-2\frac{1}{s}{\mathbf{Q}}^T{\mathbf{W}}_Q{\mathbf{P}\mathbf{R}}^T+\alpha \frac{1}{s^2}{\mathbf{tt}}^T-2\frac{1}{s^2}\ {\mathbf{tu}}^T{\mathbf{W}}_Q\mathbf{P}+\frac{1}{s^2}{\mathbf{P}}^T{\mathbf{W}}_Q\mathbf{P}\right)\end{array}} $$

(14)

where α = u^TW_Qu.

The optimization process is subject to the same constraints as in the previously considered problem; namely;

$$ {\mathbf{RR}}^T=\mathbf{I},\left|\mathbf{R}\right|=1 $$

(15)

Combining (14) and (15) Lagrangian reads:

$$ {\displaystyle \begin{array}{l}\ell \left(\mathbf{R},\mathbf{t},s\right)=\\ {}= tr\left({\mathbf{Q}}^T{\mathbf{W}}_Q\mathbf{Q}+2\frac{1}{s}{\mathbf{Q}}^T{\mathbf{W}}_Q{\mathbf{ut}}^T{\mathbf{R}}^T-2\frac{1}{s}{\mathbf{Q}}^T{\mathbf{W}}_Q{\mathbf{P}\mathbf{R}}^T+\alpha \frac{1}{s^2}{\mathbf{tt}}^T-2\frac{1}{s^2}\ {\mathbf{tu}}^T{\mathbf{W}}_Q\mathbf{P}+\frac{1}{s^2}{\mathbf{P}}^T{\mathbf{W}}_Q\mathbf{P}\right)+\\ {}+ tr\left[2\boldsymbol{\Lambda} \left({\mathbf{R}\mathbf{R}}^T-\mathbf{I}\right)\right]+2\lambda \left(\left|\mathbf{R}\right|-1\ \right)\end{array}} $$

(16)

where Λ and λ are Lagrange multipliers.

Taking partial derivatives with respect to R, t, s, and equating them to zero one obtains the following formulas:

$$ \frac{\partial \ell \left(\mathbf{R},\mathbf{t},s\right)}{\partial \mathbf{R}}=-2\frac{1}{s}{\mathbf{Q}}^T{\mathbf{W}}_Q\mathbf{P}+2\frac{1}{s}{\mathbf{Q}}^T{\mathbf{W}}_Q{\mathbf{ut}}^T+2\left({\boldsymbol{\Lambda}}^T+\boldsymbol{\Lambda} \right)\mathbf{R}+2\lambda \left|\mathbf{R}\right|\mathbf{R}=\mathbf{0} $$

(17)

$$ \frac{\partial \ell \left(\mathbf{R},\mathbf{t},s\right)}{\partial \mathbf{t}}=2\frac{1}{s}{\mathbf{R}}^T{\mathbf{Q}}^T{\mathbf{W}}_Q\mathbf{u}+2\alpha \frac{1}{s^2}\mathbf{t}-2\frac{1}{s^2}{\mathbf{P}}^T{\mathbf{W}}_Q\mathbf{u}=\mathbf{0} $$

(18)

$$ {\displaystyle \begin{array}{l}\frac{\partial \ell \left(\mathbf{R},\mathbf{t},s\right)}{\partial s}=\\ {}= tr\left(-2\frac{1}{s^2}{\mathbf{R}}^T{\mathbf{Q}}^T{\mathbf{W}}_Q{\mathbf{ut}}^T+2\frac{1}{s^2}{\mathbf{Q}}^T{\mathbf{W}}_Q{\mathbf{P}\mathbf{R}}^T-\alpha \frac{2}{s^3}{\mathbf{tt}}^T+\frac{4}{s^3}{\mathbf{tu}}^T{\mathbf{W}}_Q\mathbf{P}-\frac{2}{s^3}{\mathbf{P}}^T{\mathbf{W}}_Q\mathbf{P}\right)=0\end{array}} $$

(19)

Equation (17) gives:

$$ \frac{1}{s}{\mathbf{Q}}^T{\mathbf{W}}_Q\mathbf{P}=\frac{1}{s}{\mathbf{Q}}^T{\mathbf{W}}_Q{\mathbf{ut}}^T+\mathbf{SR}+\lambda \mathbf{R} $$

(20)

where S = (Λ^T + Λ) is a symmetric matrix and |R| is set to unity in (17).

Equation (18) yields:

$$ \mathbf{t}=\frac{{\mathbf{P}}^T{\mathbf{W}}_Q\mathbf{u}-s{\mathbf{R}}^T{\mathbf{Q}}^T{\mathbf{W}}_Q\mathbf{u}}{\alpha }=\frac{{\left(\mathbf{P}-s\mathbf{QR}\right)}^T{\mathbf{W}}_Q\mathbf{u}}{\alpha } $$

(21)

Inserting (21) into (19) and rearranging terms the scale factor may be expressed as:

$$ s=\frac{tr\left({\mathbf{P}}^T{\mathbf{W}}_Q\left(\mathbf{I}-\frac{1}{\alpha }{\mathbf{uu}}^T{\mathbf{W}}_Q\right)\mathbf{P}\right)}{tr\left({\mathbf{Q}}^T{\mathbf{W}}_Q\left(\mathbf{I}-\frac{1}{\alpha }{\mathbf{uu}}^T{\mathbf{W}}_Q\right){\mathbf{P}\mathbf{R}}^T\right)} $$

(22)

By inserting expression for t into (20) the following relation emerges:

$$ \frac{1}{s}{\mathbf{Q}}^T{\mathbf{W}}_Q\left(\mathbf{I}-\frac{1}{\alpha }{\mathbf{uu}}^T{\mathbf{W}}_Q\right)\mathbf{P}=\mathbf{MR} $$

(23)

where the right hand side of (23) is again a polar decomposition of $\frac{1}{s}{\mathbf{Q}}^T{\mathbf{W}}_Q\left(\mathbf{I}-\frac{1}{\alpha }{\mathbf{uu}}^T{\mathbf{W}}_Q\right)\mathbf{P}$. Previously, this formula includes unknown scale factor s but uniform scaling does not affect the orthogonal polar factor R (e.g., Gander 1989, 1990); hence, it is enough to find the orthogonal polar factor (rotation matrix) of ${\mathbf{Q}}^T{\mathbf{W}}_Q\left(\mathbf{I}-\frac{1}{\alpha }{\mathbf{uu}}^T{\mathbf{W}}_Q\right)\mathbf{P}$.

Algorithm II

Weighted solution of Helmert transformation parameters in error-affected source system model

• 1. Prepare coordinate matrices P, Q, and a weight matrix for a source system W_Q

• 2. Compute the weighted centering matrix C = W_Q − W_Quu^TW_Q/α, where α = u^TW_Qu and u^T = [1 1 … 1]

• 3. Compute singular value decomposition (SVD) of Q^TCP=UΣV^T and restore the rotation matrix as R = Udiag[1 1 det(U)det(V)]V^T

• 4. Compute the scale factor as $s=\frac{tr\left({\mathbf{P}}^T\mathbf{CP}\right)}{tr\left({\mathbf{R}}^T{\mathbf{Q}}^T\mathbf{CP}\right)}$

• 5. Compute the translation vector $\mathbf{t}=\frac{{\left(\mathbf{P}-s\mathbf{QR}\right)}^{\boldsymbol{T}}{\mathbf{W}}_Q\mathbf{u}}{\alpha }$

Symmetric case

Error-affected Q (source system) and P (target system) model

Now, a solution for Helmert transformation parameters under errors-in-variables model will be considered in a Procrustean framework. The functional relationship may be expressed as:

$$ \mathbf{P}-{\mathbf{E}}_P=s\left(\mathbf{Q}-{\mathbf{E}}_Q\right)\mathbf{R}+{\mathbf{ut}}^T $$

(24)

In this optimization problem, we seek transformation parameters R, t, and s that minimize the following cost function:

$$ \Phi \left({\mathbf{E}}_P,{\mathbf{E}}_Q,\boldsymbol{\Lambda} \right)= tr\left({\mathbf{E}}_P^T{\mathbf{W}}_P{\mathbf{E}}_P+{\mathbf{E}}_Q^T{\mathbf{W}}_Q{\mathbf{E}}_Q\right) $$

(25)

subject to (24).

where W_P and W_Q are positive-definite weight matrices that weigh points (point-wise weighting schema) in a target and in a source system, respectively.

Combination of these two expressions gives the Lagrange function of the form:

$$ \ell \left({\mathbf{E}}_P,{\mathbf{E}}_Q,\boldsymbol{\Lambda} \right)= tr\left[{\mathbf{E}}_P^T{\mathbf{W}}_P{\mathbf{E}}_P+{\mathbf{E}}_Q^T{\mathbf{W}}_Q{\mathbf{E}}_Q+2{\boldsymbol{\Lambda}}^T\left(\mathbf{P}-{\mathbf{E}}_P-s\mathbf{QR}+s{\mathbf{E}}_Q\mathbf{R}-{\mathbf{ut}}^T\right)\right] $$

(26)

where Λ is a Lagrange multipliers matrix.

Partial derivatives of (26) with respect to disturbance matrices E_P and E_Q read:

$$ \frac{\partial \ell \left({\mathbf{E}}_P,{\mathbf{E}}_Q,\boldsymbol{\Lambda} \right)}{\partial {\mathbf{E}}_P}=2{\mathbf{W}}_P{\mathbf{E}}_P-2\boldsymbol{\Lambda} =\mathbf{0}\to {\mathbf{E}}_P={\mathbf{W}}_P^{-\mathbf{1}}\boldsymbol{\Lambda} $$

(27)

$$ \frac{\partial \ell \left({\mathbf{E}}_P,{\mathbf{E}}_{Q,}\boldsymbol{\Lambda} \right)}{\partial {\mathbf{E}}_Q}=2{\mathbf{W}}_Q{\mathbf{E}}_Q+2s\boldsymbol{\Lambda} {\mathbf{R}}^T=\mathbf{0}\to {\mathbf{E}}_Q=-s{\mathbf{W}}_Q^{-\mathbf{1}}\boldsymbol{\Lambda} {\mathbf{R}}^T $$

(28)

Substituting these results into (24) and using the orthogonality relation R^TR = RR^T = I, one obtains:

$$ \mathbf{P}-{\mathbf{W}}_P^{-1}\boldsymbol{\Lambda} =s\mathbf{QR}+{s}^2{\mathbf{W}}_Q^{-\mathbf{1}}\boldsymbol{\Lambda} +{\mathbf{ut}}^T $$

(29)

and this further gives the expression for Λ:

$$ \boldsymbol{\Lambda} ={\left({\mathbf{W}}_P^{-1}+{s}^2{\mathbf{W}}_Q^{-1}\right)}^{-1}\left(\mathbf{P}-s\mathbf{QR}-{\mathbf{ut}}^T={\mathbf{W}}_P{\left(\mathbf{I}+{s}^2{\mathbf{W}}_Q^{-1}{\mathbf{W}}_P\right)}^{-1}\right)\left(\mathbf{P}-s\mathbf{QR}-{\mathbf{ut}}^T\right) $$

(30)

Plugging (27), (28), and then (30) into (25), one obtains the cost function expressed explicitly as a function of transformation parameters R, t, s:

$$ {\displaystyle \begin{array}{l}\Phi \left({\mathbf{E}}_P,{\mathbf{E}}_Q,\boldsymbol{\Lambda} \right)= tr\left[{\boldsymbol{\Lambda}}^T{\mathbf{W}}_P^{-1}\boldsymbol{\Lambda} +{s}^2\mathbf{R}{\boldsymbol{\Lambda}}^T{\mathbf{W}}_Q^{-1}\boldsymbol{\Lambda} {\mathbf{R}}^T\right]= tr\left[{\boldsymbol{\Lambda}}^T\left({\mathbf{W}}_P^{-1}+{s}^2{\mathbf{W}}_Q^{-1}\right)\boldsymbol{\Lambda} \right]=\\ {}= tr\left[{\left(\mathbf{P}-s\mathbf{QR}-{\mathbf{ut}}^T\right)}^T\mathbf{W}(s)\left(\mathbf{P}-s\mathbf{QR}-{\mathbf{ut}}^T\right)\right]=\Phi \left(\mathbf{R},\mathbf{t},s\right)\end{array}} $$

(31)

where $\mathbf{W}(s)={\left({\mathbf{W}}_P^{-1}+{s}^2{\mathbf{W}}_Q^{-1}\right)}^{-1}$ will be called an equivalent weight matrix.

Combining the final form of the loss function (31) with the orthogonality constraint RR^T = R^TR = I and |R| = 1, we obtain the Lagrange function to be optimized with respect to the transformation parameters:

$$ L\left(\mathbf{R},\mathbf{t},s\right)= tr\left[{\left(\mathbf{P}-s\mathbf{QR}-{\mathbf{ut}}^T\right)}^T\mathbf{W}(s)\left(\mathbf{P}-s\mathbf{QR}-{\mathbf{ut}}^T\right)\right]+ tr2{\boldsymbol{\Lambda}}_{\mathbf{R}}\left({\mathbf{R}\mathbf{R}}^{\boldsymbol{T}}-\mathbf{I}\right)+2\lambda \left(\left|\mathbf{R}\right|-1\right) $$

(32)

where Λ_R and λ are Lagrange multipliers.

Expanding the expression under the first trace operator and using its properties, we obtain the following formula:

$$ {\displaystyle \begin{array}{l}L\left(\mathbf{R},\mathbf{t},s\right)= tr\left({\mathbf{P}}^T\mathbf{W}(s)\mathbf{P}-2s{\mathbf{P}}^T\mathbf{W}(s)\mathbf{Q}\mathbf{R}-2{\mathbf{P}}^T\mathbf{W}(s){\mathbf{ut}}^T+2s{\mathbf{R}}^T{\mathbf{Q}}^T\mathbf{W}(s){\mathbf{ut}}^T+{s}^2{\mathbf{Q}}^T\mathbf{W}(s)\mathbf{Q}+\alpha {\mathbf{tt}}^T\right)+\\ {}+ tr2{\boldsymbol{\Lambda}}_{\mathbf{R}}\left({\mathbf{R}\mathbf{R}}^T-\mathbf{I}\right)+2\lambda \left(\left|\mathbf{R}\right|-1\right)\end{array}} $$

(33)

where α = u^TW(s)u

Partial derivatives with respect to the transformation parameters R, t, and s are given respectively:

$$ \frac{\partial \ell \left(\mathbf{R},\mathbf{t},s\right)}{\partial \mathbf{R}}=-2s{\mathbf{Q}}^T\mathbf{W}(s)\mathbf{P}+2s{\mathbf{Q}}^T\mathbf{W}(s){\mathbf{ut}}^T+2\left({\boldsymbol{\Lambda}}_{\mathbf{R}}^T+{\boldsymbol{\Lambda}}_{\mathbf{R}}\right)\mathbf{R}+2\lambda \left|\mathbf{R}\right|\mathbf{R}=\mathbf{0} $$

(34)

$$ \frac{\partial \ell \left(\mathbf{R},\mathbf{t},s\right)}{\partial \mathbf{t}}=2\alpha \mathbf{t}-2{\mathbf{P}}^T\mathbf{W}(s)\mathbf{u}+2s{\mathbf{R}}^T{\mathbf{Q}}^T\mathbf{W}(s)\mathbf{u}=\mathbf{0} $$

(35)

$$ {\displaystyle \begin{array}{l}\frac{\partial \ell \left(\mathbf{R},\mathbf{t},s\right)}{\mathrm{\partial s}}= tr\left[{\mathbf{P}}^T{\mathbf{W}}^{\prime }(s)\mathbf{P}\right]-2 tr\left[{\mathbf{P}}^T\mathbf{W}(s)\mathbf{Q}\mathbf{R}+s{\mathbf{P}}^T{\mathbf{W}}^{\prime }(s)\mathbf{Q}\mathbf{R}\right]-2 tr\left[{\mathbf{P}}^T{\mathbf{W}}^{\prime }(s){\mathbf{u}\mathbf{t}}^T\right]+\\ {}+2 tr\left[{\mathbf{R}}^T{\mathbf{Q}}^T\mathbf{W}(s){\mathbf{u}\mathbf{t}}^T+s{\mathbf{R}}^T{\mathbf{Q}}^T{\mathbf{W}}^{\prime }(s){\mathbf{u}}^{\boldsymbol{T}}\right]+ tr\left[2s{\mathbf{Q}}^T\mathbf{W}(s)\mathbf{Q}+{s}^2{\mathbf{Q}}^T{\mathbf{W}}^{\prime }(s)\mathbf{Q}\right]+ tr\left[{\mathbf{u}}^T{\mathbf{W}}^{\prime }(s){\mathbf{u}\mathbf{t}\mathbf{t}}^T\right]=0\end{array}} $$

(36)

From (34) we have:

$$ s{\mathbf{Q}}^T\mathbf{W}(s)\mathbf{P}=s{\mathbf{Q}}^T\mathbf{W}(s){\mathbf{ut}}^T+\mathbf{SR}+\lambda \mathbf{R} $$

(37)

where $\mathbf{S}=\left({\boldsymbol{\Lambda}}_{\mathbf{R}}^T+{\boldsymbol{\Lambda}}_{\mathbf{R}}\right)$ is a symmetric matrix and |R| in (34) was set to unity

and from (40), expression for t may be given by:

$$ \mathbf{t}=\frac{{\mathbf{P}}^T\mathbf{W}(s)\mathbf{u}-s{\mathbf{R}}^T{\mathbf{Q}}^T\mathbf{W}(s)\mathbf{u}}{\alpha }=\frac{{\left(\mathbf{P}-s\mathbf{QR}\right)}^T\mathbf{W}(s)\mathbf{u}}{\alpha } $$

(38)

By inserting the above expression for t into (42) we obtain:

$$ s{\mathbf{Q}}^T\mathbf{W}(s)\left(\mathbf{I}-\frac{1}{\alpha }{\mathbf{uu}}^T\mathbf{W}(s)\right)\mathbf{P}=\left(\mathbf{S}+\lambda \mathbf{I}-\frac{s^2{\mathbf{Q}}^T\mathbf{W}(s){\mathbf{uu}}^T\mathbf{W}(s)\mathbf{Q}}{\alpha}\right)\mathbf{R}=\mathbf{MR} $$

(39)

As in all previous cases, the solution for a rotation matrix has a form of the polar decomposition of $s{\mathbf{Q}}^T\mathbf{W}(s)\left(\mathbf{I}-\frac{1}{\alpha }{\mathbf{uu}}^T\mathbf{W}(s)\right)\mathbf{P}$. This expression, in fact, is dependent on scale factor as a multiplier and through the equivalent weight matrix being a function of scale factor too. Relying on the property of the polar decomposition that the uniform scaling does not affect the orthogonal polar factor R, the left hand side of (39) may be reduced to ${\mathbf{Q}}^T\mathbf{W}(s)\left(\mathbf{I}-\frac{1}{\alpha }{\mathbf{uu}}^T\mathbf{W}(s)\right)\mathbf{P}$. This expression is still dependent on the unknown scale factor s, thus the entire solution for transformation parameters will require an iterative approach.

An expression for a scale factor is obtained by collecting and rearranging terms in (36) what gives a quadratic equation:

$$ {as}^2+ bs+c=0 $$

(40)

where

$$ a= tr\left[{\mathbf{Q}}^T{\mathbf{W}}^{\prime }(s)\mathbf{Q}\right] $$

(41)

$$ b=2 tr\left[{\mathbf{R}}^T{\mathbf{Q}}^T{\mathbf{W}}^{\prime }(s){\mathbf{ut}}^T\right]+2 tr\left[{\mathbf{Q}}^T\mathbf{W}(s)\mathbf{Q}\right]-2 tr\left[{\mathbf{P}}^T{\mathbf{W}}^{\prime }(s)\mathbf{Q}\mathbf{R}\right] $$

(42)

$$ c= tr\left[{\mathbf{P}}^T{\mathbf{W}}^{\prime }(s)\mathbf{P}\right]-2 tr\left[{\mathbf{P}}^T\mathbf{W}(s)\mathbf{QR}\right]-2 tr\left[{\mathbf{P}}^T{\mathbf{W}}^{\prime }(s){\mathbf{u}\mathbf{t}}^T\right]+2 tr\left[{\mathbf{R}}^T{\mathbf{Q}}^T\mathbf{W}(s){\mathbf{u}\mathbf{t}}^T\right]+ tr\left[{\mathbf{u}}^T{\mathbf{W}}^{\prime }(s){\mathbf{u}\mathbf{t}\mathbf{t}}^T\right] $$

(43)

where ${\mathbf{W}}^{\prime }(s)=-2s{\left({\mathbf{W}}_P^{-1}+{s}^2{\mathbf{W}}_Q^{-1}\right)}^{-1}{\mathbf{W}}_Q^{-1}{\left({\mathbf{W}}_P^{-1}+{s}^2{\mathbf{W}}_Q^{-1}\right)}^{-1}$

Dependence of the equivalent weight matrix W(s) on the scale factor makes the solution a bit troublesome but fortunately, it does not require linearization but only iteration. Hence, the above formulas may be summarized and cast into the following iterative scheme.

Algorithm III

Weighted solution of Helmert transformation parameters for the symmetric case

• 1. Prepare coordinate matrices P, Q, and weight matrices W_P and W_Q

• 2. Find an approximate solution for R, t, and s using, e.g., Algorithm I

• 3. Update s by solving (40)

• 4. Compute the weighted centering matrix C = W(s) − W(s)uu^TW(s)/α, where α = u^TW(s)u and u = [1 1 … 1]

• 5. Compute SVD of Q^TCP=UΣV^T and restore the rotation matrix R = Udiag[1 1 det(U)det(V)]V^T or use any suitable algorithm restoring the orthogonal polar factor in the polar decomposition

• 6. Compute the translation vector $\mathbf{t}=\frac{{\left(\mathbf{P}-s\mathbf{QR}\right)}^T\mathbf{W}(s)\mathbf{u}}{\alpha }$

• 7. Return to step 3 and iterate until stopping criteria are met

It is easily verifiable that in case of W_P = W_Q = W (equally weighted points in both systems, not necessarily W = I) the equivalent weight matrix takes the form:

$$ \mathbf{W}(s)={\left({\mathbf{W}}^{-1}+{s}^2{\mathbf{W}}^{-1}\right)}^{-1}={\left[\left(1+{s}^2\right){\mathbf{W}}^{-1}\right]}^{-1}=\frac{1}{1+{s}^2}\mathbf{W} $$

(44)

what gives the objective function, counterpart of (31), of the form:

$$ \Phi \left(\mathbf{R},\mathbf{t},s\right)=\frac{1}{1+{s}^2} tr\left[{\left(\mathbf{P}-s\mathbf{QR}-{\mathbf{ut}}^T\right)}^T\mathbf{W}\left(\mathbf{P}-s\mathbf{QR}-{\mathbf{ut}}^T\right)\right] $$

(45)

If the weight matrix W is taken to be a scalar multiple of an identity matrix (particular case of 44) i.e., W = kI, then the cost function is given by:

$$ \Phi \left(\mathbf{R},\mathbf{t},s\right)=\frac{k}{1+{s}^2} tr\left[{\left(\mathbf{P}-s\mathbf{QR}-{\mathbf{ut}}^T\right)}^T{\left(\mathbf{P}-s\mathbf{QR}-{\mathbf{ut}}^T\right)}^T\right] $$

(46)

The latter expression, being a particular case of (31) or (45), gives the same loss function as given in Chang (2015) but in a more compact and comfortable matrix form.

Also, in case of ${\mathbf{W}}_P=\frac{\mathbf{1}}{k_P}\mathbf{W}$, ${\mathbf{W}}_Q=\frac{\mathbf{1}}{k_Q}\mathbf{W}$, i.e., scalar multiples of the same weight matrix W (compare Chang 2016) the equivalent weight matrix takes the form:

$$ \mathbf{W}(s)={\left({k}_P{\mathbf{W}}^{-1}+{s}^2{k}_Q{\mathbf{W}}^{-1}\right)}^{-1}={\left[\left({k}_P+{s}^2{k}_Q\right){\mathbf{W}}^{-1}\right]}^{-1}=\frac{1}{k_P+{s}^2{k}_Q}\mathbf{W} $$

(47)

and the loss function will be given as:

$$ \Phi \left(\mathbf{R},\mathbf{t},s\right)=\frac{1}{k_P+{s}^2{k}_Q} tr\left[{\left(\mathbf{P}-s\mathbf{QR}-{\mathbf{ut}}^T\right)}^T\mathbf{W}\left(\mathbf{P}-s\mathbf{QR}-{\mathbf{ut}}^T\right)\right] $$

(48)

If W is taken as a diagonal matrix, the loss function (48) is equivalent to the one presented in Chang (2016). Hence, the solution proposed here absorbs solutions presented by Chang (2015, 2016).

Discussion

Comparing final formulas for the transformation parameters (rotation, translation, and scale) in the asymmetric cases considered here, we notice that, in general, the two adjustment scenarios produce different results. If W_P ≠ W_Q, then all transformation parameters for both cases are different (compare formulas (9, 10, 11) to their counterparts (21, 22, 23)). On the other hand, if W_P = W_Q = W (not necessarily W = I) we obtain the same rotation parameter R (a rotation matrix) for these two cases but scale factors s and translations t (scale-dependent) are different. It is easy to notice that this weighting scheme leads to the full equivalence when s = 1 (a rigid body transformation—a particular case of the similarity transformation) then all transformation parameters R, s, and t in the asymmetric cases would be the same. In the most general case, if W_P ≠ W_Q, the solution for transformation parameters in the symmetric case leads to an iterative procedure (without linearization) due to the nonlinear involvement of a scale factor in the equivalent weight matrix. In this instance, it is hard to infer anything about similarities or dissimilarities to the previously mentioned asymmetric cases, but there are instances when the solution may be presented in a closed-form, i.e., when a scale factor may be unraveled from the equivalent weight matrix. Among these cases, we may list, e.g., W_P = W_Q = W; W_P = W_Q = kI; ${\mathbf{W}}_P=\frac{1}{k_P}\mathbf{W}$, ${\mathbf{W}}_Q=\frac{\mathbf{1}}{k_Q}\mathbf{W}$, . In all these cases, the cost function of type (3) is multiplied by some scalar function involving the scale factor and the equivalent weight matrix is independent of the scale factor. Hence, in these cases, one may expect the equivalence for the rotation parameter between symmetric (Gauss–Helmert) and asymmetric cases (Gauss–Markov) under the condition of the same weight matrix W. The same cannot be stated about a scale factor and translation parameter. Moreover, considering the same weighting scheme, i.e., equal weight matrices for both systems, then in the symmetric case, we will obtain the same rotation and translation parameters as in asymmetric cases for a rigid-body transformation, i.e., when s = 1.

Conclusions

We have presented closed-form and iterative solutions to the similarity transformation under various adjustment scenarios. In general, closed-form expressions, besides their elegance, may potentially give better understanding of how different factors affect the final solution. They may also serve as a reference for testing iterative methods that may turn out to be more efficient, e.g., with respect to time of execution. In this study, we have considered asymmetric cases when only one system is subject to random errors (Gauss–Markov model) and the symmetric case when both systems are contaminated by random errors (Gauss–Helmert model). To solve the stated problems, we employed multivariate Procrustes approach with point-wise weighting scheme (e.g., positional errors may be used to obtain weight matrices). The presented solutions are general and may be applied to both 2D and 3D similarity transformations without modifications. Both considered asymmetric cases lead to closed-form solutions, the symmetric one, in general, does not. The most general symmetric case considered in the paper is solved through a simple iterative procedure but there are also special instances when it has closed-form solutions. The presented solutions if not satisfactory due to the use of special weighting may be used as an initial estimate for more general weighting schemes. Step-by-step algorithms have been given for the ease of implementation. Although all derivations for restoring a rotation parameter are presented in the polar decomposition form, to obtain the latter mentioned, another factorization has been used, i.e., singular value decomposition.