Introduction

In geographic information system (GIS) medium, usually uncertain spatial features are revealed schematically. In this manner, mathematical models and simulation techniques are used in processing, analyzing, and in decision making of uncertain data (Burrough 1996). This uncertainty maybe is originated from different resources such as nature of phenomena, human knowledge, and the limitations of the meanings (Shi and Lui 2007). Despite this fact, crisp solutions are widely used in GIS for modeling the natural phenomena. These approaches impose some limitations in different disciplines such as soil science (McBratney and Odeh 1997), engineering (Kosko 1997), object-oriented modeling (Cross 2001; Jonathan et al. 2001; Ma et al. 2001), and data mining (Clementini et al. 2000). Thus, the concepts of classical set theory and crisp boundary may not be suitable for handling the uncertainty inherent in such problems (Wang et al. 1990).

The boundary, in simple words, is the outer limits of feature that is defined for better understanding and recognizing of objects. The kinds of feature boundaries depend on their material and their functional and temporal properties. Yet, other difficulties such as complexity of boundaries, large storage volume of 3D spatial data, and dynamic (spatial-temporal) entities arise. These problems caused GIS models to be more complicated and ineffective (Couclelis 1996).

There are attempts for defining topological relations between non-exact features in the literatures (Bjorke 1995; Clementini and Di Felice 1996; Cohn and Gotts 1996; Roy and Stell 2001). Many researchers believe that the difficulty lies in the selection of suitable generalization of the real world.

Leung (1987) tried to formalize the meanings of “boundary” and “core” for fuzzy regions. Other researchers (Gaal 1964; Lipschutz 1965; Schurle 1979; Ying-Ming and Mao-Kang 1997; Chang 1968) defined the boundary and interior of objects using open set concepts. Fuzzy regions were explained as a binary relation by Altman (1994). Schneider (1999) proved that Altman’s method is not acceptable, since different geometric anomalies will arise. Others (Clementini and Di Felice 1996; Clementini et al. 2000; Cohn and Gotts 1996) defined three parts for each fuzzy region which are kernel, boundary, and exterior. Zhan (1998, 2001) proposed an approximate model for fuzzy relation, using fuzzy set theory. Egenhofer and Al-Taha)1992) presented a theory for gradual changes of topological relations and proposed a measure to assess how far two relationships are different from each other. Sharif et al. (1998; Egenhofer and Herring 1991) refined the Egenhofer nine-intersection model to capture the semantics of natural language spatial terms based on the geometry of features.

Allen (1983) identified 13 topological relations between two temporal intervals. Kainz et al. (1993) investigated the topological relations from the perspective of poset and lattice theory. Randell et al. (1992) described topological relations using their Region Connection Calculus theory, which is based on logic. De Hoop et al. (1993) investigated possible relationships for 3D formal data structure. Based on the theory of fuzzy topology, Tang (2004), Tang and Kainz (2002; Tang et al. 2003), and Shi and Liu (2004) presented fuzzy topological relations between fuzzy spatial objects. Du et al. (2005a, b) work on computational methods of fuzzy topological relations, as well as a fuzzy nine-intersection model.

Fuzzy topological relations are needed to be modeled in GIS, particularly for decision making and deducing. For example, the boundaries of pollution cloud and residential area are uncertain, and we should simulate topological relations between them for deducing and deciding in a fuzzy controller based on variable condition. Therefore, in this research, our main purpose is to model 3D topological relations between two fuzzy objects A and B (3DFT). Let’s assume that 3D fuzzy object B is moving towards 3D fuzzy region A. As B gets closer to A, the relation gradually changes. Using of qualifiers like clearly, mostly, somewhat, and slightly, the topological relations between two 3D fuzzy regions can be described as clearly disjoint, somewhat disjoint, slightly touch, etc. The relation between 3D fuzzy objects can also be described by inclusion or similarity index (Bouchon-Meunier et al. 1996). These variables are entered to a knowledge-based system and analyzed using database, inference engine, and GIS tools.

The overall structure of this article is as follows. In “Definitions and concepts” section, several basic concepts of 3D fuzzy sets are presented. In “Topological relations for 3D fuzzy regions” section, 3D spatial relations are defined using binary and fuzzy concepts and the intersection matrix of Egenhofer. In addition, fuzzy relations are extracted using similarity model. In “Simulation experiment” section, decision variables and inclusion indexes are determined and entered into a knowledge-based system and deduced using a fuzzy controller. The case study in “Implementation results” section is to evaluate and demonstrate the results of the proposed method. The conclusion section outlines the final results and some possibilities for further work.

Definitions and concepts

Mathematically, point set topology can be applied as a fundamental tool for modeling crisp spatial objects in GIS. Based on this theory, each region (as A) consists of its interior (A°) and boundary (∂A). The remaining space is called exterior (Ae). The nine-intersection matrix of Egenhofer uses these concepts for defining topological relations between crisp regions. Here, we define a 3D fuzzy region based on point set theory.

Definition 1

3D fuzzy region A is characterized by its membership function as

$$ {\text{A}} = \left\{ {\left( {x,y,z} \right),{\mu_{\text{A}}}\left( {x,y,z} \right)} \right\}\;{\text{where}}\;\left( {x,y,z} \right)\;\; \in \quad {R^3}\quad {\text{and}}\;{\mu_{\text{A}}}:{R^3} \to \left[ {0,1} \right] $$
(1)

Here µ A(x, y, z) is the membership function of a set A from the points in the continues 3D space to the real numbers between 0 and 1.

Definition 2

Support of fuzzy region A, denoted by supp(A), can be defined as

$$ {\text{Supp}}\left( {\text{A}} \right) = \left\{ {\left( {x,y,z} \right),{\mu_{\text{A}}}\left( {x,y,z} \right) > 0} \right\} $$
(2)

Definition 3

α-cut of fuzzy region A, denoted by A α , will be defined as

$$ {{\text{A}}_\alpha } = \left\{ {\left( {x,y,z} \right),{\mu_{\text{A}}}\left( {x,y,z} \right) \geqslant \alpha } \right\},\;\forall \alpha \in \left[ {0,1} \right] $$
(3)

Definition 4

In fuzzy set theory, an element may have partial membership in several sets. For the fuzzy region A, the partial membership function of its interior is defined as

$$ {\mu_{{\text{A}}^\circ }}\left( {x,y,z} \right) = \left\{ {\begin{array}{*{20}{c}} {{\mu_{\text{A}}}\left( {x,y,z} \right)} \hfill & {{\text{for}}\,\left( {x,y,z} \right) \in \;{\text{supp}}\left( {\text{A}} \right)^\circ } \hfill \\ 0 \hfill & {\quad {\text{Otherwise}}} \hfill \ \end{array} } \right. $$
(4)

where supp(A)° is the interior of support A.

Definition 5

If A is considered as a fuzzy region, the partial membership function of ∂A can be defined as follows (Tarres 1997):

$$ {\mu_{\partial {\text{A}}}}\left( {x{\text{,}}y{\text{,}}z} \right) = 2\;\min \left[ {{\mu_{\text{A}}}\left( {x{\text{,}}y{\text{,}}z} \right),1 - {\mu_{\text{A}}}\left( {x{\text{,}}y{\text{,}}z} \right)} \right]. $$
(5)

This boundary is extracted based on the following conditions:

  1. (a)

    The maximum amount of min[µ A(x, y, z), 1 − µ A(x, y, z)] is 0.5 and is at ∂A.

  2. (b)

    If a point has a certain membership to interior or exterior of fuzzy region A, then \( {\mu_{\partial {\text{A}}}}\left( {x{\text{,}}y{\text{,}}z} \right) = 0 \).

  3. (c)

    The fuzzy boundary of Ae is equal to the fuzzy boundary of A°.

Definition 6

The partial membership value of Ae can be described as follows:

$$ \left\{ {\begin{array}{*{20}{c}} {{\mu_{\text{A}}}\left( {x{\text{,}}y{\text{,}}z} \right)} \hfill & {{\text{for}}\;\left( {x{\text{,}}y{\text{,}}z} \right)\; \in \;{\text{supp}}{{\left( {\text{A}} \right)}^e}} \hfill \\ {} \hfill & {{\mu_{\text{A}}}^e\left( {x{\text{,}}y{\text{,}}z} \right) = } \hfill \\ 0 \hfill & {\text{Otherwise}} \hfill \ \end{array} } \right. $$
(6)

Topological relations for 3D fuzzy regions

Egenhofer’s nine-intersection matrix (Egenhofer and Franzosa 1991) can be used for representing 3D topological relations between two simple objects.

Crisp nine-intersection matrix

In 3D space, objects can be considered as of having different dimension and, therefore, can be divided into points (P), lines (L), surfaces (S), and bodies (B). Accordingly, different kinds of relations may be defined between two spatial objects. Such relations are related to topological dimension of objects and can be denoted as R(P, L), R(L, S),…(Egenhofer and Herring 1990). The intersection between two objects depends on the space rank, topological dimension (0D, 1D, 2D, and 3D), and shape of the boundary (continuous or not). For example, two regions can not have intersection without considering their boundary.

In Fig. 1, topological elements can be defined as follows:

0DB={P1, P2, P3, P4}

0DA={P′1, P′2, P′3, P′4}

1DB={L1, L2, L3, L4, L5, L6}

1DA={L′1, L′2, L′3, L′4, L′5, L′6}

2DB={Γ1, Γ2, Γ3, Γ4}

2DA={Γ′1, Γ′2, Γ′3, Γ′4}

3DB={B}

3DA={B′}

Fig. 1
figure 1

3D topological relation between two simple objects

Full size image

Each elements of A can be related to any of the elements of B. Therefore, we could create the nine-intersection matrix and extract the number of possible relations among the 512 predicted relations. This is shown on Table 1, where the nDB denotes an n-dimension object.

Table 1 Number of possible topological relations between two simple 3D objects
Full size table

Considering Table 1, most of the relations can not be found in the real world. Using constraints and rules, real relationships can be extracted. Regarding our application, pollution cloud and residential area can be defined as two simple bodies; consequently, among all 512 states of the nine-intersection matrix, only eight are real (Egenhofer and Franzosa 1991; Fig. 2).

Fig. 2
figure 2

Topological relations between two simple 3D bodies (Egenhofer and Herring 1990)

Full size image

Therefore, nine-intersection matrix can be defined using characteristic function (χ r ) and a definite set (V9) as follows:

$$ {\text{V}}\left( {{\text{A}},{\text{B}}} \right) = \left( {\begin{array}{*{20}{c}} {{{\text{A}}^\circ } \cap {{\text{B}}^\circ }} \hfill & {{{\text{A}}^\circ } \cap \partial {\text{B}}} \hfill & {{{\text{A}}^\circ } \cap {{\text{B}}^e}} \hfill \\ {\partial {\text{A}} \cap {{\text{B}}^\circ }} \hfill & {\partial {\text{A}} \cap \partial {\text{B}}} \hfill & {\partial {\text{A}} \cap {{\text{B}}^e}} \hfill \\ {{{\text{A}}^e} \cap {{\text{B}}^\circ }} \hfill & {{{\text{A}}^e} \cap \partial {\text{B}}} \hfill & {{{\text{A}}^e} \cap {{\text{B}}^e}} \hfill \ \end{array} } \right) $$
(7)
$$ {\chi_r}(v) = \left\{ {\begin{array}{*{20}{c}} 0 \hfill & {v = 0} \hfill \\ 1 \hfill & {{\text{Otherwise}}{\text{.}}} \hfill \\ \end{array} } \right. $$
(8)

Fuzzy nine-intersection matrix

Fuzzy nine-intersection matrix (Bjorke 1995) is a generalization of the crisp nine-intersection matrix. If Fuzzy nine-intersection matrix between A and B is shown by F9, then (Yager 1982)

$$ {\mu_{{\text{F}}9}}(v) = H(v)\;{\text{for}}\;{\text{all}}\;v\; \in \;{\text{V}} $$
(9)

where H is “height” or the maximum of the intersection membership value for A and B. Then, the result will be the following notation.

$$ {\text{F}}\left( {{\text{A}},{\text{B}}} \right) = \left( {\begin{array}{*{20}{c}} {{\text{H}}\left( {{{\text{A}}^\circ } \cap {{\text{B}}^\circ }} \right)} \hfill & {{\text{H}}\left( {{{\text{A}}^\circ } \cap \partial {\text{B}}} \right)} \hfill & {{\text{H}}\left( {{{\text{A}}^\circ } \cap {{\text{B}}^e}} \right)} \hfill \\ {{\text{H}}\left( {\partial {\text{A}} \cap {{\text{B}}^\circ }} \right)} \hfill & {{\text{H}}\left( {\partial {\text{A}} \cap \partial {\text{B}}} \right)} \hfill & {{\text{H}}\left( {\partial {\text{A}} \cap {{\text{B}}^e}} \right)} \hfill \\ {{\text{H}}\left( {{{\text{A}}^e} \cap {{\text{B}}^\circ }} \right)} \hfill & {{\text{H}}\left( {{{\text{A}}^e} \cap \partial {\text{B}}} \right)} \hfill & {{\text{H}}\left( {{{\text{A}}^e} \cap {{\text{B}}^e}} \right)} \hfill \\ \end{array} } \right) $$
(10)

Since the fuzzy nine-intersection matrix is based on the interior, boundary, and exterior sets, each point of the space has associated membership values regarding A°, ∂A, and Ae. This idea of the fuzzy nine-intersection is in accordance with the fundamental principles of fuzzy sets.

Computing similarity

For any two objects having crisp and fuzzy topological relations, the type and strength of the relationships can be determined using the similarity concept. The type of relations between two objects can be described using nine-intersection matrix. To do this, it is necessary to detect the set of spatial points that certainly belong to the boundary set \( \left( {{\mu_{\partial {\text{A}}}} = 1} \right) \) (Yager 1982).

The crisp relations can be associated with a characteristic function χ r (v), where r ∈ R8 possesses the properties of fuzzy sets. Comparison between F9 and R8 can be formalized as a fuzzy relation Ф(F9, r) for all r ∈ R8. Then, the membership function \( {\mu_\Phi }\left( {{{\text{F}}_9},r} \right) \) can represent the similarity between F9 and r.

$$ {\mu_\Phi }\left( {{{\text{F}}_9},r} \right) = \gamma \left[ {\left( {{{\text{F}}_9} \wedge r} \right) \vee \left( {{\text{F}}_9^{-} \wedge {r^{-} }} \right)} \right] $$
(11)

where ∧ and ∨ show the Fuzzy minimum and maximum operators, F9− and r − are the complements of F9 and r, γ is the minimum of memberships, and µ(F9, r) demonstrates the amount of similarity between F9 and r 1, r 2, r 3, r 4, r 5, r 6, r 7, or r 8. Consequently, µ(F9, r) can determine the strength and type of 3D topological relations.

Simulation experiment

The following experiments were used as a guide in examining the properties of the presented model between 3D fuzzy regions.

Decision variables

By computing the similarity between fuzzy nine-intersection matrix and binary relations matrix, the two closest relations are selected (based on experiments results) and combined in a quad set characterized as:

$$ Q = \left\{ {q\left( {{r_i}} \right),n\left( {{r_i}} \right),q\left( {{r_j}} \right),n\left( {{r_j}} \right)} \right\} $$
(12)

In which, n(r i ) and n(r j ) are the two closest relations and are called the superior and the sub-superior relations, and q(r i ) and q(r j ) are their quantifiers. If the quantifier of the superior relation r j is “no”, only the sub-superior relation is applied.

Classifying µ Ф(F9, r) and labeling each class with a natural language term, the strength of relations will be defined using “no”, “slightly”, “somewhat”, “mostly”, and “clearly” terms.

$$ q\left( r \right) = \left\{ {\begin{array}{*{20}{c}} {\prime {\text{clearly}}\prime } \hfill & {{\text{if}}\;0.9 < {\mu _\varphi }\left( {{{\text{F}}_9}{\text{, }}r} \right)} \hfill \\ {\prime {\text{mostly}}\prime } \hfill & {{\text{if}}\;0.7 < {\mu _\varphi }\left( {{{\text{F}}_9}{\text{, }}r} \right) \leqslant 0.9} \hfill \\ {\prime {\text{somewhat}}\prime } \hfill & {{\text{if}}\;0.5 < {\mu _\varphi }\left( {{{\text{F}}_9}{\text{, }}r} \right) \leqslant 0.7} \hfill \\ {\prime {\text{slightly}}\prime } \hfill & {{\text{if}}\;0.02 < {\mu _\varphi }\left( {{{\text{F}}_9}{\text{, }}r} \right) \leqslant 0.5} \hfill \\ {\prime {\text{no}}\prime } \hfill & {{\text{if}}\;{\mu _\varphi }\left( {{{\text{F}}_9}{\text{, }}r} \right) \leqslant 0.02} \hfill \\ \end{array} } \right. $$
(13)

These classes are chosen arbitrarily. A spatial knowledge-based system is designed for alarming in a control center using decision variables and fuzzy “If–Then” rules. The center is to analyze and decide on 3D fuzzy topological relations between pollution cloud and a residential area, using a spatial knowledge-based system.

The system works online and decides when to alarm about air condition. The system is responsive to changes in the values of decision variables with respect to the conditions in the real world.

Inclusion index

Since decision variables represent only qualitative information, an inclusion measure can be defined to add quantitative information to the topological descriptions. There are several measures proposed in the literatures (Bouchon-Meunier et al. 1997; Young 1996). In this paper, we define an inclusion measure II* for fuzzy raster regions as:

$$ {\text{II*}}\left( {{\text{A}},{\text{B}}} \right) = \left| {\text{A}} \right|/\left| {{\text{B*}}} \right| $$
(14)

In which |A| and |B*| are the cardinality values for fuzzy sets A and B*, which are defined as follows:

$$ {\mu_{{\rm I}{\rm I}}}(u) = \left\{ {\begin{array}{*{20}{c}} 1 \hfill & {{\mu_{\text{B}}}(u) \geqslant {\mu_{\text{A}}}(u)} \hfill \\ 0 \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. $$
(15)
$$ {\mu_{{\text{B}}*}}(u) = \left\{ {\begin{array}{*{20}{c}} 1 \hfill & {{\mu_{\text{B}}}(u) > 0} \hfill \\ 0 \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. $$
(16)

in which u is a non-overlapped raster pixel, and II is an inclusion index calculated by Eq. 14.

Fuzzy spatial deductive system

Fuzzy spatial deductive systems work based on spatial controllers. Such systems along with proper spatial inference engines can be very useful for decision makers. Topological decision variables and quantifiers that are described conceptually can be used for recording spatial alteration in knowledge-based systems. In this regard, topological relations and decision variables should be represented as If–Then rules in a knowledge-based system. In both control theory and the theory of approximate reasoning, much of the knowledge about system behavior and system control can be stated in the form of If–Then rules. Finally, the interactive relation will be created using 3D fuzzy topology and expert knowledge (Fig. 3).

Fig. 3
figure 3

Overall view of spatial controller system

Full size image

In a spatial proposition of knowledge, a component statement can be modeled by a fuzzy set. A single spatial fuzzy IF–Then rule, which relates several components, can be regarded as a fuzzy relation. This fuzzy relation can be interpreted as the strength of relation between two fuzzy variables. Denoting the degree of memberships in fuzzy relations, they are combined using fuzzy implications by inference engines.

Inference engine can infer based on fuzzy implication operators such as Mamdani, Max–Min, Zadeh, Larson, Arithmatic, Boolean, Bonded product, Drastic product, Gogen, and Godlin. Mamdani proposed a fuzzy implication rule for fuzzy control. It is a simplified version of Zadeh (1979) operator in the form of fuzzy implication (relation (shortly R(A,B)) between the so called rule premise: x is A and rule consequence: y is B. Let x be from universe X, y from universe Y, and let x and y be linguistic variables. Fuzzy set A in X is characterized by its membership function μ. In engineering applications, the Mamdani implication is widely used and is given as:

$$ {\text{R}}\left( {{\text{A}},{\text{B}}} \right) = {\mu_{\text{A}}}(x) \wedge {\mu_{\text{B}}}(y) $$
(17)

where ∧ is fuzzy minimum operator.

The other important part of the fuzzy logic controllers is the inference mechanism. One of the widely used methods is the generalized modus ponens, in which, the inference “y is B′” is obtained.

$$ {\text{B}}\prime (y) = \vee \left( {{\text{A}}\prime (x) \wedge {{\text{R}}_{{\text{Ai\_Bi}}}}\left( {x{\text{, }}y} \right)} \right) $$
(18)

In this relation, A i (x) is the “If” part and B i (y) is the “Then” part of the rule. A′(x) is a real condition, RAi_Bi(x, y) is the Mamdani implication, and ∨ is the fuzzy supremum operator. Generally speaking, the consequence (rule output) is provided by fuzzy set B′(y), which is derived from rule consequence B(y), as a cut of the B(y).

Implementation results

The methodology is implemented using VB and Matlab programming languages. This fuzzy system models uncertainty of the input and output parameters by defining fuzzy numbers and sets as linguistic variables. Fuzzy rule-based systems are performed based on If–Then verbal rules that are overlapped through the space for handling the non-linear relations. If–Then rules, which are conditional statements, consisted of a set of conditions that are satisfied (If) and a set of consequents that can be inferred (Then).The schematic diagram of fuzzy rule-based system is shown in Fig. 5, which is composed of five operational layers including input linguistic nodes, input term nodes, rule nodes, output term nodes, and output linguistic nodes. In this structure, fuzzy linguistic node represents a fuzzy variable, term node indicates mapping degree of a fuzzy variable, and rule node demonstrates a rule that decides on severity of firing during inference. First and second layers are called premise layers, and the last two layers are called consequential layers. For more clarifying layers, they are described as follows:

Layer1

In this layer, nodes can directly transfer input values to layer2. If input vector for tth mode is I t  = (I t1, I t2,…, I tm ) with I tm input value of mth fuzzy variable for tth mode, then tth output vector of this layer will be:

$$ \begin{array}{*{20}{c}} {\mu :I \to [0,1]} \\ {\mu_{{\text{Layer}}1}^t = \left( {\left( {{I_{t11}};{I_{t12}}; \ldots; {I_{t1{n_1}}}} \right);\left( {{I_{t21}};{I_{t22}}; \ldots; {I_{t2{n_2}}}} \right); \ldots; \left( {{I_{tm1}};{I_{tm2}}; \ldots; {I_{tmn}}_{_m}} \right)} \right)} \\ \end{array} $$
(19)

where I tmk is input value of kth linguistic term in mth fuzzy variable for tth mode, and a fuzzy linguistic term is represented by membership function μ. The great advantage of these linguistic terms is that they can model what experts are actually thinking about the application.

Layer2

In layer 2, outputs of fuzzy variables are linked to the third layer’s nodes to create lawful conditions, considering some specified rules. These outputs should be obtained from linguistic nodes that are specified in fuzzy rules. Consequently, this layer carries out the first step of reasoning for calculating matching degrees of conditional nodes in the premise part of rules. So, if the input vector of this layer is \( \mu_{{\text{Layer}}1}^t \), then the output vector can be obtained as follows:

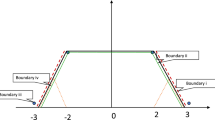
$$ \begin{array}{*{20}{c}} {\mu_{{\text{Layer}}2}^t = \left( {\left( {{{\text{M}}_{t11}};{{\text{M}}_{t12}}; \ldots; {{\text{M}}_{t1{n_1}}}} \right);\left( {{{\text{M}}_{t21}};{{\text{M}}_{t22}}; \ldots; {{\text{M}}_{t2{n_2}}}} \right); \ldots; \left( {{{\text{M}}_{tm{n_1}}};{{\text{M}}_{tm{n_2}}}; \ldots; {{\text{M}}_{tm{n_m}}}} \right)} \right)} \\ {{M_{\text{Triangular}}}(x) = \left\{ {\begin{array}{*{20}{c}} 0 & {x < {x_1}} \\ {\frac{{x - {x_1}}}{{{x_2} - {x_1}}}} & {{x_1} \leqslant x < {x_2}} \\ {\frac{{{x_3} - x}}{{{x_3} - {x_2}}}} & {{x_2} \leqslant x < {x_3}} \\ 1 & {{x_3} \leqslant x} \\ \end{array} \quad \quad {x_1} < {x_2} < {x_3}} \right.} \\ \end{array} $$
(20)

where \( {\text{M}}_{tmk}^2 \) is membership degree of kth linguistic term in mth fuzzy variable for tth mode. Membership functions can classify an input variable into varying degrees of different labels rather than “0” or “1” used in binary logic. In this paper, trapezoidal functions are used for membership functions of linguistic terms. For example, fuzzy variables of smoke persistency and wind direction are designed and introduced in the knowledge-base system.

Layer3

In this layer, each rule node represents a fuzzy If–Then rule. These 20 rules are experimentally introduced to the knowledge base as initial preconditions using expert questionnaires. In the following, calculation of matching degrees of preconditions, \( \mu_{{\text{Layer}}3}^{t - r{\text{node}}1} \), and weight of output link, \( W_{{\text{Layer}}3}^{t - r{\text{node}}1} \), is provided for rule node 1 in tth mode.

$$ \begin{array}{*{20}{c}} {\mu_{{\text{Layer}}3}^{t - r{\text{node}}1} = \min \left( {{M_{t11}}...{M_{tm{n_1}}}} \right)} \\ {W_{{\text{Layer}}3}^{t - r{\text{node}}1} = \prod\limits_{o = 1}^m {{M_{to1}}} } \\ \end{array} $$
(21)

Where, min is a fuzzy minimum operator and Π multiplies membership degrees M.

Layer4

Output fuzzy variable of fuzzy rule base is a risk value, ranging between zero and one. In Fig. 5, this output variable has been specified with five terms: “very high”, “high”, “medium”, “low”, and “very low”. Then, the output of the fourth layer can be calculated as follows:

(22)

Where C (Centroid) means the center of gravity function, which is used for defuzzyfying, and max is fuzzy maximum operator. In our case, the fuzzy reasoning method is the classical Mamdani, playing the role of the implication and conjunctive operators, and the center of gravity weighted by the matching strategy acting as defuzzification operator.

Layer5

In this layer, considering Eq. 4, y t is calculated using Eq. 5:

$$ {y_t} = \frac{{\sum\nolimits_{h = 1}^5 {{w_{th}} \times {s_{th}}} }}{{\sum\nolimits_{h = 1}^5 {{w_{th}}} }} $$
(23)

where W th is the aggregated weights of rule nodes for each output linguistic term.

The case study of Fig. 4 shows how pollution cloud A moves to residential area B and topological relations change from clearly disjoint to clearly inside. The amount of inclusion indexes which sorted in Table 2 are derived from the variation of topological relation between A and B. The means of the values for “touch/overlap” and “overlap/touch” are 0.11 and 0.32, respectively. The range of inclusion index is the broadest in overlap relationship (0.18–0.83), and the narrowest in inside and disjoint relationships.

Fig. 4
figure 4

Decision variables for pollution cloud A moves to residential area B

Full size image
Table 2 The variation of inclusion index
Full size table

The resulted system installed in the control center for online warning and making decision using fuzzy spatial knowledge-base system and entered real-time satellite data. The inputs of this system are satellite images, collected knowledge, and different GIS layers. Digital terrain model is one of the important input data for extracting relation from the map.

As shown in Fig. 5, a spatial fired rule is saved in the knowledge-base system and connected to the interface interactively.

Fig. 5
figure 5

General view of the spatial deductive system

Full size image

Conclusions

The main result of this study was to provide a spatial deductive system for modeling 3D topological relations of fuzzy spatial objects in GIS environment. The system includes a spatial knowledge-base system and is capable of making decision on dynamic 3D fuzzy features.

One significant step here was the extraction of 3D fuzzy topological relationships between two spatial regions. This can be done by computing the similarity between the 3D fuzzy nine-intersection matrix and crisp matrix. The decision variables, extracted from similarity computation, provide an intuitive, informative, and generalized description to be entered to the knowledge rules in a deductive system.

A topic for further study is to investigate how lattice theory algebra can be applied in further development of the 3D fuzzy nine-intersection.