Risk estimation of soil slope stability problems

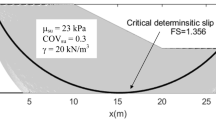
Abstract

For successful design of any real-life engineering structures, it is important to quantify the risk of failure. Most of the geotechnical engineers find it suitable to define risk mathematically in terms of well-known metric called probability of failure. The inherent spatial variability of the soil strength parameters also makes the design of soil slopes suitable for stochastic interpretations. In the present study, probabilistic slope stability analysis has been performed for both, cohesive soil as well as cohesive frictional, i.e., $c-\phi$ soil. The estimation of the factor of safety of the soil slope has been carried out using ordinary method of slices. Probabilistic analysis has been carried out using the single random variable approach with the assumption that the cohesion and angle of internal friction of soils follow lognormal distribution. The variation in soil shear strength is taken into account with the help of statistical parameter known as coefficient of variation. The effect of the coefficient of variation, the spatial correlation length, and local averaging on the probability of failure and the factor of safety has been investigated. This phenomenon indicates a gradual variation of probability of failure with respect to the factor of safety at higher coefficient of variation values. The presented analyses can be used to determine the factor of safety of a soil slope for which the slope should be designed with a predefined probability of failure.

APPENDIX

The probability of failure p_f against slope failure has been defined as the probability that the F_s value is less than 1. The derivation of the expression of p_f for different cases is shown below:

Cohesive Soil

For cohesive soil slope, the factor of safety F_s against failure is earlier mentioned in Eq. 11 and is given by

$$F_{s} = \frac{{c_{u} L_{a} R}}{Wd}.$$

(A1)

From Eq. A1, p_f is derived as follows:

$$\begin{array}{*{20}c} {p_{f} = P\left[ {F_{s} < 1} \right]} \\ { = P\left[ {\frac{{c_{u} L_{a} R}}{Wd} < 1} \right].} \\ \end{array}$$

Taking logarithm on both sides, we get

$$\begin{gathered} = P\left[ {\ln \left( {c_{u} L_{a} R} \right) - \ln \left( {Wd} \right) < 0} \right] \hfill \\ = P\left[ {ln\left( {c_{u} L_{a} R} \right) < \ln \left( {Wd} \right)} \right]. \hfill \\ \end{gathered}$$

Subtracting $\mu_{{ln\left( {c_{u} L_{a} R} \right)}}$ and dividing by $\sigma_{{ln\left( {c_{u} L_{a} R} \right)}}$ on both sides, we get

$$\begin{array}{*{20}l} { = P\left[ {\frac{{ln\left( {c_{u} L_{a} R} \right) - \mu_{{ln\left( {c_{u} L_{a} R} \right)}} }}{{\sigma_{{ln\left( {c_{u} L_{a} R} \right)}} }} < \frac{{\ln \left( {Wd} \right) - \mu_{{ln\left( {c_{u} L_{a} R} \right)}} }}{{\sigma_{{ln\left( {c_{u} L_{a} R} \right)}} }}} \right]} \hfill \\ { = P\left[ {Z < \frac{{\ln \left( {Wd} \right) - \mu_{{ln\left( {c_{u} L_{a} R} \right)}} }}{{\sigma_{{ln\left( {c_{u} L_{a} R} \right)}} }}} \right].} \hfill \\ \end{array}$$

(A2)

Cohesive Frictional Soil

In case of cohesive frictional, i.e., c – ϕ soil, different cases are considered in which soil properties such as cohesion and angle of internal friction are treated as lognormally distributed random variables. The respective expressions for factor of safety F_s against failure and the associated probability of failure are as described below.

For cohesion

In this case, the cohesion parameter is assigned lognormal distribution. The factor of safety F_s against failure is earlier mentioned in Eq. 14 and is given by

$$F_{s} = \frac{{\sum {cl} }}{{\sum {w\sin \alpha } - \sum {w\cos \alpha \tan \phi } }}.$$

(A3)

Further, the probability of failure p_f expression from A3 is derived as follows

$$\begin{array}{*{20}c} {p_{f} = P\left[ {F_{s} < 1} \right]} \\ { = P\left[ {\frac{{\sum {cl} }}{{\sum {w\sin \alpha - \sum {w\cos \alpha \tan \phi } } }} < 1} \right]} \\ { = P\left[ {\ln (\sum {cl} ) - \ln \left( {\sum {w\sin \alpha - \sum {w\cos \alpha \tan \phi } } } \right) < 0} \right]} \\ { = P\left[ {\ln (\sum {cl} ) < \ln \left( {\sum {w\sin \alpha - \sum {w\cos \alpha \tan \phi } } } \right)} \right].} \\ \end{array}$$

Subtracting $\mu_{{\ln (\sum {cl} )}}$ and dividing by $\sigma_{{\ln (\sum {cl} )}}$, we get

$$\begin{gathered} = P\left[ {\frac{{\ln (\sum {cl} ) - \mu_{{\ln (\sum {cl} )}} }}{{\sigma_{{\ln (\sum {cl} )}} }} < \frac{{\ln \left( {\sum {w\sin \alpha - \sum {w\cos \alpha \tan \phi } } } \right) - \mu_{{\ln (\sum {cl} )}} }}{{\sigma_{{\ln (\sum {cl} )}} }}} \right] \hfill \\ = P\left[ {Z < \frac{{\ln \left( {\sum {w\sin \alpha - \sum {w\cos \alpha \tan \phi } } } \right) - \mu_{{\ln (\sum {cl} )}} }}{{\sigma_{{\ln (\sum {cl} )}} }}} \right]. \hfill \\ \end{gathered}$$

(A4)

For angle of internal friction

In this case, the angle of internal friction is assigned lognormal distribution. The factor of safety F_s against failure is earlier mentioned in Eq. 15 and is given by

$$F_{s} = \frac{{\sum {w\cos \alpha \tan \phi } }}{{\sum {w\sin \alpha } - \sum {cl} }}.$$

(A5)

Further, the probability of failure p_f expression from A5 is derived as follows

$$\begin{gathered} p_{f} = P\left[ {F_{s} < 1} \right] \hfill \\ = P\left[ {\frac{{\sum {w\cos \alpha \tan \phi } }}{{\sum {w\sin \alpha - \sum {cl} } }} < 1} \right] \hfill \\ = P\left[ {\ln (\sum {w\cos \alpha \tan \phi } ) - \ln \left( {\sum {w\sin \alpha - \sum {cl} } } \right) < 0} \right] \hfill \\ = P\left[ {\ln (\sum {w\cos \alpha \tan \phi } ) < \ln \left( {\sum {w\sin \alpha - \sum {cl} } } \right)} \right]. \hfill \\ \end{gathered}$$

Subtracting $\mu_{{\ln ((\sum {w\cos \alpha \tan \phi } ))}}$ and dividing by $\sigma_{{\ln (\sum {w\cos \alpha \tan \phi } )}}$, we get

$$\begin{gathered} = P\left[ {\frac{{\ln (\sum {w\cos \alpha \tan \phi } ) - \mu_{{\ln ((\sum {w\cos \alpha \tan \phi } ))}} }}{{\sigma_{{\ln (\sum {w\cos \alpha \tan \phi } )}} }} < \frac{{\ln \left( {\sum {w\sin \alpha - \sum {cl} } } \right) - \mu_{{\ln (\sum {w\cos \alpha \tan \phi } )}} }}{{\sigma_{{\ln (\sum {w\cos \alpha \tan \phi } )}} }}} \right] \hfill \\ = P\left[ {Z < \frac{{\ln \left( {\sum {w\sin \alpha - \sum {cl} } } \right) - \mu_{{\ln (\sum {w\cos \alpha \tan \phi } )}} }}{{\sigma_{{\ln (\sum {w\cos \alpha \tan \phi } )}} }}} \right]. \hfill \\ \end{gathered}$$

(A6)

For both cohesion and angle of internal friction

In this case, both cohesion and angle of internal friction are assigned lognormal distribution. The factor of safety F_s against failure p_f is earlier mentioned in Eq. 16 and is given by

$$F_{s} = \frac{{\sum {cl} + \sum {w\cos \alpha \tan \phi } }}{{\sum {w\sin \alpha } }}.$$

(A7)

Further, the probability of failure p_f expression from A7 is derived as follows

$$\begin{gathered} p_{f} = P\left[ {F_{s} < 1} \right] \hfill \\ = P\left[ {\frac{{\sum {cl} + \sum {w\cos \alpha \tan \phi } }}{{\sum {w\sin \alpha } }} < 1} \right] \hfill \\ = P\left[ {\ln (\sum {cl} + \sum {w\cos \alpha \tan \phi } ) - \ln \left( {\sum {w\sin \alpha } } \right) < 0} \right] \hfill \\ = P\left[ {\ln (\sum {cl} + \sum {w\cos \alpha \tan \phi } ) < \ln \left( {\sum {w\sin \alpha } } \right)} \right]. \hfill \\ \end{gathered}$$

Subtracting $\mu_{{\ln (\sum {cl} + \sum {w\cos \alpha \tan \phi } )}}$ and dividing by $\sigma_{{\ln (\sum {cl} + \sum {w\cos \alpha \tan \phi } )}}$, we get

$$\begin{gathered} = P\left[ {\frac{{\ln (\sum {cl} + \sum {w\cos \alpha \tan \phi } ) - \mu_{{\ln (\sum {cl} + \sum {w\cos \alpha \tan \phi } )}} }}{{\sigma_{{\ln (\sum {cl} + \sum {w\cos \alpha \tan \phi } )}} }} < \frac{{\ln \left( {\sum {w\sin \alpha } } \right) - \mu_{{\ln (\sum {cl} + \sum {w\cos \alpha \tan \phi } )}} }}{{\sigma_{{\ln (\sum {cl} + \sum {w\cos \alpha \tan \phi } )}} }}} \right] \hfill \\ = P\left[ {Z < \frac{{\ln \left( {\sum {w\sin \alpha } } \right) - \mu_{{\ln (\sum {cl} + \sum {w\cos \alpha \tan \phi } )}} }}{{\sigma_{{\ln (\sum {cl} + \sum {w\cos \alpha \tan \phi } )}} }}} \right] = P\left[ {Z < \frac{{\ln \left( {\sum {w\sin \alpha } } \right) - \mu_{{\ln (F_{R} )}} }}{{\sigma_{{\ln (F_{R} )}} }}} \right]. \hfill \\ \end{gathered}$$

(A8)