Introduction

Estimating suspended sediment load (SSL) of rivers is a major objective in water resource planning because it has a key role in the design and construction of water-related structures and has major implications for erosion management and sediment redistribution within watersheds (Halbe et al. 2013; Rajaee 2011). Sediments removed by upstream components of turbulent flow that remain suspended for a long time are defined as suspended loads (Kaveh et al. 2017). Erosion of soil throughout a drainage basin and sediment input to river flow cause a reduction in water resource quality and the useful lifetime of hydraulic structures. Prediction of SSL could help to control water quality and increase the effectiveness of hydro-electric power installations. Measuring SSL requires the installation of hydrometric stations, which is costly financially and in terms of human labor, and it is impossible in many remote regions. In such regions, using methods that can estimate SSL, indirectly and less expensively, would be desirable for improved sediment and water resource management.

Asian countries are very sensitive to flood flows, which can carry large SSL and lead to severe socio-economic damage (Das et al. 2018). Climate change and human interference exacerbate these conditions (Das et al. 2018; Malik and Pal 2020b). Therefore, predicting natural disasters and the SSL can be effective in reducing the negative consequences of such events (Malik and Pal 2020a; Melesse et al. 2011). Several authors have already used different mathematical modeling techniques to predict SSL of rivers (Verstraeten and Poesen 2001; Ward et al. 2009; Bezak et al. 2014; Choi and Lee 2015; Wang et al. 2015; Si et al. 2017). Such mathematical modeling requires a large amount of input data that is costly and time-consuming to collect. One of the most common methods for predicting SSL is through using sediment rating curves that show the relationship between sediment load and flow. Unfortunately, there are many errors associated with using this method (Rajaee et al. 2009; Asselman 2000).

There are many different factors in watersheds that could influence the amount of SSL in watersheds. By gathering data on these factors and using them with experimental models, SSL can be estimated. So far data such as drainage characteristics, topography, river discharge, rainfall levels, and vegetation cover have been used to estimate SSL with a range of data mining techniques (Kisi 2012; Lafdani et al. 2013; Agarwal et al. 2006; Haddadchi et al. 2013; Vafakhah 2013; Nourani and Andalib 2015).

Data mining science incorporates aspects of several disciplines such as statistics, artificial intelligence, and machine learning. The methods used involve making predictions, using carefully collected data, and for each model suitably processing databases. Zounemat-Kermani et al. (2016) modeled SSL based on data-oriented models such as ANNs and SVR to allow comparison with predictions from sediment rating curves. Results indicated that SVR models produced by radial basis functions (RBFs) were the most suitable for predicting SSL. Lafdani et al. (2013) also used ANNs and SVR to forecast SSL, but they considered streamflow and precipitation as explanatory variables and showed that the SVR model produced the most reliable predictions. Kisi (2012) modeled the relationship between SSL and discharge using SVR, ANNs, and sediment rating curves at the downstream and upstream stations in California. For the upstream stations, the SVR model was the best, but for the downstream stations, sediment rating curves produced the best results. In flood studies, the boosted regression tree (BRT) model was found to be the best predicting flash flood susceptibility using climatic and geo-environmental variables (Band et al. 2020a). In another study, flood susceptibility mapping was successfully performed using logistic regression compared to multi-criteria decision analysis approaches (Malik et al. 2020a). The ensemble of MLR with an evidence belief function (EBF) has also shown good performance in predicting flood-sensitive areas (Chowdhuri et al. 2020).

Using additional climatic and hydrological data can lead to increased model accuracy in prediction of SSL. Zhu et al. (2007) modeled SSL by using ANNs and mean precipitation, temperature, precipitation intensity, and discharge data related to the Yangtse River, China. Their results showed that ANNs and these data could provide better predictions of monthly SSL compared with MLR models.

The physiographic characteristics of drainage basins have a critical role in determining the amount of water and sediment in channels as well as channel morphology downstream. Some of these characteristics are slope and elevation (Malik and Pal 2020a, b; Malik et al. 2020b). With regard to the specific role of different physiographic characteristics in erosion and sedimentation processes, only very limited research has taken place such as the work of Talebi et al. (2016) who reviewed the role of curvature and its types on the rate of erosion. With current geographic information system (GIS) software, extraction of topographic and physiographic features from digital elevation models (DEMs) is relatively simple, and they have the potential to improve prediction of suspended sediment loads compared to the studies mentioned earlier that did not use such a key group of variables as inputs to modelling.

While physiographic attributes can be easily extracted from DEMs and data from many sources can be included in modeling suspended sediment loads, there can be computational issues in terms of sufficient memory and computer storage space as well as computational time when making predictions over large geographical areas like multiple drainage basins. For many algorithms as the space used for input data is extended, the complexity of algorithm implementation is increased. Given that some input data have a small role in prediction yet they increase the space needed for input data and the computational complexity, attribute reduction techniques could decrease input data space without a significant loss in prediction accuracy (Taghizadeh-Mehrjardi et al. 2016).

Gilan and Lorestan provinces are rainy and important to the water supply of Iran. The majority of dams in Iran are on rivers that originate in these two provinces. Therefore, being aware of the minimum and average SSL in a year can assist in the proper management of the dams. In this regard, discharge data are often used to predict minimum and average sediment load (Kakaei Lafdani et al. 2013; Zounemat-Kermani et al. 2016). Due to the non-linear relationship between discharge and deposition and the complexity of sediment transport processes, and factors affecting them (Kisi 2012), this study will use geo-morphometric parameters that can be easily extracted from DEMs in addition to discharge data. This study not only investigates what are the best ML techniques for doing this, but also uses the SVM method to determine which are the most important geo-morphometric parameters for predicting SSL in these regions of Iran.

The major objective of this work was to evaluate six ML models for predicting SSL for large geographic areas covering many drainage basins. Using such methods could greatly reduce the cost of predicting SSL compared to traditional methods. The methods compared were MLR, ANNs, KNN, GP, SVM, and ESVM. The novelty of this work lies in the range of methods compared as well as the use of topographic/geo-morphometric attributes for improving prediction as they have largely been ignored in previous research. Data reduction methods should also enable this key wealth of topographic/geo-morphometric data to be utilized without a proportionate increase in computational complexity and input data storage capacity given the large size of the datasets used.

Materials and methods

Study sites

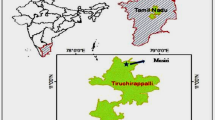
The study sites consist of 68 watersheds located in the Gilan and Lorestan provinces, Iran. These watersheds have a suitable data bank compared with other watersheds in Iran. The altitude varies between −89 and 3702 m above sea level in the study sites. The two regions have different vegetation types. The geographic location of the study regions and hydrometric stations are shown in Fig. 1.

Figure 1
figure 1

Location of hydrometric stations in the study area

Full size image

Data used

ML models need appropriate input parameters for predicting and modeling processes. In this study, discharge and geo-morphometric parameters were used as input parameters. DEM with a resolution of 30 m was downloaded from the United States Geological Survey (USGS). In addition, 26 geo-morphometric parameters were extracted as auxiliary input parameters using SAGA (System for Automated Geoscientific Analyses) GIS.

In this study, SSL recorded at the hydrometric stations for 1983–2014 were used as the target or dependent variable. Minimum and average SSL were calculated to validate the output of the models used in the study.

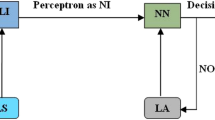
The methodology used for the current study is represented in Figure 2, and more details are described below.

Figure 2
figure 2

Flowchart of steps involved in the study

Full size image

Principal component analysis (PCA)

Reducing the number of variables is a useful tool for decreasing the volume of input data when modeling large datasets (Ebrahimi-Khusfi et al. 2021). PCA was used to decrease the complexity of computation and determine which were the most important variables (Taghizadeh-Mehrjardi et al. 2016). PCA was done prior to modeling of sediment loads by various methods. As all variables are used in the formation of the principal components, there is a low loss of information from the primary variables (Johnson and Wichern 2007).

ML methods used in predicting the SSL

In this work, minimum and average SSL were predicted using the MLR, ANNs, KNN, GP, SVM, and ESVM models. To investigate the contribution of auxiliary variables in the predicting of SSL, first minimum and average SSL were modeled with the corresponding discharge.

Multiple linear regression (MLR)

MLR aims to specify association strength between one dependent variable and several independent variables (Aiken et al. 2003). Relations among a dependent variable and one or more independent variables are modeled through fitting a linear equation to actual data, as follows (Eq. 1).

$$ y={a}_0+{a}_1{x}_1+{a}_2{x}_2+\dots +{a}_p{x}_p $$
(1)

where y is dependent variable; x1, x2, …, xp are independent variables; a0 is the y intercept; and a1, a1, …, ap are the coefficients of variables under investigation. In this study, the SSL was considered as the dependent variable, and the geo-morphometric parameters were used as the independent variables.

Artificial neural networks (ANNs)

ANNs are characterized with one or more hidden layers (Sahana et al. 2020). ANNs are a large parallel system which consists of enormous processing components connected by weight links. The most widely used ANN model is the feed-forward back-propagation network (FFBP) (Haykin and Lippmann 1994). The ANN includes some layers of parallel processing components called neurons. Each layer is completely connected to the previous one via inter-connecting weights. At each iteration, determined weight amounts are initially altered as the calibration or training process proceeds. This compares predicted outputs with real outputs and back-propagates any errors to determine appropriate weight adjustments so that errors can be minimized (Kişi 2010).

Initially, the number of hidden layers was changed from 0 to 20 to show that 16 hidden layers gave the best results. Training cycle tools were used to determine the number of training cycles that was best, and 500 training cycles were shown to give the best results. The model also had a learning rate of 3/0 and a momentum of 2/0 as analysis was conducted to optimize these parameters.

In this method, a function of sigmoid ϕ (x) was expressed by Eq 2:

$$ {d}^i=\phi {\left(\sum \limits_i{w}_i.\phi \left(\sum \limits_i{w}^{\prime } ij\left(\sum \limits_k{f}_k.{w}_{jk}+{k}_n\right)+{k}_m^{\prime}\right)+{k}^{{\prime\prime}}\right)}^{\prime } $$
(2)

where fp is a feature of input kn and k'm and k” are neurons of different layers. Also, wi, w'ij, and w'jk are weights of the different input layers.

K-nearest neighbor (KNN)

The KNN model was suggested by Nemes et al. (2006). It does not need particular assumptions about the distribution of predictors, which is regarded as one of the advantages of this algorithm. The KNN samples are categorized based on the mean values of k neighbor responses in a predictor space (Mahmoudzadeh et al. 2020). The training examples are characterized by n attributes. Every example denotes a point in an n-dimensional space. Hence, all training examples will be maintained in an n-dimensional pattern space (Jayawardena et al. 2002). In this model, model optimization results showed that k=3 gave the best results.

Gaussian process (GPs)

As a useful non-parametric ML technique, GP can be applied to build comprehensive probabilistic models of real-world issues. A GP is a stochastic procedure whose substantiation is constituted of randomized amounts which are related with every point in spatial and temporal scales such that every random variable is normally distributed (Roushangar and Shahnazi 2020). In addition, every finite set of those random variables is characterized with a multivariate normal distribution. GPs play a substantial role in statistical modeling thanks to properties inherited from the normal distribution. In GPs, multivariate Gaussian distributions are extended to unlimited dimensionality. As a whole, a GP produces data nested over some domain such that every finite subset will follow a multivariate Gaussian distribution. In GP models, different kernel functions give different model accuracies. In this study, the functions investigated included radial basis functions (RBF), Cauchy, Laplace, poly, sigmoid, Epanechnikov, Gaussian combination, and multi-quadratic functions.

Support vector machine (SVM)

The SVM (Cortes and Vapnik 1995) has been widely used to predict different target variables, such as gully erosion and SSL (Rashidi et al. 2016; Band et al. 2020b). This algorithm measures functional dependency f(x) between X and Y while assuming that these samples do not follow a specific probability distribution function \( P\left(\overrightarrow{x},y\right) \):

$$ F=\left\{f|f\left(\overrightarrow{x}\right)=\left(\overrightarrow{K},\overrightarrow{x}\right)+C:\overrightarrow{K}\in {R}^n,{R}^n\to R\right\} $$
(3)

where K and C are coefficients obtained from sampling data (X, Y). Considering that the probability distribution function of sampling data is unknown, it cannot reduce the risk function. Therefore, the empirical risk function is calculated using Eq. 4 (Cimen 2008).

$$ {R}_{emp}\left[f\left(\overrightarrow{x}\right)\right]=\frac{1}{T}\sum \limits_{i=1}^Nl\left({y}_1-f\left({\overrightarrow{x}}_i\right)\right) $$
(4)

where T denotes the number of sampled data. However, the empirical risk minimization is not appropriate to reduce the risk function. To reduce it, the regularized risk function is used as expressed by Eq. 5:

$$ {R}_{reg}\left[f\left(\overrightarrow{x}\right)\right]=d\sum \limits_{x_i\in X}{l}_{\varepsilon}\left({y}_1-f\left({\overrightarrow{x}}_i\right)\right)+\frac{1}{2}{\left\Vert \overrightarrow{K}\right\Vert}^2 $$
(5)

In Eq. 5, ||K|| and d refer to a regression vector and a coefficient constant, respectively. lε is the loss function and is defined by Eq. 6:

$$ {l}_{\varepsilon}\left({y}_1-f\left({\overset{\rightharpoonup }{x}}_i\right)\right)=\left\{\begin{array}{c}0\kern0.5em for\mid {y}_1-f\left({\overset{\rightharpoonup }{x}}_i\right)\mid <\varepsilon \\ {}{y}_1-f\left({\overrightarrow{x}}_i\right),\kern0.5em otherwise\end{array}\right. $$
(6)

The non-linear regression function is computed as (Cimen 2008; Gunn 1998):

$$ f(x)=\sum \limits_{i=1}^N\left({l}_i^{\ast }-{l}_i\right)K\left(x,{x}_i\right)+ bc $$
(7)

where bc is a bias component, \( {l}_i^{\ast } \) and li are the Lagrange multipliers, and k(x,xi) is the kernel function (Kisi and Cimen, 2011).

In the SVM and ESVM models, different kernel functions have differing accuracies. The functions investigated in this study for SVM and ESVM were Cornell dot, radial, polynomial, neural, ANOVA, Epachnenikov, Gaussian combination, and multi-quadratic.

Support vector machine evolutionary (ESVM)

The ESVM is a SVM implementation using evolutionary algorithms to deal with the dual optimization problems of a SVM. This model can be applied for several aims learning that makes parameter C selection before learning unnecessary (Huang and Chang 2007). Through designing an efficient GAFootnote 1-chromosome representation as well as an intelligent crossover operation, ESVM makes the best use of intelligent GA in optimizing system parameters. The intelligent crossover operation is contingent upon an orthogonal experimental design applying a divide-and-conquer strategy to deal with intractable optimization problems which consist of many system parameters. Common intelligent GAs are concisely presented while having the strengths of orthogonal experimental design and intelligent crossover and have shown superiority in several studies (Ho et al. 2004). Rapid Miner software (Ver. 5) was used to run all the models mentioned.

Model validation

To evaluate the efficiency of the study models, a leave-one-out (LOO) cross-validation approach was used where one data point is excluded and the included data are utilized to estimate the value at the missing point. The advantage of this method is that all data are used for evaluation, so extra data collection to provide a separate validation set is not needed and there is good coverage of the study area. However, a disadvantage of this method is that each data point is used several times for estimating other points that are spatially close to it.

To compare the ML techniques used here, the root mean squared error (RMSE) and Pearson’s correlation coefficient (r) were computed using Eqs. 7 and 8, respectively.

$$ RMSE=\sqrt{\frac{\sum \limits_{\mathrm{i}=1}^{\mathrm{n}}{\left({o}_{\mathrm{i}}-p\right)}^2}{n}} $$
(7)
$$ r=\frac{\sum \limits_{\mathrm{i}=1}^{\mathrm{n}}\left({p}_{\mathrm{i}}-\overline{p}\right)\left({o}_{\mathrm{i}}-\overline{o}\right)}{\sqrt{\sum \limits_{\mathrm{i}=1}^{\mathrm{n}}{\left({p}_{\mathrm{i}}-\overline{p}\right)}^2\sum \limits_{\mathrm{i}=1}^{\mathrm{n}}{\left({o}_{\mathrm{i}}-\overline{o}\right)}^2}} $$
(8)

where o is observed data, p is predicted data, \( \overline{p} \) is the mean value of predicted data, \( \overline{o} \) is the mean value of observed data, and n is the total number of observations.

Weighting parameters

Not all variables received equal weight in the prediction methods mentioned hereafter. Some variables showed greater correlation with the model output and therefore have a greater impact on predictions. In this study, the SVM algorithm was used for weighting variables (Sani Abade et al., 2014).

Results

Summary statistics

Summary statistics for each geo-morphometric input parameter/variable are given in Table 1. The results show that the range of most variables is wide for the 68 watersheds as they represent very different conditions that accompany a wide range in elevation from a minimum of −15.92 m (Gilan Province) to a maximum of 2785.85 m (Lorestan province). Table 2 also indicates wide variation in the area of the different watersheds studied with the smallest being just 2.63 km2 and the largest being 7733 km2. The wide range in values for these two key variables, elevation and watershed area, in turn causes a wide range in values of other variables.

Table. 1 Summary statistics of input parameters
Full size table
Table. 2 Principal component analysis results
Full size table

To reduce the amount of input data, PC analysis was used. PCA results showed that the dataset was summarized by three components. The first PC explains by far the greatest proportion of variation in the data (99 percent). The second and the third PCs determined the remaining 1% of changes in the data. The PCA results are provided in Table 2.

Modeling

Modeling with discharge parameters as inputs

The results of applying models for the collection of average SSL showed that if the discharge parameter is used to predict average SSL, all models show less accuracy than the models that used geo-morphometric parameters. The results for models applied to the dataset with discharge as the input are provided in Table 3.

Table. 3 Validation statistics of different prediction methods for estimating average suspended sediment load using discharge
Full size table

The results for the SVM method showed that this model performed best with a polynomial kernel function (minimized RMSE=63.98). Also for the ESVM method, the Epachnenikov kernel function had the lowest RMSE=181.40, and for the GP method, the RBF kernel showed the best result. Overall, when discharge was used as the input data for KNN, model h was most accurate at predicting average sediment load with RMSE=50.45 and r=0.63.

The outcomes for predicting minimum SSL also indicated that the RBF had the lowest RMSE for the SVM method. For the ESVM method, the polynomial kernel function was most accurate. The results for all methods for predicting minimum SSL using discharge as the inputs are presented in Table 4. Overall, the KNN method was the most accurate at predicting minimum SSL.

Table. 4 Validation statistics of different prediction methods for estimating minimum suspended sediment load using discharge
Full size table

Modeling with geo-morphometric parameters as inputs

For the six ML approaches used in this study, the best results for each method are summarized in Table 5, and the correlations between actual and predicted data are shown in Figure 4. The best-performing ANN model had 16 hidden layers, moment of 0.2, and learning rate 0.2 and had a RMSE =44.56 (Table 4) for predicting average SSL. For the KNN model, prediction was best when K=3 was used.

Table. 5 Validation statistics of different prediction methods for estimating average suspended sediment load using the geo-morphometric parameters
Full size table

The results showed that the GP model with a RBF kernel function had better results than other kernel functions. For average SSL with SVM, the Epachnenikov kernel function had the lowest RMSE=65.61 and highest correlation coefficient, r =0.74. In contrast, for predicting average SSL with ESVM, the ANOVA kernel function had the lowest RMSE=24.95 and highest r=0.95.

When comparing the performance of the most appropriate models for each method, Table 3 shows that the GP model had the best validation statistics (RMSE=11 and r=0.98) for estimating average SSL with geo-morphometric parameters (Table 6).

Table. 6 Validation statistics of different prediction methods for estimating minimum suspended sediment load using the geo-morphometric parameters
Full size table

The relationship between actual and predicted SSL is shown when discharge (Figure 3a) and geo-morphometric parameters (Figure 3b) were used for modeling average SSL using the best models (GP). These graphs show that the correlation between actual and estimated values is far stronger when geo-morphometric parameters are used rather than discharge.

Figure 3
figure 3

Scatter plots showing the relationship between measured and estimated amounts of average SSL produced by the GP: a using discharge, b using the geo-morphometric parameters

Full size image

The ESVM model had acceptable validation statistics close to those of the GP model (RMSE=24.95 and r=0.95) for predicting average SSL. The same range of model parameters and kernel functions was investigated for each method for predicting minimum SSL as were used for average SSL. The best parameters/kernel functions were generally the same for predicting minimum SSL as for predicting average SSL apart from for SVM and ESVM. The validation statistics for the best models for each method are shown in Table 5, and the correlations between actual and predicted SSL are shown in Figure 5. For forecasting minimum SSL with the SVM model, the Epanechnikov kernel was best with a RMSE=0.99 and r=0.82. However, for the ESVM model, the radial and Epachnenikov functions were the best performing with the same RMSEs=0.17 and r=0.99. When comparing all methods for predicting minimum SSL, the ESVM model was the best performing with RMSE=0.17 and r=0.99 (Table 6). The difference in validation statistics between ESVM and GPs was very low. Figure 4a and b show the relationship between actual and predicted SSL when minimum SSL was predicted using discharge and geo-morphometric parameters, respectively, and based on modeling using the best model (ESVM).

Figure 4
figure 4

Scatter plots showing the relationship between measured and estimated amounts of minimum SSL produced by the ESVM: a using discharge, b using the geo-morphometric parameters

Full size image

For predicting both average and minimum SSL, the difference between GPs and ESVM model was very low so it can be concluded that among the methods implemented here, GPs and ESVM would be the best to use.

Weighting parameters

In this study, geo-morphometric parameters were used as auxiliary data for predicting SSL, but it was recognized that not all of these parameters have equal importance in making such predictions. Therefore, each parameter was weighted to give effective parameters. The results of weighting input parameters showed that discharge and drainage density had the highest weight (1) and among the geo-morphometric parameters the highest weightings were for profile curvature (1), LS factor (0.819), longitudinal curvature (0.810), and flow accumulation (0.77) for predicting SSL. Maps of each of these parameters for one studied sub-basin are presented in Figure 5.

Figure 5
figure 5

Map of profile curvature, LS factor, longitudinal curvature, and flow accumulation parameters in one of the studied sub-basins

Full size image

The results of applying weighting to minimum SSL showed that stream power index (1) and Strahler order (0.98) and aspect (0.95) were the parameters with the highest weight and maximum impact for predicting minimum SSL. The maps for these parameters are presented in Figure 6 for one sub-basin.

Figure 6
figure 6

Maps of stream power index, Strahler order, aspect, and vertical distance to channel network in one of the sub-basins studied

Full size image

Discussion

In this study, the use of the geo-morphometric parameters for optimizing the estimation of river SSL using different ML models was investigated.

Cross-validation results from using six ML models for estimation of SSL indicated that the behavior of average and minimum SSL was not the same in terms of the accuracy metrics. According to our outcomes, GP was found to be the best method to forecast the average SSL (Table 5). However, the ESVM model was identified as the optimal model for predicting the minimum SSL in the study regions (Table 6). It was also found that integrating these techniques along with the geo-morphometric parameters can markedly increase the accuracy of SSL prediction.

In predicting average values of SSL using the selected models, the correlation coefficient increased from 0.63 using discharge data to about 0.98 using the geo-morphometric properties. However, the prediction error value decreased from 54 to 11 mg L−1.

In studies where only climatic data have been used to predict SSL, less accurate predictions have been reported (Cobaner et al. 2009; Liu et al. 2013; Zounemat-Kermani et al. 2016; Kisi 2012; Rajaee et al. 2011).

Comparing our findings with other researchers’ findings can highlight the effective role of geo-morphometric features in increasing the accuracy of SSL predictions.

As a whole, compared to discharge data, the use of the geo-morphometric parameters improved the accuracy of SSL predictions in our study regions by 30%.

Determining the contribution of factors affecting SSL variations is required to better understand the conditions where large SSL occur and to try and prevent adverse consequences of such large SSL (Shi et al. 2017). Our results showed that in addition to discharge and drainage density, some geo-morphometric parameters, especially profile curvature, slope factor, longitudinal curvature, and cumulative flow, had the most influence on average SSL in the study areas. However, according to the best model for predicting minimum SSL, stream power index and Strahler order and aspect had the highest share in the variations of the minimum SSL across the study regions. According to Sabzevari and Talebi (2019), the curvature shape has more effect on erosion compared to plan shape. Malik and Pal (2020a) reported that slope, HSI, TSI, and SSI were the main factors controlling channel capacity that can be a function of changes in SSL in the rivers. Also, stream power was shown as the best predictor for soil detachment rate in research done by Wu et al. (2019). These reports are quite consistent with outcomes of the current research.

Changes in longitudinal and profile curvature alter potential gradients and influence flow rates and hence transport processes in rivers. The high weighting for LS factor is understandable given that according to Moore and Wilson (1992), it was equal to the sediment transport index and represents erosion and sediment transport processes showing the impact of erosion on the slope. The flow accumulation map (Figure 3c) shows a numerical value for each cell which indicates the total number of cells that ultimately drain into that cell. The longitudinal curvature parameter indicates whether there is an acceleration or deceleration in stream flow and hence whether erosion or deposition is the dominant processes in a given cell. Stream power index is a demonstration of the power of erosion surface currents and is calculated using specific surface area and shelves. Aspect represents a line in which the greatest reduction in height takes place (see Table 1 for further definitions of geo-morphometric parameters).

The Strahler order parameter is used to define stream size based on a hierarchy of tributaries. It is clear from the definition of each of the important geo-morphometric parameters that these factors are of key importance in determining patterns of SSL and that the weightings produced are sensible theoretically and likely to produce acceptable results. In the future, such parameters could also include other variables that influence erosion processes and basin sediment load such as vegetation coverage and type as well as land use which could be extracted from satellite imagery. In addition, it would be useful to examine the efficiency of other ML models and algorithms based on artificial intelligence. This study investigates annual SSL, but temporal changes in SSL on a daily basis are very important in river engineering studies. Given the success of using geo-morphometric parameters in predicting average and minimum annual SSL, it is likely that they could be incorporated with weather data into daily or monthly predictions, but this would require a separate study.

Conclusion

In this study, six ML models, namely MLR, ANN, KNN, GPs, SVM, and ESVM, were evaluated to predict the minimum and average SSL in 68 river basins of Gilan and Lorestan provinces, in Iran. For this purpose, the optimal independent features were selected among the 26 geo-morphometric parameters using the PCA method. Lastly, model yield was evaluated based on r and RMSEs. The best models for predicting the average SSL were recognized as GPs, ESVM, ANN, SVM, KNN, and MLR, in order of accuracy. However, ESVM, GPS, MLR, SVM, ANN, and KNN models were, respectively, identified as the best predictive models to forecast the minimum SSL, using geo-morphometric characteristics. Furthermore, using discharge data, KNN was determined as the optimal predictive model for predicting minimum and average SSL. It was also found that discharge, drainage density, and profile curvature were the most important variables for predicting the average SSL. However, stream power index and Strahler order were dominant parameters for predicting minimum SSL in our study regions. These results encourage the future use of GPs and ESVM for predicting SSL at the basin scale. Indeed, this work provides a good reference for evaluating the effects of geo-morphometric parameters on SSL variation using GPs and ESVM methods. These findings are useful for mitigating the undesirable impacts of SSL in different basins, decreasing soil erosion and increasing sustainable development.