Abstract
Theme unsuitability is noted to have inhibited the accuracy of groundwater potential zones (GWPZs) mapping approach, especially in a semi-arid environment where surface water supply is inadequate. This work, therefore presents a geoscience approach for mapping high-precision GWPZs peculiar to the semi-arid area, using Buffalo catchment, Eastern Cape, South Africa, as a case study. Maps of surficial-lithology, lineament-density, drainage-density, rainfall-distribution, normalized-difference-vegetation-index, topographic-wetness-index, land use/land cover, and land-surface-temperature were produced. These were overlaid based on analytical hierarchical process weightage prioritization at a constituency ratio of 0.087. The model categorizes GWPZs into the good (187 km2), moderate (338 km2), fair (406 km2), poor (185 km2), and very poor (121 km2) zones. The model validation using borehole yield through on the coefficient of determination (R2 = 0.901) and correlation (R = 0.949) indicates a significant replication of ground situation (p value < 0.001). The analysis corroboration shows that the groundwater is mainly hosted by a fractured aquifer where the GWPZs is either good (9.3 l/s) or moderate (5.5 l/s). The overall result indicates that the model approach is reliable and can be adopted for a reliable characterization of GWPZs in any semi-arid/arid environment.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The water shortage is a global issue, owing to the nexus of water-food-energy and its influence on livelihood and global economics. In South Africa, the water shortage may persist for a longer time due to the rate of increase in population, urbanization, and industries, as well as the regional severity of aridity on water resources, which is further complicated by climate change (Owolabi et al. 2020b). Ad hoc effort towards water security has involved data gathering and evaluation, creation of impoundments and water infrastructures for water transfer schemes, water policies, optimization programs, and management measures (Schreiner and Hassan 2010). However, water supply has been outmatched and this is impacting other vital organs of development in the country. The exploitation of groundwater resources as an alternative has not been harnessed as a result of limited knowledge on its development (Cobbing 2014). Groundwater status and development were relegated to private operations with limited restrictions (Pietersen et al. 2012). As a result, vast numbers of groundwater and surface water researches have been carried out as a separate entity until the reform of the Water Act (Act 36. of 1998) which also depolarizes their disjunctive management (Tanner and Hughes 2015). Information on groundwater distribution of groundwater is still poorly documented (Cobbing and de Wit 2018). Institutional framework and arrangement for data collection, private sector data handling, integrated developmental plans, and management strategy for groundwater resources are issues yet to be properly accounted for (Pietersen et al. 2012). Till present, few aquifers have been assessed for groundwater potential. Hence, the current research attempts to improve the awareness of groundwater availability and to proffer a regional approach to map the zones of groundwater potential.
Groundwater is a component of water resources that fills soil pore spaces, joints, and voids within geologic structures and strata. Groundwater occurrence in rocks depends on the hydraulic conductivity of lithologic materials which is a function of the porosity, permeability, and the flow of fluid through the geologic aperture or structures (Barlow and Leake 2012; Burberry et al. 2018; Owolabi et al. 2020a). Identification of the water-bearing structures and stratigraphic layer with significant hydraulic conductivity is therefore considered crucial to groundwater development. Groundwater potential zones (GWPZs) are areas enclosing the occurrence of a considerable and economically exploitable quantity of groundwater resources (Mandel 2012; Waikar and Nilawar 2014; Thompson 2017). Exploration of GWPZs is essential for water resources reserve estimation, zone budgeting, water quality protection, vulnerability mapping, and environmental management (Waikar and Nilawar 2014).
Conventionally, groundwater prospect has been explored directly through geologic, geophysical, and hydrogeologic approaches. In recent times, the advancement in geoscientific knowledge of data access and processing as well as the multifarious applications of geoinformatics has enabled the regional exploration of areas of groundwater potentials. The strong awareness gained by the geospatial technology for GWPZ mapping has facilitated drastic improvement especially due to the inculcation of multi-criteria decision-making (MCDM) statistical classifier (Machiwal et al. 2011). Some of the statistical tools include the weight of evidence, evidential belief (Tahmassebipoor et al. 2016), weighted overlay (Senthilkumar et al. 2019), multi-influencing factors (Anbarasu et al. 2019), analytical hierarchical process (Sahoo et al. 2017; Sandoval and Tiburan 2019), logistic regression (Chen et al. 2018), and frequency ratio (Hong et al. 2018). Among these, the analytical hierarchical process (AHP) has been rated as the most efficient multi-criteria decision-making tool (Jha et al. 2010). The evolution in the domain of forecast modeling and the advancement in computer programming have facilitated the discovery of machine learning techniques (MLT) for resource modeling (da Costa et al. 2019). Due to the versatility of MLT for analysis of intricate structures and stochastic data, it has offered a more reliable exploration outcome for groundwater resources (Lee et al. 2020; Pourghasemi et al. 2020; Prasad et al. 2020). On this note, several regression models of MLT were proposed for GWPZ mapping. These include multivariate adaptive regression splines (MARS), boosted regression tree (Naghibi et al. 2016; Kordestani et al. 2019), support vector machine (Lee et al. 2018; Naghibi et al. 2018), artificial neural network (Lee et al. 2012; Lee et al. 2018), radial basis function, multiple-layer perception, standalone logistic regression (Pradhan 2010), and random forest (Golkarian et al. 2018; Arabameri et al. 2019). The robustness of machine learning techniques over unsupervised statistical approaches is due to its accuracy, speed, large database computation capability, and its ability to improve its self (Mueller and Massaron 2016).
Remarkable improvement in the performance of machine learning models has been intensified also. For instance, Rizeei et al. (2019) developed an ensemble multi-adoptive boosting logistic regression (MABLR) technique from the hybridization of a multi-adaptive boosting model and logistic regression. The model reports an excellent performance for groundwater aquifer potential maps for bias and variance error reduction due to insufficient sample size, oversimplification, and outliers sensitivity (Rizeei et al. 2019). Tien Bui et al. (2019) designed the hybrid computational intelligence approach called AB-ADTree from the integration of alternating decision tree classifier and adaptive boosting ensemble model for the assessment of groundwater spring potential zones. Kalantar et al. (2019) present two data mining approach based on the application of mixture discriminant analysis and linear discriminant analysis (LDA) compared with random forest for mapping the groundwater potential zone. The redundancy within the groundwater conditioning factors was controlled by normalizing the 15 conditioning factors in variance inflation factor, chi-square factor optimization, and Gini importance. Their outcome revealed the two data mining techniques are satisfactory and moderate even though the random forest approach proved to be better in performance (Kalantar et al. 2019). Also, Chen et al. (2019) developed a hybrid approach that involves the integration of Fisher’s LDA, rotation forest LDA, and bagging LDA for mapping groundwater spring potential.
The computation capability of MLT is strengthened by its meta-algorithm compartment and the ensemble learning model that facilitates the multivariate analysis of a huge dataset (Prasad et al. 2020). MLT works by improving itself scientifically as sample distribution, sizes, and randomness increase while the increase in randomness and sample size increases the skewness and operational complexity of MCDM statistics (Mueller and Massaron 2016). Due to the huge dataset that machine learning works with, decision-making is based on probability, whereas in MCDM statistics, the variance and uncertainty of statistical operands are concealed by the results (Mitchell 1997). Machine learning does not require the definition of sample distribution and does not provide any room for assumption meanwhile MCDM statistics require the definition of distribution and enables assumption, thereby, providing the chance to hypothesize (Duan et al. 2016). As a result of the huge dataset, the outcome of machine learning can only be generalized since it works on probability and best fit, while the outcome of MCDM statistics can be fit to the defined data distribution (Kelleher et al. 2015). In this work, a few datasets (seven) are being used to assess their applicability for site-specific GWPZ exploration. Hence, this study is rather research-oriented than being result-oriented, and to this end, AHP was adopted as the statistical classifier.
Pieces of literature that provide information on groundwater potential in the study area are relatively few. These include DWA (2010), Madi and Zhao (2013), Cobbing (2014), and Owolabi et al. (2020a, b). DWA (2010) characterized the regional attributes of the water management area and indicates that the study area is characterized by a groundwater yield of 2.0 l/s to 5.3 l/s range within aquifer of fractured and intergranular hydrostratigraphy domain. Madi and Zhao (2013) examined the significance of neotectonic belt to groundwater potential across Eastern Cape and noted the existence of a shallow quartzite vein with high groundwater potential in the study area through field mapping of geology structures. Cobbing (2014) assessed the factors influencing the underdevelopment of groundwater and poor management of groundwater boreholes and noted the existence of boreholes in the west of the study area that have been abandoned due to the mechanical breakdown of borehole hardware. Owolabi et al. (2020a) investigated the relationship between the environmental flow of Buffalo and the hydrostratigraphic properties of the catchment. Their work noted that the perennial attribute of the Buffalo River is due to spring and baseflow discharges from Buffalo aquifer. The work specifically indicated through flow duration curve, baseflow analysis, and hydrostratigraphy domain classification that Yellowwood, Tshoxa, and Mgqakwebe low-flow are driven by groundwater discharges, thus indicating the excellent potential for groundwater in the catchment. Owolabi et al. (2020b) assessed the degree of association and interdependence of the Buffalo streamflow on rainfall. The work indicated through bivariate statistical analysis that the hydrodynamic response of Buffalo streamflow is not only controlled by storm-flow but the existence of spring. With the numerous calls made on the need for improvement of knowledge on groundwater resources of South Africa, this work serves as a distinctive response to the call with a concentration on river basin-scale assessment (DWA 2010; Kahinda et al. 2016).
The present paper focuses on the assessment of zones of groundwater potential based on the agglomeration of statistically weighted geoscientific layers within the study area. Seven thematic layers were geospatially concerted using AHP for their weightage prioritization at a catchment scale. These include the thematic layers of surficial lithology (SL), rainfall distribution (RD), lineament density (LD), drainage density (DD), topographic wetness index (TWI), land use/land cover (LULC), and land surface temperature (LST). Importantly, the selection of the thematic factors was based on the regional geology of the study area. Hence, this work intends to address the gap in the holistic investigation of groundwater potential in the Buffalo River catchment, Eastern Cape, South Africa. It proposes to project the inter-relationship among influencing factors of groundwater development peculiar to the semi-arid environment. Based on the intent of the work, it is hoped that the selected themes would improve the application of AHP to an integrated approach for groundwater exploration.
The aim of this study is therefore to present the feasibility of developing a high-precision map of groundwater potential zone for a semi-arid environment. The rationale behind this approach is based on the integrated water resources management scheme that encourages a conjunctive development of water resources in an environmentally sensitive manner (Cosgrove and Loucks 2015).
The catchment-based geohydrological mapping is achieved based on the following objectives: (i) by producing the maps of the thematic layers (SL, RD, LD, DD, TWI, LULC, and LST maps); (ii) by quantifying their critical weights to be used for overlay analysis and their relative consistency ratio; (iii) by delineating and validating the groundwater potential zones for the assessment of the model reliability; and (iv) by corroborating and conceptualizing the geohydrology and hydrogeological variability across the environment of study. The paper presents a hybrid approach of geology, geophysics, geomorphology, and geoinformatics for the geohydrological characterization of groundwater enrichment spots. The approach developed in this study would be of tremendous benefit to the decision-makers, stakeholders, and the host community at large.
Study area
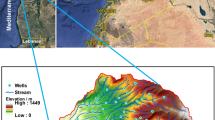
The study area, the Buffalo River catchment, is situated in the Buffalo Metropolitan District Municipality, Eastern Cape, South Africa, within the geographic coordinates of latitudes 32° 40′ 07″ S to 32° 58′ 50″ S and longitudes 27° 7′ 54″ E to 27° 33′ 16″ E (Fig. 1). It spans over an estimated area of 1237 km2, at an elevation of 258–1370 m above the sea level. Its geomorphological settings can be classified into three landform patterns: the plain (South), the dissected plain (trending from West to the Northeast), and the medium gradient mountain (Northwest). The main hydrologic feature in the catchment is the Buffalo River. It runs across a 54-km channel in Southeastern direction to the mouth of the Laing dam. It is fed by six major tributaries: Ngqokweni, Tshoxa, Mgqakwebe, Quencwe, North Zwelitsha, and Yellowwoods rivers. The catchment is characterized by a highly varying climatic pattern, with an average maximum temperature of 22.3 °C in summer and an average minimum temperature of 13.5 °C in winter (Slaughter et al. 2014). It has a mean annual rainfall of 590 mm per annum. The area is covered by two dominant soil types: the undulating and non-stratified sandy-clayey soil, occupying the entire North to the center, and the unconsolidated clayey assemblages from the center to the South.
Location and regional geological map of the Buffalo catchment (modified from the Council of Geoscience regional map sheet (Johnson et al. 2006))
The area is covered by Tatarian arenaceous mudstone of the Balfour Formation, while the extreme lower section of the area exposed the Kazarian argillaceous shaly-sandstone of the Middleton Formation, both belonging to the Adelaide Subgroup within the Karoo Supergroup (Owolabi et al. 2020a). More than half of the areal geology is interspersed by Jurassic dolerite dykes and sills. The formation develops from the episodic history of the Adelaide subgroup, with Koonap and Middleton formations, which also belongs to the Beaufort Group, and Karoo Supergroup (Johnson et al. 2006). As a finding from the Neotectonic study of the region, Madi and Zhao (2013) noted that there are potentials for the development of groundwater resources in the catchment. The paleoenvironment setting of the Formation was reported to be characterized by a humid-to-temperate climatic type (Catuneanu and Elango 2001). Buffalo aquifer was classified under the Ciskean water management area with fractured aquifer and groundwater yield of 2–5 l/s (Vegter 2006).
Materials and Methods
Indices of geomorphology and environment such as topographic wetness index (TWI), land use/land cover (LULC), lineament density (LD), and drainage density (DD) have been extensively annotated in researches to characterize groundwater recharge index (Srivastava and Bhattacharya 2006; Hojati and Mokarram 2016; Aquilué et al. 2017).
AHP enables an unbiased and consistent pair-wise prioritization approach for the computation of weightage of features. The criterion for scoring the weight of features is based on the eigenvector of the square reciprocal matrix of paired features (Saaty 1999). AHP has been successfully adopted in environmental management (Althuwaynee et al. 2014), water resource management (Saaty 1992), and numerous groundwater potential zone mapping (Rahmati et al. 2014; Mohammadi-Behzad et al. 2019; Rajasekhar et al. 2019). The interface of GIS tools presents the opportunity to integrate spatially encoded and statistically weighed groundwater influencing factors in a single map (Lillesand et al. 2014).
Preparation and computation of the thematic layers
Geology
The geology of the study area was produced from the integration of information drawn from an enhanced aeromagnetic data, borehole lithology cross-section profile, and field geologic survey on a scanned geology map as the base map. The enhancement of aeromagnetic data enables the accurate mapping of basement rocks as well as the distinct detrital of sedimentary rocks due to the differential magnetic property of a geologic environment. The effectiveness of analytical signal for mapping basement configuration and lithology variability from an aeromagnetic data have been acknowledged in numerous literature (Matter et al. 2006; Baiyegunhi and Gwavava 2017; Owolabi et al. 2020a). The aeromagnetic data gathered by Fugro Airborne Surveys, South Africa, was supplied by the Centre for Geological Survey, South Africa. The geophysical survey for the aeromagnetic data was carried out with the use of a proton procession magnetometer with a resolution of 0.01 nT, at a constant flight height of 60 m in the North-South direction within a sampling line of 250 m and line spacing of 200 m. The data was processed in Geosoft Oasis montaj by defining the domain grid to reduce the long wavelength and high amplitude effect. The reduced-to-pole filtering was carried out by adapting the data to the average magnetic inclination of 63.47 and declination of −28.67 after removing the International Geomagnetic Reference Field (Peddie 1982). This was then convolved and filtered in the wavenumber domain by applying the 2D forward and inverse fast Fourier transform algorithm. The final computation on the processed aeromagnetic data involved the calculation of the analytical signal using Eq. (1):
where AS represent the analytical signal feature, x, y, and z represent the edges of the magnetic structure, and T represents the total magnetic intensity. The resulting signal layer was classified into three: the extremely low, the intermediate, and the high amplitude signal for validation of relative surficial lithology types.
Rainfall
The data of rainfall from rain gauging stations around the study area were acquired from South Africa Weather Service. These include Stutterheim, Cata, Dimbaza, Berlin, East London, Kidd Beach, and Peddie stations. These were summated into an annual average for at least thirty years record, 1987 to 2016. In doing so, missing data are averaged out. The annual average rainfall was computed and projected to generate a rainfall thematic layer using the ordinary kriging interpolation method, and a linear semi-variogram model. The resulting spatially varying rainfall map was classified for overlaying purposes.
Land use/land cover
Landsat 8 OLI with less than 10 % cloud was downloaded from the Earth Explorer USGS website and processed in ArcGIS 10.5.1 to produce the map of land surface temperature and the land use/land cover. The downloaded imagery was rectified for spectral distortion and reflectance quality. This was used to produce the LULC, LST, and LD maps. Mapping of LULC was carried out by generating a composite band of bands 1, 2, 3, 4, 5, 6, and 7. The buffering of LULC features was guided by the band combination validated by Butler (2013). This enables the easy identification of the constituent cells associated with the LULC features of interest presented in Table 1.
Hence, training samples were digitized and the signature file was developed for supervised mapping through a maximum likelihood classifier. The approach adopted here for LULC mapping is popularly recognized in the previous literature due to its high degree of reliability (Mohammadi-Behzad et al. 2019; Rajasekhar et al. 2019). The mapped feature was validated by NDVI and Google Earth. The features of Land use/ land cover provide important environmental insight on areas of groundwater accumulation based on the natural settings and human interaction with the settings (Aquilué et al. 2017).
Land surface temperature
Landsat 8 Operational Land Imager of July 26, 2019, was downloaded from the USGS Earth Explorer website to produce the LST theme. The month represents the driest month of the year while the year was linked with the period of extremely low soil moisture (Owolabi et al. 2020b). The bands 4, 5, and 10 of the satellite data are processed in the following order:
-
1. Top of atmospheric (TOA) spectral radiance was calculated in raster algebra using Eq. (2):
where RFM = radiometric multiplicative rescaling factor for TIRS 1 which is 0.0003342, TIRS = thermal infrared sensor 1 which is Band 10, and RFA = radiometric addictive rescaling factor for TIRS 1 which is 0.1.
-
2. TOA was converted to brightness temperature (BT) using Eq. (3):
where K1 and K2 = Thermal conversion constant for Band 10 extracted from metadata, 774.885 and 1321.0789 respectively and 273.15 = constant for temperature conversion from Kelvin to Celsius.
-
3. NDVI was calculated using the expression in Eq. (4):
where NIR (near-infrared) = band 5, and red = band 4 for Landsat 8 OLI.
-
4. Vegetation proportion (Pv) was calculated from NDVI, using Eq. (5):
-
5. Emissivity was calculated from Pv, using Eq. (6):
where 0.004 is the downscaling constant for Pv and 0.986 is the correction value of the equation.
-
6. LST is deduced from the integration of BT and Emissivity, ℇ , according to Eq. (7):
The approach adopted here for LST has been extensively validated in the previous land surface temperature researches (Orimoloye et al. 2018; Suresh et al. 2016). Land surface temperature indicates zones of poor saturation thickness, high evaporation, and evapotranspiration considering the severity of semi-aridity in the study area (Urqueta et al. 2018). Hence, its spatial information is considered significant to groundwater exploration in the study environment.
Lineament density
The surficial lineaments were produced using the panchromatic band (Band 8) of Landsat 8 OLI due to its high resolution (16 m by 16 m) in PCI Geomatica, 2017 version. This was achieved through an algorithm of multi-stage line detection of Canny edge and contour detection. The contour detection enables the filtering of curves and edges. The line detection enables a four-stage transformation which includes speciation of a minimum length of the curves, maximum error, maximum angle between polylines segments, and the minimum distance between two polylines (Hashim et al. 2013). These processes produce the polylines defined as lineaments. Its density was processed in ArcGIS 10.5.1 using grid cells method based on Eq. (8) (Rahmati et al. 2014):
where LD is the lineament density, Li is the sum of the length of all the lineaments (km), i represent each linear feature in the study area, and A is the effective area of lineament cell grids (km2). The lineament plot was validated by plotting its rose diagram and comparing its orientation to that of the Neotectonic structure in the study area. LD’s significance to groundwater exploration is on account of its spatial analyst to indicates the zones of the tectonic macro-structures that serve as conduits for groundwater influx into hydrostratigraphic units (Fenta et al. 2015).
Drainage density
ASTER Digital Elevation Model (DEM) was downloaded from the USGS earth explorer website for the development of drainage density (DD) and topographic wetness index (TWI). The production of the drainage density map was achieved in the spatial analyst of ArcGIS. This begins with the transformation of the raw DEM into Fil > > Flow direction > > accumulation raster. Calculation of the effective area of drainage then enables the delineation of the watershed hydrological pattern. The drainage density index of the watershed was calculated using Eq. (9):
where DD means drainage density and A is the area.
Drainage density (DD) provides about the degree of ponding within a hydrologic unit (Srivastava and Bhattacharya 2006). Its computation is an essential inference for deciphering important hydrogeologic properties such as infiltration and permeability. Hence, it is DD is significant to groundwater exploration.
Topographic wetness index
TWI was mapped from the slope map, prepared from DEM in ArcGIS 10.5.1. This was achieved by calculating the rate of change of an aspect of a cell grid within its neighborhood-based on Eqs. (10)–(11) (Hojati and Mokarram 2016):
where a is the specific catchment area, A is the catchment area, L is the contour length, and tan(β) is the slope.
TWI map was employed as the integrator of slope, elevation, and landform impacts on groundwater development (Pourali et al. 2016). Its computation sums up the influence of topographic roughness, hillslope, and foothill on lateral groundwater flow. Areas of high TWI enables the identification of areas of soil moisture accumulation and infiltration potential peculiar to foothills (Hojati and Mokarram 2016; Neilson et al. 2018). A significant highlight in the selection of the themes is the application of a surficial lithology map as a replacement for a conventionally scanned geologic map.
Computation of priority scores for the thematic layers and their consistency ratio
To improve the accuracy of the groundwater potential zone model, the relative degree of influence of each theme to groundwater development was computed as a priority score, based on the field experience of groundwater experts. AHP was employed to generate the priority score, and this was computed in a Microsoft Excel sheet in the following order:
-
1.
Opinions of groundwater experts were sought on the degree of relevance of the groundwater factors on each other and to groundwater development. These were used to formulate the criterion rating.
-
2.
The ratings of seven groundwater factors were collated as input for the groundwater criterion pairwise comparison based on Saaty’s 1–9 scale (Saaty 1980).
-
3.
The overall sums of scores of each element under the pairwise comparison were calculated. Each criterion cell was normalized by calculating the ratio of each pairwise cell to its sum in the columns.
-
4.
Each row of the normalized matrix was computed for its average to derive the priority scores.
The consistency of criterion ratings across the pairwise comparison cells and the derived priority scores was assessed as it further enables the optimization of priority scale and subjectivity among the GWPZ factors (Jha et al. 2010). This was achieved in three stages as follow:
-
1.
The consistency measure, λmax, was deduced as a principal eigenvalue based on the eigenvector technique. This is done by computing the matrix multiplication function of criterion ratings (in the pairwise comparison matrix row) and the normalized average of all the factors (within the normalized matrix column) divided by the criterion normalized average.
-
2.
The consistency index was calculated using the consistency measure as presented in Eq. (12):
where λmax is the consistency measure and n is the number of GWPZ factors.
where CI is the consistency index based on Eq. 13 and RCI is the random consistency index obtained from Saaty’s 1–9 scale (Saaty 1980). The resulting final criteria weights are considered as the normalized values as long as the consistency ratio lies within the expected limit. For a consistent normalization, the value of CR is expected to fall within 0.01 to 0.09, otherwise, the priority scores have to be adjusted.
Overlay analysis for the delineation of groundwater potential zone
The overlay analysis of the seven thematic layers was carried out in ArcGIS 10.5.1 as a summation of the effective influence of the factors based on their criterion weight to generate the ultimate potential zone. To arrive at these, all the layers were converted into an integral raster while their units were ranked. The groundwater potential zone was calculated based on Eq. 11:
where GWPI is the groundwater potential index, Wi is the criteria weight, Ri is the ranking of parameter factors, and i denotes each of the seven influencing factors with serial number from 1 to 7.
Validation of groundwater potential zone
The delineated GWPZs were validated using data of groundwater yield of exploration boreholes acquired from the National Groundwater Archive of the Department of Water Affairs, South Africa. The 84 geo-referenced yield data was overlaid on the GWPZ map to filter out the corresponding grid code identity of the borehole spot. The regression equation of the scattered diagram of the GWPZ grid codes against the groundwater yield was obtained to simulate the expected yield value. The coefficient of determination (R2), coefficient of correlation (R), and the p-value of the relationship between the observed value and the simulated value were calculated in Microsoft Excel. R was obtained using Eq. (15):
where Oi is the observed value which is the borehole yield (l/sec), Ei is the expected value drawn from the simulation of borehole yield, O̅n is the mean borehole yield, and n is the sample size of the borehole yield involved.
The relationship between the derived GWPZs and the actual borehole yield was further interpreted using a box-and-whisker plot. Representative borehole yield for each of the class of GWPZs was computed for their minimum value, lower quartile, median, upper quartile, and maximum value. These were used to derive the estimate for the bottom, 2Q box, 3Q box, whisker− and whisker+ (Table 2; Krzywinski and Altman 2014).
Results
Surficial Lithology
The surficial lithology map has been prepared using the geological map sheet of the Council of Geological Survey at a 1:250,000 scale as the base map. The surficial lithology is dominated by Mudstone (359 km2) covering 29% of the area. Dolerite (281 km2), sandstone (189 km2), shale (56 km2), and Quaternary sediment (4 km2) cover 23%, 15%, 5%, and 0.3% of the river catchment, respectively (Fig. 2a). The mudstone and silty/sandy mudstone intercalation units were estimated to cover approximately 340 km2 (27%) and 8 km2 (0.7%) of the area respectively. Hydraulic conductivity is one of the foremost aquifer properties that determine groundwater recharge and storage potential of a lithology. Quaternary Sediment was considered as the highest importance for groundwater storage on account of its high hydraulic conductivity, followed by sandstone, silty sandstone, and silty/sandy mudstone (Barlow and Leake 2012). The least important for the groundwater storage is the dolerite rock, followed by the shale and the mudstone.
Lineament density map
The lineament density map is classified into five: the very high (4%), high (10), moderate (17), low (25), and the very low/none lineament density area (Fig. 2b). The map shows the bias of lineament concentration to the North. This aligns with the topographic complexity in the North where the relief is steep and abrupt. Importantly, the zones of very high to moderate lineament density lie around the edges of the Karoo dolerite where the intrusion of magma creates a contact zone between the dolerite and the pre-existing sedimentary rock. Areas of extensive fracture system are replicated by high lineament density (Mostafa and Bishta 2005; Khosroshahizadeh et al. 2016; Meixner et al. 2018). Hence, the zones of effectively high/moderate lineament density, therefore, serve as a modifier for high-drained fractured dolerite that was ranked as very poor for groundwater potential under the surficial lineament. Rose diagram shows that the dominant trend of the surficial lineaments is WNW-ESE. This, therefore, conforms to the direction of the Neotectonic structure shown in the study area geology map (Fig. 1). Zones of higher lineament density are expected to have higher potential for groundwater accumulation; hence, they are ranked higher.
Drainage density
The drainage density map of the Buffalo River catchment typifies dendritic drainage. Within the tributaries, only the Quencwe and Mgqakwebe rivers are characterized by dendritic drainage with well-developed stream orders while the Yellowwood, Ngqokweni, and Tshoxa rivers are associated with a trellis or subparallel drainages with underdeveloped stream orders (Figs. 1 and 2c). The dendritic drainage pattern of the Buffalo catchment and the northern sub-basins depict coarse dissection of the geomorphological layer impacted by the land cover system and climatic contribution. Meanwhile, the drainage pattern of the southern sub-basins indicates structural and lithological controls (Waikar and Nilawar 2014).
The drainage density map was classified into four with areas of high concentration surrounding the river confluence where enormous groundwater discharge to the watercourse indicates a negative influence on aquifer development (Fig. 2c). The four spots of high drainage density in the South and one at the North can be associated with the existence of springs. They are shown to be proximal to contact zones of dolerite and the country rocks where lineament density is high. As a result, areas of higher drainage density are inversely ranked while the area of very low drainage density is assigned a higher rank.
Rainfall map
The mean annual rainfall for the hydrologic year records of 1989 to 2016 in the study area ranges from 544 to 610 mm (Fig. 2d). The rainfall trend shows a positive linear variation with relief in a Northwest-Southeast trend. This suggests the possible influence of relief on atmospheric circulation in such a way that favors orographic downpour at the high relief. Similarly, Owolabi et al. (2020a, b) noted that relief exhibits a linear spatial influence on a regional hydro-climatic pattern. The spatial variation in rainfall intensity influences the distribution of groundwater recharge rate across the study area. Due to the positive influence of rainfall on groundwater recharge, the areas with higher rainfall range are ranked higher.
Topographic wetness index
The result of the topographic wetness index for the study area is presented in Fig. 2e. The complexity of Buffalo topography is revealed by the lines of concentration of the low TWI, which coincides with the edges of dolerite outcrops in the North (Fig. 2). In a way, the concentrated low TWI patches depict the influence of dolerite intrusion on the initiation, evolution, and the development of rift (Madi and Zhao 2013). Consequently, the low TWI areas are more likely to develop an overland flow rather than enabling groundwater recharge on account of the influence of the hillslope factor. Meanwhile, high TWI which lies at the foothill of low TWI is more likely to enable groundwater recharge on account of the tendency for soil moisture accumulation (Fig. 2e). Soil moisture accumulation is a significant indicator of groundwater abundance, although the hydraulic properties of soil/lithologic material are the primary determinant of infiltration (Naghibi and Dashtpagerdi 2017).
TWI has been employed to decipher the average groundwater level in a watershed characterized by low permeability soils (Rinderer et al. 2014). Since the Buffalo catchment is dominated by argillaceous sedimentary material, TWI is therefore considered applicable to groundwater potential mapping here. The very low TWI that suggests the tendency for overland flow was assigned the lowest rank while the very high TWI that indicates the tendency for soil moisture accumulation zone was assigned the highest rank. The TWI showed high concentration in the north and center and coincidence with the drainage density (Fig. 2 c and e). The distribution of TWI also shows strong geologic control, influenced by the dolerite outcrop as shown in the Northwest, East, and the South (Figs. 1 and 2e).
Land surface temperature
The land surface temperature map is classified into four: the very low, low, moderate, and high as presented in Fig. 2 f. Areas of low temperature had the largest coverage (102 km2), followed by a moderate temperature class (356 km2), the very low-temperature class (508 km2), and the least which is hot temperature class (272 km2). The similitude in the geospatial attributes of LULC and LST further depicts the relative influence of urbanization in inducing urban heat index which indirectly culminates into the spatial variability in land surface temperature. This, therefore, conforms to the findings of Orimoloye et al. (2018) on the relationship between the LULC system and LST variability. Areas of high temperatures are associated with a high evaporation rate. Evaporation is a critical issue in a water-scarce country like South Africa, where it constitutes a significant soil moisture loss and diminution to shallow unconfined aquifers. As a consequence, areas with high temperatures are assigned the lowest rank while the areas with low temperatures are assigned the highest rank.
Land use/land cover
The result of the LULC mapping among the seven land cover features indicates that the cropland (320 km2), has the highest coverage (Fig. 2 g). This is followed by the grassland (295 km2), the built-up (247 km2), the mixed forest (188 km2), the scrubs (145 km2), and the bare ground (37 km2), while water bodies have the least coverage (4 km2). The validity of the LULC plot was confirmed using Google Earth features. The Rooikrandsdam and its watercourse located by the Quencwe River were distinctly marked out just the same way as portrayed in Google Earth, The dispersed settlement across the Mgqakwebe, Tshoxa, and Ngqokweni rivers showed similar distal segmentation just as observed in Google Earth. Also, the Evergreen nature forest showed similar sectoral demarcation in the Google Earth the same way as mapped in the LULC map. Due to the varying impact of LULC changes on groundwater development, the different elements of LULC change are rated based on their significance to groundwater investigation. A mixed forest is a naturally preserved environment and an important indication of groundwater potential. Scrubs and cropland rank second to the indicators of groundwater potential; hence, they are ranked higher than others. Meanwhile, built-up area and water bodies/courses are the least important areas for groundwater investigation, followed by bare ground which is vulnerable to evaporation. Grassland is ranked higher than the bare ground because of its significance to soil moisture accumulation.
Normalization of features of GWPZ mapping
Relevant weights were assigned to the seven themes based on the influence on groundwater development during the computation of AHP as presented in Table 3. The value of CR obtained is 0.09, implying that the criteria weight was based on a reasonable level of consistency. The factors and their classes are presented in Table 4.
Delineation of groundwater potential zone
The potential zone of groundwater was classified into five: good (187 km2), moderate (338 km2), fair (406 km2), poor (185 km2), and very poor (121 km2) zones as shown in Fig. 3. The study shows that the groundwater potential is high in the north and low in the south. The potential groundwater area lies in a perpendicular direction along the West-East direction to the direction of the catchment drainage. Overall, zones with high groundwater potential are dominant in the northwest, while the extremely poor groundwater potential zone is dominant in the south and southeast.
Validation and corroboration of groundwater potential zones
The scientific significance of models depends on validation reports; hence, it is considered the most important stage of scientific research. The spatial distribution of eighty-four exploration borehole yield employed is presented in Fig. 3. The coefficient of determination (R2 = 0.901) obtained from the scattered diagram indicates that the GWPZ model is an excellent fit for the characterization of zones groundwater yield as it explains the borehole yield variability around its mean (Fig. 4).
This was further established by the coefficient of correlation and the test for significance (p value < 0.01) for the model which that the modeling procedure shows a very significant and strong positive relationship with the borehole yield (Table 5), that is, the model can provide relevant and applicable information on the availability of groundwater in place of borehole yield. A more expository relationship between borehole yield and GWP rate is presented in the box-and-whisker plots in Fig. 5. Twenty boreholes each lies within the good and the moderate GWPZs with a yield range of 6.03–12.15 l/s and 3.15–9.87 l/s respectively while 15 boreholes lie within the fair GWPZs. The poor and the very poor GWPZs were occupied by 19 and 10 boreholes with the yield range of 0.19–2.05 l/s and 0.09–1.83 l/s respectively. The good GWPZ class reports a high level of agreement with borehole yield, whereby more than half of its class is 9.3 l/sec. The moderate GWPZ class is associated with the widest range and the highest yield standard deviation with an average value is 5.5 l/sec. The good and moderate GWPZs is therefore considered the most significant groundwater capture zone. The fair, poor, and very poor GWPZ classes are associated with 3.2, 0.8, and 0.4 l/s average yield which is not considered economical for groundwater development where water demand is high. The plot reveals that groundwater borehole exploitation sited on the good and moderate GWPZs area is most likely to provide considerable yield.
Discussion
Characterization of the Buffalo catchment groundwater potential
The GWPZ mapping reveals that Buffalo groundwater resources are hosted by two hydrostratigraphic units: the fractured unit, dominant in the permissive contact zones of dolerite, and the inter-granular unit comprising of the arenaceous sedimentary materials (Figs. 2a and 3). This dominant borehole yield falls within the range of 2–5 l/s, the fair GWPZ (Fig. 3), covering 33% of the study area. These findings agree with the report of Vegter (2006) on the hydrogeology of the regional water management area of Buffalo Catchment. However, excellent borehole yield is regionally biased in the study, thus occupying the Northern half of the study area, where the lineament density is high.
The outcome of the GWPZ model suggests that the groundwater distribution in the Buffalo River catchment is strongly controlled by the permissive contact zone of dolerite and country rocks (Figs. 1 and 3). The distribution of the groundwater yield shows a cluster of high yield at the West compared with the East; meanwhile, considering the orientation of the lineaments, groundwater flow could be assumed to flow from the West to the East (Figs. 2b and 3). This study, therefore, confirms the assertion of Chevallier et al. (2014) on the groundwater potential of weathered and fractured dolerite as a viable aquifer. The poor potential of the dolerite outcrop in the South is due to the limited/non-existence of surficial lineaments in the area (Fig. 2b). Owolabi et al. (2020a) noted that the Buffalo streamflow is a perennial flow and that the river is possibly sustained by the existence of springs or leaky aquifer. The findings here agrees with the submission as the perennial attributes of Buffalo drainage is possibly due to replenishment from perpendicular groundwater discharges at the suggested spring zones (Fig. 2c).
The inter-relationship across the influencing factors of groundwater
The high lineament density area depicts the influenced by tectonic activities, which also possibly accounts for the uplift in the northwest and the hillslope that deter settlement residency (Chevallier et al. 2014). The structural evolution influenced by tectonic activities in the northwest area is depicted by the high concentration of TWI features in conformity to Mandal and Mondal (2019). Hence, the northern half was validated to be associated with an extensive fractured system, joints, and macro-scale geologic structures that can facilitate groundwater accumulation and flow. This corresponds to the highly vegetated area of the land use/cover map (Fig. 2 g) and the highly dissected area of the geomorphological area shown by the drainage density map (Fig. 2c). The coarseness of the high drainage density area in the northern half, therefore, corresponds to the areas associated with high permeable soil and rock materials in the area in conformity to Waikar and Nilawar (2014). Moreover, Johnson et al. (2006) and Katemaunzanga and Gunter (2009) noted the northern half is characterized by abundant siltstone and sandstones compared with the Middleton Formation that is mainly dominated by Mudstone and shale at the southern (Fig. 1). The geomorphic evolution of Buffalo drainage can also be explained by the similitude in the trend of precipitation and drainage texture (Fig. 2 c and d). A similar discovery was noted by Ngapna et al. (2018) whose investigation of climate and morpho-tectonic interaction was through morphometric analysis. Considering the land use/cover features (Fig. 2 g), the area covered by dense vegetation at the north is associated with a high degree of high ruggedness which implies high infiltration potential and lesser runoff while the urban area dominates the south and consequently culminates into a high degree of runoff. This inference can be drawn to describe the dependence of drainage density on the LULC features (Fig. 2 c and g) and its influence on groundwater discharge at the Buffalo catchment mouth in agreement with the assertion of Brody et al. (2014).
Overall, the computation approach used in this work presents the GIS-based GWPZ model as an excellent tool for exploring the prospective spots of groundwater for site-specific geologic investigation. In the previous GWPZ mapping involving AHP, Maity and Mandal (2019) noted that the validation provides 78% credibility while Roy et al. (2020) acknowledged a discouraging validation outcome. However, in this work, a significant 90% plus assessment accuracy was obtained by the R2 and R here. This not only validated the applicability of AHP computation but also accredited the quality of influencing factors employed and the proficiency of pairwise weightage assignment.
Conclusions
The application of the geosciences approach involving the conjunction of non-linear and spatially-independent environmental, hydrologic, and geomorphic parameters to geologic parameters for mapping the zones of groundwater potential has been demonstrated. The uniqueness in the work lies in the selection of the parameters and the conceptual steps followed to narrow down uncertainty and ensure high precision mapping. The following conclusions can be made from the study:
-
The hybridization of aeromagnetic data scanned geologic map, and field geologic survey offers a high-precision map of surficial lithology.
-
The application of the analytical hierarchical process has affirmatively revealed the feasibility of integrating the stochastic geoscience themes for environmental management.
-
The robustness of site-specific factors for the production of accurate GIS-based groundwater potential was proven achievable.
-
Strong interrelationship was shown by the correspondence between tectonically stressed zones and zones of compacted TWI features, a trend of precipitation and drainage, the zones of coarser drainage texture, and areas of permeable earth materials.
Overall, the computational approach exhibited in this work can be adopted for the characterization of groundwater potential zones and areas requiring conservative use against groundwater contamination based on the seven parameters employed in any semi-arid/arid environment with similar fractured geology.
References
Althuwaynee OF, Pradhan B, Park HJ, Lee JH (2014) A novel ensemble decision tree-based Chi-squared Automatic Interaction Detection (CHAID) and multivariate logistic regression models in landslide susceptibility mapping. Landslides 11(6):1063–1078
Anbarasu S, Brindha K, Elango L (2019) Multi-influencing factor method for delineation of groundwater potential zones using remote sensing and GIS techniques in the western part of Perambalur district, southern India. Earth Sci Inf:1–16
Aquilué N, De Cáceres M, Fortin MJ, Fall A, Brotons LA (2017) spatial allocation procedure to model land-use/land-cover changes: accounting for the occurrence and spread processes. Ecol Model 344:73–86
Arabameri A, Rezaei K, Cerda A, Lombardo L, Rodrigo-Comino J (2019) GIS-based groundwater potential mapping in Shahroud Plain, Iran. A comparison among statistical (bivariate and multivariate), data mining, and MCDM approaches. Sci Total Environ 658:160–177
Baiyegunhi C, Gwavava O (2017) Magnetic investigation and 2½ D gravity profile modeling across the Beattie magnetic anomaly in the southeastern Karoo Basin, South Africa. Acta Geophys 65(1):119–138
Barlow PM, Leake SA (2012) Streamflow depletion by wells: understanding and managing the effects of groundwater pumping on streamflow. US Geological Survey, Reston, VA
Brody S, Blessing R, Sebastian A, Bedient P (2014) Examining the impact of land use/land cover characteristics on flood losses. J Environ Planning Mgmt 57(8):1252–1265
Burberry LF, Moore CR, Jones MA, Abraham PM, Humphries BL, Close ME (2018) Study of connectivity of open framework gravel facies in the Canterbury Plains aquifer using smoke as a tracer. Geol Soc Lond, Spec Publ 440(1):327–344
Butler K (2013) Band Combinations for Landsat 8. ArcGIS blog Esri.
Catuneanu O, Elango HN (2001) Tectonic control on fluvial styles: the Balfour Formation of the Karoo Basin, South Africa. Sedtry Geol 140(3-4):291–313
Chen W, Li H, Hou E, Wang S, Wang G, Peng T (2018) GIS-based groundwater potential analysis using novel ensemble weights-of-evidence with logistic regression and functional tree models. Sci Total Environ 634:853–867
Chen W, Pradhan B, Li S, Shahabi H, Rizeei HM, Hou E, Wang S (2019) Novel hybrid integration approach of bagging-based fisher’s linear discriminant function for groundwater potential analysis. Nat Res Research 28(4):1239–1258
Chevallier LP, Goedhart ML, Woodford AC (2014) Influence of dolerite sill and ring complexes on the occurrence of groundwater in Karoo fractured aquifers: a morpho-tectonic approach: Report to the Water Research Commission. Water Research Commission, South Africa
Cobbing JE, de Wit M (2018) The Grootfontein aquifer: governance of a hydro-social system at Nash equilibrium. South Afr J Sci 114(5-6):1–7
Cobbing J (2014) Groundwater for rural water supplies in South Africa. Nelson Mandela Metropolitan University and SLR Consulting (Pty) Ltd, South Africa
Cosgrove WJ, Loucks DP (2015) Water management: current and future challenges and research directions. Water Res Res 51(6):4823–4839
da Costa KA, Papa JP, Lisboa CO, Munoz R, de Albuquerque VHC (2019) Internet of things: a survey on machine learning-based intrusion detection approaches. Compt Netw 151:147–157
Duan H, Deng Z, Deng F, Wang D (2016) Assessment of groundwater potential based on multicriteria decision-making model and decision tree algorithms. Math Probs Eng
DWA (Department of Water Affairs, South Africa) (2010) Groundwater strategy 2010. Department of Water Affairs, Pretoria
Fenta AA, Kifle A, Gebreyohannes T, Hailu G (2015) Spatial analysis of groundwater potential using remote sensing and GIS-based multi-criteria evaluation in Raya Valley, northern Ethiopia. Hydrogeol J 23(1):195–206
Golkarian A, Naghibi SA, Kalantar B, Pradhan B (2018) Groundwater potential mapping using C5.0, random forest, and multivariate adaptive regression spline models in GIS. Environ Monitoring Assessmt 190(149)
Hashim M, Ahmad S, Johari MAM, Pour AB (2013) Automatic lineament extraction in a heavily vegetated region using Landsat Enhanced Thematic Mapper (ETM+) imagery. Adv Space Res 51(5):874–890
Hojati M, Mokarram M (2016) Determination of a topographic wetness index using high-resolution digital elevation models. Eur J Geog 7(4):41–52
Hong H, Tsangaratos P, Ilia I, Liu J, Zhu AX, Chen W (2018) Application of fuzzy weight of evidence and data mining techniques in the construction of flood susceptibility map of Poyang County, China. Sci Total Environ 625:575–588
Jha MK, Chowdary VM, Chowdhury A (2010) Groundwater assessment in Salboni Block, West Bengal (India) using remote sensing, geographical information system, and multi-criteria decision analysis techniques. Hydrogeol J 18(7):1713–1728
Johnson MR, Anhauesser CR, Thomas RJ (2006) The geology of South Africa. Geological Society of South Africa.
Kahinda JM, Meissner R, Engelbrecht FA (2016) Implementing integrated catchment management in the upper Limpopo River basin: a situational assessment. Physics and Chemistry of the Earth, Parts A/B/C 93:104–118
Kalantar B, Al-Najjar HA, Pradhan B, Saeidi V, Halin AA, Ueda N, Naghibi SA (2019) Optimized conditioning factors using machine learning techniques for groundwater potential mapping. Water 11(9):1909
Katemaunzanga D, Gunter CJ (2009) Lithostratigraphy, sedimentology, and provenance of the Balfour Formation (Beaufort Group) in the Fort Beaufort–Alice area, Eastern Cape Province, South Africa. Acta Geol Sin-Engl 83(5):902–916
Kelleher J, MacNamee B, D’arcy A (2015) Fundamentals of machine learning for predictive data analytics: algorithms, worked examples, and case studies. MIT Press, Cambridge
Khosroshahizadeh S, Pourkermani M, Almasian M, Arian M, Khakzad A (2016) Lineament patterns and mineralization related to alteration zone by using ASAR-ASTER imagery in Hize Jan-Sharaf Abad Au-Ag epithermal mineralized zone (East Azarbaijan—NW Iran). Open J Geol 6(4):232–250
Kordestani MD, Naghibi SA, Hashemi H, Ahmadi K, Kalantar B, Pradhan B (2019) Groundwater potential mapping using a novel data-mining ensemble model. Hydrogeol J 27(1):211–224
Krzywinski M, Altman N (2014) Points of significance: visualizing samples with box plots.
Lee S, Hong SM, Jung HS (2018) GIS-based groundwater potential mapping using artificial neural network and support vector machine models: the case of Boryeong City in Korea. Geocarto Int 33(8):847–861
Lee S, Song KY, Kim Y, Park I (2012) Regional groundwater productivity potential mapping using a geographic information system (GIS) based artificial neural network model. Hydrogeol J 20(8):1511–1527
Lee S, Hyun Y, Lee S, Lee M (2020) Groundwater Potential mapping using remote sensing and GIS-based machine learning techniques. Remote Sensing J 12(1200)
Lillesand T, Kiefer RW, Chipman J (2014) Remote sensing and image interpretation. John Wiley & Sons
Machiwal D, Jha MK, Mal BC (2011) Assessment of groundwater potential in a semi-arid region of India using remote sensing, GIS, and MCDM techniques. Water Res Mgmt 25(5):1359–1386
Madi K, Zhao B (2013) Neotectonic belts, remote sensing, and groundwater potentials in the Eastern Cape Province, South Africa. Int J Water Res Environ Eng 5(6):332–350
Maity DK, Mandal S (2019) Identification of groundwater potential zones of the Kumari river basin, India: an RS & GIS based semi-quantitative approach. Environ Devt Sustl 21(2):1013–1034
Mandal S, Mondal S (2019) Geomorphic, geo-tectonic, and hydrologic attributes and landslide probability. In statistical approaches for landslide susceptibility assessment and prediction. Springer, Cham: 41-75
Mandel S (2012) Groundwater resources: investigation and development. Elsevier
Matter JM, Goldberg DS, Morin RH, Stute M (2006) Contact zone permeability at intrusion boundaries: new results from hydraulic testing and geophysical logging in the Newark Basin, New York, USA. J Hydrogeology 14:689–699
Meixner J, Grimmer JC, Becker A, Schill E, Kohl T (2018) Comparison of different digital elevation models and satellite imagery for lineament analysis: implications for identification and spatial arrangement of fault zones in crystalline basement rocks of the southern Black Forest (Germany). J Struct Geol 108:256–268
Mitchell TM (1997) Machine learning. McGraw-Hill, New York
Mohammadi-Behzad HR, Charchi A, Kalantari N, Mehrabi NA, Karimi VH (2019) Delineation of groundwater potential zones using remote sensing (RS), geographical information system (GIS) and analytic hierarchy process (AHP) techniques: a case study in the Leyla–Keynow watershed, southwest of Iran. Carbonates Evaporites 34(4):1307–1319
Mostafa ME, Bishta AZ (2005) Significance of lineament patterns in rock unit classification and designation: a pilot study on the Gharib-Dara area, northern Eastern Desert, Egypt. Int J Remote Sens 26(7):1463–1475
Mueller JP, Massaron L (2016) Machine learning for dummies. John Wiley & Sons
Naghibi SA, Dashtpagerdi MM (2017) Evaluation of four supervised learning methods for groundwater spring potential mapping in the Khalkhal region (Iran) using GIS-based features. Hydrogeol J 25(1):169–189
Naghibi SA, Pourghasemi HR, Abbaspour K (2018) A comparison between ten advanced and soft computing models for groundwater qanat potential assessment in Iran using R and GIS. Theor Appl Climatol 131:967–984
Naghibi SA, Pourghasemi HR, Dixon B (2016) GIS-based groundwater potential mapping using boosted regression tree, classification and regression tree, and random forest machine learning models in Iran. Environ Monitoring Assessmt 188(44)
Neilson BT, Cardenas MB, O'Connor MT, Rasmussen MT, King TV, Kling GW (2018) Groundwater flow and exchange across the land surface explain carbon export patterns in continuous permafrost watersheds. Geophys Res Lett 45(15):7596–7605
Ngapna MN, Owona S, Owono FM, Mpesse JE, Youmen D, Lissom J, Ekodeck GE (2018) Tectonics, lithology and climate controls of morphometric parameters of the Edea-Eseka region (SW Cameroon, Central Africa): Implications on equatorial rivers and landforms. J Afr Earth Sci 138:219–232
Orimoloye IR, Mazinyo SP, Nel W, Kalumba AM (2018) Spatiotemporal monitoring of land surface temperature and estimated radiation using remote sensing: human health implications for East London, South Africa. Environ Earth Sci 77(3):77
Owolabi ST, Madi K, Kalumba AM, Alemaw BF (2020a) Assessment of recession flow variability and the surficial lithology impact: a case study of Buffalo River catchment, Eastern Cape, South Africa. Environ Earth Sci 79:187
Owolabi ST, Madi K, Kalumba AM (2020b) Comparative evaluation of Spatio-temporal attributes of precipitation and streamflow in Buffalo and Tyume Catchments, Eastern Cape, South Africa. Envir, Devt & Sustl, pp 1–16
Peddie NW (1982) International geomagnetic reference field. J Geomagn Geoelectr 34(6):309–326
Pietersen K, Beekman HE, Holland M, Adams S (2012) Groundwater governance in South Africa: a status assessment. Water SA 38(3):453–460
Pourali SH, Arrowsmith C, Chrisman N, Matkan AA, Mitchell D (2016) Topography wetness index application in flood-risk-based land use planning. Applied Spatial Anal Pol 9(1):39–54
Pourghasemi HR, Sadhasivam N, Yousefi S, Tavangar S, Nazarlou HG, Santosh M (2020) Using machine learning algorithms to map the groundwater recharge potential zones. J Environ Mgmt 265:110525
Pradhan B (2010) Remote sensing and GIS-based landslide hazard analysis and cross-validation using multivariate logistic regression model on three test areas in Malaysia. Adv Space Res 45(10):1244–1256
Prasad P, Loveson VJ, Kotha M, Yadav R (2020) Application of machine learning techniques in groundwater potential mapping along the west coast of India. GI Sci Remote Sens J:1–18
Rahmati O, Nazari SA, Mahdavi M, Pourghasemi HR, Zeinivand H (2014) Groundwater potential mapping at Kurdistan region of Iran using analytic hierarchy process and GIS. Arab J Geosci
Rajasekhar M, Raju GS, Raju RS (2019) Assessment of groundwater potential zones in parts of the semi-arid region of Anantapur District, Andhra Pradesh, India using GIS and AHP approach. Modeling Earth Sys Environ 5(4):1303–1317
Rinderer M, Van Meerveld HJ, Seibert J (2014) Topographic controls on shallow groundwater levels in a steep, pre-alpine catchment: when are the TWI assumptions valid? Water Res Res 50(7):6067–6080
Rizeei HM, Pradhan B, Saharkhiz MA, Lee S (2019) Groundwater aquifer potential modeling using an ensemble multi-adoptive boosting logistic regression technique. J Hydrol 579:124172
Roy S, Hazra S, Chanda A, Das S (2020) Assessment of groundwater potential zones using multi-criteria decision-making technique: a micro-level case study from red and lateritic zone (RLZ) of West Bengal, India. Sust Water Res Mgmt 6(1):4
Saaty TL (1999) Basic theory of the analytic hierarchy process: how to make a decision. Revista de la Real Academia de Ciencias Exactas Fisicas y Naturales 93(4):395–423
Saaty TL (1980) The analytic hierarchy process: planning, priority setting, resource allocation. McGraw-Hill, New York
Saaty TL (1992) The hierarchy: a dictionary of hierarchies. RWS Publications, Pittsburgh 496
Sahoo S, Dhar A, Kar A, Ram P (2017) Grey analytic hierarchy process applied to effectiveness evaluation for groundwater potential zone delineation. Geocarto Int 32(11):1188–1205
Sandoval JA, Tiburan CL (2019) Identification of potential artificial groundwater recharge sites in Mount Makiling forest reserve, Philippines using GIS and analytical hierarchy process. Applied Geog 105:73–85
Schreiner B, Hassan R (2010) Transforming water management in South Africa: designing and implementing a new policy framework. Springer Science & Business Media 2
Senthilkumar M, Gnanasundar D, Arumugam R (2019) Identifying groundwater recharge zones using remote sensing & GIS techniques in Amaravathi aquifer system, Tamil Nadu, South India. Sust Envir Res J 29(1):15
Slaughter AR, Mantel SK, Hughes DA (2014) Investigating possible climate change and development effects on water quality within an arid catchment in South Africa: a comparison of two models.
Srivastava PK, Bhattacharya AK (2006) Groundwater assessment through an integrated approach using remote sensing, GIS, and resistivity techniques: a case study from a hard rock terrain. Int J Remote Sens 27(20):4599–4620
Suresh S, Ajay SV, Mani K (2016) Estimation of the land surface temperature of high range mountain landscape of Devikulam Taluk using Landsat 8 data. Int J Res Eng Tech 5:92–96
Tahmassebipoor N, Rahmati O, Noormohamadi F, Lee S (2016) Spatial analysis of groundwater potential using weights-of-evidence and evidential belief function models and remote sensing. Arab J Geosci 9(1):79
Tanner JL, Hughes DA (2015) Surface water–groundwater interactions in catchment-scale water resources assessments—understanding and hypothesis testing with a hydrological model. Hydrol Sci J 60(11):1880–1895
Tien Bui D, Shirzadi A, Chapi K, Shahabi H, Pradhan B, Pham BT, Singh VP, Chen W, Khosravi K, Bin Ahmad B, Lee SA (2019) Hybrid computational intelligence approach to groundwater spring potential mapping. Water 11(10):2013
Thompson SA (2017) Hydrology for water management. CRC Press
Urqueta H, Jódar J, Herrera C, Wilke HG, Medina A, Urrutia J, Custodio E, Rodríguez J (2018) Land surface temperature as an indicator of the unsaturated zone thickness: a remote sensing approach in the Atacama Desert. Sci Total Environ 612:1234–1248
Vegter JR (2006) Hydrogeology of Groundwater: Region 26: Bushmanland. WRC.
Waikar ML, Nilawar AP (2014) Identification of groundwater potential zone using remote sensing and GIS technique. Int J Innov Res Sci Eng Tech 3(5):12163–12174.l
Acknowledgments
We are grateful to Prof Oswald Gwavava of the University of Fort Hare for his assistance with aeromagnetic data provision and to Dr. (Ms.) Chinemerem Ohoro for her sacrificial support in the course of the field geologic mapping. Special thanks to Govan Mbeki Research and Development Centre for making the researching platform easy with a soft fund.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
No human or animal participant was involved or harmed in any way during the conduct of this research.
Conflict of interest
The authors declare that there is no conflict of interest
Additional information
Responsible Editor: Biswajeet Pradhan
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Owolabi, S.T., Madi, K., Kalumba, A.M. et al. A groundwater potential zone mapping approach for semi-arid environments using remote sensing (RS), geographic information system (GIS), and analytical hierarchical process (AHP) techniques: a case study of Buffalo catchment, Eastern Cape, South Africa. Arab J Geosci 13, 1184 (2020). https://doi.org/10.1007/s12517-020-06166-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12517-020-06166-0