Introduction

Understanding the incipient motion of sediment particles in sediment transport is of vital scientific importance to understand the incipient threshold of different properties sediment under various flow conditions. Also, it is of practical importance for channel sediment transportation, bank stabilization, development and management of deltas and coasts, aggradation/erosion in the upstream and downstream of the reservoirs, and so forth. When the flow-induced shear stress exceeds a certain critical value, the bed particle begins to move, and the shear stress in this situation is defined as the incipient shear stress, which equals to component force of water weight on unit bed surface in the flow direction. Shields curve is widely known for commutating critical shear stress of uniform cohesionless sediment (Singh et al. 2017). However, the relationship between the cohesive of sediment particle and the range of consolidation has been neglect. Subsequently, the following model studies have been conducted to understand the characteristics of the incipient shear stress of consolidated cohesive sediment.

In addition to common properties of sediment, cohesive sediment is characterized by clay particles with large specific surface areas. Higher complexity of the incipient motion and scouring mechanism of cohesive sediment is induced compared with those of noncohesive sediment, because the surface of cohesive particles in water is strongly influenced by the physical and chemical action (Tan et al. 2007b; Zhang et al. 2009; Wang and Cai 2014; Tan and Chen 2016).

The incipient motion of cohesive sediment has been extensively studied (Dune 1959; Chien and Wan 1999). Since 1962, many experiments testing the erosion process of cohesive sediment bed that were deposited from suspension have been conducted, including those by Mehta (1973), Mehta and Partheniades (1975), and Krone (1962, 1993). In the 1990s, the values of critical shear stress were measured in various experiments (McNeil et al. 1996; Liem et al. 1992; Roberts and Lick 1997, 1998a, b, 1999). In general, a full consolidation process involves flocculation, deposition, erosion, transport, and consolidation (Wu et al. 2004). A critical bed shear stress to initiate erosion was essential for the setup of numerical models. Toorman (2002) and Winterwerp (2002) found that different water depths hardly influenced the process of deposition for cohesive sediment. In situ erosion experiments were carried out in the York River by Maa and Kim (2002). They found that minimal variation of the critical bed shear stress for starting erosion showed at the water-sediment interface, while significant increase of the critical bed shear stress for the well-consolidated sediment occurred below the interface. To represent distribution of the bed shear stress, a probability function was used by Winterwerp (2007). Mehta and Partheniades (1975) simulated the experimental results by Krone (1962) successfully. Maa et al. (2008) studied the critical shear stress for cohesive sediment bed under steady flow. Wang and Hu (2009) suggested a critical velocity for the scouring of cohesive sediment from the Zhuwo Reservoir as a function of the deposition dry bulk density, which is being expressed as:

$$ {U}_c=4.6{\left({\rho}^{\prime}\right)}^4 $$
(1)

where Uc is the critical velocity, and ρ′ is the dry bulk density. An empirical formula was proposed by Xu et al. (2015), for the critical velocity of coastal muds at different densities, which indicated that the incipient shear stress grows exponentially with mud density. Zheng and An (2017) reanalyzed data from two experiments and found that the critical shear stress depends on bulk density and clay solid content using the data in the work of Sharif (2003), while result from Kothyari and Jain (2008) demonstrated that the critical shear stress of cohesive sediments varied with the clay solid content and clay volume content in the presence of gravel and air.

However, due to short consolidation times, different impacts of consolidation characteristics on the starting motion of cohesive sediment cannot be effectively revealed in Eq. (1). Moreover, the consolidated cohesive sediment taken from the field sites was scoured by a jet flow at the laboratory. Thus, a disturbance to the original sediment sample may affect the inner stable structure of deposition.

Hence, in this study, to improve the experiment for the two shortcomings described above, a pressure pipe system was established to conduct the incipient motion experiments of cohesive sediment with different consolidation time. Various effects of consolidation time, dry bulk density, and content of cohesive particles on the incipient motion were investigated by experiments, and a new incipient motion formula of cohesive sediment was proposed. The experiments results and theoretical analysis obtained in this study may help to deepen the understanding of the mechanism of the incipient motion of consolidated cohesive sediment.

The present study aims to measure and quantitatively explore the effects of consolidation on the critical conditions of incipient motion of cohesive sediments. Laboratory experiments were performed in a rectangular PMMA glass pipe and the influences of bulk density, water content, and yield stress on the incipient motion were systematically investigated. More specifically, the experimental material, equipment, and methodology are introduced in the “Experiments” section. In the “Influencing factors on incipient shear stress of cohesive sediment” section, the results are presented, and the influences of the various factors are compared and analyzed, especially the influence factors on incipient shear stress of cohesive sediment. In the “Incipient motion formula of cohesive sediment” section, an empirical formula for the critical parameter and a modified Shields diagram are proposed based on the experimental data, and some suggestions for further study are discussed. Finally, the “Conclusions” section presents the main conclusions of the study.

Experiments

Experimental setup

A long consolidation time can help cohesive sediment resist large flow shear stress. It is difficult for an open channel flume to steadily provide the necessary conditions for the incipient motion of cohesive sediment. For this reason, a special experiment setup was designed that consisted of a rectangular PMMA glass pipe as shown in Fig. 1. And the pipe is 3-cm wide and 12-cm long. The sediment samples were placed in a test cylinder with the same size as the test sample. The inner diameter of the test cylinder was 7 cm. Two piezometric tubes were installed 0.6 m upstream and 0.6 m downstream from the test cylinder, respectively. A rubber piston below the cylinder was used to push sediment samples upwards in the cylinder. In the experiments, in order to keep the sample surface and pipe bottom at the same level, a manual elevating screw was used to control the rubber piston so that the sample height could be adjusted according to the scouring situation.

Fig. 1
figure 1

Schematic view of the experimental installation

Full size image

Sediment samples

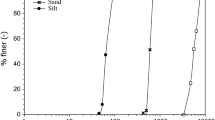
The sediment samples to be tested were selected from the deposition at Huayuankou in the Lower Yellow River as well as from the Yangtze River. Sediment samples collected from Lower Yellow River are mostly Kaolinite and Montmorillonite, and that from Yangtze River are mainly Illite and Kaolinite, the detailed properties being given in Table 1. For the four groups of tested sediment samples, 12 of different consolidation time for each group were selected, a total of 48 data sets were analyzed. The consolidation time in the experiments was 1 day, 3 days, 5 days, 8 days, 13 days, 21 days, 34 days, 55 days, 89 days, 144 days, 233 days, and 377 days, respectively. Table 1 shows the details of all data sets that were collected from these laboratory experiments; D50 represents median sediment size, is cohesive particles content, is dry bulk density, and represents incipient shear stress. These two kinds of cohesive sediment were divided into four groups using the sieving and sedimentation methods as follows: (i) group A was the sediment deposition from the Yangtze River with particle sizes smaller than 0.10 mm; (ii) group B was the sediment deposition from the deposition in the Lower Yellow River; and (iii) mixing group A with group B in the ratio of 5:1 and 2:1 was taken as groups C and D, respectively. The size distribution curves of these four groups are shown in Fig. 2. Median sediment size of groups A, B, C, and D is 0.046 mm, 0.008 mm, 0.042 mm, and 0.038 mm, respectively. Sediment with diameter finer than 0.005 mm in this study is defined as cohesive particles, and cohesive particle content is taken as weight percentage of cohesive particles to all the sediment. Cohesive particle content in groups A, B, C, and D is 2%, 38%, 8%, and 15%, respectively.

Table 1 Summary of collected data
Full size table
Fig. 2
figure 2

Size distributions of samples

Full size image

Consolidation experiment

The whole process of consolidation experiment is described as follows: First, the prepared sediment sample was put into a plastic basin after being uniformly mixed. Clear water (tap water) was sucked out as the clear water percolated slowly during the free settling stage of the sediment. Secondly, the deposition in the plastic basin was mixed uniformly by continuous whisking, and it was then put into separate sample containers. Thirdly, these sample containers were submerged in a water pool, and thus, various consolidation processes under the water surface were conducted, with different consolidation times ranging from 1 to 377 days. The sediment sample in each container was taken out for the incipient motion experiment.

Before the incipient motion experiment, sediment sample container was put on the top of experimental device firstly, one side of the container was removed, and then, the experimental device was rising slowly until all the sediment sample went into the test cylinder. This ensured that the sediment sample could not be disturbed during the whole period of experiment, because experiment operation–induced disturbance was avoided to the great extent, as sediment sample was put on the device top and went to the test cylinder gently.

In order to analyze the change of the dry bulk density of cohesive sediment during the consolidation process, another consolidation experiment of a tested sediment sample was also carried out in a measuring cylinder.

Scour experiment

A series of experiments have been carried out at the Experimental Hall of Sedimentation and Flood Control, Wuhan University, in order to investigate the incipient shear stress of cohesive sediment under different consolidation times.

The scour experiment procedure is, firstly, the sample was placed in the bottom inlet, and then made sample surface a little higher than the conduit bottom by pushing the sample up. Secondly, to ensure the conduit was fulfilled by water and the sample could be scoured, the power of a pump was increased gradually until the pump reached a specified flow rate. Thirdly, when an intermittent but discernable change occurred on the deposition surface, such as the intermittent patches or local pits, the flow shear stress in the pipe was regarded to be equal to the critical incipient shear stress of cohesive sediment. When the sample was scoured, it was pushed up gradually so that its surface was always level with the conduit bottom. Finally, the results of the experiment were recorded. It should be noted that the depth of sediment sample is 10 cm, and recorded scouring depth in the experiment is 0.47–7.91 cm. It should be noted that the vertical change of density along the depth of the sample is not considered in this study.

Shear stress calculation

According to the study of Bathurst (1985), relationship between average velocity U and wall shear stress τ in the rectangular tube should follow the common formula for the shear velocity \( {u}_{\ast }=\sqrt{\tau /\rho }=\sqrt{\lambda /8U} \) , the factor of friction λ can be expressed as follows:

$$ \lambda =\frac{8\tau }{\rho {U}^2} $$
(2)

where ρ is water density, and wall shear stress τ can be calculated if λ is known.

Additionally, previous studies such as Nicholas indicated that the factor of friction λ can be calculated using empirical formula as below:

  1. (i)

    For the hydraulically smooth area: shear Reynolds number \( {R}_{e\ast }=\frac{\Delta {u}_{\ast }}{v}<5\ \mathrm{or}\ \frac{\Delta }{\delta_0}<0.4 \),

$$ \mathrm{Paula}\ \mathrm{Theseus}\ \mathrm{formula}:\uplambda =\frac{0.316}{R_e^{1/4}}\kern0.5em 4000<{R}_e<{10}^5 $$
(3)
$$ \mathrm{Nicholas}\ \mathrm{formula}:\frac{1}{\sqrt{\lambda }}=21g\left({R}_e\sqrt{\lambda}\right)-0.8\kern0.5em {R}_e<{10}^6 $$
(4)
  1. (ii)

    For the area between hydraulically smooth and rough: \( 5\le ={R}_{e\ast}\le 70\ \mathrm{or}\ 0.4\le \frac{\Delta }{\delta_0}\le 6 \),

$$ \mathrm{White}\ \mathrm{formula}:\frac{1}{\sqrt{\lambda }}=-21g\left(\frac{2.51}{R_e\sqrt{\lambda }}+\frac{\Delta}{3.7d}\right)\kern0.5em 3000<{R}_e<{10}^6 $$
(5)
  1. (iii)

    For the hydraulically rough area: \( {R}_{e\ast }>70\ \mathrm{or}\ \frac{\Delta }{\delta_0}>6 \),

$$ \mathrm{Nicholas}\ \mathrm{formula}:\lambda =\frac{1}{{\left[21g\left(3.7\frac{d}{\Delta}\right)\right]}^2}\kern0.75em {R}_e>\frac{191}{\sqrt{\lambda }}\left(\frac{d}{\Delta }\right) $$
(6)

where, Δ is absolute roughness, and δ0 is the viscous sublayer, v is kinematic viscosity, which is related with water temperature, and d is the tube diameter.

In current experiments, the flow discharge in current experiments ranged from 3.68 to 21.64 m3/h, the Reynolds number Re in a rectangular tube can be expressed as:

$$ {R}_e=\frac{Uh_d}{v} $$
(7)

where, hd is rectangular height. Re it is less than 105 ranging from 7681 to 49607.

Additionally, sediment sample in the experiments was fine sediment; bed surface before scour experiment was generally smooth; the absolute roughness Δ was generally less than 0.046 mm (the maximum median particle size). The shear velocity u∗ in the experiment less than 0.10 m/s. When shear velocity u∗ is 0.10 m/s, the corresponding wall shear stress τ is 10 N/m2, the calculated shear Reynolds number Re∗ less than 7.2. As thus, Eqs. (3) and (4) are suitable to calculate factor of friction λ in this study, and wall shear stress τ could be obtained using Eq. (2) then.

Experimental results

According to Eq. (2), the flow velocity was obtained by dividing the discharge by the area of rectangular pipe section. During the period of consolidation, the deposition was getting denser progressively, and eventually to relatively high dry density and strong cohesion. After being consolidated from 1 to 377 days, each deposition sample’s dry bulk density was measured. Figure 3 shows the variation of dry bulk density at different consolidation stages, which reveals that (i) the dry bulk density increased rapidly at the beginning of consolidation, and followed by slow increase after several months; (ii) only a few groups could reach their steady states after a consolidation time of 377 days.

Fig. 3
figure 3

Dry bulk densities versus consolidation times

Full size image

Influencing factors on incipient shear stress of cohesive sediment

Influence of consolidation times on incipient shear stress

During the consolidation process of cohesive sediment, the deposition compressed slowly, and pore water percolated out gradually. In general, the deposition-consolidation process lasts a long time so that the values of cohesive force and shear strength vary with the consolidation time. Accordingly, the scour resistance of the deposition differs significantly for different consolidation time (Fig. 4, Tan et al. 2007a).

Fig. 4
figure 4

Relationships between the incipient shear stress and consolidation time for different groups

Full size image

Fig. 4 shows that the incipient shear stress, τc , of sediment sample increased over consolidation time. Moreover, the increased rate was different for different sediment groups. During the deposition process of 377 days, the values of incipient shear stress for group A was 0.30 to 0.47 N/m2, with a smallest increase of 57%; the values for group C ranged from 0.63 to 2.21 N/m2, with a maximum increase of 251%; and the increased percentages of incipient shear stress for group B and group D were 207% and 208%, respectively.

Since it is very difficult to accurately measure the deposition time under natural conditions, the concept of relative dry bulk density ρd was introduced herein. According to Chien and Wan (1999), a function of dry bulk density and consolidation time is expressed as:

$$ {\rho}^{\prime }={\rho}_{s1}^{\prime }+B\log t $$
(8)

where \( {\rho}_{s1}^{\prime } \) is the dry bulk density in the first year after consolidation, termed as the initial dry bulk density. And relative dry bulk density, ρ′, is defined as:

$$ {\rho}_d=\frac{\rho^{\prime }}{\rho_{s1}^{\prime }}=1+\frac{B}{\rho_{s1}^{\prime }}\log t=f(t) $$
(9)

As indicated by Eq. (6), if other factors remain unchanged, ρd is influenced by the consolidation times and can be calculated by the measured ρ′ and \( {\rho}_{s1}^{\prime } \) In this way, the difficulties of measuring the consolidation times can be effectively overcome.

Effect of dry bulk density on the incipient shear stress

The dry bulk density depends on the sediment composition and particle shape, etc. For example, the dry bulk density increased when the median diameter increased (Shu et al. 2009). However, for certain sediment deposition, the dry bulk density slowly increased as the consolidation time increased. Such different evolution of the dry bulk density for different kinds of cohesive sediment influenced the variation of incipient shear stress.

The relationships between the dry bulk density and incipient shear stress for different sediment groups are plotted in Fig. 5. It shows that the incipient shear stress increased as the dry bulk density increased. For instance, the incipient shear stress for group B increased from 1.91 to 5.86 N/m2 when the dry bulk density varied from 0.74 to 0.84 × 103 kg/m3. Moreover, these curves in Fig. 5 also indicate that dry bulk density affected the incipient shear stress differently for various deposition samples. It should be noted that the incipient shear stress increased as the content of cohesive particles increased (Fig. 6).

Fig. 5
figure 5

Relationships between the incipient shear stress and dry bulk density for different groups

Full size image
Fig. 6
figure 6

Comparison between the calculated and measured velocities

Full size image

For the same sediment sample, the incipient shear stress increased with the increasing dry bulk density, which indirectly demonstrated the relationship between the incipient shear stress and consolidation time. For different sediment samples with the same consolidation time, the larger of the particle sizes in the sample, the greater of the dry bulk density. Since the main force resisting scouring was the cohesive force, the cohesive sediment particles with larger sizes could be scoured more easily than those particles with smaller sizes.

Influence of the cohesive particle content on incipient shear stress

The content of cohesive particles in the deposition sample (Pc) is one of the most important factors that influences the magnitude of cohesive force. The cohesive sediment particles are very fine with large surface areas. Therefore, they are subjected to intensive physical and chemical effects. These effects are caused by the presence of an inner cohesive force.

However, previous researches rarely introduced the content of cohesive particles, even if this factor was closely related to the incipient shear stress. Figure 4 also shows the relationship between Pc and τc for different sediment samples under the same consolidation time. It can be seen that the higher of the content of cohesive particles, the greater of the incipient shear stress. Consequently, cohesive sediment with a higher Pc scoured less easily.

Analysis of influencing factors

As discussed earlier, the value of incipient shear stress significantly depended on the consolidation time, the dry bulk density, the content, and mineral composition of cohesive particles. Since a logarithmic relationship between the dry bulk density and consolidation time has been observed, the variable of consolidation time can be implicitly expressed as a function of the relative dry bulk density. The most important factor that influenced the cohesive force was cohesive particle content, which further affected the incipient shear stress.

For the same sediment sample, the incipient shear stress increased with the dry bulk density, which is consistent with the observation that a larger value of incipient shear stress would be obtained with a longer consolidation time. For different sediment samples, the deposition composition is different, and this may partially led to the difference in the relationship between the dry bulk density and incipient shear stress.

Generally, the consolidation time and content of cohesive particles were mutually independent, but both of them significantly influenced the incipient shear stress. The incipient shear stress increased with the increase of consolidation time and cohesive particle content.

Incipient motion formula of cohesive sediment

Preliminary analysis of the incipient motion mechanism

During consolidation, the forces and motion modes for the fine cohesive sediment were different from those for noncohesive sediment once the erosion process started. The noncohesive sediment was mainly affected by the hydrodynamic force and effective gravity, while the cohesive sediment was affected by the cohesive force between particles in addition to the two forces mentioned above (Bai et al. 2002).

During consolidation, the cohesive sediment was gradually compressed and formed a stable structure. The cohesive force between particles increased gradually, and became the main factor that resisted erosion. Thus, the stable structure and cohesive force between particles were generally the key influencing factors for the cohesive sediment erosion. During the consolidation process, the pore water between particles percolated out slowly, and the deposition was compressed slowly, so the dry bulk density increased gradually. Following Gu and Sun (2005), the inner cohesion force of soil, C, is the function of the ratio of water content to cohesive soil content m and dry bulk density ρ', which can be expressed by:

$$ C=\left(-33m+44\right)\times \left(3.75{\rho}^{\prime }-4.32\right)\kern0.5em m<1.33 $$
(10)

Thus, the content of cohesive particles for the deposited sediment kept unchanged during the process of consolidation. With the decrease of water content, the value of m decreased, and the value of ρ′ increased, which led to the increase of C. In other words, it was more difficult for scouring to occur as the consolidation time increased (Fig. 7).

Fig. 7
figure 7

The relationships between inner cohesion force C and cohesive soil content m

Full size image

Formula of incipient shear stress

As discussed earlier, the values of incipient shear stress greatly depended on the consolidation time, the dry bulk density, and the content of cohesive particles. If the cohesive content and the composition of deposition sample remained unchanged, the consolidation time influenced the dry bulk density. According to Shu et al. (2008), the incipient shear stress is given by:

$$ {\tau}_c=k{P}_c^{\eta }{\left(\frac{\rho^{\prime }}{\rho_{s1}^{\prime }}\right)}^{\varphi } $$
(11)

where k, η, and ϕ are coefficients, which can be estimated using the least square method. Based on the 48 groups of data, the estimated values of k, η, and ϕ were 18.5 N/m2, 0.88, and 10.3, respectively. Then, Eq. (8) can be rewritten as:

$$ {\tau}_c=18.5{P}_c^{0.88}{\left(\frac{\rho^{\prime }}{\rho_{s1}^{\prime }}\right)}^{10.3} $$
(12)

where Pc is a dimensionless parameter for the cohesive particle content, and the units of ρ′ and \( {\rho}_{s1}^{\prime } \) are both 103 kg/m3. This equation can be used to estimate the incipient shear stress for sediment with 2–38% of cohesive particle content.

Formula validation

In order to assess the proposed formula, the experimental data obtained by Wang and Zhang (1989) and Yang and Wang (1995) were used. These data were obtained from the deposition observations from a reservoir and the Hangzhou Bay, with the median diameters of 0.004 and 0.0104 mm, respectively and with the corresponding contents of cohesive sediment of 55% and 35%. The incipient shear stress can also be represented by the incipient velocity. Figure 6 compares the predictions using Eq. (9) and the measured incipient velocities, and it can be seen that the calculated results agree well with the measured, especially for those with smaller incipient velocities.

Conclusions

Based on experimental and theoretical methods, this paper investigates the incipient motion mechanism of cohesive sediment, especially the impact factors of incipient shear stress including the consolidation time, dry bulk density, and cohesive particle content. A formula of incipient shear stress for cohesive sediment was proposed and verified by the experimental data. The following conclusions can be drawn:

  1. 1.

    The incipient shear stress correlated closely with the consolidation time, dry bulk density, and cohesive particle content. The dry bulk density influenced the incipient motion due to the integrated influences of the consolidation time and composition of sediment mixtures. Therefore, the consolidation time and cohesive particle content were mutually independent, whereas both of them had a significant influence on the incipient shear stress. The magnitude of incipient shear stress increased with the increase of consolidation time and cohesive particle content. Consequently, cohesive sediment scoured less easily than noncohesive sediment.

  2. 2.

    The incipient motion mechanism of cohesive sediment was described. During the deposition process of cohesive sediment, with the pore water filtering out slowly, the distance between particles became shorter, and the cohesion force increased. Consequently, cohesive sediment scoured less easily as the consolidation time prolonged.

  3. 3.

    A formula of the incipient shear stress was derived for natural river conditions, and it was expressed as a function of content of cohesive particles and relative dry bulk density. Three parameters in the formula were determined by the experimental data, and the calculated values agreed well with the measured data.