Introduction

Raising the level of environmental performance in construction is one of the current problems in construction production engineering. It is very important to study the parameters creating the environmental performance (friendliness) of building solutions and their quantitative and qualitative assessment criteria. It is also important to determine the significance of environmental criteria at various stages of the investment, as well as the ways and methods of its assessment.

In construction, a major step forward has been made to raise the environmental performance of buildings. Sustainable construction and green construction studies have appeared (Al-Gahtani et al. 2016; Ali and Al Nsairat 2009; Banani et al. 2016; Bansal et al. 2017; Hatefi and Tamošaitienė 2018; Li-Yin et al. 2007; Mavi and Standing 2018; Saleh et al. 2016; Shishir et al. 2015; Sunita et al. 2015a, b, c; Swarup et al. 2011; Yu et al. 2018) and building certification systems and their applications in various countries (Castro-Lacouture et al. 2009; Cidell 2009; Cole and Valdebenito 2013; Schweber and Haroglu 2014; Suzer 2015). The formal and legal requirements for construction works have also been changed (e.g., in the field of energy efficiency, environmental friendliness)

Analyzing the requirements for building objects, it can be stated that the issue of environmental performance is a very broad problem concerning both the environment inside the building and the entire surrounding environment. Environmental performance should be taken into account throughout the building’s “life” cycle. Therefore, already at the level of pre-project studies, it is necessary to conduct analyses regarding the effects on the environment and required actions for environmental protection. Such checks are of formal and legal nature; they examine compliance with regulations and previously issued decisions.

Some authors see an improvement in the environmental performance of buildings in design (Anysz and Narloch 2019) and choosing the right building materials. For example, Ljungberg (2007) reviews current methods as well as presents models on how to develop sustainable products. Castro-Lacouture et al. (2009) proposed a mixed-integer optimization model that incorporates design and budget constraints while maximizing the number of credits reached under the Leadership in Energy and Environmental Design (LEED) rating system.

According to the author, the environmental problem should be included in the overall assessment of projects (including construction solutions) in the form of optimization. This is a necessity due to the increasingly stringent requirements set for buildings in various areas of their ecological characteristics, features, and properties.

The purpose of this article is (1) to indicate the criteria (parameters, features) that create the level of environmental performance of a given building solution by analyzing the utility requirements for building objects; (2) to demonstrate the essential characteristics (specificity) of ecological construction; (3) and to propose for a method of assessing construction projects, taking into account the criterion of environmental performance supporting decision-making.

It should be emphasized that the elements that have significance (e.g., type of material, technology) in creating the level of environmental performance of construction projects (building solutions), in construction practice, are largely chosen based on experience and intuition or based on “trend” of building if of course the contracting authority does not impose it in advance. Meanwhile, each construction solution due to their different physical, mechanical, chemical, etc. features differs. And this difference, despite meeting the formal and legal ranges, causes that each solution has a different ecological effect. To obtain rational and acceptable technical, economic, and ecological indicators, it is still necessary at the design stage to choose elements that create an environmental performance (friendliness) among the existing alternative solutions available in the given market. This requires the selection of appropriate assessment criteria that define the characteristics of a given building solution (Anysz and Buczkowski 2018; Ibadov 2017, 2018a, b; Jaśkowski and Biruk 2010; Shevchenko et al. 2019). Then, a comparative analysis (assessment) of alternative technical and technological solutions should be done and the most optimal variant in a given decision situation should be chosen.

In practice, it is usually limited to time and cost assessment. In this regard, the optimal construction solution is the one that has the most favorable cost and/or implementation time indicator. According to the author, for the “conscious” creation of ecological features of a building, it is justified to take into account, in addition to the time-cost characteristics of the considered building solutions, an additional criterion (additional criteria), taking maximum account of the priorities of a given decision situation. It can be a generally formulated criterion of the degree of environmental performance of building solutions in which, depending on the decision situation and the building solution being considered, the following aspects can be taken into account: the shape of the building body; internal zoning; thermal insulation; sound insulation; health of material solutions; energy-saving performance technology; operational energy-saving, etc.

The inclusion of many criteria in a comparative analysis (assessment) makes it difficult to make objectively optimal decisions (Ibadov and Rosłon 2015; Ibadov and Kulejewski 2019; Cole 2000). To facilitate decision-making, various methods can be used to support decision-making. There is a sufficiently extensive mathematical apparatus (Crawley and Aho 1999; Uğur and Baykan 2016; Vaagen et al. 2017; Winanda et al. 2017). What method should not be used, the decision-maker must always determine which option is “better” or “worse” according to established criteria. The traditional way to describe such a situation is: xiRxj  ⇔  xi  " better than "  xj where R is a partial order relation, defined on the elements of the set of compared variants (alternatives) X (Ibadov and Rosłon 2015). It is worth to note that the term “better” associated with its relations can be defined in many ways. It is hereby proposed to use fuzzy relations, as this linguistic term and quality criteria (in the presented case the criterion of “degree of environmental performance”) are inherently fuzzy concepts.

Materials and methods

From a methodological point of view, this article deals with the environmental performance of construction projects, along with a proposal for a method for selecting construction projects with an additional criterion—the degree of environmental performance. The proposed selection method uses elements of decision-making theory (making decisions based on multicriteria) and fuzzy set theory, in particular, fuzzy preference relationships.

Below, the theoretical foundations of the requirements for building objects are considered, along with the specifics of ecological construction to justify the selection and creation of the environmental criterion in the selection (assessment) of construction projects.

Analysis of technical and legal requirements for building objects

Requirements for objects based on user needs are as follows:

  • Security: construction; fire; using,

  • Hygiene, health, and the environment: air cleanliness; dryness; water supply; sewage disposal; garbage removal; finishing materials used; sunlight,

  • Comfort: acoustic; visual; hydrothermal; structure usability,

  • Energy-saving and thermal protection,

  • Dimensions and equipment of the apartments.

Each of the above requirements for construction works is more or less related to environmental performance. Particular attention should be paid to the requirement “hygiene, health and the environment” from which it follows that buildings should be designed and built in such a way that they do not pose a threat to hygiene or health and the environment.

It is widely believed that the three main risk factors in the building environment are formaldehyde, radon, and asbestos. Considering this and the “hygiene, health and environment” requirement, it can be said that the level of environmental performance is influenced by:

  • design (location, selection of materials, ventilation, waste disposal, etc.),

  • proper conducting of construction works,

  • finish,

  • operation.

It should be emphasized that the building is also affected by mechanical, electromagnetic, thermal, chemical, and biological factors. These factors can come from outside the building, from the atmosphere, from the ground, and from the building as a result of use or project consequences. Because of the above, it can be concluded that the environmental problem cannot be considered only as single-directional, namely as the impact of construction production on surrounding environments. It should be analyzed also as the impact of the surrounding environment on investor’s decisions (location, applied solutions, human safety, etc.)

The “fire safety” requirement, in turn, has an indirect impact on the level of environmental performance, through design and operational errors. A fire can have catastrophic effects. It affects the environment and construction. The impact on the environment occurs through the thermal effect and change in the chemical composition of the gas fractions and the appearance of areas with significant air saturation with solid particles (smoke).

The requirement of “acoustic comfort” has a human health significance. Therefore, the building should be properly located and designed. The requirement for “acoustic comfort” should be taken into consideration when assessing the level of environmental performance.

The requirement of “energy-saving and heat protection” has a very large impact on the level of environmental performance. It is considered in the production of energy and thermal insulation of external partitions (thermal insulation is related to energy demand and this in turn with energy material, which pollutes the environment). Based on this, it can be concluded that the issue of the environmental performance of building solutions is strongly related to the energy aspect of construction.

Based on the above considerations, it should be stated that the issue of the environmental performance of construction projects (building solutions) is multifaceted and multidisciplinary, which causes consideration of multicriteria of various nature (quantitative and qualitative) when assessing and selecting construction projects (building solutions). This causes a lot of problems for decision-makers (officials, designers, investors) at various stages of decision-making (in planning, designing, and implementing construction projects). This determines the need for an adequate tool for the assessment and selection of construction projects, taking into account the criteria for the environmental performance assessment if construction projects.

To better understand and properly evaluate and select construction projects, the specificity and nature of ecological construction are discussed below.

The specificity and essence of ecological construction

Ecological construction is the construction with healthy and energy-saving materials, based on energy-saving solutions and energy-saving implementation techniques that do not damage the environment. It is a construction that is friendly to nature and significantly associated with it and much less pollutes the environment than conventional construction. Ecological construction includes energy-saving construction, but one that is healthy and includes ecological aspects. In other words, ecological construction is an energy-saving construction that shapes a healthy and harmonious space of users and employees while reducing energy consumption for the construction and operation of buildings.

Ecological construction should meet the following conditions:

  • improve the health of buildings,

  • significantly minimize environmental pollution (surroundings),

  • minimize energy consumption both during the erection and operation of buildings,

  • maximize the use of renewable energy.

Ecological construction is also related to the fields of knowledge as follows: bionics, biotechnics, construction biology, climatology, and variant construction.

It should be emphasized that determining the level of the environmental performance of construction projects (solutions) is also important to analyze its technological structure. In this case, among others, construction technology should be considered as a system with a multi-level hierarchical structure. Construction technology is a relationship of elements: the erected structure, the material from which the structure is made, the technological process as business continuity in material processing, technical means, and contractors implementing the technological process. Time, cost, and the environment (conditions for works, etc.) are also inherent elements of construction technology. Therefore, when determining the level of the environmental performance of construction projects, each structural element of technology should be described by appropriate quality indicators that allow the classification of construction technologies and build a hierarchical structure. The impact of each hierarchical level on the surrounding environment will be different.

It is worth noting that according to the international ISO14001: 1996 standard, the environment is the environment in which the organization operates, including air, water, land, natural resources, flora, fauna, people and their interdependencies (in this context, the concept of the environment refers to an organization to the global system). The environmental impact is defined there as any change in the environment, both unfavorable and beneficial, which is wholly or partly caused by the activities of the organization, its products, and services. Therefore, the analysis of construction technology according to environmental performance criteria, aimed at determining its environmental impact, should be carried out by assessing each hierarchical level. This analysis should also include identifying the types and magnitude of impacts on the surrounding environment and various variants of alternative solutions. The level of impact of each variant can be assessed in different ways, for example, by the number from the range (0.1) or/and linguistically. This is also another justification for the use of fuzzy set theory elements in building design assessments.

It should be emphasized that ecological construction is based on the selection of healthy materials and energy-saving construction. It uses clean renewable energy and includes the rational exploitation of buildings and high durability of materials and buildings.

The buildings are also the subject of external impact. There is a certain balance between these impacts, the disorder of which threatens to adversely affect human health and well-being. Therefore, in ecological construction, architectural shaping, zoning, and urban location as well as adaptation to the surroundings of buildings are of great importance.

Human health is also significantly affected by internal impacts derived from the materials used and building solutions. Therefore, the environmental performance of buildings or buildings is inter alia influenced by the following factors:

  • equipment,

  • material,

  • technical shape,

  • organization of internal processes.

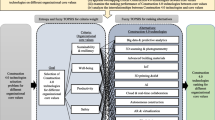
Analyzing the issues discussed above in the field of the environmental performance of construction, it can be concluded that the development of ecological buildings should be considered in the areas of materials, technology, architecture, and urban planning. Figure 1 presents the shaping of buildings in these aspects.

Fig. 1
figure 1

Shaping ecological buildings

Full size image

Given the above, the decision-maker to shape an ecological project must take into account many criteria that are important considering ecology in construction. To facilitate the selection from various projects, it is suggested to make a multi-criteria selection of alternative design solutions based on a fuzzy preference relationship.

Useful concepts of fuzzy set theory for decision-making are discussed below.

Fundamental concepts of the fuzzy set theory

The concept of a fuzzy set was introduced by Zadeh (1965), as a generalization of the conventional or nonfuzzy set concept. A fuzzy set A in a non-empty space X is a set of pairs:

$$ A=\left\{\left(x,{\mu}_A(x)\right);x\in \mathrm{X}\right\} $$
(1)

where

µA : X → [0,  1] is a membership function of the fuzzy set A. For each element x ∈ X, this function assigns a degree of membership to the fuzzy set A.

Depending on the value of the membership degree, one can distinguish three cases:

  1. 1.

    μA(x) = 1 means that element x is fully included in fuzzy set A, x ∈ A,

  2. 2.

    μA(x) = 0 means that element x is not included in fuzzy set A, x ∉ A,

  3. 3.

    0 < μA(x) < 1 means that element x is partially included (fuzzy member) in fuzzy set A.

Figure 2 shows the typical L, t, and γ class membership functions.

Fig. 2
figure 2

L, t, and γ class membership functions

Full size image

L class function is described by Eq. (2):

$$ L=\left(x,a,b\right)=\left\{\begin{array}{c}1\kern0.5em \mathrm{for}\kern0.5em x\le a\\ {}\frac{b-x}{b-a}\kern0.5em \mathrm{for}\kern0.5em a\le x\le b\\ {}\begin{array}{ccc}0& \mathrm{for}& x\ge b\end{array}\end{array}\right. $$
(2)

t class function is described by Eq. (3):

$$ t=\left(x,a,b,c\right)=\left\{\begin{array}{c}0\kern0.5em \mathrm{for}\kern0.5em x\le a\\ {}\begin{array}{ccc}\frac{x-a}{b-a}& \mathrm{for}& a\le x\le b\end{array}\\ {}\begin{array}{ccc}\frac{c-x}{c-b}& \mathrm{for}& b\le x\le c\end{array}\\ {}\begin{array}{ccc}0& \mathrm{for}& x\ge c\end{array}\end{array}\right. $$
(3)

γ class function is described by Eq. (4):

$$ \gamma =\left(x,a,b\right)=\left\{\begin{array}{c}0\kern0.5em \mathrm{for}\kern0.5em x\le b\\ {}\begin{array}{ccc}\frac{x-b}{c-b}& \mathrm{for}& b\le x\le c\end{array}\\ {}\begin{array}{ccc}1& \mathrm{for}& x\ge c\end{array}\end{array}\right. $$
(4)

Some denotations and operations on fuzzy sets such as inclusion (⊂), a complement of the fuzzy set, or standard intersection (∩) and standard union (∪) of fuzzy sets A and B, can be displayed in the following manner (Zadeh 1965):

$$ A\subset B\leftrightarrow {\mu}_A(x)\le {\mu}_B(x),\forall x\in \mathrm{X}, $$
(5)
$$ {\mu}_{\overline{A}}(x)=1-{\mu}_A(x),\forall x\in \mathrm{X}, $$
(6)
$$ {\mu}_{A\cap B}(x)=\min \left({\mu}_A(x){\mu}_B(x)\right),\forall x\in \mathrm{X}, $$
(7)
$$ {\mu}_{A\cup B}(x)=\max \left({\mu}_A(x){\mu}_B(x)\right),\forall x\in \mathrm{X}. $$
(8)

A very important feature of fuzzy sets is that they can be used for modeling certain imprecise characteristics with the use of linguistic variables, basing on the expert experience (Zadeh 1999).

Suppose that the expert determines the degree of the environmental performance of the construction project, with notions as “low,” “average,” and “high,” indicating variability in the degree of environmental performance on a numerical scale, for example, 0 to 5. The formalization of such a description can be carried out using a linguistic variable characterized by <N, T, X, G, M> data set, where:

  • N, the linguistic variable name, the degree of environmental performance;

  • T, the terms (sets)—{“low,” “average,” “high”}—representing a range of meanings for fuzzy variable on universe X;

  • X = [0, 5], the universe, which is a set of the degree of environmental performance;

  • G, the syntactic procedure that allows operating on a terms T, in particular, to generate new terms (meanings). In other words, this is a procedure used for the creation of new terms with the use of conjunctions (“and,” “or”) and modifiers (“very,” “more or less,” “approximately,” etc.), for example, “low or medium degree of environmental performance” and “very high degree of environmental performance”;

  • M, the semantic procedure, which enables one to transform any new value of the linguistic variable created by the G procedure into the fuzzy variable, namely establishing an appropriate fuzzy set. In other words, this is a procedure that allows creating within universe X fuzzy subsets А1 = “low degree of environmental performance,” А2 = “medium degree of environmental performance,” А3 = “high degree of environmental performance,” and the fuzzy sets for G (T) terms, according to the rules of fuzzy conjunctions and modifiers transmission. Sets A1, A2, and A3 can be described with the use of functions shown in Fig. 2.

In addition to the considered above base values of linguistic variable, Т = {“low degree of environmental performance,” “medium degree of environmental performance,” “high degree of environmental performance”} depending on the field of X, other values are also possible. In our case, linguistic variable values (“the degree of environmental performance”) may be defined as fuzzy numbers, for example, “approximately 2” or “approximately 4.”

The concept of fuzzy relations allows assigning a degree of membership to compared elements of a set. The degree defines the relationship (the strength of relation) between them. The problem statement in a short form is as follows. Let A be a set of alternative construction projects, which are characterized by several criteria (both qualitative and quantitative) with index numbers j = 1, …, n. Information on pairwise comparison for each criterion is presented in the form of a preference relation Rj. Therefore, there are n preference relations Rj on set A. There is a need to choose the best alternative from the set {A, R1, …, Rm}.

The fuzzy relation of preferences on the set A is any reflexive fuzzy relation defined on this set, whose membership function is calculated as follows:

$$ {\mu}_{R^S}\left(a,b\right)=\left\{\begin{array}{c}{\mu}_R\left(a,b\right)-{\mu}_R\left(b,a\right)\ if{\mu}_R\left(a,b\right)\ge {\mu}_R\left(b,a\right)\\ {}0\kern6.75em if{\mu}_R\left(a,b\right)\le {\mu}_R\left(b,a\right)\end{array}\right. $$
(9)

The concept in question is to build a set of non-dominated alternatives based on the fuzzy relation of preferences. Let A be a set of alternatives and let μR be a relation of preferences given on a set A. A fuzzy subset of non-dominated alternatives of a set {A, μR} is described by the membership function:

$$ {\mu}_R^{\mathrm{nd}}(a)=1-\underset{b\in A}{\sup}\left({\mu}_R\left(b,a\right)-{\mu}_R\left(a,b\right)\right),a\in A $$
(10)

where \( {\mu}_R^{\mathrm{nd}} \) is a degree of non-dominance of an alternative a.

It should be emphasized that when \( {\mu}_R^{nd}(a)=1 \), then the alternative a is strongly non-dominated.

The procedure for choosing and determining the degree of non-domination is presented on a numerical example.

Results and discussion

Numerical example

Let’s assume that it is possible to realize 3 alternative construction projects marked as A = {ai}, where i = 1, …, n, characterized by cost and labor intensity per 1 m2 of a building in the form of a specific quantity (1.000 PLN per 1 m2 and man-hour per 1 m2). Let’s also suppose also that decision-makers can determine the overall degree of the environmental performance of each project on a scale from 0 to 5, where the environmental performance increases with increasing value, which shows how much each project is eco-friendly. Table 1 shows the individual construction project with the relevant time-cost values and corresponding environmental performance, which contain evaluation criteria values. The set of criteria is marked as K = {kk}, where k = 1, …, 3., wherein k1 = kcost, k2 = klabor − intensity (li), k3 = kenvironmental performance (ep). It is necessary to decide which construction project to choose.

Table 1 The selection criteria values of the construction project
Full size table

The information about the alternatives compared with each criterion kk is presented in the form of a fuzzy relation of preferences Rk. As a result, m preference relations Rk on set A are obtained. The following describes how to choose the best alternative construction project from the set {A, Rk}.

The membership functions of alternative projects for each criterion are described by Eq. (11):

$$ {\mu}_{k_1}=0.3/5+0.3/5+0.15/6;{\mu}_{k_2}=0.8/2.5+1.0/2+0.9/2.3;{\mu}_{k_3}=0.6/3+0.4/2+1/5 $$
(11)

Using these data, matrixes of fuzzy relations of preferences R1, …, R3 are created according to Eq. (9).

The matrix of fuzzy relations Rk is as follows:

$$ {R}_k=\left(\begin{array}{cccc}{\mu}_R\left({a}_1,{a}_1\right)& {\mu}_R\left({a}_1,{a}_2\right)& \dots & {\mu}_R\left({a}_1,{a}_n\right)\\ {}{\mu}_R\left({a}_2,{a}_1\right)& {\mu}_R\left({a}_2,{a}_2\right)& \dots & {\mu}_R\left({a}_2,{a}_n\right)\\ {}\dots & \dots & \dots & \dots \\ {}{\mu}_R\left({a}_n,{a}_1\right)& {\mu}_R\left({a}_n,{a}_2\right)& \dots & {\mu}_R\left({a}_n,{a}_n\right)\end{array}\right) $$
(12)

Therefore, the relations for the individual criteria are as follows:

$$ {\mu}_{R_1}=\left(\begin{array}{ccc}1& 0& 0.15\\ {}0& 1& 0.15\\ {}0& 0& 1\end{array}\right);{\mu}_{R_2}=\left(\begin{array}{ccc}1& 0& 0\\ {}0.2& 1& 0.1\\ {}0.1& 0& 1\end{array}\right);{\mu}_{R_3}=\left(\begin{array}{ccc}1& 0.2& 0\\ {}0& 1& 0\\ {}0.4& 0.6& 1\end{array}\right) $$
(13)

Then, the intersection of all fuzzy relations P1 = R1 ∩ … ∩ R3 is determined, where P1 is a n × n matrix, in which individual elements \( {\mu}_{P_1}\left({a}_i,{a}_j\right) \) are defined by Eq. (14):

$$ {\mu}_{P_1}\left({a}_i,{a}_j\right)=\underset{k}{\min }{\mu}_{R_k}\left({a}_i,{a}_j\right),\kern1em k=1,\dots, 3 $$
(14)

Hence, \( {\mu}_{P_1}\left({a}_i,{a}_j\right) \) is:

$$ {\mu}_{P_1}\left({a}_i,{a}_j\right)={\displaystyle \begin{array}{cccc}& {a}_1& {a}_2& {a}_3\\ {}{a}_1& 1& 0& 0\\ {}{a}_2& 0& 1& 0\\ {}{a}_3& 0& 0& 1\end{array}} $$
(15)

Then, a subset of non-dominated alternatives ai in a set \( \left\{A,{\mu}_{P_1}\right\} \) is determined for every i and j (i ≠ j):

$$ {\mu}_{P_1}^{\mathrm{nd}}\left({a}_i\right)=1-\underset{a_j\in A}{\sup}\left({\mu}_{P_1}\left({a}_j,{a}_i\right)-{\mu}_{P_1}\left({a}_i,{a}_j\right)\right) $$
(16)

The calculated degrees of non-dominance of each alternative projects are as follows:

$$ {\displaystyle \begin{array}{l}{\mu}_{P_1}^{\mathrm{nd}}\left({a}_1\right)=1-\sup \left[\left(0-0\right),\left(0-0\right)\right]=1\\ {}{\mu}_{P_1}^{\mathrm{nd}}\left({a}_2\right)=1-\sup \left[\left(0-0\right),\left(0-0\right)\right]=1\\ {}{\mu}_{P_1}^{\mathrm{nd}}\left({a}_3\right)=1-\sup \left[\left(0-0\right),\left(0-0\right)\right]=1\end{array}} $$
(17)

The calculated values of a subset of the non-dominated alternative projects are:

$$ {\mu}_{P_1}^{\mathrm{nd}}=\left|1\ 1\ 1\right| $$
(18)

In the next step, validity coefficients wk are assigned to every criterion kk, fulfilling the condition:

$$ \sum \limits_{k=1}^m{w}_k=1,\kern0.5em {w}_k\ge 0 $$
(19)

It is assumed in the example that w1 =  w2 =  w3; therefore, \( {w}_k=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right. \).

Then, taking into account the validity of individual criteria kk, a n × n matrix of fuzzy relationship P2 is created. The elements of this matrix are defined by Eq. (20):

$$ {\mu}_{P_2}\left({a}_i,{a}_j\right)=\sum \limits_{k=1}^3{w}_k{\mu}_{R_k}\left({a}_i,{a}_j\right)=\frac{1}{3}\left({\mu}_1\left({a}_i,{a}_j\right),{\mu}_2\left({a}_i,{a}_j\right),{\mu}_3\left({a}_i,{a}_j\right)\right) $$
(20)

Hence,

$$ {\displaystyle \begin{array}{l}{\mu}_{P_2}\left({a}_1,{a}_1\right)=\frac{1}{3}\left(1+1+1\right)=1\\ {}{\mu}_{P_2}\left({a}_1,{a}_2\right)=\frac{1}{3}\left(0+0+0.2\right)=0.07\\ {}{\mu}_{P_2}\left({a}_1,{a}_3\right)=\frac{1}{3}\left(0.15+0+0\right)=0.05\end{array}} $$
(21)
$$ {\displaystyle \begin{array}{l}{\mu}_{P_2}\left({a}_2,{a}_1\right)=\frac{1}{3}\left(0+0.2+0\right)=0.07\\ {}{\mu}_{P_2}\left({a}_2,{a}_2\right)=\frac{1}{3}\left(1+1+1\right)=1\\ {}{\mu}_{P_2}\left({a}_2,{a}_3\right)=\frac{1}{3}\left(0.15+0.1+0\right)=0.08\end{array}} $$
(22)
$$ {\displaystyle \begin{array}{l}{\mu}_{P_2}\left({a}_3,{a}_1\right)=\frac{1}{3}\left(0+0.1+0.4\right)=0.17\\ {}{\mu}_{P_2}\left({a}_3,{a}_2\right)=\frac{1}{3}\left(0+0+0.6\right)=0.2\\ {}{\mu}_{P_2}\left({a}_3,{a}_3\right)=\frac{1}{3}\left(1+1+1\right)=1\end{array}} $$
(23)

Therefore, \( {\mu}_{P_2}\left({a}_i,{a}_j\right) \) is:

$$ {\mu}_{P_2}\left({a}_i,{a}_j\right)={\displaystyle \begin{array}{cccc}& {a}_1& {a}_2& {a}_3\\ {}{a}_1& 1& 0.07& 0.05\\ {}{a}_2& 0.07& 1& 0.08\\ {}{a}_3& 0.17& 0.2& 1\end{array}} $$
(24)

Then, a subset of non-dominated alternatives ai in the set \( \left\{A,{\mu}_{P_2}\right\} \) is determined for every i and j (i ≠ j):

$$ {\mu}_{P_2}^{\mathrm{nd}}\left({a}_i\right)=1-\underset{a_j\in A}{\sup}\left({\mu}_{P_2}\left({a}_j,{a}_i\right)-{\mu}_{P_2}\left({a}_i,{a}_j\right)\right) $$
(25)

The calculated degrees of non-dominance of each alternative projects are as follows:

$$ {\displaystyle \begin{array}{l}{\mu}_{P_2}^{\mathrm{nd}}\left({a}_1\right)=1-\sup \left(\left(0.07-0.07\right),\kern0.5em \left(0.17-0.05\right)\right)=0.88\\ {}{\mu}_{P_2}^{\mathrm{nd}}\left({a}_2\right)=1-\sup \left(\left(0.07-0.07\right),\kern0.5em \left(0.2-0.08\right)\right)=0.88\\ {}{\mu}_{P_2}^{\mathrm{nd}}\left({a}_3\right)=1-\sup \Big(\left(0.05-0.17\right),\kern0.5em \left(0.08-0.2\right)=1\end{array}} $$
(26)

Hence,

$$ {\mu}_{P_2}^{\mathrm{nd}}\left({a}_i\right)={\displaystyle \begin{array}{ccc}{a}_1& {a}_2& {a}_3\\ {}\left\Vert 0.88\right.& 0.88& \left.1\right\Vert \end{array}} $$
(27)

The resulting set of non-dominated alternatives is the intersection of sets \( {\mu}_{P_1}^{\mathrm{nd}} \) and \( {\mu}_{P_2}^{\mathrm{nd}} \):

$$ {\mu}_{P_1}^{\mathrm{nd}}\cap {\mu}_{P_2}^{\mathrm{nd}}=\left\{\left(1\kern0.5em 1\kern0.5em 1\right)\cap \left(\begin{array}{ccc}0.88& 0.88& 1\end{array}\right)\right\}=\left\{\left(\begin{array}{ccc}0.88& 0.88& 1\end{array}\right)\right\} $$
(28)

In conclusion, the choice of the construction project a3, which has a maximum degree of non-domination μnd, should be considered rational.

It should be emphasized that the a3 project is the most expensive project, with an average implementation time and the highest degree of environmental performance. In the absence of an environmental criterion, the decision-maker would certainly reject this project because of the highest cost. Then, the best solution would be project a2, where the value of the disregarded environmental criterion is the worst.

Projects a1and a2 are equally preferred with the same weight criteria. Considering the cost criterion, the projects are equal. While project a1 is the worst in terms of implementation time, project a2 is the best. This means that by choosing the a2 project, the project with the worst ecological parameters would be implemented. It is understandable that currently, the cost criterion is very important in construction; nevertheless, for pro-ecological action in construction, one should consider the level of value of the weight of the environmental criterion.

Conclusion

The analysis of the requirements for building objects is intended to indicate the criteria creating the level of environmental performance of construction projects. This will help to properly understand and formulate the problem of the environmental performance of construction projects and also allows choosing the right mathematical apparatus for solving problems related to making decisions.

Also, the specificity and essence of ecological construction presented in the article will be very helpful both in public perception and in creating an ecological construction project.

The proposed assessment method can be useful both at individual stages of decision-making in the implementation of construction investments and in the overall assessment of projects.

The proposed decision-making model is based on fuzzy relationships and ordering of construction projects by determining their degree of non-dominance. It is a useful and functional way of evaluation and selection based on many criteria of a different nature.

Another advantage of the proposed algorithm is that at the design stage, due to the high uncertainty level, the decision-maker may not have well-defined preferences. In such case, the use of fuzzy preference relations allows for a better way of formalizing and describing the decision-making situation.

The solved calculation example in the article presents the operation of the proposed approach. At the same time, it shows that modeling the degree of environmental performance of construction projects using fuzzy sets and creating fuzzy relationships makes it easier to decide considering the listed criteria. Thus, it justifies the practical usefulness of the developed method.

The article creates the base for deeper analysis of the ecological safety of construction projects. The article can also be useful in constructing the environmental performance of construction solutions at various stages of the life cycle of a construction project.