Skip to main content
SpringerLink
Log in

Discrete element simulation of dynamic semi-circular bend flexure tests of rocks using split Hopkinson pressure bar

  • Original Paper
  • Published:
Arabian Journal of Geosciences Aims and scope Submit manuscript

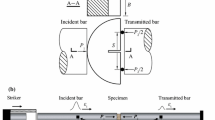
Abstract

The semi-circular bending (SCB) using a split Hopkinson pressure bar system appears to be a promising method for measuring dynamic flexural strength of rock materials due to its distinct advantages. The quasi-static analysis is adopted for determining the dynamic flexural strength, of which several vital prerequisites have not been thoroughly examined yet. In this study, dynamic flexure tests regarding dynamic force equilibrium, interfacial friction effects, and energy partitioning are numerically investigated based on discrete element method (DEM) modeling. Results show that by virtue of the ramped wave loading, the force equilibrium of the specimen can be effectively achieved and the rupture is precisely measured to synchronize with the peak force, both of which guarantee the quasi-static data reduction method employed to determine the dynamic flexural strength; while the opposite occurs for the test under a rectangular wave loading. Furthermore, dynamic flexural strengths obtained by the numerical SCB tests exhibit approximately linear rate dependence that is identical with the experimental results. The interfacial friction, which is found to significantly influence the measuring results for rather high loading rates, contributes to enhancing the rate dependence of flexural strength and must be taken into account in dynamic flexure tests. In addition, energy partitioning is first numerically performed in the dynamic SCB tests and the nominal fracture energy manifests an S type of rate dependence with loading rates.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

Abbreviations

BPM:

Bonded particle model

DEM:

Discrete element method

ISRM:

International Society for Rock Mechanics

SCB:

Semi-circular bending

SHPB:

Split Hopkinson pressure bar

A s :

Area of the fracture surface (m2)

B :

Thickness of the SCB sample (m)

F Ic :

Force on the incident end of the specimen (N)

F Tc :

Force on the transmitted end of the specimen (N)

G dc :

Fracture energy dissipated per unit area (J/m2)

U f :

Accumulated energy consumed to fracture during the failure process of SCB (J)

P 1 :

Axial force applied on the incident end of the sample (N)

P 2 :

Axial force applied on the transmitted end of the sample (N)

R :

Radius of the SCB sample (m)

S :

Span of the supporting pins (m)

t i :

Instant when the stress wave first arrives at the incident end of the specimen (s)

t t :

Instant when the stress wave first arrives at the transmitted end of the specimen (s)

t b :

Instant when the force equilibrium on both ends of the specimen is first achieved (s)

t f :

Instant when the specimen initially fractures (s)

t p :

Instant when the forces on both ends of the specimen reach the peak value

t d :

Instant when the specimen is destroyed (s)

t e :

Instant when the loading process ends (s)

t m :

Instant of a post-mortem examination (s)

εi :

Incident strain signal on the incident bar

εr :

Reflected strain signal on the incident bar

εt :

Transmitted strain signal on the transmitted bar

μ :

Force equilibrium coefficient

f :

Friction coefficient

References

  • Arabani M, Ferdowsi B (2009) Evaluating the semi-circular bending test for HMA mixtures. Int J Eng Trans A 22(1):47–58

    Google Scholar 

  • ASTM Standard C1499-05 (2005) Standard test method for monotonic equibiaxial flexural strength of advanced ceramics at ambient temperature. ASTM International

  • ASTM Standard C293/C293M-10 (2010) Standard test method for flexural strength of concrete (using simple beam with center-point loading). ASTM International

  • ASTM Standard C78/C78M-15a (2015) Standard test method for flexural strength of concrete (using simple beam with third-point loading). ASTM International

    Google Scholar 

  • ASTM Standard C880/C880M-15 (2015) Standard test method for flexural strength of dimension stone. ASTM International

  • Bohme W, Kalthoff JF (1982) The behavior of notched bend specimens in impact testing. Int J Fract 20(4):139–143

    Article  Google Scholar 

  • Chen R, Xia K, Dai F, Lu F, Luo SN (2009) Determination of dynamic fracture parameters using a semi-circular bend technique in split Hopkinson pressure bar testing. Eng Fract Mech 76:1268–1276

    Article  Google Scholar 

  • Colback PSB (1966) An analysis of brittle fracture initiation and propagation in the Brazilian test. Proc 1st Congr Int Soc Rock Mech Lisbon 1:385–391

    Google Scholar 

  • Coviello A, Lagioia R, Novam R (2005) On the measurement of the tensile strength of soft rocks. Rock Mech Rock Eng 38(4):251–273

    Article  Google Scholar 

  • Cundall PA, Strack ODL (1979) A discrete numerical model for granular assemblies. Geotechnique 29(1):47–65

    Article  Google Scholar 

  • Dai F, Xia KW, Tang LZ (2010a) Rate dependence of the flexural tensile strength of Laurentian granite. Int J Rock Mech Min 47(3):469–475

    Article  Google Scholar 

  • Dai F, Huang S, Xia K, Tan Z (2010b) Some fundamental issues in dynamic compression and tension tests of rocks using split Hopkinson pressure bar. Rock Mech Rock Eng 43(6):657–666

    Article  Google Scholar 

  • Dai F, Xia KW, Zuo JP, Zhang R, Xu NW (2013) Static and dynamic flexural strength anisotropy of Barre granite. Rock Mech Rock Eng 46(6):1589–1602

    Article  Google Scholar 

  • Davies RM (1948) A critical study of the Hopkinson pressure bar. Philosophical Trans R Soc Lond Ser A, Math Phys Sci, pp. 375–457

    Google Scholar 

  • Foster JT, Luk VK, Chen WW (2008) Dynamic initiation fracture toughness of high strength steel alloys. In: 11th International congress and exhibition on experimental and applied mechanics, vol. 3. Society for Experimental Mechanics, pp. 1414–20

  • Frew DJ, Forrestal MJ, Chen W (2001) A split hopkinson pressure bar technique to determine compressive stress-strain data for rock materials. Exp Mech 41(1):40–46

    Article  Google Scholar 

  • Frew DJ, Forrestal MJ, Chen W (2002) Pulse shaping techniques for testing brittle materials with a split Hopkinson pressure bar. Exp Mech 42(1):93–106

    Article  Google Scholar 

  • Hoek E (1964) Rock fracture around mining excavations. Proc. 4th Int. Conf. on Strata Control and Rock Mech New York

  • Hudson JA, Brown ET, Rummel F (1972) The controlled failure of rock discs and rings loaded in diametral compression. Int J Rock Mech Min Sci Geomech Abstr 9:241–248

    Article  Google Scholar 

  • Kolsky H (1953) Stress waves in solids. Clarendon Press, Oxford

    Google Scholar 

  • Kubota S, Ogata Y, Wada Y, Simangunsong G, Shimada H, Matsui K (2008) Estimation of dynamic tensile strength of sandstone. Int J Rock Mech Min 45(3):397–406

    Article  Google Scholar 

  • Li XB, Zou Y, Zhou ZL (2013) Numerical simulation of the rock SHPB test with a special shape striker based on the discrete element method. Rock Mech Rock Eng 47(5):1693–1709

    Article  Google Scholar 

  • Lu FY, Lin YL, Wang XY, Lu L, Chen R (2015) A theoretical analysis about the influence of interfacial friction in SHPB tests. Int J Impact Eng 79:95–101

    Article  Google Scholar 

  • Lundberg B (1976) A split Hopkinson bar study of energy absorption in dynamic rock fragmentation. Int J Rock Mech Min Sci Geomech Abstr 13(6):187–197

    Article  Google Scholar 

  • O’Sullivan C (2011) Particle-based discrete element modeling: geomechanics perspective. Int J Geosci 11(6):449–464

    Google Scholar 

  • Potyondy DO, Cundall PA (2004) A bonded-particle model for rock. Int J Rock Mech Min 41:1329–1364

    Article  Google Scholar 

  • Schuler H, Mayrhofer C, Thoma K (2006) Spall experiments for the measurement of the tensile strength and fracture energy of concrete at high strain rates. Int J Impact Eng 32(10):1635–1650

    Article  Google Scholar 

  • Song B, Chen W (2004) Loading and unloading split Hopkinson pressure bar pulse-shaping techniques for dynamic hysteretic loops. Exp Mech 44(6):622–627

    Article  Google Scholar 

  • Utili S, Zhao T, Houlsby GT (2015) 3D DEM investigation of granular column collapse: evaluation of debris motion and its destructive power. Eng Geol 186:3–16

    Article  Google Scholar 

  • Weatherley D, Boros V, Hancock W (2011) ESyS-Particle tutorial and user’s guide version 2.1. Earth Systems Science Computational Centre, The University of Queensland

  • Weerasooriya T, Moy P, Casem D, Cheng M, Chen W (2006) A four-point bend technique to determine dynamic fracture toughness of ceramics. J Am Ceram Soc 89(3):990–995

    Article  Google Scholar 

  • Xia K, Huang S, Dai F (2013) Evaluation of the frictional effect in dynamic notched semi-circular bend tests. Int J Rock Mech Min Sci 62:148–151

    Google Scholar 

  • Xu Y, Dai F, Xu NW, Zhao T (2016) Numerical investigation of dynamic rock fracture toughness determination using a semi-circular bend specimen in split Hopkinson pressure bar testing. Rock Mech Rock Eng 49(3):731–745

    Article  Google Scholar 

  • Zhang QB, Zhao J (2014) Quasi-static and dynamic fracture behaviour of rock materials: phenomena and mechanisms. Int J Fract 189:1–32

    Article  Google Scholar 

  • Zhang ZX, Kou SQ, Jiang LG, Lindqvist PA (2000) Effects of loading rate on rock fracture: fracture characteristics and energy partitioning. Int J Rock Mech Min 37(5):745–762

    Article  Google Scholar 

  • Zhao J, Li HB (2000) Experimental determination of dynamic tensile properties of a granite. Int J Rock Mech Min 37(5):861–866

    Article  Google Scholar 

  • Zhao GF, Kazerani T, Man K, Gao M, Zhao J (2015) Numerical study of the semi-circular bend dynamic fracture toughness test using discrete element models. Sci China Technol Sci 58(9):1587–1595

    Article  Google Scholar 

  • Zhong WZ, Rusinek A, Jankowiak T, Abed F, Bernier R, Sutter G (2015) Influence of interfacial friction and specimen configuration in split Hopkinson pressure bar system. Tribol Int 90:1–14

    Article  Google Scholar 

  • Zhou YX, Xia K, Li XB, Li HB, Ma GW, Zhao J, Zhou ZL, Dai F (2012) Suggested methods for determining the dynamic strength parameters and mode-I fracture toughness of rock materials. Int J Rock Mech Min Sci 49:105–112

    Article  Google Scholar 

Download references

Acknowledgments

The authors are grateful for the financial support from the National Program on Key Basic Research Project (no. 2015CB057903), National Natural Science Foundation of China (no. 51374149, 51579167), and the Youth Science and Technology Fund of Sichuan Province (2014JQ0004).

Author information

Authors and Affiliations

  1. State Key Laboratory of Hydraulics and Mountain River Engineering, College of Water Resources and Hydropower, Sichuan University, Chengdu, Sichuan, 610065, China

    Yuan Xu, Feng Dai, Nu-wen Xu, Tao Zhao & Cheng Zhou

Authors
  1. Yuan Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Feng Dai
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Nu-wen Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Tao Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Cheng Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Feng Dai.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Xu, Y., Dai, F., Xu, Nw. et al. Discrete element simulation of dynamic semi-circular bend flexure tests of rocks using split Hopkinson pressure bar. Arab J Geosci 9, 543 (2016). https://doi.org/10.1007/s12517-016-2574-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s12517-016-2574-8

Keywords

Search

Navigation