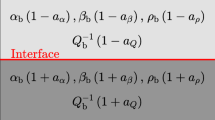Seismic spectrograms of an anelastic layer with different source-receivers configurations

Abstract

Thin and relatively thin anelastic layers (compared to the signal wavelength) generally represent hydrocarbon reservoirs, where the rock is a sandstone or a source rock saturated with brine, oil and gas. The study of the seismic response of these layers is important to detect the hydrocarbons on the basis of the reflection and transmission coefficients and the wave velocity and attenuation properties. Different seismic experiments (source-receiver configurations) can provide useful information to characterise its properties. In this work, we consider varying thicknesses and Q values of the layer and analyse the reflection and transmission coefficients. Moreover, we obtain spectrograms of surface seismic profiles and vertical and horizontal well profiles (VSP and HSP, respectively) to analyse their frequency content with offset due to variations of the attenuation properties of the layer. In addition, we compare the effects due to NMO stretching and intrinsic attenuation related to the low-frequency shadows (LFS) observed in real data after stacking, since LFS can have several causes. Ambiguity is present in this case, indicating that non-stretch NMO is required, otherwise an offset mute of the data may remove useful information regarding the intrinsic (physical) loss.

Appendix A: Anelasticity

The phase velocity, attenuation factor and quality factor of a viscoelastic medium are

$$ c_{\text{p}} \,=\, \left[ \text{Re} \left( \frac{1}{c} \right) \right]^{-1}, \ \ \ \alpha \,=\, - \omega \text{Im} \left( \frac{1}{c} \right) \ \ \ \text{and} \ \ \ Q \!=\ \frac{\text{Re} (c^{2})}{\text{Im} (c^{2})} , $$

(1)

respectively, where here c is the complex velocity of the P-wave, ω is the angular frequency ω=2π f and “Re” and “Im” take real and imaginary parts (e.g. Carcione 2015).

We consider a constant quality factor, $\bar Q$, obtained with a spectrum of L Zener relaxation mechanisms, whose peak locations are equispaced in logω scale (see Section 2.4.6 in Carcione (2015)). We then have to find the relaxation times τ _{𝜖 l} and τ _{σ l} that gives an almost constant Q in a given frequency band centred at ω _0m = 1/τ _0m . This is the location of the mechanism situated at the middle of the band, which, for odd L, has the index m = L/2 + 1. The minimum quality factor of the L peaks is the same and is given by

$$ Q_{0} = \frac{\bar Q}{L} \sum\limits_{l=1}^{L} \frac{ 2 \omega_{0m} \tau_{0l} } { 1 + \omega_{0m}^{2} \tau_{0l}^{2} } $$

(2)

Carcione (2015), where ω _0m is defined below and ω _0l = 1/τ _0l are the peak locations. Then, the relaxation times are

$$ \tau_{\epsilon l} \,=\, \frac{\tau_{0l}}{Q_{0}} \left( \sqrt{ {Q_{0}^{2}} \,+\,1 } \,+\,1 \right) \ \ \ \text{and} \ \ \ \tau_{\sigma l} \,=\, \frac{\tau_{0l}}{Q_{0}} \left( \sqrt{ {Q_{0}^{2}} \,+\,1 } \,-\,1 \right) . $$

(3)

If f ₀ is the central frequency of the source wavelet, we assume that the centre peak is located at ω _0m = 2π f ₀.

Finally, the complex P-wave modulus is given by

$$ E (\omega ) = \rho c^{2} = E_{U} \left( \sum\limits_{l=1}^{L} \frac{\tau_{\epsilon l}} {\tau_{\sigma l}} \right)^{-1} \sum\limits_{l=1}^{L} \frac{1 + \mathrm{i} \omega \tau_{\epsilon l}} {1 + \mathrm{i} \omega \tau_{\sigma l} } $$

(4)

(Carcione 2015; Eq. (2.196)), where E _U = ρ v ² is the unrelaxed, high-frequency limit modulus and v is the real-valued elastic velocity. If ω → ∞, E → E _U. Taking into account that E = ρ c ², the quality factor is given by Eq. 1.

Appendix B: Reflection and transmission coefficients

Let us denote with 1 and 2 the background medium and layer, respectively (see Fig. 2) and consider only the P-waves. The reflection and transmission coefficients of a single layer of thickness h embedded in a homogeneous medium, corresponding to an incidence wave with angle θ ₁, are

$$\begin{array}{@{}rcl@{}} R &=& \frac{r \left[ 1 - \exp (- \beta ) \right]}{1 - r^{2} \exp (- \beta )} \ \ \ \text{and}\\ T &=& \frac{4 Z_{1} Z_{2} \cos \theta_{1} \cos \theta_{2}}{ (Z_{2} \cos \theta_{1} + Z_{1} \cos \theta_{2})^{2}}\frac{ \exp (- \beta/2 )}{1 - r^{2} \exp (- \beta )} \end{array} $$

(5)

Brekhovskikh (1960), Carcione et al. (2014), respectively, where

$$ \beta = 2 \mathrm{i} h \left( \frac{\omega}{v_{2}} \right) \cos \theta_{2}, \ \ \ \ Z_{j} = \rho_{j} c_{j}, \ \ j=1,2 , $$

(6)

$\mathrm {i} = \sqrt {-1}$, ω is the angular frequency, c is the complex P-wave velocity, θ ₂ is the refraction angle

$$ r = \displaystyle \frac{Z_{2} \cos \theta_{1} - Z_{1} \cos \theta_{2} }{Z_{2} \cos \theta_{1} + Z_{1} \cos \theta_{2} } , $$

(7)

and Snell’s law is sinθ ₁/c ₁ = sinθ ₂/c ₂. Here, we use the convention exp(iω t) for the Fourier transform. The incident wave is homogeneous, i.e. the propagation and attenuation directions coincide (e.g. Carcione 2015).

Appendix C: Correction of the NMO stretch

Dunkin and Levin (1973) have explained the stretch effect after the NMO correction. Let us assume that at a given offset, the signal before the NMO correction is f(t). After the correction, the new (stretched) signal becomes

$$ g(t) = f (t/a) , $$

(8)

where a is the stretch ratio, given below. The frequency domain version of Eq. 8 is

$$ G(\omega ) = a F (a \omega) , $$

(9)

where G and F are the Fourier transforms of f and g, respectively. The stretch ratio is

$$ a = \frac{t}{t_{0}} \left( 1 - \frac{x^{2}}{t_{0} {v_{s}^{3}}} \left. \frac{dv_{s}}{d t_{0}} \right|_{t_{0}} \right)^{-1} , $$

(10)

where t is the uncorrected traveltime, t ₀ is the corrected traveltime, x is the offset and v _s is the stacking velocity.

The correction can be performed in the frequency domain, based on Eq. 9 by restoring each frequency component ω to the right value a ω and dividing the result by a, i.e. if G is the uncorrected spectrum, we have

$$ F (\omega ) = \frac{1}{a} G \left( \frac{\omega}{a}\right) . $$

(11)

Here, we use the method of Perroud and Tygel (2004). The basic processes, i.e. velocity analysis, NMO and stack, are unchanged. An extra step is required to avoid the stretch effect, the adjustment of the time-velocity function obtained from the velocity analysis.

If τ represents a time-shift since the onset of the seismic pulse, the following formula gives the adjusted NMO velocity v(τ) for an event at time t(x) for offset x and NMO velocity v _NMO (obtained from the velocity analysis) at zero-offset time t ₀:

$$ v(\tau) = v_{\text{NMO}} \left( 1+\frac{2}{ 1 + \sqrt{1 + a^{2}}} \frac{\tau}{t_{0}} \right)^{-1/2} , \ \ \ a = \frac{x}{t_{0} v_{\text{NMO}}} $$

(12)

One can observe that v(τ) decreases when τ increases, so the NMO adjusted velocity always decreases along the seismic pulse. For relatively small τ, the decrease is quasi-linear and can therefore be described by a velocity at the beginning of the pulse, and a velocity at the end of the pulse, for the maximum τ whose value should correspond to the pulse length. We can approximate the NMO velocity by the RMS velocity, v _RMS. For n layers, the traveltime is

$$ T = \sqrt{ {t_{0}^{2}} + \frac{x^{2}}{v_{\text{RMS}}} } , $$

(13)

where

$$ v_{\text{RMS}} = \frac{1}{t_{0}} \sum\limits_{k=1}^{n} {v_{k}^{2}} \tau_{k}, $$

(14)

v _k is the seismic velocity of the k layer, τ _k is the vertical two-way traveltime within layer k and $t_{0} = {{\sum }_{1}^{n}} \tau _{i}$.