Abstract
The pilgrimage to Mecca, which is called Hajj, is the largest annual pedestrian crowd management problem in the world. During the Hajj, the pilgrims are accommodated in camps. For safety reasons, exact times and directions are given to the pilgrims who are moving between holy sites. Despite the importance of complying with those schedules, violations can often be conjectured. Directing a small workforce between the camps to monitor the pilgrims’ compliance with the schedule is an important matter, which will be dealt with in this paper. A type of multi-objective multiple traveling salesperson optimization problem with time windows is introduced to generate the tours for the employees monitoring the flow of pilgrims at the campsite. Four objectives are being pursued: As many pilgrims as possible (1), should be visited with a preferably small workforce (2), the tours of the employees should be short (3) and employees should have short waiting times between visits (4). A goal programming, an enumeration, Augmecon2 and an interactive approach are developed. The topic of supported and non-supported efficient solutions is addressed by determining all efficient solutions with the enumeration approach. The suitability of the approaches is analyzed in a computational study, while using an actual data set of the Hajj season in 2015. For this application, the interactive approach has been identified as the most suitable approach to support the generation of an offer for the project.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Background
Each year the Hajj attracts two to four million people. See Haase et al. (2016) for a detailed description of the pilgrimage. During the different movements of pilgrims between the holy sites, the pilgrims can either walk, use a bus or the Mecca Metro. See Fig. 1 for images of the metro.
The movements of the pilgrims are illustrated in Figure 2.
Before moving between different locations, most of the pilgrims are located in camps in Mina. See Fig. 3 for images of the tent city of Mina.
Only registered ticket holders in dedicated camps are permitted to use the metro. Between 300, 000 and 400, 000 pilgrims use the metro each Hajj season. There are three metro stations in Mina, Muzdalifah, and Arafat, respectively. They are illustrated in Figure 4.
See Fig. 5 for images of two metro stations.
To prevent congestion and to assure a steady flow of pilgrims from their camps to the metro stations, a schedule is distributed. The schedule for a camp specifies the departure time and the path to the metro station. Since all the pilgrims of a camp cannot depart instantaneously, the expected duration needed for the pilgrims leaving the camp is given. The number of pilgrims in each camp is known.
The compliance of this schedule is crucial (Helbing et al. 2007). However, it is still frequently violated, which leads to the necessity of identifying those violations. An analysis of the pilgrims’ arrival time at the metro station during the Hajj in 2016 indicates major problems with the schedule compliance, which is illustrated in Fig. 6. It shows the fraction of pilgrims arriving on time at the corresponding metro stations. Only \(36\%\) of all pilgrims reached their metro station at the scheduled time. The compliance has been calculated with a 15-min time buffer before and after each scheduled arrival time.
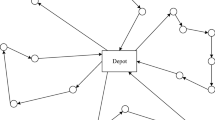
The goal of this paper is to direct a small and homogeneous workforce between the camps and detect which camps violate the schedule. It is not strictly necessary to observe all camps, but as many as possible with a reasonably scaled workforce. The employees of the workforce start their duty at any metro station and can only visit camps assigned to that station. This reduces the complexity for the employees of finding the correct camps in the tent city and empowers them to guide lost pilgrims to their correct metro station. A schematic representation of a metro station and some associated camps are given in Fig. 7.
The employees operate a smartphone with an application that instructs the employees to move to certain camps. After the arrival, the employees monitor whether the pilgrims already left, are leaving or are still waiting for their departure and enter this information into the smartphone.
Due to camp sizes of a few thousand pilgrims it is expected that the dispatching process lasts a certain period of time. To ensure that the observed dispatching status of the camp is correct, the employee is bound to stay a certain fraction of the duration of the dispatching process at the camp. The employee’s arrival time is negligible if they stay the given time during the departure.
The components of this project have already been developed and tested during the Hajj in 2015. For this prototype, a workforce was gathered and they have been directed to the camps to monitor the dispatching process. They used a mobile application to send the dispatching status to a central server, which stores the incoming data. Figure 8a is a screenshot of the mobile application. After receiving the dispatching statuses at the server, the results have been analyzed. The mobile application stored the location. An example track of an employee is displayed in Fig. 8b. The pilgrims of only \(30\%\) of the camps departed as scheduled during their scheduled departure time.
Walking to a camp and sending the dispatching status to a server is called a task. A tour consists of multiple tasks for a single employee.
A set of tours can be evaluated regarding four different goals. The first goal is to observe the dispatching process of as many pilgrims as possible. The second goal is to minimize the number of employees. The third goal is minimizing long waiting times between two tasks for the employees and the fourth goal is to minimize the total distance the employees must walk.
An offer for the responsible metro operator in Saudi Arabia should be made. This offer should contain a bundle of different solutions. Each solution contains a set of tours with their individual performance for the four goals. The offer receiver wants to be involved in the decision-making process and select their preferred solution without being overwhelmed by too many possible solutions. For the numerical studies, the real data of the camps’ locations as well as their distances are used.
The remainder of this paper has the following structure: The second section addresses literature relevant for this paper. In Sect. 3, a mixed-integer formulation is introduced. The results of a numerical study are presented in Sect. 4. First, the goal programming approach is described, followed by an enumeration approach. An interactive approach is the solution approach discussed at last. All solution approaches use the actual schedule data. This includes the actual location of the camps with their corresponding number of accommodated pilgrims as well as their scheduled departure time. Finally, a conclusion is drawn in Sect. 5.
2 Literature
Multi-objective combinatorial optimization (MOCO) is the simultaneous approach of several objectives in a finite, but often large set of feasible solutions (Czyzżak and Jaszkiewicz 1998). Those objectives are usually conflicting (Ehrgott and Gandibleux 2008). The general MOCO framework can be formulated as
subject to \(x\in S\), where S is a finite set of feasible solutions and the solution x a vector of discrete decision variables. K is the set of objective functions with \(|K|\ge 2\). MOCO problems find a lot of applications and are, therefore, well studied (Ulungu et al. 1999). A solution optimizing every objective simultaneously does generally not exist, but the best compromise for a decision maker (DM) can be found (Ehrgott and Gandibleux 2004). The best compromise of a DM is part of the set of efficient solutions and depends on their utility function (Jaszkiewicz 2002). A solution is efficient (or Pareto-optimal) if there does not exist another feasible solution that does not perform worse in any objective and better in at least one objective (Teghem et al. 2000).
The set of efficient solutions of a MOCO problem can be divided into supported and non-supported efficient solutions (Ehrgott and Gandibleux 2000). Let \(f_k\) be the objective value and \(\lambda _k\) the weight for the objective function k with \(\lambda _k\ge 0 \, \forall\ k\in K\) and \(\sum _{k\in K}\lambda _k=1\). When using the single objective function:
only the set of supported efficient solutions can be obtained (Ulungu and Teghem 1994). The set of non-supported efficient solutions, therefore, contains the solutions that cannot be found with this single objective function. For a non-supported efficient solution \(x'\) compared to the set of supported efficient solutions S, no set of weights can be found, so that:
There are several approaches for MOCO problems. Goal programming is a well-known technique even though only supported efficient solutions can be obtained. Goal programming minimizes the sum of the deviations of the individual objective values from their target value (Tamiz et al. 1998). Knowledge of the utility function of the DM is required to weigh the deviations of the different objectives (Dyer 1972). Gilbert et al. (1985) proposed an interactive method, which generates efficient solutions with the integration of the DM in the optimization process iteratively. Two more interactive approaches based on local optimality have been proposed by Paquete et al. (2007). Yet, various genetic algorithm approaches like Konak et al. (2006) and Fonseca and Fleming (1995) have been developed to find the approximated set of efficient solutions. Ulungu et al. (1999) describe a multi-objective simulated annealing method to approximate the set of efficient solutions, since the problems may be too complex for exact methods. A genetic local search approach was proposed by Jaszkiewicz (2002) to generate a set of approximated efficient solutions even for relatively large instances.
The multiple traveling salesperson problem (mTSP), a generalization of the traveling salesperson problem (TSP), describes the determination of multiple tours that cover all cities and each salesperson starts and ends their journey in the same city (Bektas 2006). When adding time-window contraints, each city can only be served after a permitted starting time and before a permitted ending time (Gendreau et al. 1998). The multi-objective TSP addresses two or more objectives, commonly minimizing the number of tours, the total time required and the total tour cost (Jozefowiez et al. 2008). Bowerman et al. (1995) proposed an approach to the urban school bus routing problem. Multiple objectives are minimized, e.g. the total bus route length, the remaining walking distance for the students, as well as balancing the length of the routes. Many heuristics have been developed to solve multi-objective TSP. Hansen (2000) illustrated the applicability of using substitute scalarizing functions to guide a tabu search heuristic. A genetic algorithm has also been used to solve the multi-objective TSP (Jaszkiewicz 2002). Florios and Mavrotas (2014) used a multi-objective mathematical programming method to generate the exact Pareto set in the multi-objective TSP.
3 Multi-objective multiple traveling salesperson problem with time windows
The problem can be formulated as a directed graph, see Fig. 7. The camps and metro stations are represented by nodes. The arcs represent compatible connections between camps and metro stations. As stated in the first section, not every camp must be visited, since a reasonable workforce should be found. Furthermore, it is assumed that the employees start their duty at a metro station and can only visit camps whose pilgrims are assigned to that station. Restrictions concerning the working hours are not taken into consideration. The following notation formalized the problem as a mathematical model.
The objective functions \(K =\{\text {pilgrims},\text {employees},\text {wait},\text {walk}\}\) are defined as the following:
where (4) minimizes the number of pilgrims who are not visited, (5) the number of employees on duty, (6) the sum of all waiting times between two tasks, which are longer than \(t^H\) and, therefore, considered as too long and (7) minimizes the total walking time over all employees.
The following constraints must be satisfied:
The constraints (8)–(10) are well-known network flow constraints. The constraint (11) detains short cycles and ensures a correct order of visits. Those constraints do not disable any connection if \(x_{ij}\) is zero and \(t_i \le s_{j}+t_{j}\) remains. It is only a matter of maintaining a correct time reference point so that \(s_j > t^{\text {max}}_{i} \forall i,j \in C\). The subtour elimination constraints can be lifted (Desrochers and Laporte 1991):
with \(1\le u_i\le |C|-1 \quad \forall i\in C\) to strengthen the formulation.
Figure 9 illustrates the parameters and variables for the movement from camp i to camp j with \(i,j \in C\).
The graph consists of camps and metro stations \(I=D \cup C\) and \(D\cap C = \emptyset\). A camp can only be associated to a single metro station \(C_{i} \cup C_{j}=\emptyset \quad \forall i,j \in D, i\ne j\). The arcs of the graph describe possible connections between the nodes. Two camps associated to the same depot \(d\in D\) are connected if it is possible to reach the destination camp before the time window closes:
Every camp is always connected to its associated metro station. There are two subsets of arcs E, which contain arcs with certain properties. The first subset \(E^H\) connects nodes with long waiting times. They should be avoided if possible, because long waiting times for employees are disadvantageous:
The second subset \(E^L\) connects nodes with similar starting times. Their time windows overlap and the order when a camp is visited may change depending on the realizations of \(t_{i}\) and \(t_{j}\):
Many computational studies have been conducted to evaluate the scalability of such problems (Solomon 1987; Cordeau et al. 2001 or Miranda and Conceição 2016). The focus of this paper is the suitability of different approaches for MOCO problems.
4 Solution approaches
4.1 Data description and model performance
This paper is based on the real data set containing three metro stations and 104 camps accommodating 178,131 pilgrims. All departures are scheduled within 8 hours. The average time to walk from one camp to another (\(w_{ij}\)) is about 10 min, and the average monitoring duration (\(a_i\)) is 8 minutes. On average, a camp must be visited not later than 7 minutes after the scheduled departure. A computer with an Intel Xeon CPU E5-2667 v3 processor, 256 GB RAM and CPLEX as a solver has been used for all studies in this paper.
Solving a single instance of the model with this data does not take longer than a second. Subtours are only possible when two camps with similar starting times and long monitoring durations are close together. This is rarely the case since the set \(E^{\text {L}}\) contains only 111 arcs. Lifting the subtour elimination constraints with (14) does not reduce the calculation time for this instance. The stronger formulation becomes more important when many camps have similar starting times, because they enable more possible subtours.
4.2 Goal programming
The goal programming approach is one method to address multiple objectives (Tamiz et al. 1998). All objective values are combined in a single objective function. This approach requires the knowledge of the objective weights of the DM to assess the deviation of the individual objectives from their optima. The objective function minimizes the sum of deviations of the objective k from its individual optima \(f^*_k\) weighted with \(\bar{\lambda }\):
Since \(f^*_k=0 \quad \forall k\in K\) in our application, the objective function can be simplified:
This simplification leads to a normalized weighted objective function and is a special case of the goal programming approach, since the individual optima of the objective are zero. In order to make a comparison between the deviations of the objectives easier for the DM, the weights can be replaced to normalize the objective value by its upper bound \(\bar{\lambda }_k=\frac{\lambda _k}{\kappa _k}\). \(\lambda _k\) is the weight of the DM for the normalized objective value \(k \in K\). The calculation of the upper bounds \(\kappa _k\) is listed in Table 1. The resulting objective function minimizes the weighted sum of normalized objective values:
The weights \(\lambda _k\) of the DM are unknown. Testing multiple sets of weights can give valuable insights in the structure of the efficient frontier. Systematically varying all goals in certain steps while ensuring that \(\sum _{k\in K}\lambda _k=1\) delivers a set of weights with constant intervals. Decreasing the step size increases the number of weight combinations. With a step size of \(10\%\) each combination of the weights \(\lambda _k\) in \(\{0;0.1;0.2;\dots ;0.9;1\}\) is applied to the objective values as long as \(\sum _{k\in K}\lambda _k=1\). An extract of the weights for a step size of \(10\%\) is listed in Table 3. All possible combinations of weights changing by \(10\%\) with a sum of 1 are used for the computational study. The results obtained by solving the goal programming approach with the objective function (20) and the constraints (8)–(13) for different step sizes are listed in Table 2.
A given step results in a certain number of instances. Each instance represents a realization of \(\lambda _k \forall k\in K\). There are more instances than distinct efficient solutions, because different weights may still result in the same solution. Decreasing the step size delivers very few additional efficient solutions compared to a high increase in instances and, therefore, calculation time. The instances and the corresponding amount of distinct and efficient solutions is illustrated in Fig. 10b. Even a very large number of instances cannot deliver the complete set of efficient solutions. Obviously, some efficient solutions may be skipped due to gaps that are too large while varying the weights. Additionally, the non-supported solutions are excluded, because the underlying problem utilizes integer variables (Ulungu and Teghem 1994). Furthermore, even 534 solutions are too many to be included, for example, in a quotation for the DM. Even if a lot of solutions are skipped, the trade-off between visited pilgrims and the number of employees for the solutions at hand can be looked at. To gain some insights of the efficient frontier, the results of the goal programming approach with a step size of 1% can be analyzed. Here, the maximum and minimum amount of pilgrims that have not been visited is illustrated in Fig. 10a for each number of employees. The remaining objective values have not been plotted in this figure, but the benefit of an additional employee can be estimated (Table 3).
a The minimum and maximum amount of non-visited pilgrims for each number of employees of the goal programming approach with a step size of 1%. b Relation of the step size and the resulting amount of distinct efficient solutions of the goal programming approach from Table 2
Another computational study has been conducted to show the conflict of objectives. Table 4 lists the objective values and weights for each objective in 12 rows. A small (0.1) a medium (0.52) and a high (0.88) weight has been assigned to each objective (bold values) with equal weights for the remaining three objectives.
As expected, a high weight reduces the corresponding objective value. A weight of 52% is already enough to push the number of non-visited pilgrims to 140. Punishing the walking distance with a high weight leads to the trivial solution of not deploying any employees at all. Increasing the number of employees from five to six decreases the number of non-visited pilgrims by 1790.
4.3 Enumeration of efficient solutions
Finding all efficient solutions is not guaranteed by using the goal programming approach. One possible way, described in Sylva and Crema (2004), of calculating all efficient solutions is to calculate one identified efficient solution iteratively and restrict all feasible solutions dominated by it, until no further solution can be found. Let \(r=1,\dots ,R\) be the iteration count with R as the amount of passed iterations. \(f_{rk}\) is the objective value of goal \(k \in K\) in iteration r. \(y_{rk}\) is a binary variable and 1 if the current solution is superior to the solution of the iteration r in goal k. Otherwise it is zero. The objective function of this approach minimizes the sum of the individual normalized objective values and is defined as \(r'=R+1\) for a new iteration:
Note that no weights are defined for the individual goals. Those weights lead only to the order in which the solutions are found. The objective values are normalized to avoid scaling issues. The constraints (8)–(13) and two additional constraint blocks are required for this approach:
The Eqs. (22) and (23) force a solution to be found, which has a better objective value in at least one of the objectives. \(\epsilon\) is a small positive number and does not exclude any solutions, since all objective values are integer. This approach can list all efficient solutions. Due to the increasing number of constraints with each iteration, the numerical study was aborted after 52 h of calculation. In that time, 254 distinct efficient solutions have been found while taking the longest time for the last iterations. The calculation time per iteration is illustrated in Fig. 11. Only 17 equal solutions have been observed when comparing the solutions with the solutions of the goal programming approach. The goal programming approach found solutions systematically distributed over the efficient frontier, whereas the enumeration approach delivered solutions relatively close to each other. The objective function in the enumeration approach does not change, so that each further iteration will deliver an adjacent solution.
Even though the calculation time is too long for a practical use, this approach still gives valuable insights in the set of supported efficient solutions. Those insights are discussed in the Sect. 4.5.
4.4 Augmecon2
Augmecon2 is an algorithm to find the exact pareto set in MOCO problems (Mavrotas and Florios 2013). This algorithm improves the Augmecon algorithm described in Mavrotas (2009). The core idea is to optimize a single objective while bounding the remaining objective values. Iteratively adjusting the bounds of all except one objective delivers many efficient solutions. Firstly, the range of every objective value is obtained by creating the payoff table. Table 5 is the payoff table and lists the objective values for all objectives while optimizing a single objective only and improving the remaining objectives afterwards in a lexicographic order.
The best case scenario for the pilgrim objective is to visit all pilgrims. To achieve this solution at least six employees are necessary. Optimally for the next objective, not a single employee is in duty with the consequence of visiting not a single pilgrim. It is possible to reduce the wait objective to zero while simultaneously visiting all pilgrims, but seven employees are necessary. Again no employee is in duty, when optimizing the last objective, because not a single step needs to be done. The range for each objective, \(\text {range}_k\), is the maximum minus the minimum value of each column in the payoff table.
With this payoff table every objective can be divided into equidistant steps, which serve as the bounds during the optimization. For example, the objective range of minimizing the number of employees can be divided by seven resulting in the bounds: \(0,1,\dots ,7\). Similarly, the objective range of wait are divided by 20 and walk by 40. Now, while optimizing a single objective, all other objectives are bound to one of the resulting values when dividing the objective range. This process is repeated for every possible combination of bounding the three objectives. Dividing each objective into more steps delivers more solutions which takes a longer computation time than solving all possible combinations when dividing the objectives in less steps.
In each iteration one of those steps \(\epsilon _k\) is chosen as a bound for each objective. The following objective function minimizes the number of pilgrims and maximizes the normalized \(\text {SLACK}_k\) variables for the three remaining objectives:
Adding weights to the normalized slack variable enforces a sequential optimization of the remaining objectives.
Despite the model relevant Eqs. (8)–(13) the following restrictions bound the remaining three objectives:
The three remaining objectives cannot be worse than the given bound \(\epsilon _k\). The objective value can be lower (better), while increasing the slack, which is normalized and maximized in the objective function (24). Solving the model for all possible combinations of the values for \(\epsilon _k\) delivers the exact pareto set. Note, that some computational improvements can be achieved by iterating over the combinations as described in Mavrotas and Florios (2013).
This solution approach found 215 solutions in 8 min. A short extract is listed in Table 6.
This mainly shows the effect of lowering the number of employees on the number of non-visited pilgrims. An increasingly growing number of pilgrims are missed when decreasing the number of employees. Employing only five instead of six employees misses 1190 pilgrims, while reducing the number of employees once again, reduces the number of missed pilgrims by 12,848. The other two objectives change simultaneously, because a reduced number of employees trivially leads to a reduced total walking time. This approach points out the trade-offs between the various objectives. Note, that the trade-off depends on the step size of the \(\epsilon _k\) bounds. A smaller step size than 1 (which was used in Table 6) is futile, because the number of employees is always integer.
Table 7 scrutinizes the effects of adjusting the walk objective. It is possible as shown in the first row, to employ only six persons and still visit all pilgrims while fulfilling the walk objective. Limiting the walk objective further, decreases the number of visited pilgrims and again this increase is growing.
Calculating those trade-off representations can help inform the DM about the connection of the underlying problem.
4.5 Gilbert et al.’s interactive approach
The two previous approaches have shown that the set of efficient solutions is too big to be included in an offer completely. The approach of Gilbert et al. includes the interaction with the DM Gilbert et al. (1985). The benefit of this approach compared to other approaches is the simple explanation and fast execution concerning the cooperation with the DM. Start with any efficient solution with the objective values \(f_k \forall k \in K\). During each iteration m, the DM selects the objective \(\bar{k} \in K\) they want to improve next. The DM defines an \(\epsilon ^m_{\bar{k}}>0\) for the objective \(\bar{k}\) based on his or her utility function. \(\epsilon ^m_{\bar{k}}\) is the amount the objective \(\bar{k}\) should be improved in iteration m if possible. Afterwards, the model with the objective function (26) subject to the constraints (8)–(13) is solved \(|K|-1\) times. Each time one of the remaining objective functions \(K\setminus \bar{k}\) is minimized. An improvement in objective \(\bar{k}\) is achieved by taking into account a loss in the objective function k while introducing an upper bound for all remaining objectives.
Constraint (27) ensures an improvement in the objective \(\bar{k}\) selected by the DM. A deterioration of the objective value for k is accepted while ensuring that all other objective values cannot increase in constraint (28). Out of the \(|K|-1\) solutions, the DM selects the feasible solution best matching their utility function, which is the starting point for the following iteration. This approach takes advantage of the utility function of the DM while their involvement additionally raises the acceptance of the offer. It also simplifies the process for the DM, because choosing from a small set of alternatives requires less effort and preparation than quantifying certain weights for various objectives that are difficult to compare.
The result of a sample implementation is given in Table 8. Each iteration contains the results of one or more solutions with their corresponding k and \(\epsilon ^m_{\bar{k}}\). The DM chose one solution of each iteration, which was used as the base for the following iteration. The solutions chosen by the DM are marked with a star \(^*\).
4.6 Comparison
Many indicators measuring the performance of MOCO problems are introduced in the literature (e.g. Okabe et al. 2003 or Zitzler et al. 2008). Four different performance indicators listed in Zitzler et al. (2008) are calculated comparing the resulting solution set of all four solution approaches. Table 9 lists all performance indicators. The first two performance indicators are cardinality-based. Overall Non-dominated Vector Generation (ONVG) counts the number of generated solutions. Very high and very low values for the ONVG indicate a bad performance. The Error Ratio, indicating the ratio of the solutions which are not efficient, is not listed in Table 9 because it is zero for all solution approaches. The Coverage of two Sets indicator compares the solution set of two approaches. It counts how many solutions are found by both approaches relatively to the total number of solutions found by either approach. The total number of solutions is hinted in each row of the coverage indicator in Table 9. Another performance indicator calculates the Distribution by taking the average difference of each solution with its closest neighbor. The closest neighbor is the solution with the smallest sum of differences in all objectives. Lastly, the Overall Pareto Spread indicates the area of the efficient solutions which is covered by one approach. The value is between 0 and 1 while bigger values indicate a better performance. It computes how much of the range of each objective is covered by the solutions found by a solution approach. For each objective the maximum minus the minimum value of all found solutions is divided by the nadir point minus the best possible value. The nadir value is the worst objective value of pareto optimal solutions. Multiplying all values for each objective delivers the Overall Pareto Spread.
Gilbert et al.’s (1985) approach delivers a reasonable small and, therefore, easy-to-grasp set of solutions. The Distribution indicates a big variety between the solutions. The spread is very small because only the area of the solutions relevant for the DM is examined. The goal programming approach spreads nearly around all solutions due to the parametrization of the weights. After 52 h the enumeration approach was stopped and, in that time, many similar solutions have been found in a small area. This means that the goal programming approach skips many supported and non-supported efficient solutions even with small changes in the weights for the objectives. Augmecon2 delivers well distributed solutions with a relatively big spread, while also finding many different solutions. Even though the number of solutions found by the Augmecon2 approach is still too big to present to the DM, they still can be utilized to illustrate the trade-offs between the different objectives as done in Sect. 4.4. Those insights can help the DM,while interacting with Gilbert et al.’s (1985) approach. Alternatively, the DM could, if he is interested, be guided through systematically structured solutions obtained by the Augmecon2 approach.
5 Managerial implications
While applying the solution approaches to the described problem, broader insights emerged apart from the performance indicators that compare the computational results. Despite being practical and applicable, the obtained solutions cannot only be used for creating a quotation for the responsible decision makers. It is also usable for the operation itself. The selected solution contains the number of employees and the sequence of camps (paths) each individual employee should visit. A smartphone application stores the path for each employee to help them locate the camps. The next camp including the shortest route to it is displayed to the employee. Upon arrival, the employee can log the dispatching status of the pilgrims in the camp.
Knowing the path for each employee before the event starts has several advantages. Firstly, the employees can be trained with their own specific path, since finding the correct camps can be difficult in crowded areas. Furthermore, no internet connection and communication between the smartphone application and a central server is necessary during the operation. The network stability cannot be guaranteed in harsh climate conditions and with a myriad of connected devices. Training the employees can, therefore, reduce the number of mistakes done during the operation. After completing the operation, the execution can be analyzed, if the smartphone tracked the positions of every employee. The planned and actual travel and waiting times can be compared and the parametrization can be tweaked for future operations. Additionally, the observations by the employees have an increased credibility, because the presence at the correct camp at the correct time is recorded. This empirical data might be important when accusing a group of pilgrims violating the schedules.
Further strategical conclusions can be made. As discussed in Haase et al. (2016), the schedule compliance is important for the safety of the pilgrims during the Hajj. This underlines the importance of monitoring and potentially increasing the schedule compliance during the operation. Decision makers on site thought about a model of penalizing schedule violations. An organizer gets less pilgrims approved for next year’s Hajj, if their pilgrims violate the schedules. The excess capacity of pilgrims can be reallocated to more compliant organizers. Monitoring the schedule compliance is essential for the effectiveness of this incentive to work. We emphasize that the effectiveness of the strategy has not been researched yet and is not subject of this paper.
6 Conclusion and outlook
If an automated system, which monitors the exact departure times of all pilgrims, is not available, manually recording the departure times is necessary. There are many different aspects which can be measured and evaluated when directing a small workforce between the camps. Four of those aspects have been considered in this paper. While solving a MOCO problem, many different OR methods with individual advantages and disadvantages can be applied. The goal programming approach illustrates the trade-off between the different goals, even if the weights of the DM are not known. Unfortunately, too many supported efficient solutions are generated to be presented to the DM. Additionally, the non-supported efficient solutions are not obtained. The enumeration approach compensates this disadvantage by listing both the supported and non-supported efficient solutions. For this problem, the time needed to list all efficient solutions is not practical. The Augmecon2 approach delivers well-spread solutions without overwhelming the DM with a myriad of solutions. It also can be used to show the trade-offs between the four objectives. Gilbert et al.’s interactive approach Gilbert et al. (1985) helps to systematically search through the efficient solutions, even if the utility function of the DM is not known. The involvement of the DM in the decision process also raises their acceptance. Due to this consideration, the interactive approach of Gilbert et al. (1985) was chosen to select an efficient solution for the described problem. The presented approach does not include any fairness criterion concerning the tasks for the employees. In further research, the resulting routes for the employees could be compared in terms of length and waiting times.
Abbreviations
- \(I\) :
-
Nodes
- C :
-
Camps \(C\subset I\)
- D :
-
Metro stations \(D\subset I, C\cap D = \emptyset\)
- \(C_i\) :
-
Camps associated to metro station \(i \in D\) \(C_i \subset C\)
- E :
-
Set of arcs connecting compatible nodes
- \(E^H\) :
-
Set of arcs with waiting times longer than \(t^H\) \(E^H \subset E\)
- \(E^L\) :
-
Set of arcs connecting camps with similar starting times \(E^L \subset E\)
- \(I^p_i\) :
-
Set of immediate predecessor nodes of node \(i \in I\)
- \(I^s_i\) :
-
Set of immediate successor nodes of node \(i \in I\)
- K :
-
Set of objective functions
- \(p_i\) :
-
Number of pilgrims located in camp \(i \in C\)
- \(s_i\) :
-
Scheduled departure time for pilgrims of camp \(i\in C\)
- \(w_{ij}\) :
-
Time needed to walk from node \(i \in I\) to \(j \in I\)
- \(a_i\) :
-
Monitoring time needed for an employee at camp \(i\in C\)
- \(t^{\text {max}}_i\) :
-
Maximum allowed delay for an employee at the camp \(i\in C\)
- \(t^H\) :
-
Maximum waiting time
- \(x_{ij}\) :
-
1 if node \(i \in I\) is visited directly after node \(j \in I\), 0 otherwise
- \(t_i\) :
-
Time after \(s_i\) when a camp \(i\in C\) is visite
References
Bektas T (2006) The multiple traveling salesman problem: an overview of formulations and solution procedures. Omega 34(3):209–219. https://doi.org/10.1016/j.omega.2004.10.004
Bowerman R, Hall B, Calamai P (1995) A multi-objective optimization approach to urban school bus routing: Formulation and solution method. Transport Res Part A 29(2):107–123. https://doi.org/10.1016/0965-8564(94)E0006-U
Cordeau J-F, Laporte G, Mercier A (2001) A unified tabu search heuristic for vehicle routing problems with time windows. J Oper Res Soc 52(8):928–936. https://doi.org/10.1057/palgrave.jors.2601163
Czyzżak P, Jaszkiewicz A (1998) Pareto simulated annealing-a metaheuristic technique for multiple-objective combinatorial optimization. J Multi-Criteria Decision Anal 7.1:34–47. https://doi.org/10.1002/(SICI)1099-1360(199801)7:1%3C34::AID-MCDA161%3E3.0.CO;2-6
Desrochers M, Laporte G (1991) Improvements and extensions to the Miller-Tucker-Zemlin subtour elimination constraints. Oper Res Lett 10(1):27–36. https://doi.org/10.1016/0167-6377(91)90083-2
Dyer JS (1972) Interactive goal programming. Manage Sci 19(1):62–70. https://doi.org/10.1287/mnsc.19.1.62
Eckart Z, Joshua K, Lothar T (2008) Quality assessment of pareto set approximations. Multiobject Optimiz Lecture Notes in Computer Science 5252:373–404. https://doi.org/10.1007/978-3-540-88908-3_14 (Springer Berlin Heidelberg)
Ehrgott M, Gandibleux X (2000) A survey and annotated bibliography of multiobjective combinatorial optimization. OR Spectrum 22(4):425–460. https://doi.org/10.1007/s002910000046
Ehrgott M, Gandibleux X (2004) Approximative solution methods for multiobjective combinatorial optimization. Top 12(1):1–63. https://doi.org/10.1007/BF02578918
Florios K, Mavrotas G (2014) Generation of the exact Pareto set in multi-objective traveling salesman and set covering problems. Appl Math Comput 237:1–19. https://doi.org/10.1016/j.amc.2014.03.110
Fonseca CM, Fleming PJ (1995) An overview of evolutionary algorithms in multiobjective optimization. Evol Comput 3(1):1–16. https://doi.org/10.1162/evco.1995.3.1.1
Gendreau M, Hertz A, Laporte G, Stan M (1998) A generalized insertion heuristic for the traveling salesman problem with time windows. Oper Res 46(3):330–335. https://doi.org/10.1287/opre.46.3.330
Gilbert KC, Holmes DD, Rosenthal RE (1985) A multiobjective discrete optimization model for land allocation. Manage Sci 31(12):1509–1522. https://doi.org/10.1287/mnsc.31.12.1509
Haase K, Al Abideen HZ, Al-Bosta S, Kasper M, Koch M, Müller S, Helbing D (2016) Improving pilgrim safety during the Hajj: An analytical and operational research approach. Interfaces 46(1):74–90. https://doi.org/10.1287/inte.2015.0833
Hansen MP (2000) Use of substitute scalarizing functions to guide a local search based heuristic: the case of moTSP. J Heuristics 6(3):419–431. https://doi.org/10.1023/A:1009690717521
Helbing D, Johansson A, Al-Abideen HZ (2007) Dynamics of crowd disasters: an empirical study. Phys Rev E 75(4):046109. https://doi.org/10.1103/PhysRevE.75.046109
Jaszkiewicz A (2002) Genetic local search for multi-objective combinatorial optimization. Eur J Oper Res 137(1):50–71. https://doi.org/10.1016/S0377-2217(01)00104-7
Jozefowiez N, Semet F, Talbi E-G (2008) Multiobjective vehicle routing problems. Eur J Oper Res 189(2):293–309. https://doi.org/10.1016/j.ejor.2007.05.055
Konak A, Coit DW, Smith AE (2006) Multi-objective optimization using genetic algorithms: a tutorial. Reliab Eng Syst Saf 91(9):992–1007. https://doi.org/10.1016/j.ress.2005.11.018
Matthias E, Xavier G (2008) Hybrid metaheuristics for multi-objective combinatorial optimization. Hybrid metaheuristics. Studies in Computational Intelligence 114:221–259. https://doi.org/10.1007/978-3-540-78295-7_8 (Springer)
Mavrotas G (2009) Effective implementation of the \(\varepsilon\)-constraint method in Multi-Objective Mathematical Programming problems. Appl Math Comput 213(2):455–465. https://doi.org/10.1016/j.amc.2009.03.037
Mavrotas G, Florios K (2013) An improved version of the augmented \(\varepsilon\)-constraint method (AUGMECON2) for finding the exact pareto set in multi-objective integer programming problems. Appl Math Comput 219(18):9652–9669. https://doi.org/10.1016/j.amc.2013.03.002
Miranda DM, Conceição SV (2016) The vehicle routing problem with hard time windows and stochastic travel and service time. Expert Syst Appl 64:104–116. https://doi.org/10.1016/j.eswa.2016.07.022
Okabe T, Jin Yaochu, Sendhoff B (2003) A critical survey of performance indices for multi-objective optimisation. In: The 2003 Congress on Evolutionary Computation. IEEE. (pp. 878–885). https://doi.org/10.1109/cec.2003.1299759
Paquete L, Schiavinotto T, Stützle T (2007) On local optima in multiobjective combinatorial optimization problems. Ann Oper Res 156(1):83–97. https://doi.org/10.1007/s10479-007-0230-0
Solomon MM (1987) Algorithms for the vehicle routing and scheduling problems with time Window constraints. Oper Res 35(2):254–265. https://doi.org/10.1287/opre.35.2.254
Sylva J, Crema A (2004) A method for finding the set of non-dominated vectors for multiple objective integer linear programs. Eur J Oper Res 158(1):46–55. https://doi.org/10.1016/S0377-2217(03)00255-8
Tamiz M, Jones D, Romero C (1998) Goal programming for decision making: an overview of the current state-of-theart. Eur J Oper Res 111(3):569–581. https://doi.org/10.1016/S0377-2217(97)00317-2
Teghem J, Tuyttens D, Ulungu EL (2000) An interactive heuristic method for multi-objective combinatorial optimization. Comput Oper Res 27(7):621–634. https://doi.org/10.1016/S0305-0548(99)00109-4
Ulungu EL, Teghem J, Fortemps PH, Tuyttens D (1999) MOSA method: a tool for solving multiobjective combinatorial optimization problems. Journal of Multi-Criteria Decision Analysis 8(4):221–236. https://doi.org/10.1002/(SICI)1099-1360(199907)8:4%3C221::AID-MCDA247%3E3.0.CO;2-O
Ulungu EL, Teghem J (1994) Multi-objective combinatorial optimization problems: a survey. J Multi-Criteria Decision Anal 3(2):83–104. https://doi.org/10.1002/mcda.4020030204
Funding
Open Access funding enabled and organized by Projekt DEAL.. Open Access funding enabled and organized by Projekt DEAL.. Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bonz, J. Application of a multi-objective multi traveling salesperson problem with time windows. Public Transp 13, 35–57 (2021). https://doi.org/10.1007/s12469-020-00258-6
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12469-020-00258-6