Abstract
This study develops a framework to optimize bus assignments and operating practices to routes considering both operating costs and environmental goals. The mixed-integer programming model is applied to the Metro Transit bus system in the Minneapolis–St. Paul metropolitan area. The model is used to derive representative solutions on the efficient frontiers between operating costs and emissions, and to demonstrate how economic factors such as fuel cost and service level affect the trade-offs between costs and environmental outcomes. An analysis of fleet composition shows that vehicle assignments can significantly affect the cost and emission performance of the fleet. We then use the model to evaluate the actual bus assignment schedule used by Metro Transit, and provide suggestions on how to reduce operating costs and emissions. The model is useful in supporting strategic decisions such as vehicle replacement and purchase, as well as operational planning.









Similar content being viewed by others
Notes
For transit planning problems that include light rail, scheduling variables may be used to assemble trains of specific sizes during particular planning periods.
The GAMS model used here is designed for analyses of a wide range of transit planning problems. For details, see Apland and Sun (2019).
References
Apland J, Sun B (2019) A multi-period, multiple objective, mixed integer programming, GAMS model for public transit planning. Staff Paper P19-3. Department of Applied Economics, University of Minnesota
Atabani AE, Badruddin IA, Mekhilef S, Silitonga AS (2011) A review on global fuel economy standards, labels and technologies in the transportation sector. Renew Sustain Energy Rev 15(9):4586–4610
Baita F, Pesenti R, Ukovich W, Favaretto D (2000) A comparison of different solution approaches to the vehicle scheduling problem in a practical case. Comput Oper Res 27:1249–1269
Banihashemi M, Haghani A (2000) Optimization model for large-scale bus transit scheduling problems. Transp Res Rec 1733:23–30
Barany M, Bertok B, Kovacs Z, Friedler F, Fan LT (2011) Solving vehicle assignment problems by process-network synthesis to minimize cost and environmental impact of transportation. Clean Technol Environ Policy 13(4):637–642
Barla P, Gilbert-Gonthier M, Castro MAL, Miranda-Moreno L (2017) Eco-driving training and fuel consumption: impact, heterogeneity and sustainability. Energy Econ 62:187–194
Bektaş T, Laporte G (2011) The pollution-routing problem. Transp Res Part B Methodol 45(8):1232–1250
Bodin L, Golden B, Assad A, Ball M (1983) Routing and scheduling of vehicles and crews: the state of the art. Comput Oper Res 10(2):63–211
Bunte S, Kliewer N (2009) An overview on vehicle scheduling models. Public Transp 1(4):299–317
Carrión M, Arroyo JM (2006) A computationally efficient mixed-integer linear formulation for the thermal unit commitment problem. IEEE Trans Power Syst 21(3):1371–1378
Ceder AA (2011) Public-transport vehicle scheduling with multi vehicle type. Transp Res Part C Emerg Technol 19(3):485–497
Clark NN, Kern JM, Atkinson CM, Nine RD (2002) Factors affecting heavy-duty diesel vehicle emissions. J Air Waste Manag Assoc 52(1):84–94
Costa A, Branco IM, Paixão JMP (1995) Vehicle scheduling problem with multiple type of vehicles and a single depot. In: Daduna JR, Branco I, Paixão JMP (eds) Computer-aided transit scheduling. Springer, Berlin, pp 115–129
Demir E, Bektaş T, Laporte G (2014) The bi-objective pollution-routing problem. Eur J Oper Res 232(3):464–478
Dessouky M, Rahimi M, Weidner M (2003) Jointly optimizing cost, service, and environmental performance in demand-responsive transit scheduling. Transp Res Part D Transp Environ 8(6):433–465
Ehrgott M (2005) Multicriteria optimization. In: Lecture notes in economics and mathematical systems, vol 491. Springer, Berlin
Ehrgott M (2006) A discussion of scalarization techniques for multiple objective integer programming. Ann Oper Res 147(1):343–360
Energy Information Administration (2017) How much carbon dioxide is produced from burning gasoline and diesel fuel? https://www.eia.gov/tools/faqs/faq.php?id=307&t=11. Accessed 21 Dec 2017
Environmental Protection Agency (2010) Integrated science assessment for particulate matter. Office of Research and Development, National Center of Environment Assessment. https://www.epa.gov/isa/integrated-science-assessment-isa-particulate-matter. Accessed 21 Dec 2017
Environmental Protection Agency (2016) Integrated science assessment for oxides of nitrogen—health criteria. Office of Research and Development, National Center of Environment Assessment. https://www.epa.gov/isa/integrated-science-assessment-isa-nitrogen-dioxide-health-criteria. Accessed 21 Dec 2017
Environmental Protection Agency (EPA) (2016) Draft inventory of US greenhouse gas emissions and sinks: 1990–2014. https://www3.epa.gov/climatechange/Downloads/ghgemissions/US-GHG-Inventory-2016-Main-Text.pdf. Accessed 21 Dec 2017 (see also https://www.epa.gov/ghgemissions/inventory-us-greenhouse-gas-emissions-and-sinks-1990-2015. Accessed 17 Apr 2019)
Figliozzi M (2010) Vehicle routing problem for emissions minimization. Transp Res Rec 2197:1–7
Forbes MA, Holt JN, Watts AM (1994) An exact algorithm for multiple depot bus scheduling. Eur J Oper Res 72(1):115–124
Freling R, Wagelmans AP, Paixão JMP (2001) Models and algorithms for single-depot vehicle scheduling. Transp Sci 35(2):165–180
Geng Y, Ma Z, Xue B, Ren W, Liu Z, Fujita T (2013) Co-benefit evaluation for urban public transportation sector—a case of Shenyang, China. J Clean Prod 58:82–91
Goodkind AL, Polasky S (2013) Health & environmental costs of electricity generation in Minnesota. https://www.minnpost.com/sites/default/files/attachments/Polasky%20report%20on%20externality%20costs.pdf. Accessed 22 Dec 2017 (see also https://de.slideshare.net/mnceeInEx/value-of-externalities. Accessed 17 Apr 2019)
Gouge B, Dowlatabadi H, Ries FJ (2013) Minimizing the health and climate impacts of emissions from heavy-duty public transportation bus fleets through operational optimization. Environ Sci Technol 47(8):3734–3742
Guan X, Xu Z, Jia QS (2010) Energy-efficient buildings facilitated by microgrid. IEEE Trans Smart Grid 1(3):243–252
Hedberg E, Gidhagen L, Johansson C (2005) Source contributions to PM10 and arsenic concentrations in Central Chile using positive matrix factorization. Atmos Environ 39(3):549–561
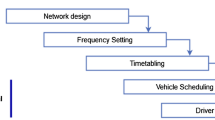
Ibarra-Rojas OJ, Delgado F, Giesen R, Muñoz JC (2015) Planning, operation, and control of bus transport systems: a literature review. Transp Res Part B Methodol 77:38–75
IBM (2015) IBM ILOG CPLEX optimization studio getting started with CPLEX. IBM ILOG CPLEX Optimization Studio V12.6.3 documentation. https://www.ibm.com/support/knowledgecenter/SSSA5P_12.6.3/ilog.odms.studio.help/pdf/gscplex.pdf. Accessed 16 May 2018
Li JQ, Head KL (2009) Sustainability provisions in the bus-scheduling problem. Transp Res Part D Transp Environ 14(1):50–60
Löbel A (1997) Optimal vehicle scheduling in public transit. PhD thesis, Technische Universität Berlin
Metro Transit (2013a) “2013 Fact Sheet”. https://www.metrotransit.org/Data/Sites/1/media/about/facts/2013/2013_metrotransit_facts.pdf. Accessed 22 Dec 2017
Metro Transit (2013b) Buses going big on biodiesel. Metro Transit Blog. https://www.metrotransit.org/buses-going-big-on-biodiesel. Accessed 22 Dec 2017
Mobility Investment Priorities. Express bus service. Texas A&M Transportation Institute. https://mobility.tamu.edu/mip/strategies-pdfs/system-modification/technical-summary/Express-Bus-Service-4-Pg.pdf. Accessed 29 May 2017
Sanchez M, Pradenas L, Deschamps JC, Parada V (2016) Reducing the carbon footprint in a vehicle routing problem by pooling resources from different companies. Netnomics 17:29–45. https://doi.org/10.1007/s11066-015-9099-2
Schouwenaars T, De Moor B, Feron E, How J (2001) Mixed integer programming for multi-vehicle path planning. In: Control conference (ECC), 2001 European. IEEE, pp 2603–2608
Visentini MS, Borenstein D, Li JQ, Mirchandani PB (2014) Review of real-time vehicle schedule recovery methods in transportation services. J Sched 17(6):541–567
Acknowledgements
This work is part of the project “Enabling the Next Generation of Super Hybrid Transit Bus”, which was jointly funded by the Initiative for Renewable Energy and the Environment (Grant number RL-0013-13) and the Center for Transportation Studies, both at University of Minnesota, and Metro Transit—the public transportation operator in the Minneapolis–St. Paul Metropolitan Area. We would like to thank Janet Hopper, David Haas and Chuck Wurzinger at Metro Transit for providing extensive datasets. We are also very grateful for the advice and assistance from Steven Taff, William Northrop, David Kittelson, Win Watts, Andrew Kotz, Shashank Singh and Kieran McCabe at the University of Minnesota, and the anonymous reviewers.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix 1: Equation used to calculate NOx and PM emission levels
where: N = gNOX/Bhp-hr—CARB emission standard for NOX, D = Bhp-hr/gal-Diesel—Diesel fuel energy content per gallon, B = Bhp-hr/gal-Biodiesel—Biodiesel fuel energy content per gallon, x = Volume fraction of biodiesel—The fraction varies by season. The summer level is 20%, while the winter level is 2.5%. MPG = Miles per gallon of fuel—Determined by total miles divided by total fuel, G = Gallons Fuel—From Fuel consumption, ηth = Thermal Efficiency— % of energy in fuel tuned into useful work.
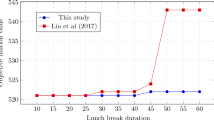
Appendix 2: Weights and values of efficient solutions in Fig. 2, 3, 5 and 6
Rights and permissions
About this article
Cite this article
Sun, B., Apland, J. Operational planning of public transit with economic and environmental goals: application to the Minneapolis–St. Paul bus system. Public Transp 11, 237–267 (2019). https://doi.org/10.1007/s12469-019-00199-9
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12469-019-00199-9