Abstract
Lead (Pb) is a naturally occurring heavy metal that received, in the last decades, much attention in the human health risk assessment community. In the European Human Biomonitoring Initiative (HBM4EU), Pb was identified as a priority substance as various scientific and policy questions were open and still to be answered. They included the further investigation of the internal exposure to Pb, the factors determining it, and its variations within European populations. The aim of this work was to develop an integrative modeling framework for the assessment of the aggregated long-term exposure to Pb in Belgium, Czech Republic, Germany, and Norway. This framework enabled predicting the concentrations of Pb in human blood (PbB) from estimates of the external exposure. The effect of past and current exposure events was accounted for, as multiple country-specific Pb concentration data in environmental compartments and diet, and estimates of the dietary intake of Pb covering a period from the 1970s until the present times were compiled. This modeling approach allowed, using a two-dimensional Monte Carlo (MC2D) approach, running a population-based simulation and characterizing the inter-individual variability within the simulated populations and the uncertainty on the external exposure estimates. The predicted PbB levels were compared with the results drawn from HBM data. To the best of our knowledge, this holistic modeling approach combines for the first time temporal and country-specific trends in environmental lead concentrations to derive internal exposure, in order to get better insights into the relationship between environmental and human lead exposure, and to characterize individual exposure at different ages.
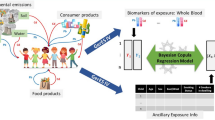
Graphical Abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
During the 20th Century, high exposure to lead was mainly due to the addition of Pb in gasoline that generated important Pb emissions in the atmosphere (Bergdahl and Skerfving 2022). From the 1970s to the 1980s, regulatory measures were implemented in Europe to mitigate the environmental burden by gradually removing lead out of gasoline (Hagner 2000). Over the years, these measures resulted in a significant reduction of Pb air concentrations, but also revealed additional relevant sources of exposure to Pb, which have gained a growing attention recently (von Storch et al. 2000). Multiple pathways can potentially result in high exposure to Pb including the intake through food consumption due to the long-term accumulation of Pb in soils and its transfer to the food chain, through drinking water contaminated by the Pb in plumbing systems, or the ingestion of house dust containing residues of lead-based paints (WHO 2010).
To better quantify the level of (internal) exposure to Pb or to identify potentially specific cases of high exposure to Pb within the general population, human biomonitoring (HBM) programs focusing on Pb have extensively been conducted in Europe during many years (Hahn et al. 2022; Lermen et al. 2021; Schulz et al. 2007; Smolders et al. 2010). By using systematic standardized measurement of the concentration of selected compounds and their metabolites in human biological matrices, HBM studies provide an estimate of the human exposure to those compounds and their potential adverse effects (Angerer et al. 2007). In human health risk assessment, HBM studies are at a global scale increasingly seen as a reliable research approach, as they offer an insight, at the individual and the population levels, into the internal exposures aggregated over all sources and pathways and reflecting the past and the current exposure events (Angerer et al. 2007). In Europe, the use of HBM to inform exposure and risk assessments and to advance chemical safety received a substantial impulse with the European Human Biomonitoring Initiative called HBM4EU (Ganzleben et al. 2017). HBM4EU is coordinating and advancing human biomonitoring in Europe with the aim to generate science-based evidence to support policy making (Gilles et al. 2021; Uhl et al. 2021). As part of the HBM4EU prioritization process (Ougier et al. 2021), a list of substances including Pb were identified for which according to EU institutions and national agencies responsible in the field of risk assessment and risk management in the HBM4EU partner countries open policy relevant questions were determined. Globally, these questions intended to investigate the current internal exposures to Pb in European countries, to identify the major sources of this exposure, and to understand age-dependent differences within the European population and the impact of the ban of leaded gasoline on Pb concentrations in human blood (HBM4EU 2022). In order to provide relevant answers to these policy questions the collection of existing ancillary data informing the external exposure to Pb is paramount as HBM data alone do not enable accounting for the different exposure sources. An evaluation of the external exposure to Pb in conjunction with HBM data is therefore required.
Bierkens et al. (2011) conducted, as part of a European effort to develop and test methods for the integrated assessment of health risks from environmental stressors, a study with the goal to find correlations between blood Pb concentrations (abbreviated PbB thereafter) and Pb concentrations in environmental matrices and consumer sources (drinking water and food products). In their work, they implemented the collection of PbB data, Pb concentrations in air, soil, dust, and drinking water, and estimates of the dietary intake of Pb for different age groups and covering several decades (starting from the 1980s) and various European countries. Despite the compilation of such a large database, the authors acknowledged the inability of the developed regression models to accurately predict actual and future simultaneous exposure to Pb from various environmental compartments (Bierkens et al. 2011). The quantitative interpretation of HBM data for instance to relate estimates of the external exposure with the internal exposure is a complex challenge as it may be affected by data carrying insufficient information or models being incapable to replicate the processes driving the internal exposure (Angerer et al. 2007; Clewell et al. 2008).
Recently, a growing attention has been directed toward the development of in silico approaches capable to reproduce complex (biological) systems to advance exposure and risk assessments (Egeghy et al. 2016; Wambaugh et al. 2019). Specifically, physiologically based pharmacokinetic/toxicokinetic (PBPK/PBTK) models, which are developed to simulate the time-dependent fate of chemicals in humans and animals by following principles of mass transport, fluid dynamics, and biochemistry to reproduce the physiology in the considered organism, are well-established and valuable approaches (Campbell et al. 2012). PBPK models, which transcribe mathematically the processes involved in the absorption, distribution, metabolism, and excretion (ADME) of a potentially hazardous substance in the human body, are often applied to perform forward dosimetry that consists in predicting the concentration of the candidate substance in human tissues and body fluids from measurements of the external exposure (Ruiz and Fowler 2015). For Pb and similar bone seeking elements, a PBPK model that simulates the fate of Pb in the human body was developed and presented in a series of articles published in the 1990s and the beginning of 2000s by O’Flaherty (1991a, 1991b, 1991c, 1993, 1995, 1998, 2000). The O’Flaherty (hereinafter abbreviated as OF) model sets a special emphasis on the age-dependent exchanges of Pb in and out of the bone compartment by accounting for the different phases of the anatomical development of human body and bones in a lifespan (Fleming et al. 1999). By integrating time-varying estimates of the external exposure to Pb and using these as inputs, the OF model enables to predict the lifelong internal Pb exposure resulting from past and current exposure sources at individual and population levels.
In this study, the main objective was to develop an integrative modeling framework for the assessment of the aggregated long-term (external as well as internal) exposure to Pb in Europe. Four European countries, namely Belgium, Czech Republic, Germany, and Norway were selected, due to their extensive history in the monitoring of Pb levels in the general population (and the environment) and the availability of country-specific HBM study data within the HBM4EU network (Cerná et al. 2007; Kolossa-Gehring et al. 2012; Rønningen et al. 2006; Schoeters et al. 2017). Furthermore, the selection of these countries should allow the analysis of the geographical variations of Pb exposure in Europe. The developed approach enables the quantification of the individual exposure at different ages and time periods, and the identification of the major sources of this exposure. Therefore, the present approach should help to analyze the impact of policy not only on the current exposure levels but also on projections of the future exposure to Pb in Europe. To combine historical data describing temporal trends with current external and internal exposure data into one model, the modeling framework was organized in three inter-connected modules:
-
(i)
A toxicokinetic module built on the O’Flaherty (OF) model, which is central in this analysis as it predicts at each time point (i.e., each individual age and de facto corresponding to a calendar year) PbB levels using the information imputed from the two additional modules. For its detailed representation of human body growth and physiological processes occurring in bones, and the integration of an exposure module allowing to evaluate in a straightforward setting various exposure scenarios over a human’s life span, the OF model was selected. Specifically, the OF model was preferred to existing lead-based kinetic models such as the integrated exposure uptake biokinetic (IEUBK) model of the US Environmental Protection Agency (EPA) because it considers Pb kinetics only in children, and the PBPK model of Leggett, which does not propose a detailed characterization of physiological variability that could occur after the age of 25 years (Dede et al. 2018; Leggett 1993; US EPA 1994).
-
(ii)
A growth module that helps simulating individual trajectories of anthropometric parameters (body weight, body height, body mass index) at different ages based on country-specific growth information.
-
(iii)
An exposure module that provides at each time point (i.e., calendar year) the estimates of the external exposure to Pb from air, soil, outdoor and indoor dust, drinking water, and diet.
In order to account for the effect of past and current Pb exposures, multiple country-specific sources of data on the concentrations of Pb in environmental compartments, in drinking water, and food products, as well as estimate of the dietary intake of Pb covering the time frame starting from the 1970s until the present times were compiled. Furthermore, we developed a dietary exposure model based on the age-specific energy intake because of the lack of age-specific dietary intake data for the considered time frame. A two-dimensional Monte Carlo (MC2D) simulation was implemented to characterize the inter-individual variability within the simulated populations and the uncertainty on external exposure estimates. Finally, the predicted PbB levels were compared with the results drawn from HBM studies collected under the umbrella of HBM4EU, with the aim to evaluate the predictivity of our approach (i.e., collected data and modeling framework) to emulate blood Pb levels observed in the considered four countries.
Materials and Methods
Integrative Modeling Framework
An integrative modeling framework was built to evaluate the long-term exposure to Pb in four European countries (i.e., Belgium, Czech Republic, Germany, and Norway). This modeling approach was implemented with the background objective to consider, at the individual level and by replication at the population level, several pathways of Pb exposure including far-field sources such as outdoor air, dust, and soils, and near-field sources such as indoor dust, drinking water, and dietary products. At the individual level, the developed framework consists of three inter-connected components (or modules), namely a growth module, an exposure module and a toxicokinetic model. In Fig. 1, the modeling framework, its components, and the interconnection between them are illustrated. This stepwise approach enabled: (i) to randomly simulate over a lifetime (i.e., until 79 years) individuals characterized by anthropometric parameters such as year of birth, sex, and body weight using country-specific anthropometric data, (ii) to estimate for each simulated individual and at each time point the external aggregated exposure to Pb using country-specific exposure-related data, and (iii) to predict the resulting blood Pb levels (PbB) to be considered as an estimate of the internal exposure and comparing them to empirical HBM data collected within the HBM4EU network in order to evaluate our modeling approach and the collected exposure data. The maximum age of our simulation was set to 79 years, which is close to life expectancy in Europe and because anthropometric data are lacking for elderly people over 80 years (Raleigh 2019). Furthermore, the integration of country-specific exposure-related data covering several decades from the 1970s to the present times allowed not only accounting for the historical exposure to Pb but also enabling making projections in the future. Indeed, for individuals born in the 2000s predictions until a time horizon around 2080 were possible by assuming similar Pb concentrations in the different matrices from the 2020s until approximately 2080. In the following sections each component of the modeling framework and their associated data and models are described in more details.
Toxicokinetic Module
The toxicokinetic module, which is central to predict the internal Pb exposure, was built based on the PBPK model developed for rats and further adapted for humans in the 1990s by O’Flaherty (1991a, 1991b, 1991c, 1993, 1995, 1998). The model of O’Flaherty (or OF model) is a multi-compartment model that emulates the distribution of Pb from blood plasma into liver, kidneys, other well-perfused tissues, cortical and trabecular bones, and other poorly perfused tissues (Fleming et al. 1999). This model intends to reproduce the disposition of Pb in the human body by accounting for the age-dependent variations induced by the growth of the human body with a special focus on the growth of bones. Physiological parameters such as the volume of bones, the volume of other organs, the cardiac output, the organ-specific blood flows, and body clearance rates are varying as a function of body weight and thus age. In addition, the exposure to Pb is assumed to occur via the inhalation route (with a fractional bioavailability assumed constant over a lifetime) and the oral route (with a fractional bioavailability varying depending on age as it is assumed to be higher in infants and drop after the age of 10 years).
The main characteristics of the OF model reside in its description of the age-dependent exchanges of Pb taking place in human bone compartments and the distinction between mature and juvenile bones. Indeed, the cortical bones representing about 80% of the volume of total bones are constituted of (i) a metabolically active region where the modeling of juvenile bone and the remodeling of mature bone affects Pb kinetics, and (ii) a diffusion region where slow diffusion-limited exchanges within the bone compartment and between blood and bone takes place (Fleming et al. 1999; O’Flaherty 1998). The trabecular bones (about 20% of the volume of total bones) are essentially constituted of a metabolically active region similar to the metabolically active region of the cortical bones.
In 2000, the OF model was further refined in order to integrate the loss of bone weight occurring later in life for both men and women and intensively during the menopause period for women between 55 and 65 years (O’Flaherty 2000).
In this work, this later version of the OF model was adopted and the original model code written in the Advanced Continuous Simulation Language (ACSL) that was made available in (O’Flaherty 2000) was transcribed in R using the package deSolve (Mitchell and Gauthier 1976; Soetaert et al. 2010; R Core Team 2022). The scripts in R language can be made available by the corresponding author MS upon request. Prior verifications of the model code were implemented independently by the authors DE and MS (in alphabetical order and with an equal contribution) to ensure an exact reproduction of the model for numerically solving the ordinary differential equations (ODEs).
Growth Module
We have developed a stepwise procedure consisting in four main different steps in order to generate for each simulated individual age-dependent body weight values that account for the anthropometric characteristics proper to each country (Robinson et al. 2015; Rodriguez-Martinez et al. 2020).
Firstly, growth charts and reference values for body weight, body height, and BMI specific to Belgium, Czech Republic, Germany, and Norway were retrieved from the literature. For Belgium, reference tables for individuals from birth until 21 years published by Roelants et al. (2009) were used and complemented for adults and the elderly by BMI data derived from the Belgian Health Interview Survey (BHIS) conducted in 2001 (Demarest et al. 2013). For Czech Republic, body weight, body height, and BMI data were drawn from the results of the national anthropological survey of children and adolescents conducted in 2001 and published by Vignerová et al. (2006). For individuals over 18 years, BMI data published by Cifkova et al. (2004) were used. In Germany, the German Health Interview and Examination Survey for Children and Adolescents (KiGGS) conducted by the Robert Koch Institute (RKI) between 2003 and 2006 provided reference percentiles for anthropometric measures for children and teenagers from birth until 18 years (RKI 2016). For individuals aged between 19 and 79 years reference values of BMI were drawn from Hemmelmann et al. (2010). For Norway, reference anthropometric data published by Júlíusson et al. (2013) for children and adolescents until 18 years and by Droyvold et al. (2006) for adults over 18 years were considered.
Secondly, the collected anthropometric data were compiled to derive country- and sex-specific parameters lambda, mu, and sigma (LMS) of the method developed by Cole and Green (1992) for the smoothing of growth curves. This method is based on the use of the Box-Cox transformation, which is a parametric approach used to construct reference percentiles in growth charts (Flegal 2013). For a given anthropometric variable X, the value of the desired percentile \(X_{\alpha } \left( T \right)\) of X at age T (in years) is given by the following equation.
L(T), M(T), and S(T) are the parameters of the LMS method evaluated at T, and \(Z_{\alpha }\) that is also called Z-score stems from a standard Gaussian distribution. The value of \(Z_{\alpha }\) corresponds to the \(\alpha {\text{th}}\) percentile of a standard normal distribution. The R package gamlss was applied to estimate the LMS parameters (Rigby and Stasinopoulos 2005).
Thirdly, the country- and gender-specific LMS parameters estimated at the previous stage for the body weight, body height, and BMI variables were applied to randomly simulate individual body weight trajectories from birth to the age of 79 years based on Z-scores randomly generated using a standard normal distribution.
Finally, the generated individual body weight trajectories are used to calibrate the parameters of the growth equation used by O’Flaherty in conjunction with the PBPK model as described below (O’Flaherty 1993).
For a given individual \(i\) from a country \(c\), \(BW_{i}^{c} \left( T \right)\) is the body weight (in kg) at age T (in years), the parameter \(BW0^{c}\) represents the country-specific mean body weight (in kg) at birth, \(W_{child}^{i}\) is the maximum weight (in kg) for the initial hyperbolic section of the growth curve corresponding to the rapid growth during early childhood, and \(T_{half}^{i}\) represents the midpoint age (in years) of this hyperbolic section. The parameters \(W_{adult}^{i} , \kappa\), and \(\lambda^{i}\) characterize the logistic behavior of the growth curve during adolescence and early adulthood. The parameter \(W_{adult}^{i}\) (in kg) is defined so that the sum \(W_{adult}^{i} + W_{child}^{i}\) equals the individual’s body weight at approximately 25–30 years, \(\kappa\) is a weighting factor for young ages fixed at 600 and \(\lambda^{i}\) that is sex-dependent is fixed at 0.017 year/kg for women and 0.0095 year/kg for men.
Exposure Module
Data
The collected data included not only Pb concentrations in air, soil, indoor and outdoor dust, drinking water, and food products, but also age-dependent or age group-specific dietary intake rate values with the aim to cover several decades starting from the 1970s. Whenever possible, country-specific data relevant at either national or regional levels were considered and supplemented with data at the European level (e.g., European average or German data) to bridge the gaps in case of missing knowledge. The compiled data, which were presented as either raw data or aggregated records (i.e., descriptive statistics such as mean, standard deviation, or percentiles), were retrieved from various sources including peer-reviewed papers, reports published by national and international committees or in publicly available databases from national or international environmental monitoring programs (see Supplementary Information S1 stored as an Excel spreadsheet for details). The results published by Bierkens et al. (2011) and the references listed in the article served as point of departure of our search for evidence. These data sources were complemented, for the years after the 2010s, by more recent references found in the literature.
For each country in each decade starting from the 1970s, the collected data were compiled to derive probability distribution functions characterizing the uncertainty on the Pb concentrations in exposure sources (i.e., environmental matrices, drinking water, and food products) as well as the uncertainty on age group-specific dietary intake rates. See Supplementary Information S2, for more details on the derivation of the probability distributions. The resulting dataset of probability distributions and associated references are presented in the Supplementary Information S1.
Exposure Models
Environmental Matrices: Air, Soil, and Dust
The external exposure to Pb via the inhalation of air, and the ingestion of soil and indoor and outdoor dust was estimated as described below by multiplying the inhalation or ingestion rate by the concentration of Pb in the considered matrix as described in the guidelines document on exposure assessment of the US Environmental Protection Agency (US EPA 2019).
The superscripts \(i, a, c \,{\text{and}}\, y\) correspond, respectively, to the \(i{\text{th}}\) individual, their age (in years) and country, and the simulated year. The quantities \(E_{air}^{i,a,c,y} , E_{soil}^{i,a,c,y} , {\text{and}} E_{dust}^{i,a,c,y}\)(in mg/y) denote the rates of Pb intake through the inhalation of air, and the ingestions of soil and dust, respectively. The exposures to soil and dust were calculated using the weighting factor \(f_{outdoor}^{a}\) describing the relative age-dependent time an individual spent outdoors drawn from the handbook of exposure factors published by US EPA (2011). The quantities \(Q_{air}^{y,c} , Q_{soil}^{y,c} , Q_{in\_dust}^{y,c} , {\text{and}} Q_{out\_dust}^{y,c}\) refer to Pb concentrations in air, soil, indoor and outdoor dust, respectively. The variable \(IR_{air}^{i,a}\) (in m3/yeary weight normalized inhalation rate presented in the Table 6.14 of US EPA (2011). The variables \(IR_{soil}^{i,a}\) and \(IR_{dust}^{i,a}\) (in kg/year) corresponds to the annual soil and dust ingestion rate, respectively, which are calculated using the ingestion rates provided by O’Flaherty (2000) for children under six years and complemented, for children (over 6 years), teenagers, adults, and elderly by the ingestion rates published by Wilson et al. (2013).
Drinking Water
The exposure to Pb via the consumption of drinking water was estimated as follows.
The quantity \(E_{water}^{i,a,c,y}\) (in µg/year and converted to mg/year) represents Pb exposure from drinking water, the variable \(Q_{water}^{y,c}\) denotes the concentration of Pb in drinking water expressed in µg/kg, and the variable \(C_{water}^{i,a}\) (in kg/y) corresponds to the age-dependent consumption of water by the \(i{\text{th}}\) individual. Here, the age-specific behavior influencing the consumption of water was accounted for. Indeed, before the age of 6 months water consumption is assumed to exclusively come from the consumption of breast milk or infant formula (denoted baby milk thereafter), whereas from six months to two years water consumption is assumed to be the sum of baby milk and water consumptions. The annual consumption of baby milk was derived using the equation developed by Yeung et al. (2020) combined with the individuals’ body weights from birth to the age of two years. The consumption of drinking water was calculated based on the equation of O’Flaherty (2000).
Dietary Exposure: Food Products
Two options were considered to quantify the dietary exposure to Pb. In the first option, the dietary exposure data collected in the literature and stored in the tab “E_food” of the Supplemental Material S1 were used and directly imputed in the OF model. The second option, which is model-centric was considered due to the sparsity observed in the collected dietary exposure data. Indeed, for each time point (i.e., calendar year or decade) country-specific and age or age group-dependent dietary exposure estimates are required, which we could not achieve with the compiled database. The model-centric approach was applied as the standard approach in the simulations for all four countries. A comparison of both approaches was implemented using German data as described in the next section.
In the model-centric approach, the dietary exposure model was built on an energy intake-based approach using age-specific energy intakes to derive the annual quantity of consumed food products (see Supplemental Material S2 for more details). The global structure of the model is described as follows:
The quantity \(E_{diet}^{i,a,c,y}\) expressed in mg/year is the dietary intake rates aggregated over \(J = 18\) food groups corresponding to food classes in the German food classification system “Bundeslebensmittelschlüssel (BLS)” (Hartmann et al. 2014). The variables \(Q_{F,j}^{y,c} {\text{with}} j = 1, \ldots , J\) (in µg/g) denote the concentrations of Pb in each food group. The parameters \(e_{j} {\text{with}} j = 1, \ldots , J\) (in Kcal/g) represent the mean relative energy content of each food group drawn from the database of the 2nd German National Nutrition Survey (NVS II) conducted by the Max Rubner Institute (MRI) (MRI 2008). These German data were also used for the other considered countries, as data related to these parameters \(e_{j}\) and specific to the other countries were not available. Preliminary statistical analyses (not shown here) exhibited differences before and after 19 years. Two sets of food energy content data were then provided according to this threshold of 19 years. See the tab “Food_Energy_Content” of the Supplemental Material S1 for details. The variable \(E_{T}^{i,a}\) (in Kcal/year) refers to the age- and sex-dependent total energy intake, which was estimated using the regression models of Henry (2005) built as function of body weight.
Simulations and Uncertainty Analysis
We intended to characterize the impact on the long-term internal Pb exposure of the inter-individual variability induced by the individual-dependent and country-specific anthropometric characteristics and the uncertainty on time-varying Pb concentrations in the environmental matrices, drinking water, and food products as well as the uncertainty on the dietary intake estimates collected in the literature. To this end, the simulations were implemented using a two-dimensional Monte Carlo (MC2D) approach that enabled to separate the inter-individual variability from the uncertainty dimension described by a lower bound (LB), a medium bound (MB), and a upper bound (UB) uncertainty levels equivalent to the 2.5th, 50th, and 97.5th percentiles of the probability distributions of the Pb concentrations in considered matrices.
The MC2D approach is equivalent to the use of two nested one-dimensional or classical Monte Carlo simulations consisting each in generating for each input variable a set of N random numbers (using probability distributions) and feed them into a model to produce a set of N random model outputs (Nauta 2000). The obtained random numbers reflect the extent of the variations of a modeled system considering the variations in the input variables. The MC2D approach is proven to be useful in risk assessment as it enables to differentiate variations attributable to the inter-individual variability and variations due to imprecision or a lack of knowledge (Kelly and Campbell 2000; Ragas et al. 2009).
In our specific case, the resulting outputs are the internal exposure estimates that were compared to the HBM data drawn from several studies conducted in the four considered countries over several years and gathered under the umbrella of HBM4EU. Data on the population characteristics (e.g., number of male and female participants, and the age of participants at the time of sampling) and descriptive statistics of PbB calculated at the population level were available for a total of fifty-eight (58) study populations and sub-populations. These study populations are briefly presented in Table 1. These study populations or sub-populations correspond to various cohorts that were investigated to derive the actual extent of Pb exposure in these groups of the population and more broadly in the considered country at a given time period. See Supplementary Material S2 for details. In addition, the results of the dietary exposure model introduced in the previous section and of the dietary intake data collected from the data compilation process were compared focusing on one German study conducted in 2010, part of the Environmental Specimen Bank campaigns, for which the results are separated between female and male participants (see Table 1 and Supplementary Material S2 for further details).
Results
A first MC2D simulation run was conducted in which hundred (100) individuals were randomly generated for each of the fifty-eight (58) study populations leading to 5800 simulated individuals based on the demographic characteristics and study information described in Table 1 (i.e., study year of sampling, age class and number of female and male study participants). As mentioned in the previous section, LB, MB, and UB are the three levels of uncertainty considered to characterize the uncertainty on the predictions stemming from the uncertainty on the Pb concentrations in air, dust, soil, drinking water, and food products. For each given level of uncertainty, the predicted PbB levels of the 5800 simulated individuals characterized the resulting inter-individual variability. In the following sub-section, the results based on the LB level of uncertainty are presented.
Comparison with HBM Data
The predictions based on the MC2D simulation were summarized by calculating, for each study cohort and for each of the uncertainty levels (i.e., LB, MB, and UB), the 5th, 50th, and 95th percentiles of the inter-individual variability distributions of predicted PbB levels. For each considered study cohort, the summarized predictions and the descriptive statistics of the levels of PbB observed in the study cohort at the study-specific year of sampling are reported in Table 1. The adequacy between predicted and observed PbB values varied depending on the given country and from one uncertainty level to another. The LB case produced the closest results to the HBM data in comparison to MB and UB as ratios of the predicted PbB levels to the observed PbB levels (MC2D/HBM) oscillated on average around 1.45, 0.71, 0.97, and 2.39 for Belgium, Czech Republic, Germany, and Norway, respectively, whereas factors ranged from 10 to 37 for MB and from 15 to 75 for UB. In addition, predictions related to individuals from studies in Norway showed a tendency to be largely higher than HBM data observations, and for Czech Republic to be slightly lower in comparison to predictions drawn for studies from Belgium, and Germany. This shows, that our approach to use the German data for estimation of the dietary intake and in part for complementing missing information in the Czech Republic’s and Norway’s dataset is inappropriate to characterize Pb exposure in those countries.
Long-Term Exposure to Pb
The individual trajectories of PbB (in mg/L) obtained for LB, MB, and UB were summarized per year and per country using population-based median values and illustrated in Fig. 2, and Figures S1 and S2 of the supplementary material S2, respectively. Various phases having different dynamics of PbB are observed over the years in each country. The first phase covers the beginning of the 1970s to the end of the 1980s with PbB levels reaching a peak of about 0.18 mg/L followed by a rapid decline with Pb concentrations around 0.02 mg/L at the end of the 1980s. In this period, individuals from Norwegian studies showed a different pattern in comparison to individuals from Belgium, Czech Republic, and Germany since the predicted PbB levels are lower with a peak around 0.08 mg/L in 1972 and a stabilization of the decline starting in 1976 around 0.02 mg/L. The second phase starts at the beginning of the 1990s with a significant increase of PbB levels reaching peaks around 0.04 mg/L in mid 1990s in Belgium and 0.03 mg/L at the beginning of the 2000s in Czech Republic, Germany, and Norway. This peak is followed by a decrease of PbB levels observed in Czech Republic, Germany, and Norway during the 2000s with PbB median levels about 0.025 mg/L in 2009. For Belgium, the situation is different as a subsequent increase of PbB levels is observed until the end of the 2000s with a population median of approximately 0.03 mg/L. The last phase that starts from the 2010s predicts a steady decrease of Pb concentrations in individuals from all four countries.
Graphical illustration of the variation over time of the median PbB levels (in mg/L) in Belgium (BE), Czech Republic (CZ), Germany (DE), and Norway (NO) predicted based on the LB uncertainty level. The error bars represent the 5th and 95th percentiles of the inter-individual variability distribution
To have a better understanding of the observed time-dependent dynamics, the relative contribution of each source of exposure to the total intake rates of Pb was computed by averaging relative contributions (at an individual level) for each country and each calendar year. The resulting relative contributions are presented in Fig. 3 for the LB level of uncertainty and Figures S3 and S4 of the supplementary material S2 for MB and UB, respectively. In the 1970s, the inhalation of air and the ingestion of drinking water represented the major sources of Pb exposure in Belgium, Czech Republic, and Germany, whereas the ingestion of dust was the major source of Pb exposure in Norway. Starting from the mid-1970s until the end of the 1980s, the ingestion of dust and the dietary pathway became more important in all four countries. From the beginning of the 1990s the major source of Pb exposure was observed to be the diet. In Figure S5 of the Supporting Information S2, the predicted PbB levels illustrated for randomly selected individuals born in different decades confirmed this increasing internal Pb exposure in the 1990s and the 2000s suggesting a significant increase of the external Pb exposure. In addition, the individual trajectories in Figure S5 showed that individuals born in the 1970s reached at early age higher PbB levels than individuals born in other decades and that individuals born in the 1980s, due to rather low external exposures, presented the lowest peak in early age. Consequently, this suggests a generation effect with the influence of the decade in which the individuals are born.
Relative contribution of air, dust, soil, drinking water, and diet to the total Pb intake rates for the LB uncertainty level. Values were averaged over individuals in each country and at each calendar year. BE, CZ, DE, and NO refer to Belgium, Czech Republic, Germany, and Norway, respectively (*Individuals from Germany and Norway were essentially born before the 2000s, which explains the gap observed in the graph as the lifelong simulations could not reach the horizon 2080)
Finally, differences on the long-term internal exposure to Pb between sexes were investigated by evaluating at each calendar year the population-based medians of PbB discriminated by sexes and calculated for Belgium, Czech Republic, and Germany. Studies from Norway were excluded as results for male individuals were not available. The results are presented in Figure S6 of the supporting material S2. Based on the derived results, no significant influence of sex was demonstrated.
Uncertainty and Variability
To analyze the inter-individual variability and uncertainty on Pb occurrence data, a second MC2D simulation run focusing on the two study sub-populations “DE10_ESB_F” and “DE10_ESB_M” was performed. We focused on German studies since the model-centric approach was built mainly on German data and selected these two study populations among German studies arbitrarily. This simulation run consisted in generating 274 and 180 individuals for “DE10_ESB_F” and “DE10_ESB_M,” respectively, which equal the number of study participants in each cohort (see Table 1). The obtained results are summarized in Table 2.
The uncertainty on Pb dietary intake rates and Pb concentrations in the different exposure source matrices resulted in a large uncertainty on PbB values. Indeed, Pb levels in blood differ between LB and MB and between LB and UB by factors of approximately 15 and 30, respectively.
On the contrary, the inter-individual variability drawn for the three levels of uncertainty LB, MB, and UB was observed to be rather small in comparison to the inter-individual variability in the corresponding HBM data in Table 1. Ratios of the 95th percentiles to the 50th and 2.5th percentiles of the variability distributions for the HBM data were estimated at 2 and 3.33 for “DE10_ESB_F” and at 1.85 and 3 for “DE10_ESB_M,” respectively, whereas the ratios for the LB, MB, and UB cases ranged from 1.07 to 1.33 and from 1.02 to 1.12. This observation is especially valid when comparing the ratios calculated for the LB case with the ratios of the HBM data.
Evaluation of the used Dietary Exposure Model
Figure 4 illustrates the distributions of the predictions of Pb concentrations obtained using the dietary exposure model introduced in “Exposure Models” section and the dietary intake data collected in the literature. The Pb levels in blood predicted using the data-based approach are globally lower than the predictions derived from the model-based approach and closer to the HBM data. Specifically for LB, the data-based approach underestimates the observed PbB levels while the model-based approach slightly overestimates them. Furthermore, the resulting uncertainty is significantly lower in the data-based approach than in the model-based approach. In both cases, an underrepresentation of the inter-individual variability in comparison to the inter-individual variability contained in the HBM data is observed.
Comparison of the distributions of PbB levels (in mg/L) predicted for the cohort DE10_ESB_M using the dietary intake rates collected in the literature (option 1 in green) and the dietary exposure model introduced in “Exposure Models” section (option 2 in red). The red solid lines correspond to the 5th and 95th percentiles of the variability distributions of HBM data, and the blue dashed line depicts the 50th percentile of HBM data
Discussion
Integrative Modeling of the Past and Current Exposure to Lead
We conducted a population-based simulation, which enabled estimating the long-term external and internal exposures to Pb of individuals from Belgium, Czech Republic, Germany, and Norway. The proposed framework combined a growth module simulating the variations of the human body weight over time, an exposure module estimating the external exposure to Pb, and a toxicokinetic model used to predict the lifetime internal exposure to Pb.
The growth module enabled to generate individual body weight trajectories specific to each country since it was built on country-specific growth curves of anthropometric variables (body weight, body height, and body mass index). The exposure module allowed estimating the aggregated exposure to Pb by considering the inhalation of air and the ingestion of dust, soil, drinking water, and food products as exposure pathways. These pathways are often identified in the literature as the major sources of Pb exposure (Heinemeyer and Bösing 2020; Jan et al. 2015; Järup 2003; Tchounwou et al. 2012). In the characterization of the relevant sources of Pb exposure, the present approach appeared to be useful since it allowed describing the time-varying influence of each considered pathway on the external Pb exposure and a posteriori on the resulting internal exposure. The ban of lead in gasoline induced a paradigm shift as the inhalation of air became over the years less influential on Pb exposure while the dietary sources became more influential as it was observed by analyzing the intake rates estimated using the exposure module and the relative contribution of each exposure pathway. In addition, the steady decrease of PbB levels observed from mid-1970s to the end of the 1980s also supports the impact of this regulatory change on the environmental burden of Pb and a posteriori on human exposure. This assertion is also confirmed when considering Figure S7 of the supplementary material S2 in which the average Pb intake rates normalized by the body weight calculated for each exposure pathway in each country are illustrated. Furthermore, the increasing importance of the dietary pathway in the 1990s and 2000s is also demonstrated as shown by average intake rates illustrated in Figure S7. This imposes to risk managers and policy makers to identify and better understand the sources of this dietary exposure when it comes to the implementation of regulatory measures to reduce Pb exposure within the general population.
Here, the retrieval of relevant data on the occurrences of Pb in each of the considered exposure sources for different time periods in current and past times was a key challenge. The data collection that was conducted in this work provided a large amount of relevant data covering several decades for each of the four considered countries. However, these data did not cover every time point from 1970 to the present times as data gaps were noticed especially for the dietary pathway. These data limitations will be discussed in more details in the “Study Limitations” section. The toxicokinetic module, which is central in this modeling framework to predict the concentrations of Pb in human blood and other human tissues and organs, was constructed based on the PBPK model developed by O’Flaherty (1991a, 1991b, 1991c, 1993, 1995, 1998). The O’Flaherty model simulates the kinetic path of Pb within the human body with an emphasis on the exchange of Pb within the bone structure as a result of the physiological bone formation and resorption processes occurring at different life stages. This model depicts the bone compartment as a reservoir of lead, which could release Pb into the systemic circulation over several months or years. The O’Flaherty model was therefore a valuable tool to estimate the internal exposure to Pb over a lifespan.
The population-based simulation was run by adopting a two-dimensional Monte Carlo approach with the aim to separate the uncertainty related to the variations of Pb levels in air, dust, soil, and dietary sources from the inter-individual variability inherent to the simulated individuals and also stemming from the demographic differences between countries. The obtained results were compared to the descriptive statistics calculated from HBM study data collected within the HBM4EU Initiative. Three levels of uncertainty, namely a lower, medium, and upper bound, corresponding, respectively, to the 2.5th, 50th, and 97.5th percentiles of the probability distributions of Pb levels in the different exposure sources were adopted. Globally, the predicted concentrations of Pb in blood exceed largely the blood concentrations derived from the HBM data. More precisely, only the results related to the LB uncertainty scenario are close to the HBM data. This overestimation could be attributed to the dietary intake rates estimated using the dietary exposure model introduced in “Exposure Models” section since the predictions derived using the dietary intake rates collected in the literature produced lower Pb levels in blood as described in “Evaluation of the used Dietary Exposure Model” section. This exhibits the influence of the modeling approach used to estimate the dietary exposure on the external and internal exposures to Pb. Despite the global overestimation of the predicted Pb levels in comparison to the observed HBM data, the predictions produced for Germany during the 1980s are rather similar to the historical concentrations of Pb in blood drawn from the German Environmental Specimen Bank data for young adults between 20 and 29 years in Germany and reported by Lermen et al. (2021). For Belgium, Czech Republic, and Norway, predictions in the same order of magnitude were obtained for this specific time period. These predictions are also similar to the values reported by Bierkens et al. (2011) and Smolders et al. (2010) for the 1980s. This observation illustrates the importance of the collection of relevant evidence for risk and exposure assessments as the rebound of the internal Pb exposures predicted in the 1990s, which highly exceed the levels found in the literature, can be linked with an overestimation of the external exposure attributable to the data available for this time period.
Uncertainty and Variability
A rather large uncertainty resulted from the simulations as approximately factors ranging from 12 to 15 and 22 to 35 were observed between the LB and MB and between LB and UB levels, respectively. This uncertainty can be attributed to the variations in the published measurements of Pb levels in the different exposure sources that could stem from the spatial differences between highly contaminated areas (qualified as hotspots) and areas with low or medium Pb levels. Furthermore, this uncertainty also questions the global quality of the compiled exposure data and specifically their representativeness that is their capacity to replicate the exposure conditions and scenarios that could have conducted to the observed blood lead levels. The compiled information corresponded mainly to population averages, which could be inadequate to capture more extreme exposures or exposures of more vulnerable subgroups of the population. For instance, geographical clusters of elevated Pb (and other heavy metals) blood levels, which correlated with the geographical variability of Pb levels in the environment, were identified in King et al. (2015).
The inter-individual variability was on the contrary rather small in comparison to the inter-individual variability contained in the HBM data. The “artificial” cohorts that were simulated in our analysis did not enable us to reproduce the actual inter-individual variability specific to the considered HBM study cohorts.
Study Limitations
One limitation in this work lies on the incapacity of the “artificially” generated populations to emulate the inter-individual variability enclosed in the data drawn from the HBM study cohorts presented in Table 1. An initial explanation could be oriented toward the growth module, and the inter-connection between the country-specific growth curves and the growth equation of O’Flaherty (see “Growth Module” section). Indeed, the growth curves were randomly generated from country-specific growth charts, which are constructed by smoothing the age-dependent anthropometric data representative of the demographic characteristics in a given country. Randomly picking body weight trajectories from this smoothed curves implied that the generated curves did not lead to wide variations among individuals. Furthermore, the growth equation of O’Flaherty is built such that it required for each simulated individual to fit the equation to the corresponding random growth curve. This translation of the random growth curves into the five-parameter equation of O’Flaherty and the loss of information potentially resulting for this derivation did not prevent shrinking the variability between the simulated individuals.
Another limitation arose from the overestimation of Pb blood levels that could be attributed to the dietary exposure model introduced in “Exposure Models” section as it was illustrated by the comparison between the data-centric and model-centric options presented in “Evaluation of the used Dietary Exposure Model” section. Particularly, data gaps related to the collected Pb concentration data in food products were noticed. These gaps were filled using available data from the other considered countries or data at a European level, which could potentially be responsible in some cases for an overestimation of the food concentrations. The discrepancies between the estimated dietary intake rates and the collected dietary intake rate data could have also stemmed from the derivation of the age-dependent consumption of food products. The age-dependent food consumption was emulated by using estimates of the age-dependent energy intake, which could have resulted in an overestimation of the actual amount of food consumed at an individual level. Furthermore, this energy-based approach was built on German data mainly, which could also explain the discrepancies between the predictions and the observed data for the other considered countries. Specifically when considering the LB scenario of uncertainty that provided the “best” results, the PbB levels predicted for Norway are systematically higher than the HBM study data, whereas the inverse is noticed for Czech Republic with an underestimation of the observed PbB levels as presented in Table 1. In addition, difficulties were encountered while calculating the inverse of the matrix of the quadratic product of the parameters \(e_{j}\) with \(j = 1, \ldots , J\) referring to the relative energy content of each food group (see Eq. (7) in “Exposure Models” section). To solve these issues, the generalized Moore–Penrose inverse also called pseudoinverse of Moore–Penrose was applied (Moore 1920; Penrose 1955). Despite the demonstrated existence and uniqueness of the pseudoinverse, the use of the Moore–Penrose method could raise questions about the general uniqueness of the calculated inverse and consequently about the reliability of the derived food intake rates.
Conclusion
This work, which is an implementation of a total exposure approach toward the reconstruction of human exposure via exposure pathways across different regulatory niches, intended to provide evidences to answer policy questions raised within the HBM4EU Initiative around the exposure to Pb (HBM4EU 2022). These questions sought to characterize the level of Pb exposure in European populations, to investigate the major sources and pathways leading to this exposure, and to understand its variability within the European population and the impact of the ban of leaded gasoline on Pb concentrations in human blood. The developed approach offers an appealing toolbox to support policy making relative to lead as it enabled advancing the characterization of the long-term exposure to lead and the identification of its main determinants. The developed integrative modeling framework enabled to relate, under a forward dosimetry approach, the internal human exposure to Pb with estimates of the occurrences of Pb in environmental matrices and dietary sources of exposure by focusing on four European countries, namely Belgium, Czech Republic, Germany, and Norway. The overall decreasing trend observed in PbB levels over the years in Europe could then be associated with decreasing trends observed in the levels of Pb in environmental matrices and dietary exposure sources. This exhibited the significant value that high tier approaches such as PBPK models could bring to the assessment of human exposure to potentially hazardous substance such as Pb. Based on our modeling framework, it was possible to identify the paradigm shift observed with dietary exposure becoming the major exposure pathway, which could imply to put more attention on the compilation of relevant data informing, for instance, the exposure attributable to diet.
The integration of the growth, exposure and toxicokinetic modules and their application on the collected data helped generating populations simulating the main characteristics of the real populations and accommodating the related inter-individual variability and the variations of Pb concentration values in the environment and diet. The inter-individual variability observed in the HBM data was however higher than the variability produced by the developed modeling framework. With the availability of individual HBM data, more precise information about the study participants, and individually based physiologic data, the growth and toxicokinetic modules could be improved and possibly provide a better representation of the inter-individual variability.
Finally, the compiled database constitutes, to the best of our knowledge, one of the most extensive databases of exposure data for lead. This database provides an insightful source of knowledge for European countries by covering several decades of lead exposure. However, this study also highlighted the necessity to retrieve or to generate more country- and age-specific relevant data to improve the estimation of the exposure and to refine the assessment of the risk. For future work the collated lead HBM data can be used for exposure reconstruction, namely the estimation of lead intake for the various age groups. Given the long biological half-life of lead, the respective intake estimates would reflect the mean daily intake over a long period in relation to the respective periods for which the bottom-up estimates given in this paper have been accounted for, i.e., for a year. Then, the respective estimates of intake could be used to validate the bottom-up estimates and to foster the refinement of route-specific contributions that have been already characterized by the highest uncertainty levels. We would expect that the delivered estimates would corroborate well with the LB estimates of the bottom-up approach, due to the conservative nature of bottom-up methodologies. Methodologically speaking, the results of the exposure reconstruction via reverse dosimetry modeling can serve as a validation of the overall approach, providing thus the necessary robustness that would be necessary for regulatory decision-making.
Supplementary Information
The supplementary materials are consisted of an Excel Spreadsheet containing the distributions of Pb dietary intake rates and Pb concentrations in exposure source matrices collected in the literature and a Word document with complementary materials. Both files can be accessed online via the journal’s website.
Data Availability
Enquiries about data availability should be directed to the authors and the corresponding supplementary materials were provided to be made available online via the journal’s website.
References
Angerer J, Ewers U, Wilhelm M (2007) Human biomonitoring: state of the art. Int J Hyg Environ Health 210:201–228
Bergdahl IA, Skerfving S (2022) Chapter 19: Lead. In: Handbook on the toxicology of metals, 5th ed. Academic Press, pp 427–493. https://doi.org/10.1016/B978-0-12-822946-0.00036-2.
Bierkens J, Smolders R, Van Holdeberke M, Cornelis C (2011) Predicting blood lead levels from current and past environmental data in Europe. Sci Total Environ 409:5101–5110. https://doi.org/10.1016/j.scitotenv.2011.08.034
Campbell JL, Clewell RA, Gentry PR, Andersen ME, Clewell HJ (2012) Chapter 18: Physiologically based pharmacokinetic/toxicokinetic modeling. In: Reisfeld B, Mayeno AN (eds) Computational toxicology: volume I, methods in molecular biology, vol 929. https://doi.org/10.1007/978-1-62703-050-2_18
Cerná M, Spevácková V, Batáriová A, Smíd J, Cajchanová M, Ocadlíková D et al (2007) Human biomonitoring system in the Czech Republic. Int J Hyg Environ Health 210(3–4):495–499. https://doi.org/10.1016/j.ijheh.2007.01.005
Cífková R, Skodová Z, Lánská V, Adámová V, Novozámská E, Jozífová M, Plásková M et al (2004) Prevalence, awareness, treatment, and control of hypertension in the Czech Republic. Results of two nationwide cross-sectional surveys in 1997/1998 and 2000/2001, Czech Post-MONICA Study. J Hum Hypertens 18:571–579. https://doi.org/10.1038/sj.jhh.1001686
Clewell HJ, Tan YM, Campbell JL, Andersen ME (2008) Quantitative interpretation of human biomonitoring data. Toxicol Appl Pharmacol 231:122–133. https://doi.org/10.1016/j.taap.2008.04.021
Cole TJ, Green PJ (1992) Smoothing reference centile curves: the LMS method and penalized likelihood. Stat Med 11(10):1305–1319
Dede E, Tindall M, Cherrie J, Hankin S, Collins C (2018) Physiologically-based pharmacokinetic and toxicokinetic models for estimating human exposure to five toxic elements through oral ingestion. Environ Toxicol Pharmacol 57:104–114. https://doi.org/10.1016/j.etap.2017.12.003
Demarest S, Van der Heyden J, Charafeddine R, Drieskens S, Gisle L, Tafforeau J (2013) Methodological basics and evolution of the Belgian helath interview survey 1997–2008. Arch Public Health 71(24):1–10
Droyvold WB, Nilsen TIL, Krüger O, Holmen TL, Krokstad S, Midthjell K, Holmen J (2006) Change in height, weight and body mass index: Longitudinal data from the HUNT Study in Norway. Int J Obes 30:935–939. https://doi.org/10.1038/sj.ijo.0803178
Egeghy PP, Sheldon LS, Isaacs KK, Özkaynak H, Goldsmith M-R, Wambaugh JF, Judson RS, Buckley TJ (2016) Computational exposure science: an emerging discipline to support 21st-century risk assessment. Environ Health Perspect 124(6):697–702. https://doi.org/10.1289/ehp.1509748
Flegal KM (2013) Construction of LMS parameters for the centers for disease control and prevention 2000 Growth charts. National Health Statistics Reports. 63. February 2013
Fleming DEB, Chettle DR, Webber CE, O’Flaherty EJ (1999) The O’Flaherty model of lead kinetics: an evaluation using data from a lead smelter population. Toxicol Appl Pharmacol 161:100–109
Ganzleben C, Antignac J-P, Barouki R, Castano A, Fiddicke U, Klánová J, Lebret E, Olea N et al (2017) Human biomonitoring as a tool to support chemicals regulation in the European Union. Int J Hyg Environ Health 220(2):94–97. https://doi.org/10.1016/j.ijheh.2017.01.007
Gilles L, Govarts E, Rambaud L, Vogel N, Castano A, Esteban López M, Rodriguez Martin L et al (2021) HBM4EU combines and harmonises human biomonitoring data across the EU, building on existing capacity – the HBM4EU survey. Int J Hyg Environ Health. https://doi.org/10.1016/j.ijheh.2021.113809
Hagner C (2000) European regulations to reduce lead emissions from automobiles—did they have an economic impact on the German gasoline and automobile markets? Reg Environ Change 1:135–151. https://doi.org/10.1007/s101130000019
Hahn D, Vogel N, Höra C, Kämpfe A, Schmied-Tobies M, Göen T, Greiner A, Aigner A, Kolossa-Gehring M (2022) The role of dietary factors on blood lead concentration in children and adolescents—results from the nationally representative German Environmental Survey 2014–2017 (GerES V). Environ Pollut 299:118699. https://doi.org/10.1016/j.envpol.2021.1186699
Hartmann BM, Schmidt C, Sandfuchs K (2014) Bundeslebensmittelschlüssel (BLS). Version 3.02. Max Rubner-Institut (MRI) 2014 (in German)
HBM4EU (2022) Lead. https://www.hbm4eu.eu/hbm4eu-substances/lead/. Accessed 25 Mar 2022
Heinemeyer G, Bösing U (2020) Eintragspfade von Blei in den menschlichen Organismus]. Abschlussbericht. Umwelt und Gesundheit 02-2020 (in German). https://www.umweltbundesamt.de/publikationen/eintragspfade-von-blei-in-den-menschlichen
Hemmelmann C, Brose S, Vens M, Hebebrand J, Ziegler A (2010) Percentiles of body mass index of 18–80-year-old German adults based on data from the 2nd National Nutrition Survey. Deutsch Med Wochenschr. 135:848–852. https://doi.org/10.1055/s-0030-1253666. (in German)
Henry CJK (2005) Basal metabolic rate studies in humans: measurement and development of new equations. Oublich Health Nutrition 8(7A):1133–1152. https://doi.org/10.1079/PHN2005801
Jan AT, Azam M, Siddiqui K, Ali A, Choi I, Haq QMR (2015) Heavy metals and human health mechanistic insight into toxicity and counter defense system of antioxidants. Int J Mol Sci 16(12):29592–29630
Järup L (2003) Hazards of heavy metal contamination. Br Med Bull 68:167–182. https://doi.org/10.1093/bmb/ldg032
Júlíusson RB, Roelants M, Nordal E, Furevik L, Eide GE, Moster D, Hauspie R, Bjerknes R (2013) Growth references for 0–19 year-old Norwegian children for length/height, weight, body mass index and head circumference. Ann Hum Biol 40(3):220–227. https://doi.org/10.3109/03014460.2012.759276
Kelly EJ, Campbell K (2000) Separating variability and uncertainty in environmental risk assessment—making choices. Hum Ecol Risk Assess 6(1):1–13. https://doi.org/10.1080/10807030091124419
King KE, Darrah TH, Money E, Meentemeyer R, Maguire RL, Nye MD, Michener L, Murtha AP et al (2015) Geographic clustering of elevated blood heavy metal levels in pregnant women. BMC Public Health 15:1035. https://doi.org/10.1186/s12889-015-2379-9
Kolossa-Gehring M, Becker K, Conrad A, Schröter-Kermani C, Schulz C, Seiwert M (2012) Chapter 2A: Health-related Environmental Monitoring in Germany: German Environmental Survey (GerES) and Environmental Specimen Bank (ESB). In: Knudsen L, Merlo D (eds) Biomarkers and Human Biomonitoring, vol 1: Ongoing programs and exposures, vol 1. RSC Publishing, Cambridge, pp 16–45
Leggett R (1993) An age-specific kinetic model of lead metabolism in humans. Environ Health Perspect 101:598–616
Lermen D, Weber T, Göen T, Bartel-Steinbach M, Gwinner F, Mueller SC, Conrad A, Rüther M et al (2021) Long-term time trend of lead exposure in young German adults—evaluation of more than 35 years of data of the German Environmental Specimen Bank. Int J Hyg Environ Health 231:113665. https://doi.org/10.1016/j.ijheh.2020.113665
Max Rubner Institute (MRI) (2008). Nationale Verzehrsstudie II. Ergebnisbericht Teil 1. (in german). MRI reports W1946. https://nbn-resolving.org/urn:nbn:de:gbv:ka51-2008080507
Mitchell EEL, Gauthier JS (1976) Advanced Continuous Simulation Language (ACSL). SIMULATION 26(3):72–78. https://doi.org/10.1177/003754977602600302
Moore EH (1920) On the reciprocal of the general algebraic matrix. Bull Am Math Soc 26(9):394–395. https://doi.org/10.1090/S0002-9904-1920-03322-7
Nauta M (2000) Separation of uncertainty and variability in quantitative microbial risk assessment models. Int J Food Microbiol 57(1–2):9–18. https://doi.org/10.1016/S0168-1605(00)00225-7
O’Flaherty EJ (1991a) Physiologically based models for bone-seeking elements: I. Rat Skeletal and Bone Growth. Toxicol Appl Pharmacol 111:299–312
O’Flaherty EJ (1991b) Physiologically based models for bone-seeking elements: II. Kinetics of lead disposition in rats. Toxicol Appl Pharmacol 111:313–331
O’Flaherty EJ (1991c) Physiologically based models for bone-seeking elements: III. Human skeletal and bone growth. Toxicol Appl Pharmacol 111:332–341
O’Flaherty EJ (1993) Physiologically based models for bone-seeking elements: IV. Kinetics of lead disposition in humans. Toxicol Appl Pharmacol 118:16–29
O’Flaherty EJ (1995) Physiologically based models for bone-seeking elements: V. Lead absorption and disposition in childhood. Toxicol Appl Pharmacol 131:297–308
O’Flaherty EJ (1998) A physiologically based kinetic model for lead in children and adults. Environ Health Perspect 106(Suppl 6):1495–1503
O’Flaherty EJ (2000) Modeling normal aging bone loss, with consideration of bone loss in osteoporosis. Toxicol Sci 55:171–188
Ougier E, Ganzleben C, Lecoq P, Bessems J, David M, Schoeters G, Lange R, Meslin M et al (2021) Chemical prioritisation strategy in the European Human Biomonitoring Initiative (HBM4EU) – development and results. Int J Hyg Environ Health 236:113778. https://doi.org/10.1016/j.ijheh.2021.113778
Penrose R (1955) A generalized inverse for matrices. Proc Camb Philos Soc 51(3):406–413
R Core Team (2022) R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna. https://www.R-project.org/
Ragas A, Brouwer F, Büchner F, Hendricks H, Huijbregts M (2009) Separation of uncertainty and interindividual variability in human exposure modeling. J Eposure Sci Environ Epidemiol 19:201–212. https://doi.org/10.1038/jes.2008.13
Raleigh V (2019) Trends in life expectancy in EU and other OECD countries: why are improvements slowing? OECD Health Working Papers, No. 108, OECD Publishing, Paris. https://doi.org/10.1787/223159ab-en
Rigby RA, Stasinopoulos DM (2005) Generalized additive models for location, scale and shape (with discussion). Appl Stat 54:507–554
Robert Koch Institute (RKI) (2016) Reference percentiles for anthropometric measures and blood pressure based on the German Health Interview and Examination Survey for Children and Adolescents 2003–2006 (KiGGS). Federal Health Reporting. https://doi.org/10.17886/RKI-GBE-2016-032
Robinson MR, Hemani G, Medina-Gomez C, Mezzavilla M, Esko T, Shakhbazov K, Powell JE et al (2015) Population genetic differentiation of height and body mass index across Europe. Nat Genet 47(11):1357–1364. https://doi.org/10.1038/ng.3401
Rodriguez-Martinez A, Zhou B, Sophiea M, Bentham J, Paciorek C, Iurilli M, Carrillo-Larco R et al (2020) Height and body-mass index trajectories of school-aged children and adolescents from 1985 to 2019 in 200 countries and territories: a pooled analysis of 2181 population-based studies with 65 million participants. The Lancet 396(10621):1511–1524. https://doi.org/10.1016/S0140-6736(20)31859-6
Roelants M, Hauspie R, Hoppenbrouwers K (2009) References for growth and pubertal development from birth tio 21 years in Flanders, Belgium. Ann Hum Biol 36(6):680–694. https://doi.org/10.3109/03014460903049074
Rønningen KS, Paltiel L, Meltzer HM, Nordhagen R, Lie KK, Hovengen R, Haugen M et al (2006) The biobank of the Norwegian mother and child cohort Study: a resource for the next 100 years. Eur J Epidemiol 21:619–625. https://doi.org/10.1007/s10654-006-9041-x
Ruiz P, Fowler BA (2015) Chapter 7: Exposure assessment, forward and reverse dosimetry. In: Handbook on the toxicology of metals, 4th ed, pp 141–153. https://doi.org/10.1016/B978-0-444-59453-2.00007-X
Schoeters G, Govarts E, Bruckers L, Den Hond E, Nelen V, De Henauw S, Sioen I et al (2017) Three cycles of human biomonitoring in Flanders—time trends observed in the Flemish Environment and Health Study. Int J Hyg Environ Health 220(2):36–45. https://doi.org/10.1016/j.ijheh.2016.11.006
Schulz C, Conrad A, Becker K, Kolossa-Gehring M, Seiwert M, Seifert B (2007) Twenty years of the German Environmental Survey (GerES): human biomonitoring—temporal and spatial (West Germany/East Germany) differences in population exposure. Int J Hyg Environ Health 210(3–4):271–297. https://doi.org/10.1016/j.ijheh.2007.01.034
Smolders R, Alimonti A, Cerna M, Den Hond E, Kristiansen J, Palkovicova L, Ranft U et al (2010) Availability and comparability of human biomonitoring data across Europe: a case-study on blood-lead levels. Sci Total Environ 408:1437–1445. https://doi.org/10.1016/j.scitotenv.2009.11.025
Soetaert K, Petzoldt T, Setzer RW (2010) Solving differential equations in R: Package deSolve. J Stat Softw 33(9):1–25. https://doi.org/10.18637/jss.v033.i09
Tchounwou P, Yedjou C, Patlolla AK, Sutton D (2012) Heavy metals toxicity and the environment. EXS 101:133–164. https://doi.org/10.1007/978-3-7643-8340-4_6
Uhl M, Santos RR, Costa J, Santos O, Virgolino A, Evans DS, Murray C, Mulcahy M et al (2021) Chemical exposure: European citizens’ perspectives, trust, and concerns on human biomonitoring initiatives, information needs, and scientific results. Int J Environ Res Public Health 18:1532. https://doi.org/10.3390/ijerph18041532
US EPA (Environmental Protection Agency) (1994) IEUBK. Guidance Manual for the Integrated Exposure Uptake Biokinetic Model for Lead in Children. EPA/540/R-93/081; U.S. Environmental Protection Agency, Washington
US EPA (Environmental Protection Agency) (2011) Exposure factors handbook. National Center for Environmental Assessment, Washington, DC; EPA/600/R-09/052F. Available from the National Technical Information Service, Springfield, VA. http://www.epa.gov/ncea/efh
US EPA (Environmental Protection Agency) (2019). Guidelines for Human Exposure Assessment. EPA/100/B-19/001. https://www.epa.gov/sites/default/files/2020-01/documents/guidelines_for_human_exposure_assessment_final2019.pdf
Vignerová J, Riedlová J, Bláha P, Kobzová J, Krejcovský L, Brabec M, Hrusková M (2006) 6th nation-wide anthropological survey of children and adolescents 2001 Czech Republic: summary results. ISBN 80-86561-30-5
Von Storch H, Costa-Cabral M, Feser F, Hagner C (2000). Reconstruction of lead (Pb) fluxes in Europe during 1955–1995 and evaluation of gasoline lead-content regulations. In: Proceedings of the 11th joint conference on the applications of air pollution meteorology with the air and waste management association 9–14 Jan 2000, Long Beach, California, USA, pp 1–6
Wambaugh JF, Bare JC, Carignan CC, Dioniso KL, Dodson RE, Jolliet O, Liu X, Meyer DE et al (2019) New approach methodologies for exposure science. Curr Opin Toxicol 15:76–92. https://doi.org/10.1016/j.cotox.2019.07.001
WHO (2010) Exposure to lead: a major public health concern. World Health Organization. ISBN: 9789240037632. https://www.who.int/publications/i/item/9789240037632
Wilson R, Jones-Otazo H, Petrovic S, Mitchell I, Bonvalot Y, Williams D, Richardson M (2013) Revisiting dust and soil ingestion rates based on hand-to-mouth transfer. Hum Ecol Risk Assess 19(1):158–188. https://doi.org/10.1080/10807039.2012.685807
Yeung CHT, Fong S, Malik PRV, Edington AN (2020) Quantifying breast milk intake by term and preterm infants for input into paediatric physiologically based pharmacokinetic models. Matern Child Nutr 16:e12938. https://doi.org/10.1111/mcn.12938
Acknowledgements
This work is a fulfillment of the implication of the German Federal Institute for Risk Assessment in the activities of the Work Package 12 entitled “From HBM to Exposure” within the European Initiative HBM4EU. Authors are grateful to the colleagues from the Work Packages 12 and 10 of “Data Management” for their efforts and assistance in compiling and providing quality data. Finally, authors are thankful to their BfR colleagues PD Dr. Christine Müller-Graf and PD Dr. Ralph Pirow for their useful comments to improve the quality of the manuscript.
Funding
Open Access funding enabled and organized by Projekt DEAL. The BfR is financed by the German Federal Ministry of Food and Agriculture. HBM4EU is funded under Horizon 2020 Research and Innovation Program of the European Union with grant agreement N° 733032. The funding of German HBM studies by the German Ministry for the Environment, Nature Conservation, Nuclear Safety and Consumer Protection is gratefully acknowledged.
Author information
Authors and Affiliations
Contributions
MS: was responsible for the study, the methodology, the collection, management and processing of data, the implementation of methods, the analysis and interpretation of results, and manuscript reviewing and editing; DE: contributed to the implementation of the methods, interpretation of the results, and manuscript reviewing and editing; CJ: contributed to the methodology, implementation of the methods, interpretation of the results, and manuscript review and editing; SK and DS coordinated the work in the WP12 of HBM4EU and contributed to the methodology and the manuscript review and editing; TW and MK: contributed as providers of HBM data to HBM4EU and to the manuscript review and editing; OL: co-supervised the study, and contributed to the methodology, interpretation of the results, and manuscript reviewing and editing and MG: initiated research to total exposure approach (together with OL), co-supervised the study, and contributed to the interpretation of the results and manuscript reviewing and editing.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sy, M., Eleftheriadou, D., Jung, C. et al. Assessment of the Long-Term Exposure to Lead in Four European Countries Using PBPK Modeling. Expo Health 16, 21–39 (2024). https://doi.org/10.1007/s12403-023-00535-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12403-023-00535-2