1 Introduction

Currently, ultra-lightweight designs are obtained in materials engineering by applying the ideas of structural engineers to ever smaller scales (e.g. [11]). We see microstructures in lattice materials, with length scales barely visible to the human eye, that follow the same principles as found in the centuries old engineering length scales of buildings, bridges, aeroplanes and ships. Thus, the distinction between materials and structural engineering has become fuzzy. Traditionally the larger length scale structures have been designed by using frame, finite element and finite strip methods where the actual discrete topology is modeled explicitly. This is a computationally expensive approach when we add structural hierarchy to our designs so that we need to extend detailed modeling over several length scales. Therefore, computationally efficient multiscale structural design methods are needed. Non-classical continuum mechanics theories can provide a solid theoretical platform for such computational multiscale modeling.

Non-classical continuum mechanics theories have evolved considerably over the recent years (for extensive reviews see for example [2, 8, 9, 29, 40]). These theories employ material models that have intrinsic length scales in them, whereas classical continuum mechanics does not account for the effect of the microstructure within the material. Roughly put, non-classical theories consider multiple length scales in detail simultaneously and, thus, are ideal for multiscale modeling. There are numerous formulations for non-classical continuum mechanics theories based on different engineering needs. Of these formulations, the micropolar theory has been shown to produce reliable results for sandwich structures that have structural hierarchy (e.g. [6, 20, 28, 29, 33]). However, the applications of these theories to structural design are still lacking. In order to understand the true value of these developments, practical case studies are of fundamental importance. Here a case of ship structural design is selected as representative case to demonstrate the meaning of these developments in practice.

The design of large engineering structures such as ships is often carried in several steps [13, 14], see Fig. 1a and it is always a compromise between different design disciplines [1, 10]. Structural design is one of the most critical design stages as it secures the safety of the vessel and also defines to large extent the lightweight of the ship affecting this way the payload of the vessel. The loading is due to ship operations in random environment, i.e. waves and ice. The ship responds to these loads by bending at length-scales of hull girder, cargo holds and individual beams, plates and shells, see Fig. 1b. The resulting deformations and stresses are superimposed and compared with relevant strength criteria. In the concept design stage, the main dimensions of the ships are defined along with the initial structural scantlings as well as the functionalities in connection to other design disciplines (e.g. machinery systems, ship resistance and seakeeping). The main aim of this stage from structural design viewpoint is to secure that the design space is feasible. Often closed form expressions, provided by ship classification societies, are used for quick check of strength of beams, plates and shells, see Fig. 1c, while the assessment of structural stresses requires finite element analysis. In the classification society rules adopted at this stage, the Euler-buckling of a simply supported beam or plate forms the basic assumption made. After the concept design stage is completed, the design is more or less feasible or very close to feasibility, which allows moving to the next stages of design. In basic design stage, the structural analysis for response and strength is carried out with 3D-FEA. At this stage more realistic boundary conditions can be used as well as the initial imperfections that affect the buckling strength. These imperfections are dependent on manufacturing process. Naturally, at this stage the accuracy of design space exploration increases, but as time is limited, the exploration can be focused only in specific regions of the design space. As the design moves to the next stage it is possible to check the influence of structural details such as brackets and openings to the strength and also perform validating experiments. At this detail design stage, the exploration of the design space is limited even more. Due to this split of design process and cumulative nature of it, it is important that in the conceptual design stage right decisions are made with correct analytical models based on realistic assumptions. Otherwise, we may neglect regions of the feasible design space due to modeling errors.

Fig. 1
figure 1

a Classical design ship design spiral by Evans [10], b division of structural analysis to different structural length-scales and c Euler-buckling equations for plates as present in ship structural design rules [7]

Full size image

The comparison of response and strength can be treated by use of partial safety factors or by different levels of reliability methods where the load and capacity and their statistical distributions are compared. The limit state function forms a key element in this assessment. The structural limit states in thin-walled structures can be based on serviceability, fatigue strength, ultimate strength and accidental conditions. For thin-walled structures, the ultimate limit state is of great importance and the ultimate strength analysis is often initiated by buckling. In structural core sandwich panels buckling assessment is often split to local and global buckling. Local buckling refers to buckling of the faces and/or webs locally with wave length equal to the distance between the hard points of the core. Global buckling refers to buckling of the entire panel. While the local buckling is often assessed by the isotropic plate theory such as shown in Fig. 1c, global buckling requires due to orthotropy of entire structural assembly orthotopic plate theory formulations of “smeared” homogenous structure, fine mesh FE simulations of the actual structure or experiments.

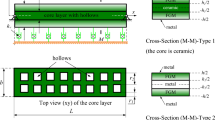
Web-core sandwich panels have been applied for numerous engineering applications, such as bridges, ships and industrial machinery (see e.g. [39]). The connection between webs and faces can be made by adhesive bonding, brazing or laser-welding. In heavily loaded steel sandwich panels, laser-welding forms strong connection and is due to this the main manufacturing method of the panels. The local buckling of the faces and webs of the laser-welded web-core sandwich panels has been investigated for example by analytically, FEA and experiments for example by Kolsters and Wennhage [21] and Kolsters and Zenkert [22,23,24]. The main influence of laser-welding in this context is the rotational support it provides for local buckling. In global buckling, occurring at the panel level, the global buckling formulations based on orthotropic plate theory are often based on equivalent single layer (ESL) modeling principle where plate quantities are formulated through single layer. In this context, the early works to be mentioned are those of First order shear deformation theory (FSDT) as formulated by Holmberg [12] for web-core panels Libove and Batdorf [25], Libove and Hubka [26] for corrugated core panels. Since that time several formulations have been presented for analytical solutions, finite element solutions and their numerical and experimental validations, see Lok et al. [27], Nordstrand [30, 31], in laser-welded web-core panels by Jelovica et al. [16, 18, 19] Jelovica and Romanoff [17] and further to cases where local buckling interacts with global buckling, see for example Patel et al. [32] and interacting local and global buckling by Reinaldo Goncalves et al. [35]. All these investigations show that at the conceptual level of structural design, linear bifurcation (eigenvalue) buckling forms the first estimate for the limit state function. These investigations also show that the strength predictions between different methods are in good agreement when the loading is in the direction of webs. When loading is turned to the weaker direction, problems occur as presented by Jelovica and Romanoff [15] and Karttunen et al. [20] in global, but not in local buckling.

These investigations by Jelovica and Romanoff [15] and Karttunen et al. [20] showed that in web-core and corrugated core sandwich panels modeled by 2-D equivalent single-layer (ESL) plates based on classical continuum mechanics, certain type of size-dependency on buckling strength is observed. Figure 2 shows that for an ESL-FSDT plate based on classical continuum mechanics, the number of buckling half-waves increases indefinitely when the minimum buckling load is searched for and the model does not converge to a physically correct minimum. The model used for validation is based on 3D-FE-model of the actual geometry. The physical reason for this is high orthotropy ratio in out-of-plane shear [38] in classical ESL-FSDT formulation that causes to the Navier-based analytical solution decreasing buckling load for increasing number of buckling waves in weaker direction. If the same problem is solved with FEA for minimum buckling load, the answer becomes mesh size dependent and finer mesh produces lower buckling load. In essence the error is introduced partly by the model and partly by the numerical solution. An analogous situation can be found, for example, in plasticity where localization of damage is known to result in mesh size dependent solutions unless non-local formulations are used (e.g. [3,4,5]). When using a stabilizing mesh on top of classical ESL-FSDT mesh [36], Jelovica and Romanoff [15], or a micropolar ESL-FSDT plate model [20], such size-dependency does not exist. The technological reason for this orthotropy ratio is caused by laser-welding that lowers the rotation stiffness of the laser-stake welds and due to this reduces the classical out-of-plane shear stiffness opposite to the direction of the web plates [37]. When antisymmetric shear is considered, as in micropolar theories, we get rid of this phenomenon [36]. Early on, this was done with the stabilizing mesh [36], but the recent works of Karttunen et al. [20] and Nampally et al. [28] forms solid and validated theoretical framework for this type of structural engineering aspect.

Fig. 2
figure 2

(Figures are modified from Jelovica and Romanoff [15] and Karttunen et al. [20])

a Introduction of a stabilizing mesh on an ESL-FSDT plate based on classical elasticity. b Simply-supported web-core sandwich panel under compressive loads. c Buckling load for uniaxial compression and d bi-axial compression, where Nxx/Nyy = 1/4

Full size image

In this light, the current paper presents the effect of ESL-FSDT plate theories based on classical and micropolar continuum mechanics on the (eigenvalue) buckling design space of web-core sandwich panels. The paper first reviews briefly the differential equations of a 2-D micropolar ESL-FSDT plate theory for a web-core sandwich panel and the analytical Navier solution as presented by Karttunen et al. [20]. In order to show the impact of the size effects on the design of thin-walled structures, representative case studies of structures used in practice are performed for different load and plate aspect ratios. This is motivated by the fact that the buckling assessment of large structures is often based on structural analysis performed by the aid of the finite element method and on comparing the results to design rules, which at the conceptual design stage are based on closed-form expressions forming the design space, see Fig. 3. The results of the buckling assessment can be shown in the type of schematic plot shown in Fig. 3, where the symbols represent the stress resultant state from finite element analysis and the lines represent the limit values given by analytical solutions. With this idea in mind it becomes clear that the feasibility of structure is dependent on the utilized plate formulation. Therefore, we investigate here only the impact of the plate formulations to the extent and shape of the design space.

Fig. 3
figure 3

Schematic comparison of the finite element stress resultants values against the design rule values. The symbols represent the stress resultants from FEA of the actual structure (model on the left) and the lines the limit values given by different plate theories and their analytical solutions

Full size image

2 Review of the micropolar and classical ESL-FSDT plate theories

2.1 Micropolar ESL-FSDT plate model and analytical buckling solution by Karttunen et al. [20]

The micropolar plate model used here as reference is presented by Karttunen et al. [20] in detail. The model is derived based on energy methods and the resulting differential equations are solved there analytically by using Navier-method (series solution). The model is validated with 3D-FEA and shown to be accurate in bending and buckling problems. The displacements for this micropolar plate can be written as [20]

$${U}_{x}\left(x,y,z\right)={u}_{x}\left(x,y\right)+z{\phi }_{x}\left(x,y\right),$$
(1)
$${U}_{y}\left(x,y,z\right)={u}_{y}\left(x,y\right)+z{\phi }_{y}\left(x,y\right)$$
(2)
$${U}_{z}\left(x,y,z\right)={u}_{z}\left(x,y\right)$$
(3)
$${\Psi }_{x}\left(x,y,z\right)={\varphi }_{x}\left(x,y\right)$$
(4)
$${\Psi }_{y}\left(x,y,z\right)={\varphi }_{y}(x,y)$$
(5)
$${\Psi }_{z}\left(x,y,z\right)=0$$
(6)

where the classical mid-surface displacements u and normal rotations \(\phi\) are complemented by non-classical microrotations φ and an assumption of incompressibility is made (uz is independent of z-coordinate).

The non-zero linear strains for the plate are [9]

$${\varepsilon }_{xx}={u}_{x,x}+z{\phi }_{x,x}={\varepsilon }_{xx}^{0}+z{\kappa }_{xx}$$
(7)
$${\varepsilon }_{yy}={u}_{y,y}+z{\phi }_{y,y}={\varepsilon }_{yy}^{0}+z{\kappa }_{yy}$$
(8)
$${\varepsilon }_{xy}={u}_{y,x}+{\phi }_{y,x}={\varepsilon }_{xy}^{0}+z{\kappa }_{xy}$$
(9)
$${\varepsilon }_{yx}={u}_{x,y}+{\phi }_{x,y}={\varepsilon }_{yx}^{0}+z{\kappa }_{yx}$$
(10)
$${\varepsilon }_{xz}={u}_{z,x}+{\psi }_{y}$$
(11)
$${\varepsilon }_{zx}={\phi }_{x}-{\psi }_{y}$$
(12)
$${\varepsilon }_{yz}={u}_{z,y}-{\psi }_{x}$$
(13)
$${\varepsilon }_{zy}={\phi }_{y}+{\psi }_{x}$$
(14)
$${\chi }_{xx}={\psi }_{x,x,}$$
(15)
$${\chi }_{yy}={\psi }_{y,y}$$
(16)
$${\chi }_{xy}={\psi }_{y,x}$$
(17)
$${\chi }_{yx}={\psi }_{x,y}$$
(18)
$${\gamma }_{x}^{s}={\varepsilon }_{xz}+{\varepsilon }_{zx}={u}_{z,x}+{\phi }_{x}$$
(19)
$${\gamma }_{y}^{s}={\varepsilon }_{yz}+{\varepsilon }_{zy}={u}_{z,y}+{\phi }_{y}$$
(20)
$${\gamma }_{x}^{a}={\varepsilon }_{xz}-{\varepsilon }_{zx}={u}_{z,x}-{\phi }_{x}{+2\psi }_{y}$$
(21)
$${\gamma }_{y}^{a}={\varepsilon }_{yz}-{\varepsilon }_{zy}={u}_{z,y}-{\phi }_{y}{-2\psi }_{x}$$
(22)

Note that the shear strains are divided into symmetric and antisymmetric parts, see Eqs. (19)–(22). The symmetric part has the same form as the shear strain in the conventional first-order shear deformation theory. In vector form the strains are

$${\varvec{\varepsilon}}={\left\{\begin{array}{cc}\begin{array}{cc}{{\varvec{\varepsilon}}}^{0}&{\varvec{\kappa}}\end{array}& \begin{array}{cc}{\varvec{\gamma}}&{\varvec{\chi}}\end{array}\end{array}\right\}}^{T},$$
(23)
$${{\varvec{\varepsilon}}}^{0}={\left\{\begin{array}{cc}\begin{array}{cc}{\varepsilon }_{xx}^{0}& {\varepsilon }_{yy}^{0}\end{array}& \begin{array}{cc}{\varepsilon }_{xy}^{0}& {\varepsilon }_{yx}^{0}\end{array}\end{array}\right\}}^{T},{\varvec{\kappa}}={\left\{\begin{array}{cc}\begin{array}{cc}{\kappa }_{xx}& {\kappa }_{yy}\end{array}& \begin{array}{cc}{\kappa }_{xy}& {\kappa }_{yx}\end{array}\end{array}\right\}}^{T}$$
$${\varvec{\gamma}}={\left\{\begin{array}{cc}\begin{array}{cc}{\gamma }_{x}^{s}& {\gamma }_{x}^{a}\end{array}& \begin{array}{cc}{\gamma }_{y}^{s}& {\gamma }_{y}^{a}\end{array}\end{array}\right\}}^{T},{\varvec{\chi}}={\left\{\begin{array}{cc}\begin{array}{cc}{\chi }_{xx}& {\chi }_{yy}\end{array}& \begin{array}{cc}{\chi }_{xy}& {\chi }_{yx}\end{array}\end{array}\right\}}^{T}$$

The micropolar stress resultants are

$${\varvec{S}}={\left\{\begin{array}{cc}\begin{array}{cc}{\varvec{N}}& {\varvec{M}}\end{array}& \begin{array}{cc}{\varvec{Q}}& {\varvec{P}}\end{array}\end{array}\right\}}^{T}$$
(24)

\({\varvec{N}}={\left\{\begin{array}{cc}\begin{array}{cc}{N}_{xx}& {N}_{yy}\end{array}& \begin{array}{cc}{N}_{xy}& {N}_{yx}\end{array}\end{array}\right\}}^{T}\), \({\varvec{M}}={\left\{\begin{array}{cc}\begin{array}{cc}{M}_{xx}& {M}_{yy}\end{array}& \begin{array}{cc}{M}_{xy}& {M}_{yx}\end{array}\end{array}\right\}}^{T}\)

\({\varvec{Q}}={\left\{\begin{array}{cc}\begin{array}{cc}{Q}_{x}^{s}& {Q}_{x}^{a}\end{array}& \begin{array}{cc}{Q}_{y}^{s}& {Q}_{y}^{a}\end{array}\end{array}\right\}}^{T}\), \({\varvec{P}}={\left\{\begin{array}{cc}\begin{array}{cc}{P}_{xx}& {P}_{yy}\end{array}& \begin{array}{cc}{P}_{xy}& {P}_{yx}\end{array}\end{array}\right\}}^{T}\) and the constitutive equations read

$$\left\{\begin{array}{c}\begin{array}{c}{\varvec{N}}\\ {\varvec{M}}\end{array}\\ \begin{array}{c}{\varvec{Q}}\\ {\varvec{P}}\end{array}\end{array}\right\}=\left[\begin{array}{cc}\begin{array}{cc}\mathbf{A}& 0\\ 0& \mathbf{D}\end{array}& \begin{array}{cc}0& 0\\ 0& 0\end{array}\\ \begin{array}{cc}0& 0\\ 0& 0\end{array}& \begin{array}{cc}\mathbf{G}& 0\\ 0& \mathbf{H}\end{array}\end{array}\right]\left\{\begin{array}{c}\begin{array}{c}{{\varvec{\varepsilon}}}^{0}\\{\varvec{\kappa}}\end{array}\\ \begin{array}{c}{\varvec{\gamma}}\\{\varvec{\chi}}\end{array}\end{array}\right\}$$
(25)
$$\mathbf{A}=\left[\begin{array}{cc}\begin{array}{cc}{A}_{11}& {A}_{12}\\ {A}_{12}& {A}_{22}\end{array}& \begin{array}{cc}0& 0\\ 0& 0\end{array}\\ \begin{array}{cc}0& 0\\ 0& 0\end{array}& \begin{array}{cc}{A}_{33}& {A}_{34}\\ {A}_{34}& {A}_{44}\end{array}\end{array}\right],\mathbf{D}=\left[\begin{array}{cc}\begin{array}{cc}{D}_{11}& {D}_{12}\\ {D}_{12}& {D}_{22}\end{array}& \begin{array}{cc}0& 0\\ 0& 0\end{array}\\ \begin{array}{cc}0& 0\\ 0& 0\end{array}& \begin{array}{cc}{D}_{33}& {D}_{34}\\ {D}_{34}& {D}_{44}\end{array}\end{array}\right],$$
$$\mathbf{G}=\left[\begin{array}{cc}\begin{array}{cc}{G}_{11}& {G}_{12}\\ {G}_{12}& {G}_{22}\end{array}& \begin{array}{cc}0& 0\\ 0& 0\end{array}\\ \begin{array}{cc}0& 0\\ 0& 0\end{array}& \begin{array}{cc}{G}_{33}& {G}_{34}\\ {G}_{34}& {G}_{44}\end{array}\end{array}\right],\mathbf{H}=\left[\begin{array}{cc}\begin{array}{cc}{H}_{11}& {H}_{12}\\ {H}_{12}& {H}_{22}\end{array}& \begin{array}{cc}0& 0\\ 0& 0\end{array}\\ \begin{array}{cc}0& 0\\ 0& 0\end{array}& \begin{array}{cc}{H}_{33}& {H}_{34}\\ {H}_{34}& {H}_{44}\end{array}\end{array}\right].$$

Constitutive relation (25) can be derived through two-scale micromechanical analysis of the unit cell of a web-core panel [20]. The constitutive equation takes the same form also for a number of other lattice cores than the web-core such as a pyramidal core [28]. The equilibrium equations of the plate in terms of the stress resultants are

$${N}_{xx,x}-{N}_{xy,y}=0$$
(26)
$${N}_{yy,y}-{N}_{xy,x}=0$$
(27)
$${Q}_{x,x}^{s}+{Q}_{x,x}^{a}+{Q}_{y,y}^{s}+{Q}_{y,y}^{a}=-N-q$$
(28)
$${M}_{xx,x}+{M}_{xy,y}-{Q}_{x}^{s}+{Q}_{x}^{a}=0$$
(29)
$${M}_{yy,y}+{M}_{xy,x}-{Q}_{y}^{s}+{Q}_{y}^{a}=0$$
(30)
$${P}_{xx,x}+{P}_{yx,y}+2{Q}_{y}^{a}=0$$
(31)
$${P}_{yy,y}+{P}_{xy,x}-2{Q}_{x}^{a}=0$$
(32)

where the contribution from nonlinear von Kármán strains included in the formulation after the micromechanical constitutive analysis is

$$N=\frac{\partial }{\partial x}\left({N}_{xx}{u}_{z,x}+{N}_{xy}{u}_{z,y}\right)+\frac{\partial }{\partial y}\left({N}_{yy}{u}_{z,y}+{N}_{xy}{u}_{z,x}\right)$$
(33)

It should be highlighted here that this inconsistency in assumed linear strains and non-linear equilibrium equations is taken only to model the bifurcation point, i.e. Euler-buckling. The equilibrium equations can also be written as

$${N}_{xx,x}-{N}_{xy,y}=0$$
(34)
$${N}_{yy,y}-{N}_{xy,x}=0$$
(35)
$${Q}_{x,x}^{s}+{Q}_{x,x}^{a}+{Q}_{y,y}^{s}+{Q}_{y,y}^{a}=-N-q$$
(36)
$${M}_{xx,x}+{M}_{xy,y}-{Q}_{x}^{s}+\left(\frac{{P}_{yy,y}+{P}_{xy,x}}{2}\right)=0$$
(37)
$${M}_{yy,y}+{M}_{xy,x}-{Q}_{y}^{s}-\left(\frac{{P}_{xx,x}+{P}_{yx,y}}{2}\right)=0$$
(38)

which reduce to the same general form as in the classical ESL-FSDT formulation when the couple-stress moments in the brackets and the antisymmetric shear forces are zero. The resulting differential equations are given as

$${A}_{11}\left(\frac{{d}^{2}{u}_{x}}{d{x}^{2}}\right)+{A}_{12}\left(\frac{{d}^{2}{u}_{y}}{dxdy}\right)+{A}_{33}\left(\frac{{d}^{2}{u}_{x}}{d{y}^{2}}+\frac{{d}^{2}{u}_{y}}{dxdy}\right)=0$$
(39)
$${A}_{22}\left(\frac{{d}^{2}{u}_{y}}{d{y}^{2}}\right)+{A}_{12}\left(\frac{{d}^{2}{u}_{x}}{dxdy}\right)+{A}_{33}\left(\frac{{d}^{2}{u}_{y}}{d{x}^{2}}+\frac{{d}^{2}{u}_{x}}{dxdy}\right)=0$$
(40)
$$\left({G}_{11}+{G}_{12}\right)\left(\frac{{d}^{2}{u}_{z}}{d{x}^{2}}+\frac{d{\phi }_{x}}{dx}\right)+\left({G}_{12}+{G}_{22}\right)\left(\frac{{d}^{2}{u}_{z}}{d{x}^{2}}-\frac{d{\phi }_{x}}{dx}+2\frac{d{\psi }_{y}}{dx}\right)+\left({G}_{33}+{G}_{34}\right)\left(\frac{{d}^{2}{u}_{z}}{d{y}^{2}}+\frac{d{\phi }_{y}}{dy}\right)+\left({G}_{34}+{G}_{44}\right)\left(\frac{{d}^{2}{u}_{z}}{d{y}^{2}}-\frac{d{\phi }_{y}}{dy}-2\frac{d{\psi }_{x}}{dy}\right)=-N-q$$
(41)
$${D}_{11}\frac{{d}^{2}{\phi }_{x}}{d{x}^{2}}+\left({D}_{12}{+D}_{33}\right)\frac{{d}^{2}{\phi }_{y}}{dxdy}-\left({G}_{11}+{G}_{12}\right)\left(\frac{d{u}_{z}}{dx}+{\phi }_{x}\right)+{D}_{33}\frac{{d}^{2}{\phi }_{x}}{d{y}^{2}}+{2G}_{12}\left({\phi }_{x}-{\psi }_{y}\right)+\frac{\left({H}_{12}+{H}_{34}\right)\frac{{d}^{2}{\psi }_{x}}{dxdy}+{H}_{22}\frac{{d}^{2}{\psi }_{y}}{d{y}^{2}}+{H}_{33}\frac{{d}^{2}{\psi }_{y}}{d{x}^{2}}}{2}=0$$
(42)
$${D}_{22}\frac{{d}^{2}{\phi }_{y}}{d{y}^{2}}+\left({D}_{12}{+D}_{33}\right)\frac{{d}^{2}{\phi }_{x}}{dxdy}-\left({G}_{33}+{G}_{34}\right)\left(\frac{d{u}_{z}}{dy}+{\phi }_{y}\right)+{D}_{33}\frac{{d}^{2}{\phi }_{y}}{d{x}^{2}}+{2G}_{34}\left({\phi }_{y}+{\psi }_{x}\right)-\frac{\left({H}_{12}+{H}_{34}\right)\frac{{d}^{2}{\psi }_{y}}{dxdy}+{H}_{11}\frac{{d}^{2}{\psi }_{x}}{d{x}^{2}}+{H}_{44}\frac{{d}^{2}{\psi }_{x}}{d{y}^{2}}}{2}=0$$
(43)

As shown by Karttunen et al. [20], Navier-type bending and buckling solutions for simply-supported micropolar plates can be developed. The series approximations are:

$${u}_{z}=\sum_{n=1}^{\infty }\sum_{m=1}^{\infty }{W}_{mn}{\sin}\alpha x{\sin}\beta y$$
(44)
$${\varnothing }_{x}=\sum_{n=1}^{\infty }\sum_{m=1}^{\infty }{X}_{mn}{\cos}\alpha x{\sin}\beta y$$
(45)
$${\varnothing }_{y}=\sum_{n=1}^{\infty }\sum_{m=1}^{\infty }{Y}_{mn}{\sin}\alpha x{\cos}\beta y$$
(46)
$${\psi }_{x}=\sum_{n=1}^{\infty }\sum_{m=1}^{\infty }{R}_{mn}{\sin}\alpha x{\cos}\beta y$$
(47)
$${\psi }_{y}=\sum_{n=1}^{\infty }\sum_{m=1}^{\infty }{P}_{mn}{\cos}\alpha x{\sin}\beta y$$
(48)

For buckling, setting the determinant of the matrix of the following system equal to zero yields the buckling load \({N}_{0}\)

$$\left[ {\begin{array}{*{20}c} {k_{{11}} } & {\alpha \left( {G_{{11}} - G_{{22}} } \right)} & {2\alpha \left( {G_{{12}} - G_{{22}} } \right)} & {\beta \left( {G_{{33}} - G_{{44}} } \right)} & { - 2\beta \left( {G_{{34}} + G_{{44}} } \right)} \\ {} & {k_{{22}} } & {2\left( {G_{{12}} - G_{{22}} } \right)} & {\alpha \beta \left( {D_{{12}} + D_{{33}} } \right)} & 0 \\ {} & {} & {k_{{33}} } & {} & {~\alpha \beta \left( {H_{{12}} + H_{{34}} } \right)} \\ {} & {sym} & {} & {k_{{44}} } & {2\left( {G_{{44}} - G_{{34}} } \right)} \\ {} & {} & {} & {} & {k_{{55}} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {W_{{mn}} } \\ {X_{{mn}} } \\ {P_{{mn}} } \\ \end{array} } \\ {\begin{array}{*{20}c} {Y_{{mn}} } \\ {R_{{mn}} } \\ \end{array} } \\ \end{array} } \right\} = \left\{ 0 \right\}$$
(49)

where

$$\alpha =\frac{m\pi }{a},\beta =\frac{n\pi }{b}$$
(50)
$${k}_{11}={\alpha }^{2}\left({G}_{11}+{2G}_{12}+{G}_{22}-k{N}_{0}\right)+{\beta }^{2}\left({G}_{33}+{2G}_{34}+{G}_{44}-{N}_{0}\right)$$
(51)
$${k}_{22}={G}_{11}-{2G}_{12}+{G}_{22}{+\alpha }^{2}{D}_{11}{+\beta }^{2}{D}_{33}$$
(52)
$${k}_{33}=4{G}_{22}{+\beta }^{2}{H}_{22}{+\alpha }^{2}{H}_{33}$$
(53)
$${k}_{44}={G}_{33}-{2G}_{34}+{G}_{44}{+\beta }^{2}{D}_{22}{+\alpha }^{2}{D}_{33}$$
(54)
$${k}_{55}=4{G}_{44}{{+\alpha }^{2}{H}_{11}+\beta }^{2}{H}_{44}$$
(55)
$${N}_{xx}=-k{N}_{0},{N}_{yy}=-{N}_{0},k=\frac{{N}_{xx}}{{N}_{yy}}$$
(56)

and Wmn, Xmn, Ymn, Rmn and Pmn correspond the mid-surface variables \({{u}_{z},\phi }_{x},{\phi }_{y}\), \({\psi }_{x}\) and \({\psi }_{y}\), respectively. The buckling load \({N}_{0}\) is calculated numerically in the micropolar case.

2.2 Classical ESL-FSDT plate model and analytical buckling solution

For the ESL-FSDT plate based on classical elasticity the equilibrium equations can be written in displacement form as [34]

$${A}_{11}\left(\frac{{d}^{2}{u}_{x}}{d{x}^{2}}\right)+{A}_{12}\left(\frac{{d}^{2}{u}_{y}}{dxdy}\right)+{A}_{33}\left(\frac{{d}^{2}{u}_{x}}{d{y}^{2}}+\frac{{d}^{2}{u}_{y}}{dxdy}\right)=0$$
(57)
$${A}_{22}\left(\frac{{d}^{2}{u}_{y}}{d{y}^{2}}\right)+{A}_{12}\left(\frac{{d}^{2}{u}_{x}}{dxdy}\right)+{A}_{33}\left(\frac{{d}^{2}{u}_{y}}{d{x}^{2}}+\frac{{d}^{2}{u}_{x}}{dxdy}\right)=0$$
(58)
$${G}_{11}\left(\frac{{d}^{2}{u}_{z}}{d{x}^{2}}+\frac{d{\phi }_{x}}{dx}\right)+{G}_{33}\left(\frac{{d}^{2}{u}_{z}}{d{y}^{2}}+\frac{d{\phi }_{y}}{dy}\right)=-N-q$$
(59)
$${D}_{11}\frac{{d}^{2}{\phi }_{x}}{d{x}^{2}}+{D}_{12}\frac{{d}^{2}{\phi }_{y}}{dxdy}+{D}_{33}\left(\frac{{d}^{2}{\phi }_{x}}{d{y}^{2}}+\frac{{d}^{2}{\phi }_{y}}{dxdy}\right)-{G}_{11}\left(\frac{d{u}_{z}}{dx}+{\phi }_{x}\right)=0$$
(60)
$${D}_{22}\frac{{d}^{2}{\phi }_{y}}{d{y}^{2}}+{D}_{12}\frac{{d}^{2}{\phi }_{x}}{dxdy}+{D}_{33}\left(\frac{{d}^{2}{\phi }_{y}}{d{x}^{2}}+\frac{{d}^{2}{\phi }_{x}}{dxdy}\right)-{G}_{33}\left(\frac{d{u}_{z}}{dy}+{\phi }_{y}\right)=0$$
(61)

where differences to micropolar formulated is seen only in bending related equations, Eqs. (59)–(61) and additional stiffness properties and displacements associated with antisymmetric shear strains. For a classical, specially orthotropic ESL-FSDT plate under biaxial compression with simply-supported edges, the buckling load is [34]

$${N}_{0}=\frac{1}{{\alpha }^{2}+k{\beta }^{2}}\frac{{c}_{33}+{c}_{1}\left(\frac{{\alpha }^{2}}{{G}_{33}}+\frac{{\beta }^{2}}{{G}_{11}}\right)}{1+\left(\frac{{c}_{1}}{{G}_{11}{G}_{33}}+\frac{{c}_{2}}{{G}_{11}}+\frac{{c}_{3}}{{G}_{33}}\right)}=\frac{\frac{1}{{\alpha }^{2}}}{1+k\frac{{\beta }^{2}}{{\alpha }^{2}}}\frac{{c}_{33}+\frac{{c}_{1}{\alpha }^{2}}{{G}_{33}}\left(1+\frac{{\beta }^{2}}{{\alpha }^{2}}\frac{{G}_{33}}{{G}_{11}}\right)}{1+\frac{{c}_{1}}{{G}_{33}}\left(\frac{1}{{G}_{11}}+\frac{{c}_{2}}{{c}_{1}}\frac{{G}_{33}}{{G}_{11}}+\frac{{c}_{3}}{{c}_{1}}\right)}$$
(62)
$${c}_{33}={{D}_{11}\alpha }^{4}\left(1+2\left(\frac{{D}_{12}}{{D}_{11}}+2\frac{{D}_{33}}{{D}_{11}}\right)\frac{{\beta }^{2}}{{\alpha }^{2}}+\frac{{D}_{22}{\beta }^{4}}{{{D}_{11}\alpha }^{4}}\right)$$
(63)
$${c}_{1}={c}_{2}{c}_{3}-{({c}_{4})}^{2}$$
(64)
$${c}_{2}={{D}_{11}\alpha }^{2}+{{D}_{33}\beta }^{2}={{D}_{11}\alpha }^{2}\left(1+\frac{{{D}_{33}\beta }^{2}}{{{D}_{11}\alpha }^{2}}\right)$$
(65)
$${c}_{3}={{D}_{33}\alpha }^{2}+{{D}_{22}\beta }^{2}={{D}_{33}\alpha }^{2}\left(1+\frac{{{D}_{22}\beta }^{2}}{{{D}_{33}\alpha }^{2}}\right)$$
(66)
$${c}_{4}=\left({D}_{12}+{D}_{33}\right)\alpha \beta ={D}_{33}\left(1+\frac{{D}_{12}}{{D}_{33}}\right)\alpha \beta$$
(67)

and

$$\frac{{c}_{1}}{{c}_{2}}={c}_{3}-\frac{{\left({c}_{4}\right)}^{2}}{{c}_{2}}={{D}_{33}\alpha }^{2}\left[\left(1+\frac{{{D}_{22}\beta }^{2}}{{{D}_{33}\alpha }^{2}}\right)-\frac{{D}_{33}}{{D}_{11}}\frac{{\left(1+\frac{{D}_{12}}{{D}_{33}}\right)}^{2}}{\left(1+\frac{{{D}_{33}\beta }^{2}}{{{D}_{11}\alpha }^{2}}\right)}\frac{{\beta }^{2}}{{\alpha }^{2}}\right]$$
(68)

\(\frac{{c}_{1}}{{c}_{3}}={c}_{2}-\frac{{({c}_{4})}^{2}}{{c}_{3}}\) = \({{D}_{11}\alpha }^{2}\left[\left(1+\frac{{{D}_{33}\beta }^{2}}{{{D}_{11}\alpha }^{2}}\right)-\frac{{D}_{33}}{{D}_{11}}\frac{{\left(1+\frac{{D}_{12}}{{D}_{33}}\right)}^{2}}{\left(1+\frac{{{D}_{22}\beta }^{2}}{{{D}_{33}\alpha }^{2}}\right)}\frac{{\beta }^{2}}{{\alpha }^{2}}\right]\)

The comparison of the Eqs. (41)–(43) and (59)–(61) for the micropolar and classical ESL-FSDT respectively reveals interesting facts about the web-core panels. As the stiffeners are in one direction only, the shear stiffness in classical ESL-FSDT parallel to stiffener direction is one order of magnitude larger than normal to this direction, i.e. G11 << G33. Due to this, in Eqs. (59)–(61) the deformation terms \(\left({d}^{2}{u}_{z}/d{x}^{2}+d{\phi }_{x}/dx\right)\) increase. As a result, the bifurcation solution in Eq. (57) is strongly affected by the large shear stiffness ratio G33/G11 >> 1. Due to this, the α2/β2-ratio must be large, which indicates for fixed plate aspect ratio, a/b, that the ratio of buckling half waves m/n must be large. Thus, in classical ESL-FSDT the number of buckling half-waves m in the weaker x-direction is large. In micropolar case due to the additional deformation terms and coupling between deformations in x- and y-direction this effect does not occur, see Eqs. (41)–(43).

3 Case studies

3.1 General

The structures to be studied are taken from Karttunen et al. [20], where the validation of the micropolar model was done by 3-D FEA, the 2-D micropolar buckling results are generally in good agreement with 3-D FEA results. The web-core plate is made from steel with Young’s modulus E = 206 GPa and Poisson ratio ν = 0.3. The web-plates have a thickness of tw = 2 mm and spacing l = 120 mm. The distance between the mid-surfaces of the face plates is h = 44 mm. The face plate thickness is varied between tf = 2 mm and 10 mm. The stiffness parameters, derived by micromechanical analysis in Karttunen et al. [20], and their ratios are shown in Table 1 for micropolar and classical ESL-FSDT plates, respectively. A simply-supported rectangular plate with aspect ratios a/b = 1 (a = b = 17l), a/b = 3 (a = 51l) and a/b = 5 (a = 85l) and their inverse values a/b = 1/3 (b = 17l) and a/b = 1/5 (b = 85l) are considered. The aim is to identify the feasibility of the classical solution in terms of orthotropy of the panels. Therefore, we focus here only on the comparison of the results produced by current models.

Table 1 Micropolar FSDT-ESL stiffness parameters and stiffness ratios
Full size table

As Table 1 shows, the panels are highly orthotropic in shear in the classical continuum solution as the stiffness ratios range between G33/G11 = 126 and 170. When micropolar solution is considered, the corresponding numbers are from G33/G11 = 2.683 to 29.95. This indicates directly that the number of buckling half-waves is order of magnitude larger in classical solution than in the micropolar solution as for fixed plate aspect ratio, see also Sect. 2.2. When other stiffness ratios used in classical solution are considered the stiffness ratios are much more moderate and very close to those found in the micropolar case.

3.2 Failure maps and the design space for different load ratios

The failure maps for different plate aspect ratios a/b = 1, a/b = 3 (and a/b = 1/3) and a/b = 5 (and a/b = 1/5) are given in Figs. 4, 5 and 6 respectively. Face plate thickness is varied here between tf = 2 mm and 4 mm as these values are typically used in practical solutions. These maps are created by ranging the buckling half-wave values from m = 1, 2,..., 25 and n = 1, 2,..., 25 in the Navier solution and by finding the combination that minimizes the buckling load. The lines in the maps indicate the combination of Nxx and Nyy where the buckling happens. Kinks in the lines indicate a mode shift, i.e. changes in the number of half-waves that minimize the buckling load.

Fig. 4
figure 4

Stress resultants and split of shear resultants Qxz and Qzx into symmetric and antisymmetric parts for the micropolar plate

Full size image
Fig. 5
figure 5

Comparison of the biaxial buckling strength predicted by micropolar and classical ESL-FSDT. Plate aspect ratio a/b = 1. The 2-D micropolar plates is generally in good agreement with 3-D FE results [20]

Full size image
Fig. 6
figure 6

Comparison of the biaxial buckling strength predicted by micropolar and classical ESL-FSDT. Plate aspect ratio a/b = 3

Full size image

As Figs. 5, 6 and 7 indicate, the classical and micropolar solutions produce nearly the same results when loading is in the direction of the stiffeners, i.e. Nyy is the main load direction. This is due the fact that in this direction the resistance of the plate against buckling is mostly due to bending deformations as the shear stiffness in this direction is very high, resulting in low shear deformations, i.e. D22/G33l2 ratio is low. As the loading Nxx increases, the difference between the two models increases and the micropolar solution results in higher buckling loads than the solutions based on the classical ESL-FSDT,this difference is highlighted by the grey areas in Figs. 4, 5 and 6. This effect is largest at plate aspect ratio a/b = 1, indicating that when plate deformation wavelengths are equal, the error becomes largest. This can be seen also through the stiffness ratios,the G33/G11-ratio can be compensated in Eq. (57) only by the wavelength ratio β2/α2 and more specifically the by ratio n2/m2. When the plate aspect ratio a/b is increased ratio to a/b = 3 or a/b = 5 or decreased to a/b = 1/3 or a/b = 1/5, the difference between the two models reduces. At high aspect ratios this can be explained by the fact that the plate bends close to a cylindrical shape. At low aspect ratios this reduced difference is due to the fact that the transverse direction has little effect on the number of buckling half-waves in the longitudinal direction, but does effect the deformation in the transverse direction.

Fig. 7
figure 7

Comparison of the biaxial buckling strength predicted by micropolar and classical FSDT-ESL. Plate aspect ratio a/b = 5

Full size image

Figure 8 summarizes the difference of micropolar and classical ESL-FSDT for different plate aspect ratios and plate thicknesses in terms of size of the design space. The measure here is equivalent load length, \({N}_{cr}=\sqrt{{A}_{map}}\), that produces the area enclosed by the failure maps, in Figs. 5, 6 and 7,the area has been integrated by trapezoidal rule. It is clear from Fig. 8 that the largest impact of micropolar formulation is for plate aspect ratio of a/b = 1. For low aspect ratios the influence is not as significant and for high aspect ratios. This effect increases when the plate thickness increases.

Fig. 8
figure 8

Comparison of the effective design space length for biaxial buckling predicted by micropolar and classical FSDT-ESL

Full size image

4 Conclusions

The strength of web-core sandwich panels is often limited by buckling and at early design stages such as conceptual design the bifurcation buckling forms the basis for buckling strength assessment. This paper reviewed briefly the differential equations of a 2-D micropolar plate theory and the Navier solution for biaxial compression with the aim to identify the reasons observed by Jelovica and Romanoff [15] and Karttunen et al. [20] for the differences between classical and micropolar ESL-FSDT plate models and 3-D FEA. It was shown for web-core panels that while most of the stiffness parameters related to in-plane stretching and bending are of the same order of magnitude in the stiffener direction and in the weak direction opposite to stiffeners, there are few orders of magnitude differences in shear stiffness when classical solution is concerned. Due to this difference, in buckling a large number of buckling half-waves in the direction opposite to stiffeners is needed in comparison to direction along the stiffeners to compensate the shear stiffness difference. When the micropolar formulation is used, such compensation is not needed. This is due to the fact that even the shear stiffness ratios are close to each other. The outcome of these findings is that there is significant error in classical buckling loads for plate aspect ratios close to unity when the loading direction is opposite to the stiffener direction. When loading is along stiffener direction, the differences between classical and micropolar ESL-FSDT are much smaller. The same can be concluded for plate aspect ratios much smaller or larger than unity.

The present study was limited to simply-supported rectangular plates undergoing biaxial compression. In real structures in-plane shear is also often present. In addition, it is possible that the loading is a combination of compression and tension. Moreover, plates may be exposed to initial deformations. Recently Nampally et al. [28] derived a geometrically nonlinear plate finite element for bending problems based on the micropolar plate theory presented here. With suitable extensions, the plate element will enable further study of web-core plate buckling problems. Finally, as shown by Reinaldo Goncalves et al. [35] by classical ESL-FSDT and 3-D FEA, in case of geometrical non-linearity it is possible that the microstructure buckles locally instead of global buckling which was discussed in this paper. This calls for two-scale geometrical non-linear solution. Developing a micropolar plate model suitable for both local and global buckling is left for future work.