Skip to main content
SpringerLink
Log in

Inferring material parameters from imprecise experiments on soft materials by virtual fields method

  • Original Article
  • Published:
Annals of Solid and Structural Mechanics

Abstract

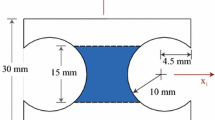
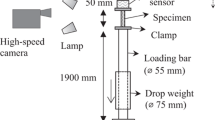
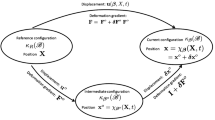
Inferring material parameters of soft materials, especially soft tissues from experiments, has always been a challenge because of the inaccuracy of specimen geometry, difficulty in proper gripping and difficulty in obtaining reliable displacement data. If one is able to obtain full field data with Digital Image Correlation or other similar techniques, we show that in spite of poor quality experimental data, it is still possible to get the material parameters using Virtual Fields Method with carefully chosen virtual fields. We demonstrate the approach by two cases. The first is Ecoflex (silicone rubber) under biaxial deformations at controlled loading rates, and the second is rat skin samples with imperfect shape under biaxial deformations at controlled loading rates. In both cases, rather than trying to obtain homogeneous deformation conditions, we use a technique based on the Virtual Fields Method to extract the material properties from the deformation of the specimen collected by Digital Image Correlation (DIC) and the force load measured by the load sensor. In order to apply loads in two principal directions simultaneously, a custom biaxial set-up was built and mounted into a uniaxial Instron tensile set-up. We show here that in spite of significant inhomogeneity in the deformation, errors, and missing data in the measured displacement field, we are still able to recover the material properties of the soft solid by suitable choices of virtual fields.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21

Similar content being viewed by others

References

  1. Afsar-Kazerooni N, Srinivasa A, Criscione J (2020) Experimental investigation of the inelastic response of pig and rat skin under uniaxial cyclic mechanical loading. Exp Mech pp. 1–17

  2. Avril S, Badel P, Duprey A (2010) Anisotropic and hyperelastic identification of in vitro human arteries from full-field optical measurements. J Biomech 43(15):2978–2985

    Article  Google Scholar 

  3. Avril S, Grédiac M, Pierron F (2004) Sensitivity of the virtual fields method to noisy data. Comput Mech 34(6):439–452

    Article  Google Scholar 

  4. Benias PC, Wells RG, Sackey-Aboagye B, Klavan H, Reidy J, Buonocore D, Miranda M, Kornacki S, Wayne M, Carr-Locke DL et al (2018) Structure and distribution of an unrecognized interstitium in human tissues. Sci Rep 8(1):4947

    Article  Google Scholar 

  5. Berardesca E, Elsner P, Wilhelm KP, Maibach HI (1995) Bioengineering of the skin: methods and instrumentation, vol 3. CRC Press, Boca Raton

    Google Scholar 

  6. Billiar KL, Sacks MS (2000) Biaxial mechanical properties of the natural and glutaraldehyde treated aortic valve cusp-part i: experimental results. J Biomech Eng 122(1):23–30

    Article  Google Scholar 

  7. Brieu M, Diani J, Bhatnagar N (2006) A new biaxial tension test fixture for uniaxial testing machine-a validation for hyperelastic behavior of rubber-like materials. J Test Eval 35(4):1–9

    Google Scholar 

  8. Capek L, Lochman Z, Dzan L, Jacquet E (2010) Biaxial extensometer for measuring of the human skin anisotropy in vivo. In: 2010 5th Cairo International Biomedical Engineering Conference, pp. 83–85. https://doi.org/10.1109/CIBEC.2010.5716059

  9. Evans SL, Holt CA (2009) Measuring the mechanical properties of human skin in vivo using digital image correlation and finite element modelling. J Strain Anal Eng Design 44(5):337–345. https://doi.org/10.1243/03093247JSA488

    Article  Google Scholar 

  10. Flynn D, Peura G, Grigg P, Hoffman A (1998) A finite element based method to determine the properties of planar soft tissue. J Biomech Eng 120(2):202–210

    Article  Google Scholar 

  11. Fung YC (2013) Biomechanics: mechanical properties of living tissues. Springer Science & Business Media, Berlin

    Google Scholar 

  12. Geerligs M (2006) In vitro mechanical characterization of human skin layers: stratum corneum, epidermis and hypodermis. Ph.D. thesis, Ph. D. Thesis, Technische Universiteit Eindhoven

  13. Grédiac M, Pierron F (1998) At-shaped specimen for the direct characterization of orthotropic materials. Int J Numer Methods Eng 41(2):293–309

    Article  Google Scholar 

  14. Grédiac M, Pierron F (2004) Numerical issues in the virtual fields method. Int J Numer Methods Eng 59(10):1287–1312

    Article  MathSciNet  Google Scholar 

  15. Grediac M, Pierron F, Avril S, Toussaint E (2006) The virtual fields method for extracting constitutive parameters from full-field measurements: a review. Strain 42(4):233–253

    Article  Google Scholar 

  16. Grédiac M, Toussaint E, Pierron F (2002) Special virtual fields for the direct determination of material parameters with the virtual fields method. 1—-principle and definition. Int J Solids Struct 39(10):2691–2705

    Article  Google Scholar 

  17. Grédiac M, Toussaint E, Pierron F (2002) Special virtual fields for the direct determination of material parameters with the virtual fields method. 2—-application to in-plane properties. Int J Solids Struct 39(10):2707–2730

    Article  Google Scholar 

  18. Haut R (1989) The effects of orientation and location on the strength of dorsal rat skin in high and low speed tensile failure experiments. J Biomech Eng 111(2):136–140

    Article  Google Scholar 

  19. Holzapfel GA, Gasser TC, Ogden RW (2000) A new constitutive framework for arterial wall mechanics and a comparative study of material models. J Elast Phys Sci Solids 61(1):1–48

    Article  MathSciNet  Google Scholar 

  20. Kazerooni NA, Srinivasa A, Freed A (2019) Orthotropic-equivalent strain measures and their application to the elastic response of porcine skin. Mech Res Commun 101:103404

    Article  Google Scholar 

  21. Kim JH, Avril S, Duprey A, Favre JP (2012) Experimental characterization of rupture in human aortic aneurysms using a full-field measurement technique. Biomech Model Mechanobiol 11(6):841–853

    Article  Google Scholar 

  22. Lanir Y, Fung Y (1974) Two-dimensional mechanical properties of rabbit skin—i. experimental system. J Biomech 7(1):29–34

    Article  Google Scholar 

  23. Lanir Y, Fung Y (1974) Two-dimensional mechanical properties of rabbit skin—ii. experimental results. J Biomech 7(2):171–182. https://doi.org/10.1016/0021-9290(74)90058-X

    Article  Google Scholar 

  24. Maiti R, Gerhardt LC, Lee ZS, Byers RA, Woods D, Sanz-Herrera JA, Franklin SE, Lewis R, Matcher SJ, Carré MJ (2016) In vivo measurement of skin surface strain and sub-surface layer deformation induced by natural tissue stretching. J Mech Behav Biomed Mater 62:556–569

    Article  Google Scholar 

  25. Marek A, Davis FM, Rossi M, Pierron F (2018) Extension of the sensitivity-based virtual fields to large deformation anisotropic plasticity. Int J Mater Form. https://doi.org/10.1007/s12289-018-1428-1

    Article  Google Scholar 

  26. McGrath JA, Uitto J (2010) Anatomy and Organization of Human Skin, Chap. 3, pp. 1–53. Wiley-Blackwell . https://doi.org/10.1002/9781444317633.ch3

  27. Mooney M (1940) A theory of large elastic deformation. J Appl Phys 11(9):582–592

    Article  Google Scholar 

  28. Nolan D, Gower A, Destrade M, Ogden R, McGarry J (2014) A robust anisotropic hyperelastic formulation for the modelling of soft tissue. J Mech Behav Biomed Mater 39:48–60. https://doi.org/10.1016/j.jmbbm.2014.06.016

    Article  Google Scholar 

  29. Rivlin RS (1948) Large elastic deformations of isotropic materials. iv. further developments of the general theory. Philos Trans R Soc Lond A: Math, Phys Eng Sci 241(835): 379–397. https://doi.org/10.1098/rsta.1948.0024. http://rsta.royalsocietypublishing.org/content/241/835/379

  30. Sacks MS (2000) Biaxial mechanical evaluation of planar biological materials. J Elast Phys Sci Solids 61(1):199. https://doi.org/10.1023/A:1010917028671

    Article  MATH  Google Scholar 

  31. Seibert H, Scheffer T, Diebels S (2014) Biaxial testing of elastomers-experimental setup, measurement and experimental optimisation of specimen’s shape. Tech Mech 34(2):72–89

    Google Scholar 

  32. Shergold OA, Fleck NA, Radford D (2006) The uniaxial stress versus strain response of pig skin and silicone rubber at low and high strain rates. Int J Impact Eng 32(9):1384–1402. https://doi.org/10.1016/j.ijimpeng.2004.11.010. http://www.sciencedirect.com/science/article/pii/S0734743X04002325

  33. Sommer G, Haspinger DC, Andrä M, Sacherer M, Viertler C, Regitnig P, Holzapfel GA (2015) Quantification of shear deformations and corresponding stresses in the biaxially tested human myocardium. Ann Biomed Eng 43(10):2334–2348. https://doi.org/10.1007/s10439-015-1281-z

    Article  Google Scholar 

  34. Tonge TK, Atlan LS, Voo LM, Nguyen TD (2013) Full-field bulge test for planar anisotropic tissues: Part i-experimental methods applied to human skin tissue. Acta Biomater 9(4):5913–5925. https://doi.org/10.1016/j.actbio.2012.11.035

    Article  Google Scholar 

  35. Toussaint E, Grédiac M, Pierron F (2006) The virtual fields method with piecewise virtual fields. Int J Mech Sci 48(3):256–264

    Article  Google Scholar 

  36. Yin FC, Strumpf RK, Chew PH, Zeger SL (1987) Quantification of the mechanical properties of noncontracting canine myocardium under simultaneous biaxial loading. J Biomech 20(6):577–589

    Article  Google Scholar 

  37. Zemánek M, Burša J, Děták M (2009) Biaxial tension tests with soft tissues of arterial wall. Eng Mech 16(1):3–11

    Google Scholar 

Download references

Acknowledgements

The authors gratefully thank Dr. Terry Creasy for allowing us to use his facilities and Dr. Goenezen for lending us, the DIC set-up.

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Texas A&M University, College Station, TX, 77843, USA

    N. Afsar Kazerooni & A. R. Srinivasa

  2. Health Sciences, Ontario Tech University, 2000 Simcoe St N, Oshawa, ON, L1G 0C5, Canada

    Z. Wang

  3. Department of Biomedical Engineering, Texas A&M University, College Station, TX, 77843, USA

    J. C. Criscione

Authors
  1. N. Afsar Kazerooni
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Z. Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. A. R. Srinivasa
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. J. C. Criscione
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. R. Srinivasa.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kazerooni, N.A., Wang, Z., Srinivasa, A.R. et al. Inferring material parameters from imprecise experiments on soft materials by virtual fields method. Ann. Solid Struct. Mech. 12, 59–72 (2020). https://doi.org/10.1007/s12356-020-00062-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12356-020-00062-8

Keywords

Search

Navigation