Third-order nonlocal elasticity in buckling and vibration of functionally graded nanoplates on Winkler-Pasternak media

Abstract

The focus of the present work is to present an analytical approach for buckling and free vibrations analysis of thick functionally graded nanoplates embedded in a Winkler-Pasternak medium. The equations of motion are derived according to both the third-order shear deformation theory, proposed by Reddy, and the nonlocal elasticity Eringen's model. For the first time, the equations are solved analytically for plates with two simply supported opposite edges, the solutions also turning helpful as shape functions in the analysis of structures with more complex geometries and boundary conditions. Sensitivity analyses are finally performed to highlight the role of nonlocal parameters, aspect and side-to-thickness ratios, boundary conditions, and functionally graded material properties in the overall response of plates and cylindrical shells. It is felt that the proposed strategy could be usefully adopted as benchmark solutions in numerical routines as well as for predicting some unexpected behaviors, for instance, in terms of buckling load, in thick nanoplates on elastic foundations.

1 Introduction

In the last years, a new class of composites known as Functionally Graded Materials (FGMs) has been subjected to extensive research activities. In a FGM the microstructural variation of the material composition is intentionally designed to build up new composites with optimal physical performance under specific functional requirements. Their superior properties make them applicable in a wide range of engineering fields. Examples are micro- and nano- electro-mechanical systems, thin films, cutting tools and machine parts, which are all extensively discussed in the literature [1,2,3]. Recently, functionally graded models have been successfully employed to describe the mechanical behavior and scale effects in nanoplates, by enriching the classical continuum mechanics with size-dependent continuum theories, such as nonlocal elasticity [4,5,6,7], to overcome the drawbacks of standard (local) approaches [8,9,10]. In particular, in Reddy [11] the author applied Eringen's theory of elasticity to formulate a nonlocal version for bending, buckling and vibration of different beam theories, including Bernoulli, Timoshenko, Levinson and Reddy ones. The same author in [12] developed a microstructure-dependent nonlinear Euler–Bernoulli and Timoshenko beam theory accounting for though-thickness power-law variation of a two-constituent material. Remarkable attention is also paid to the buckling and vibration analysis of nonlocal FG nano-plates. For instance, in [13] the authors adopted a nonlocal strain gradient model to study the buckling of nanoplates in the context of Classical Plate Theory (CPT) and, in the same framework, Pradhan and Murmu [14] studied the stability of single-layer graphene sheets using a Levy approach to solve the governing equations, while Ansari et al. [15] developed a nonlocal finite element plate model to analyze vibration of multilayered graphene sheets embedded in an elastic medium.

The first-order shear deformation theory extends the kinematics of the Kirchhoff plate by relaxing the normality restriction that allows an arbitrary constant rotation across the plate thickness. Hosseini-Hashemi and Samaei [16] derived an analytical solution for the buckling analysis of rectangular nanoplates resting on a Pasternak elastic foundation. The formulation is based on an updated Mindlin plate theory, which includes nonlocal elasticity, first-order shear deformation, and plate-foundation interaction. This model was then adopted in further works [17, 18] to analyze the effect of geometric imperfections on the buckling and vibration of micro- and nanoplates. In higher-order shear deformation theories, the shear deformation effects are taken into account and do not need a shear correction factor.

The third-order shear deformation theory proposed by Reddy [19, 20] assumes a displacement field that is cubic through the plate thickness. Since it provides results that are close to 3D elasticity solutions [21], its use ensures accurate results in studying the mechanical behavior of thick plates [22, 23]. In [24], Daneshmehr et al., investigated the free vibration of FG nano-plates considering a higher-order theory and by solving the corresponding equations through the generalized differential quadrature method. Furthermore, in [25], the authors studied the small-scale effects on the buckling and vibration of rectangular nanoplates based on the Reddy plate theory.

In the present work, the nonlocal Eringen model is employed to examine buckling and vibration behavior of nanoplates obeying the Reddy theory, exhibiting material properties changing gradually through the thickness. The governing equations are derived by starting from Hamilton's principle and, to the best of the authors knowledge, for the first time solved analytically in the case of rectangular plates simply supported on two opposite edges. To extend the approach to nano-structures with relatively complex geometries, the obtained analytical solutions are exploited to gain insights into the mechanical response of thick cylindrical shells and also used as shape functions in a finite-strip method. At the end, the influence of different parameters such as aspect ratio, boundary conditions, and power-law index of FGMs on buckling and vibration is investigated and discussed, by highlighting how the comparison of the obtained outcomes with results available in the literature suggests effectiveness and robustness of the proposed strategy.

2 Remarks on the nonlocal functionally graded plate theory

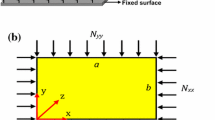
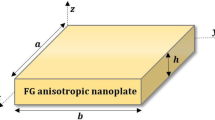
Consider a FG nanoplate of length a, width b and thickness h with applied in-plane loads in x- and y-direction. Despite what follows, we approach the problems in a general way, the plate is thought as composed of two different phases, pure ceramic on the top surface and pure metal at the bottom surface. Poisson's ratio $\nu$ is assumed constant, whereas the Young modulus $E = E\left( h \right)$ and the mass density $\rho = \rho \left( h \right)$ are instead considered continuously variable along with the thickness (Fig. 1) with the following power-law distribution:

$$ \left[ \begin{gathered} E\left( z \right) \hfill \\ \rho \left( z \right) \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} E_{c} \hfill \\ \rho_{c} \hfill \\ \end{gathered} \right]\left( {\frac{2z + h}{{2h}}} \right)^{n} + \left[ \begin{gathered} E_{m} \hfill \\ \rho_{m} \hfill \\ \end{gathered} \right]\left( {1 - \left( {\frac{2z + h}{{2h}}} \right)^{n} } \right) $$

(1)

Fig. 1

Coordinate system, geometry and applied loads of FGM nanoplate

where z is the distance from the neutral plane of the FG nanoplate, $\left( {c,m} \right)$ indicate ceramic and metal, and n is the power-law index of material distribution, assumed to be positive.

According to Eq. (1), as the power-law index approaches zero or infinity, the plate is isotropic, composed of fully ceramic or metal, respectively (Fig. 2).

Fig. 2

Effect of power-law parameter n on FGM

Typical values for metal and ceramic properties usually adopted in the FG nanoplates are listed in Table 1. The plate model is continuously supported in its plane by a two-layer Winkler-Pasternak medium, playing the role of an elastic foundation, whose properties depend on both its normal and shear elastic moduli.

Table 1 Material properties used in the numerical analysis

By indicating with $\nabla^{2}$ the Laplace operator in $\left( {x,y} \right)$, the load–displacement relationship of the foundation can be written as:

$$ q = \left( {K_{w} - K_{s} \nabla^{2} } \right)w $$

(2)

where the terms $\left( {K_{w} ,K_{s} } \right)$ represent the Winkler and Pasternak parameters, respectively, and the out-of-plane displacement is defined as:

$$ w\left( {x,y,t} \right) = u_{3} \left( {x,y,0,t} \right) $$

(3)

As it is well-known, the nonlocal models call into play a length scale parameter in order to account for the size effects. By assuming that the stress at a point in a continuum body is a function of the strain at the neighboring points, Eringen [6] proposed the following nonlocal constitutive model:

$$ {{\varvec{\upsigma}}}^{NL} = \int_{{}}^{{}} {K\left( {\left| {{\mathbf{x^{\prime}}} - {\mathbf{x}}} \right|,\tau } \right){{\varvec{\upsigma}}}\left( {{\mathbf{x^{\prime}}}} \right)dx^{\prime}} $$

(4)

In Eq. (4) the nonlocal kernel function $K\left( {\left| {{\mathbf{x^{\prime}}} - {\mathbf{x}}} \right|,\tau } \right)$ depends on the Euclidean distance $\left| {{\mathbf{x^{\prime}}} - {\mathbf{x}}} \right|$ and on the material constants $\tau$ determined by internal and external characteristic lengths, whereas:

$$ {{\varvec{\upsigma}}}\left( {\mathbf{x}} \right) = {\mathbf{C}}\left( {\mathbf{x}} \right):{{\varvec{\upvarepsilon}}}\left( {\mathbf{x}} \right) $$

(5)

represents, concerning the 2D problems addressed in the present work, the classical (local) macroscopic stress tensor at a point ${\mathbf{x}} = \left( {x,y} \right)$ of the middle plane of the plate.

In a later publication, Eringen [7] proposed a Green function of a linear differential operator differential to describe the kernel $K\left( {\left| {{\mathbf{x^{\prime}}} - {\mathbf{x}}} \right|,\tau } \right)$, in order to represent Eq. (4) in the simplified, equivalent differential form:

$$ {\mathcal{L}}{{\varvec{\upsigma}}}^{NL} \left( {\mathbf{x}} \right) = {{\varvec{\upsigma}}}\left( {\mathbf{x}} \right) = {\mathbf{C}}\left( {\mathbf{x}} \right):{{\varvec{\upvarepsilon}}}\left( {\mathbf{x}} \right),\,\,\,\,\,\,{\mathcal{L}} = \left( {1 - \mu \nabla^{2} } \right),\,\,\,\,\mu = e_{0}^{2} a^{2} $$

(6)

in which $\nabla^{2}$ a is the internal length and $e_{0}$ represents a material constant to be determined experimentally.

3 Mathematical modeling for plane stress problems in nonlocal Reddy nano-plates

In plane-stress analyses, the relation (6) can be written in terms of Young modulus distribution as follows:

$$ {\mathcal{L}}{{\varvec{\upsigma}}}^{NL} = {\mathcal{L}}\left[ \begin{gathered} \sigma_{x}^{NL} \hfill \\ \sigma_{y}^{NL} \hfill \\ \tau_{xy}^{NL} \hfill \\ \end{gathered} \right] = {\mathbf{E}} \cdot {{\varvec{\upvarepsilon}}},\,\,\,\,\,\,\,\,{\mathcal{L}}{{\varvec{\uptau}}}^{NL} = {\mathcal{L}}\left[ \begin{gathered} \tau_{xz}^{NL} \hfill \\ \tau_{yz}^{NL} \hfill \\ \end{gathered} \right] = {\mathbf{G}} \cdot {{\varvec{\upgamma}}} $$

(7)

with E related to the proposed power-law distribution (1) as:

$$ {\mathbf{E}} = \left[ {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } & 0 \\ {Q_{21} } & {Q_{22} } & 0 \\ 0 & 0 & {Q_{66} } \\ \end{array} } \right] = \frac{E\left( z \right)}{{1 - \nu^{2} }}\left[ {\begin{array}{*{20}c} 1 & \nu & 0 \\ \nu & 1 & 0 \\ 0 & 0 & {\frac{1 - \nu }{2}} \\ \end{array} } \right];\,\,\,{\mathbf{G}} = \left[ {\begin{array}{*{20}c} {Q_{44} } & 0 \\ 0 & {Q_{55} } \\ \end{array} } \right] = \frac{E\left( z \right)}{{2\left( {1 + \nu } \right)}}\left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ \end{array} } \right] $$

(8)

and:

$$ {\mathbf{G}} = \left[ {\begin{array}{*{20}c} {Q_{44} } & 0 \\ 0 & {Q_{55} } \\ \end{array} } \right] = \frac{E\left( z \right)}{{2\left( {1 + \nu } \right)}}\left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ \end{array} } \right] $$

(9)

The strain components, under the von Karman hypothesis, can be split into the sum of the linear and nonlinear contributes as:

$$ {{\varvec{\upvarepsilon}}} = \frac{1}{2}\left( {u_{i,j} + u_{j,i} } \right) + \frac{1}{2}\left( {u_{3,i} u_{3,j} } \right) $$

(10)

the comma denoting differentiation with respect space variables, whereas, in what follows, the dot is used to indicate differentiation with respect to the time t.

In presence of body $X_{i}$ and inertia forces, the equilibrium requires:

$$ \sigma_{ij,j}^{NL} + X_{i} - \rho \ddot{u}_{i} = 0 $$

(11)

from which the substitution of Eq. (6) in (11) gives

$$ \sigma_{ij,j} + {\mathcal{L}}\left( {X_{i} - \rho \ddot{u}_{i} } \right) = 0 $$

(12)

According to Reddy plate theory, the displacement field $\left( {s_{x} ,s_{y} ,s_{z} } \right)$ at an arbitrary point within the plate can be entirely expressed in terms of both rotations $\varphi_{x} = \varphi_{x} \left( {x,y,t} \right),\;\;\varphi_{y} = \varphi_{y} \left( {x,y,t} \right)$ and displacements $\left( {u,v,w} \right) = \left( {u\left( {x,y,t} \right),v\left( {x,y,t} \right),w\left( {x,y,t} \right)} \right)$ of the middle plate surface as follows:

$$ \begin{gathered} s_{x} \left( {x,y,z,t} \right) = u + z\left( {\varphi_{x} - c_{1} z^{2} \left( {\varphi_{x} + w,_{x} } \right)} \right) \hfill \\ s_{y} \left( {x,y,z,t} \right) = v + z\left( {\varphi_{y} - c_{1} z^{2} \left( {\varphi_{y} + w,_{y} } \right)} \right) \hfill \\ s_{z} \left( {x,y,z,t} \right) = w \hfill \\ \end{gathered} $$

(13)

with $\,c_{1} = {4 \mathord{\left/ {\vphantom {4 {3h^{2} }}} \right. \kern-\nulldelimiterspace} {3h^{2} }}$. Accordingly, the strain components can be obtained by substituting Eqs. (13) into (10):

$$ \begin{gathered} {{\varvec{\upvarepsilon}}} = \left[ \begin{gathered} \varepsilon_{x} \hfill \\ \varepsilon_{y} \hfill \\ \gamma_{xy} \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} u,_{x} + \varphi_{x,x} - c_{1} z^{2} \left( {\varphi_{x,x} + w,_{xx} } \right) + \frac{1}{2}w,_{x}^{2} \hfill \\ v,_{y} + \varphi_{y,y} - c_{1} z^{2} \left( {\varphi_{y,y} + w,_{y,y} } \right) + \frac{1}{2}w,_{y}^{2} \hfill \\ \left( {\varphi_{x,y} + \varphi_{y,x} } \right) - c_{1} z^{2} \left( {\varphi_{x,y} + \varphi_{y,x} + 2w,_{xy} } \right) + \frac{1}{2}w,_{x} w,_{y} \hfill \\ \end{gathered} \right] \hfill \\ {{\varvec{\upgamma}}} = \left[ \begin{gathered} \gamma_{xz} \hfill \\ \gamma_{yz} \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} \left( {\varphi_{x} + w,_{x} - 3c_{1} z^{2} \left( {\varphi_{x} + w,_{x} } \right)} \right) \hfill \\ \left( {\varphi_{y} + w,_{y} - 3c_{1} z^{2} \left( {\varphi_{y} + w,_{y} } \right)} \right) \hfill \\ \end{gathered} \right] \hfill \\ \end{gathered} $$

(14)

The governing equilibrium equations and the corresponding boundary conditions of the FG nanoplates can be derived minimizing the total energy, sum of the elastic and the kinetic contributions, that is

$$ \int_{0}^{t} {\left( {\delta W + \delta K} \right)dt} = 0 $$

(15)

in which

$$ \delta W = \frac{1}{2}\int_{A}^{{}} {\int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\sigma_{ij}^{NL} \delta \varepsilon_{ij} dzdA} } + \int_{A}^{{}} {\left( {K_{w} w\delta w + K_{s} w,_{i} \delta w,_{i} } \right)} dA,\quad \delta K = \int_{A}^{{}} {\int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\rho \dot{s}_{i} \delta \dot{s}_{i} } dzdA} $$

(16)

By substituting Eqs. (14) into (16), the strain energy per unit area can be written as:

$$ \int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\sigma_{ij}^{NL} \delta \varepsilon_{ij} dz = } {\mathbf{N}}^{NL} {\mathbf{\delta \eta }} + {\mathbf{M}}^{NL} \delta {{\varvec{\upchi}}} + {\mathbf{P}}^{NL} \delta {{\varvec{\upzeta}}} + \left( {{\mathbf{Q}}^{NL} - 3c_{1} {\mathbf{R}}^{NL} } \right)\delta {{\varvec{\upgamma}}} $$

(17)

where the generalized Reddy strain are collected in the form:

$$ {{\varvec{\upeta}}} = \left[ \begin{gathered} u,_{x} \hfill \\ v,_{y} \hfill \\ u,_{y} + v,_{x} \hfill \\ \end{gathered} \right];\;\;\delta {{\varvec{\upchi}}} = \left[ \begin{gathered} \varphi_{x,x} \hfill \\ \varphi_{y,y} \hfill \\ \varphi_{x,y} + \varphi_{y,x} \hfill \\ \end{gathered} \right];\,\,\delta {{\varvec{\upzeta}}} = - c_{1} \left[ \begin{gathered} \left( {\varphi_{x,x} + w,_{xx} } \right) \hfill \\ \left( {\varphi_{y,y} + w,_{y,y} } \right) \hfill \\ \left( {\varphi_{x,y} + \varphi_{y,x} + 2w,_{xy} } \right) \hfill \\ \end{gathered} \right];\;\delta {{\varvec{\upgamma}}} = \left[ \begin{gathered} \left( {\varphi_{x,x} + w,_{xx} } \right) \hfill \\ \left( {\varphi_{y,y} + w,_{y,y} } \right) \hfill \\ \end{gathered} \right] $$

(18)

and

$$ \left[ \begin{gathered} {\mathbf{N}} \hfill \\ {\mathbf{M}} \hfill \\ {\mathbf{P}} \hfill \\ \end{gathered} \right]^{NL} = \int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {{{\varvec{\upsigma}}}^{NL} \left[ \begin{gathered} 1 \hfill \\ z \hfill \\ z^{3} \hfill \\ \end{gathered} \right]dz} ;\,\,\,\,\left[ \begin{gathered} {\mathbf{Q}} \hfill \\ {\mathbf{R}} \hfill \\ \end{gathered} \right]^{NL} = \int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {{{\varvec{\uptau}}}^{NL} \left[ \begin{gathered} 1 \hfill \\ z^{2} \hfill \\ \end{gathered} \right]dz} $$

(19)

are the corresponding dual stress, obtained as integrals of the nonlocal stress components defined in Eq. (7). Analogously, by integrating along the thickness, the kinetic energy one has:

$$ m_{0} \left( {{\dot{\mathbf{u}}}\delta {\dot{\mathbf{u}}} + \dot{w}\delta \dot{w}} \right) + m_{1} \left( {{\dot{\mathbf{\varphi }}}\delta {\dot{\mathbf{u}}} + {\dot{\mathbf{u}}}\delta {\dot{\mathbf{\varphi }}}} \right) + m_{2} {\dot{\mathbf{\varphi }}}\delta {\dot{\mathbf{\varphi }}} - c_{1} m_{3} \left( {{\dot{\mathbf{\theta }}}\delta {\dot{\mathbf{u}}} + {\dot{\mathbf{u}}}\delta {\dot{\mathbf{\theta }}}} \right) - c_{1} m_{4} \left( {{\dot{\mathbf{\theta }}}\delta {\dot{\mathbf{\varphi }}} + {\dot{\mathbf{\varphi }}}\delta {\dot{\mathbf{\theta }}}} \right) + c_{1}^{2} m_{6} {\dot{\mathbf{\theta }}}\delta {\dot{\mathbf{\theta }}} $$

(20)

with

$$ m_{i} = \int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {z^{i} \rho \left( z \right)dz} $$

(21)

and

$$ {\dot{\mathbf{u}}} = \left[ {\dot{u}\,\,\,\,\,\dot{v}} \right],\quad {\dot{\mathbf{\varphi }}} = \left[ {\dot{\varphi }_{x} \,\,\,\,\,\dot{\varphi }_{y} } \right],\quad {\dot{\mathbf{\theta }}} = \left[ {\left( {\dot{\varphi }_{x} + \dot{w},_{x} } \right)\,\,\,\,\,\left( {\dot{\varphi }_{y} + \dot{w},_{y} } \right)} \right] $$

(22)

the vectors containing the generalized displacement field rate.

By substituting Eqs. (17) and (20) into Eq. (15) and invoking the fundamental lemma of calculus of variations, we then obtain the following in-plane and out-of-plane equilibrium equations respectively as

$$ \begin{gathered} \delta u:\,\,\,\,\,\,\mathcal{L}\left( {N_{x,x}^{NL} + N_{xy,y}^{NL} - \ddot{\mathcal{U}}} \right) = 0 \hfill \\ \delta v:\,\,\,\,\,\,\mathcal{L}\left( {N_{xy,x}^{NL} + N_{y,y}^{NL} - \ddot{\mathcal{V}}} \right) = 0 \hfill \\ \end{gathered} $$

(23)

and

$$ \begin{gathered} \delta w:\,\,\,\,\,\mathcal{L}\left( {\overline{Q}_{x,x}^{NL} + \overline{Q}_{y,y}^{NL} + \mathcal{N} + q - \ddot{\mathcal{W}}} \right) = 0 \hfill \\ \delta \phi_{x} :\,\,\,\,\,\mathcal{L}\left( {M_{x,x}^{NL} + M_{xy,y}^{NL} - T_{x}^{NL} - \ddot{\mathcal{F}}_{x} } \right) = 0 \hfill \\ \delta \phi_{y} :\,\,\,\,\,\mathcal{L}\left( {M_{xy,x}^{NL} + M_{y,y}^{NL} - T_{y}^{NL} - \ddot{\mathcal{F}}_{y} } \right) = 0 \hfill \\ \end{gathered} $$

(24)

where q is defined in Eq. (2) while:

$$ \begin{gathered} \ddot{\mathcal{U}} = m_{0} \ddot{u} + \overline{m}_{1} \ddot{\varphi }_{x} - c_{1} m_{3} \ddot{w},_{x} ,\;\;\ddot{\mathcal{V}} = m_{0} \ddot{v} + \overline{m}_{1} \ddot{\varphi }_{y} - c_{1} m_{3} \ddot{w},_{y} \hfill \\ \ddot{\mathcal{W}} = \left( {m_{0} \ddot{w} - c_{1}^{2} m_{6} \nabla^{2} \ddot{w} + c_{1} \left( {m_{3} \left( {\ddot{u},_{x} + \ddot{v},_{y} } \right) + \overline{m}_{4} \left( {\ddot{\varphi }_{x,x} + \ddot{\varphi }_{y,y} } \right)} \right)} \right) \hfill \\ \ddot{\mathcal{F}}_{x} = \overline{m}_{1} \ddot{u} + \tilde{m}\ddot{\varphi }_{x} - c_{1} m_{4} \ddot{w},_{x} ,\;\;\ddot{\mathcal{F}}_{y} = \overline{m}_{1} \ddot{v} + \tilde{m}\ddot{\varphi }_{y} - c_{1} m_{4} \ddot{w},_{y} \hfill \\ \mathcal{N} = \left( {N_{x} w,_{x} + N_{xy} w,_{y} } \right),_{x} + \left( {N_{xy} w,_{x} + N_{y} w,_{y} } \right),_{y} \hfill \\ \overline{m}_{i} = m_{i} - c_{1} m_{i + 2} ,\,\,\,\,\tilde{m} = m_{2} - 2c_{1} m_{4} + c_{1}^{2} m_{6} \hfill \\ \overline{Q}_{x}^{NL} = Q_{x}^{NL} - 3c_{1} R_{x}^{NL} ,\;\;\overline{Q}_{y}^{NL} = Q_{y}^{NL} - 3c_{1} R_{y}^{NL} - c_{1} \left( {P_{xy,x}^{NL} + P_{y,y}^{NL} } \right) \hfill \\ T_{x}^{NL} = \overline{Q}_{x}^{NL} + \left( {P_{x,x}^{NL} + P_{xy,y}^{NL} } \right),\;\;T_{y}^{NL} = \overline{Q}_{y}^{NL} + \left( {P_{xy,x}^{NL} + P_{y,y}^{NL} } \right) \hfill \\ \end{gathered} $$

(25)

By considering the nonlocal model (6), Eqs. (23) and (24) can be rewritten as:

$$ \begin{gathered} N_{x,x} + N_{xy,y} = \mathcal{L}\left( {\ddot{\mathcal{U}}} \right) \hfill \\ N_{xy,x} + N_{y,y} = \mathcal{L}\left( {\ddot{\mathcal{V}}} \right) \hfill \\ T_{x,x} + T_{y,y} + \mathcal{L}\left( \mathcal{N} \right) + \mathcal{L}\left( q \right) = \mathcal{L}\left( {\ddot{\mathcal{W}}} \right) \hfill \\ M_{x,x} + M_{xy,y} - \overline{Q}_{x} = \mathcal{L}\left( {\ddot{\mathcal{F}}_{x} } \right) \hfill \\ M_{xy,x} + M_{y,y} - \overline{Q}_{y} = \mathcal{L}\left( {\ddot{\mathcal{F}}_{y} } \right) \hfill \\ \end{gathered} $$

(26)

from which, by recalling the constitutive Eqs. (7), one has the first two equations in the form:

$$ \begin{gathered} A_{11} u,_{xx} + A_{66} u,_{yy} + \left( {A_{12} + A_{66} } \right)v,_{xy} + \overline{B}_{11} \varphi_{x,xx} + \overline{B}_{66} \varphi_{x,yy} + \left( {\overline{B}_{12} + \overline{B}_{66} } \right)\varphi_{y,xy} - \left( {\overline{C}_{11} w,_{xxx} + \left( {\overline{C}_{12} + 2\overline{C}_{66} } \right)w,_{xyy} } \right) = \mathcal{L}\left( {\ddot{\mathcal{U}}} \right) \hfill \\ A_{22} v,_{yy} + A_{66} v,_{xx} + \left( {A_{12} + A_{66} } \right)u,_{xy} + \overline{B}_{22} \varphi_{y,yy} + \overline{B}_{66} \varphi_{y,xx} + \left( {\overline{B}_{12} + \overline{B}_{66} } \right)\varphi_{x,xy} - \left( {\overline{C}_{22} w,_{yyy} + \left( {\overline{C}_{12} + 2\overline{C}_{66} } \right)w,_{xxy} } \right) = \mathcal{L}\left( {\ddot{\mathcal{V}}} \right) \hfill \\ \end{gathered} $$

(27)

and the others have rewritten as follows:

$$ \begin{gathered} \left( {\overline{C}_{11} u,_{x} + \overline{C}_{12} v,_{y} } \right),_{xx} + \left( {C_{12} u,_{x} + \overline{C}_{22} v,_{y} } \right)_{yy} + 2\overline{C}_{66} \left( {u,_{y} + v,_{x} } \right),_{xy} + \left( {\overline{F}_{11} \varphi_{x,x} + \overline{F}_{12} \varphi_{y,y} } \right),_{xx} + \left( {\overline{F}_{12} \varphi_{x,x} + \overline{F}_{22} \varphi_{y,y} } \right),_{yy} + \hfill \\ \;\;\; - \left( {\overline{H}_{11} w,_{xx} + \overline{H}_{12} w,_{yy} } \right),_{xx} - \left( {\overline{H}_{12} w,_{xx} + \overline{H}_{22} w,_{yy} } \right),_{yy} + 2\left( {\overline{F}_{66} \left( {\varphi_{x} ,_{y} + \varphi_{y} ,_{x} } \right) - 2\overline{H}_{66} w,_{xy} } \right),_{xy} + \overline{A}_{55} \left( {w,_{x} + \varphi_{x} } \right),_{x} \hfill \\ \;\;\; + \overline{A}_{44} \left( {w,_{y} + \varphi_{y} } \right),_{y} = - \mathcal{L}\left( \mathcal{N} \right) - \mathcal{L}\left( q \right) + \mathcal{L}\left( {\ddot{\mathcal{W}}} \right) \hfill \\ \;\;\overline{B}_{11} u,_{xx} + \overline{B}_{66} u,_{yy} + \left( {\overline{B}_{12} + \overline{B}_{66} } \right)v,_{xy} + \left( {\overline{D}_{11} \varphi_{x} ,_{x} + \overline{D}_{12} \varphi_{y} ,_{y} - \left( {\overline{F}_{11} w,_{xx} + \overline{F}_{12} w,_{yy} } \right)} \right),_{x} \hfill \\ \;\; + \left( {\overline{D}_{66} \left( {\varphi_{x} ,_{y} + \varphi_{y} ,_{x} } \right) - 2\overline{F}_{66} w,_{xy} } \right),_{y} - \overline{A}_{55} \left( {w,_{x} + \varphi_{x} } \right) = \mathcal{L}\left( {\ddot{\mathcal{F}}_{x} } \right) \hfill \\ \;\;\;\overline{B}_{22} v,_{yy} + \overline{B}_{66} v,_{xx} + \left( {\overline{B}_{12} + \overline{B}_{66} } \right)u,_{xy} + \left( {\overline{D}_{12} \varphi_{x} ,_{x} + \overline{D}_{22} \varphi_{y} ,_{y} - \left( {\overline{F}_{12} w,_{xx} + \overline{F}_{22} w,_{yy} } \right)} \right),_{y} \hfill \\ \;\; + \left( {\overline{D}_{66} \left( {\varphi_{y} ,_{x} + \varphi_{x} ,_{y} } \right) - 2\overline{F}_{66} w,_{xy} } \right),_{x} - \overline{A}_{44} \left( {w,_{y} + \varphi_{y} } \right) = \mathcal{L}\left( {\ddot{\mathcal{F}}_{y} } \right) \hfill \\ \end{gathered} $$

(28)

where the coefficients are related to the plate stiffness properties as

$$ \begin{gathered} \left( {A_{ij} ,B_{ij} ,D_{ij} ,C_{ij} ,F_{ij} ,H_{ij} } \right) = \left( {\int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {Q_{ij} dz,} \;\;\int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {Q_{ij} z^{{}} dz,} \;\;\int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {Q_{ij} z^{2} dz,} \;\;\int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {Q_{ij} z^{3} dz,} \;\;\int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {Q_{ij} z^{4} dz,} \;\;\int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {Q_{ij} z^{6} dz,} } \right) \hfill \\ \left( {\overline{A}_{ij} ,\overline{B}_{ij} ,\overline{C}_{ij} ,\overline{D}_{ij} ,\overline{F}_{ij} ,\overline{H}_{ij} } \right) = \left( {A_{ij} - 3c_{1} \left( {2D_{ij} - 3c_{1} F_{ij} } \right),B_{ij} - c_{1} C_{ij} ,c_{1} C_{ij} ,D_{ij} - c_{1} \left( {2F_{ij} - c_{1} H_{ij} } \right),c_{1} \left( {F_{ij} - c_{1} H_{ij} } \right),c_{1}^{2} H_{ij} } \right) \hfill \\ \end{gathered} $$

(29)

the in-plane and out-of-plane Reddy stress being given by

$$ {\mathbf{N}} = \left[ \begin{gathered} N_{x} \hfill \\ N_{y} \hfill \\ N_{xy} \hfill \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}c} {A_{11} } & {A_{12} } & 0 \\ {} & {A_{22} } & 0 \\ {sym} & {} & {A_{66} } \\ \end{array} } \right]\left[ \begin{gathered} u,_{x} \hfill \\ v,_{y} \hfill \\ u,_{y} + v,_{x} \hfill \\ \end{gathered} \right] + \left[ {\begin{array}{*{20}c} {\overline{B}_{11} } & {\overline{B}_{12} } & 0 \\ {} & {\overline{B}_{22} } & 0 \\ {sym} & {} & {\overline{B}_{66} } \\ \end{array} } \right]\left[ \begin{gathered} \varphi_{x,x} \hfill \\ \varphi_{y,y} \hfill \\ \varphi_{x,y} + \varphi_{y,x} \hfill \\ \end{gathered} \right] - \left[ {\begin{array}{*{20}c} {\overline{C}_{11} } & {\overline{C}_{12} } & 0 \\ {} & {\overline{C}_{22} } & 0 \\ {sym} & {} & {\overline{C}_{66} } \\ \end{array} } \right]\left[ \begin{gathered} w,_{xx} \hfill \\ w,_{yy} \hfill \\ 2w,_{xy} \hfill \\ \end{gathered} \right] $$

(30)

and

$$ \begin{gathered} {\mathbf{M}} = \left[ \begin{gathered} M_{x} \hfill \\ M_{y} \hfill \\ M_{xy} \hfill \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}c} {\overline{D}_{11} } & {\overline{D}_{12} } & 0 \\ {} & {\overline{D}_{22} } & 0 \\ {sym} & {} & {\overline{D}_{66} } \\ \end{array} } \right]\left[ \begin{gathered} \varphi_{x,x} \hfill \\ \varphi_{y,y} \hfill \\ \varphi_{x,y} + \varphi_{y,x} \hfill \\ \end{gathered} \right] - \left[ {\begin{array}{*{20}c} {\overline{F}_{11} } & {\overline{F}_{12} } & 0 \\ {} & {\overline{F}_{22} } & 0 \\ {sym} & {} & {\overline{F}_{66} } \\ \end{array} } \right]\left[ \begin{gathered} w,_{xx} \hfill \\ w,_{yy} \hfill \\ 2w,_{xy} \hfill \\ \end{gathered} \right] + \left[ {\begin{array}{*{20}c} {\overline{B}_{11} } & {\overline{B}_{12} } & 0 \\ {} & {\overline{B}_{22} } & 0 \\ {sym} & {} & {\overline{B}_{66} } \\ \end{array} } \right]\left[ \begin{gathered} u,_{x} \hfill \\ v,_{y} \hfill \\ u,_{y} + v,_{x} \hfill \\ \end{gathered} \right]\,\,\, \hfill \\ {\mathbf{P}} = \left[ \begin{gathered} P_{x} \hfill \\ P_{y} \hfill \\ P_{xy} \hfill \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}c} {\overline{F}_{11} } & {\overline{F}_{12} } & 0 \\ {} & {\overline{F}_{22} } & 0 \\ {sym} & {} & {\overline{F}_{66} } \\ \end{array} } \right]\left[ \begin{gathered} \varphi_{x,x} \hfill \\ \varphi_{y,y} \hfill \\ \varphi_{x,y} + \varphi_{y,x} \hfill \\ \end{gathered} \right] - \left[ {\begin{array}{*{20}c} {\overline{H}_{11} } & {\overline{H}_{12} } & 0 \\ {} & {\overline{H}_{22} } & 0 \\ {sym} & {} & {\overline{H}_{66} } \\ \end{array} } \right]\left[ \begin{gathered} w,_{xx} \hfill \\ w,_{xy} \hfill \\ 2w,_{yx} \hfill \\ \end{gathered} \right] - \left[ {\begin{array}{*{20}c} {\overline{C}_{11} } & {\overline{C}_{12} } & 0 \\ {} & {\overline{C}_{22} } & 0 \\ {sym} & {} & {\overline{C}_{66} } \\ \end{array} } \right]\left[ \begin{gathered} u,_{x} \hfill \\ v,_{y} \hfill \\ u,_{y} + v,_{x} \hfill \\ \end{gathered} \right] \hfill \\ \hfill \\ {\mathbf{Q}} = \left[ \begin{gathered} Q_{x} \hfill \\ Q_{y} \hfill \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}c} {\overline{A}_{55} } & 0 \\ 0 & {\overline{A}_{44} } \\ \end{array} } \right]\left[ \begin{gathered} \left( {w,_{x} + \varphi_{x} } \right) \hfill \\ \left( {w,_{y} + \varphi_{y} } \right) \hfill \\ \end{gathered} \right]. \hfill \\ \end{gathered} $$

(31)

4 Explicit solutions and computational approach

In the present study, we assume harmonic motion and simply supported conditions at $x = \pm \,{a \mathord{\left/ {\vphantom {a 2}} \right. \kern-\nulldelimiterspace} 2}$:

$$ \begin{array}{*{20}l} {u\left( {x,y,t} \right) = \overline{u}\left( y \right)\sin \left( {\lambda_{m} x} \right)e^{i\omega t} } \hfill \\ {v\left( {x,y,t} \right) = \overline{v}\left( y \right)\cos \left( {\lambda_{m} x} \right)e^{i\omega t} } \hfill \\ {w\left( {x,y,t} \right) = \overline{w}\left( y \right)\cos \left( {\lambda_{m} x} \right)e^{i\omega t} } \hfill \\ {\varphi_{x} \left( {x,y,t} \right) = \overline{\varphi }_{x} \left( y \right)\sin \left( {\lambda_{m} x} \right)e^{i\omega t} } \hfill \\ {\varphi_{y} \left( {x,y,t} \right) = \overline{\varphi }_{y} \left( y \right)\cos \left( {\lambda_{m} x} \right)e^{i\omega t} } \hfill \\ \end{array} \,\,\,\,\,\,\,\,\,\,\,\lambda_{m} = m\pi a^{ - 1} $$

(32)

in this way automatically satisfying the boundary conditions

$$ v = N_{xy} = w = M_{x} = P_{x} = 0\,\,\,\,\,\,\,\,\,\,\,\,at\,\,\,\,\,x = \pm \frac{a}{2},\;\;t = 0 $$

(33)

By substituting Eqs. (32) in (27) and (28) we obtain the following system of five one-dimensional linear and homogeneous fourth-order differential equations, split as

$$ \begin{gathered} a_{11} \overline{w},_{yy} + a_{12} \overline{w} + a_{13} \overline{\varphi }_{x,yy} + a_{14} \overline{\varphi }_{x} + a_{15} \overline{\varphi }_{y,y} + b_{11} \overline{v},_{y} + b_{12} \overline{u},_{yy} + b_{13} \overline{u} = 0 \hfill \\ a_{21} \overline{w},_{yyy} + a_{22} \overline{w},_{y} + a_{23} \overline{\varphi }_{x,y} + a_{24} \overline{\varphi }_{y,yy} + a_{25} \overline{\varphi }_{y} + b_{21} \overline{v},_{yy} + b_{22} \overline{v} + b_{23} \overline{u},_{y} = 0 \hfill \\ \end{gathered} $$

(34)

and

$$ \begin{gathered} a_{31} \overline{w},_{yyyy} + a_{32} \overline{w},_{yy} + a_{33} \overline{w} + a_{34} \overline{\varphi }_{x,yy} + a_{35} \overline{\varphi }_{x} + a_{36} \overline{\varphi }_{y,yyy} + a_{37} \overline{\varphi }_{y,y} + b_{31} \overline{v},_{yyy} + b_{32} \overline{v},_{y} + b_{33} \overline{u},_{yy} + b_{34} \overline{u} \hfill \\ a_{41} \overline{w},_{yy} + a_{42} \overline{w} + a_{43} \overline{\varphi }_{x,yy} + a_{44} \overline{\varphi }_{x} + a_{45} \overline{\varphi }_{y,y} + b_{41} \overline{v},_{y} + b_{42} \overline{u},_{yy} + b_{43} \overline{u} = 0 \hfill \\ a_{51} \overline{w},_{yyy} + a_{52} \overline{w},_{y} + a_{53} \overline{\varphi }_{x,y} + a_{54} \overline{\varphi }_{y,yy} + a_{55} \overline{\varphi }_{y} + b_{51} \overline{v},_{yy} + b_{52} \overline{v} + b_{53} \overline{u},_{y} = 0 \hfill \\ \end{gathered} $$

(35)

where the functions $\left( {\overline{u}\left( y \right),\overline{v}\left( y \right),\overline{w}\left( y \right),\overline{\varphi }_{x} \left( y \right),\overline{\varphi }_{y} \left( y \right)} \right)$ represent the unknowns of the problem and $a_{ij} = a_{ij} \left( {N_{x} ,N_{y} ,\omega } \right)$ are real-valued coefficients explicitly reported in the Appendix.

After some algebraic manipulations, Eqs. (34) and (35) can be collected and written in the compact form

$$ \partial {\mathbf{U}} = {\mathbf{A}} \cdot {\mathbf{U}} $$

(36)

where

$$ \begin{gathered} \partial {\mathbf{U}} = \left[ {\overline{w},_{yyyy} \,\,\,\,\,\overline{w},_{yyy} \,\,\,\,\,\overline{w},_{yy} \,\,\,\,\overline{w},_{y} \,\,\,\,\,\overline{\varphi }_{x,yy} \,\,\,\,\,\overline{\varphi }_{x,y} \,\,\,\,\,\overline{\varphi }_{y,yy} \,\,\,\,\,\overline{\varphi }_{y,y} \,\,\,\,\,\overline{u},_{yy} \,\,\,\,\overline{u},_{y} \,\,\,\,\,\overline{v},_{yy} \,\,\,\,\,\overline{v},_{y} } \right]^{T} \hfill \\ {\mathbf{U}}\,\,\,\,\, = \left[ {\overline{w},_{yyy} \,\,\,\,\,\,\,\overline{w},_{yy} \,\,\,\,\,\,\,\overline{w},_{y} \,\,\,\,\,\overline{w}\,\,\,\,\,\,\,\,\overline{\varphi }_{x,y} \,\,\,\,\,\,\,\overline{\varphi }_{x} \,\,\,\,\,\,\,\,\overline{\varphi }_{y,y} \,\,\,\,\,\,\,\overline{\varphi }_{y} \,\,\,\,\,\,\overline{u},_{y} \,\,\,\,\,\,\overline{u}\,\,\,\,\,\,\,\,\,\overline{v},_{y} \,\,\,\,\,\,\overline{v}\,\,\,\,} \right]^{T} \hfill \\ \end{gathered} $$

(37)

are vectors containing the generalized displacements, and A is a matrix whose coefficients are explicitly reported in Appendix. As a consequence, the general solution of Eq. (36) is

$$ {\mathbf{U}} = \left( {{{\varvec{\upalpha}}} \cdot e^{{{{\varvec{\uprho}}} \cdot y}} \cdot {{\varvec{\upalpha}}}^{ - 1} } \right){\mathbf{c}} $$

(38)

depending on eigenvalues and eigenvectors of the matrix coefficients in A, collected in $\left( {{{\varvec{\uprho}}},{{\varvec{\upalpha}}}} \right)$, c being a $12 \times 1$ constant vector whose values have to be determined by imposing proper boundary conditions. In Eqn. (38) ${{\varvec{\upalpha}}}$ indicates a nonsingular linear transformation matrix containing the generalized eigenvectors of ${\mathbf{A}}$, ${\mathbf{A}}^{ - 1}$ the corresponding inverse matrix and ${{\varvec{\uprho}}} = {\mathbf{H}}^{ - 1} {\mathbf{AH}}$ is the Jordan normal form for the given matrix ${\mathbf{A}}$. In order to finalize the process in a Matlab code, both $\left( {{{\varvec{\uprho}}},{{\varvec{\upalpha}}}} \right)$ matrices has been obtained numerically.

Finally, by collecting the nodal displacement ${\mathbf{w}}_{N}$ and the corresponding dual forces ${\mathbf{q}}_{N}$, evaluated on the boundary points $\left( {A,B} \right)$ of coordinates $y = \pm b/2$, as:

$$ \begin{gathered} {\mathbf{w}}_{N} = \left[ {\bar{u}^{A} \,\,\,\,\bar{v}^{A} \,\,\,\bar{u}^{B} \,\,\,\,\bar{v}^{B} \,\,\,\,\,\,\bar{\varphi }_{y}^{A} \,\,\,\,\bar{\varphi }_{x}^{A} \,\,\,\bar{w},_{y}^{A} \,\,\,\,\bar{w}^{A} \,\,\,\,\bar{\varphi }_{y}^{B} \,\,\,\,\bar{\varphi }_{x}^{B} \,\,\,\bar{w},_{y}^{B} \,\,\,\,\bar{w}^{B} } \right]^{T} \hfill \\ {\mathbf{q}}_{N} = \left[ {\bar{N}_{{xy}}^{A} \,\,\,\,\,\bar{N}_{y}^{A} \,\,\,\,\bar{N}_{{xy}}^{B} \,\,\,\,\,\bar{N}_{y}^{B} \,\,\,\,\,\bar{M}_{y}^{A} \,\,\,\,\,\bar{M}_{{xy}}^{A} \,\,\,\,\bar{P}_{y}^{A} \,\,\,\,\,\bar{T}_{y}^{A} + \bar{P}_{{xy,x}}^{A} \,\,\,\,\,\bar{M}_{y}^{B} \,\,\,\,\,\bar{M}_{{xy}}^{B} \,\,\,\,\bar{P}_{y}^{B} \,\,\,\,\,\bar{T}_{y}^{B} + \bar{P}_{{xy,x}}^{B} } \right]^{T} \hfill \\ \end{gathered} $$

(39)

it is possible to derive, for any plate characterizing the investigated structure, a local stiffness matrix ${\mathbf{k}}_{loc}$ and, with a proper matrix rotation ${{\varvec{\uptheta}}}$, the global stiffness matrix ${\mathbf{k}}_{glob}$, thus obtaining:

$$ {\mathbf{k}}_{loc} = {\mathbf{q}}_{N} \cdot {\mathbf{w}}_{N}^{ - 1} ,\quad \quad {\mathbf{k}}_{glob} = {{\varvec{\uptheta}}}^{T} {\mathbf{k}}_{loc} {{\varvec{\uptheta}}} $$

(40)

Because ${\mathbf{w}}_{N}^{ - 1}$ is a $12 \times 12$ non-singular square matrix, the inverse can be easily obtained.

Finally, adopting as shape functions the displacement field represented in Eq. (32), a standard finite strip assembly procedure provides the stiffness matrix ${\mathbf{K}}$ of the whole structure, whose eigenvalues and eigenvectors, obtained with a trial and error approach, represent respectively the critical buckling loads—or, equivalently, the frequencies of oscillations—and the corresponding shape modes, the analytical nature of the adopted shape functions also ensuring reliable results with the minimum number of elements.

5 Numerical results and discussion

In the following examples, unless otherwise stated, it is assumed that the nanoplate is characterized by the material properties listed in Table 1 and a length $a = 10\;\;{\mu m}$.

Capital letters F, S, G, C indicate respectively free, simply supported, guided and clamped boundary conditions, so that, for instance, SCSF stays for a plate simply supported at $x = \pm a/2$, clamped at $y = b/2$ and free at $y = - b/2$.

For convenience, the results are represented in terms of the following dimensionless frequency parameter and buckling load

$$ \overline{\omega } = \omega h\sqrt {\frac{{\rho_{c} }}{{G_{c} }}} ,\,\quad \,\overline{N} = \frac{{N_{cr} a^{2} }}{{\pi^{2} D_{c} }} $$

(41)

and expressed in terms of the ceramic in-plane and bending stiffness

$$ G_{c} = \frac{{E_{c} }}{{2\left( {1 + \nu } \right)}},\quad D_{c} = \frac{{E_{c} h^{3} }}{{12\left( {1 - \nu^{2} } \right)}} $$

(42)

Also, by indicating with $\overline{\omega }^{L}$ and $\overline{N}^{L}$ the local values obtained by posing $\mu = 0$, the frequency and buckling ratios

$$ \Omega = \frac{{\overline{\omega }}}{{\overline{\omega }^{L} }},\quad \,\eta = \frac{{\overline{N}}}{{\overline{N}^{L} }} $$

(43)

are evaluated and compared with their counterparts available in the literature.

5.1 Benchmarks and comparative analyses

In order to assess the accuracy and robustness of the proposed approach, natural frequencies and buckling loads were numerically evaluated and compared with those obtained in the literature [9, 25] for local and nonlocal isotropic plate models, with or without elastic foundation. Besides, the analytical solutions for Reddy nano-plates with all the edges simply supported reported in [11], here enriched with the new terms due to the presence of Winkler-Pasternak foundation, were used as a benchmark for sensitivity analyses.

Table 2 shows the dimensionless mode frequency $\overline{\omega }$ of a SSSS square plate, compared with those reported by Aghababaey and Reddy [9] assuming a sinusoidal displacement field in both x and y directions. The results are in excellent agreement for any nonlocal parameter $\mu$ and geometrical ratios $\left( {a/b,\,a/h} \right)$ considered, with low discrepancies ranging between $0.02$ and $0.5\%$.

Table 2 Non-dimensional first mode frequency of SSSS plate

The first three dimensionless fundamental natural frequencies, obtained for different numbers of half-waves m in x-direction, are reported in Table 3 for rectangular plates with four different boundary conditions (namely SCSC, SCSS, SCSF and SSSF plates) and compared with those obtained in [25] by Hosseini et al.

Table 3 Non-dimensional higher mode frequencies of plates with different boundary conditions

The results show that, by increasing the nonlocal parameter, the reduction of the frequency ratios is more pronounced for higher frequencies. For instance, the range $0.7315 \le \Omega_{{\left( {1,1} \right)}} \le 0.3356$ of the first frequency obtained for SCSC plates by considering $0.6 \le \sqrt \mu /a \le 0.2$, becomes $0.4479 \le \Omega_{{\left( {3,1} \right)}} \le 0.1647$ for the highest frequency considered, with a reduction of about 85% if compared with the corresponding value of the local model, an analogous behavior being observed for the other considered boundary conditions.

Table 4 represents a comparison of the critical buckling load ratios with those obtained by Hosseini et al. [25] for square nanoplates with different values of the length a and of the nonlocal parameter $\mu$, the agreement among the results being very good indeed, with percentage differences always lower than $0.2\%$.

Table 4 Non-dimensional critical buckling load and buckling load ratio of SSSS nanoplates

Finally, Table 5 compares the dimensionless buckling load $\eta$ for a FGM nanoplate achieved with the proposed procedure with the one derived for a simply supported plate by employing the Navier approach, that is by considering, instead of the more general displacement field reported in Eq. (32), the following one:

$$ \begin{array}{*{20}l} {u\left( {x,y,t} \right) = U_{pm} \cos \left( {\lambda_{p} y} \right)\sin \left( {\lambda_{m} x} \right)e^{i\omega t} } \hfill \\ {v\left( {x,y,t} \right) = V_{pm} \sin \left( {\lambda_{p} y} \right)\cos \left( {\lambda_{m} x} \right)e^{i\omega t} } \hfill \\ {w\left( {x,y,t} \right) = W_{pm} \cos \left( {\lambda_{p} y} \right)\cos \left( {\lambda_{m} x} \right)e^{i\omega t} } \hfill \\ {\varphi_{x} \left( {x,y,t} \right) = X_{pm} \left( {\cos \lambda_{p} y} \right)\sin \left( {\lambda_{m} x} \right)e^{i\omega t} } \hfill \\ {\varphi_{y} \left( {x,y,t} \right) = Y_{pm} \left( {\sin \lambda_{p} y} \right)\cos \left( {\lambda_{m} x} \right)e^{i\omega t} } \hfill \\ \end{array} $$

(44)

Table 5 Non-dimensional buckling load η for a SSSS nanoplate on a Pasternak-Winkler foundation

with $\lambda_{m} = m\pi a^{ - 1} ,\;\;\lambda_{p} = p\pi b^{ - 1}$. By substituting Eqs. (44) into (27) and (28), and solving the corresponding eigenvalue problem, the required critical load for different half-waves (m,p) in x- and y- direction is finally obtained.

Furthermore, the results obtained for different values of the power-law parameter n and the nonlocal parameter $\mu$ are still in excellent agreement, with percentage differences never greater than 2% and Levy-type results always slightly higher than Navier ones. It is worth to highlight that a stringent proof of the robustness and accuracy of the proposed model for thick nonlocal FGM nanoplates should be made by comparing results with outcomes from numerical codes implementing nonlocal three-dimensional elasticity. However, in absence of commercial software dealing with these nonlocal model, the authors assumed that an enrichment of the kinematical description of the field of interest across the thickness can lead to improved results.

5.2 Parametric analyses on functionally graded plates

The analyses are performed on the curved nano-beam represented in Fig. 3 for different boundary conditions and values of both geometrical ratio $\overline{h} = h/t$ and nonlocal parameter $\mu$.

Fig. 3

Parametric example: geometry and applied loads

Figure 4 shows the influence of $\left( {\overline{h},\mu } \right)$ on the critical load of a SSSS, FGM nanoplate with dimensions $a \times a$, $t = 0.1a$ and power-law coefficient $n = 2$, highlighting the beneficial effects of increasing curvatures on the buckling behavior of simply supported structures.

Fig. 4

Dimensionless critical load for different value of geometrical and nonlocal parameter on SSSS microplate

Also, it is worth noting that for local plates (i.e. $\mu = 0$) the critical load increases with $\overline{h}$ up to $\eta = 1.8$ when $h = t$, essentially doubling the critical load obtained for a flat plate. However, such effects decrease by increasing the nonlocal parameter $\mu = 0$, giving $\eta = 0.65$ with $\left( {\mu = 2,\overline{h} = 0} \right)$ and $\eta = 0.71$ for $\left( {\mu = 2,\overline{h} = 1} \right)$.

A different behavior can be instead observed by varying the boundary conditions, as illustrated in Fig. 5, where the results obtained for a SFSF plate exhibit a reduced dependence on the nonlocal parameter and a constant growth of $\eta$ with $\overline{h}$.

Fig. 5

Dimensionless critical load for different value of geometrical and nonlocal parameter on SFSF microplate

6 Conclusions

In the present study, buckling and vibration of thick FGM nano-plates embedded in elastic Winkler-Pasternak media were studied. To take into account size effects typically encountered when dealing with the mechanical behavior of structures at the nanoscale, the governing equations of the problem were written by incorporating the nonlocal theory of elasticity by Eringen, also employing the third-order Reddy plate model in order to gain accuracy and faithfully describe stress fields, shear deformation regimes, buckling and vibrations of nanoplates and cylindrical nano-shells with varying elastic properties along their thickness. In this framework, some explicit analytical solutions were given for simple geometry and selected boundary conditions. Levy-type method and numerical procedures, ad hoc rewrote to include the above-mentioned modeling features, were employed to determine buckling and vibrations of nano-structure. Finally, a number of sensitivity analyses on flat and curved FGM systems under different boundary conditions to assess the robustness and effectiveness of the proposed approach were proposed. As in detail shown in Sect. 5Numerical results and discussion, the presence of scale effects at the nanoscale, combined with possible variations of the material properties along with the thickness of two-dimensional structures, can influence—in some cases also significantly—their mechanical response, with significant qualitative and quantitative effects on both the elastic stability and the dynamics of nanoplates eventually interacting with elastic substrates.

Appendix

The coefficients occurring in Eqs. (34) and (35) are:

$$ \begin{gathered} a_{31} = \left( {\overline{H}_{22} - \mu \left( {K_{s} - N_{y} + c_{1}^{2} m_{6} \omega^{2} } \right)} \right) \hfill \\ a_{32} = - \left( {\lambda_{m}^{2} \left( {2\left( {\overline{H}_{12} + 2\overline{H}_{66} } \right)} \right) + \overline{A}_{44} + N_{x} + \left( {1 + \mu } \right)N_{y} - K_{s} \left( {1 + 2\lambda_{m}^{2} \mu } \right) - \mu K_{w} - \omega^{2} \left( {\mu m_{0} + c_{1}^{2} m_{6} \left( {1 + \lambda_{m}^{2} \mu } \right)} \right)} \right) \hfill \\ a_{33} = \left( {\lambda_{m}^{2} \left( {\lambda_{m}^{2} \left( {\overline{H}_{11} + \mu N_{x} } \right) + N_{x} + \overline{A}_{55} - K_{s} \left( {1 + \lambda_{m}^{2} } \right)} \right) - K_{w} \left( {1 + \lambda_{m}^{2} } \right) - \left( {1 + \lambda_{m}^{2} \mu } \right)\left( {m_{0} + c_{1}^{2} \lambda_{m}^{2} m_{6} } \right)} \right) \hfill \\ a_{34} = - \lambda_{m} \left( {\overline{F}_{12} + 2\overline{F}_{66} - c_{1} \overline{m}_{4} \omega^{2} \mu } \right) \hfill \\ a_{35} = \lambda_{m} \left( {\lambda_{m}^{2} \overline{F}_{11} - \overline{A}_{55} - c_{1} \overline{m}_{4} \omega^{2} \left( {1 + \lambda_{m}^{2} } \right)} \right) \hfill \\ a_{36} = - \left( {\overline{F}_{22} - c_{1} \overline{m}_{4} \omega^{2} \mu } \right) \hfill \\ a_{37} = \left( {\lambda_{m}^{2} \left( {\overline{F}_{12} + 2\overline{F}_{66} } \right) - \overline{A}_{44} - c_{1} \overline{m}_{4} \omega^{2} \left( {1 + \lambda_{m}^{2} } \right)} \right) \hfill \\ b_{31} = - \overline{C}_{22} \hfill \\ b_{32} = \left( {\lambda_{m}^{2} \left( {\overline{C}_{12} + 2\overline{C}_{66} } \right) - c_{1} m_{3} \omega^{2} \left( {1 + \lambda_{m}^{2} \mu } \right)} \right) \hfill \\ b_{33} = - \lambda_{m} \left( {\overline{C}_{12} + 2\overline{C}_{66} - c_{1} m_{3} \omega^{2} \mu } \right) \hfill \\ a_{34} = \lambda_{m} \left( {\lambda_{m}^{2} \overline{C}_{11} - c_{1} m_{3} \omega^{2} \left( {1 + \lambda_{m}^{2} \mu } \right)} \right) \hfill \\ a_{41} = \lambda_{m} \left( {\overline{F}_{12} + 2\overline{F}_{66} - c_{1} m_{4} \omega^{2} \mu } \right) \hfill \\ a_{42} = - \lambda_{m} \left( {\lambda_{m}^{2} \overline{F}_{11} - \overline{A}_{55} - c_{1} m_{4} \omega^{2} \left( {1 + \lambda_{m}^{2} \mu } \right)} \right) \hfill \\ a_{43} = \left( {\overline{D}_{66} - \tilde{m}\omega^{2} \mu } \right) \hfill \\ a_{44} = - \left( {\lambda_{m}^{2} \overline{D}_{11} + \overline{A}_{55} - \tilde{m}\omega^{2} \left( {1 + \lambda_{m}^{2} \mu } \right)} \right) \hfill \\ a_{45} = - \lambda_{m} \left( {\overline{D}_{12} + \overline{D}_{66} } \right) \hfill \\ b_{41} = - \lambda_{m} \left( {\overline{B}_{12} + \overline{B}_{66} } \right) \hfill \\ b_{42} = \left( {\overline{B}_{66} - \overline{m}_{1} \omega^{2} \mu } \right) \hfill \\ b_{43} = - \left( {\lambda_{m}^{2} \overline{B}_{11} - \overline{m}_{1} \omega^{2} \left( {1 + \lambda_{m}^{2} \mu } \right)} \right) \hfill \\ a_{51} = \left( {\overline{F}_{22} - c_{1} m_{4} \omega^{2} \mu } \right) \hfill \\ a_{52} = - \left( {\lambda_{m}^{2} \left( {\overline{F}_{12} + 2\overline{F}_{66} } \right) - \overline{A}_{44} - c_{1} m_{4} \omega^{2} \left( {1 + \lambda_{m}^{2} \mu } \right)} \right) \hfill \\ a_{53} = - \lambda_{m} \left( {\overline{D}_{12} + \overline{D}_{66} } \right) \hfill \\ a_{54} = - \left( {\overline{D}_{22} - \tilde{m}\omega^{2} \mu } \right) \hfill \\ a_{55} = \left( {\lambda_{m}^{2} \overline{D}_{66} + \overline{A}_{44} - \tilde{m}\omega^{2} \left( {1 + \lambda_{m}^{2} \mu } \right)} \right) \hfill \\ b_{51} = - \left( {\overline{B}_{22} - \overline{m}_{1} \omega^{2} \mu } \right) \hfill \\ b_{52} = \left( {\lambda_{m}^{2} \overline{B}_{66} - \overline{m}_{1} \omega^{2} \left( {1 + \lambda_{m}^{2} \mu } \right)} \right) \hfill \\ b_{53} = - \lambda_{m} \left( {\overline{B}_{12} + \overline{B}_{66} } \right) \hfill \\ \end{gathered} $$

(45)

In the present form the system of Eqs. (34), (35) does not admit a closed form solution. It does if rewritten as:

$$ \begin{gathered} u,_{yy} - \overline{a}_{11} \overline{u},_{y} - \overline{a}_{12} \overline{u} - \overline{a}_{13} \overline{v},_{y} - \overline{a}_{14} \overline{v} - \overline{b}_{11} \overline{w},_{yyy} - \overline{b}_{12} \overline{w},_{yy} - \overline{b}_{13} \overline{w},_{y} - \overline{b}_{14} \overline{w} - \overline{b}_{15} \overline{\varphi }_{x,y} - \overline{b}_{16} \overline{\varphi }_{x} - \overline{b}_{17} \overline{\varphi }_{y,y} - \overline{b}_{18} \overline{\varphi }_{y} = 0 \hfill \\ v,_{yy} - \overline{a}_{21} \overline{u},_{y} - \overline{a}_{22} \overline{u} - \overline{a}_{23} \overline{v},_{y} - \overline{a}_{24} \overline{v} - \overline{b}_{21} \overline{w},_{yyy} - \overline{b}_{22} \overline{w},_{yy} - \overline{b}_{23} \overline{w},_{y} - \overline{b}_{24} \overline{w} - \overline{b}_{25} \overline{\varphi }_{x,y} - \overline{b}_{26} \overline{\varphi }_{x} - \overline{b}_{27} \overline{\varphi }_{y,y} - \overline{b}_{28} \overline{\varphi }_{y} = 0 \hfill \\ w,_{yyyy} - \overline{a}_{31} \overline{u},_{y} - \overline{a}_{32} \overline{u} - \overline{a}_{33} \overline{v},_{y} - \overline{a}_{34} \overline{v} - \overline{b}_{31} \overline{w},_{yyy} - \overline{b}_{32} \overline{w},_{yy} - \overline{b}_{33} \overline{w},_{y} - \overline{b}_{34} \overline{w} - \overline{b}_{35} \overline{\varphi }_{x,y} - \overline{b}_{36} \overline{\varphi }_{x} - \overline{b}_{37} \overline{\varphi }_{y,y} - \overline{b}_{38} \overline{\varphi }_{y} = 0 \hfill \\ \overline{\varphi }_{x} ,_{yy} - \overline{a}_{41} \overline{u},_{y} - \overline{a}_{42} \overline{u} - \overline{a}_{43} \overline{v},_{y} - \overline{a}_{44} \overline{v} - \overline{b}_{41} \overline{w},_{yyy} - \overline{b}_{42} \overline{w},_{yy} - \overline{b}_{43} \overline{w},_{y} - \overline{b}_{44} \overline{w} - \overline{b}_{45} \overline{\varphi }_{x,y} - \overline{b}_{46} \overline{\varphi }_{x} - \overline{b}_{47} \overline{\varphi }_{y,y} - \overline{b}_{48} \overline{\varphi }_{y} = 0 \hfill \\ \overline{\varphi }_{y} ,_{yy} - \overline{a}_{51} \overline{u},_{y} - \overline{a}_{52} \overline{u} - \overline{a}_{53} \overline{v},_{y} - \overline{a}_{54} \overline{v} - \overline{b}_{51} \overline{w},_{yyy} - \overline{b}_{52} \overline{w},_{yy} - \overline{b}_{53} \overline{w},_{y} - \overline{b}_{54} \overline{w} - \overline{b}_{55} \overline{\varphi }_{x,y} - \overline{b}_{56} \overline{\varphi }_{x} - \overline{b}_{57} \overline{\varphi }_{y,y} - \overline{b}_{58} \overline{\varphi }_{y} = 0 \hfill \\ \end{gathered} $$

(46)

that requires a reformulation of the Eq. (34) for the presence of $\overline{\varphi }_{x,yy}$ and $\overline{\varphi }_{y,yy}$, and of Eq. (35) for the presence of $\overline{v},_{yyy} ,\overline{v},_{yy} ,\overline{u}_{yy} ,\overline{\varphi }_{x,yy} ,\overline{\varphi }_{y,yyy}$.

By solving Eqs. (33) and (34₍₂₎, 34₍₃₎) we obtain:

$$ \begin{gathered} \overline{\varphi }_{x,yy} = A_{11} \overline{w},_{yy} + A_{12} \overline{w} + A_{14} \overline{\varphi }_{x} + A_{15} \overline{\varphi }_{y,y} + B_{11} \overline{v},_{y} + A_{17} \overline{u} \hfill \\ \overline{u},_{yy} = A_{41} \overline{w},_{yy} + A_{42} \overline{w} + A_{43} \overline{\varphi }_{x} + A_{45} \overline{\varphi }_{y,y} + B_{41} \overline{v},_{y} + B_{42} \overline{u} \hfill \\ \overline{\varphi }_{y,yy} = A_{21} \overline{w},_{yyy} + A_{22} \overline{w},_{y} + A_{23} \overline{\varphi }_{x,y} + A_{24} \overline{\varphi }_{y} + A_{25} \overline{v} + A_{26} \overline{u},_{y} \hfill \\ \overline{v},_{yy} = A_{51} \overline{w},_{yyy} + A_{52} \overline{w},_{y} + A_{53} \overline{\varphi }_{x,y} + A_{54} \overline{\varphi }_{y} + A_{55} \overline{v} + A_{56} \overline{u},_{y} \hfill \\ \end{gathered} $$

(47)

So that Eqs. (33) and (34₍₂₎, 34₍₃₎) can be rewritten as:

$$ \begin{gathered} \overline{u},_{yy} - \tilde{A}_{11} \overline{w},_{yy} - \tilde{A}_{12} \overline{w} - \tilde{A}_{14} \overline{\varphi }_{x} - \tilde{A}_{15} \overline{\varphi }_{y,y} - \tilde{B}_{11} \overline{v},_{y} - \tilde{B}_{13} \overline{u} = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {\left( {\tilde{A}_{ij} ,\tilde{B}_{ij} } \right) = - \frac{{a_{ij} + a_{13} \left( {A_{ij} ,B_{ij} } \right)}}{{b_{12} }}} \right) \hfill \\ \hfill \\ \overline{v},_{yy} - \hat{A}_{21} \overline{w},_{yyy} - \hat{A}_{22} \overline{w},_{y} - \hat{A}_{23} \overline{\varphi }_{x,y} - \hat{A}_{25} \overline{\varphi }_{y} - \hat{B}_{22} \overline{v} - \hat{B}_{23} \overline{u},_{y} = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {\left( {\hat{A}_{ij} ,\hat{B}_{ij} } \right) = - \frac{{a_{ij} + a_{24} \left( {A_{ij} ,B_{ij} } \right)}}{{b_{21} }}} \right) \hfill \\ \hfill \\ \overline{\varphi }_{x,yy} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{41} \overline{w},_{yy} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{42} \overline{w} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{44} \overline{\varphi }_{x} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{45} \overline{\varphi }_{y,y} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{B}_{41} \overline{v},_{y} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{B}_{43} \overline{u} = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{ij} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{B}_{ij} } \right) = - \frac{{a_{ij} + b_{42} \left( {A_{ij} ,B_{ij} } \right)}}{{a_{43} }}} \right) \hfill \\ \overline{\varphi }_{y,yy} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A}_{51} \overline{w},_{yyy} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A}_{52} \overline{w},_{y} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A}_{53} \overline{\varphi }_{x,y} - a\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A}_{55} \overline{\varphi }_{y} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{B}_{52} \overline{v} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{B}_{53} \overline{u},_{y} = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A}_{ij} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{B}_{ij} } \right) = - \frac{{a_{ij} + b_{51} \left( {A_{ij} ,B_{ij} } \right)}}{{a_{54} }}} \right) \hfill \\ \end{gathered} $$

(48)

Equation (48) replace Eqs. (33) and (34₍₂₎, 34₍₃₎). By Eqs. (48₍₂₎, 48₍₄₎) it is possible to obtain a suitable form of $\overline{v},_{yyy}$ and $\overline{\varphi }_{y,yyy}$. Replacing such expressions in (34₍₁₎) returns a system in the desired form (46).