Abelian Integrals and Non-generic Turning Points

Abstract

In this paper we initiate the study of the Chebyshev property of Abelian integrals generated by a non-generic turning point in planar slow-fast systems. Such Abelian integrals generalize the Abelian integrals produced by a slow-fast Hopf point (or generic turning point), introduced in Dumortier et al. (Discrete Contin Dyn Syst Ser S 2(4):723–781, 2009), and play an important role in studying the number of limit cycles born from the non-generic turning point.

1 Introduction

In this work we are concerned with the study of the Abelian integrals

$$\begin{aligned} I_{j}(h)=\int _{\gamma _h}e^{-2n{\bar{y}}}{\bar{x}}^{2n+2j+1} d{\bar{y}}, \ n\in {\mathbb {N}}, \ j=-n,0,1,2\dots \end{aligned}$$

and with their derivatives

$$\begin{aligned} \frac{d}{dh}I_j(h)=-\frac{2n+2j+1}{4n^2}{\bar{I}}_{j}(h) \ \text { where } \ {\bar{I}}_{j}(h)=\int _{\gamma _h}{\bar{x}}^{2j+1}d{\bar{y}}. \end{aligned}$$

(1)

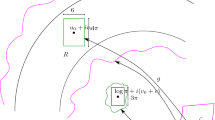
A proof of (1) is given in Sect. 2. Here $\gamma _h$, with $h\in ]0,1[$, denotes the oval surrounding the origin described by the level of energy $\{H({\bar{x}},{\bar{y}})=h\}$ where $H({\bar{x}},{\bar{y}})=2ne^{-2n{\bar{y}}}({\bar{y}}-{\bar{x}}^{2n}+\frac{1}{2n})$. We assume that the ovals are oriented clockwise. The boundary of the period annulus formed by $\{\gamma _h\}_{h\in ]0,1[}$ consists of the origin $({\bar{x}},{\bar{y}})=(0,0)$ and the curve ${\bar{y}}={\bar{x}}^{2n}-\frac{1}{2n}$ (see Fig. 1). They correspond to the level sets $h=1$ and $h=0$, respectively.

Fig. 1

The blow-up locus and indication of the period annulus formed by $\{\gamma _h\}_{h\in ]0,1[}$ and its boundary (see Sect. 3)

When $n=1$, the above Abelian integrals arise from a slow-fast Hopf point at the origin $(x,y)=(0,0)$ in slow-fast family of Liénard systems

$$\begin{aligned} \left( y-x^2+O(x^3)\right) \frac{\partial }{\partial x}+\epsilon ^2(\epsilon \alpha -x)\frac{\partial }{\partial y}, \end{aligned}$$

(2)

where $\epsilon \ge 0$ is a small singular perturbation parameter and $\alpha \sim 0$ is a regular parameter. This has been observed in [5] where the cyclicity of $(x,y)=(0,0)$ (i.e., the maximum number of limit cycles in an $(\epsilon ,\alpha )$-uniform neighborhood of $(x,y)=(0,0)$) in the Liénard family (2) has been studied using so-called family blow-up. If the Liénard family is analytic or $C^\infty$-smooth with finite codimension, then the cyclicity of the origin is finite (see [5, Theorem 7.3]). To find a good upper bound for the cyclicity, the following conjecture formulated in [5] has to be solved:

Conjecture Let $n=1$. For each $m\ge 0$, the functions $\bar{I}_j$ $j=-1,0,1,\dots ,m-1$, defined in (1), form an extended complete Chebyshev system on $[h_0,1]$ for any $h_0\in ]0,1[$.

Extended complete Chebyshev systems (shortly, ECT-systems) are defined in Sect. 2. For $m\le 2$, the conjecture is proved in [7] or [13]. The conjecture is also true near the center $h=1$, i.e. for each $m\ge 0$ there exists $\epsilon >0$ such that $({\bar{I}}_{-1},{\bar{I}}_0, \dots , {\bar{I}}_{m-1})$ is an ECT-system on $[1-\epsilon ,1]$ (see [7, Corollary 3.5]). Furthermore, in [14, Theorem A] it has been shown that for each $m\ge 0$ there exists $\epsilon >0$ such that $({\bar{I}}_{-1},{\bar{I}}_0, \dots , {\bar{I}}_{m-1})$ is an ECT-system on $]0,\epsilon ]$. The conjecture has been solved recently by Chengzhi Li and Changjian Liu in the paper [12].

The main purpose of this paper is to study the Chebyshev property of $({\bar{I}}_{-n},{\bar{I}}_0, {\bar{I}}_1, \dots , {\bar{I}}_{m-1})$, with $m=0,1,\dots$, on the interval ]0, 1[ for any fixed integer $n>1$. When $m=0$, the set of functions is only formed by ${\bar{I}}_{-n}.$ Our motivation is the following generalization of system (2):

$$\begin{aligned} \left( y-x^{2n}+O(x^{2n+1})\right) \frac{\partial }{\partial x}+\epsilon ^{2n}(\epsilon ^{2n-1}\alpha -x^{2n-1})\frac{\partial }{\partial y}, \end{aligned}$$

(3)

where $n>1$, $\epsilon \ge 0$ is the singular perturbation parameter and $\alpha \sim 0$. We say that slow-fast Liénard family (3) has a non-generic turning point at the origin $(x,y)=(0,0)$. Like in the generic case ($n=1$), to study the cyclicity of $(x,y)=(0,0)$ inside (3), one typically uses a family blow-up at $(x,y,\epsilon )=(0,0,0)$. After desingularization of (3) near the origin, one has to deal with the Chebyshev property of the integrals $({\bar{I}}_{-n},{\bar{I}}_0, {\bar{I}}_1, \dots , {\bar{I}}_{m-1})$. For more details about the connection between the non-generic turning point (3) and the Abelian integrals $({\bar{I}}_{-n},{\bar{I}}_0, {\bar{I}}_1, \dots , {\bar{I}}_{m-1})$, we refer the reader to Sect. 3.

Large canard limit cycles of (3), of size O(1) in the (x, y)-phase space, have been treated in [2]. As far as we know, the cyclicity of $(x,y)=(0,0)$ in (3) has not been studied. For the study of the cyclicity of some other slow-fast points, different from the Liénard systems (2) and (3), see e.g. [3, 8, 9, 11].

We stress that the goal of this paper is not to prove finite cyclicity of non-generic turning points, which is a result that needs further research to approach and it is beyond the scope of this manuscript. We mostly focus on the ECT-property of the ordered set $({\bar{I}}_{-n},{\bar{I}}_0, {\bar{I}}_1, \dots , {\bar{I}}_{m-1})$.

We prove that a result similar to [7, Corollary 3.5] and [14, Theorem A] is true for each fixed $n>1$ (see Theorems 1 and 2 in Sect. 2). The main difference between the statement of [7, Corollary 3.5] ($n=1$) and Theorem 1 ($n>1$) is that for $n>1$ the boundary point $h=1$ is not included in the interval on which the ECT-property holds. The function ${\bar{I}}_{-n}$ goes to infinity as $h\rightarrow 1^-$ (see Lemma 2).

Applying methods from [13] to the case where $n>1$ it can be seen that, for any fixed integer $n >1$, $({\bar{I}}_{-n},{\bar{I}}_0)$ is an ECT-system on $[\epsilon ,1-\epsilon ]$. The proof is analogous to the proof for $n=1$ and we therefore omit it for the sake of brevity. We did not succeed in using [13] to prove the same for the ordered set $({\bar{I}}_{-n},{\bar{I}}_0, {\bar{I}}_1)$ when $n>1$. This is a topic of further study.

Further, we prove the monotonicity property of the quotient $I_0/I_{-n}$ on the interval ]0, 1[ for each $n>1$ (see Theorem 3). Theorem 3 naturally generalizes [4, Theorem 18] which covers the case of $n=1$. Theorem 3 can be used to prove existence and uniqueness of limit cycles of planar systems obtained after desingularization of non-generic turning points. For more details see Theorem 4 in Sect. 3.

In Sect. 2 we recall the definition of ECT-systems and state the main results of this paper. As already mentioned above, in Sect. 3 we motivate our study of the Abelian integrals. We prove the main results in Sect. 4.

2 Definitions and Statement of Results

Definition 1

Let $f_0,f_1,\dots ,f_{n-1}$ be analytic functions on a real interval with nonempty interior I. The ordered set of functions $(f_0,f_1,\dots ,f_{n-1})$ is an extended complete Chebyshev system (in short, ECT-system) on I if, for all $k=1,2,\dots n$, any nontrivial linear combination

$$\begin{aligned} \alpha _0 f_0(x)+\alpha _1f_1(x)+\cdots + \alpha _{k-1}f_{k-1}(x) \end{aligned}$$

has at most $k-1$ isolated zeros on I counted with multiplicity.

(Notice that in this abbreviation "T" stands for Tchebycheff, which in some sources is the transcription of the Russian name Chebyshev.)

One can prove (see [7, Lemma 3.7]) that $(f_0,f_1,\dots ,f_{n-1})$ is an ECT-system on I if and only if the sequence ${\mathcal {F}}^1,\dots ,{\mathcal {F}}^{n-1}$, with ${\mathcal {F}}^k=\{f^k_k,f^k_{k+1},\dots ,f^k_{n-1}\}$, can be constructed such that:

• 1. Defining $f^1_i:=\frac{f_i}{f_0}$, $i=1,\dots ,n-1$, the functions $f_i^{k+1}:=\frac{(f_i^k)'}{(f_k^k)'}$, for $k=1,\dots ,n-2$ and $i=k+1,\dots ,n-1$, are analytic on I and

• 2. $f_0$ and $(f_k^k)'$, $k=1,\dots ,n-1$, are nowhere zero on I.

This equivalent definition of ECT-system has been used in [5] with I being a closed interval [a, b]. If $I=[a,b]$, then we have the following stability property of ECT-system (see [5, Proposition 7.6]): If $(f_0,f_1,\dots ,f_{n-1})$ is an ECT-system on [a, b] and if $g_i$ is an analytic function sufficiently close to $f_i$ in the ${\mathcal {C}}^{n-1}$-topology, for $i=0,\dots ,n-1$, then $(g_0,g_1,\dots ,g_{n-1})$ is also an ECT-system on [a, b]. We will use this stability property in Sect. 3.

The following results show that the number of zeros of any nontrivial linear combination of the Abelian integrals are bounded locally near the endpoints of the interval ]0, 1[. We note that in the following statements, when $m=0$ the set of functions is only formed by ${\bar{I}}_{-n}.$

Theorem 1

For each $m\ge 0$ there exists $\epsilon >0$ such that $({\bar{I}}_{-n},{\bar{I}}_0, {\bar{I}}_1, \dots , {\bar{I}}_{m-1})$ is an ECT-system on $[1-\epsilon ,1[$.

Theorem 1 will be proved in Sect. 4.1.

Theorem 2

For each $m\ge 0$ there exists $\epsilon >0$ such that $({\bar{I}}_{-n},{\bar{I}}_0, {\bar{I}}_1, \dots , {\bar{I}}_{m-1})$ is an ECT-system on $]0,\epsilon ]$.

We prove Theorem 2 in Sect. 4.2.

Theorem 3

Let $P(h)=\frac{I_0(h)}{I_{-n}(h)}$. Then $P(h)>0$ and $P'(h)<0$, for all $h\in ]0,1[$, and $\lim _{h\rightarrow 1^-}P(h)=0$.

For $n=1$, Theorem 3 has been proved by Chengzhi Li in [4] using the method from [1]. We use the same technique to prove it in the case where $n>1$ (see Sect. 4.3).

Lemma 1

The formula in (1) holds for every positive integer n and $j=-n,0,1,2\dots$.

Proof

Notice that the oval $\gamma _h=\{H({\bar{x}},{\bar{y}})=h\}$, where H is defined in Sect. 1, has two components: ${\bar{x}}={\bar{x}}_-({\bar{y}},h)<0$ and ${\bar{x}}={\bar{x}}_+({\bar{y}},h)>0$. We have ${\bar{x}}_+=-{\bar{x}}_-$, due to the symmetry of $\gamma _h$, and $\frac{\partial {\bar{x}}_\pm }{\partial h}=-\frac{e^{2n{\bar{y}}}}{4n^2{\bar{x}}_\pm ^{2n-1}}$. Now, it easily follows that

$$\begin{aligned} \frac{d}{dh}I_j(h)=&(2n+2j+1)\int _{\gamma _h}e^{-2n{\bar{y}}}{\bar{x}}^{2n+2j}\left( -\frac{e^{2n{\bar{y}}}}{4n^2{\bar{x}}^{2n-1}}\right) d{\bar{y}}\\ =&-\frac{2n+2j+1}{4n^2}\int _{\gamma _h}{\bar{x}}^{2j+1}d{\bar{y}} \end{aligned}$$

where we use the notation ${\bar{x}}$ for ${\bar{x}}_\pm$. This gives (1). $\square$

3 Motivation

Consider slow-fast polynomial Liénard equations

$$\begin{aligned} X_{\epsilon ,\alpha ,a}: {\left\{ \begin{array}{rcl} {\dot{x}} &{}=&{}y-\bigl (x^{2n}+\sum _{k=1}^ma_kx^{2n+k}\bigr ) \\ {\dot{y}} &{}=&{}\epsilon ^{2n}\bigl (\epsilon ^{2n-1}\alpha -x^{2n-1} \bigr ), \end{array}\right. } \end{aligned}$$

(4)

where $m,n\ge 1$, $a:=(a_1,\dots ,a_m)$ is kept in a compact set $K\subset {\mathbb {R}}^{m}$, $\epsilon \ge 0$ is a small singular perturbation parameter and $\alpha \sim 0$ is a small regular parameter. To study the number and configurations of limit cycles of (4), we can use geometric singular perturbation theory. The theory is essentially composed of two parts, one of which, called Fenichel theory [6], describes the dynamics of $X_{\epsilon ,\alpha ,a}$ near normally hyperbolic manifolds. The other part is family blow-up [4, 11]; it is used to desingularize $X_{\epsilon ,\alpha ,a}$ for example near the origin $(x,y)=(0,0)$ where the normal hyperbolicity is lost.

Fig. 2

Dynamics of $X_{0,\alpha ,a}$ in a neighborhood of the contact point

More precisely, the fast subsystem $X_{0,\alpha ,a}$ has the curve of singularities $S=\{(x,y)\in {\mathbb {R}}^2|y=x^{2n}+\sum _{k=1}^ma_kx^{2n+k}\}$ and horizontal fast movements. The critical curve S contains near the origin $(x,y)=(0,0)$ a normally repelling part $x<0$, a normally attracting part $x>0$ and a nilpotent contact point $x=0$ which separates them (see Fig. 2). The contact point is generic (resp. non-generic) when $n=1$ (resp. $n>1$). For $\epsilon >0$ and $\epsilon \sim 0$, the dynamics of $X_{\epsilon ,\alpha ,a}$, uniformly away from S, can be described using regular horizontal orbits of the fast subsystem $X_{0,\alpha ,a}$. Near the normally hyperbolic parts of S, the dynamics of $X_{\epsilon ,\alpha ,a}$ is given by the slow flow (often called slow dynamics)

$$\begin{aligned} x'=-\frac{x^{2n-1}}{\frac{\partial F}{\partial x}(x,a)}\ \end{aligned}$$

where $F(x,a):=x^{2n}+\sum _{k=1}^ma_kx^{2n+k}$. When $x\sim 0$ and $x\ne 0$, the slow dynamics points from the attracting part of S to the repelling part of S (note that $x'=-\frac{1}{2n}+O(x)<0$). Thus, we call the contact point $(x,y)=(0,0)$ a turning point.

To see how the Abelian integrals defined in Sect. 1 come into play, we blow up the origin $(x,y,\epsilon )=(0,0,0)$ in $X_{\epsilon ,\alpha ,a}+0\frac{\partial }{\partial \epsilon }$ using the following “singular" coordinate change (see [2, 10])

$$\begin{aligned} (x,y,\epsilon )=(r\bar{x},r^{2n}\bar{y},r{\bar{\epsilon }}), \ r\ge 0,\ \bar{\epsilon }\ge 0, \ ({\bar{x}},{\bar{y}},{\bar{\epsilon }})\in {\mathbb {S}}^2. \end{aligned}$$

(5)

We work with different charts in (5).

Family directional chart $\{{\bar{\epsilon }}=1\}$. In this chart we have $(x,y)=(\epsilon \bar{x},\epsilon ^{2n}{\bar{y}})$, with $\epsilon =r$, where we keep $({\bar{x}},{\bar{y}})$ in a large compact set in ${\mathbb {R}}^2$. In these new coordinates the system $X_{\epsilon ,\alpha ,a}$, defined in (4), becomes (after division by $\epsilon ^{2n-1}>0$)

$$\begin{aligned} X^F_{\epsilon ,\alpha ,a}: {\left\{ \begin{array}{rcl} \dot{{\bar{x}}} &{}=&{}{\bar{y}}-\bigl ({\bar{x}}^{2n}+\sum _{k=1}^ma_k\epsilon ^k{\bar{x}}^{2n+k}\bigr ) \\ \dot{{\bar{y}}} &{}=&{}\alpha -{\bar{x}}^{2n-1}. \end{array}\right. } \end{aligned}$$

(6)

When $\epsilon =\alpha =0$, system (6) is given by

$$\begin{aligned} {\left\{ \begin{array}{rcl} \dot{{\bar{x}}} &{}=&{}{\bar{y}}-{\bar{x}}^{2n} \\ \dot{{\bar{y}}} &{}=&{}-{\bar{x}}^{2n-1}. \end{array}\right. } \end{aligned}$$

(7)

System (7) has a center at the origin $({\bar{x}},{\bar{y}})=(0,0)$, with

$$\begin{aligned} H({\bar{x}},{\bar{y}})=2ne^{-2n{\bar{y}}}\left( {\bar{y}}-{\bar{x}}^{2n}+\frac{1}{2n}\right) \end{aligned}$$

as a first integral, and the invariant curve $\{{\bar{y}}={\bar{x}}^{2n}-\frac{1}{2n}\}$ is the boundary of the period annulus (Fig. 1).

The phase directional charts $\{\bar{x}=\pm 1,\bar{y}=\pm 1\}$. The most interesting phase directional chart is the chart $\{{\bar{y}}=+1\}$. In this chart we find two semi-hyperbolic singularities $p_\pm$ located on the equator of the blow up locus (they are the end points of the invariant curve $\{{\bar{y}}={\bar{x}}^{2n}-\frac{1}{2n}\}$). For a detailed study of $X_{\epsilon ,\alpha ,a}$ in the $\{{\bar{y}}=+1\}$-direction see e.g. [10]. The other phase directional charts ($\{\bar{x}=\pm 1,\bar{y}=-1\}$) are not relevant when we study limit cycles of $X_{\epsilon ,\alpha ,a}$ near the origin in the (x, y)-space.

To find the cyclicity of $(x,y)=(0,0)$ in $X_{\epsilon ,\alpha ,a}$, we have to study three different types of limit periodic sets, for $\epsilon =\alpha =0$, which may produce limit cycles after perturbations: the center $\gamma _1$ represented by $\{H({\bar{x}},{\bar{y}})=1\}$, closed orbits of (7) surrounding the origin, denoted by $\gamma _h=\{H({\bar{x}},{\bar{y}})=h\}$ where $h\in ]0,1[$, and the polycycle $\gamma _0$ consisting of the singularities $p_\pm$ and heteroclinic orbits between them. Let $\rho >0$ be arbitrarily small and fixed. Limit cycles bifurcating from $\cup _{h\in [\rho ,1]} \gamma _h$ can be studied inside $X^F_{\epsilon ,\alpha ,a}$ using the family chart $\{{\bar{\epsilon }}=1\}$. In order to treat $\gamma _0$, the charts $\{{\bar{\epsilon }}=1\}$ and $\{{\bar{y}}=+1\}$ have to be combined. In this paper we don’t study limit cycles produced by $\gamma _0$ (see Remark 2).

Define a section $\Sigma =\{{\bar{x}}=0,{\bar{y}}\ge 0\}$ parametrized by $h\in ]0,1]$ by means of the relation $H(0,{\bar{y}})=h$ and a section $\Sigma _0\subset \{{\bar{x}}=0,{\bar{y}}>0 \}$ parametrized by $h\in [\rho ,1-\rho ]$. For $\epsilon \ge 0$ small enough we define the Poincaré map ${\mathcal {P}}(h,\epsilon ,\alpha ,a)$ of $X^F_{\epsilon ,\alpha ,a}$ from $\Sigma _0\subset \Sigma$ to $\Sigma$. Notice that we focus on the return map ${\mathcal {P}}$ with $(\epsilon ,\alpha )\sim (0,0)$, $\epsilon \ge 0$ and $a\in K$, defined uniformly away from $\gamma _0$ and $\gamma _1$. We have

Proposition 1

The Poincaré map ${\mathcal {P}}(h,\epsilon ,\alpha ,a)$ of $X^F_{\epsilon ,\alpha ,a}$ can be written as

$$\begin{aligned} {\mathcal {P}}(h,\epsilon ,\alpha ,a)&=h+4n^2\alpha \left( -\int _{\gamma _h}e^{-2n\bar{y}}d{\bar{x}}+U_{-n}(h,\epsilon ,\alpha ,a)\right) \nonumber \\&\quad +4n^2\sum _{j=0}^la_{2j+1}\epsilon ^{2j+1}\left( -\int _{\gamma _h}e^{-2n\bar{y}}\bar{x}^{2(n+j)+1}d{\bar{y}}+U_{j}(h,\epsilon ,\alpha ,a)\right) \end{aligned}$$

(8)

where l is the largest integer with the property $2l+1\le m$ and $U_{-n}, U_j$ are analytic functions identically zero when $(\epsilon ,\alpha )= (0,0)$: $U_{-n}(h,0,0,a)=0$ and $U_{j}(h,0,0,a)=0$ for $j=0,\dots ,l$.

Proof

We first study the Poincaré map $\widetilde{{\mathcal {P}}}(h,\alpha ,A)$ of

$$\begin{aligned} {\left\{ \begin{array}{rcl} \dot{{\bar{x}}} &{}=&{}{\bar{y}}-\bigl ({\bar{x}}^{2n}+\sum _{k=1}^mA_k{\bar{x}}^{2n+k}\bigr ) \\ \dot{{\bar{y}}} &{}=&{}\alpha -{\bar{x}}^{2n-1} \end{array}\right. } \end{aligned}$$

(9)

where $\alpha \sim 0$ and $A=(A_1,\dots ,A_m)\sim (0,\dots ,0)$. (If $A_k=a_k\epsilon ^k$, then system (9) becomes $X^F_{\epsilon ,\alpha ,a}$ and ${\mathcal {P}}(h,\epsilon ,\alpha ,a_1,\dots ,a_m)=\widetilde{{\mathcal {P}}}(h,\alpha ,a_1\epsilon ,\dots ,a_m\epsilon ^m)$.) For $(\alpha ,A)=(0,0)$, the function H is the Hamiltonian of the (Hamiltonian) vector field (9), multiplied by $4n^2 e^{-2n{\bar{y}}}$. If we denote by $\Omega$ the dual $1-$form of (9), then we have

$$\begin{aligned} 4n^2 e^{-2n{\bar{y}}}\Omega =dH+4n^2\alpha e^{-2n{\bar{y}}}d{\bar{x}}+4n^2\sum _{k=1}^mA_k e^{-2n{\bar{y}}}{\bar{x}}^{2n+k}d{\bar{y}}. \end{aligned}$$

Since $\int _{\gamma _{h,\alpha ,A}}4n^2 e^{-2n{\bar{y}}}\Omega =0$ and $\int _{\gamma _{h,\alpha ,A}}dH=\widetilde{{\mathcal {P}}}(h,\alpha ,A)-h$, where $\gamma _{h,\alpha ,A}$ is a part of the orbit of (9) (multiplied by $4n^2 e^{-2n{\bar{y}}}$) between $h\in \Sigma _0$ and the next intersection $\widetilde{{\mathcal {P}}}(h,\alpha ,A)\in \Sigma$ in forward time, we obtain

$$\begin{aligned} \widetilde{{\mathcal {P}}}(h,\alpha ,A)&=h+4n^2\alpha \left( -\int _{\gamma _h}e^{-2n\bar{y}}d{\bar{x}}+V_{-n}(h,\alpha ,A)\right) \nonumber \\&\quad +4n^2\sum _{k=1}^m A_k\left( -\int _{\gamma _h}e^{-2n\bar{y}}\bar{x}^{2n+k}d{\bar{y}}+V_{k}(h,\alpha ,A)\right) , \end{aligned}$$

(10)

where $V_{-n},V_k$ are analytic functions, $V_{-n}(h,0,0)=0$ and $V_{k}(h,0,0)=0$ for $k=1,\dots ,m$. Here we used the fact that $\gamma _{h,\alpha ,A}$ converges uniformly to the oval $\gamma _h$ when $(\alpha ,A)\rightarrow (0,0)$, where the section $\Sigma _0$ is parametrized by $h\in [\rho ,1-\rho ]$. On the other hand, $\widetilde{{\mathcal {P}}}(h,\alpha ,A)=h$ for $\alpha =A_{2j+1}=0$, $j=0,\dots ,l$, due to the symmetry $(x,t)\rightarrow (-x,-t)$. This, together with (10) and a Taylor expansion, implies

$$\begin{aligned} \widetilde{{\mathcal {P}}}(h,\alpha ,A)&=h+4n^2\alpha \left( -\int _{\gamma _h}e^{-2n\bar{y}}d{\bar{x}}+V_{-n}(h,\alpha ,A)\right) \\&\quad +4n^2\sum _{j=0}^l A_{2j+1}\left( -\int _{\gamma _h}e^{-2n\bar{y}}\bar{x}^{2n+2j+1}d{\bar{y}}+V_{j}(h,\alpha ,A)\right) \end{aligned}$$

for some new analytic functions $V_{-n},V_j$ with $V_{-n}(h,0,0)=0$ and $V_{j}(h,0,0)=0$ for $j=0,\dots ,l$. This implies (8). $\square$

Theorem 4

Let ${\mathcal {U}}$ be any compact set in the interior of the period annulus of (7) and let $\kappa >0$ be arbitrary and fixed. Then there exist sufficiently small $\epsilon _0>0$ and $\alpha _0>0$ such that system $X^F_{\epsilon ,\alpha ,a}$–given in (6)–has at most one periodic orbit in ${\mathcal {U}}$, for all $(\epsilon ,\alpha ,a)\in [0,\epsilon _0]\times [-\alpha _0,\alpha _0]\times K$, $(\epsilon ,\alpha )\ne (0,0)$ and $|a_1|\ge \kappa$.

Proof

Let $\rho >0$ be small enough such that ${\mathcal {U}}\subset \cup _{h\in [\rho ,1-\rho ]} \gamma _h$ and let $\kappa >0$ be small and fixed. If $|a_1|\ge \kappa$, then the Poincaré map given in (8) can be written as

$$\begin{aligned} {\mathcal {P}}(h,\epsilon ,\alpha ,a)=&h+4n^2\alpha \left( -\int _{\gamma _h}e^{-2n\bar{y}}d{\bar{x}}+U_{-n}(h,\epsilon ,\alpha ,a)\right) \nonumber \\&+4n^2 a_1\epsilon \left( -\int _{\gamma _h}e^{-2n\bar{y}}\bar{x}^{2n+1}d{\bar{y}}+U_{0}(h,\epsilon ,\alpha ,a)\right) \end{aligned}$$

(11)

where $h\in [\rho ,1-\rho ]$ and $U_{-n}, U_0$ are analytic functions and are equal to zero when $(\epsilon ,\alpha )=(0,0)$. Following Theorem 3, $(I_{-n},I_0)$, with $I_{-n}(h)=\frac{1}{2n}\int _{\gamma _h}e^{-2n\bar{y}}d{\bar{x}}$ since $\int _{\gamma _h}d\left( e^{-2n{\bar{y}}}{\bar{x}}\right) =0$ and $I_{0}(h)=\int _{\gamma _h}e^{-2n{\bar{y}}}{\bar{x}}^{2n+1} d{\bar{y}}$, is an ECT-system on $[\rho ,1-\rho ]$. This implies that $(-2n I_{-n},-I_0)$ is an ECT-system on $[\rho ,1-\rho ]$. Now, using the stability property (Sect. 2) of $(-2n I_{-n},-I_0)$ on the segment $[\rho ,1-\rho ]$, we have that $(-2n I_{-n}+U_{-n},-I_0+U_0)$ is an ECT-system on $[\rho ,1-\rho ]$, for each $(\epsilon ,\alpha )\sim (0,0)$, $a\in K$ and $|a_1|\ge \kappa$ (note that $U_{-n}, U_0$ are equal to zero when $(\epsilon ,\alpha )=(0,0)$). Now, using (11), the equation $\{ {\mathcal {P}}(h,\epsilon ,\alpha ,a)-h=0\}$ has at most one solution in $[\rho ,1-\rho ]$ counted with multiplicity, for each $(\epsilon ,\alpha )\sim (0,0)$, $(\epsilon ,\alpha )\ne (0,0)$, $a\in K$ and $|a_1|\ge \kappa$. This solution corresponds to a periodic orbit of $X^F_{\epsilon ,\alpha ,a}$. $\square$

Remark 1

Theorem 4 gives the uniqueness of limit cycles of $X^F_{\epsilon ,\alpha ,a}$ in the compact set ${\mathcal {U}}$, for $|a_1|\ge \kappa$. Using (11) and The Implicit Function Theorem we see that $X^F_{\epsilon ,\alpha ,a}$ has a limit cycle near $\gamma _h$, with $h\in [\rho ,1-\rho ]$, for

$$\begin{aligned}\alpha =-\frac{a_1\epsilon }{2n}\left( \frac{I_0}{I_{-n}}(h)+o(1)\right) \end{aligned}$$

where $o(1)\rightarrow 0$ as $\epsilon \rightarrow 0$.

Remark 2

To find an optimal upper bound for the number of limit cycles of (4) in a fixed neighborhood of $(x,y)=(0,0)$, independent of $\epsilon \rightarrow 0$, it is more suitable to study the Chebyshev property of $({\bar{I}}_{-n},{\bar{I}}_0, {\bar{I}}_1, \dots , {\bar{I}}_{l})$. These integrals appear in the expression for the derivative of ${\mathcal {P}}$ given in (8). The reason for this comes from [5] where the same has been done for $n=1$. In fact, the Chebyshev property of the derivatives is relevant in a gluing process with the polycycle $\gamma _0$ (see for example [5, Proposition 7.17] or [8]). As already observed in [14] for $n=1$, we recall that the Chebyshev property of $({\bar{I}}_{-n},{\bar{I}}_0, {\bar{I}}_1, \dots , {\bar{I}}_{l})$ in the limit $h\rightarrow 0$, obtained in Theorem 2, does not say anything about the number of limit cycles produced by $\gamma _0$ for $n>1$. One has to use different techniques to study the cyclicity of $\gamma _0$ (see [5]). This topic is therefore not a subject of the present paper.

4 Proofs of Theorem 1–Theorem 3

4.1 Proof of Theorem 1

Lemma 2

For each $j\in \{-n,0,1,2,\dots \}$, ${\bar{I}}_j(h)=(1-h)^{\frac{2j+1+n}{2n}}(a_j+g_j(h))$ where $a_j\ne 0$ and $g_j$ is an analytic function at $h=1$ with $g_j(1)=0$.

Proof

When $n=1$, this has been proved in [7, Lemma 3.4]. When $n>1$, Lemma 2 can be proved in similar fashion. However, for the sake of completeness, we will give a sketch of the proof of this lemma. We know that $\gamma _h$ can be described by $\{C({\bar{y}})+D({\bar{y}}){\bar{x}}^{2n}=1-h\}$, with $C({\bar{y}})=1-2n e^{-2n{\bar{y}}}({\bar{y}}+\frac{1}{2n})$ and $D({\bar{y}})=2n e^{-2n{\bar{y}}}$. The oval $\gamma _h$, with $h\in ]0,1[$, intersects the ${\bar{y}}$-axis at $-\frac{1}{2n}<{\bar{y}}_-(h)<0<{\bar{y}}_+(h)<+\infty$. Clearly, $C({\bar{y}}_\pm (h))=1-h$. Since $C({\bar{y}})=2n^2{\bar{y}}^2(1+O({\bar{y}}))$ near ${\bar{y}}=0$, it follows that $g({\bar{y}})=\text {sgn}({\bar{y}})\sqrt{C({\bar{y}})}$ is an analytic diffeomorphism on $]-\frac{1}{2n},+\infty [$. We have ${\bar{y}}_\pm (h)=g^{-1}(\pm \sqrt{1-h})$ and

$$\begin{aligned} {\bar{I}}_{j}(h)&=\int _{\gamma _h}{\bar{x}}^{2j+1}d{\bar{y}}=-2\int _{g^{-1}(-\sqrt{1-h})}^{g^{-1}(\sqrt{1-h})}\left( \frac{1-h-C({\bar{y}})}{D({\bar{y}})}\right) ^{\frac{2j+1}{2n}}d{\bar{y}}\\&=-2(1-h)^{\frac{2j+1+n}{2n}}\int _{-1}^1\frac{(g^{-1})'(\sqrt{1-h}s)}{(D^{\frac{2j+1}{2n}})(g^{-1}(\sqrt{1-h}s))}(1-s^2)^{\frac{2j+1}{2n}}ds, \end{aligned}$$

with $j=-n,0,1,\dots$. In the last step we use the change of coordinates $g({\bar{y}})=\sqrt{1-h}s$ and $C({\bar{y}})=g({\bar{y}})^2$. Note that the function

$$\begin{aligned}z\mapsto \frac{(g^{-1})'(z)}{(D^{\frac{2j+1}{2n}})(g^{-1}(z))}\end{aligned}$$

is analytic at $z=0$, and thus can be written as $\sum _{k\ge 0}b_kz^k$. We obtain now

$$\begin{aligned} {\bar{I}}_{j}(h)&= -2(1-h)^{\frac{2j+1+n}{2n}}\int _{-1}^{1}\Big (\sum _{k\ge 0}b_k(\sqrt{1-h}s)^k\Big )(1-s^2)^{\frac{2j+1}{2n}}ds \\&=-2(1-h)^{\frac{2j+1+n}{2n}}\sum _{k\ge 0}b_{2k}(1-h)^k\int _{-1}^1s^{2k}(1-s^2)^{\frac{2j+1}{2n}}ds. \end{aligned}$$

This implies the analyticity of ${\bar{I}}_{j}(h)/(1-h)^{\frac{2j+1+n}{2n}}$ at $h=1$, for each $j=-n,0,1,\dots$. As $(g^{-1})'(0)=\frac{1}{\sqrt{2}n}$ and $D(0)=2n$, we have

$$\begin{aligned} \lim _{h\rightarrow 1^-}\frac{{\bar{I}}_{j}(h)}{(1-h)^{\frac{2j+1+n}{2n}}}=-2b_0\int _{-1}^1(1-s^2)^{\frac{2j+1}{2n}}ds=\frac{-2\sqrt{2\pi }\Gamma (\frac{2j+1+2n}{2n})}{(2n)^{\frac{2j+1+2n}{2n}}\Gamma (\frac{2j+1+3n}{2n})}=:a_j\end{aligned}$$

where $\Gamma$ is the Gamma function.$\square$

Proof of Theorem 1

For each $\alpha \in {\mathbb {Q}}$ we say that a function f belongs to the set ${\mathcal {R}}_{\alpha }$ if there exists $\epsilon >0$ such that $f(h)=(1-h)^{\alpha }F(h)$ for all $h\in [1-\epsilon ,1[$, where F is an analytic function at $h=1$ satisfying $F(1)\ne 0.$ We notice that if $f\in {\mathcal {R}}_{\alpha }$ and $g\in {\mathcal {R}}_{\beta }$ with $\alpha >\beta$ then $(\frac{f}{g})'\in {\mathcal {R}}_{\alpha -\beta -1}$.

Let us fix $0\le k \le m-1$ and consider any function in the linear span of ${\bar{I}}_{-n},{\bar{I}}_0,\dots ,{\bar{I}}_k$, that is

$$\begin{aligned} \ell (h)=\eta _{-n} {\bar{I}}_{-n}(h)+\eta _0 {\bar{I}}_0(h)+ \cdots +\eta _k {\bar{I}}_k(h) \end{aligned}$$

where $\eta _{-n},\eta _0,\dots ,\eta _k\in {\mathbb {R}}.$ We can consider $\eta _k\ne 0$ since otherwise $\ell (h)$ belongs to the linear span with lesser index k. For the sake of compactness we rewrite the previous equality as

$$\begin{aligned} \ell ^0 = \eta _{-n} {\bar{I}}_{-n}^0 + \eta _0 {\bar{I}}_0^0 + \cdots + \eta _k{\bar{I}}_k^0. \end{aligned}$$

From Lemma 2 we know that ${\bar{I}}_{-n}^0\in {\mathcal {R}}_{\frac{1-n}{2n}}$. In particular, there exists $\epsilon _0>0$ such that ${\bar{I}}_{-n}^0(h)\ne 0$ for all $h\in [1-\epsilon _0,1[$. This allows the first step of the division-derivation algorithm, producing the function

$$\begin{aligned} \ell ^1 := \left( \frac{\ell ^0}{{\bar{I}}_{-n}^0}\right) ' = \eta _0 \left( \frac{{\bar{I}}_0^0}{{\bar{I}}_{-n}^0}\right) ' + \eta _1 \left( \frac{{\bar{I}}_1^0}{{\bar{I}}_{-n}^0}\right) '+\cdots + \eta _k \left( \frac{{\bar{I}}_k^0}{{\bar{I}}_{-n}^0}\right) '. \end{aligned}$$

For an analytic function f, let us denote by ${\mathcal {Z}}(f,\epsilon )$ the number of zeros of f on the interval $[1-\epsilon ,1[$ counted with multiplicity. By Rolle’s Theorem, we have that ${\mathcal {Z}}(\ell ^0,\epsilon _0)\le {\mathcal {Z}}(\ell ^1,\epsilon _0)+1$. Let us denote ${\bar{I}}_i^1\!:=(\frac{{\bar{I}}_i^0}{{\bar{I}}_{-n}^0})'$ for all $i=0,1,\dots ,k$. We point out that, from Lemma 2 and the remark at the beginning of the proof, ${\bar{I}}_i^1\in {\mathcal {R}}_{\frac{i}{n}}$. Therefore ${\bar{I}}_0^1\in {\mathcal {R}}_0$ and so there exists $0<\epsilon _1<\epsilon _0$ such that ${\bar{I}}_0^1(h)\ne 0$ for all $h\in [1-\epsilon _1,1[.$ We can then perform the second step of the division-derivation algorithm, obtaining

$$\begin{aligned} \ell ^2 := \left( \frac{\ell ^1}{{\bar{I}}_0^1}\right) ' = \eta _1 \left( \frac{{\bar{I}}_1^1}{{\bar{I}}_0^1}\right) ' + \eta _2 \left( \frac{{\bar{I}}_2^1}{{\bar{I}}_0^1}\right) ' + \cdots + \eta _k \left( \frac{{\bar{I}}_k^1}{{\bar{I}}_0^1}\right) '. \end{aligned}$$

Therefore we can ensure that ${\mathcal {Z}}(\ell ^0,\epsilon _1)\le Z(\ell ^2,\epsilon _1)+2.$ Now, denoting ${\bar{I}}_i^2\!:=(\frac{{\bar{I}}_i^1}{{\bar{I}}_0^1})'$ we have that ${\bar{I}}_i^2\in {\mathcal {R}}_{\frac{i-n}{n}}$ for $i=1,2,\dots ,k$. In particular, ${\bar{I}}_1^2\in {\mathcal {R}}_{\frac{1-n}{n}}$ and we can perform the next step in the division-derivation algorithm. Following this procedure, the $(j+1)$-step in the algorithm is

$$\begin{aligned} \ell ^{j+1}:= \left( \frac{\ell ^{j}}{{\bar{I}}_{j-1}^{j}}\right) '= \eta _{j}\left( \frac{{\bar{I}}_j^j}{{\bar{I}}_{j-1}^j}\right) ' + \cdots + \eta _k\left( \frac{{\bar{I}}_k^j}{{\bar{I}}_{j-1}^j}\right) ' \end{aligned}$$

with ${\bar{I}}_i^{j+1}\!:=(\frac{{\bar{I}}_{i}^j}{{\bar{I}}_{j-1}^j})'$ for $i=j,j+1,\dots ,k$ and ${\bar{I}}_j^{j+1} \in {\mathcal {R}}_{\frac{1-n}{n}}$. Thus we can perform it since the $(k+1)$-step, obtaining

$$\begin{aligned} \ell ^{k+1}:=\left( \frac{\ell ^k}{{\bar{I}}_{k-1}^k}\right) ' = \eta _k\left( \frac{{\bar{I}}_k^k}{{\bar{I}}_{k-1}^k}\right) ', \end{aligned}$$

with ${\bar{I}}_{k}^{k+1}\!:=(\frac{{\bar{I}}_k^k}{{\bar{I}}_{k-1}^k})'\in {\mathcal {R}}_{\frac{1-n}{n}}$ and $\eta _k\ne 0$. In particular ${\bar{I}}_k^{k+1}$ does not vanish on $[1-\epsilon _{k+1},1[$ for some $0<\epsilon _{k+1}<\epsilon _k<\cdots <\epsilon _0$ and ${\mathcal {Z}}(\ell ^0,\epsilon _{k})\le Z(\ell ^{k+1},\epsilon _{k})+k+1.$ Since the sequence of $\epsilon _0,\epsilon _1,\dots ,\epsilon _{k+1}$ does not depend on $\ell$ but only on the Abelian integrals ${\bar{I}}_{-n},{\bar{I}}_0,\dots ,{\bar{I}}_k$, this shows that, by taking $\epsilon =\epsilon _{k+1}$, any function in the linear span of ${\bar{I}}_{-n},{\bar{I}}_0,\dots ,{\bar{I}}_k$ has at most $k+1$ zeros, counted with multiplicity, on the interval $[1-\epsilon ,1[$. $\square$

4.2 Proof of Theorem 2

The oval $\gamma _h$ intersects the ${\bar{y}}$-axis in two points $(0,{\bar{y}}_{\pm }(h))$ for each $h\in ]0,1[$, where ${\bar{y}}_{-}(h)<0<{\bar{y}}_{+}(h)$ are the two solutions of

$$\begin{aligned} f({\bar{y}}):= H(0,{\bar{y}}) = 2ne^{-2n{\bar{y}}}\left( {\bar{y}}+\frac{1}{2n}\right) = h.\end{aligned}$$

From the definition of $\gamma _h$, we have that any $(x,y)\in \gamma _h$ satisfies the equality ${\bar{x}}^{2n}={\bar{y}} + \frac{1}{2n}-\frac{h}{2n}e^{2n{\bar{y}}}$. Therefore we can write the Abelian integrals (1) as

$$\begin{aligned} {\bar{I}}_j(h) = 2\int _{{\bar{y}}_{-}(h)}^0 [{\bar{y}}+\tfrac{1}{2n}-\tfrac{h}{2n}e^{2n{\bar{y}}}]^{\frac{2j+1}{2n}} d{\bar{y}} + 2\int _{0}^{{\bar{y}}_{+}(h)} [{\bar{y}}+\tfrac{1}{2n}-\tfrac{h}{2n}e^{2n{\bar{y}}}]^{\frac{2j+1}{2n}} d{\bar{y}} \end{aligned}$$

for $j=-n,0,1,2,\dots$ Let us denote by ${\bar{I}}_{j}^-(h)$ (resp. ${\bar{I}}_j^+(h)$) the left-hand side integral (resp. right-hand side integral) of the splitting of ${\bar{I}}_j(h)$. We point out that the functions ${\bar{y}}_{\pm }(h)$ are analytic on ]0, 1[. Moreover, since $f'(-\frac{1}{2n})\ne 0$, the function ${\bar{y}}_{-}(h)$ can also be extended analytically to $h=0$ by ${\bar{y}}_{-}(0):=-\frac{1}{2n}.$ In consequence, the functions ${\bar{I}}_j^-(h)$ are analytic at $h=0$ since $\frac{2j+1}{2n}>-1$ for $j\in \{-n,0,1,2,\dots \}$. Following the steps in [14] we perform the change of variable

$$\begin{aligned} h = f(\tfrac{1}{2ns}) = e^{-1/s}(\tfrac{1}{s}+1) \end{aligned}$$

and we define ${\hat{I}}_j(s) = {\bar{I}}_j(f(\frac{1}{2ns})).$ We also define ${\hat{I}}_j^{\pm }(s)$ accordingly.

Lemma 3

For each $j\in \{-n,0,1,2,\dots \}$, ${\hat{I}}_j^{+}(s) =(2ns)^{-\frac{2n+2j+1}{2n}}\psi _{\frac{2j+1}{2n}}(s)$ for all $s>0$, where $\psi _{\alpha }(s):= \int _0^1 [(1+s)(1-e^{-t/s})-t]^{\alpha } dt$, for $\alpha >-1$.

Proof

From the fact that ${\bar{y}}_{+}(h)$ is the positive solution of $f({\bar{y}})=h$ we have that ${\bar{y}}_{+}(f(u))=u$. Then, performing the change of variable ${\bar{y}} = \frac{1-t}{2ns}$ we get

$$\begin{aligned} {\hat{I}}_j^+(s) = {\bar{I}}_j^+(f(\tfrac{1}{2ns}))&= \int _0^{\frac{1}{2ns}} [{\bar{y}} + \tfrac{1}{2n} - \tfrac{1}{2n}f\bigl (\tfrac{1}{2ns}\bigr )e^{2n{\bar{y}}}]^{\frac{2j+1}{2n}}d{\bar{y}}\\&= (2ns)^{-\frac{2n+2j+1}{2n}}\int _0^{1} [(1+s)(1-e^{-t/s})-t]^{\frac{2j+1}{2n}}dt \end{aligned}$$

with $\frac{2j+1}{2n}>-1$ for all $j=-n,0,1,2,\dots$ This proves the result. $\square$

Let us define the function

$$\begin{aligned} J_{\alpha }(s):=\int _0^{1-e^{1-\frac{1}{s}}} [x+s\ln (1-x)]^{\alpha }dx, \text { for }s>0. \end{aligned}$$

Next two results are proved in [14, Lemma 2.3] and [14, Lemma 2.4] respectively.

Lemma 4

$\psi _{\alpha }(s) = -\frac{1}{\alpha +1}[(1+s)(1-e^{-1/s})-1]^{\alpha +1}+(1+s)^{\alpha +1}J_{\alpha }(\frac{s}{1+s}).$

Lemma 5

For every $\alpha >-1$, $\lim _{s\rightarrow 0^+} J_{\alpha }(s)=\frac{1}{1+\alpha }$. Moreover, for every $\ell \in {\mathbb {N}}$, $\lim _{s\rightarrow 0^+}s^{\ell }\partial _s^{\ell } J_{\alpha }(s)=0$.

Proof of Theorem 2

For each $\alpha \in {\mathbb {Q}}$ we say that a function f belongs to the set ${\mathcal {S}}_{\alpha }$ if there exists $\epsilon >0$ such that $f(s)=s^{\alpha }F(s)$ for all $s\in ]0,\epsilon [$, with

$$\begin{aligned} \lim _{s\rightarrow 0^+}s^{\ell }\partial _{s}^{\ell }F(s) = {\left\{ \begin{array}{ll} a &{} \text { if } \ell = 0,\\ 0 &{} \text { if } \ell >0, \end{array}\right. } \end{aligned}$$

for some $a\ne 0$. We claim at this point that if $f\in {\mathcal {S}}_{\alpha }$ and $g\in {\mathcal {S}}_{\beta }$ with $\alpha \ne \beta$ then $(f/g)'\in {\mathcal {S}}_{\alpha -\beta -1}$. Indeed, deriving the quotient we obtain

$$\begin{aligned} \left( \frac{f(s)}{g(s)}\right) ' = s^{\alpha -\beta -1} \left[ (\alpha -\beta )\frac{F(s)}{G(s)} + s \left( \frac{F(s)}{G(s)}\right) '\right] . \end{aligned}$$

Let us denote $Q_0(s)=\tfrac{F(s)}{G(s)}$ and $Q(s)=(\alpha -\beta ) Q_0(s)+sQ_0'(s)$. A simple computation shows that

$$\begin{aligned} Q^{(k)}(s) = (k+\alpha -\beta )Q_0^{(k)}(s) + s Q_0^{(k+1)}(s), \end{aligned}$$

and so

$$\begin{aligned} s^kQ^{(k)}(s) = (k+\alpha -\beta )s^kQ_0^{(k)}(s) + s^{k+1}Q_0^{(k+1)}(s). \end{aligned}$$

Let us show that $\lim _{s\rightarrow 0^+}s^k Q_0^{(k)}(s)=0$ for all $k>0$ by induction. For $k=1$ we have

$$\begin{aligned} s\left( \frac{F(s)}{G(s)}\right) '=\frac{sF'(s)G(s)-sF(s)G'(s)}{G(s)^2}. \end{aligned}$$

Since $\lim _{s\rightarrow 0^+}sF'(s)=\lim _{s\rightarrow 0^+}sG'(s)=0$ and $\lim _{s\rightarrow 0^+}G(s)$ is a non-zero constant, $\lim _{s\rightarrow 0^+}sQ_0'(s)=0$. Assuming the property to be true up to $k-1$ we use the following recursive expression for the derivative of the quotient of two functions proposed in [15],

$$\begin{aligned} \left( \frac{F(s)}{G(s)}\right) ^{(k)} = \frac{1}{G(s)}\left( F^{(k)}(s) - k!\sum _{j=1}^k \frac{G^{(k+1-j)}(s)}{(k+1-j)!}\frac{\bigl (\frac{F(s)}{G(s)}\bigr )^{(j-1)}}{(j-1)!}\right) . \end{aligned}$$

Then multiplying by the term $s^k$ the property follows by $\lim _{s\rightarrow 0^+}s^kF^{(k)}=0$, $\lim _{s\rightarrow 0^+}s^{k+1-j}G^{(k+1-j)}(s)=0$ and $\lim _{s\rightarrow 0^+}s^{j-1}Q_0^{(j-1)}(s)=0$ for $j=1,\dots ,k$. This shows $\lim _{s\rightarrow 0^+}s^k Q_0^{(k)}(s)=0$ for all $k>0$ and so $\lim _{s\rightarrow 0^+}s^kQ^{(k)}(s) = 0$ for all $k>0$. Moreover,

$$\begin{aligned} \lim _{s\rightarrow 0^+} Q(s) = \lim _{s\rightarrow 0^+}(\alpha -\beta )\frac{F(s)}{G(s)} = a \end{aligned}$$

for some $a\ne 0$. This proves the claim.

The fact that the map $s\mapsto f(\frac{1}{2ns})$ is an analytic diffeomorphism from $]0,+\infty [$ to ]0, 1[ and $\lim _{s\rightarrow 0^+}f(\frac{1}{2ns})=0$ imply the equivalence between proving Theorem 2 and showing that the set $({\hat{I}}_{-n},{\hat{I}}_0, {\hat{I}}_1, \dots , {\hat{I}}_{m-1})$ is an ECT-system on $]0,\epsilon ]$. According to the notation introduced at the beginning of the section,

$$\begin{aligned} {\hat{I}}_j(s) = 2 {\hat{I}}_j^-(s) + 2 {\hat{I}}_j^+(s), \text { where }{\hat{I}}_j^{\pm } = {\bar{I}}_j^{\pm }(f(1/2ns)). \end{aligned}$$

Since ${\bar{I}}_j^-(h)$ can be extended analytically at $h=0$ and the map $s\mapsto f(\tfrac{1}{2ns})$ is flat at $s=0$ the function ${\hat{I}}_j^-(s)$ can be written as ${\hat{I}}_j^-(s) = a_j + g_j(s)$, where $a_j$ is a constant and $g_j$ is a flat function at $s=0$. In consequence, by Lemma 3,

$$\begin{aligned} {\hat{I}}_j(s) = 2(2ns)^{-\frac{2n+2j+1}{2n}}\bigl ((2ns)^{\frac{2n+2j+1}{2n}}(a_j+g_j(s)) + \psi _{\frac{2j+1}{2n}}(s)\bigr ), \end{aligned}$$

and by Lemma 4,

$$\begin{aligned} {\hat{I}}_j(s) = 2(2ns)^{-\frac{2n+2j+1}{2n}}\bigl (s^{\frac{2n+2j+1}{2n}}({{\tilde{a}}}_j + {{\tilde{g}}}_j(s))+(1+s)^{\frac{2n+2j+1}{2n}}J_{\frac{2j+1}{2n}}(\tfrac{s}{1+s})\bigr ), \end{aligned}$$

where ${{\tilde{a}}}_j$ is a constant and ${{\tilde{g}}}_j$ is a flat function at $s=0$. The last equality together with Lemma 5 allows to write ${\hat{I}}_j(s) = 2(2ns)^{-\frac{2n+2j+1}{2n}} L_j(s)$ with

$$\begin{aligned} \lim _{s\rightarrow 0^+}s^{\ell }\partial _s^{\ell } L_j(s) = {\left\{ \begin{array}{ll} \frac{2n}{2n+2j+1} &{} \text { if } \ell = 0,\\ 0 &{} \text { if } \ell >0, \end{array}\right. } \end{aligned}$$

for each $j\in \{-n,0,1,2,\dots \}$. Let us fix $0\le k\le m-1$ and consider any function in the linear span of ${\hat{I}}_{-n},{\hat{I}}_0, {\hat{I}}_1, \dots , {\hat{I}}_{k}$,

$$\begin{aligned} \ell (s) = \eta _{-n} {\hat{I}}_{-n}(s) + \eta _0 {\hat{I}}_0(s) + \cdots + \eta _k {\hat{I}}_k(s), \end{aligned}$$

where $\eta _{-n},\eta _0,\dots ,\eta _k\in {\mathbb {R}}$. We can consider $\eta _k\ne 0$ since otherwise $\ell (s)$ belongs to the linear span with lesser index k. For the sake of compactness we rewrite

$$\begin{aligned} \ell ^0 = \eta _{-n} {\hat{I}}^0_{-n} + \eta _0 {\hat{I}}^0_0 + \cdots + \eta _k {\hat{I}}^0_k. \end{aligned}$$

From the previous discussion, we have ${\hat{I}}_{-n}^0 \in {\mathcal {S}}_{-1/2n}$. In particular, there exists $\epsilon _0>0$ such that ${\hat{I}}_{-n}^0(s)\ne 0$ for all $s\in ]0,\epsilon _0]$ and the first step of the division-derivation algorithm can be performed, producing

$$\begin{aligned} \ell ^1 = \left( \frac{\ell ^0}{{\hat{I}}_{-n}^0} \right) ' = \eta _0 \left( \frac{{\hat{I}}^0_0}{{\hat{I}}^0_{-n}}\right) ' + \cdots + \eta _k \left( \frac{{\hat{I}}^0_k}{{\hat{I}}^0_{-n}}\right) '. \end{aligned}$$

Let us denote ${\hat{I}}_j^1\!:= \bigl (\frac{{\hat{I}}^0_j}{{\hat{I}}^0_{-n}}\bigr )'$ for all $j\in \{0,1,2,\dots \}$. From the claim before ${\hat{I}}_j^1 \in {\mathcal {S}}_{-\frac{2n+j}{n}}$. In particular, ${\hat{I}}_0^1\in {\mathcal {S}}_{-2}$ and there exists $0<\epsilon _1<\epsilon _0$ such that ${\hat{I}}_0^1(s)\ne 0$ for all $s\in ]0,\epsilon _1]$ and a second step of the division-derivation algorithm can be performed. Following this procedure, the $(j+1)$-step in the algorithm is

$$\begin{aligned} \ell ^{j+1}:= \left( \frac{\ell ^{j}}{{\hat{I}}_{j-1}^{j}}\right) '= \eta _{j}\left( \frac{{\hat{I}}_j^j}{{\hat{I}}_{j-1}^j}\right) ' + \cdots + \eta _k\left( \frac{{\hat{I}}_k^j}{{\hat{I}}_{j-1}^j}\right) ' \end{aligned}$$

with ${\hat{I}}_i^{j+1}\!:=(\frac{{\hat{I}}_i^j}{{\hat{I}}_{j-1}^j})'$ with ${\hat{I}}_j^{j+1} \in {\mathcal {R}}_{-\frac{1+n}{n}}$. Thus we can perform it since the $(k+1)$-step to obtain

$$\begin{aligned} \ell ^{k+1}:=\left( \frac{\ell ^k}{{\hat{I}}_{k-1}^k}\right) ' = \eta _k\left( \frac{{\hat{I}}_k^k}{{\hat{I}}_{k-1}^k}\right) ', \end{aligned}$$

with ${\hat{I}}_{k}^{k+1}\!:=(\frac{{\hat{I}}_k^k}{{\hat{I}}_{k-1}^k})'\in {\mathcal {R}}_{-\frac{1+n}{n}}$ and $\eta _k\ne 0$. In particular ${\hat{I}}_k^{k+1}$ does not vanish on $]0,\epsilon _{k+1}]$ for some $0<\epsilon _{k+1}<\epsilon _k<\cdots <\epsilon _0$ and, if we denote by ${\mathcal {Z}}(f,\epsilon )$ the number of zeros of an analytic function f on the interval $]0,\epsilon ]$ counted with multiplicity, ${\mathcal {Z}}(\ell ^0,\epsilon _{k})\le Z(\ell ^{k+1},\epsilon _{k})+k+1.$ Since the sequence of $\epsilon _0,\epsilon _1,\dots ,\epsilon _{k+1}$ does not depend on $\ell$ but only on the Abelian integrals ${\hat{I}}_{-n},{\hat{I}}_0,\dots ,{\hat{I}}_k$, this shows that, by taking $\epsilon =\epsilon _{k+1}$, any function in the linear span of ${\hat{I}}_{-n},{\hat{I}}_0,\dots ,{\hat{I}}_k$ has at most $k+1$ zeros, counted with multiplicity, on the interval $]0,\epsilon ]$. This proves that $({\hat{I}}_{-n},{\hat{I}}_0, {\hat{I}}_1, \dots , {\hat{I}}_{m-1})$ is an ECT-system on $]0,\epsilon ]$ and thus the result. $\square$

4.3 Proof of Theorem 3

Let $P(h):=\frac{I_0(h)}{I_{-n}(h)}$ for $h\in ]0,1[$. It is clear that $I_{-n}(h)<0$ and $I_0(h)<0$ (and hence $P(h)>0$) for all $h\in ]0,1[$ due to the chosen orientation of the oval $\gamma _h$. Near $h=1$, the function P can be written as

$$\begin{aligned} P(h)=\left( 1-h\right) (c+o(1)), \end{aligned}$$

(12)

where c is a positive constant and o(1) is an analytic function at $h=1$ and equal to zero for $h=1$. From (12) follows that $P'(h)<0$, for $h\sim 1$ and $h<1$, and that $\lim _{h\rightarrow 1^-}P(h)=0$.

In the rest of the proof we show that $P'(h)<0$ for all $h\in ]0,1[$. Suppose that this is not true on ]0, 1[. Then there exists the largest $h_0<1$ such that $P'(h_0)=0$. We prove that $P(h)>P(h_0)$ for $h>h_0$ and $h\sim h_0$ (this will produce a contradiction with the largest $h_0$ such that $P'(h_0)=0$).

If we define $q(h):=I_{-n}(h_0)I_0(h)-I_{-n}(h)I_0(h_0)$, then we have $q(h_0)=0$ and, for $h>h_0$,

$$\begin{aligned} P(h)-P(h_0)=&\frac{I_0(h)}{I_{-n}(h)}-\frac{I_0(h_0)}{I_{-n}(h_0)}\nonumber \\ =&\frac{q(h)}{I_{-n}(h)I_{-n}(h_0)}=\frac{q(h)-q(h_0)}{I_{-n}(h)I_{-n}(h_0)}\nonumber \\ =&\frac{h-h_0}{I_{-n}(h)}\cdot \frac{q'({{\tilde{h}}})}{I_{-n}(h_0)}\nonumber \\ =&\frac{h-h_0}{I_{-n}(h)}\cdot \left( I_0'({{\tilde{h}}})-P(h_0) I_{-n}'({{\tilde{h}}}) \right) \end{aligned}$$

(13)

where ${{\tilde{h}}}\in ]h_0,h[$. In the last step we differentiate q and use the definition of P. If we write $Q(h):=I_0'( h)-P(h_0) I_{-n}'(h)$, then, using (13) and the fact that $I_{-n}<0$, it suffices to prove that $Q(h)<0$ for $h>h_0$ and $h\sim h_0$.

Fig. 3

The ovals $\gamma _{h_0}$ and $\gamma _{h}$, with $h>h_0$ and $h\sim h_0$, and the region $\Omega =\Omega _1\cup \Omega _2\cup \Omega _3\cup \Omega _4$ with the orientation on the boundary

We have $Q(h_0)=0$ because $P'(h_0)=0$. Since $I_{-n}'(h)=-\frac{1}{4n^2}\bar{I}_{-n}(h)$ and $I_0'(h)=-\frac{2n+1}{4n^2}\bar{I}_0(h)$, with $\bar{I}_{-n}$ and $\bar{I}_0$ defined in (1), we get

$$\begin{aligned} Q(h)=&-\frac{2n+1}{4n^2}\int _{\gamma _h}{\bar{x}} d{\bar{y}}-P(h_0)\left( -\frac{1}{4n^2}\right) \int _{\gamma _h}{\bar{x}}^{1-2n} d{\bar{y}}\nonumber \\ =&-\frac{1}{4n^2}\int _{\gamma _h}\frac{(2n+1){\bar{x}}^{2n}-P(h_0)}{{\bar{x}}^{2n-1}}d{\bar{y}}. \end{aligned}$$

(14)

Consider two vertical lines ${\bar{x}}=\pm \root 2n \of {\frac{P(h_0)}{2n+1}}$. These two vertical lines intersect the oval $\gamma _{h_0}$ through the interior (Fig. 3) since $Q(h_0)=0$. See also (14). Let’s denote by $\Omega$ the region between $\gamma _h$ and $\gamma _{h_0}$, with $h>h_0$ and $h\sim h_0$. We can write $\Omega =\Omega _1\cup \Omega _2\cup \Omega _3\cup \Omega _4$ (see Fig. 3). Then we have

$$\begin{aligned} Q(h)=&Q(h)-Q(h_0)\nonumber \\ =&-\frac{1}{4n^2}\left( \int _{\gamma _h}\frac{(2n+1){\bar{x}}^{2n}-P(h_0)}{{\bar{x}}^{2n-1}}d{\bar{y}}-\int _{\gamma _{h_0}}\frac{(2n+1){\bar{x}}^{2n}-P(h_0)}{{\bar{x}}^{2n-1}}d{\bar{y}}\right) \nonumber \\ =&-\frac{1}{4n^2}\int _{\partial \Omega }\frac{(2n+1){\bar{x}}^{2n}-P(h_0)}{{\bar{x}}^{2n-1}}d{\bar{y}}\nonumber \\ =&-\frac{1}{4n^2}\left( \int _{\partial \Omega _1\cup \partial \Omega _3}+\int _{\partial \Omega _2\cup \partial \Omega _4}\right) \frac{(2n+1){\bar{x}}^{2n}-P(h_0)}{{\bar{x}}^{2n-1}}d{\bar{y}}\nonumber \\ =&-\frac{1}{4n^2}\int _{\Omega _1\cup \Omega _3}\frac{(2n+1){\bar{x}}^{2n}+P(h_0)(2n-1)}{{\bar{x}}^{2n}}d{\bar{x}} d{\bar{y}}\nonumber \\&-\frac{1}{4n^2}\int _{\Omega _2\cup \Omega _4}\frac{P(h_0)-(2n+1){\bar{x}}^{2n}}{({\bar{x}}^{2n}-{\bar{y}})^2}d{\bar{x}} d{\bar{y}}. \end{aligned}$$

(15)

In the last step we used Green’s Theorem and

$$\begin{aligned} \int _{\partial \Omega _2\cup \partial \Omega _4}\frac{(2n+1){\bar{x}}^{2n}-P(h_0)}{{\bar{x}}^{2n-1}}d{\bar{y}}=\int _{\partial \Omega _2\cup \partial \Omega _4}\frac{(2n+1){\bar{x}}^{2n}-P(h_0)}{{\bar{x}}^{2n}-{\bar{y}}}d{\bar{x}}, \end{aligned}$$

using $dH({\bar{x}},{\bar{y}})=0$ and the fact that the numerator in the above integrals vanishes along the vertical lines ${\bar{x}}=\pm \root 2n \of {\frac{P(h_0)}{2n+1}}$. It is clear that the first integral in (15) is positive. Since the curve $\{{\bar{x}}^{2n}-{\bar{y}}=0\}$ does not intersect $\Omega _2$ and $\Omega _4$ (more precisely, the curve $\{{\bar{x}}^{2n}-{\bar{y}}=0\}$ intersects $\gamma _{h_0}$ in its right-most point and its left-most point), we have that the second integral in (15) is also positive. We conclude that $Q(h)<0$ for $h>h_0$ and $h\sim h_0$. This completes the proof of Theorem 3.