On the Uniqueness of Limit Cycles in a Generalized Liénard System

Abstract

Kooij and Sun (J Math Anal Appl 208:260–276, 1997) proposed a theorem to guarantee the uniqueness of limit cycles for the generalized Liénard system $dx/dt=h(y)-F(x),\ dy/dt=-g(x)$. We will give a counterexample to their theorem. Moreover, we shall give some sufficient conditions for the existence, uniqueness and hyperbolicity of limit cycles.

1 Introduction

Consider the generalized Liénard system

$$\begin{aligned} \frac{dx}{dt}= & {} h(y)-F(x), \nonumber \\ \frac{dy}{dt}= & {} -g(x), \end{aligned}$$

(1)

where the functions in (1) are assumed to be continuous and such that uniqueness for solutions of initial value problems is guaranteed. We define, as usual, $G(x):=\int _0^xg(s)ds$ and $H(y):=\int _0^yh(s)ds$. Huang and Sun [8] have shown a theorem to guarantee the uniqueness of limit cycles for system (1) as following (see [8, Theorem 2.3]).

Theorem 1.1

(Huang and Sun [8, Theorem 2.3]) If the following conditions (i–v) hold. Then system (1) has exactly one limit cycle which is stable.

• (i) $h(0)=0$, h(y) is strictly increasing, and $h(\pm \infty )=\pm \infty$;

• (ii) $xg(x)>0$ for $x\ne 0$ and $G(\pm \infty )=\infty$;

• (iii) there exist constants $x_1$, $x_2$ with $x_1<0<x_2$ such that $F(x_1)=F(0)=F(x_2)=0$ and $xF(x)<0$ for $x \in (x_1, x_2)\backslash \{0\}$;

• (iv) there exist constants $M>0$, K, $K_0$ with $K>K_0$, such that $F(x)>K$ for $x \ge M$ and $F(x)<K_0$ for $x \le -M$;

• (v) one of the following holds:

  • (a) $G(x_1)=G(x_2)$, or

  • (b) $G(-x) \ge G(x)$ for $x>0$. Furthermore, let $W(x):=\int _0^{h^{-1}(F(x))}h(y)dy$, where $h^{-1}$ is the inverse function of h. Then

    ($\alpha$):

    if $x_2 \le |x_1|$ then $max_{0 \le x \le x_2} [{G(x)+W(x)}]\ge G(x_1)$,

    ($\beta$):

    if $0<|x_1|<x_2$ then $max_{x_1 \le x \le 0} [{G(x)+W(x)}]\ge G(x_2)$.

Kooij and Sun [9] pointed out that Theorem 1.1 is incorrect. In fact, in their proof Huang and Sun compare the values of the differential of the function $G(x)+H(y)$ integrated along two limit cycles. However, this comparison is valid only if the following condition is added:

$$\begin{aligned} F(x)~ \mathrm{is\ nondecreasing\ for}\ x \in (-\infty ,x_1)\cup (x_2,\infty ). \end{aligned}$$

(2)

Kooij and Sun [9] gave a modified theorem as following

Theorem 1.2

(Kooij and Sun [9, Theorem 2.1]) If conditions $(i)-(v)$ of Theorem 1.1 and (2) hold. Then system (1) has exactly one closed orbit, a hyperbolic stable limit cycle.

We shall give an example such that the conditions of Theorem 1.2 are satisfied, but there are at least two limit cycles. Our investigation shows that the conditions of Theorem 1.2 cannot ensure that all closed orbits of system (1) have to intersect both $x=x_1$ and $x=x_2$. In fact, we will give an example to show that under the conditions of Theorem 1.2 there may be at least two limit cycles which intersect $x=x_2$ but do not intersect $x=x_1$. Therefore, Theorem 1.2 is incorrect. Moreover, we will give some sufficient conditions for the existence, uniqueness and hyperbolicity of limit cycles of system (1).

The idea of the proof of the uniqueness of limit cycles for the classical Liénard system (i.e. system (1) with $h(y)\equiv y$), via a comparison of integral curves, appears already in the paper by Liénard [12], and other references in this direction [1, 5, 10, 11, 13,14,15,16]. By utilizing the traditional comparison method, we obtain that system (1) with $h(y)\equiv y$ has exactly one nontrivial periodic solution which is orbitally stable, however, we cannot show that the limit cycle of system (1) with $h(y)\equiv y$ is hyperbolic (i.e. exponentially asymptotically stable).

The Proof of Theorem 3.1 for system (1) with $h(y)\equiv y$ appears for the first time in [4], but the problem is also treated in [2] and generalized in [6] and [15]. The monotonicity assumption on F(x) is relaxed in [16]. In this paper, we estimate the divergence of corresponding system integrated along a limit cycle and apply suitable transformations ( see, for example, [3, 17, 19, 20]). By this we can show that the limit cycle of system (1) is unique, hyperbolic and stable.

2 A Counterexample to Theorem 1.2

In this section we give a counterexample such that the conditions of Theorem 1.2 are satisfied, but there are at least two limit cycles which intersect $x=x_2$ but do not intersect $x=x_1$.

Example 1

Consider the Liénard system

$$\begin{aligned} \frac{dx}{dt}= & {} y-F(x), \nonumber \\ \frac{dy}{dt}= & {} -g(x), \end{aligned}$$

(3)

which satisfies the following assumptions:

• (1) g(x) is continuous on $\mathbf R$, $xg(x)>0$ for $x\ne 0$ and $G(\pm \infty )=\infty$;

• (2) F(x) is continuously differential on $\mathbf R$, $F(0)=0$.

By the transformation $u=\sqrt{2G(x)} \mathrm{sgn}x$, then system (3) is transformed into

$$\begin{aligned} \frac{du}{dt}= & {} y-F[x(u)]=y-H(u), \nonumber \\ \frac{dy}{dt}= & {} -u, \end{aligned}$$

(4)

where $x=x(u)$ is the inverse function of $u=\sqrt{2G(x)}\mathrm{sgn}x$.

Fig. 1

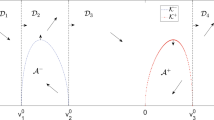
The construction graph for system (4)

The main ideas in the construction of the counterexample are as follows: Denote $\varphi (u)=H'(u)$; and construct H(u) such that (4) has at least two limit cycles. Then construct the function g(x) such that it satisfies the conditions of Theorem 1.2, and after the transformation $u=\sqrt{2G(x)}\mathrm{sgn}x$, the function

$$\begin{aligned} F(x)=\int _0^xf(s)ds=\int _0^xH'(u)u'_sds=\int _0^x\frac{\varphi [u(s)]g(s)}{u(s)}ds \end{aligned}$$

satisfies the conditions of Theorem 1.2. The system (3) will then have at least two limit cycles.

As indicated in Fig. 1, let $\widehat{POEDG}$ be part of the graph for $y=H(u)$. $D=(1,0)$. On arc $\widehat{OED}$, we have $H(u)\le 0$ and $H''(u)>0$. On line segments $\overline{PO}$, $\overline{DG}$, we have $H(u)\ge 0$. On $\overline{PO}$, $H'(u)=c_2$, and on $\overline{DG}$, $H'(u)=c_1$, with $-\frac{6}{5}c_2>c_1>-c_2$, $-c_2<1$. The function H(u) is continuously differentiable if $u_P\le u\le u_G$.

For the system (4), perform the Filippov’s transformation $z=u^{2}/2$ to transform (4) into

$$\begin{aligned} \frac{dz}{dy}= & {} H_1(z)-y,\ H_1(z)=H(\sqrt{2z}),\ z>0. \nonumber \\ \frac{dz}{dy}= & {} H_2(z)-y,\ H_2(z)=H(\sqrt{-2z}),\ z>0. \end{aligned}$$

(5)

From the construction of $y=H(u)$, Eq. (5) satisfies:

• (1) there exists $\delta >0$ such that $H_1(z)\le H_2(z)$ for $0<z<\delta$, $(H_1(z)\not \equiv H_2(z))$, $H_1(z)<a\sqrt{z}$, $H_2(z)>-a\sqrt{z}\ (a<\sqrt{8})$;

• (2) there exists $z_0>\delta$ such that $\int _0^{z_0}(H_1(z)-H_2(z))dz>0$; when $z \ge z_0$, $H_1(z) \ge H_2(z)$, $H_1(z)>-a\sqrt{z}$, $H_2(z)=H(-\sqrt{2z})=-c_2\sqrt{2z}<\sqrt{2z}<a\sqrt{z}\ (a<\sqrt{8}$).

Using Theorem 1.3 in [21, pp. 181–188], we can construct inner and outer boundaries $l_1\subset l_2$ for Eq. (5) or system (4) such that orbits starting from $l_1$, $l_2$ can only enter the annular region bounded between $l_1$ and $l_2$ as time increases. Thus there must exist a limit cycle in the annular region. Let the outer boundary $l_2$ intersect the curve $y=H(u)$ on the right halfplane at the point G. In order that system (4) has at least two limit cycles, we continue to construct the curve $\widehat{GMN}$ as part of the graph of $y=H(u)$ where $H'(u)>0$. Moreover, $H''(u)=\lambda <0$ on $\widehat{GM}$, $H'(u)=c_3>0$ on $\overline{MN}$, where $\frac{3}{2}c_3>c_1>-c_2>c_3$. For such curve $y=H(u)$, there exists $z_1>z_0$ such that the above condition (2) is satisfied with the role of $H_1(z)$ and $H_2(z)$ interchanged. That is, there exists $z_1>z_0$ such that $\int _0^{z_1}(H_2(z)-H_1(z))dz>0$; when $z \ge z_1$, $H_2(z) \ge H_1(z)$, $H_2(z)>-a\sqrt{z}$, $H_1(z)=H(\sqrt{2z})=H(u_M)+c_3\sqrt{2z}<H(u_M)+\sqrt{2z}<a\sqrt{z}$ (here $z_1$ is sufficiently large, $a<\sqrt{8}$).

Using Theorem 1.3 in [21] again, we can construct an outer boundaries $l_3\supset l_2$ such that any orbit starting at $l_2$, $l_3$ will enter the annular region bounded between $l_3$ and $l_2$ as time decreases. Thus there must exist at least one limit cycle $L_2 \supset L_1$ in the annular region between $l_2$ and $l_3$.

The construction for $y=H(u)$ is nearly complete. We continue to extend its graph to both the left and right such that $H'(u)=c_3$ if $u>u_N$, $H''(u)<0$ if $u<u_P$; $u_Q\le -2$, $H'(u)\ge 1$ for $u\le u_Q$, $H(u)\in C^1(-\infty , \infty )$. In this way, Eq. (4) has at least two limit cycles.

We further construct the function g(x) as follows:

$$\begin{aligned} g(x) = \left\{ \begin{array}{ll} kx &{} \quad \mathrm{for}\ \ x\le 0, \\ x &{} \quad \mathrm{for}\ \ x>0, \end{array} \right. \end{aligned}$$

where $k=4c_0^2$, $c_0=|u_Q|$.

It is clear that the conditions (i), (ii), (iv) and (2) are satisfied. Since $G(x)=kx^2/2$ for $x\le 0$, $G(x)=x^2/2$ for $x>0$, $u_Q=-c_0\le -2$, $u_D=1$, by the transformation $u=\sqrt{2G(x)}\mathrm{sgn}x$, we have $x_1=-\frac{1}{2}$, $x_2=1$, it follows that $0<|x_1|<x_2$, $G(x_1)=\frac{c_0}{2}>\frac{1}{2}=G(x_2)$, and $G(-x)>G(x)$ for $x>0$. Thus, the conditions (iii) and ($\beta$) in (v) are also satisfied. This concludes the construction of the counterexample.

3 Existence, Uniqueness and Hyperbolicity of Limit Cycles

In this section we give some sufficient conditions for the existence, uniqueness and hyperbolicity of limit cycles of system (1).

Theorem 3.1

If conditions $(i)-(iv)$ of Theorem 1.2 and (2) hold, F(x) and h(y) are continuously differentiable on $\mathbf R$, and condition $(v^*)$ holds if one of the following conditions

• (i) $G(x_1)=G(x_2)$;

• (ii) if $G(x_1)<G(x_2)$ then $max_{x_1 \le x \le 0}[{G(x)+W(x)}]\ge G(x_2)$;

• (iii) if $G(x_1)>G(x_2)$ then $max_{0 \le x \le x_2}[{G(x)+W(x)}]\ge G(x_1)$.

is satisfied. Then system (1) has exactly one closed orbit, a hyperbolic stable limit cycle.

This theorem will be proved by showing that if $\gamma$ is a closed orbit then its characteristic exponent $\int _{\gamma }-f(x)dt<0$, where $f(x)=(d/dx)F(x)$. This shows that $\gamma$ is hyperbolic and stable (see, for example, [3, 17, 19, 20]).

Because two adjacent limit cycles cannot both be stable, the uniqueness of $\gamma$ follows. In order to estimate the characteristic exponent we need the following lemma by Zeng [19].

Lemma 3.1

Let $\gamma$ be arc of an orbit of the system (1), described by y(x), $\alpha \le x \le \beta$. Then

$$\begin{aligned} \int _{\gamma }-f(x)dt= & {} \mathrm{sgn}(h(y(\alpha ))-F(\alpha ))\left[ \ln |\frac{F(\beta )-h(y(\alpha ))}{F(\alpha )-h(y(\alpha ))}\Bigg |\right. \\&\left. +\int _{\alpha }^{\beta }\frac{(F(\beta )-F(x))g(x)(dh/dy)}{(F(\beta )-h(y(x)))(F(x)-h(y(x)))^2}dx\right] . \end{aligned}$$

Proof of Theorem 3.1

By [7] or [18], it follows from the conditions of Theorem 3.1 that system (1) has at least one limit cycle $\gamma$. Let $\gamma$ be a closed orbit of system (1). Hence, the closed orbit $\gamma$ must contain (0, 0) in its interior. Consider the function

$$\begin{aligned} E(x,y)=G(x)+H(y) \end{aligned}$$

and evaluate the derivative of the function E(x, y) with respect to system (1),

$$\begin{aligned} \frac{dE}{dt}=-g(x)F(x)\ge 0\ \mathrm{for}\ x_1\le x\le x_2. \end{aligned}$$

(6)

Since $xF(x)<0$ for $0<|x|\ll 1$, the equilibrium (0, 0) is unstable and no closed orbit of system (1) lies wholly in the interval $x_1\le x\le x_2$. Hence, one of the points $(x_1,0)$ and $(x_2,0)$ is in the interior of $\gamma$. It is obvious that the point $(x_1,0)$ must be in the interior of $\gamma$ if $G(x_1)<G(x_2)$, and $(x_2,0)$ must be in the interior of $\gamma$ if $G(x_2)<G(x_1)$, both $(x_1,0)$ and $(x_2,0)$ are in the interior of $\gamma$ if $G(x_2)=G(x_1)$. Without loss of the generality, we assume $G(x_2)<G(x_1)$, the point $(x_2,0)$ is in the interior of $\gamma$. Let B, C and D be the points at which $\gamma$ intersects the line $x=x_2$, the negative y-axis and the negative x-axis, respectively as time t increases, where $y_B<0$, $y_C<0$ and $x_D<0$. Let P be a point on the arc $\widehat{BC}$ of $\gamma$. Then the coordinates $(x_P,y_P)$ of P satisfy $0\le x_P\le x_2$, $y_P<0$. Hence, $h(y_P)<F(x_P)<0$. $\square$

Next we prove that the point $(x_1,0)$ is in the interior of $\gamma$. Suppose it is not the case, then $x_1\le x_D<0$.

From (6), we have

$$\begin{aligned} G(x_D)=E(x_D,0)>E(x_P,y_P) \end{aligned}$$

and by $y_P<h^{-1}(F(x_P))<0$,

$$\begin{aligned} E(x_P,y_P)=G(x_P)+H(y_P)>G(x_P)+H(h^{-1}(F(x_P))). \end{aligned}$$

Thus, by the condition (iii) in condition $(v^*)$ of Theorem 3.1, we have

$$\begin{aligned} G(x_1)\ge G(x_D)>max_{0 \le x \le x_2}[{G(x)+W(x)}]\ge G(x_1) \end{aligned}$$

This is a contradiction. Therefore, the closed orbit $\gamma$ must contain the segment $(x_1,x_2)$ of the x-axis in its inner region.

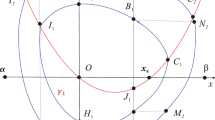
Denote the intersection point of $\gamma$ with the positive y-axis by A. Let B and C be the intersections of $\gamma$ with $x=x_2$ in the first and fourth quadrant( see Fig. 2), respectively. If we denote the arc of $\gamma$ between A and B by $\gamma _1$, then applying Lemma 3.1 with $\alpha =0$ and $\beta =x_2$ yields

$$\begin{aligned} \int _{\gamma _1}-f(x)dt=\int _0^{x_2}\frac{F(x)g(x)(dh/dy)}{h(y(x))(F(x)-h(y(x)))^2}dx. \end{aligned}$$

Fig. 2

The phase portraits on $\Sigma$ of class 29 with interior fixed point. The fixed point notation is as in [19]

This integral is negative because the integrand is negative by virtue of (i)-(iii). Thus we have proved

$$\begin{aligned} \int _{\gamma _1}-f(x)dt<0. \end{aligned}$$

For $\gamma _2$, the arc of $\gamma$ between B and C, we obtain by condition (2) and $f(x)=(d/dx)F(x)$

$$\begin{aligned} \int _{\gamma _2}-f(x)dt<0. \end{aligned}$$

Proceeding in this way we can prove that $\int _{\gamma }-f(x)dt<0$. This completes the Proof of Theorem 3.1.