Limit Sets, Attractors and Chaos

Abstract

The aim of this paper is a study on relations between $\omega$-chaos and the structure of $\omega$-limit sets. We propose a definition of $\hat{\omega }$-chaos which requires stronger relations between limit sets of points from tuples. We present example with relatively simple dynamics (almost equicontinuous system) which is $\omega$-chaotic and propose further restrictions on the conditions in the definition.

1 Introduction

The qualitative theory of dynamical systems focuses on the understanding how the trajectories of all points from the state space behave in long time. There appear situations when the motion is periodic or almost periodic however also more complicated, irregular patterns can appear during evolution of a point. Roughly speaking, the last case can usually be identified with some kind of chaos, and was intensively studied by many authors from different points of view, introducing several notions of chaos (e.g. see [1]).

The notion of omega chaos was introduced by Li [15] in 1993 for interval maps and was later generalized for continuous maps on compact metric spaces. An uncountable subset of the state space is called $\omega$-scrambled if for any nondiagonal pair in the set: (i) difference of omega limit sets is uncountable, (ii) intersection of omega limit sets is nonempty and (iii) each omega limit set is not contained in the set of periodic points. It provides yet another characterization of the situation when interval map has positive entropy or other chaotic phenomena, equivalent in this one-dimensional context.

Omega chaos is still not well understood and many open questions remains unsolved. The main difficulty in studies on this notion is that it more relies on geometric structure of attractors in the space, rather than evolution of single points. Simply, points with completely different, unrelated trajectories can lead at the end to the same omega limit set (e.g. two points with dense trajectory). In [16] authors discussed omega chaos for the circle maps and [11, 12] studied cardinality of omega scrambled sets and relations to the chaos in the sense of Li and Yorke. Later in [4, 23] authors discussed Lebesgue measure of omega scrambled sets for continuous maps on the interval. Recently in [14] the specification property was used to study omega chaos and [19] relates limit shadowing with $\omega$-chaos. In [8] the notion of $\omega$-chaos was transferred from individual dynamics to collective one. For further reading on the topic see e.g. [9] and [22]. An important notion tightly bonded with $\omega$-chaos is minimality. It is worthy to note at this point, that by the definition, $\omega$-chaos is not present in minimal dynamical systems. So intuitively it seems that $\omega$-chaos may not appear if the structure of minimal systems is not rich. This is somehow misleading.

In [6] authors construct space which is $\omega$-chaotic but the only minimal sets are periodic orbits. Furthermore, $\omega$-chaos can appear in dynamical system with one minimal subset, even in the case when the minimal system is rigid and dynamics is almost equicontinuous (see Sect. 5). To avoid the above situation and induce a more complicated structure of limit sets we will modify the definition of $\omega$-chaos. Let us first recall mathematically strict definition of $\omega$-chaos introduced first by Li in [15].

Definition 1.1

A set $\Omega \subset X$ containing at least two points is called an $\omega$ -scrambled set for dynamical system (X, f) if, for any two $x\ne y$ in $\Omega$,

• (1) $\omega _{f}(x){\setminus }\omega _{f}(y)$ is uncountable,

• (2) $\omega _{f}(x) \cap \omega _{f}(y) \ne \emptyset$ and

• (3) $\omega _{f}(x) {\setminus } Per(f) \ne \emptyset$.

The map f is $\omega$-chaotic if there is an uncountable $\omega$-scrambled set. By an $\omega$-chaotic pair we mean any $\omega$-scrambled set of cardinality 2.

It was pointed out in [15] that the third condition is superfluous when $X=I=[0,1]$. In [13] it was shown, however, that even in dimension one there are systems where the third condition is essential. Recent progress in theory of dynamical systems revealed big advantages of studies of dynamics of tuples, especially when studying topological entropy (e.g. see [20] for a survey on recent results). Following this approach, we will require that tuples in scrambled set satisfy a stronger property, which is a natural generalization of chaotic pairs (in particular, 2-tuple is chaotic pair in the standard sense).

Definition 1.2

A tuple of points $(x_1,\ldots , x_n)\in X^n$, $n\ge 2$, is an $\omega$-scrambled n-tuple if the following three conditions are satisfied:

• (1) $\left( \omega _{f}(x_{\pi (1)})\cap \ldots \cap \omega _{f}(x_{\pi (n-1)})\right) {\setminus } \omega _{f}(x_{\pi (n)})$ is uncountable for any permutation $\pi$ of the set $\left\{ 1,\ldots ,n\right\}$,

• (2) $\bigcap _{i=1}^n \omega _{f}(x_i) \ne \emptyset$ and

• (3) $\omega _{f}(x_i) {\setminus } Per(f) \ne \emptyset$ for $i=1,\ldots ,n$.

An uncountable set $Q\subset X$ is $\hat{\omega }$ -scrambled set if for any $n\ge 2$, any choice of distinct points $x_1,\ldots ,x_n\in Q$ forms and $\omega$-scrambled n-tuple $(x_1,\ldots ,x_n).$ If an uncountable $\hat{\omega }$-scrambled set exists, the map f is called $\hat{\omega }$ -chaotic.

Remark 1.3

It may happen in practice that conditions (1)–(3) in Definition 1.2 are satisfied but the structure of the dynamical system is quite simple (see example of dynamical system $(\mathcal {X},G)$ constructed in Sect. 5). Then we propose to replace (1)–(3) by the following two stronger conditions:

• (i) $\left( \omega _{f}(x_{\pi (1)})\cap \ldots \cap \omega _{f}(x_{\pi (n-1)})\right) {\setminus } \omega _{f}(x_{\pi (n)})$ contains an uncountable minimal set for any permutation $\pi$ of the set $\left\{ 1,\ldots ,n\right\}$,

• (ii) $\bigcap _{i=1}^n \omega _{f}(x_i)$ contains an uncountable minimal set.

Observe that for $n=2$ Definition 1.2 immediately gives Definition 1.1. On the other hand it is possible to construct an example of $\omega$-chaotic map with $\omega$-chaotic pairs without $\omega$-chaotic triples; the construction is just simplification of the proof of Proposition 1 from [23] while picking the initial set A as two point set of sequences containing infinitely many zeros and ones.

In the article (in Sect. 3) we will show that every interval map with positive topological entropy is $\hat{\omega }$-chaotic, obtaining yet another condition equivalent to positive topological entropy. We strongly believe that this definition (after update proposed in Remark 1.3) should lead to dynamics with complicated structure of limit sets (both theoretically and geometrically, which should be visible in computer simulations).

2 Definitions and Notations

By a dynamical system we mean a pair (X, f), where X is a compact metric space with a metric d, and f is a continuous map from X to itself. The orbit of $x \in X$ is the set $\text{ O }^+(x):=\{f^{k}(x): k\ge 0\}$, where as usual $f^k$ stands for the k fold composition of f. For $x \in X$ the $\omega$-limit set is the set

$$\begin{aligned} \omega _f(x):= \left\{ y\in X: \exists _{\{n_k\}^{\infty }_{k=1}, n_k \nearrow \infty } ~ f^{n_k}(x)\rightarrow y\right\} . \end{aligned}$$

A set $A \subset X$ is invariant under f if $f(A) \subset A$ and minimal if it is nonempty, closed and invariant under f and it does not contain any proper subset which satisfy these three conditions. When X is a minimal set, then we say that the dynamical system (X, f) is minimal. It is known that (X, f) is minimal iff each $x\in X$ has dense orbit or equivalently $\omega _f (x) =X$ for any $x \in X$. If $x\in \omega _f(x)$ then x is recurrent.

We say that f is (topologically) transitive if for any two nonempty open sets $U,V \subset X$ there exist $n>0$ such that $f^{n}(U)\cap V \ne \emptyset$ and is (topologically) weakly mixing if for any three nonempty open sets $U,V,W \subset X$ there exist $n>0$ such that $f^{n}(W)\cap U \ne \emptyset$ and $f^{n}(W)\cap V \ne \emptyset$ (see [2] for a list of equivalent conditions). If for every two nonempty sets $U,V \subset X$ there exist $N>0$ such that $f^{n}(U)\cap V \ne \emptyset$ for all $n>N$ then we say that f is (topologically) mixing.

Now let us present some standard notation related to symbolic dynamics. Let $\mathcal {A}$ be any finite set (an alphabet) and let $\mathcal {A}^*$ denote the set of all finite words over $\mathcal {A}$. In what follows, for simplicity of notation, we assume that symbol $0\in \mathcal {A}$. For any word $w \in \mathcal {A}^*$ we denote by |w| the length of w, that is the number of letters which form this word. If w is empty word then we put $|w|=0$. An infinite word is a mapping $w: \mathbb {N}\rightarrow \mathcal {A}$, hence we may view it as an infinite sequence $w_1 w_2, \ldots$ where $w_i \in \mathcal {A}$ for any $i \in \mathbb {N}$. The set of all infinite words over alphabet $\mathcal {A}$ is denoted by ${\mathcal {A}}^{\mathbb {N}}$. By $0^{\infty }$ we will denote the infinite word $0^{\infty }=000 \ldots .$ If $x \in \mathcal {A}^\mathbb {N}$ and $i \le j$ are integers then we denote $x_{[i,j)}=x_{i}x_{i+1} \ldots x_{j-1}$ and by $\mathcal {L}(X)$ we denote the language of subshift X, that is, the set $\mathcal {L}(X):=\{x_{[0,k)}: x \in X, k\ge 0 \}$. If a word $u\in \mathcal {A}^*$ appears in $z\in {\mathcal {A}}^{\mathbb {N}}$ (the same for $z\in \mathcal {A}^*$), then we denote it by $u \sqsubset z$ and say that u is a subword of z. If $u_k$ is a sequence of words such that $|u_k|\longrightarrow \infty$ then we write $z=\lim _{k\rightarrow \infty } u_k$ if the limit $z=\lim _{k\rightarrow \infty } u_k 0^\infty$ exists in $\mathcal {A}^\mathbb {N}$.

The set $\mathcal {A}$ is provided with the discrete topology and $\mathcal {A}^\mathbb {N}$ is endowed with the product topology that is equivalently metrizable by the metric $d:\mathcal {A}^\mathbb {N}\times \mathcal {A}^\mathbb {N}\rightarrow \mathbb {R}$

$$\begin{aligned} d(x,y)= {\left\{ \begin{array}{ll} 2^{-k} &{}\text {if } x \ne y, \\ 0 &{}\text {otherwise} \end{array}\right. } \end{aligned}$$

where k is the length of maximal common prefix of x and y, that is $k=\max \{ i: x_{[0,i)}=y_{[0,i)}\}.$ By $\Sigma ^{+}_{n}$ we denote the dynamical system $(\{0, \ldots , n-1\}^{\mathbb {N}} , \sigma )$, where $\sigma$ is a shift map defined by

$$\begin{aligned} (\sigma (x))_i=x_{i+1}. \end{aligned}$$

By $C[w]=\{x \in \Sigma _n^+: x_{[0,|w|)}=w\}$ we denote an open set in $\Sigma _n^+$ (the so-called cylinder set) and by $C_{A}[w]=C[w]\cap A$ we denote trace of cylinder set C[w] in a set $A\subset \Sigma _n^+$. The collection of all cylinder sets form a basis of the topology of $\Sigma ^{+}_{n}$.

Observe that $x \in \Sigma _n^+$ is a minimal point for $\sigma$ if for any open and nonempty set U there exist a positive number m such that for any $i>0$ there exist $j \in [i, i+m]$ such that $\sigma ^{j}(x) \in U$. By N(U, V) we denote set of all positive numbers i such that $\sigma ^{i}(U) \cap V \ne \emptyset .$

A Hausdorff space X is perfect if it has no isolated points, and a Cantor space if it is non-empty, compact, totally disconnected, perfect metrizable space. We say that a subset in a Hausdroff space is a Cantor set if it is a Cantor space with respect to relative topology, and a Mycielski set if it can be presented as a countable union of Cantor sets.

We present here a simplified version of Mycielski’s theorem ([17], Theorem 1) that will play a crucial role in the proof of Theorems 4.1 and 4.3.

Theorem 2.1

(Mycielski) Let X be perfect complete metric space and let $R_n \subset X^n$ be residual subsets in $X^n$ for each $n\in \mathbb {N}$. Then there is a dense Mycielski set $S \subset X$ with the property that $(x_1,x_2, \ldots , x_n) \in R_n$ for any $n \in \mathbb {N}$ and any pairwise distinct points $x_1,x_2, \ldots ,x_n \in S$.

Remark 2.2

Clearly, we may apply Mycieski theorem when $R_n$ are defined only for $n\in F$ where $F\subset \mathbb {N}$. Simply, for $n\not \in F$ we can put $R_n=X^n$.

3 Construction of $\hat{\omega }$-Chaotic Set in Full Shift

In what follows, we will need the following simple fact (e.g. see [18, Lemma 3.8]):

Lemma 3.1

For every dynamical system (X, f) the following conditions are equivalent:

• (1) (X, f) is topologically weakly mixing,

• (2) there is a point $x\in X$ with dense orbit such that for any non-empty and open neighbourhood U of x there is an integer $n>0$ such that $n,n+1\in N(U, U)$.

Fix $k>0$ and put $A=0^k$ and $B=0^{k}1$. Define $a_0^{(k)}=AAB$, $b_0^{(k)}=ABB$ and then recursively $a_{n+1}^{(k)}=a_{n}^{(k)}a_{n}^{(k)}b_{n}^{(k)}$, $b_{n+1}^{(k)}=a_{n}^{(k)}b_{n}^{(k)}b_{n}^{(k)}$. Let

$$\begin{aligned} z^{(k)}=\lim _{n\rightarrow \infty } a_{n}^{(k)}, \end{aligned}$$

that is, the point $z^{(k)}$ is the unique element of the set $\bigcap _{n\in \mathbb {N}}C[a_n^{(k)}]$. Finally, we put

$$\begin{aligned} X_k=\overline{\text{ O }^+_\sigma (z^{(k)})}. \end{aligned}$$

(3.1)

Lemma 3.2

For $k=1,2,\ldots$ the subshift $X_k$ defined by (3.1) has following properties:

• (i) $X_k$ is minimal and infinite (thus uncountable),

• (ii) $X_k$ is weakly mixing,

• (iii) $X_m\cap X_n =\emptyset$ provided that $m\ne n$.

Proof

Fix any $k>0$. First we claim, that if we fix any integer $r\ge 0$ then for all non-negative integers j, both $a^{(k)}_{r+j}$ and $b^{(k)}_{r+j}$ can be presented as concatenations of $a^{(k)}_r$ and $b^{(k)}_r$. We prove this fact by induction on j. Indeed, for $j=0$ the claim follows by the definition. Now assume, that the claim holds for some $j \ge 0$. By the definition

$$\begin{aligned} a^{(k)}_{r+j+1}=a^{(k)}_{r+j}a^{(k)}_{r+j}b^{(k)}_{r+j} \end{aligned}$$

and

$$\begin{aligned} b^{(k)}_{r+j+1}=a^{(k)}_{r+j}b^{(k)}_{r+j}b^{(k)}_{r+j} \end{aligned}$$

and by assumption, each $a^{(k)}_{r+j}$ and $b^{(k)}_{r+j}$ can be presented as concatenation of $a^{(k)}_r$ and $b^{(k)}_r$ hence also $a^{(k)}_{r+j+1}$ and $b^{(k)}_{r+j+1}$ are concatenation of $a^{(k)}_r$ and $b^{(k)}_r$. The claim is proved.

To prove (i) that $X_k$ is minimal we show that any point x from $X_k$ is a minimal point. To do so, fix any $z^{(k)}$, its open neighbourhood U and let $p>0$ be an integer such that $C[u]\subset U$, where $u=z_{[0,p)}^{(k)}$. There exist $l>0$ such that $|a^{(k)}_l| \ge |u|$. Observe that from the above claim we get that, $z^{(k)}=u_1u_2u_3 \ldots$, where $u_i \in \{a^{(k)}_{l-1}, b^{(k)}_{l-1} \}$ for every $i=1,2, \ldots$. Denote $N=6|b^{(k)}_{l}| \ge 2|b^{(k)}_{l+1}|$. Observe that for any i, word $z^{(k)}_{[i,i+N)}$ contains $b^{(k)}_{l+1}$ or $a^{(k)}_{l+1}$ as a subword and both of them contain $a^{(k)}_{l}$ as a subword. This shows that $z_{[i, i+N)}^{(k)}$ has u as a subword, and hence there is $j \in [i,i+N)$ such that $\sigma ^{j}(z^{(k)})\in C[u] \subset U$.

We will prove (ii) by reducing to Lemma 3.1. Let us fix any non-empty open neighbourhood $z^{(k)}\in U \subset X_k$. There exist $r>0$ such that $C[a^{(k)}_r] \subset U$.

We claim that there are $u_t$ and $u_{t+1}$ such that

$$\begin{aligned} z^{(k)}=\ldots a^{(k)}_r u_{t} a^{(k)}_r \ldots a^{(k)}_r u_{t+1} a^{(k)}_r \ldots \end{aligned}$$

(3.2)

and $|u_{t+1}|=|u_{t}|+1$ for some $t >0$. To prove this fact, we firstly show that for every positive number r we have $|b_{r}^{(k)}|=|a_{r}^{(k)}|+1$. It is obviously true for $r=0$. Now assume, that the following equalities $|b_{r}^{(k)}|=|a_{r}^{(k)}|+1$ is true for some $r>0$. By the definition

$$\begin{aligned} a_{r+1}^{(k)}=a_{r}^{(k)}a_{r}^{(k)}b_{r}^{(k)} \end{aligned}$$

and

$$\begin{aligned} b_{r+1}^{(k)}=a_{r}^{(k)}b_{r}^{(k)}b_{r}^{(k)}. \end{aligned}$$

hence by the induction it is clear that

$$\begin{aligned} |b_{r+1}^{(k)}|=|a_{r+1}^{(k)}|+1. \end{aligned}$$

But $a^{(k)}_{r+2}$ is a prefix of $z^{(k)}$, hence both $a^{(k)}_{r+1}$, $b^{(k)}_{r+1}$ are its subwords, which gives (3.2). Since U was arbitrarily chosen, $X_k$ is weakly mixing by Lemma 3.1.

To show (iii) let us suppose that $X_m\cap X_n \ne \emptyset$ for some $m \ne n$. We may assume that $m>n$. Let $z \in X_m\cap X_n$. Then there is $z \in \overline{\text{ O }^+_\sigma (z^{(m)})}\cap \overline{\text{ O }^+_\sigma (z^{(n)})}$. It means that there exist $j > 0$ such that word $a^{(m)}_j$ appears in $z^{(n)}$. But $a_1^{(m)}=0^{3m} 1$ is a subword of $a_j^{(m)}$ and $z^{(n)}$ is a concatenation of words $a^{(n)}_1$, $b^{(n)}_1$ where each of these words ends with 1. Hence the longest allowed block of consecutive zeros in $z^{(n)}$ is bounded by

$$\begin{aligned} |b^{(n)}_1|=3n+2<3(n+1)\le 3m \end{aligned}$$

which is a contradiction. This completes the proof. $\square$

Now we continue with the construction of an $\hat{\omega }$-chaotic map. Let $x\in \Sigma _2^+$ and let $P=\left\{ p_i\right\} _{i=1}^\infty =\left\{ 2,3,5,\ldots \right\}$ be an increasing sequence consisting of all prime numbers.

We define a map $\psi =(\psi _1,\psi _2) :\mathbb {N}\rightarrow \mathbb {N}\times \mathbb {N}$ by putting $\psi (n)=(i_1,k_1)$ provided that $n=p_{i_1}^{k_1}\ldots p_{i_s}^{k_s}$ where $s\ge 1$ and $i_1<i_2<\ldots <i_s$. Fix any $x\in \Sigma _2^+$ and define

$$\begin{aligned} \phi _x(n)={\left\{ \begin{array}{ll} a_{\psi _2(n)}^{(\psi _1(n))}&{} \text { if } x_{\psi _1(n)}=1,\\ 0^n &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

We define $z_x=\phi _x(2) 0 \phi _x(3) 0^2 \phi _x(4) 0^3 \ldots$.

Lemma 3.3

Fix any $z\in \omega _{\sigma }(z_x)$. Then one of the following conditions is satisfied:

• (i) $z=0^\infty$,

• (ii) there is j such that $x_j=1$ and $z=0^m y$ for some $m\ge 0$ and $y\in X_j$,

• (iii) there is j such that $x_j=1$ and $z=0^s w 0^\infty$ for some $w\in \mathcal {L}(X_j)$ and some $s \ge 0$,

Proof

Let $x\in \Sigma _2^+$ and fix $z\in \omega _{\sigma }(z_x).$ Note that by the definition, we have $z_x=\phi _x(2) 0 \phi _x(3) 0^2 \phi _x(4) 0^3 \ldots$. Let us analyze the structure of $u_k=(z_{x})_{[s_k,s_k+k)}$ where $s_k$ is an increasing sequence such that

$$\begin{aligned} z=\lim _{k\rightarrow \infty } \sigma ^{s_k}(z_{x})=\lim _{k\rightarrow \infty } u_k 0. \end{aligned}$$

We have exactly four possibilities on the structure $u_k$ depending on the relative position of $u_k$ in $z_x$ with respect to blocks $0^n$ connecting words $\phi _x(n)$.

• (a) First case is when $u_k=0^k$, for every k. Then we immediately get $z=\lim _{k\rightarrow \infty } u_k=0^{\infty }$ which is condition (i).

• (b) Another possibility is when $u_k=0^{m}\phi _x (n)_{[0,p)}$ for some $m\ge 0$, $n>0$ and $p\le |\phi _x (n)|$. Then

  $$\begin{aligned} \lim _{n \rightarrow \infty } \phi _x(n)_{[0,p)} = \lim _{n \rightarrow \infty } {a^{(j)}_{n}}_{[0,p)}={z^{(j)}}_{[0,p)} \in \mathcal {L}(X_j) \end{aligned}$$

  which proves the setting of (ii), that is $z=0^{m}y$ for some $y \in X_j$.

• (c) Similarly we show that it may happen that $z=w0^{\infty }$ for some $w \in \mathcal {L}(X_j)$ which appears when $u_k={\phi _x (n)}_{[|\phi _x (n)|-p, |\phi _x (n)|)}0^{k-p}$ for every k, where n depends on k and p is fixed and has the same value for all k. Note that ${\phi _x (n)}_{[|\phi _x (n)|-p, |\phi _x (n)|)}$ is finite hence is the same for infinitely many n (and as a result infinitely many k). In other words, since $z=\lim _{k\rightarrow \infty } u_k$ exists, we obtain that $z={\phi _x (n)}_{[|\phi _x (n)|-p, |\phi _x (n)|)}0^\infty$ for some n. This is the case (iii) with $s=0$, provided that $x_j=1$, ${\phi _x (n)}=a_{\psi _2(n)}^{(j)}$ and its suffix is w.

• (d) The remaining situation that we have in (iii) is $z=0^s w0^{\infty }$ for some $s>0$. Note that if $x_j$ is 1 and n has decomposition into primes $n=p_j^r....$ where, $p_j$ is smallest prime in decomposition, we may obtain $u_k$ of the form

  $$\begin{aligned} u_k=0^{t}\phi _x(n) 0^{n-1} w_k=0^{t}a^{(j)}_r 0^{n-1} w_k \end{aligned}$$

  where t is the same for all k and words $w_k$ are possibly changing with k. But n tends to infinity, so without loss of generality we may assume that $w_k$ is an empty word. If r increases with n then $|a^{(j)}_r| \rightarrow \infty$, which reduces to the case (ii). The other situation is that r stabilizes, but then $z=0^t a^{(j)}_r 0^\infty$ which is the case (iii).

We considered all the possibilities of the structure of $u_k$, hence the proof is completed. $\square$

Lemma 3.4

There is a Cantor set $Q\subset \Sigma _2^+$ such that for any $n\ge 2$ and for any distinct $x_1,\ldots , x_n\in Q$ there is $i> 0$ such that

$$\begin{aligned} x_1(i)=x_2(i)=\cdots = x_n(i)=1 \end{aligned}$$

and there is $j> 0$ such that

$$\begin{aligned} 1=x_1(j)=x_2(j)=\cdots = x_{n-1}(j)\ne x_{n}(j)=0. \end{aligned}$$

Proof

For each $n\ge 2$ define the set $R_n \subset (\Sigma _2^+)^n$ by putting

$$\begin{aligned} R_n= & {} \left\{ (x_1,x_2,\ldots , x_n) \in (\Sigma _2^+)^n: x_1(i)=x_2(i)=\cdots =x_{n-1}(j)=1\right. \\&\left. \text { and } x_{n-1}(j) \ne x_n(j) \text { for some }j>0\right\} . \end{aligned}$$

where $(\Sigma _2^+)^n$ is endowed with the maximum metric $d_n$, i.e.

$$\begin{aligned} d_n((x_1,\ldots ,x_n),(y_1,\ldots ,y_n))=\max _{i=1,\ldots ,n}d(x_i,y_i). \end{aligned}$$

Observe that each set $R_n$ is open, because for every j there is $\varepsilon >0$ such that if $d_n((x_1,\ldots ,x_n), (y_1,\ldots , y_n))<\varepsilon$ then $x_k(j)=y_k(j)$ for $k=1,2,\ldots , n$. Note that $R_n$ is also dense, because if we fix any nonempty words $w_1,\ldots , w_n$ and put $v_i=w_i w_{i+1}\ldots w_n w_1\ldots w_{i-1}$, then $|v_1|=|v_2|=\cdots =|v_n|$ and clearly

$$\begin{aligned} \left( v_1 1 0^\infty , \ldots , v_{n-1} 10^\infty , v_n 0^\infty \right) \in R_n \cap \left( C[w_1]\times \cdots \times C[w_n]\right) . \end{aligned}$$

By Mycielski theorem there is a Cantor set $Q\subset \Sigma _2^+$ such that for any $n\ge 2$ and for any distinct $x_1,\ldots , x_n\in Q$ we have $(x_1,\ldots ,x_n)\in R_n$, that is there is $j> 0$ such that $1=x_1(j)=x_2(j)=\cdots = x_{n-1}(j) \ne x_{n}(j)$. But Q is a Cantor set, hence there is also $x_{n+1}\in Q$ such that $x_1,\ldots , x_{n+1}$ are pairwise distinct. Then there is i such that $1=x_1(i)=x_2(i)=\cdots = x_{n}(i) \ne x_{n+1}(i)$. The proof is completed. $\square$

Lemma 3.5

Function $\zeta :x\mapsto z_x$ is continuous and $\zeta (Q)$ is a Cantor set (where Q is provided by Lemma 3.4). If $x_1,\ldots ,x_n\in Q$ then there are $k,s\ge 1$ such that

$$\begin{aligned} X_k\subset & {} \bigcap _{i=1}^n\omega _\sigma (z_{x_i}) \end{aligned}$$

(3.3)

$$\begin{aligned} X_s\subset & {} \left( \bigcap _{i=1}^{n-1} \omega _\sigma (z_{x_i}) \right) {\setminus }\omega _\sigma (z_{x_{n}}). \end{aligned}$$

(3.4)

Proof

First we show that function $\zeta :x\mapsto z_x$ is continuous, i.e. for every $\varepsilon >0$ exist $\delta >0$ such that $d(x_1,x_2)<\delta$ gives $d(z_{x_1},z_{x_2})<\varepsilon$. Fix any $\varepsilon >0$ and take $k>0$ such that $\varepsilon >2^{-k}$. It is enough to provide $\delta >0$ such that $z_{x_{1}}$ and $z_{x_{2}}$ have common prefix of length at least k, since then $d(z_{x_1},z_{x_2})<\varepsilon$. Note that

$$\begin{aligned} \max _{i=0,\ldots ,k} \psi _1(i)\le k, \end{aligned}$$

hence if $(x_1)_{[0,k]}=(x_2)_{[0,k]}$ then also $(z_{x_1})_{[0,k]}=(z_{x_2})_{[0,k]}$, and so it is enough to put $\delta =2^{-k}$. Indeed, $\zeta$ is continuous.

Let Q be the Cantor set provided by Lemma 3.4. Since $\zeta$ is continuous, $\zeta (Q)$ is compact. But $\zeta$ is also injective, hence Q does not have isolated points. This shows that $\zeta (Q)$ is a perfect subset in a totally disconnected space, hence is a Cantor set.

Now, fix any $x_1,\ldots ,x_n\in Q$. There is k such that $x_1(k)=x_2(k)=\cdots = x_n(k)=1$. Then by the definition of $z_{x_i}$ we obtain that $X_k \subset \omega _{\sigma }(z_{x_i})$ for $i=1,\ldots ,n$. Similarly, there is s such that $x_1(s)=x_2(s)=\cdots = x_{n-1}(s)=1$ and $x_n(s)=0$. Then $X_s \subset \omega _{\sigma }(z_{x_i})$ for $i=1,\ldots ,n-1$ and by Lemma 3.3 we obtain that $X_s \cap \omega _{\sigma }(z_{x_n})=\emptyset$. Indeed, conditions (3.3) and (3.4) are satisfied and the proof is finished. $\square$

By Lemma 3.5 (see also Lemma 3.2) we directly obtain the following. Simply, it is enough to put $D=\zeta (Q)$.

Theorem 3.6

There exists a Cantor set $D\subset \Sigma _2^+$ such that for any $n\ge 2$ and any distinct $z_1,\ldots , z_n\in D$ there are $s,k>0$ such that:

• (1) $\left( \omega _{\sigma }(z_1)\cap \ldots \cap \omega _{\sigma }(z_{n-1})\right) {\setminus } \omega _{\sigma }(z_n)$ contains an uncountable weakly mixing minimal set,

• (2) $\bigcap _{i=1}^n \omega _{\sigma }(z_i)$ contains an uncountable weakly mixing minimal set (hence is nonempty).

In particular D is an $\hat{\omega }$-scrambled set for $\sigma$.

4 Dimension One and Beyond

Theorem 4.1

Let $f:[0,1]\rightarrow [0,1]$ be transitive. Then there exists a dense Mycielski $\hat{\omega }$-scrambled set $M\subset [0,1]$.

Proof

Let $\{V_j: j \in \mathbb {N}\}$ be countable base for the topology of [0, 1] consisting of nonempty open sets of [0, 1], and for each $j \in \mathbb {N}$, let $U_j \subset (0,1)$ be a nonempty open interval with $\overline{U_j} \subset V_j$. Let D be a Cantor set provided by Theorem 3.6 and let $C_1, C_2, \ldots \subset D$ be pairwise disjoint Cantor sets.

Since f is a transitive interval map, there exists $p\in (0,1)$ such that for every $\varepsilon >0$ and every j there is n such that $(\varepsilon ,p-\varepsilon )\subset f^n(U_j)$ and $(p+\varepsilon ,1-\varepsilon )\subset f^{n+1}(U_j)$. In particular, there is n and a Cantor set $C_j'$ such that $f^n(U_j)\cap C_j=C_j'$. By [24, Remark4.3.6], there exists a Cantor set $D_j\subset U_j$ such that $f^n|_{D_j}$ is one-to-one and $f^n(D_j)\subset C_j'\subset C_j$.

Putting $M=\bigcup _{j=1}^{\infty } D_j$ we obtain a dense Mycielski set. But for every n we have $\omega _f(x)\,{=}\,\omega _f(f^n(x))$, and sets $C_j$ were pairwise disjoint, hence M is $\hat{\omega }$-scrambled. $\quad \square$

Before proceeding, we will need the following result by Oxtoby and Ulam (see [21, Thm. 9]).

Theorem 4.2

(Oxtoby and Ulam) Let $B\subset [0,1]^k$ and suppose that there exists a sequence $\left\{ S_n\right\} _{n=1}^\infty$ of perfect sets $S_n\subset B$ such that $\bigcup _{n\in \mathbb {N}} S_n$ is dense in $I^k$. Then there exists a homeomorphism $\eta :[0,1]^k \rightarrow [0,1]^k$ such that $\eta |_{\partial [0,1]^k}=id$ and $\mathscr {L}(\eta (B))=1$, where $\mathscr {L}$ denotes the Lebesgue measure on $[0,1]^k$.

Theorem 4.3

For every $n\ge 2$ there exists a continuous $\hat{\omega }$-chaotic map $F:[0,1]^n\rightarrow [0,1]^n$ and a dense Mycielski $\hat{\omega }$-scrambled set $M\subset [0,1]^n$ for F such that its Lebesgue measure $\mathscr {L}(M)=1$.

Proof

Take a mixing map $f:[0,1]\rightarrow [0,1]$ (e.g. the standard tent map) and denote $G=f\times \cdots \times f:[0,1]^n\rightarrow [0,1]^n$. Since there is a fixed point $p\in (0,1)$ for f, the set $J=[0,1]\times \left\{ p\right\} ^{n-1}$ is invariant under G and we may identify $G|_J$ with a map acting on [0, 1]. Let $D\subset J$ be a Cantor $\hat{\omega }$-scrambled set for $G|_J$ (hence also for G) provided by Theorem 3.6. Taking a Cantor subset of D if necessary, we may assume that $D\subset (0,1)^n$. Observe that since f is mixing, for every open set $U\subset [0,1]^n$ and every $\varepsilon >0$ there is $k>0$ such that $(\varepsilon ,1-\varepsilon )^n\subset G^k(U)$, so there is $k>0$ such that $D\subset G^k(U)$. Repeating all the arguments from the proof of Theorem 4.1 we obtain a dense Mycielski $\hat{\omega }$-scrambled set B for G. By Oxtoby-Ulam theorem we obtain a homeomorphism $\eta :[0,1]^k \rightarrow [0,1]^k$ such that $\eta |_{\partial [0,1]^k}=id$ and $\mathscr {L}(\eta (B))=1$. Since $\hat{\omega }$-scrambled sets are preserved by topological conjugacy, the proof is completed by putting $F=\eta \circ G \circ \eta ^{-1}$ $\square$

Fig. 1

$\omega$-scrambled triple $x_1,x_2,x_3\in [0,1]^2$ with $(0,0)\in \bigcap _{i=1}^3\omega _T(x_i)$

Clearly $T=f\times f$ is a special type of triangular map, hence we have also the following.

Corollary 4.4

There exists a transitive triangular map $T:[0,1]^2\rightarrow [0,1]^2$ with a dense Mycielski $\hat{\omega }$-scrambled set $M\subset [0,1]^2$.

A computer simulation, showing how $\omega$-limits sets of a triple in a map $T=f\times f$ when f is the standard tent map can look like is presented on Fig. 1. Points $x_1,x_2,x_3\in [0,1]^2$ were chosen in such a way that $(0,0)\in \bigcap _{i=1}^3\omega _T(x_i)$.

5 Almost Equicontinuous Example

The aim of this section is to construct a compact set X and an $\hat{\omega }$-chaotic homeomorphism F on it which is almost equicontinuous (however is not transitive). We will construct the space $\mathcal {X}$ (and the map F) in a few steps. Let us first recall the definition of equicontinuity and almost equicontinuity (see [10])

Definition 5.1

Let (X, f) be a dynamical system.

• (1) The set $\mathcal {E} \subseteq X$ of equicontinuous points of (X, f) is defined by

  $$\begin{aligned} x \in \mathcal {E} \Leftrightarrow \forall _{\varepsilon >0} \ \exists _{\delta >0} \ \forall _{ y \in B_{\delta }(x)} \ \forall _{ n \ge 0} \ d\left( f^n(x), f^n(y)\right) < \varepsilon . \end{aligned}$$

• (2) We say that (X, f) is equicontinious if $\mathcal {E}=X.$

• (3) We say that (X, f) is almost equicontinious if $\mathcal {E}$ is a residual set.

Denote by $\mathbb {S}^1$ the unit circle with metric induced from the complex plane. Start with the irrational rotation of the unit circle $R:\mathbb {S}^1\rightarrow \mathbb {S}^1$ and for $n=1,2,\ldots$ select points $x_0^{(n)}\in \mathbb {S}^1$ with pairwise disjoint orbits, i.e. $R^i(x_0^{(n)})\ne R^j(x_0^{(m)})$ for all $i,j\in \mathbb {Z}$ provided that $m\ne n$. Denote $x^{(n)}_j=R^j(x_0^{(n)})$ for all $j\in \mathbb {Z}$. We will perform a construction similar to that of a Denjoy map (see [5, Example 14.9] or [3, Theorem 7.2.3]). As the first step of our construction we remove all points $x^{(n)}_j$ from $\mathbb {S}^1$ and fill each obtained hole with a closed interval $I_j^n$ of length $4^{-|j|-n}$. Clearly $\sum _{n=1}^\infty \sum _{j\in \mathbb {Z}} 4^{-|j|-n}<\infty$ so this new extended space can be identified again with $\mathbb {S}^1$. Denote by $\pi :\mathbb {S}^1\rightarrow \mathbb {S}^1$ factor map which collapses back intervals $I_j^n$. There is also a natural induced homeomorphism g (Denjoy map) defined on the extended circle:

• (1) each interval $I^n_j$ is mapped homeomorphicaly onto $I_{j+1}^n$,

• (2) if all intervals $I^n_j$ are collapsed back into single points $x^{(n)}_j$ then g reverts back to the map R.

In particular condition $R\circ \pi =\pi \circ g$ is satisfied. If we denote $C=\mathbb {S}^1{\setminus } \bigcup _{n>0, j\in \mathbb {Z}}I_j^n$ then clearly $\pi |_C$ is one to one (and C is an open set).

Note that ${{\mathrm{diam}}}I^n_j\le 4^{-n}$ for every j and for every m there is $N_m$ such that

$$\begin{aligned} \sum _{n=1}^\infty \sum _{j\in \mathbb {Z}} 4^{-|j|-n} - \sum _{n=1}^{N_m} \sum _{j=-N_m}^{N_m} 4^{-|j|-n} < 4^{-m}. \end{aligned}$$

(5.1)

Fix a point z in $\mathbb {S}^1$ which does not belong to the orbit of any $x_0^{(n)}$. Since orbit of z under R is dense, we can find sequence of integers $a^{(n,m)}$ increasing with respect to m such that:

• (i) $\left[ a^{(n,m)},a^{(n,m)}+3m\right] \cap \left[ a^{(i,j)},a^{(i,j)}+3j\right] =\emptyset$ provided that $(n,m)\ne (i,j)$

• (ii) $\left| R^{a^{(n,m)}}(z)-x^{(n)}_{-m}\right| <4^{-m}$.

• (iii) $\left| R^{a^{(n,m)}}(z)-x^{(n)}_{-m}\right| < \left| R^{a^{(n,m)}}(z)-x^{(i)}_{j}\right|$ for $i\le N_m$ ,$|j|\le N_m+2m$, $(i,j)\ne (n,-m)$.

Roughly speaking, condition (iii) means that $x^{(n)}_{-m}$ is closer to $R^{a^{(n,m)}}(z)$ than points $x^{(i)}_{j}$ for small values of i, j.

Denote by $\hat{z}\in C$ the unique point such that $\pi (\hat{z})=z$ and for any n denote by $b^n_m$ one of the endpoints of $I^n_m$ in such a way that $g(b^n_m)=b^n_{m+1}$ for every $m\in \mathbb {Z}$. Simply it is enough to fix $b^n_0$ as one of the endpoints of $I^n_0$ and then put $b_m^n=g^m(b_0^n)$ for every $m\in \mathbb {Z}$. Since we have freedom when choosing $a^{(n,m)}$, in particular we can choose “the side” of $x_m^n$ approached by orbit of z, we may assume that $b_m^n$ is closer to $\hat{z}$ than the other endpoint of $I^n_m$.

Define a sequence $\xi _j$ by replacing segments of the orbit of z for iterations $j=a^{(n,m)},\ldots ,a^{(n,m)}+2m$, putting $\xi _j=g^{j-a^{(n,m)}}(b^n_m)$ for all these j and keeping $\xi _j=g^j(z)$ otherwise. Furthermore, we consider only pairs (n, m) with $m\ge n$. For $j=a^{(n,m)},\ldots ,a^{(n,m)}+2m$ the distance between $\xi _j$ and $g^j(z)$ is bounded from the above by $\left| R^{a^{(n,m)}}(z)-x^{(n)}_{-m}\right|$ increased by the diameters of intervals inserted into points between $R^{j}(z)$ and $R^{j-a^{(n,m)}}(x^{(n)}_{-m})$. But by condition (iii) and (5.1) these diameters are bounded from the above, hence $|\xi _j-g^j(z)|<4^{-m+1}$ for $j=a^{(n,m)},\ldots ,a^{(n,m)}+2m$. This shows that the constructed sequence is asymptotic to the orbit of z, that is $\lim _{j\rightarrow \infty } |\xi _j-g^j(z)|=0$.

Take a dense sequence $\left\{ q_i\right\} _{i=1}^\infty$ in (0, 1) and denote by $q_m^{(n,i)}$ an isometric image of $q_i$ in the set $I^n_{m}$ (in particular $g(q_m^{(n,i)})=q_{m+1}^{(n,i)}$ and $\overline{\left\{ q_m^{(n,i)}: i\in \mathbb {N}\right\} }=I_m^n$). Clearly for every $q\in I^{n}_m$ there exists an increasing sequence $m_i$ such that $q=\lim _{i\rightarrow \infty } q_{m}^{(n,m_i)}$. For each $\alpha \in \Sigma _2^+$ define a sequence $\left\{ p^\alpha _i\right\} _{i\in \mathbb {Z}}$ by:

$$\begin{aligned} p^\alpha _i= {\left\{ \begin{array}{ll} g^i(z) &{}\text { if } i\not \in \bigcup _{n\ge 0}\bigcup _{m\ge n}[a^{(n,m)},a^{(n,m)}+2m],\\ b_{-m+i-a^{(n,m)}}^{n}&{} \text { if } i\in [a^{(n,m)},a^{(n,m)}+2m] \text { and }\alpha _n=0, m\ge n\\ q_{-m+i-a^{(n,m)}}^{(n,m)}&{} \text { if } i\in [a^{(n,m)},a^{(n,m)}+2m] \text { and }\alpha _n=1, m\ge n. \end{array}\right. } \end{aligned}$$

Observe that for any fixed $\alpha$, by the definition of numbers $a^{(n,m)}$ the sequence $\left\{ p^\alpha _i\right\} _{i\in \mathbb {Z}}$ contains arbitrarily long segments of the orbit $\left\{ g^i(z)\right\} _{i\in \mathbb {N}}$, which means that $\overline{C}$ is contained in the set of accumulation points of each such sequence.

Now we will construct main space for our example. Let $Q\subset \Sigma _2^+$ be the set obtained by Lemma 3.4. For each $i\in \mathbb {Z}$ define $t_i=1-2^{-i}$ for $i\ge 0$ and $t_i=-1+2^{-i}$ for $i<0$. Define quotient space $\mathcal {X}=Y/\mathord {\sim }$ where

$$\begin{aligned} Y=(Q\times \mathbb {S}^1\times \left\{ -1,1\right\} )\cup \bigcup _{\alpha \in Q}\bigcup _{i\in \mathbb {Z}} \left\{ (\alpha ,p_i^\alpha , t_i\right\} . \end{aligned}$$

and $\sim$ is an equivalence relation defined by $(\alpha ,x,t)\sim (\alpha ',x',t')$ provided that one of the conditions is satisfied: $x=x'$ and $t=t'=1$; $x=x'$ and $t=t'=-1$; or $(\alpha ,x,t)= (\alpha ',x',t')$. We endow $\mathcal {X}$ with the metric $\rho$ given by

$$\begin{aligned} \rho \left( (\alpha ,x,t), (\alpha ',x,t') \right) =\max \left\{ |t-t'|, |t|\cdot d(\alpha ,\alpha '), |x-x'| \right\} \end{aligned}$$

where $(\alpha ,x,t)$ is any member of the class $[(\alpha ,x,t)]_{\sim }$. If we fix any $r=t_i$ for some $i\in \mathbb {Z}$ then we have two possibilities. Either

$$\begin{aligned} Y_r=\left\{ (\alpha ,x,t)\in Y : t=r\right\} =Q\times \left\{ (x,r)\right\} \end{aligned}$$

or there are two $b,q\in \mathbb {S}^1$ and n such that

$$\begin{aligned} Y_r= & {} \left\{ (\alpha ,x,t)\in Y : t=r\right\} \\= & {} \left\{ \alpha \in Q: \alpha _n=0\right\} \times \left\{ (b,r)\right\} \cup \left\{ \alpha \in Q: \alpha _n=1\right\} \times \left\{ (q,r)\right\} . \end{aligned}$$

In both cases the set $Y_r$ is compact. Furthermore, each $Y_r\subset Q\times S^1\times \left\{ r\right\}$ which immediately implies that Y is compact (and as a result $\mathcal {X}$ is compact too, since $\sim$ is a closed equivalence relation).

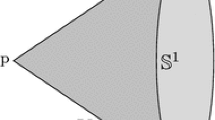
Observe that $\rho$ is well defined, it induces topology which coincides with the quotient topology on $\mathcal {X}$, and hence $(\mathcal {X},\rho )$ is a compact metric space (Fig. 2). In what follows, we will write $(\alpha ,x,t)\in \mathcal {X}$ identifying each such element with the class it represents under $\sim$. Of course for $|t|\ne 1$ we have

$$\begin{aligned}{}[(\alpha ,x,t)]_\sim =\left\{ (\alpha ,x,t)\right\} \end{aligned}$$

Define a selfmap $\varphi$ on the set $\left\{ t_i : i\in \mathbb {Z}\right\} \cup \left\{ -1,1\right\}$ by

$$\begin{aligned} \varphi (t)={\left\{ \begin{array}{ll} t_{n+1}&{} \text { if }t=t_n,\\ t&{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

and then we define $G:\mathcal {X}\rightarrow \mathcal {X}$ by

$$\begin{aligned} G([\alpha ,x,t]_\sim )= {\left\{ \begin{array}{ll} {[}\alpha ,p^\alpha _{i+1},\varphi (t)]_{\sim } &{} \text { if }x=p^\alpha _i \text { and }|t|<1,\\ {[}\alpha ,g(x),t]_\sim &{} \text { if }|t|=1. \end{array}\right. } \end{aligned}$$

It is not hard to see that G is a continuous map.

Fig. 2

Sketch of the space $\mathcal {X}$

Lemma 5.2

Dynamical system $(\mathcal {X},G)$ is almost equicontinuous.

Proof

Fix any $[\alpha ,x,t]_\sim \in \mathcal {X}$ with $|t|<1$. Then $x=p_i^\alpha$ and $t=t_i$ for some $i\in \mathbb {Z}$. Fix any $\varepsilon >0$ and let n be such that $4^{-n}<\varepsilon$. Let $\gamma >0$ be such that $(t_i-\gamma ,t_i+\gamma )\cap (t_{i-1},t_{i+1})=\left\{ t_i\right\}$ and $\gamma <2^{-n} t_i$, $\gamma <\varepsilon$. Then $d(\alpha ,\beta )<\gamma$ implies $\alpha _{[0,n]}=\beta _{[0,n]}$. Let

$$\begin{aligned} U=B_\gamma ([\alpha ,x,t])\subset \left\{ [\beta ,y,s]_\sim : d(\alpha ,\beta )<\gamma , |s-t|<\gamma \right\} . \end{aligned}$$

If we take any $[\beta ,y,s]_\sim \in U$ then $s=t=t_i$ and $y=p^\beta _i$ and for any $j\ge 0$ we have

$$\begin{aligned} G^j\left( \left[ \beta ,y,s\right] _\sim \right) =\left[ \beta ,p^\beta _{i+j}, \varphi ^j(t)\right] ,\quad G^j([\alpha ,x,t]_\sim )=\left[ \alpha ,p^\alpha _{i+j}, \varphi ^j(t)\right] . \end{aligned}$$

Observe that it follows from the definition of $\rho$ that if $\left| p^\beta _{i+j}-p^\alpha _{i+j}\right| <\varepsilon$ then $\rho \left( [\beta ,y,s]_\sim ,[\alpha ,x,t]_\sim \right) <\varepsilon$. But since $\alpha _i=\beta _i$ for all $i\le n$ then $p^\beta _{i+j}\ne p^\alpha _{i+j}$ is possible only when $p^\beta _{i+j},p^\alpha _{i+j}\in I^k_l$ for some $k>n$ and some $l \in \mathbb {Z}.$ But then

$$\begin{aligned} \left| p^\beta _{i+j}-p^\alpha _{i+j}\right| \le {{\mathrm{diam}}}(I_l^k)\le 4^{-k}\le 4^{-n}<\varepsilon . \end{aligned}$$

We have just proved that G is equicontinuous at each point $[\alpha ,x,t]_\sim$ with $|t|<1$. In particular the set of equicontinuity points is an open dense set, completing the proof. $\square$

Lemma 5.3

Dynamical system $(\mathcal {X},G)$ is $\hat{\omega }$-chaotic.

Proof

We claim that the set $S=\left\{ [\alpha ,x,t]_\sim \in \mathcal {X}: t=0\right\}$ is $\hat{\omega }$-scrambled. As we mentioned earlier, for every $\alpha \in Q$ we have that accumulation points of the sequence $\left\{ p^\alpha _i\right\} _{i=1}^\infty$ contain $\overline{C}$, hence we have

$$\begin{aligned} \omega _G\left( [\alpha ,x,0]_\sim \right) \supset Q\times \overline{C}\times \left\{ 1\right\} /_\sim . \end{aligned}$$

This shows that S satisfies conditions (2) and (3) in Definition 1.2. On the other hand, by the definition of Q, for any choice of $\alpha ^1,\ldots ,\alpha ^n\in Q$ we can always find i such that $\alpha ^1_i=\alpha ^2_i=\cdots =\alpha ^{n-1}_i=1$ and $\alpha ^{n}_i=0$. But then the set of accumulation points of the sequence $\left\{ p^{\alpha ^j}_i\right\} _{i=1}^\infty$ for $j<n$ contains the set $I^n_0$ while none of the points from interior of $I^n_0$ can be obtained as a limit of a subsequence of $\left\{ p^{\alpha ^n}_i\right\} _{i=1}^\infty$. This shows that

$$\begin{aligned} \bigcap _{i=1}^{n-1}\omega _G\left( [\alpha _i,x,0]_\sim \right) {\setminus } \omega _G\left( [\alpha _n,x,0]_\sim \right) \supset Q\times \left( \text {Int}I_n^0\right) \times \left\{ 1\right\} /_\sim . \end{aligned}$$

proving that (1) in Definition 1.2 also holds. The proof is completed. $\square$

It is enough to combine Lemmas 5.2 and 5.3 to obtain the following.

Theorem 5.4

There exists an almost equicontinuous $\hat{\omega }$-chaotic dynamical system.

Remark 5.5

Note that the set S in the proof of Lemma 5.3 is open (because $t=0$ is isolated in the sequence $\left\{ t_n\right\} _{n\in \mathbb {Z}}$), but $G^n(S)\cap S=\emptyset$ for every $n>0$. In particular $(\mathcal {X},G)$ is not transitive.

Remark 5.6

We can identify antipodal points in $\mathcal {X}$ by putting relation $[(\alpha ,x,t)]_\sim \approx [(\beta ,x,s)]_\sim$ when $|s|=|t|=1$, obtaining this way a system with exactly one minimal subset.

Almost equicontinuous systems are to some extent very regular. They leave some space for sensitivity, but this space is quite narrow. In that sense we may view almost equicontinuous systems as systems with quite regular dynamics. From this point of view it seems that the definition of $\omega$-chaos (and $\hat{\omega }$-chaos) should be strengthened. In our opinion, the smallest demand should be conditions in Remark 1.3. It also seems reasonable to require in place of Remark 1.3 (ii) a stronger condition:

• (ii’) $\bigcap _{i=1}^n \omega _{f}(x_i)$ contains an uncountable family of pairwise disjoint uncountable minimal set.