A memetic algorithm for a real-world dynamic pickup and delivery problem

Abstract

The dynamic pickup and delivery problem (DPDP) is essential in supply chain management and logistics. In this study, we consider a real-world DPDP from daily delivery scenarios of a company. In the problem, orders are generated randomly and released periodically. The orders should be completed as soon as possible to minimize the cost. We propose a novel memetic algorithm (MA) to address this problem. The proposed MA consists of a genetic algorithm and a local search strategy that periodically solves a static pickup and delivery problem when new orders are released. We have conducted extensive experiments on 64 real-world instances to assess the performance of our method. Three state-of-the-art algorithms are chosen as the baseline algorithms. Experimental results demonstrate the effectiveness of the MA in solving the real-world DPDP.

1 Introduction

The vehicle routing problem (VRP) is one of the most widely studied problems in operations research [1]. It has practical significance because many real-world problems in applications, such as transportation, supply chain management and production planning, can be formulated as VRP [2]. The classic VRP aims to determine a route plan for a fleet of vehicles to serve a set of customers. In recent decades, the VRP and its variants have been intensively studied [1, 3].

The pickup and delivery problem (PDP) [4] is an essential variant of VRP in which goods must be delivered from different origins to different destinations. Based on the availability of information, PDP can be classified into two categories: static and dynamic. In static PDP, all problem information is known at the beginning, while in dynamic PDP, there is little prior information available, and vehicle actions have to be decided dynamically. In this paper, we focus on a real-world dynamic PDP (DPDP) arising from Huawei’s daily delivery scenarios.¹ The problem was presented in a competition held by Huawei in 2021. During the manufacturing process, many cargoes need to be delivered to factories. However, most delivery requirements cannot be given in advance due to the uncertainties of customers’ requirements and production processes. The information for delivery orders includes the pickup factory, the delivery factory, the amount of cargo, and the time requirement. These orders occur randomly, and a fleet of homogenous vehicles is periodically scheduled to serve these orders. Due to a large number of delivery requests, even a tiny improvement in logistics efficiency can bring significant benefits. Therefore, it is necessary to develop an effective method to tackle this problem.

The real-world DPDP considered in this study has the following characteristics:

• Limited vehicle capacity A vehicle has a maximum load capacity.

• Time windows Orders need to be completed within the time windows. Otherwise, the penalty cost is incurred.

• Order split Splitting is only allowed for orders that exceed the loading capacity of the vehicle.

• Last-in-first-out (LIFO) loading The last loaded cargo should be unloaded first.

• Open VRP The vehicle does not need to return to its initial location.

• Large-scale problem Thousands of orders are considered.

• Dynamic orders Orders are generated periodically.

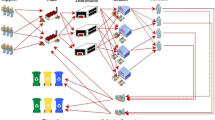
Figure 1 gives an example of the real-world DPDP. Two vehicles are available, and the initial locations of the vehicles are generated randomly. Delivery orders with the information on the pickup and delivery factories, cargo amount, and time windows are generated dynamically. At 9:00, two orders, $O_1$ and $O_2$, are generated and assigned to the vehicle $V_1$ and $V_2$, respectively. Let us suppose $O_1$ and $O_2$ need to transport cargoes from F1 to $F_2$ and from $F_3$ to $F_5$, respectively. According to $O_1$, $V_1$ takes cargoes at $F_1$ and sends them to $F_2$. Similarly, according to $O_2$, $V_2$ first takes cargoes at $F_3$. At 9:30, a new order $O_3$ which needs to transport cargoes from $F_4$ to $F_5$ is generated and assigned to $V_2$. Therefore, $V_2$ travels to $F_4$ to take cargoes and finally to $F_5$ for delivery. The LIFO loading constraint should be satisfied. Thus, the cargoes taken from $F_4$ should be unloaded from $V_2$ first.

From the perspective of objective functions, two objective functions need to be optimized in the problem. The first is to minimize the average traveling distance of vehicles, and the second is to reduce the penalty cost caused by violating the time window constraint. The real-world DPDP is hard since it is an extension of the classical VRP that has been proven to be NP-hard [5]. To the best of our knowledge, although several researchers have addressed the DPDP, few have ever considered all the above characteristics simultaneously. There is still a gap between the recent research and the need of real-world applications. Because of its complexity, the exact algorithms cannot effectively solve the real-world DPDP, particularly for large-scale instances. Instead, metaheuristics can provide high-quality solutions within a reasonable time [6], which are expected to be effective for the considered problem.

Evolutionary algorithms (EAs) are a type of metaheuristic used to manipulate a population of solutions. An EA is suitable for dynamic problems because: (1) the solutions scattering over the search space are beneficial to capture the dynamic changes in dynamic problems. (2) It can transfer problem-specific knowledge from one generation to another, which helps deal with a cyclic dynamic environment [7]. It is well known that combining population-based evolutionary search with problem-specific local search is an effective way to design powerful evolutionary computation methods [8]. These kinds of algorithms are often called memetic algorithms (MAs). MAs are the most famous representative methods in the field of memetic computing, which is a combination of multiple branches of computer science and the transfer of other scientific methods such as biology, sociology, and physics [9]. During the past few decades, MAs have been successfully applied to various complex problems [10]. Following the discipline of MAs, we design a MA to solve the real-world DPDP effectively. The proposed MA consists of two components: (1) the first component is a genetic algorithm that obtains a diverse population and explores the search space. (2) The second component is a local search that helps the search find high-quality solutions. Simultaneously using these two components can balance the exploration and exploitation well. Experimental results on small-scale to large-scale (up to 4000 orders) DPDP instances show the effectiveness of the proposed MA compared with that of the state-of-the-art methods.

The contributions of this study are summarized as follows:

• We focus on an application-oriented DPDP variant with multiple constraints.

• We provide a memetic algorithm, MA, to solve the real-world DPDP. MA consists of a genetic algorithm and a local search. The former component explores the search space, while the latter aims to find high-quality solutions in a search region. Therefore, the proposed MA can balance exploration and exploitation well, and high-quality solutions can be expected to be obtained.

• Compared with the state-of-the-art algorithms, the experimental results show that MA can obtain high-quality solutions for large-scale instances in a reasonable running time. The proposed MA can be seen as a benchmark algorithm for comparison in future works.

The rest of this paper is organized as follows. In Sect. 2, we present the background, including the problem definition and the literature review. In Sect. 3, we describe the proposed MA. Section 4 contains the dataset description, analysis of the MA and experimental results. Finally, in Sect. 5 we give the conclusion and future work.

2 Background

2.1 Problem definition

The real-world DPDP can be defined as a complete directed graph $G=\{\varvec{F}, \varvec{E}\}$, where

• 1. $\varvec{F}=\{F_{1},\ldots ,F_{M}\}$ represents a set of factories, where $F_i$ ($i \in \{1,\ldots ,M$}) is the ID of the ith factory. Each factory has several cargo docks. When a vehicle arrives at a new factory $F_i$, it is assigned to a cargo dock for loading and unloading, which takes dock approaching time $Dock_i$.

• 2. $\varvec{E}=\{E_{i,j}\mid i,j \in \{1,\ldots ,M\} \}$ represents the arcs between the factories. Each arc $E_{i,j}$ has a travel distance $d_{i,j}$ and a travel time $t_{i,j}$ from the ith factory to the jth factory.

The orders are dynamically generated in the problem. Let $\varvec{O}=\{O_1,\ldots ,O_N\}$ be the order set. Each order $O_j$ ($j\in \{1,\ldots , N\}$) has the following attributes:

$$\begin{aligned} O_{j}=\left\{ F^{j}_p, F^{j}_d, q_j, tw_j\right\} . \end{aligned}$$

(1)

where

$F^{j}_p$:

The pickup factory of $O_j$.

$F^{j}_d$:

The delivery factory of $O_j$.

$q_j$:

The amount of cargo. There are three types of cargoes, namely standard pallet, small pallet and box. Thus, $q_j$ consists of the standard pallet amount $q_j^{standard}$, the small pallet amount $q_j^{small}$, and the box amount $q_j^{box}$, i.e., $q_j=(q_j^{standard}, q_j^{small},q_j^{box})$. The demands of the standard pallet amount, small pallet and box are 1, 0.5 and 0.25, respectively.

$tw_j$:

The service time window of $O_j$. $tw_j=[b_j,e_j]$, where $b_j$ and $e_j$ represent the order creation time and committed completion time, respectively.

Let $\varvec{V}=\{V_{1},\ldots ,V_{K}\}$ be a set of homogeneous vehicles. Each vehicle $V_k$ ($k\in \{1,\ldots , K\}$) has a maximum load capacity Q. The initial locations of the vehicles are randomly set to the factories. For the real-world DPDP, we need to plan K routes $\varvec{R}=\{R_1,\ldots ,R_K\}$ with the lowest cost. Each route is served by a vehicle. Let $R_k=\langle P_{1,k}, \dots , P_{N_k,k} \rangle$ be the kth route visited by $V_k$. Each node $P_{i,k}$ has the following attributes:

$$\begin{aligned} P_{i,k}=\{O_{i,k}, F_{i,k}\}. \end{aligned}$$

(2)

where

$O_{i,k}$:

The ith order served by $V_k$.

$F_{i,k}$:

The factory ID where $V_k$ is going to visit. $F_{i,k}=F^{i,k}_p$ if the vehicle is to pick up cargoes of $O_{i,k}$. Otherwise, $F_{i,k}=F^{i,k}_d$.

Fig. 1

Illustration of the real-world DPDP

Based on these notations, the travel distance of $R_k$ is calculated as:

$$\begin{aligned} Dist_{k} = \sum _{i=1}^{N_k-1}d_{F_{i,k},F_{i+1,k}} \end{aligned}$$

(3)

and the average traveling distance of all routes is calculated as:

$$\begin{aligned} { AD} = \frac{1}{K}\sum _{k=1}^K Dist_k \end{aligned}$$

(4)

Let $a_{i,k}$ be the arrival time of $V_k$ at the factory $F_{i,k}$ and $l_{i,k}$ be the leaving time. The arrival time $a_{i,k}$ ($i\in \{1,\ldots ,N_k\}$) is calculated as:

$$\begin{aligned} a_{i,k} = l_{i-1,k} + t_{F_{i-1,k},F_{i,k}} \end{aligned}$$

(5)

where $l_{0,k}$ denotes the time $V_k$ was assigned the first order, i.e., $V_k$ starts from the initial location immediately after receiving the first order. $t_{F_{0,k},F_{1,k}}$ denotes the travel time between $V_k$’s initial location $F_{0,k}$ and the first visited factory $F_{1,k}$. The leaving time $l_{i,k}$ ($i\in \{1,\ldots ,N_k\}$) is calculated as:

$$\begin{aligned} l_{i,k} = a_{i,k} + { DAT}_{i,k}+ s_{i,k} \end{aligned}$$

(6)

where ${ DAT}_{i,k}$ is the dock approaching time of $V_{k}$ at $F_{i,k}$, which is defined as:

$$\begin{aligned} { DAT}_{i,k}=\left\{ \begin{array}{ll} Dock_i&{}\quad \text {if} \ F_{i-1,k} \ne F_{i,k} \\ 0&{}\quad \text {otherwise} \\ \end{array} \right. \end{aligned}$$

(7)

$s_{i,k}$ is the service time of $V_{k}$ for serving $O_{i,k}$, which is calculated as:

$$\begin{aligned} s_{i,k} = s_{i,k}^{standard} + s_{i,k}^{small} + s_{i,k}^{box} \end{aligned}$$

(8)

where $s_{i,k}^{standard}$, $s_{i,k}^{small}$ and $s_{i,k}^{box}$ are the loading/unloading time for standard pallet, small pallet and box of $O_{i,k}$, respectively.

Each order should be dispatched by exactly one vehicle. Besides, all orders should be completed within the time windows. Otherwise, the violation of the time window constraint of $O_{i,k}$ results in a delay time $dt_{i,k}$, which is calculated as:

$$\begin{aligned} dt_{i,k} = \max \left( l_{i,k} - e_{i,k}, 0\right) \end{aligned}$$

(9)

The penalty cost ${ PC}$ is defined as the total delay time of all orders, which is calculated as follows:

$$\begin{aligned} { PC} = \sum _{k=1}^{K} \sum _{i=1}^{N_k} dt_{i,k} \end{aligned}$$

(10)

The optimization objective of the real-world DPDP is to minimize the average traveling distance of all routes ${ AD}$ and the penalty cost ${ PC}$. The two functions are in conflict [11]. One specific scenario is that many orders are generated with the same pickup and delivery factories at different time. Then, when every order is generated and served immediately by a vehicle, the objective function ${ PC}$ has the minimum value, while the objective function ${ AD}$ has the maximum value. On the contrary, when the orders are delayed until the orders with the same pickup and delivery nodes are packed to be served by a vehicle, the objective function ${ PC}$ has the maximum value, while the objective function ${ AD}$ has the minimum value. In the real business scenario, if a delay occurs, the subsequent assembling and selling are canceled or delayed, resulting in significant economic loss [12]. Therefore, the orders should be completed as soon as possible. The fitness function of the real-world DPDP is defined as:

$$\begin{aligned} \min f = { AD} + \lambda \times { PC} \end{aligned}$$

(11)

where $\lambda$ is a large positive value (e.g., 10,000). This definition shows that the penalty cost is more important than is the average traveling distance due to the large $\lambda$.

The constraints of the problem can be defined as follows:

• 1. Limited vehicle capacity For each vehicle $V_k$, the demand of loaded cargoes cannot exceed the maximum load capacity Q. More specifically, let us suppose $V_k$ is to pick up cargoes of $O_{i,k}$ and let $c_{i-1,k}$ be the capacity of $V_k$ before serving $O_{i,k}$. The following condition must hold:

  $$\begin{aligned} c_{i-1,k} + q_{i,k}^{standard} + 0.5\times q_{i,k}^{small} + 0.25\times q_{i,k}^{box} \le Q \end{aligned}$$

  (12)

• 2. An order can be split into small orders if the demand for its cargo exceeds the maximum load capacity of the vehicle. The smallest units of different types of cargoes are one standard pallet, one small pallet and one box. For example, let us suppose the maximum load capacity of a vehicle is 5, and an order with $q=(6,0,1)$ (total demand is 6.25) is assigned to the vehicle. Since the demand exceeds the maximum load capacity, the order can be split into several combinations of small orders that meet the capacity constraint, i.e., two orders with $q=(5,0,0)$ and $q=(1,0,1)$, respectively. However, splitting is not allowed for orders that do not exceed the maximum load capacity.

• 3. Time window constraint Orders should be completed within the time windows. Otherwise, the penalty cost is calculated according to Eq. (10).

• 4. LIFO loading constraint The last loaded cargo must be first unloaded.

For example, in Fig. 1, there are five factories $\varvec{F}=\{F_{1},F_2,F_3,F_4,F_{5}\}$, three orders $\varvec{O}=\{O_1,O_2,O_3\}$ and two vehicles $\varvec{V}=\{V_1,V_2\}$. The orders are detailed as follows:

• $O_1=\{F_1,F_2,(1,0,1),[9:00,13:00]\}$

• $O_2=\{F_3,F_5,(2,0,0),[9:00,13:00]\}$

• $O_3=\{F_4,F_5,(3,1,0),[9:30,13:30]\}$

There are two routes $\varvec{R}=\{R_1,R_2\}$ in the figure, where $R_1$ and $R_2$ are served by $V_1$ and $V_2$, respectively. Following the problem defined above, the routes can be defined as follows:

• 1. $R_1 = \langle \{O_1,F_1\}, \{O_1,F_2\}\rangle$

• 2. $R_2 = \langle \{O_2,F_3\}, \{O_3,F_4\}, \{O_3,F_5\}, \{O_2,F_5\}\rangle$

2.2 Related work

The VRP is to plan a set of least-cost routes for a fleet of vehicles to satisfy the demand of customers. VRP was formulated by Dantzig and Ramser [13]. Since then, many variants of VRP have been successfully applied in practice. In VRP, if all information is known before solving the problem, the problem is regarded as static VRP. Until now, most researchers have focused on static VRPs. However, the information may be dynamic and not known in advance in real-world scenarios such as ride-sharing and home delivery. This type of VRP is referred to as dynamic VRP (DVRP). Compared to the static VRP, the dynamic VRP has yet to be thoroughly studied. Psaraftis et al. [14] presented a comprehensive review of the works on DVRPs over 3 decades, and recent literature [15] reviewed the research in this area in 2015–2021. The DVRP is NP-hard. Thus, exact methods such as branch-and-price [16] can only apply to the small-scale DVRP within reasonable computing time. Most methodologies for large-scale DVRPs are heuristics or metaheuristics, which can be further divided into two categories: insertion methods and reoptimization methods.

In the insertion methods, a feasible solution is constructed by adding a newly generated order to the current routing plan. This kind of method has been widely used in the field of DVRP. To name a few, Pureza and Laporte [17] proposed a constructive–deconstructive heuristic with waiting strategies for the DPDP with time windows. Ulmer [18], Ulmer and Thomas [19], Ulmer et al. [20] first modeled the same-day delivery problem with soft deadlines, the same-day delivery with heterogeneous fleets of drones and vehicles, and the restaurant meal delivery problem as a Markov decision process, respectively, and then applied the insertion methods to solve these problems. Xu et al. [21] proposed a dynamic programming-based insertion operator for dynamic ridesharing. In their work, a partition-based framework was proposed to reduce the time complexity of a generic insertion operator.

In the reoptimization methods, the problem was addressed again when new orders arrive. Mitrović-Minić and Laporte [22] proposed an approach based on waiting strategies for the DPDP with time windows. The proposed algorithm consists of a cheapest insertion and a tabu search procedure. AbdAllah et al. [23] proposed an enhanced genetic algorithm to solve a DVRP. For each period, a genetic algorithm is called to solve a static VRP-like instance generated by an event manager subsystem. Fikar [24] proposed an insertion heuristic to solve a problem in e-grocery deliveries. In the heuristic, all new requests are evaluated and inserted into the best positions in the current solution. Then, local search is applied to improve the solution. Park et al. [25] proposed a genetic algorithm to solve a dynamic version of VRP with simultaneous pickup and delivery. The period of the reoptimization process is determined by a waiting strategy. Karami et al. [26] proposed a periodic approach to solve the DPDP with time windows. The proposed method is a two-step scheduling heuristic consisting of a cheapest insertion and a local search. Archetti et al. [27] proposed a variable neighborhood search method to solve the online vehicle routing problem with occasional drivers. Xu and Wei [28] proposed a heuristic incorporating Clarke–Wright saving algorithm and adaptive large neighborhood search for DPDP with transshipments and LIFO constraints.

Following the second category, MA has been successfully applied to several DVRPs. Euchi et al. [29] proposed an ant colony based on a 2-opt local search for a DVRP. Necula et al. [30] proposed an ant colony optimization with a local search procedure for a DPDP with time windows. Mańdziuk and Żychowski [31] proposed a MA with a starting delay mechanism for a DVRP with dynamic requests. Berahhou and Benadada [32] proposed a MA combining a genetic algorithm and a local search for a DVRP with simultaneous delivery and pickup. da Silva Júnior et al. [33] proposed a multiple ant colony system with random variable neighborhood descent to solve a DPDP with time windows. The algorithm has two phases. The first is a static routing for known customers, and the second is to reoptimize the routes continuously or periodically for dynamic customers.

The real-world DPDP considered in this study contains multiple constraints and sources from the competition held by Huawei in 2021. There were 153 teams participating in the competition. Three metaheuristic algorithms, namely variable neighborhood search with multiple local search strategies and an efficient disturbance (VNSME) [11], insertion method (IM) and local search (LS), won gold, silver, and bronze prizes respectively in the competition. The winning algorithms are briefly described as follows:

• 1. VNSME An initial solution is first constructed by using the cheapest insertion method for each period. Then, the VNS method is utilized to improve this solution. It consists of several local searches, including couple-exchange, couple-relocate, block-exchange, and block-relocate. Moreover, the 2-opt is utilized as the perturbation operator.

• 2. IM An insertion strategy is utilized to construct a solution for each period.

• 3. LS The idea of LS is similar to VNS. For each period, an initial solution is constructed by an insertion strategy which first inserts urgent orders into the route plan and then inserts the remaining orders in decreasing travel time order. A local search strategy then improves the solution.

Table 1 Related work for DVRPs

Table 2 Abbreviations for problem constraint

Table 1 summarizes the related work for the DVRPs. The abbreviations for problem constraints in Table 1 are specified in Table 2. Although several methods exist for solving the DVRPs, few have ever applied to the considered DPDP. Because of the different problem structures, those applied to other DVRP variants may not directly apply to the considered DPDP. Unlike the winning algorithms that manipulate a single solution, the proposed MA controls a population during the search. Therefore, MA can explore the search space and get more chances to find high-quality solutions. The experimental results in Sect. 4 show the superiority of the proposed MA over the competitors.

3 Memetic algorithm

3.1 Main framework

In the real-world DPDP, the orders are released periodically at a time interval $\Delta T$. When new orders are released at time t, a static PDP problem is first formed by all the orders that have not been completed. Then, MA is applied to solve the static problem and returns a route plan $\varvec{R}(t)$. The route plan is a set of routes defined in Sect. 2.1. Algorithm 1 presents the framework of the proposed MA. Each period generates a new batch of orders, and all unstarted orders are collected (Line 4). Then, the status of all vehicles is updated (Line 5). Based on the information of orders and vehicles at time t, a population containing N solutions is first initialized (Line 6). Then, the population undergoes the evolutionary process to obtain a feasible route plan (Lines 8–17). At each generation, N offspring solutions are generated by a crossover operator (Line 11) and improved by a local search (Line 12). The crossover operator is a diversification mechanism for discovering promising unexplored areas in the search space, while the local search is an intensification mechanism for obtaining high-quality solutions within the search areas [34]. Combining these two operators leverages their advantage to find better solutions. After that, the fitness values of parent and offspring solutions are calculated by Eq. (11), and the best N solutions are selected as the new parent solutions for the next generation (Line 15). We repeat this process until the stopping criterion is met. Finally, the best solution in the population is regarded as the route plan $\varvec{R}(t)$ at time t.

Algorithm 1

MA for the Real-world DPDP

3.2 Collecting orders and updating status

3.2.1 Collecting orders

First, we collect all unstarted orders $\varvec{O}(t)$ at time t. The unstarted orders include the new orders and those that have been assigned but not started. For each order $O_i \in \varvec{O}(t)$, it is necessary to check whether $O_i$’s demand exceeds the vehicle’s maximum load capacity. If it does, $O_i$ is split into multiple small orders with the smallest cargo unit. For example, suppose the vehicle’s maximum load capacity is five, and there is an order O with $q=(5,1,1)$ (total demand is 5.75). Since the demand of O exceeds the vehicle’s maximum load capacity, O is split into seven small orders, i.e., five orders with $q=(1,0,0)$, one order with $q=(0,1,0)$ and one order with $q=(0,0,1)$.

3.2.2 Updating status

Given the route plan $\varvec{R}(t-\Delta T)$ at previous time $t-\Delta T$, the status of the vehicles at time t needs to be updated, and an initial route plan at time t is obtained. Specifically, let $R_k$ denote the route served by the vehicle $V_k$. We first update $V_k$’s location at time t; then, we remove the orders that have been completed and those that have not yet started at time t.

For example, let the route at time $t-\Delta T$ be

$$\begin{aligned}&R_k(t-\Delta T)=\langle \{O_1,F_1\}, \{O_1,F_2\}, \{O_2,F_2\}, \{O_2,F_3\},\\&\quad \quad \{O_3,F_4\}, \{O_3,F_5\}\rangle \end{aligned}$$

and the vehicle $V_k$ was serving the order $O_1$ at $F_2$. The updating process consists of the following two steps:

• 1. First, the location of $V_k$ at time t is calculated according to Eqs. (3)–(8). Assume that after the calculation, $V_k$ arrives at $F_3$ and begins to serve the order $O_2$ at time t.

• 2. Then, we remove the completed order $O_1$ and the unstarted order $O_3$ from $R_k$ so the route contains only the ongoing order $O_2$ at time t.

Therefore, after the updating process, the route at time t is $R_k(t)=\langle \{O_2,F_2\}, \{O_2,F_3\} \rangle$.

3.3 Population initialization

For each static DPDP at time t, we initialize the population $\varvec{P}$ with N solutions based on the route plan $\varvec{R}(t)$ and the set of unstarted orders $\varvec{O}(t)$. Each solution $p^i \in \varvec{P}$ is a route plan with K routes. Algorithm 2 presents the initialization procedure. First, we check if there are orders whose pickup factories are the same factory where the vehicles are currently located and whose delivery factories are the same as the next destinations of the vehicles. If they exist, these orders are assigned to the vehicles one by one without violating the capacity constraint and without increasing the total delay of the routes (Line 1). This strategy can help construct a high-quality initial solution with less delay time, as it saves dock approaching time when a vehicle serves multiple orders sequentially at the same factory, compared to serving multiple orders at different factories. The assigned orders are removed from $\varvec{O}(t)$ (Line 2). For example, we suppose the unstarted order set is $\varvec{O}=\{O_3, O_4, O_5\}$ at time t, where

• $O_3=\{F_4,F_3,(1,0,1),[9:00,13:00]\}$

• $O_4=\{F_2,F_3,(1,1,0),[8:30,12:30]\}$

• $O_5=\{F_2,F_3,(2,1,0),[9:30,13:30]\}$

Besides, suppose that one of the routes in $\varvec{R}(t)$ is $R_k=\langle \{O_2,F_2\}, \{O_2,F_3\} \rangle$. The vehicle is currently at $F_2$ and the next destination is $F_3$. Since the pickup factory of $O_4$ and $O_5$ is $F_2$, which is the vehicle’s current location. Meanwhile, the delivery factory of both orders is $F_3$, which is the next destination of the vehicle. Therefore, after serving $O_2$ at $F_2$, the vehicle should continue to serve $O_4$ and $O_5$ in turn at $F_2$ if the vehicle’s capacity constraint is not violated and the total delay time of $R_k$ does not increase. After assigning $O_4$ and $O_5$ to the vehicle, the route $R_k$ is updated as:

$$\begin{aligned} R_k= & {} \langle \{O_2,F_2\}, \varvec{\{O_4, F_2\}, \{O_5, F_2\}, \{O_5, F_3\}, \{O_4, F_3\}},\\ {}{} & {} \quad \{O_2,F_3\} \rangle \end{aligned}$$

$O_4$ and $O_5$ are removed from $\varvec{O}(t)$, and only $O_3$ remains in $\varvec{O}(t)$.

Second, the population $\varvec{P}$ is initialized based on the updated $\varvec{R}(t)$ and $\varvec{O}(t)$ (Lines 3–8). For each solution $p^i \in \varvec{P}$, we first copy $\varvec{R}(t)$ to $p^i$, then randomly assign all orders in $\varvec{O}(t)$ to $p^i$. After this procedure, N feasible initial solutions are generated.

Algorithm 2

Population Initialization at Time t

3.4 Crossover operator

The crossover operator is the main operator in MA. It produces a new population of solutions (i.e., offspring solutions) by combining the parent solutions. To obtain high-quality solutions, the crossover operator should be designed to ensure that offspring solutions inherit good features of both parents [35]. In this study, the crossover operator for the real-world DPDP is designed to combine two parent solutions into one offspring solution, which is described as follows. Given two parent solutions $p^1$ and $p^2$, we first calculate the total delay time of each route. The routes with less delay time are selected and copied into the offspring solution. Then, we check whether the offspring solution is feasible, i.e., there are duplicate orders served by multiple vehicles. If there are, duplicate orders are removed from the routes to ensure that each order is served exactly by one vehicle. Finally, all unallocated orders are randomly assigned to the vehicles of the offspring solution.

Figure 2 illustrates the process of the crossover operator. For simplicity, each solution contains three routes served by three vehicles, and each route contains only the orders (the pickup and delivery factories are ignored). The process is described as follows.

• 1. First, the delay time of each route is calculated. For example, the delay time of $R_1$, $R_2$, and $R_3$ in $p^1$ is calculated as 0, 150, and 50, respectively, while the delay time of $R_1$, $R_2$, and $R_3$ in $p^2$ is calculated as 0, 100, and 300, respectively.

• 2. Second, the routes with less delay time, i.e., $R_3$ in $p^1$ and $R_2$ in $p^2$, are selected and combined to form an offspring solution. Since the delay time of $R_1$ in both parents is the same, we randomly choose a route (e.g., $R_1$ in $p^1$) and copy it into the offspring solution. However, the offspring solution is not feasible because the order $O_5$ has been assigned to two vehicles $R_2$ and $R_3$. Since the delay time of $R_2$ is larger than $R_3$, we remove $O_5$ from $R_2$ to (1) obtain a feasible solution and (2) further reduce the delay time.

• 3. Third, we check whether any unallocated orders exist in the offspring solution. Because the order $O_3$ is in the parent solutions but not in the offspring solution, it is randomly inserted into the offspring solution. For example, it is appended at the end of $R_2$ in the offspring solution in the figure.

Fig. 2

Illustration of the crossover operator

The proposed crossover operator can transfer elite components (i.e., the routes with less delay time) from the parent solutions to the offspring solutions. Moreover, the search space is explored by introducing randomness into the crossover operator. Therefore, the crossover operator is expected to be effective for the real-world DPDP.

3.5 Local search

The offspring solution produced by the crossover operator is further improved by local search. The local search consists of iterative exploitation of neighborhood move to search for high-quality solutions in a search region. Algorithm 3 presents the local search procedure. Given an initial solution x, two steps are performed sequentially in each iteration:

Algorithm 3

Local Search

• 1. In the first step, we calculate each order’s delay time in x. Then, the roulette wheel selection [36] is performed to select an order from x according to the delay time. The order with a larger delay time has a larger chance to be chosen.

• 2. In the second step, the selected order is removed from x and reinserted into the best feasible position to obtain a better neighborhood solution $x^{\prime }$. The best feasible position is the position that leads to the minimum fitness value calculated by Eq. (11) and without violating any constraints.

3.6 Complexity analysis

The proposed MA mainly consists of the genetic algorithm and local search. In the genetic algorithm, two steps are sequentially performed:

• 1. Population initialization Generate a feasible solution takes $O(N_{O(t)})$, where $N_{O(t)}$ denotes the number of orders at time t. Since N feasible solutions are generated at this step, it takes $O(N \cdot N_{O(t)})$.

• 2. Crossover operator The worst case to generate an offspring solution is to reassign all orders to the solution, which takes $O(N_{O(t)})$. Thus, it takes $O(N\cdot N_{O(t)})$ to generate N offspring solutions at each generation.

The local search iteratively performs neighborhood moves to improve the solution quality. A neighborhood move selects an order and removes it from the solution, which takes $O(N_{O(t)})$. Then, the selected order is reinserted into the best position of the solution, which takes $O(N_{O(t)}^2)$. Therefore, the local search takes $O({ LS}_{MAX}\cdot N_{O(t)}^2)$, where ${ LS}_{MAX}$ denotes the depth of the local search.

In summary, the complexity of the MA mainly depends on local search, which takes $O(N\cdot { LS}_{MAX}\cdot N_{O(t)}^2)$ at each generation.

4 Computational experiments

In this section, experiments are carried out on a server (Eight CPUs with Intel Xeon (Cascade Lake) Platinum 8269CY at 2.5 GHz, 16.0 GB of RAM) to assess the performance of the proposed MA. The MA is implemented in C++ and compiled by g++ with C++ 11 support on Ubuntu 14.04. The dataset description, parameter settings and experimental results are presented in the following sections.

4.1 Dataset description

We use 64 instances extracted from the company’s delivery scenarios [37] to validate the effectiveness of the MA. These instances can be categorized into eight sets: Set 1–Set 8. Each set contains eight instances of different sizes. Each instance contains information on all orders for a working day (24 h). The information is detailed in Sect. 2.1. According to the real business scenarios, the time interval $\Delta t$ is set to 10 min, i.e., the period for order release is 10 min. Therefore, a working day is split into 144 time intervals. A static PDP is formed at each interval and needs to be solved within 10 min. More details of the datasets can be found in Table 3.

From the perspective of factories, there are 154 factories in total. The travel distance and travel time metrics between the factories are asymmetry. The vehicles have the same load capacity. Due to the traffic conditions, the triangle inequality may not hold for travel time in the real world.

Table 3 Dataset settings

4.2 Parameter settings

The proposed MA has three parameters to be tuned, i.e., the population size N, the number of generations $G_{MAX}$, and the depth of local search ${ LS}_{MAX}$. To achieve the best performance, it is necessary to detect the best settings for the algorithmic parameters [2]. To this end, the Taguchi orthogonal arrays experimental design method [38] is utilized for parameter turning. Table 4 shows the different values of these parameters. According to the number of parameters and levels, we choose the orthogonal array $L_{16}(4^3)$ to carry out the experiments. Therefore, there are 16 combinations of parameters to be tested. All 64 instances are used for testing. The MA with each combination of parameters runs ten times on each instance.

Table 4 Parameter values

Table 5 Orthogonal table for the MA

Fig. 3

Mean effect of each parameter

Table 6 Results of MA_no_ls, MA_no_x and MA on eight datasets

Table 7 Statistical results of performance comparisons of MA with MA_no_ls and MA_no_x by Wilcoxon’s test and Friedman test

Table 8 Results of VNSME, IM, LS and MA on eight datasets

Table 5 shows the average values and running time on all instances for the MA with various combinations of parameters. The best average value is highlighted in bold. According to the results in Table 5, we illustrate the mean effect of each parameter setting in Fig. 3. We observe that in terms of solution quality, larger parameters lead to better results. The parameter N controls the population size. Larger N helps preserve a diverse population and facilitates the exploration of the search space. The parameter ${ LS}_{MAX}$ controls the depth of the local search. Larger ${ LS}_{MAX}$ helps better exploit a specific region in the search space. Therefore, MA with larger parameters can enhance search ability and obtain better solutions. Nevertheless, MA with larger parameters uses more running time, as shown in Fig. 3. Therefore, if time permits, it is recommended to use larger parameters to obtain better results. We adopt the setting $\{N=20, G_{MAX}=20, { LS}_{MAX}=20\}$ for the rest of the experiments.

4.3 Effectiveness of components in MA

The main components in MA are the crossover operator and the local search. To validate the effectiveness of the two components, two variants of MA, MA_no_ls and MA_no_x, are proposed to be compared with MA. In MA_no_ls, the local search is removed from the MA, while in MA_no_x, the crossover operator is removed from the MA. All algorithms run ten times on each instance.

Table 6 shows the results of all algorithms on each dataset. The best and average values are presented in the “Best Value” and “Average Value” columns. The best values are highlighted in bold. Moreover, nonparametric statistical tests, i.e., the Friedman test and Wilcoxon signed-rank test [39, 40] at 5 % significance level, are carried out further to show the difference between the MA and the competitors. Table 7 shows the statistics summarizing all performance comparisons. The column w/t/l indicates the MA significantly outperforms the competitor on w instances, performs similarly to the competitor on t instances, and is outperformed by the competitor on l instances, respectively. The last row shows the average rankings of algorithms calculated according to the Friedman method. A smaller ranking means better performance.

From Tables 6 and 7, MA performs best among all algorithms. Specifically, MA significantly outperforms the MA_no_ls and MA_no_x on 18 and 51 instances, respectively, and is outperformed by the MA_no_ls and MA_no_x on 4 and 1 instances, respectively. MA obtains the best average values on all instances and gets the first rank, followed by MA_no_ls and MA_no_x. This indicates that the crossover operator has a significant impact on the performance of the algorithm. The proposed crossover operator can explore the search space while preserving the elite components of the parent solutions, increasing the chance of finding more promising search regions. Therefore, it is essential to utilize the crossover operator for exploration. However, if only the crossover operator is used, the MA_no_ls is still inferior to the MA. The reason may be that some high-quality solutions cannot be found in a search region. The local search can dive into a search region to find a high-quality solution. Combining the crossover operator and local search can scatter the search into different regions and find better solutions in these regions. Therefore, the MA achieves the best results among all algorithms. The experimental results confirm the effectiveness of the crossover operator and the local search.

4.4 Comparing MA with baseline algorithms

To assess the performance of the proposed MA, the winning algorithms in the competition held by Huawei, i.e., VNSME [11], IM and LS, are adopted as the competitors. The source codes and video talks are available on the website.² Since we focus on the same DPDP problem as these three algorithms, we regard them as state-of-the-art algorithms and utilize them as baseline algorithms. The source codes of VNSME, IM, and LS are implemented in Java, Python, and C++, respectively. For a fair comparison, the baseline algorithms adopt their original parameter settings. All algorithms run under the same environment. Since VNSME and MA are stochastic algorithms, they run ten times independently on each instance, while the IM and LS are deterministic and run once on each instance.

Table 9 Statistical results of performance comparisons of MA with VNSME, IM and LS by Wilcoxon’s test and Friedman test

Fig. 4

Objective values obtained by VNSME, IM, LS and MA on 64 instances. Best viewed in color

Fig. 5

Total running time of VNSME, IM, LS and MA on 64 instances. Best viewed in color

Table 8 shows the results of all algorithms on each dataset. Moreover, the Friedman test and the Wilcoxon signed-rank test [39, 40] at 5 % significance level are carried out further to show the difference between the MA and the competitors. Table 9 shows the statistics summarizing all performance comparisons. From Tables 8 and 9, MA obtains the best results on most instances and gets the first rank. Specifically, MA significantly outperforms the VNSME, IM and LS on 36, 62 and 55 instances, respectively, and is outperformed by the VNS and LS on 9 and 4 instances, respectively. The numeric results show the effectiveness of the MA in solving the real-world DPDP.

In addition, Fig. 4 visually shows the values obtained by VNSME, IM, LS and the proposed MA on all instances. The average values obtained by VNSME and MA on each instance are presented in the figure. It is clear that MA can obtain the best solutions on most instances. The main difference between MA and the competitor is that MA is a population-based method that manipulates a set of solutions, while the competitors only operate on a single solution during the search process. The crossover operator in MA enhances the diversity and increases the chance of finding promising areas where high-quality solutions may exist. In contrast, the competitors may not fully explore the search space as MA because only one solution is used. Therefore, MA performs the best among all algorithms.

Finally, we compare the total running time of the competitors on all instances to show the efficiency of the algorithms. As different algorithms are implemented in different programming languages, i.e., VNSME, IM, LS, and MA are implemented in Java, Python, C++, and C++, respectively, their running time cannot be directly compared. According to [41], Java and Python execute applications 1.43 $\times$ and 29.50 $\times$ slower on average than their C++ counterparts respectively. Therefore, we recalculate the running time of VNSME and IM based on these factors, making them comparable with LS and MA. Figure 5 shows the total running time of the competitors on all instances. IM solves the problem with the shortest running time, followed by LS, MA and VNSME, respectively. The proposed MA runs slower than are IM and LS because of its population-based nature. Nevertheless, the MA can obtain much better solutions than those of IM and LS. Moreover, the longest total running time for a large-scale instance with 4000 orders is 6600 s, i.e., the running time for solving a static DPDP for each time interval is about 45 s, much lower than the threshold (10 min). Therefore, the proposed MA can solve large-scale instances in a reasonable running time.

In summary, from the experimental results, the proposed MA has the best overall performance in terms of solution quality and running time. Therefore, the effectiveness of MA in solving the real-world DPDP is confirmed.

5 Conclusion and future work

In this study, we propose a memetic algorithm (MA) for solving a real-world DPDP with multiple constraints. In the DPDP, orders are periodically released and should be completed as soon as possible. When the new orders are released, a static PDP is formed by all uncompleted orders and solved by the proposed MA. The MA consists of a genetic algorithm for exploring the promising search space and a local search for exploiting the best solution in a search region. To validate the effectiveness of the MA, experiments are carried out on 64 real-world DPDP instances. Three metaheuristics, i.e., VNSME, IM and LS, are adopted as the baseline algorithms. Experimental results show the effectiveness of the MA in solving the DPDP.

However, the proposed MA still has some limitations. First, the problem-specific knowledge may not be fully used since only one neighborhood operator is utilized in the MA. To enhance the exploitation ability, more sophisticated local search strategies can be adopted in the future, e.g., (1) by incorporating more neighborhood operators and (2) by using tabu search, simulated annealing, or VNS instead of the simple local search. Second, although the MA solves the DPDP in a reasonable running time, it still requires a long time to achieve good results and may not be suitable in real-time scenarios. In the future, learning-based algorithms [12, 42] can be adopted as the local search to accelerate the running speed of the MA.