1 Introduction

The average annual domestic standard electricity bills by households and non-home suppliers have been increased \(\pounds 707\) in 2020, based on an annual consumption of 3600 kWh [1]. The non-hydro renewable energy source (RES) such as solar, wind, tidal and geothermal energy continue to enter the electricity market substantially. The percentage of RES increased from 10.3\(\%\) in 2008 to 18\(\%\) in 2018 in the EU [2]. It is well known that wholesale price fluctuation is the essential feature of deregulation in the electricity market. Energy buyers who are sensitive to electricity price may change their consumption habits according to dynamic price signals [3]. This means that dynamic energy tariffs can decrease energy demand during peak load periods and increase valley loads. While the use of RES and energy storage can significantly reduce the use of fossil fuels, thereby reducing power generation costs and greenhouse gas emissions.

In the dynamic tariff design, extensive research on demand-side management is carried out. A demand response method based on dynamic energy pricing is proposed in [4], which realizes the optimal load control of equipment by building a virtual power trading process. A smart grid decision-making model considering demand response and market energy pricing is proposed to interact between market retail price and energy consumers [5]. In [6], a cooperative operation procedure of the electricity and gas integrated energy system in a multi-energy system is proposed to develop the system performance and optimize the power flow. However, the above demand side management (DSM) research only optimizes energy prices from the perspective of operation, and does not recognize the impact of electricity market price changes and consumer demand fluctuation. In addition, most of the current papers only study single-objective optimization problems, such as modelling demand figure [7], maximizing customer utility [8] and reducing total cost [9]. When planning a multi-microgrid system, there will be a coupling interaction among power grid, independent system operator (ISO) and microgrids. These participants usually have some conflicts in the planning process. The impact of the dynamic tariff on a multi-microgrid system with a multi-objective problem has not been fully investigated.

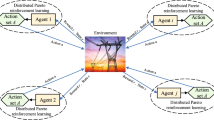
For a comprehensive design and coordination of all participants, we consider designing a multi-microgrid system, including three microgrids, one independent system operator (ISO), and one main power grid [10]. In general, microgrids are disconnected from each other with no exchange of renewable energy power. In this multi-microgrid system, a dynamic tariff scheme is implemented to evaluate the system performance of all participants. It is necessary to use a multi-objective optimal method to balance the requirement of all participants without biasing towards any single one. In [11], a multi-objective genetic algorithm (MOGA), which adapts some changes to the physical features of the load dispatch problem, is utilized to address a multi-objective problem to optimize the time distribution of domestic loads within the 36-h time-period in a smart grid scenario. An energy optimization method, based on multi-objective wind-driven optimization method and multi-objective genetic algorithm, is employed to optimize operation cost and pollution emission with/without the involvement in hybrid demand response programs and incline block tariff [12]. However, the genetic algorithm needs many iterations to obtain good convergence results, the reinforcement learning can train policies in advance and obtain the optimal solution faster based on the trained policies [13].

Multi-objective reinforcement learning (MORL) is an excellent algorithm that can solve multi-objective problems of complicated strategic intercommunications. Reinforcement learning algorithms learn policies when interacting with the environment, while evolutionary algorithms do not do. In many cases, reinforcement learning algorithms can use the interactive details of individual behaviours to be more effective than evolutionary algorithms. Although evolution and reinforcement learning algorithms share many features and naturally work together, they can autonomously learn with experience and adaptively reuse data pulled from relevant problems as prior knowledge in new tasks. However, evolutionary algorithms ignore most of the advantageous structure of reinforcement learning problems. Such information should enable algorithms to achieve more effective searches [14]. In [15], the reinforcement learning environment is usually formalized by adopting the Markov Decision Process (MDP). A Q-learning algorithm is introduced to iteratively approximate the best Q value [16]. In a multi-objective optimization problem, the objectives contain two or more dimensions, and the conventional MDP will be generalized to multi-objective MDPs. The common straightforward approach is to transform the multi-objective problem into a standard single-objective problem using a scalar function [17]. Most MORL methods rely on a single-policy strategy to learn the Pareto optimal solution [15, 18, 19].

However, this transformation may not be suitable for solving the nonlinear problem in the non-convex domain at the Pareto front. In addition, when multi-objective problems are investigated, MORL methods based on the Pareto-optimality criterion may not accomplish a meaningful search. Incorporating preferences to the MORL optimization enhances the specificity of the selection and facilitates better decisions that consider all participants. Accordingly, the solutions will focus on preferred alternative areas, and it is unnecessary to generate the entire Pareto optimal set with equal accuracy. This article developed a preference-based MORL algorithm (PMORL) to achieve high-quality solutions with nonlinear multi-objective functions. The proposed PMORL adopts the \(L_p\) metric to design a balanced multi-microgrid system plan in terms of the approximate Pareto front (APF). To the best of our knowledge, it is the first time for PMORL to be employed in a multi-objective optimization scenario. The system planner implements the Pareto front to examine the connection and importance among different objective functions, which can provide the system planner with an option that is fair to all participants. The main three contributions of this article are as follows:

  1. (1)

    This paper combines real-time dynamic energy tariff for actual planning scenarios, considering the impact of real-time fluctuation in energy tariff and renewable energy on the design of a multi-microgrid system. Three conflict objectives are proposed for a multi-microgrid system in this paper: maximizing sales revenue from main grid suppliers, maximizing the life of energy storage, minimizing energy consumption costs of consumers.

  2. (2)

    We have developed a MORL algorithm based on the \(L_p\) metric to solve this multi-objective problem that considers dynamic energy tariff and energy storage operations (such as charge/discharge/idle). It can provide the entire Pareto front if enough exploration is given. The performance of the proposed algorithm is verified by comparing multi-objective genetic algorithm (MOGA) and preference-based MOGA (PMOGA).

  3. (3)

    An extended MORL algorithm using a preference model based on the Gaussian process is proposed to design a self-governing and rational decision-making agent and control the multi-microgrid system. The preferences of individuals in the same selection are essential for simulating human decision-making behaviour. The human’s emotional system is capable of adjusting the perception and evaluation of cases.

The rest of this article is arranged as follows. Section 2 outlines the main outline of the multi-microgrid system and explains the mathematical models for the three participants. The multi-objective problem is presented in Sects. 3, 4 describes the proposed preference-based MORL method in detail. In Sect. 5, the approximate Pareto front and dynamic tariff based on the experimental results are given. Finally, the conclusion is discussed in Sect. 6.

2 Multimicrogrid description

This paper is concerned with the design of a high-level three-microgrid optimization system. An information and communication technology (ICT) system is performed to transfer the information among the three microgrids, including the load demand, energy tariff and renewable energy generation. The mathematical models of the multi-microgrid system, including the microgrid, the ISO and the main power grid, will be described in detail in the following subsections. Let \({\mathcal {N}}={1,2,\ldots ,N}\) be the set of microgrids and \({\mathcal {N}}_s={1,2,\ldots ,N_s}\) be the set of microgrids with energy storage system, where \(N_s \le N\).

2.1 Microgrid model

The microgrid system model shows the power balance among energy storages (if available), local energy generation, other microgrids, and main power grid. For microgrid n without an energy storage system, the mathematical model can be given as

$$\begin{aligned} \begin{array}{rcl} p_{d_n}(t)=p_{g_n}(t)+p_{r_n}(t). \end{array} \end{aligned}$$
(1)

If \(p_{g_n}(t)\) is positive, the power flows from the grid to the microgrid n, otherwise, the power flows from the microgrid n to the grid, i.e., sell the extra electricity to the main power grid.

For microgrid n with an energy storage system, the power balance equation is given by

$$\begin{aligned} \begin{array}{rcl} p_{d_n}(t)=p_{g_n}(t)+p_{r_n}(t)+s_n(t)-s_n(t-1). \end{array} \end{aligned}$$
(2)
$$\begin{aligned}&subject \ to \quad \forall \ t \in {\mathcal {T}}\nonumber \\&|s_n(t)-s_n(t-1) |\le \Delta s_n \end{aligned}$$
(3a)
$$\begin{aligned}&{\underline{s}}_n \le s_n(t) \le {\overline{s}}_n \end{aligned}$$
(3b)

where (3a) represents the constraints of maximum charging/discharging rating power. 3b) is the constraints of the maximum capacity of the storage. Note that we do not consider self-discharge effect of the energy storage system because the energy loss in a short-term period is too small to be negligible [20].

Considering the shiftable loads, the load demand term \(p_{d_n}(t)\) can also be given as

$$\begin{aligned} \begin{aligned} p_{d_n}(t)&=f_{d_n}(\lambda (t),l_{b_n}(t)) = (1+h_n(\lambda (t)))l_{b_n}(t) \end{aligned} \end{aligned}$$
(4)

where \(l_{b_n}(t)\) is equal to the load demand in (2) without considering the shiftable loads. \(h(\lambda (t))=a_1\lambda (t)^2+a_2\lambda (t)+a_3\) and \(p_{d_n}(t)=(1+h(\lambda (t))l_{b_n}(t))\) is the load demand based on the baseload, \(n=1,2,\ldots ,N\) is the index of microgrid. The baseload forecasting technology can achieve high-precision forecasting outcomes because there are almost no fluctuations in practice for the baseload. Therefore, we presuppose that \(l_{b_n}(t)\) is a known data in advance.

Different domestic consumers may have different responses to the same tariff. Different tariff plans can be established by choosing an objective function of microeconomics [21]. For each consumer, the objective function means the consumer’s comfort corresponding to the total power consumption. Up-to-date investigations show that certain objective functions can precisely trace the behaviour of energy consumers [22]. The overall objective function of multi-microgrid can be demonstrated as [23, 24]

$$\begin{aligned} \begin{aligned} \max _{\lambda (t)}: F_w&=f_w(p_{d_1}(t),\ldots ,p_{d_N}(t),\lambda (t)) \\&=\sum ^{N}_{n=1}(f_u(p_{d_n}(t),\omega _n)-f_c(\lambda (t),p_{d_n}(t))) \end{aligned} \end{aligned}$$
(5)

where

$$\begin{aligned} \begin{aligned}&f_c(\lambda (t),p_{d_n}(t))=\lambda (t)*p_{d_n}(t) \end{aligned} \end{aligned}$$
(6a)
$$\begin{aligned} \begin{aligned}&f_u(p_{d_n}(t), \omega _n) \\&=\left\{ \begin{aligned}&(\omega _n+\alpha )p_{d_n}(t) \\&-\frac{\beta }{2}p_{d_n}(t)^2+\gamma p_{d_n}(t)^3, if \ 0\le p_{d_n}(t) \le \frac{\omega _n}{\beta } \\&\frac{\omega _n}{\beta }, if \ p_{d_n}(t) \ge \frac{\omega _n}{\beta } \end{aligned} \right. \end{aligned} \end{aligned}$$
(6b)

\(f_u(p_{d_n}(t), \omega _n)\) is corresponding to the marginal benefit which is concave [22, 25]. The different power consumption \(p_{d_n}(t)\) responses of a consumer with a marginal benefit to different electricty prices \(\lambda (t)\). \(f_c(\lambda (t),p_{d_n}(t))\) is inflicted by the electricity provider. For example, a use that consumers \(p_{d_n}(t)\) kW electricity during the time period between t and \(t+1\) at a rate of \(\lambda (t)\) is charged \(\lambda (t)*p_{d_n}(t)\). \(b_n(t)\) is the base load. \(\omega _n\) is the parameter that can change between consumers and at different time intervals of the day. \(\alpha , \beta \) and \(\gamma \) are the pre-determined coefficients to be calibrated [26]. Every consumer tries to adjust the energy usage to maximize its welfare for each displayed tariff \(\lambda (t)\) at time t. This can be achieved by placing the derivative of \(F_w\) to zero, which means that the consumer’s marginal revenue will equal the advertising tariff.

2.2 ISO model

The ISO described in this subsection mainly acts as an emergency power provider to support emergency demand response plans. In general, the ISO will store as much energy as possible to reach a safe level. In order to provide maximum emergency power and extend battery life, the objective function can be expressed as:

$$\begin{aligned} \begin{aligned} \max _{\lambda (t), p_{g_n}(t)}: F_s= \sum _{n=1}^{N_s}s_n(t). \end{aligned} \end{aligned}$$
(7)
$$\begin{aligned} \begin{aligned} subject \ to \quad \forall \ t \in {\mathcal {T}} \\ {\underline{s}}_n \le s_n(t) \le {\overline{s}}_n. \end{aligned} \end{aligned}$$
(8)

2.3 Power grid model

The main power grid releases energy into the microgrid when renewable energy generation is insufficient. However, when there is a surplus of renewable energy in the microgrid, it can also absorb electricity from the microgrid. The objective problem of the main power grid model can be given as

$$\begin{aligned} \begin{aligned} p_g(t)=\sum _{n=1}^{N}p_{g_n}(t). \end{aligned} \end{aligned}$$
(9)

The derivation of the maximum interest of the main power grid based on the power distribution \(p_g(t)\) can be denoted as

$$\begin{aligned} \begin{aligned} \max _{\lambda (t), p_{g_n}(t)}: F_g&= f_g(\lambda (t), p_{g}(t))\\&= \lambda (t)p_{g}(t)-C_{ p_g }(t) \end{aligned} \end{aligned}$$
(10)

where

$$\begin{aligned} \begin{aligned} C_{ p_g }(t)=a_g p_g (t)^2+b_g p_g (t)+c_g \end{aligned} \end{aligned}$$
(11)

where \(a_g > 0\) and \(b_g, c_g \ge 0\).

Load demand and renewable generation data are based on that of the Penryn Campus, University of Exeter. The university office of general affairs acts as the ISO to buy energy from the utility company and connect the energy storage system and renewable energy sources (RESs) to create a time-varying electricity tariff. The current electricity tariff of the campus is fixed. If the energy tariff varies at different times, students may adjust their electricity consumption habits for household appliances to reduce energy bills. Students living in student apartments will decide when to use various electrical appliances such as washing machines and dryers based on dynamic electricity tariffs. In addition, the university office can manage the time-varying electricity tariff to decrease the peak load demand, optimize the energy storage system operation, and reduce the energy purchase from the utility companies. The design of this scenario has very practical significance for the operation of the smart microgrid, especially when smart meters are installed in every household. In 2019, nearly 1 million smart meters were installed in British households [27]. As of Jun 30 2020, smart and advanced meters increased to 21 million in homes and small businesses, of which 17.4 million were in a smart mode [28].

3 Multi-objective problem formulation

In this section, a multi-objective problem (MOP) formula will be proposed to design and maximize the benefits of three objectives for a multi-microgrid system. The following content will discuss the definition of the Pareto Optimality.

In order to solve the three objectives \(F_w\), \(F_s\) and \(F_g\) mentioned above simultaneously, a MOP formula is rewritten as

$$\begin{aligned}&\max _{\lambda (t)} \ F_w=f_w(p_{d_1}(t),\ldots ,p_{d_N}(t),\lambda (t)) \end{aligned}$$
(12a)
$$\begin{aligned}&\max _{\lambda (t), p_{g_n}(t)} \ F_s=\sum _{n=1}^{N_s}s_n(t) \end{aligned}$$
(12b)
$$\begin{aligned}&\max _{\lambda (t), p_{g_n}(t)} \ F_g=f_g(\lambda (t), p_{g}(t)) \end{aligned}$$
(12c)
$$\begin{aligned} subject \ to \quad (1)-(4), (8) and (9) \end{aligned}$$

where \(\lambda (t)\) and \(p_{g_n}(t)\) are the two variables correlated with the ISO and they are restricted by the current renewable energy generation and the charging/discharging status of energy storage between time \(t-1\) and t. A supplementary function is presented to solve the problem considering all the constraints as bellow:

$$\begin{aligned} \begin{aligned} F_a =&\sum _{n=1}^{N_s}[max(|s_n(t)-s_n(t-1)|-\Delta s_n,0) \\&+ max(s_n(t)-{\overline{s}}_n,0) + max({\underline{s}}_n-s_n(t),0)] \end{aligned} \end{aligned}$$
(14)

where the stored energy in the energy storage system manages \(F_a\). When all constraints is satisifed, if and only if \(F_a=0\). Otherwise, \(F_a\) is equal to a large positive penalty coefficient. In terms of the formulation (14), the MOP in (12) can be revised as

$$\begin{aligned} \begin{aligned} \max _{\lambda (t), p_{g_n}(t)} \ F_{mo}=[F_w \ F_s \ F_g \ \ -F_a]^T \end{aligned} \end{aligned}$$
(15)

To resolve the MOP, the Pareto optimality is employed to prove the performance. The general discussion can be seen as follows.

Definition - Pareto Dominance Let \(\mathbf{H}(x) \) be a MOP function and \(\Omega \) is a feasible solution space. The MOP is optimized to obtain a solution \(u \in \Omega \) that satisfies the MOP function \(\mathbf{H}(x) \). It is defined that solution u dominates \(u^{'}\) (written as \(u \prec u^{'}\)) if \(H_i(u) \le H_i(u^{'})\) holds true for all i and at least one i has \(H_i(u) < H_i(u^{'})\). It means that if a solution is better on one objective function and equal on other objective functions, this solution is better than others.

Definition - Pareto Optimal If there is no feasible solution \(u^{'} \prec u^*\) in the solution space that dominates it, then the solution \(u^*\) is Pareto optimal.

Definition - Pareto Optimal Set \(P^*=\{u^* \in \Omega \}\) is defined as the Pareto optimal set of the MOP, which means the solution set of all Pareto optimal.

Definition - Pareto Front The Pareto front is the boundary determined by the set of all solutions mapped by the Pareto optimal set.

4 Proposed algorithm for multi-microgrid optimization

4.1 Multi-objective reinforcement learning

To obtain the Pareto front for the MOP, a multi-objective Q-learning framework is introduced in this subsection. This MORL structure is based on a single-policy strategy that applies scalarization functions to decrease the dimensionality of the MOP. In other words, the problem is solved by converting the multi-objective problem into a single-objective problem.

A scalarization function can be described as

$$\begin{aligned} \begin{aligned} F=f(\mathbf{x },\mathbf{w }) \end{aligned} \end{aligned}$$
(16)

where \(\mathbf{x }\) and \(\mathbf{w }\) are the Q-value vector and the weight vector in the Q-learning environment, respectively. The scalar Q value in a single-objective problem is replaced by a Q vector that includes different Q values for all objectives, such as:

$$\begin{aligned} \begin{aligned} \mathbf{Q }(s,a)=(Q_1(s,a_1),\ldots ,Q_m(s,a_m)) \end{aligned} \end{aligned}$$
(17)

A single and scalar Q-value value SQ(s, a) is obtained as:

$$\begin{aligned} \begin{aligned} SQ(s,a)=\sum _{m=1}^{M}{w}_m \cdot {Q}_m(s,a_m) \end{aligned} \end{aligned}$$
(18)

where all weight values \(w_m\) should satisfy \( \sum _{m=1}^{M}{w}_m=1 \).

However, the estimated SQ(s, a) value has a major weakness in that the Pareto front can only be found in the convex region based on the linear scalarization [29, 30]. For multiobjective optimization problems, the weighting coefficients in the three objective functions can be set equal and normalization method can also be utilized to avoid favoring a particular participant. However, when the multi-objective optimization problem has a concave Pareto front (PF), both methods may not be effective. Even if PF is convex, it can introduce other challenges by using utility functions derived from various weights to approximate PF [30,31,32]. Therefore, this paper develops the scalar function by adapting the \(L_p\) metric to solve this issue [33]. The \(L_p\) metric measures the distance between the utopian point \(\mathbf{z }^{*} \) and the selected point \(\mathbf{x }\) in the multi-objective space. \(\mathbf{z }^{*} \) is an adjustable value in the iteration process. The \(L_p\) metric between \(\mathbf ( x) \) and \( \mathbf ( z)^* \) for each function can be measured by

$$\begin{aligned} \begin{aligned} L_p(x)=\left( \sum _{m=1}^{M}{w}_m |x_m-z_m^*|^p\right) ^{1/p}. \end{aligned} \end{aligned}$$
(19)

where \(1 \le p \le \infty \). If \(p = \infty \), the metric can be acknowledged as the weighted \(L_{\infty }\) or the Chebyshev metric

$$\begin{aligned} \begin{aligned} L_{\infty }(x)=\max _{m=1,\ldots ,M}w_m |x_m-z_m^*|. \end{aligned} \end{aligned}$$
(20)

\(x_m\) can be substituted by \(Q_m(s,a)\) to update the SQ(s, a) for the multi-objective problems

$$\begin{aligned} \begin{aligned} SQ(s,a)=\max _{m=1,\ldots ,M}w_m |Q_m(s,a)-Q_m^*(s,a)|. \end{aligned} \end{aligned}$$
(21)

The elements of RL are explained below. These include state space, action space, and reward functions, including learning and exploration rates, and discount factors.

4.1.1 State Space

The state space is time of day (\(ToD_j\)) and State of charge (\(SoC_k\)).

$$\begin{aligned} \begin{aligned} s|s_{j,k}=(ToD_j, SoC_k)\\ \end{aligned} \end{aligned}$$
(22)

where ToD is divided into 24 h (\(j=1,2,\ldots ,24\)), and the SoC is discretised into 8 values which are set from 30 to 100%.

4.1.2 Action space

Action space is a mixture of tariff and charging/discharging/idle status.

$$\begin{aligned} \begin{array}{rcl} A=\{a|(Tariff, Storage Command)\} \end{array} \end{aligned}$$
(23)

where the Tariff is discretized into 8 values from 1.5 to 5.0 and the StorageCommand into three values: Charge, discharge and idle.

4.1.3 Reward

The reward value \(r_m(t)\) for each objective is the stimulation obtained by taking an action while at state s. The reward function is created to maximize the objective function. All obtained reward values will be updated to the expanded Q table accordingly.

$$\begin{aligned} \begin{array}{rcl} r_{m,nor}(s,a_m)=C_m \cdot F_{_m} \end{array} \end{aligned}$$
(24)

where \({r}_{m,nor}(s,a_m)\) is corresponding to the value of each objective function \(F_{m}\) \((e.g., F_w,F_s,F_g)\). \(C_m\) is a constant value for each objective which avoids favouring a particular participant. In terms of the SQ(s, a) table, the action selection policy is updated and the appropriate action can be chosen to receive the maximum reward, such as scalar \(\epsilon \) greedy strategy. The detailed scalar \(\epsilon \) greedy strategy in this paper can be discovered in Algorithm 1.

figure a

4.2 Preference-based multi-objective reinforcement learning

Essential RL considers a scenario where an agent runs in state space by executing different actions. Reward signals provide the agent with feedback about its behaviour. The aim of RL is to maximize the expected total rewards. However, the computational cost of comprehensive interactions among different objectives with a decision-maker is expensive. Therefore, extending the essential reinforcement learning framework is necessary by using a preference learning model.

The basic idea of the proposed preference model is to prefer various reward functions in terms of a human’s emotional system. In this paper, the proposed PMORL employs a preference reward function to enable the agent to learn and perceive different preferences. The preference reward function is introduced to learn various policies based on a Gaussian distribution. We have used a multi-objective Q-learning algorithm with a scalar \(\epsilon \) greedy strategy to discover the optimal policy. The employed preference reward function leads to a bias for one particular objective, which is most common to choose good actions for this specific objective while reducing the probability of selecting good actions for other objectives.

Then the reward function of each objective for updating the scalar \(\textit{SQ(s,a)}\) table can be revised as follows.

$$\begin{aligned} \begin{aligned} r_m(s,a_m)={r}_{m,nor}(s,a_m)+r_{m,pre}(s,a_m). \ \forall \ m \in {\mathcal {M}} \end{aligned} \end{aligned}$$
(25)

For \(r_{m,pre}(s,a_m) \sim {\mathcal {N}}(\mu _m(s,a_m),\sigma _m^2(s,a_m))\), where the term \({\mathcal {N}}(\mu _m(s,a_m),\sigma _m^2(s,a_m))\) is the normal distribution, \(\mu _m(s,a_m)\) is the mean and \(\sigma (s,a_m)\) is the standard variation. For example, when an action preference model (reward) with \(\mu _2(s,a_2)=20,\mu _1(s,a_1)=\mu _3(s,a_3)=1\) and \(\sigma _1(s,a_1)=\sigma _2(s,a_2)=\sigma _3(s,a_3)=1\) is applied. Introducing a preference model for action \(a_2\) based on specific target \(F_s\) will lead to bias against action \(a_2\). In other words, the probability of action \(a_2\) being selected is high while the probability of actions \(a_1\) and \(a_3\) being selected will be reduced.

The proposed PMORL strategy is explained in Algorithm 2. First, three \(Q_m(s,a)\) tables for each objective and one SQ(s,a) table are initialized. Then the algorithm starts each episode beginning with state s and picks action via the scalar \(\epsilon \) greedy strategy. Once the action is taken, the agent will land to a new state \(s^{'}\) and generate three reward values \(r_m(s,a)\) in equation (25) for each objective. In other words, these reward values are calculated independently for each objective. Then the scalar \(\textit{SQ(s,a)}\) will be updated on the determined action via (21). And the next state \(s^{'}\) is determined and new action \(a^{'}\) will be taken to repeat steps 4–11 until the termination condition is met.

figure b
Fig. 1
figure 1

Demand and RES generation of Microgrid 1 on Nov 17, 2019

Full size image

5 Simulation results and performance

The simulation results are demonstrated to evaluate the performance of the proposed PMORL algorithm. In the experimental environment, three microgrids (\({\mathcal {N}}=3\)) are considered in which two of them have energy storage (\(\mathcal {N_s}=2\)). The sizes of the two energy storages are 250 kWh and 200 kWh, respectively. Let \(\Delta s_n\) be set to 10\(\%\) of the capacity for each storage. The average power demand responding to tariff \(\lambda \) can be achieved as explained in [34]. The baseload \(l_{b_n}\) is from the Penryn Campus, University of Exeter. The total baseload and renewable generation on Nov 17, 2019 are displayed in Fig. 1. The actual load demand can fluctuate according to the tariff when the price signal changes. The baseload of three microgrids has been given in Fig. 2.

Fig. 2
figure 2

Sample of load demand for three microgrids

Full size image
Fig. 3
figure 3

Sample of convergence rate of MORL

Full size image

Figure 3 presents a case of the preference-based results of Approximated Pareto Front (APF) that maximize the objective function \(F_w\). At the beginning of the iteration, all actions are randomly selected, and the optimal policy is also random. Therefore, it can be seen from Fig. 3 that the objective function corresponding to the randomly selected action in each iteration fluctuates wildly. However, when the number of iterations reaches 100, the simulation results begin to converge and stabilize slowly. Finally, after 150 iterations, the results converge to the optimal results. There are inevitable fluctuations after 150 iterations because the action selection strategy still has a very low probability that some actions will be randomly selected. Nevertheless, the results of the other two objective functions (2 and 3) are not optimized and do not converge to their minimums. Obviously, the objective functions are in conflict with each other, and it is impossible to find an optimal result that meets all objective functions. However, we can find an optimal solution that is biased towards a specific objective function or a compromise solution that is fair to all three objectives.

Fig. 4
figure 4

APFs and non-dominated vectors \(F(p^*)\) sampled

Full size image

Figure 4 presents the results of APF based on MORL. The experimental results show that there is a conflict between different objective functions. When \(F_w\) is large, the other two objectives will deviate from their optimal values, and vice versa. Three different solutions \(p^*_1\), \(p^*_2\) and \(p^*_3\) are the extreme dominance solutions of the three objective functions, respectively. This means that every solution will benefit every single objective function only. In order to ensure the fairness of all objective functions, a specific APF-based solution \(P^*\) will be selected so as not to give any single objective an advantage. In Fig. 4, there is a relatively special solution \(P^*\) in the Pareto optimal solution set, which is located in the centre of the Pareto optimal set. The distance between \(P^*\) to the three objective functions is the same, which indicates that the provided point \(P^*\) is a relative fair solution to three objective functions.

Fig. 5
figure 5

APFs for different objectives by using the PMORL approach

Full size image

The Pareto optimal set of the test outcomes in Fig. 4 reveals that MORL can preference a single objective function or balance all objective functions. As the learned \(\textit{SQ(s,a)}\) table comprises the experience of the agent without re-solving the decision-making problem, it can determine multi-objective issues quicker than conventional optimization methods. In short, all empirical results confirm the performance of MORL. However, the extension of multi-objective reinforcement learning is necessary to develop psychological and neurophysiological findings. For the sake of simulating human decision-making behaviour, the expert preferences based optimal policy is emulated. The favoring policy based on three objective functions is presented independently over 300 independent runs in Fig. 5. The performance in Fig. 5 has a good preference compared to the results in Fig. 4. The outcomes in Fig. 5 are straightforward and in line with our expectations. It shows that the extra rewards controlled by human’s emotional states can introduce preferences for the optimal policy of traditional multi-objective reinforcement learning. This enables the smart grid designers to use the preference model to develop MORL agents with specific preferences. The extra reward functions could be used to simulate rational components of decision making while retaining the main reward process to maximize the expected objectives. Table 1 provide the average results for three objectives over 500 independent runs. It is clear that the PMORL can achieve the preference-based optimal results for each objective function as described in (12). The PMORL allows for developing agents with preferences and specific targets. The extra reward value (like Gaussian distribution) could simulate rational decision-making components while keeping the primary potential reward process to maximize the expected benefit. The PMORL can find the best solution area according to the preference for the specific function. In order to verify the accuracy of the algorithm, we also compared the results of the MOGA and PMOGA. It can be seen from Table 2 that the experimental results of PMOGA and PMORL are very close. The results of both PMOGA and PMORL are better than those of MOGA. The proposed PMORL can achieve the best results. In addition, we also compared the running time of these three algorithms. Compared with MOGA’s optimization time of 350 s and PMOGA’s optimization time of 352 s, the trained PMORL can complete the iteration in a very short time and obtain excellent results. Grid designers can design different multi-objective optimization models according to their preferences.

Table 1 PMORL based results
Full size table
Table 2 Comparison with multi-objective genetic algorithm
Full size table

Fluctuations in tariff signals play an important role in smart grid energy management. Figure 6a shows that the proposed method can generate appropriate dynamic tariffs, and the energy storage system status is also demonstrated in Fig. 6b. Ideally, high electricity tariffs will produce peak reduction and discharge energy storage, while low electricity prices will fill the trough load and charge energy storage. The results in Fig. 6a illustrate the relationship between electricity tariffs and energy storage systems. At hour 3, the electricity tariff is relatively high. Although the power storage is relatively low, the selected action based on the optimal policy does not charge the energy storage system but maintains the idle state. The high electricity tariff means that we need to buy more electricity from the grid. All three objectives desire to maximize their benefits, the ISO does not worry about tariffs and only concerns about emergency energy storage, the main grid only considers its own profit maximization, and consumers consider how to reduce electricity bills without affecting the use of household appliances. This result is not biased towards objective three, so the agent needs to try not to charge the energy storage system when the electricity tariff is high, and at the same time, in order to ensure the largest possible emergency energy, the agent will try not to discharge it.

Fig. 6
figure 6

Dynamic price signal \(\lambda \) by using the proposed MORL approach

Full size image

6 Conclusion

In this paper, a preference-based multi-microgrid planning model considering dynamic electricity tariffs and renewable energy generation is proposed. Designing scenarios are analyzed through a preference-based multi-objective reinforcement learning algorithm to optimize energy storage operations and electricity tariffs. In addition, the dynamic tariff of the microgrid system is restricted by the power demand of the main grid, which takes into account the interests of all three objectives. The experimental outcomes reveal that the MORL algorithm can produce a fair and effective operation plan for all participants by controlling the operation of energy storage and modifying the real-time electricity tariff. Meanwhile, the proposed PMORL can introduce preferences for an optimal policy through additional reward functions and develop agents based on preference objectives for grid designers. It proves the ability of PMORL to learn the optimal control strategy, and the proposed PMORL can also be applied to other multi-objective environments. The coordinated operation of the microgrid system benefits to increase the utilization rate of renewable energy, improve the service life of energy storage batteries, decrease the operating cost of the microgrid, save electricity bills for consumers, and maximize grid profits.