Introduction

The study on bioabsorbable metallic vascular stents, which provide a mechanical opening support for blood vessels, has emerged as an research topic in the medical field [1,2,3,4]. Microtubes used in stents have a limited outer diameter at most 3.0 mm and wall thickness of 100–150 μm [5]. Usually, magnesium (Mg) alloy microtubes are currently the most popular metallic materials for stents, which are typically made by laser-cutting a thin-walled microtube [6]. Die drawing such as hollow sinking has been used for fabricating microtubes [7,8,9,10]. However, tubes made of materials with low plasticity, such as Mg and Ni–Ti alloys, often break under a large reduction in the cross-sectional area during cold die drawing [5, 11,12,13]. Therefore, fabricating microtubes by using cold die drawing is inefficient. By contrast, large reduction in the cross-sectional area can be achieved by applying die-less drawing, even for Mg alloy tubes, by pulling with localized heating [14,15,16,17]. For example, Furushima and Manabe achieved a reduction of 50% in the cross-sectional area in a single pass in the die-less drawing of AZ31 Mg alloy tubes [18]. Furthermore, Furushima and Manabe recently developed a die-less mandrel drawing method, which resulted in the active thinning of the wall thickness by suppressing the decrease in inner diameter [19]. They reported a reduction of 54% in the wall thickness was obtained in a single pass of this process using AZ31 Mg alloy tubes.

A major concern with Mg microtubes in the medical field is their rapid corrosion in body fluids; stents degrade before healing of the tissue is complete. The corrosion speed of Mg alloys is directly proportional to the surface roughness [20, 21]. Sun et al. reported that the area of corrosion pits increased as the surface roughness increased [22]. Therefore, the Mg alloy microtube fabrication process must ensure both a thin wall and a low average surface roughness value of below 0.5 μm [23]. The aim of this study is to achieve a thin wall and low surface roughness in the fabrication process of Mg alloy tubes. Although die-less mandrel drawing is suitable for fabricating thin-walled microtubes, it often increases the outer surface roughness [24, 25]. Kishimoto et al. reported that the slip deformation of the pyramidal slip system was mainly responsible for the roughening of the outer surface in die-less mandrel drawing [26]. The outer surface quality of a die-less mandrel drawn tube should be improved to improve the corrosion property reported by Du et al. [27].

Usually, tools such as a die flatten the surface of the material in metal-working processes. Several researchers have investigated the mechanism of surface flattening. Bay et al. reported that the real contact area, which is the surface area flattened by the tool, increased as contact pressure and friction shear stress increased in an asperity flattening process [28]. Wang et al. reported that the average frictional stress increased linearly with an increasing average pressure [29]. Ike and Makinouchi reported that lateral tension enhanced bulk plasticity and increased the real contact area for a given mean contact pressure [30]. Therefore, contact pressure, friction shear stress, and bulk deformation are required for asperity flattening. Hollow sinking is suitable for asperity flattening because it can apply contact pressure, friction shear stress, and bulk deformation to materials. Furushima and Manabe developed the combined process of hollow sinking after die-less mandrel drawing to decrease the outer surface roughness of the die-less mandrel drawn tube [19]. However, the optimal conditions for achieving both a thin wall and high surface quality in the combined process have not yet been clarified. Usually, the contact pressure, such as die pressure p, against the yield stress Y is > 1 in wire drawing. By contrast, p against Y of tubes is < 0.3 in hollow sinking [31]. Even in wire drawing, the concave part on the wire surface remains after drawing [32, 33]. Therefore, a part of the concave is considered to remain on the outer surface of die-less drawn tubes after hollow sinking.

Hence, based on these, the asperity flattening behavior in the combined process of hollow sinking after die-less mandrel drawing should be investigated to obtain the optimal condition for achieving high surface quality. Therefore, the objective of this study was to clarify the flattening behavior of asperity on the outer surface and the optimal condition for achieving a thin wall and high surface quality in the combined process. To this end, Mg alloy tubes were drawn using a die after die-less mandrel drawing to investigate the conditions for obtaining a thin wall and high surface quality. Furthermore, a finite element method (FEM) simulation was performed to investigate the flattening behavior of the asperity on the outer surface of the die-less mandrel drawn tubes in hollow sinking.

Experimental and analytical procedures

Figure 1 shows an overview of the experimental and analytical procedures in this study, the details of which are described in Sects. "Materials" to "Finite element method of hollow sinking".

Fig. 1
figure 1

Overview of the experiment and analysis processes in this study

Full size image

Materials

Mg alloy (ZM21) tubes (outer diameter D0 of 6.0 mm and wall thickness t0 of 1.1 mm) were used as the original tubes. They were manufactured by using the cold die drawing process after extrusion by Macrw Co. Ltd. (Shizuoka, Japan).

Tube drawing

The original tubes were drawn using a die after the die-less mandrel drawing process. Each drawing method is described below.

Die-less mandrel drawing

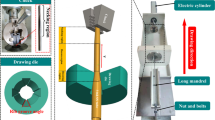
Figure 2 shows a schematic diagram of the die-less mandrel drawing machine used in this study. The principle of drawing using this machine has been presented in our previous paper [26]. The cooling coil was placed 10 mm away from the heating coil exit. A stainless (SUS304) rod (diameter 3.6 mm) was used for the mandrel. When the mandrel diameter and the inner diameter of the original tube are the same, breakage occurs easily. Therefore, the mandrel diameter was set to be slightly smaller than the inner diameter of the original tubes. A graphite spray (Fine Chemical Japan Co. LTD., FC-169, Tokyo, Japan) was applied as a lubricant inside the original tube. The feeding speed V0 was 5.0 mm/s. The original tube was drawn for a single pass at drawing speed V1 of 8.5, 9.0, and 10.0 mm/s such that the drawn tubes are provided at various speed ratio V1 / V0 of 1.7, 1.8, and 2.0, respectively. A high-frequency induction heating device (Ameritherm Inc., 114060–11030294, New York, USA) with a power of 10 kW and a frequency in the range of 150–400 kHz maintained the tube temperature inside the heating coil at 400 °C. Infrared thermography (Optris GmbH, X1400, Berlin, Germany) was used for the temperature proportional integral differential controller of the tube.

Fig. 2
figure 2

Schematic diagram of the die-less mandrel drawing machine used in this study. Parameters V0 and V1 are the feeding and drawing speeds, respectively

Full size image

Hollow sinking

Square-shaped marking lines were drawn on the outer surfaces of the die-less mandrel drawn tubes using a height gage (Mitutoyo, 192–106, Kanagawa, Japan) to evaluate the outer surface roughness of the die-less mandrel drawn tube and the hollow sunken tube over the same measurement area. This measurement aimed at investigating the flattening behavior of outer surface roughness in hollow sinking after die-less mandrel drawing. Sect. "Surface roughness measurement" describes the details of this method.

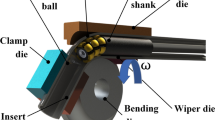
A universal testing machine (AG-IG 50kN, SHIMADZU Co., Kyoto, Japan) was used to draw the die-less mandrel drawn tubes. Figure 3 shows a schematic illustration of the universal testing machine. The die fixed to the die holder was attached to the cross-head. The die-less mandrel drawn tubes were drawn using a die by moving the cross-head upward at 1 mm/s. Machine oil was used as a lubricant. Die reduction, calculated as Re (= 1 – Ddie2 / D2), which shows the degree of outer diameter reduction in hollow sinking was 0.02–0.14, and the die half-angle was 6°. Parameters D and Ddie indicate the outer diameter of the die-less mandrel drawn tubes and the die diameter, respectively. The remaining tube in the die during hollow sinking was collected to evaluate the change in surface roughness while the tube passed through die.

Fig. 3
figure 3

Schematic diagram of the universal testing machine used in this study

Full size image

Measuring method

Dimension measurement

The mechanically polished cross sections of the tubes were observed using a three-dimensional microscope (VR-5000, Keyence, Osaka, Japan). The outer diameter D and inner diameter d were measured for four specimens using a proprietary programming language, MATLAB™ (R2022a, Mathworks, Natick, MA, USA), according to a previous paper [26]. The wall thickness of the drawn tube t was calculated (D \(-\) d)/2. The average value and standard deviation were calculated.

Surface roughness measurement

Outer and inner surface roughness was evaluated as the arithmetic average roughness of area Sa [34] using a confocal laser microscope (VK-100, Keyence, Osaka, Japan). The surface roughness was measured for four drawn tubes and the tube remaining in the die. The average surface roughness and standard deviation of the original and drawn tubes were calculated. Figure 4 shows the method of measuring the outer surface roughness of the die-less mandrel drawn tube and hollow sunken tube over the same measurement area. In this study, symbols DD, CD, and ND indicate the drawing direction, circumferential direction, and normal direction to the surface, respectively. The outer surface roughness of the die-less mandrel drawn tubes and hollow sunken tubes were measured over the same measurement area using the square-shaped marking lines mentioned in Sect. "Hollow sinking". A measurement point with a height h smaller than the average value (h = 0) was defined as concave. The measurement area was divided, and the concave fraction v was calculated by dividing the number of pixels corresponding to the concave part nc by the number of pixels in the measurement area na using MATLAB™. The concave fractions of the die-less mandrel drawn tubes and hollow sunken tubes are defined as vH and vD, respectively.

Fig. 4
figure 4

Process for evaluating the outer surface roughness of the die-less mandrel drawn tubes and hollow sunken tubes in the same measurement area. Symbols DD, CD, and ND indicate the drawing direction, circumferential direction, and normal direction of the surface, respectively

Full size image

Tensile test at room temperature

Tensile tests were performed to obtain the stress–strain curve of the die-less mandrel drawn tubes using a universal testing machine. Figure 5 shows schematics of the specimen and universal testing machine used in this study. As shown in Fig. 5(a-1), the die-less mandrel drawn tubes were cut into a dog-bone shape, similar to a previous study [35], to prevent fractures near the grippers. Figure 5(a-2) shows an image of the whole specimen. The dimensions shown in Fig. 5(a-1) was same for die-less mandrel drawn tubes with speed ratios of 1.7 and 2.0. Only the tube outer diameter D and wall thickness t of the specimens differ, as shown in Sect. "Dimensions". The gage length was 15 mm. The mandrel was inserted into the tube at the gripper. The test speed was 1 mm/s. The test load was measured using a 50 kN-load cell (SFL-50kNAG, SHIMADZU Co., Kyoto, Japan) attached to the cross-head. The stroke was measured using a non-contact extensometer (DVE-101, SHIMADZU Co., Kyoto, Japan). Three tensile tests were conducted on each of the die-less mandrel drawn tubes at the speed ratios of 1.7 and 2.0. The tensile tests were performed at room temperature. The strength coefficient K and hardening exponent n were calculated by fitting the stress–strain curves using the equation σtrue = K εtruen. Figure 6 shows the stress–strain curves of the die-less mandrel drawn tubes drawn at the speed ratios of 1.7 and 2.0, which had average strength coefficients K of 414 and 435 MPa, respectively. Furthermore, the average hardening exponent n of both was 0.17. The calculated values were used in the FEM.

Fig. 5
figure 5

Schematic diagrams showing the tensile test of the die-less mandrel drawn tubes. (a-1) Specimen geometry, (a-2) image of the whole specimen, and (b) universal testing machine

Full size image
Fig. 6
figure 6

Stress–strain curves of the die-less mandrel drawn tubes drawn at speed ratios of 1.7 and 2.0

Full size image

Finite element method of hollow sinking

The flattening mechanism of asperity in hollow sinking was not investigated because experimentally measuring the stress state of asperity during hollow sinking is difficult. Therefore, to investigate the driving force that flattened the asperity, the stress state of the asperity on the outer surface was examined by FEM analysis of hollow sinking using LS-DYNA™ (R11, JSOL, Tokyo, Japan). Figure 7 shows the two-dimensional axis symmetry model of the die-less mandrel drawn tubes before hollow sinking. A two-dimensional elastoplastic body was used as an element of the tube. A two-dimensional rigid body was used for the die and chuck. The flow stress of the tube was defined by the power hardening law σtrue = K εtruen. The strength coefficient K and hardening exponent n were obtained in Sect. "Tensile test at room temperature". The friction coefficient between the tube and die μ was set to 0.05, similar to a previous study [36]. The die reduction Re was set to 0.01–0.14 and the die-half angle θ to 6°. The asperity geometry, convex or concave height, was defined refer to the measurement results of the outer surface roughness, as shown in Fig. 7b. The asperity had a triangular shape, similar to a previous study [30]. The flank angles of the asperity of the die-less mandrel drawn tube with speed ratios of 1.7 and 2.0 were 4° and 7°, respectively. The wave length was 400 μm. Sect. "Deformation behavior of outer surface in hollow sinking after die-less mandrel drawing" explains the details. The rigid reaction force between the tube and chuck in the drawing direction was considered as the drawing force in hollow sinking. To evaluate macroscopic deformation of asperity in a simple model, hydrodynamic lubrication [37] was not considered in this study.

Fig. 7
figure 7

FEM model of the hollow sinking in this study. (a) Entire view; magnified view of the asperity of the die-less mandrel drawn tube drawn at the speed ratios of (b-1) 1.7 and (b-2) 2.0 before hollow sinking. Symbols DD, CD, and ND indicate the drawing direction, circumferential direction, and normal direction of the surface, respectively

Full size image

Results

Dimensions

Figure 8 shows the cross-sectional images of the original and drawn tubes. Figure 9 presents the magnified view of the walls of the tubes in Fig. 8. The cross-sectional size of the original tube decreased significantly as the speed ratio increased in the die-less mandrel drawing. Furthermore, the wall of the original tube became thinner as speed ratio increased in the die-less mandrel drawing.

Fig. 8
figure 8

Observed results of the cross section of the tubes. Cross-sectional images of the (a) original tube and (b) drawn tubes

Full size image
Fig. 9
figure 9

Magnified view of the walls of the tubes. Walls of (a) original tube and (b) drawn tubes

Full size image

The cross-sectional size of the die-less mandrel drawn tubes decreased as the die reduction increased in hollow sinking. Furthermore, the walls of the die-less mandrel drawn tubes increased slightly as the die reduction increased in hollow sinking.

Figure 10 shows the measurement results of the dimensions of the drawn tubes. Equations (1) and (2) represent the total reductions in the cross-sectional area RA and wall thickness RW, respectively. Parameters A0 and t0 indicate the cross-sectional area and wall thickness of the original tube, respectively. Parameters A and t indicate the cross-sectional area and wall thickness of the drawn tubes, respectively.

Fig. 10
figure 10

Experimental measurement results of the dimensions. (a) Outer diameter, (b) wall thickness, (c) reduction in area, and (d) reduction in wall thickness. The error bars indicate the standard deviation. The dotted lines are the eye guides. The measurement results of the die-less mandrel drawn tubes are plotted at the die reduction Re of 0

Full size image
$${{R}}_{A}=\frac{{{A}}_{0}-{A}}{{{A}}_{0}}\times100$$
(1)
$${{R}}_{W}={ }\frac{{{t}}_{0}-{t}}{{{t}}_{0}}\times100$$
(2)

The measurement results of the die-less mandrel drawn tubes are plotted at the die reduction Re of 0. Compared to the original tubes, in die-less mandrel drawing, the outer diameter and wall thickness decreased as the speed ratio increased. Based on the constant volume law, the wall thickness decreased as the speed ratio increased because the outer diameter decreased while the inner diameter remained constant. The details are shown in our previous paper [19]. Furthermore, in hollow sinking, the outer diameter of the die-less mandrel drawn tubes decreased, whereas the wall thickness increased as the die reduction increased.

The total reduction in the cross-sectional area increased as the speed ratio increased in die-less mandrel drawing and as the die reduction increased in hollow sinking (Fig. 10c). The total reduction in the wall thickness increased as the speed ratio increased in die-less mandrel drawing (Fig. 10d), while it decreased as the die reduction increased in hollow sinking, owing to the increased wall thickness (Fig. 10b).

Surface quality

Figures 11 and 12 show the height maps of the outer and inner surfaces of the tubes, respectively. The areas of the convex (red) and concave (blue) parts on both the outer and inner surfaces increased compared to those of the original tube in die-less mandrel drawing. The area of the concave parts increased after initially decreasing as the die reduction increased in hollow sinking. The area of the convex and concave parts on the inner surface increased as the die reduction increased in hollow sinking. Figure 13 shows the measurement results of the surface quality of the tubes. The outer surface roughness increases as the speed ratio increases because the longitudinal strain increases. The details are shown in our previous paper [26]. The die reduction at which the outer surface roughness was the least was 0.10, 0.06, and 0.04 in hollow sinking of the die-less mandrel drawn tube drawn at speed ratios of 1.7, 1.8, and 2.0, respectively, as shown in Fig. 13a. Therefore, the die reduction at which the outer surface roughness was the least in hollow sinking decreased as the speed ratio of the die-less mandrel drawing increased. The inner surface roughness increased by the die-less mandrel drawing. There was no significant difference in the inner surface roughness with increasing speed ratio in die-less mandrel drawing. Furthermore, the inner surface roughness increased as the die reduction increased in hollow sinking (Fig. 13b) due to free surface roughening, as reported by Osakada et al. [38].

Fig. 11
figure 11

Observation results of the outer surface roughness. Height maps of the (a) original tube and (b) drawn tubes. Symbols DD, CD, and ND indicate the drawing direction, circumferential direction, and normal direction of the surface, respectively

Full size image
Fig. 12
figure 12

Observation results of the inner surface roughness. Height maps of the (a) original tube and (b) drawn tubes. Symbols DD, CD, and ND indicate the drawing direction, circumferential direction, and normal direction of the surface, respectively

Full size image
Fig. 13
figure 13

Experimental measurement results of the surface roughness. Surface roughness of (a) the outer surface and (b) inner surface. The dotted line and curves are the eye guides

Full size image

Figure 14 shows height distributions of the die-less mandrel drawn tubes in the drawing direction. The asperity height of the die-less mandrel drawn tube drawn at the speed ratio of 2.0 was nearly twice that of the tube drawn at the speed ratio of 1.7. Therefore, the flank angle of the die-less mandrel drawn tube drawn at the speed ratio of 2.0 was larger than that drawn at the speed ratio of 1.7. Hence, the asperity height of the die-less mandrel drawn tube drawn at the speed ratio of 2.0 in the FEM was set to twice that of the tube drawn at the speed ratio of 1.7 (Fig. 7b). Nielsen et al. reported that the real contact area increased as the flank angle decreased in asperity flattening [39]. This study also focused on the flank angle of asperity.

Fig. 14
figure 14

Experimental height distributions of the outer surfaces of the die-less mandrel drawn tubes in the DD (drawing direction). Parameter V1 / V0 is the speed ratio in the die-less mandrel drawing

Full size image

Outer surface geometry in FEM

Figure 15 shows the outer radius distributions of the die-less mandrel drawn tube and hollow sunken tubes in the DD obtained through FEM. Visually, the outer radius dispersion of the die-less mandrel drawn tube is decreased by hollow sinking. Therefore, the outer surface of the die-less mandrel drawn tube was flattened by hollow sinking. Particularly, the outer surface was the smoothest at the die reduction of 0.04 and speed ratio of 2.0. Figure 16 depicts the dispersion of the outer surface height evaluated by using the line surface roughness Ra [40] through FEM. Line surface roughness is calculated using Eq. (3). Parameter L represents the length of the evaluation region.

Fig. 15
figure 15

Outer radius distributions of the die-less mandrel drawn tube and hollow sunken tubes for the drawing direction obtained by the FEM. Parameters V1 / V0 and Re indicate the speed ratio in die-less mandrel drawing and the die reduction in hollow sinking, respectively. Symbol DD indicates the drawing direction

Full size image
Fig. 16
figure 16

Line outer surface roughness of the hollow sunken tube after die-less mandrel drawing obtained through FEM. Parameters V1 / V0 and Re indicate the speed ratio in die-less mandrel drawing and the die reduction in hollow sinking, respectively

Full size image
$$R\mathrm{a} = \frac{1}{{L}}{\int}_{0}^{L}\left|{{h}} ({{x}})\right|{\mathrm{dx}}$$
(3)

The FEM in this study was based on the assumption that asperities existed continuously on the outer surface before hollow sinking, unlike in the experiment. Therefore, the initial surface roughness in the FEM was larger than that in the experiment. The line surface roughness was the least at the die reduction of 0.04 in hollow sinking when the speed ratio was 2.0 in die-less mandrel drawing. However, the line surface roughness was the least at the die reduction of 0.08 in hollow sinking when the speed ratio was 1.7. Therefore, the die reduction at which the outer surface roughness was the least decreased when the speed ratio increased. This tendency agreed with the measurement results in Fig. 13a.

Discussion

Flattening behavior of outer surface in hollow sinking after die-less mandrel drawing

The outer surface roughness of the die-less mandrel drawn tube and hollow sunken tube were measured over the same measurement area to investigate the outer surface flattening behavior in hollow sinking after die-less mandrel drawing. Figure 17 shows the measurement results of the outer surface of the die-less mandrel drawn tubes drawn at the speed ratio of 1.8 and hollow sunken tubes in the same measurement area. The dotted lines in Fig. 17b are the approximate lines derived using the least squares method. The measurement values when the concave part of the die-less mandrel drawn tube exhibits no change are plotted as a black line in Fig. 17b. The measurement values when the concave part of the die-less mandrel drawn tube completely disappeared are plotted on the horizontal axis. As shown in Fig. 17a, most of the concave parts on the outer surface of the die-less mandrel drawn tube remained after hollow sinking at the die reduction of 0.02. The area of the residual concave parts of the hollow sunken tube decreased as the die reduction increased to 0.06. However, the area of the residual concave parts increased when the die reduction increased from 0.06 to 0.10. Moreover, the slope of the approximate line of the concave fraction of the die-less mandrel drawn tube was the least when the die reduction was 0.06, where the outer surface roughness was the least in hollow sinking. Therefore, the concave fraction on the outer surface was the least under die reduction when the outer surface roughness was the least in hollow sinking. Similar results were obtained under other speed ratio conditions.

Fig. 17
figure 17

Experimental observation results of the outer surface of the hollow sunken tube and die-less mandrel drawn tube drawn at the speed ratio of 1.8 in the same measurement area. (a) Surface height maps before and after hollow sinking over the same measurement area. (b) Concave fraction of the hollow sunken tube against that of die-less mandrel drawn tube. The dotted lines are the approximate lines derived by the least squares method. Symbols DD, CD, and ND indicate the drawing direction, circumferential direction, and normal direction of the surface, respectively. Parameter Re is the die reduction in hollow sinking

Full size image

Deformation behavior of outer surface in hollow sinking after die-less mandrel drawing

Bay et al. reported that the real contact area (i.e., the surface area flattened by the tool) increased as the contact pressure increased in the asperity flattening process [28]. Ike and Makinouchi reported that lateral tension enhanced bulk deformation and increased the real contact area for a given mean contact pressure [30]. It is considered that the contact pressure and bulk deformation correspond to die pressure and drawing stress in hollow sinking, respectively. Therefore, die pressure and drawing stress were evaluated by the slab method and FEM to investigate the reason for the minimum value of the outer surface roughness against die reduction, as shown in Fig. 13a. Additionally, the reason for the decrease in the die reduction value corresponding to the minimum value of the outer surface roughness as the speed ratio increased was investigated.

The drawing stress ratio σl’ (= drawing stress σl / yield stress of tube Y) and die pressure ratio, p’ (= die pressure p / yield stress of tube Y), are calculated using Eqs. (4) and (5), respectively, which are derived from the slab method in a previous study [7].

$${\sigma}_{\mathrm{l}}^{\prime}= \left(\ (1+\frac{1}{{B}}\right)\left\{{1}-{(1-{R}_{\mathrm{e}})}^{{B}/2}\right\}+{\alpha }_{\mathrm{BT}}{(1-{R}_{\mathrm{e}})}^{{B}{/2}}$$
(4)
$${{p}}^{\prime}=\frac{-{t}\cdot ({\sigma }_{\mathrm{l}}^{\prime}-{1)}\cdot {\mathrm{cos}{\theta}}}{({{r}}+\frac{{t}}{{2}}{\mathrm{cos}{\theta}})}$$
(5)

The parameter B represents μ cot θ. The friction coefficient between the tube and die μ was set to 0.05, similar to that in a previous study [36]. The die half angle θ was set to 6°. Parameter αBT represents the dimensionless back stress, which is the stress acting in the direction opposite to the DD. In this study, back stress was not applied to the tube during hollow sinking. Therefore, the dimensionless back stress was set to zero. The die pressure ratio when the tube began to contact the die was calculated. Subsequently, the measured outer radius r and wall thickness t of the die-less mandrel drawn tube for each speed ratio were substituted into Eq. (5). The drawing stress σl was also calculated through FEM by dividing the drawing force by the analytical cross-sectional area of the hollow sunken tube. The strain at the yield point in the FEM, ε  =  εY, was defined as the intersection of the elastic function (= Eε) and strain hardening function (= K εn). The yield stress Y in the FEM was calculated by substituting the strain at the yield point, ε =  εY, into K εn. Figure 18 shows the relationship between the drawing stress ratio, die pressure ratio, and die reduction in hollow sinking. The drawing stress ratio increased as die reduction increased in both the slab method and FEM. Typically, the yield stress of the materials before deformation or the average of the values before and after deformation is used in the slab method. Therefore, the drawing stress ratio calculated by using the slab method was larger than that obtained by using FEM because strain hardening was not considered in the slab method. Die pressure ratio decreased as die reduction increased. Wanheim et al. reported that the tensile bulk deformation enhanced the asperity deformation towards the center of a bulk flattened using a tool by the slip-line field method [41]. Sutcliffe suggested that bulk plastic deformation caused local reduction of yield stress in the asperity region [42]. In this study, the die pressure, which was the driving force for flattening the asperity, was large when the die reduction was small. However, the drawing stress, which affected the bulk plastic deformation, was small. Therefore, it is considered that low drawing stress led to less flattening when the die reduction was small. Furthermore, the low die pressure led to less flattening when the die reduction was large. Therefore, it is considered that large flattening was achieved in the middle die reduction, as the die pressure and drawing stress in this reduction were relatively larger than those in the other die reductions.

Fig. 18
figure 18

Results of the dynamic analysis of hollow sinking using the slab method and FEM. (a) Drawing stress and (b) die pressure against die reduction. Parameter V1 / V0 is the speed ratio in the die-less mandrel drawing

Full size image

Figure 19 shows a schematic illustration of the asperity flattening process in hollow sinking after die-less mandrel drawing. The die pressure decreased, and the drawing stress increased as the die reduction increased. It is considered that low drawing stress led to less flattening when the die reduction was small. Additionally, it can be concluded that the low die pressure led to less flattening when the die reduction was large. Therefore, the middle reduction was suitable for asperity flattening, because the die pressure and drawing stress in this reduction were relatively larger than those in the other die reductions.

Fig. 19
figure 19

Schematic illustration of the asperity flattening process in hollow sinking after die-less mandrel drawing

Full size image

Figure 20 shows the measured change in the surface roughness of the outer surface while the tube passed through die in hollow sinking. The outer surface roughness of the tube decreased significantly upon contacting the die but only changed slightly while the tube passed through die. It is considered that the asperity was flattened at the moment when the convex part of tube first contacted the die. Therefore, the stress state of the asperity when the tube began to contact die in hollow sinking was evaluated using FEM to investigate the asperity flattening behavior.

Fig. 20
figure 20

Measured surface roughness change of outer surface while the tube passed through die in hollow sinking. (a) Photomicrography of the outer surface of the tube and (b) outer surface roughness of each position

Full size image

Figure 21 shows the stress state of the asperity region in hollow sinking calculated by using the FEM. The stress state was evaluated by dividing the stress σ and deviatoric stress σd by the effective stress σe at the instant when the die began to contact the tube. The deviatoric stress was used to clarify the stress components that contributed to flattening the asperity towards the ND. Compressive stress was applied to the asperity when the asperity contacted the die in DD, CD, and ND. For the die-less mandrel drawn tube (large speed ratio in die-less mandrel drawing), no significant changes were observed in the compressive stress in the DD at the large flank angle of asperity, whereas the compressive stress increased in the ND as die reduction decreased. Furthermore, the compressive deviatoric stress in the ND was larger when the die reduction was small. Wanheim et al. reported that tensile bulk deformation enhanced the asperity deformation towards the center of the bulk [41]. However, in hollow sinking, when the flank angle was large (large speed ratio), we consider that enhancing the flattening of the asperity due to tensile bulk plastic deformation was difficult, even when the drawing stress increased. Zwicker et al. also reported that stretching an asperity with a large flank angle owing to large compressive stress in the longitudinal direction was difficult even when the bulk was in tension [43]. Therefore, we consider that the outer surface roughness was the least at the smaller die reduction when the flank angle was large, as the die pressure (approximately equal to ND compressive stress) at this die reduction was large.

Fig. 21
figure 21

Stress state of the convex part of the asperity in hollow sinking calculated by the FEM. (a-1) Stress distribution; (a-2) stress ratio and deviatoric stress ratio distribution when the die began to contact the tube drawn at the speed ratio V1 / V0 of 2.0; (b-1) stress distribution; (b-2) stress ratio and deviatoric stress ratio distribution when the die began to contact the tube drawn at the speed ratio V1 / V0 of 1.7. Parameters σ, σd, and σe are the stress, deviatoric stress, and effective stress, respectively

Full size image

Conversely, the compressive stress in the DD decreased as the die reduction increased when the flank angle was small. The compressive deviatoric stress in the ND became larger when the die reduction was large. At the small flank angle (small speed ratio), the flattening of the asperity due to tensile bulk plastic deformation with increasing drawing stress was easily enhanced. Hence, the die reduction where the outer surface roughness was the least in hollow sinking of the die-less mandrel drawn tube with a small flank angle (small speed ratio) was larger than that of the die-less mandrel drawn tube with a large flank angle (large speed ratio).

Figure 22 shows the analysis results of the concave part of the asperity in hollow sinking (Re = 0.10) after die-less mandrel drawing with speed ratio of 2.0. The concave part was not flattened significantly, as shown in Fig. 22a. Furthermore, deviatoric stress in the ND was almost zero while the concave passed through the die approach. Therefore, it is considered that the deformation of the concave part did not affect the asperity flattening during hollow sinking.

Fig. 22
figure 22

Analysis results of concave part of the asperity in hollow sinking (Re = 0.10) after die-less mandrel drawing with speed ratio of 2.0 calculated by the FEM. (a) Stress distribution in ND of the asperity during drawing and (b) stress ratio and deviatoric stress ratio distribution in the concave region. Dotted squares in Fig. 22(a) corresponds to position in Fig. 22(b)

Full size image

Figure 23 shows a schematic illustration of the deformation behavior of the outer surface in hollow sinking after die-less mandrel drawing. The die reduction increases by the reduced die diameter in hollow sinking of the die-less mandrel drawn tubes at a large or small speed ratio. When the flank angle was large (large speed ratio), enhancing the flattening of the asperity due to tensile bulk plastic deformation was difficult even when the drawing stress increased. Therefore, large flattening was achieved in the small die reduction by a large die pressure. Conversely, when the flank angle was small (small speed ratio), enhancing the flattening of the asperity due to tensile bulk plastic deformation became easy when the drawing stress increased. Therefore, we consider that the die reduction where the outer surface roughness was the least in hollow sinking of the die-less mandrel draw tube with the small flank angle (small speed ratio) was larger than that of the die-less mandrel drawn tube with the large flank angle (large speed ratio).

Fig. 23
figure 23

Schematic illustration of the deformation behavior of the outer surface in hollow sinking after die-less mandrel drawing

Full size image

Optimal conditions for achieving thin wall and high inner and outer surface qualities in combined process

Figure 24a shows the reduction in wall thickness and surface quality against die reduction in hollow sinking after die-less mandrel drawing. The reduction in wall thickness increases as the die reduction decreases in hollow sinking after die-less mandrel drawing, as depicted in Fig. 10d. The total reduction in wall thickness increases as the die reduction decreases in hollow sinking after die-less mandrel drawing. Furthermore, the total reduction in wall thickness in hollow sinking of the die-less mandrel drawn tube with the large speed ratio is larger than that of the die-less mandrel drawn tube with a small speed ratio for a given die reduction. Therefore, the optimal condition for thinning wall thickness is a small die reduction in hollow sinking after die-less mandrel drawing at a large speed ratio.

Fig. 24
figure 24

Fabrication method for Mg alloy tubes with thin wall and high surface quality. (a) Optimal condition for achieving thin wall and high surface quality in the combined process. (b) Optical microscope photograph of the original tube and drawn tubes drawn under the optimal condition

Full size image

The outer surface roughness increases after an initial decrease with increasing die reduction in hollow sinking after die-less mandrel drawing, as shown in Fig. 13a. The die reduction at which the outer surface roughness was the least in hollow sinking decreased as the speed ratio of the die-less mandrel drawing increased. Additionally, the inner surface roughness decreases as the die reduction decreases in hollow sinking, as shown in Fig. 13b. Therefore, the optimal condition for achieving high inner and outer surface qualities is the die reduction at which the outer surface roughness is the least in hollow sinking after die-less mandrel drawing at a large speed ratio. This condition is also effective for wall thinning in the combined process. Therefore, the conditions for achieving the thin wall and high outer and inner surface qualities are the die reduction at which the outer surface roughness is the least after the die-less mandrel drawing at a large speed ratio. Finally, Mg alloy tubes with thin walls and high surface quality were fabricated under the above condition, as shown in Fig. 24b.

Typically, the outer diameter becomes smaller than the die diameter (excessive thinning of the outer diameter) in the new hollow sinking process, in which the drawing speed is controlled on both the entrance and exit sides of the die [44]. Therefore, in this study, conventional hollow sinking, in which only the drawing speed on the die exit side was controlled, was performed to investigate the flattening behavior using a simple model such that excessive thinning of the outer diameter does not occur. Wall thinning is more prominent in the new hollow sinking process. Furthermore, the die half-angle also affects the excessive thinning of outer diameter [8]. Therefore, further investigations of die half-angle and excessive thinning of the outer diameter are necessary to determine the optimal conditions for achieving thin wall and high surface quality in the combined process of the new hollow sinking after die-less mandrel drawing.

The final surface roughness achieved in this study could not meet market requirements. Performing multiple drawing or die-mandrel drawing is expected to improve the surface roughness. Therefore, further investigation of multiple drawing and die-drawing using inner tools is a potential topic for future work. Additionally, optimization of the conditions that consider the crystal plasticity, such as crystal orientation [45] and slip deformation [46], in hollow sinking remains a potential topic for future work.

Conclusion

In this study, the flattening behavior of the outer surface asperity and the optimal condition for achieving a thin wall and high outer and inner surface qualities in the combined process of hollow sinking after die-less mandrel drawing were clarified, and conclusions are as follows.

  1. 1)

    Outer surface roughness increases after an initial decrease as the die reduction increases in hollow sinking. The die reduction at which the outer surface roughness was the least in hollow sinking decreased as the speed ratio of die-less mandrel drawing increased.

  2. 2)

    Under the die reduction at which the outer surface roughness is the least in hollow sinking, the concave fraction on the outer surface decreased significantly because the die pressure and drawing stress are relatively higher than those in the other conditions.

  3. 3)

    Enhancing the flattening of the asperity in hollow sinking due to tensile bulk plastic deformation is difficult even if the drawing stress increases when the speed ratio in die-less mandrel drawing is large. Therefore, when the speed ratio in die-less mandrel drawing is large, the largest outer surface flattening was achieved under low die reduction in hollow sinking, where the die pressure is large.

  4. 4)

    Both a thin wall and high inner and outer surface qualities can be achieved at the low die reduction where the outer surface roughness is the least in the hollow sinking after die-less mandrel drawing at a large speed ratio.

Hence, this study presented the fabrication method for a Mg alloy tubes with thin walls and high surface quality used for the development of biodegradable materials.