An analytical model for designing defect-free sheet metal profiles with height-variable cross sections manufactured by Flexible Roller Beading

Abstract

Following the industrial change from mass production towards serial customization flexible technologies are becoming increasingly important. Therefore, the novel forming process “flexible roller beading” (FRB) is developed, which enables the continuous production of sheet metal profiles with customizable variable cross-sectional height and exploits the lightweight potential of profile-based constructions. To guarantee the quality and further processability of the profiles, component defects—primarily sheet wrinkling in the profile flange—must be avoided. The occurrence of wrinkling is affected by various geometric parameters of the targeted profile. This makes an empirical determination of the material-dependent process limits inefficient due to the expensive computational times of numerical simulations and effort of experimental test executions. Therefore, a mathematical model is developed which allows the analytical prediction of the process instabilities causing sheet wrinkling. The presented paper includes the description of the mechanical characteristics of FRB based on numerical and experimental investigations. The predictive analytical model derived from these findings determines the maximum longitudinal compressive stress in the profile flange, which is responsible for the wrinkling formation, based on the relevant geometric characteristics. By the comparison of the calculated occurring longitudinal compressive stress with the material-specific critical stress, sheet wrinkling can be predicted and failure-free profile geometries can be efficiently designed. The generality of the analytical model, independent of the profile geometry, is validated by experimental tests.

Introduction

The development of the industrial production sector goes hand in hand with social and ecological change, which determines the economic and political situation, as it were. Abrupt changes in market demand pose new challenges for consumer goods manufacturers. This is due to the interplay of economic globalization, saturated markets and rapid technological progress [1]. The result is a fragmented market and ever-shorter product life cycles, whereby products with higher quality and lower costs as well as fast reaction times to market fluctuations represent significant competitive advantages. As a result, companies are confronted with the challenges of the resulting product variance and cost pressure. According to a study [2], between 1997 and 2012, cross-industry product variance increased by 120%, while the duration of product life cycles decreased by 24%. From a macroscopic perspective on industrial manufacturing, this trend is embodied by the shift from conventional mass production to mass customization [3]. The need for customized special components in simultaneously smaller batch sizes motivates the new and further development of manufacturing technologies to increase production flexibility.

In addition, the rising ecological awareness brings political climate targets with the demand for resource conservation and energy saving. The industrial sector bears a special responsibility as the source of about 55% of global energy demand [4] and 35% of global CO2 emissions, 25% of which are attributable to steel production and processing [5]. In North America, sheet metal profile components comprise 35–45% of products made from flat steel [6]. Globally, about 8–10% of steel production is processed into cold-formed profile components [7], so reducing the amount of material used in profile-based constructions offers significant benefits for the environment. One resource-saving approach is provided by lightweight design through the use of load-oriented components with efficient material utilization [8], whereby some applications, for example in vehicle construction, also benefit from energy savings through the reduction of moving mass.

The implementation of the lightweight design concept combined with the economic pressure for on-demand production of changing product ranges brings the relevance of flexible processes into focus. In addition to the production of application-specific components, flexible processes are also capable of manufacturing different product variants on a single line, ideally without additional setup effort and loss of productivity. According to a study by Mehrabi et. al. [1], the main motive for implementing flexible technologies is the substitution of existing processes and a future-oriented approach. However in application, only 50–65% of the potential of flexible systems is currently exploited and only one in five users takes full advantage of a large product variance of at least 20 variants on a system. Among other things, this is due to the lack of planning and reliability as well as insufficient process know-how and training of specialist personnel, which means that adapting to new products is associated with long start-up times. Transparent process understanding and user-friendliness are therefore essential for creating acceptance when introducing a new flexible technology.

The lack of acceptance of flexible forming processes is rooted in the challenging controllability of process limits due to complex stress conditions. Prediction of wrinkling is one of the major challenges in the numerical simulation of sheet metal forming processes [9]. In FEA the chosen approach crucially depends on the computational method [10, 11]. Explicit solvers, due to their dynamic approach, are able to geometrically represent instability-related shape defects such as wrinkling by accumulated error propagation. However, the occurrence and growth of buckling in explicit simulations are very sensitive to the simulation parameters (e.g. element type, mesh discretization, boundary conditions) [11]. Implicit calculation methods tend to better represent deformations in sheet metal forming, resulting in more realistic stress states [12]. Implicit codes are preferred for reliable and accurate analysis of part behavior after unloading [13]. However, it is difficult to model the initiation of wrinkles without taking imperfections in the initial material into account, which is why implicit methods for predicting wrinkling are usually based on residual stress approaches [11].

Although a deep understanding of the wrinkling mechanisms is available, an accurate prediction of the stress states in combination with a sufficient representation of the component geometry is necessary for a prediction of the wrinkling in the process design. Since meeting this level of detail is very costly due to the computational effort required, simplified analytical models often provide an adequate alternative. These are mostly used in process and component design to predict the wrinkling onset and to derive measures to avoid this critical condition [14]. The advantage of analytical models is that known process-critical areas can be described with only a few geometry variables and examined for failure with negligible time expenditure.

State of the art

The ecological urge to use raw materials efficiently is expressed in the constant effort to make the industrial manufacturing landscape more sustainable and flexible. The flexibilization of manufacturing processes allows the realization of application-oriented products through load-adapted material distribution in the component without tool changes and significant loss of productivity. The lightweight design approach achieved in this way is particularly important for the future in vehicle construction, which has to meet the demands of energy consumption reduction with weight savings. In safety-relevant structures of the automobile, the demands for higher stiffness at low weight cannot yet be met satisfactorily [15]. The NSB concept from Thyssen-Krupp [16] shows that the weight of the vehicle body, as the main driver of the overall weight, can be significantly reduced by intensifying the profile design. In order to establish the use of profiles in the automotive sector, which is characterized by high product diversification, flexible forming processes must be developed to ensure the economical production of individual load-oriented components.

In forming technology, or more precisely in profile production, load-adapted component design can be achieved by varying material thicknesses, cross-section shapes and cross-section curves or developments [17]. The most widespread manufacturing process for profile components is roll forming. In roll forming, the sheet metal is conveyed in stages through several pairs of rotationally driven rolls which are mounted in roll forming stands and change their gap geometry from stage to stage. As the sheet passes through the roll forming stands, the sheet undergoes incremental bending forming to the desired target cross section. The bending increment of each forming step and thus the planned intermediate states of the cross-sectional geometry are specified by the gaps between the forming rolls. The realization of geometric variability in the profile cross-section requires flexible production technologies. The flexibilization of roll forming processes has been steadily advanced on the research side, resulting in various roll-forming-like technologies [18,19,20], which, however, have limitations with respect to geometry flexibility or economic efficiency. Despite numerous efforts to increase the technological flexibility of profile production, it was not possible to produce height-variable profiles in a continuous process independent of the tooling before flexible roller beading.

Flexible roller beading (FRB)

The developed forming process "flexible roller beading" (FRB) closes this gap in design freedom and contributes to the further development of the lightweight potential of profile-based construction. The novel flexible manufacturing technology is demonstrably capable of producing sheet metal profiles with individually designable cross sections that can be changed in height in the longitudinal direction [21]. In the following, the target part geometry, the functional principle of flexible roller beading and the tool system related state of the art are presented.

Target geometry of height-variable profiles

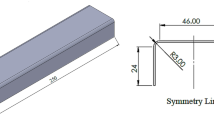
The target component in flexible roller beading is an open top hat profile whose cross-sectional geometry has an individually variable profile bottom depth h_P(x) in the longitudinal direction. The height-variable profile is longitudinally symmetrical with respect to the x–z plane, which is why Fig. 1 shows the characteristic geometry parameters of the profile based on one half of the cross-section. The cross-section can be divided into three areas: the profile bottom, the profile leg and the profile flange, which ends in the profile edge (Fig. 1b). These areas are separated from each other by the upper and lower bending edges. The bending radii r_o and r_u are specified by the forming tools. The variable profile depth h_P(x) and the profile width a_P determine the local bending angle α and the leg length l_S (Fig. 1d). The flange width b_F depends on the width of the initial plate. The longitudinal section along the line of symmetry depicts the variable profile bottom curve, which consists of the infeed and outfeed sections, the immersing height transition zone, the even profile bottom section and the emerging height transition zone (Fig. 1c). The infeed and outfeed areas at the beginning and end of the sheet are not formed, but are necessary for introducing the sheet feed by the prototypical test facility. The immerging height transition zone is represented by a linear gradient between two transition radii R_h. The emerging height transition zone has a corresponding inverse course. The even area of the profile bottom curve with constant maximum profile depth is longitudinally located between both height transitions. The shape of the profile bottom curve is defined by the total length of the height-variable profile l_P, the length of the immerging and emerging height transition zones l_h and the maximum profile depth h_P,max. The difference between the total height-variable profile length and the transition lengths results in the length of the even profile bottom section.

Fig. 1

a Target component of flexible roller beading; b relevant paths of the target profile, shown in the detailed view of the half profile section; c geometric parameters of the profile bottom curve; d geometric parameters of the profile cross-section

Functional principle of FRB

Flexible roller beading is a continuous forming process which produces top hat profiles with height-variable cross-sections, as shown in Section 2.1.1, starting from flat sheet blanks, strips or coils. Depending on the target geometry and process limits, the forming procedure can be performed in a single forming step or incrementally in multiple passes. During the process, the sheet material is fed into and through the flexible tooling system at a constant feed rate (Fig. 2a). The tool system consists of an upper forming roller and a lower forming roller as well as the blank holder plates. The blank holders are located laterally symmetrical and thus have the same distance to the center of the profile. Each blank holder assembly consists of an upper and a lower plate. The gap between the upper and lower blank holder plates can be adjusted to the present sheet thickness during setup (Fig. 2b). The setting of the distance between the blank holders in the transverse direction determines the profile width a_P (Fig. 2d). The contour shape of the lower blank holders determines the tool-dependent upper bending radius r_o (12 mm). During forming, the blank holders remain stationary and hold the flange of the hat profile vertically at the zero level, i.e. the initial height.

Fig. 2

Functional principle of FRB in the lateral and frontal view and degrees of freedom of the tool system during the forming process ((a) initial state - lateral view; (b) initial state - frontal view; (c) forming process - lateral view; (d) forming process - frontal view)

The variable height of the profile cross-section, or the profile bottom, is introduced by the upper forming roller. It has a vertical degree of freedom which allows the implementation of individual control curves. The tool-dependent profile bottom width b_PB (24 mm) and the lower bending radius r_u (6 mm) are specified by the contour of the upper roller (Fig. 2d). The lower roller has a supporting function on the underside of the profile to improve the shape and dimensional accuracy of the profile bottom curve. To ensure orthogonal contacts of both forming rollers on the profile bottom surfaces in the height transition areas as well, a horizontal degree of freedom of the lower roller in the feed direction must be provided in addition to the vertical degree of freedom (Fig. 2c) [22].

The shaping of the variable profile bottom curve results from the flexible positioning of the forming tools relatively to each other in the process. In order to avoid sheet thinning or to make sure that it remains within tolerable limits, the aim is to ensure that as much material as possible is drawn in from the profile flange to achieve the desired cross section. This is referred to as "lateral material inlet". Characteristic for lightweight profiles with variable cross-section is the equally variable material requirement in the longitudinal direction, which depends on the local cross-section dimensions. In previous flexible profiling processes, tailored sheet blanks with target geometry-dependent width contours are used [20, 23]. In FRB tailored sheet blanks that account for variable material feed can also be used. Alternatively, protruding material can be cut off at the profile edges by trimming the final profile.

Flexible forming processes, such as FRB, introduce new part defect types due to inhomogeneous process mechanisms. Sheet wrinkling in the profile flange or rather in the profile edges due to excessive longitudinal compressive stresses represent the major part error pattern of FRB. Mastering and predicting these process limits is fundamental for technology transfer to industry. The presented paper introduces the mechanical characteristics leading to sheet wrinkling as such as an analytical approach for the prediction of its occurrence.

Experimental procedure and measurement concept

In the developed test facility, the presented tool components are equipped to a servo-motor press. In this way, the customizable vertical trajectories of the upper and lower rollers are provided by the press ram and drawing cushion. The horizontal movement is implemented by a linear axis which the lower roller is mounted on (Fig. 3). The sheet feeder, depicted in Fig. 3 is implemented by external driving rollers which are located in a separate framework in front of the forming stand.

Fig. 3

Experimental setup: FRB tool system equipped to a servo-motor press (left); part geometry measurement by 3D-digitalizer “GOM Atos”

For experimental tests, 3 m long DC04 sheet blanks are used, which are cut to the constant, target geometry-dependent width. Forming takes place only in the central 1200 mm of the sheet. Due to the design of the prototype tool system, the 900 mm long areas in the infeed and outfeed are used to introduce the feed velocity and to guide the sheet during the forming pass. The profile geometry is measured using the camera-based "GOM Atos Q" measuring system, which generates a three-dimensional scan of the profile surface (Fig. 4). In this 3D model, evaluation paths can be defined and analyzed. To improve component handling and fixation during the measuring process, the infeed and outfeed areas are separated in advance by shear cutting. For the present work, the vertical curves (in z-direction) along the profile bottom h_P (x) and the profile edge z_E (x) are relevant. The profile exhibits overall part curvatures, which are mainly due to deformations of the initial sheet, for example caused by transport and material handling, as well as process-related residual stresses and deformations caused by the separation of the inlet and outlet areas. To eliminate the influence of component curvature, the basic profile path (path 1) and two paths (paths 2 and 3) per flange are measured (Fig. 4). As the edges of the profile cannot be measured continuously due to limitations of the measuring system, path 2 runs parallel to the profile at a distance of 5 mm. Path 3 runs along the inner flange area in the immediate proximity of the bending edge and is used to determine the total part curvature. To evaluate the profile bottom curve, the curvature (path 3) is subtracted from path 1 measured in the center of the profile. Accordingly, the measured curve at the outer flange edge (path 2) minus the curvature (path 3) results in the vertical profile edge curve.

Fig. 4

Evaluation paths in the measured 3D-model of the profile and evaluation concept; measured profile bottom curve and sheet wrinkling in the profile edge

Figure 4 shows the measured profile bottom curve h_P(x) and profile edge z_E (x) of a profile with h_max = 8 mm, remaining non-formed inlet and outlet lengths of 200 mm, height transition lengths l_h of 200 mm and an even profile bottom length of 400 mm. It can be seen that the shape accuracy of the profile bottom curve decreases from the longitudinal position where h_max is reached after the height transition (x = 400 mm) towards the profile end. This is due to process-related mechanical characteristics during continuous forming, which are explained in more detail in Section 5. Whereas the evaluation of the dimensional accuracy of the profile bottom curve is based on the comparison between the maximum profile height h_max achieved immediately after the immerging height transition (x = 400 mm) and the target profile height of the nominal geometry. In the example profile shown, the maximum profile depth is 7.91 mm and thus deviates from the target height by 1.1%.

The deviation is due to springback effects and must be evaluated on the basis of component-specific requirements in industrial applications. In the context of this work, the profile bottom is described as dimensionally accurate for deviations of less than 5% from the desired maximum nominal height. The shape accuracy of the profile geometry is defined as the average relative deviation of the entire profile bottom curve. Due to the above-mentioned process-related increasing deviation of the profile bottom towards the end of the profile, good shape accuracy is defined at relative deviations below 10%.

The focus of the work is the analysis of the wrinkle formation in the profile flange as a process limit of FRB. The propagation of the wrinkles in the longitudinal direction indicates process-related longitudinal compressive stresses in the flange, or in the profile edge, as the cause. The occurrence of wrinkles is detected by measuring the vertical profile edge shape z_E(x). It can be seen in Fig. 4 that by subtracting the vertical path measured in path 3, the curvatures in the profile edge cannot be entirely eliminated. Therefore, wrinkles must be differentiated in their identification from profile curvatures. Wrinkles are defined as wave-shaped instationarities whose amplitude is greater than 0.1 mm and wavelength less than 100 mm. Wrinkles of this dimension can already cause a recognizable deterioration of the appearance, which has high requirements especially for visible components, for example in building facades.

The initiation of wrinkling is reproducibly observed immediately after the immerging height transition zone at the beginning of the even profile bottom section (cf. z_E(x) in Fig. 4 from x = 400 mm). The wrinkle formation in the flange thus starts in the same area in the longitudinal direction where the profile bottom curve also reaches the maximum height h_max (x ≈ 400 mm). From this it is deduced that already a local exceeding of the critical state results in instabilities.

Process modelling with the Finite Element Method (FEM)

To evaluate the correlation of sheet wrinkling with the profile depth and potentially other parameters the mechanical stress and strain characteristics of FRB are to be investigated. As described in Chapter 1, the realistic representation of wrinkling based on numerical simulations requires a high level of detail in the modeling of the component geometry, material behavior as well as imperfections and has a high sensitivity to the simulation parameters [11]. Therefore, the purpose of the presented FEM model is not the illustration of wrinkles itself, but rather the accurate determination of the residual stresses causing wrinkling failure.

The flexible roller beading process is numerically modelled with MARC Mentat. Since the process is assumed to be quasi-static an implicit solver is used which is beneficial for accurate residual stress analyses [11, 13]. Rebelo [24] made a comparison between implicit and explicit algorithms in sheet metal forming simulations with the result that implicit calculation was less sensitive to interferences and show a better conformity with experimental results. To reduce the computation time, only one half of the system, which includes the blank and the tool rollers, is simulated under consideration of symmetry conditions. The tool system is abstracted into the main tool components upper and roller forming rollers as well as the blank holder plates and the feed and guidance rolls only. Contrary to the real process where the sheet metal is fed through the forming unit, in the simulation the motion curves are applied to the tool rollers via position control. Gehring [25] showed that friction only has a small influence on roll forming processes. Therefore a frictionless numerical model with non-rotating rolls was chosen. The definition of the forming rollers as analytical rigid bodies appears to be sufficient for the pursued investigations. The updated Lagrange procedure is used, which is applicable in large strain plasticity problems and can be implemented by using additive or multiplicative decomposition. In this case, multiplicative decomposition shows better conformity with the experimental results and is therefore chosen. The sheet metal is modelled with the element type 117 of MARC [26], which is an eight-node isoparametric arbitrary hexahedral for general three-dimensional applications with a single integration point and therefore using reduced integration. Lower order reduced integration elements, such as type 117, are formulated with an additional contribution to the stiffness matrix to eliminate hourglassing normally associated with reduced integration elements [26]. The Newton–Raphson method is chosen, which provides good results for most nonlinear problems. Figure 5 depicts an overview of the simulation properties and the applied flow curve.

Fig. 5

FEM simulation parameters and DC04 material flow curve

The initial numerical and experimental process investigations were carried out using sheets of the low-strength deep-drawing steel DC04 and a sheet thickness of 1.0 mm. The elastic–plastic behavior of the material is modelled using the von Mises yield criterion and the flow curve is obtained from tensile tests. In simulations the sheet length is 1200 mm which corresponds to the maximum forming length in experimental tests. The infeed and outfeed areas of 900 mm length required in the real test for the feed velocity introduction are not modeled in the simulation in order to save computing time. The sheet width depends on the target geometry of the profile. The reference sheet metal of the investigations has a width of 280 mm, which means a sheet width of 140 mm in the half-symmetrical FEM model.

Figure 6 shows the assembly of the FEM model. 18 nodes in the flange on the leading end of the deformable sheet metal are fixed in longitudinal direction keeping it in position while the forming rollers perform their individual motion. In order to analyze the in-plane (x–y) mechanical conditions in the profile flange, the interfering impact of profile curvature is eliminated by locking the vertical displacement of the profile flange in z-direction. This second boundary condition is applied to the laterally outer areas of the flange while the three inner nodes located close to the upper bending edge are not fixed vertically. Thus, the process-related stresses in the profile flange can be examined without affecting the forming behavior in the bending edge.

Fig. 6

FEM model of the FRB process and the applied boundary conditions

The numerical results of the FEM simulations show good agreement with the experimental investigations. Taking the profile bottom curves with 3, 4, 5 and 6 mm profile depths shown in Fig. 7 as an example, there is a high degree of shape fidelity between the results. The profile bottom geometry from the simulation deviates on average by 2.61% from the experiments.

Fig. 7

Validation of the numerical results by comparison of the profile bottom curves with experimental results

Process characteristics of FRB

The process view purely from the perspective of the cross section shows analogies to deep drawing. In order to avoid or minimize material thinning, the component geometry or the forming strategy must be selected in such a way that the material required to form the profile cross-section can be drawn in laterally from the flange (cf. Fig. 2d). Ideally, the lateral material inlet u_y,E corresponds to the additional amount of material required in the center of the profile. Accordingly, a variable profile height in the longitudinal direction implies a correspondingly variable material inlet along the profile edge. In reality, the plastic deformation of the bending edges leads to inhomogeneous material properties due to strain hardening as well as the increased geometric stiffness caused by the profile shape. These impair the lateral material inlet with the consequence that the ideal drawn-in material quantity cannot be achieved. It stands to reason that an increasing bending angle α means higher forming degrees and strain hardening in the bending edges. This impedes the material to be drawn from the flange into the profile and enhances the risk of sheet thinning accordingly. Figure 8 depicts the lateral material inlet u_y and the lateral strain along the part cross-section during the penetration process of the forming roller for two profiles with the same theoretical nominal material inlet of 4 mm. Profile 1 has a bending angle of 40° and the bending angle of profile 2 is 30°. In order to fulfill the condition of equal nominal material inlet, profile 2 needs a larger profile width than profile 1. It is evident, that profile 1 with a larger bending angle allows less lateral material inlet. By implication, the tensile stresses along the cross-section are higher than in profile 2. Thus, higher tensile elongation is observed in the cross-section of the forming zone [27].

Fig. 8

Influence of the profile bending angle on the lateral material inlet and the strains in the cross-section [27]

Since no strain hardened bending edges are yet present in the first forming pass, comparatively more material can be drawn in than in subsequent forming steps. Figure 9 shows the numerical results of three exemplary profile variants, each produced in one forming pass and in two forming passes. Shown are the sheet thickness distributions in the cross section located at the end of the immerging height transition (cf. x = 400 mm in Fig. 4). Due to the maximum profile depth h_max at this point, the greatest reduction in sheet thickness takes place in this cross section. Figure 9a shows the comparison of the sheet thickness distribution for a profile with h_max = 8 mm for single-stage and two-stage forming with 4 mm + 4 mm profile depth increase. Figure 9b shows the results of the forming strategy with 6 mm + 2 mm depth increase. Figure 9c compares the sheet thickness distributions in the cross section of a profile with h_max = 10 mm for the single-stage and two-stage forming strategy (6 mm + 4 mm).

Fig. 9

Effect of single-stage and two-stage forming strategies on the sheet thickness distribution in the profile cross-section at x = 400 mm in FRB; ((a) 8 mm single stage vs. 4+4 mm two-stage; (b) 8 mm single stage vs. 6+2 mm two-stage; (a) 10 mm single stage vs. 6+4 mm two-stage)

Despite the low thinning, it is evident that a multi-stage forming strategy leads to larger maximum sheet thickness reductions in the final part. Figure 10 shows the maximum thinning in the cross-section determined from simulations as well as the local lateral material inlet at the considered longitudinal position of the profile. A decrease in lateral material inlet is shown to correlate with an increase in sheet thinning.

Fig. 10

Correlation between sheet thinning and the lateral material inlet

It follows that to minimize material thinning, the forming potential in the first pass, which is limited by the wrinkling, must be exploited to the maximum. Accordingly, the following process investigations and analytical modeling focus on the first forming pass. The mechanical conditions of FRB along the profile cross-section and in the profile edge during the process have been presented in [23]. Then again, the cause of sheet wrinkling can be found in the process characteristics in the profile bottom leading to longitudinal residual stresses in the profile flange and edge.

Longitudinal stress and strain state in the profile bottom during the process

Due to the height-variable curve of the profile bottom longitudinal strain in the profile bottom is inevitable for the process since the length of the target profile bottom always exceeds the initial length of the sheet metal. Furthermore, the feed motion of the sheet metal brings additional effects into the stress and strain formation which is why the load applied to the profile bottom cannot be simplified as pure stretching. In fact, the mechanical load condition depends on the current process state for which six significant time stages are to be distinguished (cf. Fig. 11). The process states (PS) include the initial penetration of the upper roller (PS1 / x = 245 mm), the end of the descending height transition (PS2 / x = 400 mm), the longitudinal center position of the profile bottom (PS3 / x = 600 mm), the state of accessing the ascending height transition (PS4 / x = 800 mm) and the moment shortly before withdrawing the upper roller (PS5 / x = 950 mm). The last process state (PS6) represents the condition after releasing the tool rollers post forming.

Fig. 11

Process states of forming the profile bottom curve

The representative longitudinal path of the profile bottom is located close to the lower bending edge where the maximum upper roller force is applied instead of the symmetry axis. The numerical results of the profile bottom curve depicted in Fig. 11 shows an inferior geometrical accuracy towards the ascending transition zone (700 mm < x < 1000 mm), which can also be found in the experimental results (cf. Fig. 4). The cause of the increasing deviation can be explained by the longitudinal stress conditions in the profile bottom during the considered process states shown in Fig. 12.

Fig. 12

Longitudinal stress in the profile bottom during FRB in the significant process states 1–6

In PS1 the tool roller induces a uniform tensile stress into the profile bottom which spreads evenly in positive and negative x-direction. This symmetric stress distribution is held up as long as the deformation remains elastic. As soon as the yield strength of the material is exceeded and therefore plastic elongation of the profile bottom occurs, the springback behavior of the already formed section causes longitudinal profile curvature and therefore residual stresses expressed in compression of the entire profile bottom including the not yet reached areas lengthwise. As a consequence, the upcoming section of the profile bottom which yet has not been formed intentionally is already pre-stressed. The superposition with the constant process load induced by the tool roller results in decreasing effective longitudinal stresses in the profile bottom (cf. Fig. 12). Figure 13 schematically depicts the development of the cumulative longitudinal strain in the profile bottom in different process states (∑ε_x,PS) in relation to the profile flange and the residual springback induced stress (σ_xx,sb,PS) when the tool induced stress during the process (σ_xx,p,PS) exceeds the yield strength (YS) of the material.

Fig. 13

Development of the longitudinal strain and residual stress in the profile bottom

On the basis of the presented results, it is evident, that with the progressive movement of the tool roller, the springback induced pre-compression increases due to the cumulative total plastic elongation of the profile bottom. This can be observed in the growing compressive stress values from PS2 to PS4 and the resulting reduction of the superposed tensile stress, which leads to diminishing accuracy of the profile bottom curve toward the end. In PS5 the pre-compression even nullifies the tool induced tensile stress entailing no elongation at this point at all.

The development of the plastic strain in the profile bottom depicted in Fig. 14 supports the findings and reveals additional information about the forming behavior. The stretching of the profile bottom can be divided into a depth descending slope area with double sided elongation (200 mm < x < 400 mm) and the section width constant profile depth where only one-sided elongation occurs (450 mm < x < 800 mm) with a short transition zone in between. At first, the longitudinal elongation of the profile bottom distributes on both the front and rear side of the tool contact lengthwise. After reaching the maximum depth of the profile curve at x = 400 mm, a condition occurs where the rear-sided profile bottom of the tool roller is already plastically formed so that elongation is only necessary on the front-sided unformed sheet material. This change of elongation characteristics is expressed by a sudden drop of the longitudinal plastic strain down to approximately half of its value.

Fig. 14

Plastic strain development in different process states and total strain post forming

In consequence of the slightly fading superposed stress due to pre-compression the plastic strain decreased accordingly in the section 450 mm < x < 800 mm. The unsteadiness at x = 800 mm is caused by the elevation of the upper tool roller and therefore the momentary release of the pre-compression. In the ascending slope area (800 mm < x < 1000 mm) the tool induced tensile stress decreases until the superposed stress undercuts the yield strength at x = 935 mm and no plastic strain remains. Since PS5 occurs beyond that point at x = 950 mm, the plastic strain distribution is congruent with PS6.

Residual stress and strain state of the final part

The comparison of the plastic strain with the actual total strain in the profile bottom post forming (Fig. 14) shows the effects of longitudinal curvature in the form of residual stresses compressing the profile bottom and therefore lowering the remaining longitudinal strain. The orientation of the part curvature is consistent with the residual longitudinal stresses in Fig. 12. In order to characterize the mechanisms of wrinkle formation in the profile flange, the spreading of the post forming stress conditions is retraced starting from the profile bottom where the forming force is applied through the profile leg into the flange.

Figure 15 depicts the longitudinal stress, total strain and plastic strain in the profile bottom and two differential paths in the profile leg. The lower leg path is located close but beyond the lower bending edge while the upper leg path is situated near the upper bending edge. The profile bottom and the lower leg path undergo plastic elongations leading to compressive stresses after springback. The lower leg path shows the same distinctive stress and strain conditions as the profile bottom only to a lesser extent due to the smaller depth and therefore lower elongation of the path. Conversely, the upper leg path exhibits different characteristics, since it is not plastically stretched but even compressed lengthwise instead. Still, the present strain after the process is positive entailing residual longitudinal tensile stresses. The disparate stress and strain characteristics indicate a change of mechanical conditions in the profile leg. In fact, the forming zone which spreads over the entire profile cross-section can be divided into a direct and an indirect forming zone. The direct forming zone covers the profile bottom and the section of the leg in which the dominating stress condition is introduced by the forming roller force. The mechanical stress condition in the indirect forming zone is decisively a result of the stress and strain states in the direct forming zone. In specific, the upper leg path is not stretched by the tool engagement directly but from the elongated profile bottom involving elastic longitudinal strain and tensile residual stresses.

Fig. 15

Development of longitudinal stress and strain in the profile leg post forming

The clarified stress and strain distribution of the upper leg path is transferred into the inner area of the profile flange being a part of the indirect forming zone. Therefore the characteristics of the flange near the upper bending edge and the upper leg path resemble with the exception that no plastic strain occurs in the flange. The open profile edge acts as the counterpart of the inner flange sections and shows contrary stress distributions accordingly. The stress and strain distribution of an inner flange path and the profile edge are depicted in Fig. 16.

Fig. 16

Post process stress and strain condition in the profile flange

As a consequence of the purely elastic stress condition in the flange, the residual stress and strain exhibit the same characteristics qualitatively in the same path. While the longitudinal stress in the inner flange path shows tensile stresses in the height transition sections (0 mm ≤ x ≤ 400 mm and 800 mm ≤ x ≤ 1200 mm) and compressive stresses in the even profile bottom (400 ≤ x ≤ 800 mm), the stress condition in the profile edge behaves inversely.

Figure 17 depicts the longitudinal residual stress distribution after the forming process and illustrates the contrasting tensile and compressive zones in the inner flange sections and the profile edge. The observed stress condition is reminiscent of a beam fixed at both ends and burdened with two converse torsional moments.

Fig. 17

Residual longitudinal stress distribution in the profile flange post process

The maximum value of the compressive longitudinal stress is located at the beginning of the even profile bottom section. In the exemplary profile with the profile depth h_max = 3 mm depicted in Fig. 18, the maximum longitudinal compression appears at x = 445 mm. The location of the maximum longitudinal compressive stress matches with the position where sheet wrinkling is initiated, which consistently occurs shortly after the immerging height transition (cf. Fig. 4). This states that the maximum longitudinal compression in the profile edge represents the indication for profile failure by sheet wrinkling and therefore the process limits.

Fig. 18

Position of the maximum longitudinal stress σ_xx,max in the profile edge ((a) longitudinal stress in die profile edge (FEM); (b) profile bottom curve)

Process limit influencing factors of FRB

Besides the material properties and the sheet metal thickness [21] the process limits are mainly depending on the geometric characteristics of the target profile. Various geometric parameters are expected to have an effect on the maximum compressive stress in the profile flange and therefore on the risk of sheet wrinkling which is the main focus of the following investigations. The relevant parameters (Fig. 19) represented by the profile depth, the total and even profile length, the profile width as such as the flange width are varied in isolation in order to determine their impact sensitivity on the process limits of FRB. It is expected, that the mentioned parameters either affect the longitudinal strain of the profile bottom and therefore the stress condition in the entire part or the longitudinal stress distribution in the profile edge directly.

Fig. 19

Influencing geometric parameters

By means of the given results in Section 5.2 it is evident, that the degree of compressive stresses in the profile flange and edge is strongly determined by the longitudinal strain in the profile bottom which correlates with its shape (h_max, l_P, l_h). The cross-section geometry expressed by the section width a_P and flange width b_F additionally influences the propagation of stresses from the force application in the profile bottom to the failure critical profile edge even if the profile bottom curve remains constant. For this reason, the sensitivities of the influencing parameters are evaluated with the respectively generated maximum residual longitudinal stress values σ_xx,max post process in both the profile edge and the profile bottom. The isolated variation of the influencing parameters shown in Fig. 20 is performed starting from the reference geometry Fig. 19 (highlighted in bold). The profile width of 66 mm corresponds to the minimum feasible value due to tool-side restrictions. The sensitivity analysis is based on the example of a DC04 steel material with a thickness of 1.0 mm.

Fig. 20

Parameter variation for the evaluation of influencing sensitivities

The variation of the profile depth proves the logical correlation that an increasing h_max is accompanied by larger longitudinal stress peaks in the profile bottom and also in the profile edge (Fig. 21).

Fig. 21

Sensitivity of the maximum residual longitudinal stress in the profile edge and the profile bottom of the final part with variation of the profile depth h_max

By varying the profile length the gradient of the depth transition slope stays unaffected. With increasing total profile length, the compression of the profile edge decreases significantly while the maximum stress in the profile bottom remains unchanged (Fig. 22). Since the maximum stress in the profile bottom is observed immediately after the depth transition area (cf. Fig. 18), it is not unexpected that it mainly depends on the transition gradient and the profile depth rather than the length of the profile bottom. By enlarging the profile length l_P the resulting compressive stress in the profile edge is eased due to a greater spreading surface.

Fig. 22

Sensitivity of the maximum residual longitudinal stress in the profile edge and the profile bottom of the final part with variation of the profile length l_P

As a consequence of shortening the height transition length l_h the length of the even profile bottom section is enlarged and the height transition gradient is simultaneously increased. This leads to enhanced maximum longitudinal stresses in the profile bottom as previously discussed. Still, the positive effect of a larger spreading surface for the compressive stresses in the profile edge of the even profile bottom section dominates the increasing stress in the profile bottom by which means the maximum longitudinal stress σ_xx,max in the profile edge decreases (Fig. 23).

Fig. 23

Sensitivity of the maximum residual longitudinal stress in the profile edge and the profile bottom of the final part with variation of the height transition length l_h

Regarding the cross-sectional geometric characteristics the profile width affects the lateral material inlet as shown in Fig. 8. Widening the profile cross-section implies a reduction of the bending angle, which leads to more material inlet. As a result, less longitudinal profile bottom stretching is needed to achieve the target shape whereby the maximum stress is reduced. Accordingly, the compressive longitudinal stress in the profile edge decreases as well (Fig. 24).

Fig. 24

Sensitivity of the maximum residual longitudinal stress in the profile edge and the profile bottom of the final part with variation of the profile width a_P

As anticipated, the stress state in the profile bottom is not affected by the width of the profile flange since it only changes the condition of the indirect forming zone. However, the compressive stress in the profile edge decreases with increasing flange widths for the same reason of larger spreading surfaces (Fig. 25).

Fig. 25

Sensitivity of the maximum residual longitudinal stress in the profile edge and the profile bottom of the final part with variation of the flange width b_F

An analytical model for the prediction of sheet wrinkling

The starting point for the development of the analytical model for FRB is the failure-critical profile flange. Based on the characteristic residual longitudinal stress condition in the flange (cf. Fig. 17) and the results of the sensitivity analysis in Section 5.3, the model is developed with the aid of general laws of mechanics.

The analytical bending beam model

The analytical model for predicting sheet wrinkling is based on a residual stress approach in which the failure-relevant stress feature is mathematically calculated on the basis of the parameterized profile geometry and compared with a critical stress. The parameterization of the profile geometry is based on the geometric influence parameters identified in Section 5.3 (cf. Fig. 19). As described in Section 5.2, the residual stress state in the flange of the final component shows analogies to a bending beam clamped on both sides (Fig. 26).

Fig. 26

Transfer of the failure-critical profile flange to a simplified approach based on beam theory

Sheet wrinkling results from longitudinal compressive stresses in the flange, which, with respect to the longitudinal direction, are maximum in the profile edge section of the even profile bottom (cf. Fig. 18). Also in experimental investigations, wrinkling is observed in this area (cf. Fig. 4). The failure criterion states that wrinkling occurs as soon as the maximum longitudinal compressive stress in the flange exceeds a critical value. By transferring the failure-critical flange of the height-variable profile section to the bending beam equivalent model, the maximum prevailing compressive residual stress can be determined analytically using beam theory [28] with a known load.

The assumption of the mechanical laws of beam theory presupposes a purely elastic strain state of the profile flange. Consideration of the equivalent plastic strains of all elements in the deformed section in the FEM simulation shows that, in the failure-free state, only small areas located directly at the upper bending edge are slightly plastically deformed. In the case of the profile with a depth of 4.5 mm shown as an example in Fig. 27, the plastic deformation in the flange (33 mm < y < 140 mm) already ends at y = 40 mm. Due to the negligible plasticization, the purely elastic strain state can be assumed for the profile flange.

Fig. 27

Equivalent plastic strain on the surface of the formed profile

Determination of the equivalent load on the bending beam

The equivalent load in the bending beam model represents the influences of the residual stresses coming from the process-related strains in the profile bottom and leg, which results in the characteristic residual stress state in the profile flange. Since the equivalent load acts in the transverse direction, the transverse stresses in the y-direction σ_yy are considered along the transition borderline between the leg and the flange (inner flange path). The transverse residual stress distribution in the intersection corresponds to the equivalent line load in the analytical model.

Residual stresses in the transverse direction are predominantly present in the height transition areas. In this context, the zones of the transition area lying on the outside in the longitudinal direction (200 mm ≤ x ≤ 316 mm and 868 mm ≤ x ≤ 1000 mm) exhibit compressive transverse stresses, while tensile transverse stresses prevail in the transition areas lying on the inside (316 mm ≤ x ≤ 400 mm and 800 mm ≤ x ≤ 868 mm) (Fig. 28). The distribution of σ_yy exhibits a qualitative symmetry with respect to the profile center (x = 600 mm), which can be attributed to the symmetrical shape of the profile bottom curve. The stresses at the immerging height transition are slightly larger than at the emerging height transition due to the higher degrees of deformation in the profile bottom (Section 5.1).

Fig. 28

Distribution of the transverse residual stress σ_yy along the boundary between flange and upper bending edge (inner flange path)

The present transverse residual stress (RS) distribution is the result of inhomogeneous plastic transverse strains of the profile leg in the transition areas. If the profile is unwound in the transition area, the result is an approximately triangular profile leg which, due to its geometry, has a higher plastic transverse strain at the lower end of the transition than at the upper end (Fig. 29a). The consequences are tensile residual stresses (TRS) at the outer end, since the plastically stretched leg areas stretch the less elongated leg areas. Conversely, due to the compressive effect of the less plastically stretched leg regions, compressive residual stresses (CRS) are present at the inner end of the transition (Fig. 29b).

Fig. 29

Inhomogeneous transverse strain in the profile leg (a) resulting in the residual stress distribution in the cut edge between profile flange (c) and leg (b)

According to the actio-reactio principle, the transverse residual stresses must be compensated within the profile. Since the profile bottom is stretched in the same way as the profile leg, the stress compensation can only take place through the profile flange. As a result, residual stresses are present in the cut edge between the flange and the leg that are converse to the transverse residual stresses of the leg (Fig. 29c) and thus result in the curve shown in Fig. 28.

A precise description of the transverse residual stress curve is difficult to realize analytically due to the complex mechanisms involved. For this reason, the transverse stresses acting on the profile flange and ultimately representing the line load of the beam model are mathematically approximated with simplified assumptions and depending on the parameterized profile geometry. It is shown that the transverse stress on the flange results from the strain distribution of the leg section in the height transition regions. For the longitudinal symmetry of the profile bottom, it is thus assumed in a simplified way that the line load also has longitudinal symmetry with respect to the profile center and that the transverse stresses at the non-formed sheet infeed and outfeed as such as in the even profile bottom section are zero. In the height transitions, the profile leg experiences an inhomogeneous length change in the transverse direction. The x-position-dependent theoretical length change ∆l is composed of the length change ∆l_elongation achieved by transverse stretching of the leg and the length change ∆l_retraction resulting from the lateral material inlet.

$$\Delta l(x)=\Delta {l}_{retraction}(x)+ \Delta {l}_{elongation}(x)$$

(1)

It is assumed that the elongation components are proportional to each other:

$$\Delta l_{retraction}(x)=k_1\cdot\Delta l_{elongation}(x)$$

(2)

Consequently, ∆l can be expressed by ∆l_elongation:

$$\Delta l(x)=(k_1+1)\cdot\Delta l_{elongation}(x)$$

(3)

The residual stresses at the inner flange edge can be decomposed into tensile and compressive residual stresses according to the principle of superposition. The curves of both residual stress components are exactly inverse to each other in the x-direction (Fig. 30).

Fig. 30

Determination of the equivalent line load of the beam model by superposition of the tensile and compressive residual stress distributions in the height transition region

Since the residual stresses result directly from the non-uniform transverse strain distribution in the leg at the height transitions, the tensile residual stress distribution σ_RS,tensile can be expressed in proportion to the derivative of ∆l_elongation:

$$\sigma_{RS,tensile}=k_2\cdot\frac{\partial\Delta l_{elongation}\left(x\right)}{\partial x}$$

(4)

From the formulas 3 and 4 the following is obtained:

$$\sigma_{RS,tensile}=\frac1{k_1+1}\cdot k_2\cdot\frac{\partial\Delta l\left(x\right)}{\partial x}=k_s\cdot\frac{\partial\Delta l\left(x\right)}{\partial x}$$

(5)

The tensile component of the line load of the bending beam q_tensile is then represented as the product of σ_(RS,tensile) and the sheet thickness s₀:

$$q_{tensile}=\sigma_{RS,tensile}\cdot s_0=k_s\cdot\frac{\partial\Delta l\left(x\right)}{\partial x}\cdot s_0$$

(6)

Here, the previous coefficients are summarized by the comprehensive constant k_S with the unit N/mm². It is assumed that k_S represents a material-specific constant which, among other things, also includes the Young's modulus of the sheet material with k₂ and does not depend on the profile geometry.

The theoretical length change ∆l(x) describes the difference in length between the unwound length of the instantaneous cross-section without material inlet and that of the initial state, which corresponds to the sheet width. Neglecting the bending radii, the length changes ∆l(x) result from the difference between the profile leg length l_S and the width of the leg b_S (Fig. 31b).

Fig. 31

Geometric parameters of the simplified profile longitudinal (a) and cross-sectional geometry (b)

For l_S(x) applies:

$${l}_{S}(x)=\sqrt{{{b}_{S}}^{2}+{{h}_{P}(x)}^{2}}$$

(7)

The width of the leg can be calculated from the profile width a_P and the profile bottom width b_PB:

$${b}_{S}=\frac{{a}_{P}-{b}_{PG}}{2}$$

(8)

The tool-dependent profile bottom width b_PG is 24 mm for the present upper roller geometry. The maximum elongation ∆l is given by formula 7 and 8:

$$\Delta l(x)={l}_{S}(x)-{b}_{S}=\sqrt{{{b}_{S}}^{2}+{{h}_{P}(x)}^{2}}{-b}_{S}$$

(9)

The depth of the profile bottom in the transition area can be described by a linear function whose gradient corresponds to the quotient of the maximum profile height h_max and the transition length l_h:

$$h_P(x)=\frac{h_{max}}{l_h}\cdot x$$

(10)

From this follows for ∆l(x):

$$\Delta l(x)=\sqrt{b_S^2+({\frac{h_{max}}{l_h}\cdot x)}^2}{-b}_S$$

(11)

Thus, ∆l can be expressed as a function of the geometric parameters of the profile shape. Nevertheless, ∆l represents a relatively complex function of x, which means even more complicated integrations of ∆l(x) and thus difficulties in the application of the beam theory. For this reason, the expression for ∆l(x) described in formula 11 is approximated by an exponential function (Fig. 32):

Fig. 32

Approximation of the function ∆l(x) by an exponential function with the exponent 2.3

$$\Delta l\left(x\right)\approx\Delta l_{approx}\left(x\right)=k_3\cdot x^{2.3}$$

(12)

The boundary condition is:

$$\Delta l\left({l}_{h}\right)=\Delta {l}_{approx}({l}_{h})$$

(13)

Thus k₃’ can be determined as follows:

$${k}_{3} =\frac{\sqrt{{{b}_{S}}^{2}+{{h}_{max}}^{2}}{-b}_{S}}{{l}_{h}^{2.3}}$$

(14)

Substituting the approximated function ∆l_approx(x) into formula 6 results in:

$$\begin{array}{c}q_{tensile}\left(x\right)=\sigma_{ES,Zug}\cdot s_0=2.3\cdot k_s\cdot k_3\cdot s_0\cdot x^{1.3}\\=2.3\cdot k_s\cdot\frac{\sqrt{b_S^2+h_{max}^2}{-b}_S}{l_h^2}\cdot s_0\cdot x^{1.3}\end{array}$$

(15)

Thus, the tensile residual stress and correspondingly the tensile component of the line load can be described as an exponential function of x with the exponent 1.3. Based on the assumption that the residual compressive stress distribution is inverse to the tensile residual stress (Fig. 30), the compressive component of the line load can be described as follows:

$$\begin{array}{c}q_{compressive}\left(x\right)={-q}_{Zug}\left(l_h\right)+q_{Zug}\left(x\right)\\=2.3\cdot k_s\cdot k_3\cdot s_0\cdot{(-l_h+x)}^{1.3}\\=2.3\cdot k_s\cdot\frac{\sqrt{b_S^2+h_{max}^2}{-b}_S}{l_h^2}\cdot s_0\cdot{(-l_h+x)}^{1.3}\end{array}$$

(16)

If the product of 2.3 ∙ k_s, k₃, and s₀ is combined into a term q₀, the formulas 15 and 16 can be formulated as follows:

$$q_{tensile}\left(x\right)=q_0\cdot x^{1.3}$$

(17)

$$q_{compressive}\left(x\right)=q_0\cdot{(-l_h+x)}^{1,3}$$

(18)

The superposition of both load components according to Fig. 30 results in the equivalent line load acting on a height transition area. The calculation of the line load in the second height transition area is carried out analogously to the described procedure and shows a correspondingly mirrored course for a symmetrical profile bottom curve (Fig. 33).

Fig. 33

Approximation of the numerically determined transverse residual stresses (line load) by the analytical model

The analytically determined line load approximates the existing transverse residual stresses at the inner edge of the profile flange by means of approximately linear load profiles (exponent n = 1.3). Despite the simplifications made, the characteristic features of the transverse residual stresses determined with the aid of the FEM are thereby reproduced. In the areas of the height transitions directed toward the inlet and outlet, compressive residual stresses are present, which in each case change into tensile residual stresses toward the even profile bottom section. Deviations in the approximated line load, which have a direct influence on the predicted compressive stresses in the profile edge, can be compensated by the material-specific factor k_S, which will be discussed in more detail below.

Transfer of the bending beam model to the overall model for the prediction of wrinkle formation

Transferring the line load determined analytically from the transverse residual stresses to the modeling approach of the bending beam leads to the equivalent model shown in Fig. 34.

Fig. 34

Bending beam model with analytically determined line loads

The line loads in the height transition areas can be formulated as follows using the laws of beam theory [28]:

$$EI\omega^{IV}=f\left(x\right)=q_0{\cdot x^{1.3}-q_0\cdot x^{1.3}\langle x-l_h\rangle}^0+{q_0\cdot{(l_P-x)}^{1.3}\cdot\langle x-\left(l_P-l_h\right)\rangle}^0-(q_0\cdot\left(l_h-x\right)^{1.3}-q_0{\cdot\left(l_h-x\right)^{1.3}\langle x-l_h\rangle}^0+q_0{\cdot\langle x-\left(l_P-l_h\right)\rangle}^{1.3})$$

(19)

For the expressions with pointed brackets applies:

$${\langle x-a\rangle}^n=\left\{\begin{array}{l}0\;f\;or\;x\leq a\\{(x-a)}^n\;f\;or\;x>a\end{array}\right.$$

(20)

According to the beam theory, multiple integrations of formula 19 lead to:

$$EI\omega'''=-Q=\int f\left(x\right)+C_1$$

(21)

$$EI\omega''=-M=\iint f\left(x\right)+C_1\cdot x+C_2$$

(22)

$$EI\omega'=\iiint f(x)+\frac12C_1\cdot x^2+C_2\cdot x+C_3$$

(23)

$$EI\omega=\iint\iint f(x)+\frac16C_1\cdot x^3+\frac12C_2\cdot x^2+C_3\cdot x+C_4$$

(24)

Here, E stands for the Young's modulus, I for the geometrical moment of inertia about the axis to be bent, Q for the prevailing shear force and M for the resulting bending moment in the beam. The displacement of the beam ω corresponds to the lateral material inlet. The moment of inertia I of the profile flange can be expressed by the plate thickness s₀ and the flange width b_F [28]:

$$I=\frac{s_0\cdot b_F^3}{12}$$

(25)

Since the beam is fixed on both sides in the assumed model, the boundary conditions are as follows:

$$\omega \left(0\right)=0; {\omega }^{^{\prime}}\left(0\right)=0; \omega \left({l}_{P}\right)=0; {\omega }^{^{\prime}}\left({l}_{P}\right)=0$$

(26)

The four integration constants C₁, C₂, C₃ and C₄, are determined from the above boundary conditions. The longitudinal stress at the profile edge of the formed section σ_{xx,analytical} is calculated according to [28] by the bending moment M, which is determined using formula 22, and the geometric moment of inertia I as well as the distance of the profile edge to the neutral fiber. Due to the negligible deflection, it is assumed that the neutral fiber is centered in the flange in width direction and thus has a distance of b_F/2 to the profile edge:

$$\sigma_{xx,analytical}=-\frac{M{\cdot b}_F}{2I}$$

(27)

The calculation of σ_{xx,analytical} according to formula 27 includes the formulas 8, 9, 10, 19 and 25. This shows that all five geometrical influencing variables of the parameterized representation of the profile geometry (cf. Fig. 19) are considered in the calculation of the maximum longitudinal compressive stress in the profile edge. For the determination of σ_{xx,analytical}, the material-specific constant k_S included in the line load (cf. formula 6) is required. This scales the calculated longitudinal stress values to obtain realistic absolute values. To determine k_S, a single FEM simulation must be performed for each sheet material. For any defined profile geometry with the corresponding material, the maximum longitudinal compressive stress is to be determined numerically σ_FEM on the one hand and analytically with k_S = 1 (σ_{k_s=1}) on the other. The material constant k_S results from the ratio between σ_FEM and σ_{k_s=1} and remains unchanged for the material used, regardless of the profile geometry:

$${k}_{s}=\frac{{\sigma }_{FEM}}{{\sigma }_{{k}_{s}=1}}$$

(28)

After determining k_S, the analytical model can be used to realistically calculate the maximum longitudinal stresses in the profile edge σ_{xx,analytical} for any profile geometries. By comparing σ_{xx,analytical} and the critical stress σ_crit, a statement can be made about the occurrence of wrinkling. For a failure-free forming applies:

$${\sigma }_{xx,analytical}< {\sigma }_{crit}$$

(29)

In the analytical model, σ_crit is assumed to be a constant that depends on the material properties and the plate thickness and can be determined empirically by experiments. This implies that the influence of the flange width on σ_crit is neglected. This assumption is permissible because, in the case of failure, the critical stress is exceeded only in a very limited area of the profile edge (cf. Fig. 17) and thus there is no correlation between σ_crit and the profile geometry.

The critical stress and thus the process limit of wrinkle formation can be determined empirically with affordable effort by an efficient experimental design. For a defined material and sheet thickness, the experimental determination of σ_crit is required only once and is valid for all geometric profile variations. By isolated variation of an influencing parameter, the process window can be defined by approximating the wrinkling limit. The analytical model calculates the maximum longitudinal compressive stress in the profile edge present in the limit case, which thus corresponds to σ_crit. Since the variation of the profile height h_max, the profile length l_P or the height transition length l_h only requires an adjustment of the tool motion curves, it is preferable to vary one of these parameters. An exemplary empirical determination of σ_crit is described in Section 6.5.

Verification of the analytical model

With the aid of the analytical bending beam model the compressive stresses σ_xx,max in the strip edge can be calculated. These are compared with the numerical results of the FEM model using the DC04 material with a plate thickness of 1.0 mm to verify the substitute model by varying the geometric influence parameters. Figure 35 shows the comparison between the numerically and analytically determined σ_xx,max for the parameter variations of h_max, l_P, l_h, a_P and b_F.

Fig. 35

Verification of the analytically calculated maximum longitudinal stresses with variation of the influencing parameters (a) profile depth, (b) profile length, (c) transition length, (d) profile width and (e) flange width

The maximum longitudinal compressive stresses in the profile edge σ_xx,max can be predicted accurately with the parameter-specific accuracies shown in Fig. 36. The maximum error with isolated variation of the influencing parameters is 5.99% with a mean absolute deviation of 0.943 N/mm² and a mean relative deviation of 2.98%.

Fig. 36

Parameter-specific prediction accuracy of the maximum longitudinal compressive stress in the flange σ_xx,max by the analytical model

Validation of the analytical model

In a two-stage test plan, various profile geometries are manufactured, which are examined for wrinkling using the GOM Atos. In the first stage, by varying the profile height h_max, starting from the reference geometry shown in Fig. 18, the critical stress is determined using the equivalent model. In the second stage, the variation of the remaining parameters l_P, l_h, b_F and a_P is based on the profile geometry determined in stage 1, which shows the first wrinkle formations and has thus exceeded the process limit. According to the parameter sensitivities presented in Section 5.3 the maximum longitudinal stress in the profile edge can be reduced by appropriate adjustment of the geometric variables until the mechanical condition undercuts the process limit again. In the test plan shown in Fig. 37, the reference dimensions are highlighted in color.

Fig. 37

Two-stage test plan for the validation of the analytical model

Test stage 1—variation of the profile height

In the first test stage carried out according to Fig. 36, the process-related ascent of the profile bottom curve towards the end of the profile (as described in Section 6.1) can be observed for all specimens. The specimens with small profile depth (PD) have low shape accuracy because the springback effects have a large relative influence in relation to the nominal depth of the profile. The profile shape deviates from the nominal geometry by 23.76% for PD = 3 mm and by 23.24% for PD = 4 mm. The profiles with PD = 5 mm (deviation: 1.45%), 6 mm (deviation 0.58%) and 7 mm (deviation: 7.57%) have good shape accuracy. With PD = 8 mm, it decreases again with a deviation of 14.49% due to increasing springback-related pre-compression effects (cf. Section 5.1). In addition, with PD = 8 mm, due to the high longitudinal tensile stresses in the profile bottom, areas of the infeed and outfeed zones are also unintentionally formed during forming (cf. Fig. 38: PT8 in section 150 mm ≤ x ≤ 200 mm). On the other hand, with a maximum deviation of 4.4% and an average deviation of 2.25%, the test results show good dimensional accuracy of the desired maximum profile height h_max at x = 400 mm.

Fig. 38

Profile bottom curves with various profile depths

As previously stated, the local exceeding of the process limit, for example by reaching the critical profile height, is sufficient to generate instability. The occurrence of the resulting wrinkling is thereby limited to the section of the flange in the longitudinal direction where the critical state is reached. It follows that the good dimensional stability of h_max in all test results is sufficient to validate the analytical model, despite insufficient shape accuracy in some cases.

The variation of h_max shows wrinkling in the measured trajectories along the profile edge as from a profile depth of 8 mm (h_max = 8 mm, 9 mm, 10 mm). All profiles with h_max ≤ 7 mm show overall curvatures due to transport- and handling-related deformations and residual stresses, but are wrinkle-free. Figure 39 shows the profile edge of the profile with h_max = 7 mm, which is still within the process window, and the sheet wrinkling at 8 mm profile depth, since here the process limit is exceeded in the section 400 mm ≤ x ≤ 685 mm.

Fig. 39

Wrinkle-free profile edge of the profile with h_max = 7 mm and sheet wrinkling in the profile edge with h_max = 8 mm

The resulting longitudinal compressive stresses in the profile edge calculated with the aid of the analytical model are plotted for all h_max in Fig. 40. The profile variants with wrinkling are highlighted in gray. For the critical stress follows:

Fig. 40

Analytically determined maximum compressive longitudinal stresses σ_{xx,analytical} with varying profile depth h_max

$${\sigma }_{crit}\in (\mathrm{70,1842}\frac{N}{{mm}^{2}}, \mathrm{93,9921}\frac{N}{{mm}^{2}}]$$

The stress range of σ_crit is further narrowed down by the investigations in the second stage of the experiments by varying the remaining influence parameters starting from the reference geometry but with h_max = 8 mm.

Test stage 2—variation of all influencing parameters

The variation of the remaining geometric parameters leads to an increase or decrease of the maximum longitudinal compressive stress according to the results of the sensitivity analysis in Section 5.3. Figure 41 shows the analytically calculated σ_{xx,analytical} for all profile variants. A favorable adaptation of the parameters can bring the failure-critical case with h_max = 8 mm back into the process window which results in wrinkle-free profile edges.

Fig. 41

Analytically calculated maximum longitudinal compressive stresses in the profile edge for each profile variant of test stage 2

Figure 42 demonstrates that for all parameter variations, wrinkle formation is associated with exceeding a constant critical stress σ_crit. Based on the experimental results, σ_crit can be narrowed down to the range σ_crit ∈ (70.2842 N/mm², 73.4766 N/mm²], which allows to define the process limit at about 71 N/mm². The experimental investigations validate that the analytical model provides a reliable prediction of the occurrence of sheet wrinkling by realistically determining the maximum compressive longitudinal stresses in the profile edge.

Fig. 42

Validation of the analytically determined maximum longitudinal compressive stresses, the parameter sensitivities and the constant critical stress σ_crit

Conclusions

With flexible roller beading, a new process has been developed, enabling the production of open profiles with configurable, height-variable cross-sections. The variable cross-section height can be individually adapted to application-specific load cases. No tool exchange is required, only the adaptation of the tool kinematics, so that product changes do not entail any additional setup effort or product downtime.

The flexible process is restricted by its process limit, which, when exceeded, manifests itself in the form of wrinkles in the profile edge of the component. The process limit is expressed by a critical residual longitudinal compressive stress in the profile flange. An FEM model is presented which has a high accuracy in the determination of the longitudinal compressive stresses. The level of maximum longitudinal compressive stress determines the location of the process state inside or outside the process window. Sensitivity analyses demonstrate that the present compressive stress state depends on the geometrical influencing variables of the target profile. These parameters h_max (profile depth, l_P (profile length), l_h (height transition length), a_P (profile width) and b_F (flange width) represent a parameterized description of the component geometry.

A process or product design based on numerical or experimental investigations is associated with a high expenditure of time and is therefore not practicable in case of frequent product changes and increased time and cost pressure. An adequate analytical model represents an efficient and target-oriented approach to anticipate the forming mechanisms of flexible roller beading by simplifications. The presented bending beam model provides a robust method for predicting the compressive stresses in the profile edge as a function of all relevant geometric influence parameters. The analytical approach is based on the abstraction of the wrinkling endangered profile flange as a bending beam clamped at both ends. The load on the beam corresponds to the transverse stress distribution along the cutting edge between flange and upper bending edge. The line load is mathematically determined from the profile leg elongations due to the forming process. After calculating the line load, the maximum longitudinal compressive stress σ_xx,max is determined analytically by applying the beam theory. By contrasting σ_xx,max with the material-specific critical stress, a statement can be made about the existence of wrinkles. The proposed systematic experimental test design minimizes the empirical effort to determine the critical compressive stress.

With a mean deviation of 2,98% for variation of all influencing parameters, the calculated σ_xx,max have an precise conformity with the numerical results. Experimental investigations confirm that the critical stress, independent of the profile geometry, is a material specific constant. The analytical model is validated experimentally with different profile geometries. For each profile geometry variant and parameter variation, the analytical model is able to determine the compressive stress maxima in the profile edge and reliably predict the occurrence of wrinkle failure.