Introduction

Since automotive and commercial vehicle manufacturers have to continuously reduce the risk of injury to occupants in the form of prescribed crash scenarios and at the same time reduce the vehicle weight concerning the reduction in nitrogen oxide emissions, formed components with a high degree of functional integration made from high-strength and ultra-high-strength steel grades are integrated into the body and chassis of passenger cars or frame structures of commercial vehicles. To realize these reductions, sheet materials with high formability and high material strength are required, with initial sheet thicknesses between 0.8–8.0 mm. In this context, the processing industry is increasingly turning to dual-phase steels. Due to the lack of experience in handling these steels, the high material strength, and the outdated standards and guidelines, new challenges often arise during processing commonly caused by the formation of so-called edge cracks on shear cut surfaces during component forming. When shear cutting, high strains occur in the shear-affected zone [1, 2], the material is work hardened in this area, and consequently, the residual formability of the cut surface or the component edge is reduced compared to the undeformed base material. The component edge is subjected to an approximate uniaxial tension during component manufacture. This stress can lead to the formation of an edge crack [3]. Numerous test methods such as the hole expansion test according to ISO 16630 [4], the collar-forming test according to VDI 3359 [5], and the Diabolo test [6] have been developed to determine the edge crack sensitivity of a material. In most test methods, the failure of the specimen edge is forced and there is frictional contact at the edge to be characterized during the test, which affects the quality of the results. In addition, the edge of the specimen is not necessarily subjected to a tensile stress equivalent to the stress in the manufacturing process of the component. Only such test methods as the half-a-dog-bone test [7], the dog-bone tensile test, the strip tensile test (also called sheared edge tension test) [8], the tensile test with notched specimen [9] as well as the Edge-Fracture-Tensile-Test enable the specimen edge to be tested under uniaxial tensile stress [10]. Since the Edge-Fracture-Tensile-Test [11] can be used to investigate the effect of various shear cutting parameters on the residual formability, it is used in this study.

Motivation

The effect of numerous shear cutting process parameters on the residual formability of metallic materials has already been discussed in many publications. The influence of the die clearance on the edge crack sensitivity was studied by [12] and [13]. [14] and [15] investigated the geometries impact, of the cutting edge, on the residual forming capacity. [16] and [17] examined the influence of shear rake angle. Since the material separation during component production does not only occur on the undeformed base material, the influence of the shear cutting process on the edge cracks sensitivity when using pre-formed sheets that are subsequently further formed needs to be discussed. The process analysis is especially relevant for dual-phase steels.

Within the scope of this work, an investigation of the dependence of the edge crack sensitivity on the pre-deformation state, including the degree of pre-deformation, will be carried out. The resulting study proves that pre-deformation should not be considered as pre-damage, which would increase the edge crack sensitivity when using multi-phase steels. Due to the interaction of the interfaces, this new effect cannot be represented or discussed by a theoretical model, and experimental testing is mandatory. The following steps are necessary for the implementation:

  • Introduction of explicit reproducible pre-forming.

  • Application of the presented and validated Edge-Fracture-Tensile-Test, to objectively evaluate specimen failure and onset of local necking.

  • Preparation of the determined parameters for the implementation in the forming simulation.

To understand the procedure, the Edge-Fracture-Tensile-Test, the tools used, the experimental design, and the results are described in the following.

Edge-Fracture-Tensile-Test

Process Description and Recorded Parameters

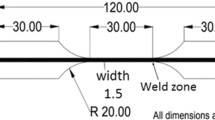
The Edge-Fracture-Tensile-Test was developed, tested, and validated against other edge crack testing methods at the Chair of Metal Forming and Casting at the Technical University of Munich. [11] In this test method, the specimen is subjected without friction to the tensile test according to [18]. The specimen fails at the onset of local necking under a uniaxial stress state at the component’s edge. The geometry of the Edge-Fracture-Tensile-Test specimen [19] is designed based on the specimens from the standard tensile test. To avoid bending stresses induced during the test, it is designed symmetrically. If the to be characterized specimen edge is produced by shear cutting, the initial starting blank geometry (see Fig. 1) must be selected depending on the type of cutting line. The geometry of the initial blank was designed so that one side of the specimen is produced by a non-damaging manufacturing process. The opposite side of the Edge-Fracture-Tensile-Test specimen can be manufactured by different production processes varying many process parameters. Figure 1 shows the individual process steps for realizing an Edge-Fracture-Tensile-Test specimen. The steps are discussed in detail in [20]. Due to the selected specimen geometry in combination with a conventional tensile test, the test specimen can fail due to the formation of an edge crack or a deformation fracture. To record the strain distribution and the type of failure, a stochastic pattern is applied to the measuring area of the specimen. The use of the Aramis 1.3 M (GOM GmbH, Braunschweig, Germany) digital image correlation system allows the logarithmic major strain to be recorded up to the time of specimen failure (onset of local necking and crack initiation). An algorithm according to Volk and Hora [21] is used to determine the time step to identify the onset of local necking. Subsequently, the logarithmic major strain is read from the recorded image sequence at the determined time step at the failure location. The Edge-Crack-Sensitivity-Factor \({K}_{\mathrm{ec}}\) (Formula 1) can be calculated from the logarithmic major strain recorded according to [20].

Fig. 1
figure 1

Schematic draft of the production process of an Edge-Fracture-Tensile-Test specimen; using a closed (a) or open (b) cutting line according to [19]; c) represents the geometry of a reference specimen

Full size image
$${K}_{\mathrm{ec}}= \frac{{\overline{\epsilon }}_{1,\mathrm{loc},{\mathrm{y}}_{1}}}{{\overline{\epsilon }}_{1,\mathrm{loc},{y}_{\mathrm{ref}}}}$$
(1)

  • \({K}_{\mathrm{ec}}\) Edge-Crack-Sensitivity-Factor

  • \({\overline{\epsilon }}_{1,\mathrm{loc},{\mathrm{y}}_{1}}\) Average logarithmic major strain at the onset of local necking, production process \({y}_{1}\), EFTT specimens sheared on one side

  • \({\overline{\epsilon }}_{1,\mathrm{loc},{\mathrm{y}}_{\mathrm{ref}}}\) Average logarithmic major strain at the onset of local necking, production process \({y}_{\mathrm{ref}}\), reference specimen

The Edge-Crack-Sensitivity-Factor includes characteristic values of the base material and the specimen edge to be characterized. The material parameters of the base material are determined on test specimens whose edges are not previously damaged. Depending on the material to be tested, the edges can be made, for example, by milling or wire-eroding. In commercially available finite element simulation tools, it is possible to implement the Edge-Crack-Sensitivity-Factor \({K}_{\mathrm{ec}}\) in the failure criterion of the finite elements of the specimen edge. Using empirically determined limit values metallic materials can be classified into the following categories regarding their edge crack sensitivity:

  • 0.9 < \({K}_{\mathrm{ec}}\)  ≤ 1.0 Insensitive to edge cracking

  • 0.8 < \({K}_{\mathrm{ec}}\)  ≤ 0.9 At risk of edge cracking

  • \({K}_{\mathrm{ec}}\) ≤ 0.8 Sensitive to edge cracking

The limit values were determined by linking the calculated Edge-Crack-Sensitivity-Factor with the false-color plot of the recorded strain fields and with the failure mode of the specimen edge. This comparison was carried out for many metallic materials, from the material groups unalloyed and micro-alloyed steels, multiphase steels, austenitic steels, bake hardening steels, and aluminum alloys. The mainly used shear cutting process parameters were single-stage full-edge shear cutting process, open cutting line, a width of the offcut 4 mm, sharp cutting edges, die clearance 10%.

A detailed process description of the Edge-Fracture-Tensile-Test can be found in [20].

Shear Cutting Tool

The shear cutting tool is used to produce the sheared edge of the Edge-Fracture-Tensile-Test specimen, according to Fig. 2.

Fig. 2
figure 2

3D cross-section of the Edge-Fracture-Tensile-Test shear cutting tool according to [11]

Full size image

All relevant shear cutting process parameters can be varied to realize a customer-specific specimen edge due to the modular design of the shear cutting tool and the use of the two starting blank geometries (Fig. 1). The relevant shear cutting process parameters include: the type of cutting line, the center waste width or the width of the offcut, die clearance, blank holder force, shear slant angle or the number of cutting steps of the cutting process. The design, assembly, and use of the cutting tool, is described in detail in [22].

Material

Sheet Material CR440Y780T-DP

The sheet material used is a hot-dip galvanized dual-phase steel CR440Y780T-DP [23] with a sheet thickness of 1.2 mm. Dual-phase steels have a microstructure of ferritic matrix with included martensitic or bainitic phases. The cold-rolled material is often used for complex structural parts such as longitudinal and transverse beams due to its excellent deep-drawing properties. In addition, dual-phase steels have excellent hardening properties.

The alloying elements of Table 1, in percent by weight, were determined by an optical emission spectrometer analysis. For completeness, one should note that the steel alloys and the base material iron contain other alloying elements that are not listed.

Table 1 Chemical composition in weight percentage of the steel CR440Y780T-DP
Full size table

The initial structure of the steel is visualized in Fig. 3. The etching was done with Nital. Sampling and preparation were carried out following DIN 50,602 [24] and the steel-iron test sheet SEP 1520 [3].

Fig. 3
figure 3

Micrograph of the base material of the steel CR440Y780T-DP; sampling a) along the rolling direction, b) across the rolling direction; etchant Nital

Full size image

The recorded mechanical parameters of the steel from the tensile test are visualized in Table 2. The hardness of the basic structure, according to Vickers, is 225 HV 0.1 (standard deviation 5.2 HV 0.1).

Table 2 Mechanical parameters of the dual-phase steel CR440Y780T-DP
Full size table

Material used for the Active Elements of the Shear Cutting Tool

The active elements of the shear cutting tool (Fig. 2) are made from the secondary hardening cold-work steel X155CrMoV12-1 with material number 1.2379. The materials’ application for cutting and forming tools is based on its high resistance to abrasive and adhesive wear. However, the unevenly lined-up carbides have a disadvantageous effect on material toughness and thus on the breakout behavior [25, 26]. The addition of the alloying elements, vanadium and molybdenum, results in hard and chromium-rich M7C3 carbides with an average carbide length of 10 µm [27] during heat treatment. The cold-work steel was tempered to a hardness of 58 + 2 HRC. The chemical composition meets the requirements of the standard.

Experimental Design and Forming Tool

Process Parameters and Equipment

The influence of the following process parameters (Table 3) on the edge crack sensitivity was determined using the described material with a sheet thickness of 1.2 mm.

Table 3 Process parameter
Full size table

The influence of the shear cutting process and the introduced pre-deformation on the residual formability of a shear-cut edge is discussed using the parameter of the logarithmic major strain \({\epsilon }_{1}\) at specimen failure due to cracking and at the onset of local necking. The major strains recorded on five specimens with an Aramis 1.3 M were summarized in the characteristic value \({\overline{\epsilon }}_{1}\) by averaging.

Forming Tool with Marciniak-punch

To realize and examine the influence of pre-forming on the residual formability of Edge-Fracture-Tensile-Test specimens sheared on one side, a forming tool (Fig. 4) with a Marciniak-punch was used.

Fig. 4
figure 4

3D cross-section of the forming tool with Marciniak-punch

Full size image

The drawing die diameter is 230 mm, that of the punch is 220 mm. To reduce the material flow, the drawing die has a braking bead (height 0.5 mm, width 10 mm). A continuous drawing gap between the drawing die and punch is achieved by inserting a sleeve, which is disassembled after the tool components have been installed on the press table and ram.

Results

Effective Strain

Undeformed Sheet Material

The averaged logarithmic major strain \({\overline{\epsilon }}_{1}\) at crack initiation and the onset of local necking is shown in Fig. 5 for the reference specimen milled on both sides (termed ‘Ref’) and for Edge-Fracture-Tensile-Test specimens sheared on one side with various relative die clearances \(u\).

Fig. 5
figure 5

Averaged logarithmic major strain determined at crack initiation and at the starting point of local necking depending on the relative die clearance for CR440Y780T-DP; sampling in the rolling direction

Full size image

The second sample edge was produced by milling. The specimens are taken from the undeformed sheet steel CR440Y780T-DP with a sheet thickness of 1.2 mm in the rolling direction.

The quotient between the major strain at the onset of local necking of the EFTT specimen and the reference specimen milled on both sides results in the Edge-Crack-Sensitivity-Factor \({K}_{\mathrm{ec}}\). The Edge-Crack-Sensitivity-Factor is smallest for a relative die clearance of \(u\) = 10.7 % (\({K}_{\mathrm{ec}}\) = 0.52) and is highest for a relative die clearance of \(u\) = 20 % (\({K}_{\mathrm{ec}}\) = 0.61). For a relative die clearance of \(u\) = 15%, this factor is located between these two values with \({K}_{\mathrm{ec}}\) = 0.55. According to the classification based on the Edge-Crack-Sensitivity-Factor in Sect. “Process Description and Recorded Parameters”, the cutting edges with all three die clearances examined are rated as sensitive to edge cracks (\({K}_{\mathrm{ec}}\) ≤ 0.8), with the smallest die clearance of \(u\) = 10.7% showing the greatest sensitivity to edge cracks.

Pre-formed Sheet Material

Sheets were deformed using a forming tool with a Marciniak-punch (see Sect. “Forming Tool with Marciniak-punch”) to investigate the influence of pre-forming on the sensitivity to edge cracks. The type and degree of deformation can be set by selecting the appropriate blank starting geometry and drawing depth. The orientation of the sheet is chosen such that the logarithmic major strain \({\epsilon }_{1}\) is parallel to the rolling direction. First, the pre-forming types uniaxial tension, plane strain, and equi-biaxial tension with a logarithmic major strain of \({\epsilon }_{1}\) = 0.05 were each implemented (see also Fig. 7).

Attention was paid to ensure that the EFTT specimen are taken from a homogeneously pre-formed area. For this purpose, a point pattern (point diameter 1 mm, point spacing 2 mm) was applied to the blank before the pre-forming. The point pattern was printed on foil and transferred to the sheet metal to ensure that the sheet surface was not affected through etching. After the pre-forming process, the major and minor strains were determined by comparing the deformed pattern with the initial pattern using an optical forming analysis system GOM Argus (see Fig. 6).

Fig. 6
figure 6

Homogeneous distribution of major strain \({\epsilon }_{1}\) after equi biaxial sheet metal pre-forming

Full size image

In addition to the change of the major and minor strain, the sheet metal pre-forming also results in a reduction in sheet thickness. Since the shear cutting of the EFTT specimens for both the undeformed and the pre-formed specimens is carried out with the same set of active elements with an absolute die clearance of 0.128 mm, this decrease in sheet thickness also results in a change of the relative die clearance \(u\). Table 4 gives an overview of the sheet thickness and the associated relative die clearance depending on the pre-forming applied.

Table 4 Overview of the sheet thicknesses and the resulting relative die clearances\(u\)after sheet metal pre-forming
Full size table

While for an undeformed sheet, the sheet thickness is 1.2 mm and the relative die clearance is 10.7 %, after pre-forming the relative die clearance ranges between 10.7 % and 12.8 %, depending on the type and amount of pre-forming.

Figure 7 shows the strain paths that result for different types of pre-forming (uniaxial tension, plane strain, and equi-biaxial tension) with a logarithmic major strain of \({\epsilon }_{1,\mathrm{pre}}\) = 0.05 each. After pre-forming, the specimen is tested in the subsequent uniaxially loaded Edge-Fracture-Tensile-Test with reference specimens milled on both sides and with specimens that are shear cut on one side.

Fig. 7
figure 7

Strain paths for different types of pre-forming (blue) and subsequent uniaxial tensile forming (red)

Full size image

Uniaxial Tension – Pre-forming

With uniaxial pre-forming, the sheet is first stretched from point \(O\) to point \(A\) by \(\overrightarrow{OA}\). Then both a reference specimen (milled on both sides) and an EFTT specimen (shear cut on one side) are taken from the same pre-formed sheet and subjected to another uniaxial tension. Local necking can be detected with the reference specimen that is milled on both sides at point \(B\) after further tensile forming by \(\overrightarrow{AB}\). With the EFTT specimen that is shear cut on one side, local necking already starts at point \(C\) after forming by \(\overrightarrow{AC}\).

Plane Strain – Pre-forming

For plane strain pre-forming, the first forming operation is located between points \(O\) and \(D\) by \(\overrightarrow{OD}\). In the following Edge-Fracture-Tensile-Tests, local necking starts with the milled reference specimen at point \(E\) by \(\overrightarrow{DE}\) and the shear-cut specimen at point \(F\) by \(\overrightarrow{DF}\).

Biaxial Tension – Pre-forming

The equi-biaxial pre-forming is performed between points \(O\) and \(G\) by \(\overrightarrow{OG}\). Performing the Edge-Fracture-Tensile-Test with the milled reference specimen, local necking can be detected at point \(H\) by \(\overrightarrow{GH}\), whereas local necking with the shear-cut specimen starts at point \(J\) by \(\overrightarrow{GJ}\).

An overview of the averaged logarithmic major strains determined at the start of local necking in the Edge-Fracture-Tensile-Tests is given in Fig. 8 for reference specimens milled on both sides and for specimens shear cut on one side for undeformed specimens and specimens with various types of pre-forming with \({\epsilon }_{1,\mathrm{pre}}\) = 0.05. The values presented for the pre-formed milled reference specimens correspond to the amounts of the logarithmic major strains of the vectors \(\overrightarrow{AB}\), \(\overrightarrow{DE}\), and \(\overrightarrow{GH}\); the values of the pre-formed shear-cut EFTT specimens correspond to the amounts of the major strains of the vectors \(\overrightarrow{AC}\), \(\overrightarrow{DF}\), and \(\overrightarrow{GJ}\).

Fig. 8
figure 8

Averaged logarithmic major strain determined at the starting point of local necking depending on the type of pre-forming for milled and shear-cut specimens made of CR440Y780T-DP; \({\epsilon }_{1,pre}\) = 0.05; sampling in the rolling direction

Full size image

The logarithmic major strains that result for the milled reference specimens show that all pre-formed specimens have reduced residual formability in the uniaxial direction compared to the undeformed specimen. If the amount of pre-forming is included, the sum of \({\epsilon }_{1,\mathrm{pre}}\) (0.05) and the residual formability of the uniaxially pre-formed specimen (0.246) results in the forming capacity of the undeformed specimen (0.296). Thus, the logarithmic major strain that can be achieved in the single-stage uniaxial tensile test is the same as in a two-stage uniaxial tensile test, as already described by other authors [28, 29]. If the strain path is no longer linear, this addition of the major strains is no longer possible. This miscorrelation results from different types of pre-forming and post-straining.

With the one-sided shear-cut EFTT specimens, lower logarithmic major strains are achieved for both the undeformed and the pre-formed variants, compared to the milled reference specimens. A comparison of the logarithmic major strains of the shear-cut specimens shows the highest residual formability for the undeformed specimen with 0.154, followed by the uniaxial pre-forming with 0.151, the plane strain pre-forming with 0.147, and the lowest residual formability for equi-biaxially pre-formed specimens with 0.137. However, it should be noted that the error bars for the standard deviation overlap.

The logarithmic major strains determined at the start of local necking are given in Fig. 9 for a higher pre-forming with \({\epsilon }_{1,\mathrm{pre}}\) = 0.10. Here, uniaxial pre-forming, equi-biaxial pre-forming, and undeformed specimens are considered. The investigation of a plane strain pre-forming with \({\epsilon }_{1,\mathrm{pre}}\) = 0.10 was not possible due to premature cracks during the pre-forming process.

Fig. 9
figure 9

Averaged logarithmic major strain determined at the starting point of local necking depending on the type of pre-forming for milled and shear-cut specimens made of CR440Y780T-DP; \({\epsilon }_{1,pre}\) = 0.10; sampling in the rolling direction

Full size image

As with a pre-forming of \({\epsilon }_{1,\mathrm{pre}}\) = 0.05, the pre-formed specimens show lower residual formability than the undeformed specimens. The uniaxially pre-formed milled reference specimens have a residual formability of 0.192, the biaxially pre-formed specimens of 0.106. The residual formability is further reduced to 0.136 (Ts) and 0.098 (Bi) using the one-sided shear-cut EFTT specimens.

The results from Fig. 9 highlight the tendency identified in Fig. 8, namely that the residual formability of an equi-biaxially pre-formed, one-sided shear-cut EFTT specimen is lower than that of a uniaxially pre-formed one with the same major strain of pre-forming \({\epsilon }_{1,\mathrm{pre}}\). In addition, the difference in residual formability between the milled reference and the shear-cut specimen is less with biaxial pre-forming than with uniaxial pre-forming. This reduction in the difference in residual formability can also be observed when the amount of pre-forming is increased.

However, it is not reasonable to only determine the Edge-Crack-Sensitivity-Factor \({K}_{\mathrm{ec}}\) for shear-cut, pre-formed specimens without considering the deformation history of the sheet metal. Therefore, it is difficult to compare the different types of pre-forming regarding edge crack sensitivity. In addition, the pre-forming also causes a change in the relative die clearance. Compared to uniaxial pre-forming, biaxial pre-forming leads to more thinning of the sheet metal and thus to a larger relative die clearance (see Table 4). This correlation is relevant because with larger die clearances, a lower edge crack sensitivity could be determined with undeformed specimens (see Figure Fig. 5).

Application of the Generalized-Forming-Limit-Concept

The deformation history must also be considered, to determine the influence of the type and amount of pre-forming on the edge crack sensitivity. This can be realized using the Generalized-Forming-Limit-Concept (GFLC) in combination with the principle of equivalent pre-forming. This principle implies that every deformation state built up of two linear strain increments can be transformed to a pure linear strain path with the same formability of the material. [30] Thus, any arbitrary pre-strain state can be related to an equivalent uniaxial pre-strain state. This transformation is presented as an example in Fig. 10. Here, an equi-biaxial pre-forming of \({\epsilon }_{1,\mathrm{pre}}\) = 0.05 is performed between the points \(O\) and \(G\) by \(\overrightarrow{OG}\). A reference specimen milled on both sides, and a one-sided shear-cut EFTT specimen, are made from the pre-formed sheet metal. In the following Edge-Fracture-Tensile-Tests, local necking starts with the milled reference specimen at point \(H\) by \(\overrightarrow{GH}\) and with the shear-cut specimen at point \(J\) by \(\overrightarrow{GJ}\). Using a undeformed reference specimen milled on both sides, local necking starts under uniaxial tensile load at point \(B\) by \(\overrightarrow{OB}\). With this knowledge, point \(G\) can be transferred to an equivalent uniaxial pre-strain state to point \({G}^{*}\) by subtracting the vector \(\overrightarrow{GH}\) from point \(B\). Using the same procedure, point \(J\) can also be transformed to \({J}^{*}\). Since any pre-strain condition can be transferred to an equivalent uniaxial strain state, it is possible to add the logarithmic major strains from the pre-forming and the following uniaxial EFTT. This also allows the Edge-Crack-Sensitivity-Factor \({K}_{\mathrm{ec}}\) to be calculated analogously to Formula 1, whereby the sum of the major strains of the equivalent uniaxial pre-strain and the following EFTT is used for \({\overline{\epsilon }}_{1,\mathrm{lok},{\mathrm{y}}_{1}}\). An overview of the major strains, related to a uniaxial strain state, and the associated Edge-Crack-Sensitivity-Factors \({K}_{\mathrm{ec}}\) that can be determined with specimens milled on both sides as well as shear cut on one side is given for various types of pre-forming with \({\epsilon }_{1,\mathrm{pre}}\) = 0.05 in Fig. 11 and \({\epsilon }_{1,\mathrm{pre}}\) = 0.10 in Fig. 12. It is apparent that all pre-formed and shear-cut specimens achieve higher logarithmic major strains than those with the undeformed shear-cut specimen. This is also expressed in the Edge-Crack-Sensitivity-Factors, which are all greater than in the case of the undeformed specimen (\({K}_{\mathrm{ec}}\) > 0.52). With a constant pre-forming of \({\epsilon }_{1,\mathrm{pre}}\) = 0.05, the plane strain specimens show the lowest edge crack sensitivity (\({K}_{\mathrm{ec}}\) = 0.84), followed by the equi-biaxial (\({K}_{\mathrm{ec}}\) = 0.79) and the uniaxial pre-formed specimens (\({K}_{\mathrm{ec}}\) = 0.68), see Fig. 11. The same tendency can be seen in Fig. 12 (above), with a pre-forming of \({\epsilon }_{1,\mathrm{pre}}\) = 0.10. In addition, the sensitivity to edge cracks decreases with increasing pre-forming \({\epsilon }_{1,\mathrm{pre}}\). While with \({\epsilon }_{1,\mathrm{pre}}\) = 0.05 uniaxial pre-formed sheet metal a \({K}_{\mathrm{ec}}\) of 0.68 is determined, this factor increases to \({K}_{\mathrm{ec}}\) = 0.81 with a uniaxial pre-forming of \({\epsilon }_{1,\mathrm{pre}}\) = 0.10. The same tendency can be observed with equi-biaxial pre-formed specimens, with the Edge-Crack-Sensitivity-Factor increasing from \({K}_{\mathrm{ec}}\) = 0.79 (\({\epsilon }_{1,\mathrm{pre}}\) = 0.05) to \({K}_{\mathrm{ec}}\) = 0.97 (\({\epsilon }_{1,\mathrm{pre}}\) = 0.10).

Fig. 10
figure 10

Transformation of an equi-biaxial pre-strain with a following uniaxial EFTT into an equivalent uniaxial strain state based on the principle of the equivalent pre-forming

Full size image
Fig. 11
figure 11

Averaged logarithmic major strain with consideration of the pre-forming determined at the starting point of local necking depending on the type of pre-forming for milled and shear-cut specimens made of CR440Y780T-DP; \({\epsilon }_{1,pre}\) = 0.05; sampling in the rolling direction

Full size image
Fig. 12
figure 12

Averaged logarithmic major strain with consideration of the pre-forming determined at the starting point of local necking depending on the type of pre-forming for milled and shear-cut specimens made of CR440Y780T-DP; \({\epsilon }_{1,pre}\) = 0.10; sampling in the rolling direction

Full size image

Table 4 shows that pre-forming results in a slight increase in the relative die clearance of a few percent due to the reduction in sheet thickness. However, this enlargement is not the decisive factor for the reduced sensitivity to edge cracks. Figure 5 shows that even with significantly larger die clearances, it was impossible to determine nearly as high Edge-Crack-Sensitivity-Factors as in Fig. 11 and Fig. 12. Therefore, it can be assumed that the type and amount of pre-forming have a significant influence on the sensitivity to edge cracks. The reasons for this are the changes in the geometry of the cut surface and the hardening of the material in the shear-affected zone, as well as the changed structure of the material due to the pre-forming. In addition, the hardness of the individual microstructural phases can influence the edge crack sensitivity.

Conclusion and Outlook

The investigations show that it is essential to discuss the sensitivity of material edge cracks depending on the type and amount of pre-forming. Also, it is imperative to use the Generalized-Forming-Limit-Concept to correctly take into account the introduced pre-forming in the formation of the Edge-Crack-Sensitivity-Factor \({K}_{\mathrm{ec}}\), and to be able to use it in the finite element simulation. The procedure selected could be used to extend the findings of initial studies conducted by Le et al. (2014) [31] and Held, Liewald and Sindel [32] on the influence of pre-forming. Due to the chosen procedure and the holistic view, it was possible to show that the pre-forming of CR440Y780T-DP is not to be considered as damage as in the previous explanations since the edge crack sensitivity is reduced.

In further investigations, the influence of a constant relative die clearance should be determined when the pre-forming is varied. Also, it is desirable to vary the sampling after pre-deformation to force anisotropic behavior. Besides, the aim of investigations can also be to describe a relationship between pre-deformation and residual formability. For this purpose, any pre-forming that differs in type and amount should be introduced into the material. The degrees of deformation to be introduced are limited by the edge areas of uniaxial tension and biaxial stretch forming, as well as the forming limit curve. The residual formability determined by the downstream Edge-Fracture-Tensile-Test corresponds to discrete points on the surface to be covered. This surface, in turn, can be implemented in finite element simulations to represent the pre-deformation influence to its full extent.