Abstract
For affordable high-volume manufacture of sandwich panels with complex curvature and varying thickness, fabric skins and a core structure are simultaneously press-formed using a set of matched tools. A finite-element-based process simulation was developed, which takes into account shearing of the reinforcement skins, multi-axial deformation of the core structure, and friction at the interfaces. Meso-scale sandwich models, based on measured properties of the honeycomb cell walls, indicate that panels deform primarily in bending if out-of-plane movement of the core is unconstrained, while local through-thickness crushing of the core is more important in the presence of stronger constraints. As computational costs for meso-scale models are high, a complementary macro-scale model was developed for simulation of larger components. This is based on experimentally determined homogenised properties of the honeycomb core. The macro-scale model was employed to analyse forming of a generic component. Simulations predicted the poor localised conformity of the sandwich to the tool, as observed on a physical component. It was also predicted accurately that fibre shear angles in the skins are below the critical angle for onset of fabric wrinkling.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Composite sandwich panels offer high specific bending stiffness, delivering opportunities for lightweight design. However, sandwich components of complex shapes can be costly to manufacture, as machining operations on the core are required in addition to moulding processes for the skins.
In well-established high-volume applications, such as lightweight automotive interior load floor components, a comparatively low-cost composite sandwich is manufactured by pressing the core material into shape simultaneously with the skins, in a single forming operation. While the forming process causes local buckling or crushing of the core structure, the mechanical performance of the finished component has been found sufficient for this type of application [1,2,3,4,5,6,7]. Typical material combinations for press-formed sandwich structures include glass fibre composite skins, usually made from chopped strand mat with fibre lengths greater than 25 mm, hexagonal paper cores and polyurethane foaming resin. The reinforcement in the skins is wet out with the resin. As the resin expands during cure, it partially fills the open cells of the core (at the interface with the skins), which allows strong bonds between the core and skins to develop. Variants of this process exist, using different types of cores and carbon fibre textile skins, for higher structural requirements.
During manufacture of panels with variable cross-sections and complex curvature, the core can be subjected to multi-axial deformation modes including in-plane tension, compression and shear, as well as through-thickness compression and out-of-plane bending [8,9,10]. Simultaneously, the reinforcement skins are subjected to in-plane shear and out-of-plane bending while the fabric is formed. There may also be relative movement between the core and the skins during forming. Typical issues occurring in the process are wrinkling of the skins due to local fibre buckling, tearing of the core due to excessive in-plane stresses, and poor conformity of the sandwich assembly to the tool surfaces due to low through-thickness stiffness of the crushed core.
The application of simulation techniques facilitates assessing the feasibility of the process prior to implementation. However, a modelling approach to capture forming induced issues and to enable optimisation of process parameters does not currently exist. Almost all available modelling techniques address sandwich load-carrying capability including damage prediction [11,12,13,14]. A model would be required for simulation of the sandwich forming process in order to predict forming-induced defects. While through-thickness crushing of the honeycomb core is considered a failure mode in structural engineering [15,16,17], it is a forming mechanism in component manufacture. Also, existing finite element (FE) models are developed for sandwich structures where the skins are bonded to the core which is essential for load transfer [18,19,20]. However, the forming process relies on relative slippage between skins and core. Hence, core-skin adhesion is not an issue here.
A complete process model requires integration of three concurrent effects: forming of the reinforcement skins, multi-axial deformation of the core structure, and frictional effects (tool-reinforcement and reinforcement-core). High-fidelity predictive modelling of reinforcement forming (draping) is well advanced. Typically, woven and non-crimp fabrics can be modelled using a non-orthogonal constitutive model, incorporating multiple plies and frictional effects [21,22,23,24,25,26,27,28,29,30,31,32]. The multi-axial deformation behaviour of the core is complex, requiring a material model that reflects the forming characteristics arising from the distortion of the cellular structure and through-thickness crushing of the core, resulting from inelastic buckling and folding of the cell walls. The core structure can be modelled in detail at the meso-scale using shell elements to represent the cell walls at an appropriate mesh density to capture the inelastic crushing process. However, this approach is not feasible for component-scale models, as a large number of finite elements would be required, which would result in long CPU times.
As an alternative, macro-scale models for the core material can be developed, which are based on volumetric finite elements and homogenisation of the core structure to obtain effective mechanical properties. These can reduce the overall number of degrees of freedom in the model and minimise the risk of numerical instability. A disadvantage of this approach is that it requires multi-axial, non-linear material properties as input, which may be hard to characterise experimentally. In addition, the interaction between skins and core is complex.
The present work aims to develop a non-linear explicit FE model of the sandwich panel forming process and to validate it against experimental studies, including a full-scale technology demonstrator.
Sandwich structure
Geometry
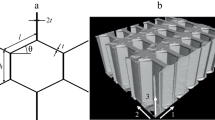
As shown in Fig. 1, sandwich panels discussed in this paper are constructed from two outer composite skins and a hexagonal honeycomb core, which is made from low-cost recycled cardboard. The low density of the porous core, compared to the composite skins, results in a significant weight-saving compared to a monolithic composite panel of the same bending stiffness. Crushing the core allows geometrically complex sandwich panels with locally varying thickness to be produced, without the need to pre-machine the core to the desired shape.
Reinforcement fabric skin
The two skins are made from FCIM359 biaxial carbon fibre non-crimp fabric (NCF), supplied by Hexcel, Leicester, UK. Each ply is 0.4 mm thick and consists of 440 gsm of carbon fibre in 24 K tow format. The fibre architecture is ±45° with a pillar stitch at 0° (in the roll direction). The material shows an asymmetric shear behaviour (Fig. 2) as a consequence of the pillar stitch pattern. This has previously been modelled by the authors using a homogenised non-orthogonal constitutive model [21,22,23,24,25], which exhibited sufficient fidelity for fabric forming process modelling and optimisation.
Shear resistance curves for NCF used in skins; derived from picture frame shear testing. [24]
Resin system
The resin is a highly reactive polyurethane system that cures within 90 s. It is applied to the outer surfaces of the skins prior to the sandwich assembly being transferred to the forming tool. During the forming process, the resin is a low viscosity liquid, which turns into a foam and cures upon application of heat.
As the resin will only fully penetrate through the skins as it is heated and expands, there is no resin at the interface between the core and skins during the forming process. Hence, the resin has no significant effect on the relative movement between core and skins. Also, the effect of the resin on the shear properties of the reinforcement fabric was neglected in the present work, which enabled an existing validated model of the fabric forming behaviour to be employed. For frequently employed fabric shear test methods (picture frame or bias extension testing [33, 34]), the time for set-up and testing is of the same order as the resin cure time, making testing of wetted fabrics infeasible. Hence, a modification to existing in-plane shear test methods would be required if the effect of resin on fabric shear was to be incorporated in the model.
Core
The core is manufactured by a well-established process of adhesively bonding multiple layers of paper and expanding the lay-up to obtain hexagonal cells with the dimensions indicated in Fig. 3. Here, cardboard paper is used because of its low cost and low environmental impact.
For geometrical characterisation, the cell dimensions of the honeycomb core were measured at 5 different positions. The corresponding average values are indicated in Fig. 3. The properties of the cardboard material used for manufacture of the core (cell walls) were assumed to be isotropic. Uniaxial tensile tests were performed on specimens from flat cardboard using a universal testing machine at a strain rate of 0.03 s−1. A 5 kN load cell and an extensometer were used to measure the tensile force and the axial strain, respectively. Material properties listed in Table 1 were obtained using average values from five repeats.
Material characterisation
In-plane tensile testing
In-plane tensile tests were performed on the honeycomb core along the longitudinal and transverse directions as shown in Fig. 4. Results show that the core exhibits the same in-plane tensile stiffness (0.2 MPa) in the two test directions up to ~0.32 effective strain. The longitudinal tensile modulus (i.e. the slope of the curve) between 0.40 and 0.45 effective strain is ~0.39 MPa, where the cell walls are generally aligned with the tensile loading direction. In longitudinal tensile loading, the specimen debonds from the testing rig at ~0.46 effective strain. In contrast, damage starts at 0.44 effective strain for the transverse core specimen and complete failure occurs at ~0.70. There is no significant increase in tensile modulus in the transverse direction, as debonding occurs at the double-thickness walls (Fig. 3), where adjacent cardboard plies are glued together to produce the core architecture.
Shear testing
The through-thickness shear behaviour of the honeycomb core was tested according to ASTM C273 (Fig. 5a). As shown in Fig. 5b, gradients of the stress-strain curves from three shear tests are consistent, indicating reproducibility of shear moduli derived from the tests. The average shear modulus is 1.56 MPa. Failure occurred in the adhesive used to bond the core to the aluminium tabs during the tests, therefore the peak stress and strain in Fig. 5 are not representative of the ultimate values of the core.
Through-thickness compression testing
The honeycomb core was tested in through-thickness compression according to ASTM C365 (Fig. 6a). In the acquired stress-strain curves (Fig. 6b), a small linear region is present due to cell wall bending at low strains. This is followed by a long plateau region where buckling of the cell walls occurs. Densification begins after 15 mm of crushing (i.e. 0.75 effective strain). At this point, the cell structure has fully collapsed (Fig. 6c), causing a rapid increase in stress with further increase in strain. The 20 mm thick core material characterised here can be compressed to a final thickness of approximately 2 mm (i.e. 0.90 effective strain). The crush response of the material was tested at 3 different strain rates (1 mm/min, 10 mm/min, 50 mm/min). As no significant difference was observed, it was concluded that the response is rate insensitive (Fig. 6b).
Friction between materials
The friction between the core and the NCF skins was tested following ASTM D1894, ISO8295. A 50 mm × 100 mm core sample was bonded to a moving sled using double-sided adhesive tape, while the NCF used in the skins was bonded to a static aluminium table. The adhesive tape, NCF and core specimen were replaced after every test. Friction coefficients were calculated from the ratio of the tangential (pulling) force and the applied normal force (10 N, corresponding to a normal pressure of 2 kPa) during relative movement at a constant velocity (100 mm/min). The average value was calculated from five repeat tests for each surface pairing [25]. The friction behaviour does not depend on which face of the NCF is in contact with the honeycomb core, as the pillar stitch pattern is identical on both faces of the NCF. It depends on the direction of relative displacement at the interface. Multiple orientations of NCF and core were tested. As shown in Fig. 7, the coefficient of friction varies from 0.47 to 0.57 along different orientations of the core relative to the yarn direction of the NCF. However, the friction behaviour was assumed to be isotropic in the simulations, using an average value of 0.52. While this assumption may affect the precision of the simulation results, it greatly reduces complexity since it enables the in-built isotropic Coulomb friction model to be used in Abaqus/Explicit. Friction coefficients were previously obtained by the authors for other surface pairings, including 0.23 for tool-fabric contact and 0.36 for tool-core contact [23,24,25].
Friction coefficients between NCF fabric and core. L and T denote the longitudinal and the transverse directions of the core, respectively; Y and S denote the yarn and the stitch directions of the NCF on the contact surface; the pulling direction of the sled is the reference direction (i.e. 0°); all of the numbers in these contact pairing codes are the angles in degrees with respect to the reference direction
Core modelling
General considerations
The mechanical behaviour of the honeycomb core can be modelled at multiple scales, as shown in Fig. 8. At the meso-scale, the architecture of the core can be represented by a unit cell. The high geometrical fidelity of this model enables the deformation modes of the core to be studied in detail, as the mechanical response is replicated explicitly. However, simulations at this level of detail are computationally expensive, and consequently the size of the structure that can be analysed is limited.
Alternatively, the core can be modelled at the macro-scale, where it is treated as a continuum and the material behaviour is homogenised. The macro-scale response should be equivalent to the corresponding meso-scale model in terms of representative overall performance. It is important that the influence of the different deformation modes is captured, such as bending of the cell walls which contributes to the initial linear region on the stress strain curve in Fig. 6b. Therefore, the meso-scale model was employed to identify what mechanisms of core deformation (such as cell wall bending, cell wall buckling and densification in Fig. 6) occur during sandwich forming. These mechanisms were then correlated with suitable macro-scale indicators (such as effective through-thickness strain) for formability.
The honeycomb core was constructed from a series of shell elements at the meso-scale (S4R in Abaqus/Explicit) or continuum brick elements (C3D8R in Abaqus/Explicit) following homogenisation at the macro-scale. Since the walls of the honeycomb core (properties as listed in Table 1) are perpendicular to the rigid surface in compression, unrealistically high stress concentrations and contact penetration occurred when the load was directly applied to the meso-scale model. Consequently, the simulation failed to converge (Table 2). Two methods were introduced to refine the contact behaviour to improve numerical stability, by increasing the surface area of the core material in contact with the tool and hence reducing local stresses. For the first method, dummy flanges were added to the free edges of each cell wall. These were assigned a much lower stiffness than the wall material, i.e. less than 1.0% (Table 3), to limit their influence on the overall cell response. The second method used a dummy infill material to occupy the cell pores. The honeycomb structure was embedded into a solid volume using the *EMBEDDED ELEMENT command in Abaqus/Explicit. Thus, contact with the skins was initiated at the solid surfaces rather than the edges of the corresponding cell walls. The infill material had the same overall dimensions as the representative volume and the material properties were 1.0% of the homogenised core material (Table 3). A small fracture strain (0.010) was assigned for element deletion to minimise additional resistance to buckling. As shown in Table 2, both methods facilitate numerical convergence for meso-scale models, resulting in realistic deformation modes during through-thickness compression. Moreover, effective stress-strain curves (Fig. 9) were obtained from through-thickness compression simulations using these meso-scale models. The results imply that predicted effective material properties are consistent with experimental data. The shape of the stress-strain curves indicates that the introduction of the dummy flanges or the infill material does not significantly influence the effective compressive behaviour of the core, but is suitable to overcome the difficulty with convergence of the original meso-scale model.
At the macro-scale, the core was modelled using a crushable foam model available in Abaqus/Explicit [35], which is suitable for modelling buckling of cell walls in compression. The macro-scale model only replicates the equivalent behaviour of the homogenised continuum and does not indicate detailed deformation behaviour. Experimentally determined data for the properties of the honeycomb core in though-thickness and in-plane loadings (Sections 3.1 to 3.3) were used as inputs for the macro-scale model. Comparison of the overall averaged response in compression (Fig. 9) shows that the stress-strain curve for the macro-scale model is representative of those determined experimentally and from the meso-scale models. The RMSE (Root Mean Square Error) of the simulated stress-strain curve from the macro-scale model is less than 5% compared to the experimental curve, indicating adequate agreement. The in-plane behaviour of the core is less important, as the forming behaviour of the sandwich assembly is dominated by the properties of the fabric skins. As shown in Table 2, macro-scale models take much less time to converge than equivalent meso-scale models.
Core bending
The meso-scale model was employed to investigate which mechanisms are relevant for different scenarios of forming a core with complex curvature. A hemispherical punch with 100 mm diameter was used in combination with a die with 144 mm diameter, as shown in Fig. 10. All parts of the tooling were defined as rigid bodies, including the punch, the die and the blank holder. The die and the blank holder were fixed during forming, while a vertical displacement of the punch simulated the 50 mm forming stroke. A penalty contact algorithm was employed to define the interfacial behaviour. An isotropic Coulomb friction model was used for the tool-core contact, using a friction coefficient of 0.36.
In a first simulation, where the blank holder was omitted, the central area of the core conformed to the hemisphere (Fig. 11). Permanent through-thickness deformation (i.e. crushing) was limited, since the core was able to deform out-of-plane due to lack of constraints in regions around the perimeter. Results indicate that, for this scenario, the formability of a core with complex curvature is primarily derived from core bending at minimum local core compression.
The forming simulation was repeated with a blank holder to apply additional constraints during forming of the hemisphere. As shown in Fig. 11, the shape of the formed hemisphere is more defined when using a blank holder, as large out-of-plane deformation is limited. As a result of the constraints on core bending for this scenario, the level of core crushing increases in areas in contact with the punch during forming.
Core crushing
A meso-scale model was used to simulate the compressive response of a cardboard core sample, which had dimensions of 120 mm × 120 mm × 20 mm. Forming was investigated using an 80 mm × 80 mm square punch with a fillet (radius 20 mm) at the edges. A 10 mm stroke (i.e. half of the core thickness) was applied in the thickness direction. The core was compressed against a flat plate, where all tools were modelled as rigid bodies.
As shown in Fig. 12, the cell walls buckle or fold around the compression surface, which has a negligible effect on the core material outside the punch area. Crushing starts at the top of the specimen in contact with the punch surface and propagates through the thickness towards the base of the specimen. Minimal crushing can be observed at the bottom surface. The simulation results are in good agreement with the deformation modes exhibited by test specimens (Fig. 12). These results show that forming of a core to a shape with variable thickness is related to core crushing and that in-plane deformation (draw-in) is negligible due to low in-plane stiffness of the cellular core.
Demonstrator forming simulation
Macro-scale model for demonstrator
A generic composite component was chosen to demonstrate the feasibility of forming sandwich panels into complex curved configurations. As shown in Fig. 13, a set of matched tools were modelled as rigid bodies, where the lower tool was fixed and the upper tool was subjected to a displacement in the z-direction. A single-layer of FCIM359 NCF [24] (at ±45° relative to the x-axis) was positioned on both the top surface and bottom surface of the core to form a sandwich.
Shape optimisation
The macro-scale FE model described above was used to optimise the blank shape for the forming process. An initial forming simulation was run for a rectangular blank of dimensions 720 mm × 590 mm (initial thickness of the core 20 mm, thickness of the skins 0.4 mm), as illustrated in Fig. 14a. In total, 9 simulations were performed and excess material outside of the final trim line on the formed component was removed iteratively. In each iteration, the fabric blank was trimmed to the same shape as the core blank.
Forming-induced defects
Physical demonstrator components were manufactured to validate the simulation-based predictions (Fig. 15a). The predicted shear angles in the reinforcement of the sandwich skins (Fig. 15b) are in the range from −30° to 12°, which does not exceed the critical shear angles for onset of wrinkling (42° in positive shear and − 50° in negative shear [23, 25]). Hence, simulations indicate that no out-of-plane wrinkling occurs in either of the skins after forming.
As the skins are made from bi-directional NCF, fibres in only one material direction are visible on each surface of the sandwich. Therefore, inter-fibre angles or shear angles cannot be measured, and quantitative comparison with the simulation results in terms of angles is not possible. However, observations on the physical component indicate that there is no fabric wrinkling on the surfaces of the sandwich, which is in agreement with the prediction and implies that the inter-fibre angles are not in the critical range for wrinkling.
A cross-section of the physical component was taken at an arbitrary position to identify other forming-induced issues. It was found that the top edges of the component in the thickest region, i.e. the edges in the longitudinal direction appearing dark in Fig. 15a and Fig. 16a, consist of foamed resin only and do not contain reinforcement. These resin rich regions are related to bridging of the fabric reinforcement in the concave regions of the tool. During the forming process, the fabric skins are highly compressed in the thinnest regions of the component, i.e. localised friction forces are high. As a result, high in-plane tensile forces occur in the fabric plies in the region of lowest material compression. These forces prevent the fabric from conforming to the tool surface and cause the core to crush locally, creating gaps along the edges of the geometry which consequently fill with resin.
The simulation results in Figs. 15b and 16b show the formed sandwich assembly, ignoring the effect of resin expansion and filling of the gaps between the mould surface and skins. The cross-sectional shape of the sandwich, including the locally crushed core, was predicted accurately in the simulations, as shown in Fig. 16. This indicates that the relevant mechanisms of the forming process are reproduced in the macro-scale model, proving the suitability of this approach.
Conclusions
To simulate the process of forming sandwich panels comprising composite skins and honeycomb cores into complex shapes with variable thickness, FE models considering effects of shearing of the reinforcement skins, multi-axial deformation of the core structure, and frictional effects at the interfaces were developed. The behaviour of the core was modelled at two different scales. Predominant forming mechanisms and limits of formability were identified for different forming scenarios using a meso-scale model, which was based on measured properties of the honeycomb cell walls. Results indicate that the formability for sandwich panels with complex curvature is primarily derived from bending, if the core is free to deform, whereas local through-thickness crushing of the core becomes more important in the presence of stronger constraints. As computational costs are high, meso-scale models are only suitable for simulations of sandwich panels of limited size. A macro-scale model was developed for simulation of larger components, implementing homogenised properties determined from a series of experiments on the honeycomb structure. Here, mechanical field variables were used to correlate deformation mechanisms observed at the meso-scale. Forming of a flat sandwich panel blank into a generic 3D component was simulated at the macro-scale. The developed macro-scale FE model was employed to optimise iteratively the blank shape for net-shape forming. For the optimum blank shape, predictions from the simulations were compared with properties of a physical component. Simulation results were found to be accurate in predicting localised fibre bridging and poor conformity of the sandwich to the tool as well as fibre shear angles in the skins which are below the threshold for fabric wrinkling. This validation indicates the suitability of the proposed modelling approach for industrial application.
References
PUR-CSM Technology, <https://www.hennecke.com/sites/default/files/downloads/purcsm_de_en.pdf>. Accessed July 2019
Bright Lite Structures, <https://www.blstructures.com/>. Accessed July 2019
Vehicle underbody structure with lightweight PU composite, <https://www.gupta-verlag.com/news/technology/9357/vehicle-underbody-structure-with-lightweight-pu-composite>. Accessed July 2019
BMS recommends polycarbonate core for PU sandwich composites, <https://utech-polyurethane.com/news/bms-recommends-polycarbonate-core-for-pu-sandwich-composites/>. Accessed July 2019
Sloan, J., JEC World 2019 preview: Huntsmand, <https://www.compositesworld.com/products/jec-world-2019-preview-huntsman(2)>. Accessed July 2019
Automotive interior resin system, <https://www.materialstoday.com/composite-processing/products/automotive-interior-resin-system/>. Accessed July 2019
Lightweight parts interior, <https://koller-gruppe.de/en/lightweight-parts-interior/>. Accessed July 2019
Gordon Murray Design, <www.iStreamtechnology.co.uk>. Accessed June 2017
Pflug, J., EconCore, Composite Panels: Thermoplastic Solution for Demanding Applications, <http://www.econcore.com/en/products-applications/composite-panels>. Accessed June 2017
Cai Z-Y, Zhang X, Liang X-B (2018) Multi-point forming of sandwich panels with egg-box-like cores and failure behaviors in forming process: analytical models, numerical and experimental investigations. Mater Des 160:1029–1041
Chen Z, Yan N, Sam-Brew S, Smith G, Deng J (2014) Investigation of mechanical properties of sandwich panels made of paper honeycomb core and wood composite skins by experimental testing and finite element (FE) modelling methods. Eur J Wood Wood Prod 72(3):311–319
Mozafari H, Khatami S, Molatefi H (2015) Out of plane crushing and local stiffness determination of proposed foam filled sandwich panel for Korean tilting train eXpress–numerical study. Mater Des 66:400–411
Gibson LJ, Ashby MF (1999) Cellular solids: structure and properties. Cambridge university press
Foo C, Chai G, Seah L (2008) A model to predict low-velocity impact response and damage in sandwich composites. Compos Sci Technol 68(6):1348–1356
Petras A, Sutcliffe M (1999) Failure mode maps for honeycomb sandwich panels. Compos Struct 44(4):237–252
Aktay L, Johnson AF, Holzapfel M (2005) Prediction of impact damage on sandwich composite panels. Comput Mater Sci 32(3–4):252–260
Chawla A, Mukherjee S, Kumar D, Nakatani T, Ueno M (2003) Prediction of crushing behaviour of honeycomb structures. Int j crashworthiness 8(3):229–235
Abrate S (1998) Impact on composite structures. Cambridge University Press, Cambridge
Burton WS, Noor A (1997) Structural analysis of the adhesive bond in a honeycomb core sandwich panel. Finite Elem Anal Des 26(3):213–227
Dear J, Lee H, Brown S (2005) Impact damage processes in composite sheet and sandwich honeycomb materials. Int J Impact Eng 32(1–4):130–154
Chen S, Endruweit A, Harper L, Warrior N (2015) Inter-ply stitching optimisation of highly drapeable multi-ply preforms. Compos A: Appl Sci Manuf 71:144–156
Chen S, Harper L, Endruweit A, Warrior N (2015) Formability optimisation of fabric preforms by controlling material draw-in through in-plane constraints. Compos A: Appl Sci Manuf 76:10–19
Chen S, McGregor O, Endruweit A, Elsmore M, De Focatiis D, Harper L, Warrior N (2017) Double diaphragm forming simulation for complex composite structures. Compos A: Appl Sci Manuf 95:346–358
Chen S, McGregor O, Harper L, Endruweit A, Warrior N (2016) Defect formation during preforming of a bi-axial non-crimp fabric with a pillar stitch pattern. Compos A: Appl Sci Manuf 91:156–167
Chen S, McGregor O, Harper L, Endruweit A, Warrior N (2018) Optimisation of local in-plane constraining forces in double diaphragm forming. Compos Struct 201:570–581
Yu W-R, Harrison P, Long A (2005) Finite element forming simulation for non-crimp fabrics using a non-orthogonal constitutive equation. Compos A: Appl Sci Manuf 36(8):1079–1093
Xue P, Peng X, Cao J (2003) A non-orthogonal constitutive model for characterizing woven composites. Compos A: Appl Sci Manuf 34(2):183–193
Peng X, Cao J (2005) A continuum mechanics-based non-orthogonal constitutive model for woven composite fabrics. Compos A: Appl Sci Manuf 36(6):859–874
Khan MA, Mabrouki T, Vidal-Sallé E, Boisse P (2010) Numerical and experimental analyses of woven composite reinforcement forming using a hypoelastic behaviour. Application to the double dome benchmark. J Mater Process Technol 210(2):378–388
Boisse P, Hamila N, Helenon F, Hagege B, Cao J (2008) Different approaches for woven composite reinforcement forming simulation. Int J Mater Form 1(1):21–29
Boisse P, Aimène Y, Dogui A, Dridi S, Gatouillat S, Hamila N, Khan MA, Mabrouki T, Morestin F, Vidal-Sallé E (2010) Hypoelastic, hyperelastic, discrete and semi-discrete approaches for textile composite reinforcement forming. Int J Mater Form 3(2):1229–1240
Boisse P, Hamila N, Helenon F, Aimene Y, Mabrouki T (2007) Draping of textile composite reinforcements: continuous and discrete approaches. Adv Compos Lett 3(4):125–131
Cao J, Akkerman R, Boisse P, Chen J, Cheng H, De Graaf E, Gorczyca J, Harrison P, Hivet G, Launay J (2008) Characterization of mechanical behavior of woven fabrics: experimental methods and benchmark results. Compos A: Appl Sci Manuf 39(6):1037–1053
Harrison P, Clifford MJ, Long A (2004) Shear characterisation of viscous woven textile composites: a comparison between picture frame and bias extension experiments. Compos Sci Technol 64(10–11):1453–1465
Dassault Systèmes, Abaqus (2016) Analysis User’s Guide. 2016
Acknowledgements
This work was funded by the Engineering and Physical Sciences Research Council [Grant number: EP/P006701/1], as part of the “EPSRC Future Composites Manufacturing Research Hub”.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Chen, S., McGregor, O.P.L., Endruweit, A. et al. Simulation of the forming process for curved composite sandwich panels. Int J Mater Form 13, 967–980 (2020). https://doi.org/10.1007/s12289-019-01520-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12289-019-01520-4