3D Modeling of squeeze flows occurring in composite laminates

Abstract

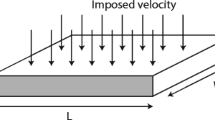
Nowadays thermoplastic composite materials are more and more used due to their specific excellent mechanical properties and a good recyclability. However, many difficulties are encountered during their forming processes, specially in the case of thermoplastic composites –TPC–. Therefore, consolidation of thermoplastic composites is becoming one of the most active research topics in composite manufacturing. Many processes proceed by heating prepregs to melt the polymer, then apply a compression in order to remove residual porosity trapped at the layers interfaces and consolidate the material. Thus the different layers containing the molten thermoplastic resin are compressed and squeeze flow occurs. Even if some modeling has been addressed, the flow occurring in the laminate, inside the yarns and in between the yarns requires rich 3D numerical descriptions with a fine enough description of the complex kinematics taking place in the laminate thickness. In this work we analyze the limits of lubrication based descriptions, justifying the necessity of proceeding with 3D descriptions. In order to alleviate the cost that such simulations involve, we employ an advanced discretization technique making use of an efficient in-plane-out-of-plane separated representation of the different fields involved in the model. Thus very fine descriptions are possible with a computational cost characteristic of 2D descriptions, as the ones making use of the lubrication hypotheses.

Appendices

Appendix A: Monolayer squeeze flow of a Newtonian resin

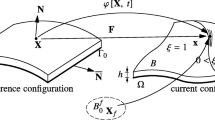
We consider a layer of a Newtonian fluid characterized by a viscosity η filling the domain Ξ = Ω × ℐ, where Ω ⊂ ℛ ² and ℐ = [−h/2, h/2] ⊂ ℛ. The domain thickness h is assumed small enough (with respect to the in-plane characteristic dimensions) and it is assumed constant.

The Stokes’s equations for an incompressible Newtonian fluid read:

$$ \nabla p = \eta \cdot \Delta \mathbf{v} $$

(28)

where v is the velocity vector with components v = (u, v, w) and p the pressure field. Eq. 28 results in the following three scalar equations:

$$ \left \{ \begin{array}{l} \frac{\partial p}{\partial x}=\eta \left(\frac{\partial^{2} u}{\partial x^{2}}+\frac{\partial^{2} u}{\partial y^{2}}+\frac{\partial^{2} u}{\partial z^{2}}\right)\\ \frac{\partial p}{\partial y}=\eta \left(\frac{\partial^{2} v}{\partial x^{2}}+\frac{\partial^{2} v}{\partial y^{2}}+\frac{\partial^{2} v}{\partial z^{2}}\right)\\ \frac{\partial p}{\partial z}=\eta \left(\frac{\partial^{2} w}{\partial x^{2}}+\frac{\partial^{2} w}{\partial y^{2}}+\frac{\partial^{2} w}{\partial z^{2}}\right) \end{array} \right. $$

(29)

When the layer thickness is much lower than the characteristics in-plane dimensions involved in Ω the following hypotheses (known as lubrication hypotheses) apply:

$$ \left \{ \begin{array}{l} \frac{\partial u}{\partial z} \gg \frac{\partial u}{\partial x} \\ \frac{\partial u}{\partial z} \gg \frac{\partial u}{\partial y}\\ \frac{\partial v}{\partial z} \gg \frac{\partial v}{\partial x} \\ \frac{\partial v}{\partial z} \gg \frac{\partial v}{\partial y}\\ w \approx 0 \end{array} \right. $$

(30)

reducing the Stokes’s equations (29) to:

$$ \left \{ \begin{array}{l} \frac{\partial p}{\partial x}=\eta \frac{\partial^{2} u}{\partial z^{2}} \\ \frac{\partial p}{\partial y}=\eta \frac{\partial^{2} v}{\partial z^{2}} \\ \frac{\partial p}{\partial z} = 0 \end{array} \right. $$

(31)

Now, by integrating Eq. 31 with respect to z and taking into account that p = p(x) = p(x, y) as well as the non-slip boundary conditions

$$ \left \{\begin{array}{c} u(z=-h/2)=u(z=h/2)=0\\ v(z=-h/2)=v(z=h/2)=0 \end{array} \right. $$

(32)

it results:

$$\left\{ \begin{array}{l} u=\frac{1}{2\eta}\frac{\partial p}{\partial x}\left(z^2-\left(\frac{h}{2}\right)^{2}\right)\\ v=\frac{1}{2 \eta}\frac{\partial p}{\partial y}\left(z^2-\left(\frac{h}{2}\right)^{2}\right)\end{array}\right\}$$

(33)

that integrated in the thickness allows calculating the flow rates q _x and q _y

$$ \left \{ \begin{array}{l} q_x=\int\limits^{h/2}_{-h/2} u \ dz= -\frac{1}{12 \eta} \frac{\partial p}{\partial x} h^{3}\\ q_y=\int\limits^{h/2}_{-h/2} v \ dz= -\frac{1}{12 \eta} \frac{\partial p}{\partial y} h^3 \end{array} \right . $$

(34)

The mass conservation, taking into account the fluid incompressibility and the compression rate ḣ, reads:

$$ \dot h = \frac{dh}{dt} = \nabla \cdot \mathbf q $$

(35)

or more explicitly:

$$ \dot h = \frac{\partial q_{x}}{\partial x}+\frac{\partial q_{y}}{\partial y} $$

(36)

that allows deriving the equation related to the pressure field:

$$ \dot h = -\frac{1}{12 \eta}\left(\frac{\partial}{\partial x}\left(h^{3} \frac{\partial p}{\partial x}\right)+\frac{\partial}{\partial y}\left(h^{3} \frac{\partial p}{\partial y}\right)\right) $$

(37)

that when the thickness is the same everywhere reduces to:

$$ \dot h = -\frac{h^{3}}{12 \eta} \Delta p $$

(38)

B: Monolayer squeeze flow of a power-law resin

In order to address a more complex resin rheology we consider it described by the power law constitutive equation

$$ \eta = K \cdot D_{eq}^{n-1} \cdot \mathbf D $$

(39)

where K and n are two material parameters, D the strain rate tensor and D _eq the equivalent strain rate

$$ D_{eq} = \sqrt{2 \ (\mathbf D : \mathbf D) } $$

(40)

where ” : ” denotes the tensor product twice contracted.

Now, the momentum balance writes

$$ \nabla p = K \cdot \nabla( D_{eq}^{n-1} \cdot \nabla \mathbf{v}) $$

(41)

Within the lubrication framework the equivalent strain reduces to

$$ D_{eq}=\sqrt{\left(\frac{\partial u}{\partial z}\right)^2+\left(\frac{\partial v}{\partial z}\right)^{2}} $$

(42)

with p = p(x). By integrating Eq. 41 in the z-coordinate and taking into account that the velocity derivatives vanish at z = 0 because the flow symmetry with respect to the mid-plane, it results

$$ \left \{ \begin{array}{l} D_{eq}^{n-1} \cdot \frac{\partial u}{\partial z}=\frac{1}{K}\frac{\partial p}{\partial x} \cdot z \\ D_{eq}^{n-1} \cdot \frac{\partial v}{\partial z}=\frac{1}{K}\frac{\partial p}{\partial y}\cdot z \end{array} \right. $$

(43)

By taking the square of both equalities in Eq. 43 and then adding both (taking into account Eq. 42) it results

$$ D_{eq}=\left(\frac{|z|}{K} \sqrt{(\nabla p)^{2}}\right)^{1/n} $$

(44)

By introducing Eq. (44) into Eq. 43, integrating again in the layer thickness ℐ and considering the non-sliping condition at z = h/2 (or z = − h/2) it finally results:

$$ \left \{ \begin{array}{l} u= \frac{\partial p}{\partial x}\frac{1}{K} \alpha^{(1-n)/n} \frac{n}{n+1} \cdot\left( |z|^{(1+n)/n} - \left(\frac{h}{2} \right)^{(1+n)/n} \right)\\ v= \frac{\partial p}{\partial y}\frac{1}{K} \alpha^{(1-n)/n} \frac{n}{n+1} \cdot\left( |z|^{(1+n)/n} - \left(\frac{h}{2} \right)^{(1+n)/n} \right) \end{array} \right. $$

(45)

with

$$ \alpha =\frac{1}{K} \sqrt{ (\nabla p)^{2}} $$

(46)

Now, the flow rate q can be computed by using Eq. 34 and the mass balance enforced

$$ \dot h = \nabla \cdot \mathbf q $$

(47)

that results in a second order non-linear partial differential equation that allows computing the 2D pressure. Knowing the pressure field, the velocity can be obtained from Eq. 45.