Abstract
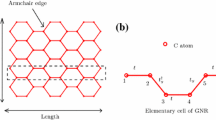
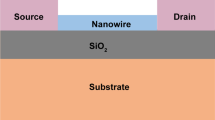
We present a semi-analytical model incorporating the effects of edge bond relaxation, the third nearest neighbor interactions, and edge scattering in graphene nanoribbon field-effect transistors (GNRFETs) with armchair-edge GNR (AGNR) channels. Unlike carbon nanotubes (CNTs) which do not have edges, the existence of edges in the AGNRs has a significant effect on the quantum capacitance and ballistic I-V characteristics of GNRFETs. For an AGNR with an index of m=3p, the band gap decreases and the ON current increases whereas for an AGNR with an index of m=3p+1, the quantum capacitance increases and the ON current decreases. The effect of edge scattering, which reduces the ON current, is also included in the model.

Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
Novoselov, K. S.; Geim, A. K.; Morozov, S. V.; Jiang, D.; Zhang, Y.; Dubonos, S. V.; Grigorieva, I. V.; Firsov, A. A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669.
Zhang, Y.; Tan, Y. W.; Stormer, H. L.; Kim, P. Experimental observation of the quantum Hall effect and Berry’s phase in graphene. Nature 2005, 438, 201–204.
Berger, C.; Song, Z.; Li, X.; Wu, X.; Brown, N.; Naud, C.; Mayou, D.; Li, T.; Hass, J.; Marchenkov, A. N.; Conrad, E. H.; First, P. N.; de Heer, W. A. Electronic confinement and coherence in patterned epitaxial graphene. Science 2006, 312, 1191–1196.
Li, X.; Wang, X.; Zhang, L.; Lee, S.; Dai, H. Chemically derived, ultrasmooth graphene nanoribbon semiconductors. Science 2008, 319, 1229–1232.
Gunlycke, D.; White, C. T. Tight-binding energy dispersions of armchair-edge graphene nanostrips. Phys. Rev. B 2008, 77, 115116.
Son, Y. W.; Cohen, M.; Louie, S. Energy gaps in graphene nanoribbons. Phys. Rev. Lett. 2006, 97, 216803.
White, C. T.; Li, J.; Gunlycke, D.; Mintmire, J. W. Hidden one-electron interactions in carbon nanotubes revealed in graphene nanostrips. Nano Lett. 2007, 7, 825–830.
Sasaki, K.; Murakami, S.; Saito, R. Stabilization mechanism of edge states in graphene. Appl. Phys. Lett. 2006, 88, 113110.
Natori, K. Ballistic metal-oxide-semiconductor field-effect transistor. J. Appl. Phys. 1994, 76, 4879–4890.
Lundstrom, M.; Guo, J. Nanoscale Transistors: Device Physics, Modeling and Simulation; Springer: New York, 2006.
Wong, H.-S. P.; Deng, J.; Hazeghi, A. Krishnamohan, T.; Wan, G. C. Carbon nanotube transistor circuits: Models and tools for design and performance optimization. Proc. Intl. Conf. Computer-aided Design 2006, p. 651.
Ouyang, Y.; Yoon, Y.; Fodor, J.; Guo, J. Comparison of performance limits for carbon nanoribbon and carbon nanotube transistors. Appl. Phys. Lett. 2006, 89, 203107.
Liang, G.; Neophytou, N.; Nikonov, D. E.; Lundstrom, M. Performance projections for ballistic graphene nanoribbon field-effect transistors. IEEE T. Electron Dev. 2007, 54, 677–682.
Rahman, A.; Guo, J.; Datta, S.; Lundstrom, M. Theory of ballistic transistors. IEEE T. Electron Dev. 2003, 50, 1853–1864.
Fiori, G.; Iannaccone, G. Simulation of graphene nanoribbon field effect transistors. IEEE Electr. Device L. 2007, 28, 760–762.
Ouyang, Y.; Yoon, Y.; Guo, J. Scaling behaviors of graphene nanoribbon FETs: A three-dimensional quantum simulation study. IEEE T. Electron Dev. 2007, 54, 2223–2231.
Liang, G. C.; Neophytou, N.; Lundstrom, M.; Nikonov, D. E. Ballistic graphene nanoribbon metal-oxide-semiconductor field-effect transistors: A full real-space quantum transport simulation. J. Appl. Phys. 2007, 102, 054307.
Guan, X.; Zhang, M.; Liu, Q.; Yu, Z. Simulation investigation of double-gate CNR-MOSFETs with a fully self-consistent NEGF and TB method. IEDM Tech. Dig. 2007, 761–764.
Wang, X.; Ouyang, Y.; Li, X.; Wang, H.; Guo, J.; Dai, H. Room temperature all semiconducting sub-10 nm graphene nanoribbon FETs. Phys. Rev. Lett. 2008, 100, 206803.
Perebeinos, V.; Tersoff, J.; Avouris, P. Electron-phonon interaction and transport in semiconducting carbon nanotubes. Phys. Rev. Lett. 2005, 94, 086802.
Lundstrom, M. Elementary scattering theory of the Si MOSFET. IEEE Electr. Device L. 1997, 18, 361–363.
Han, M. Y.; Ozyilmaz, B.; Zhang, Y.; Kim, P. Energy bandgap engineering of graphene nanoribbons. Phys. Rev. Lett. 2007, 98, 206805.
Chen, Z. H.; Lin, Y. M.; Rooks, M. J.; Avouris, P. Graphene nanoribbon electronics. Physica E 2007, 40, 228–232.
Fast Field Solvers. http://www.fastfieldsolvers.com (accessed 2008).
Datta, S. Quantum Transport: Atom to Transistor; Cambridge University Press: Cambridge, 2005, pp. 170–176.
Yoon, Y.; Fiori, G.; Hong, S.; Iannaccone, G.; Guo, J. Performance comparison of graphene nanoribbon FETs with Schottky contacts and doped reservoirs. IEEE T. Electron Dev. 2008, 55, 2314–2323.
Author information
Authors and Affiliations
Corresponding author
Additional information
This article is published with open access at Springerlink.com
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License ( https://creativecommons.org/licenses/by-nc/2.0 ), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Zhao, P., Choudhury, M., Mohanram, K. et al. Computational model of edge effects in graphene nanoribbon transistors. Nano Res. 1, 395–402 (2008). https://doi.org/10.1007/s12274-008-8039-y
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12274-008-8039-y