Skip to main content
SpringerLink
Log in

Predicting roof-surface wind pressure induced by conical vortex using a BP neural network combined with POD

  • Research Article
  • Indoor/Outdoor Airflow and Air Quality
  • Published:
Building Simulation Aims and scope Submit manuscript

Abstract

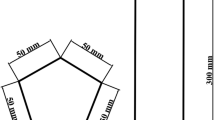
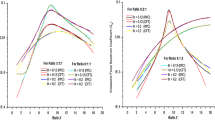
This study aims to examine the feasibility of predicting surface wind pressure induced by conical vortex using a backpropagation neural network (BPNN) combined with proper orthogonal decomposition (POD), in which a 1:150 scaled model with a large-span retractable roof was tested in wind tunnel under both laminar and turbulent flow conditions. The distributions of mean and fluctuating wind pressure coefficients were first described, and the effects of inflow turbulence, wind direction, roof opening were examined separately. For the prediction of wind pressure, the POD-BPNN model was trained using measurement data from adjacent points. The prediction results are overall satisfactory. The root-mean-square-error (RMSE) between test and predicted data lies mostly within 10%. In particular, the prediction of mean wind pressure is found to be better than that of fluctuating wind pressure. The outcomes in this study highlight that the proposed POD-BPNN model can be well used as a useful tool to predict surface wind pressure.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Ahmed R, El Sayed M, Gadsden SA, et al. (2015). Automotive internal-combustion-engine fault detection and classification using artificial neural network techniques. IEEE Transactions on Vehicular Technology, 64: 21–33.

    Article  Google Scholar 

  • Banks D, Meroney RN, Sarkar PP, et al. (2000). Flow visualization of conical vortices on flat roofs with simultaneous surface pressure measurement. Journal of Wind Engineering and Industrial Aerodynamics, 84: 65–85.

    Article  Google Scholar 

  • Carassale L, Solari G, Tubino F (2007). Proper orthogonal decomposition in wind engineering — Part 2: Theoretical aspects and some applications. Wind and Structures, 10: 177–208.

    Article  Google Scholar 

  • Chen Y, Kopp GA, Surry D (2002). Interpolation of wind-induced pressure time series with an artificial neural network. Journal of Wind Engineering and Industrial Aerodynamics, 90: 589–615.

    Article  Google Scholar 

  • Chen CH, Wu JC, Chen JH (2008). Prediction of flutter derivatives by artificial neural networks. Journal of Wind Engineering and Industrial Aerodynamics, 96: 1925–1937.

    Article  Google Scholar 

  • Chen F, Zhan Z, Zhou J, et al. (2021a). A fast partition method for wind pressure coefficient of large-span roof based on modified GK clustering. Structures, 30: 518–530.

    Article  Google Scholar 

  • Chen FB, Wang XL, Li X, et al. (2021b). Prediction of wind pressures on tall buildings using wavelet neural network. Journal of Building Engineering,: 103674.

  • Cheung JCK, Holmes JD, Melbourne WH, et al. (1997). Pressures on a 110 scale model of the texas tech building. Journal of Wind Engineering and Industrial Aerodynamics, 69: 529–538.

    Article  Google Scholar 

  • De Cillis G, Cherubini S, Semeraro O, et al. (2021). POD-based analysis of a wind turbine wake under the influence of tower and nacelle. Wind Energy, 24: 609–633.

    Article  Google Scholar 

  • Ding Z, Tamura Y (2013). Contributions of wind-induced overall and local behaviors for internal forces in cladding support components of large-span roof structure. Journal of Wind Engineering and Industrial Aerodynamics, 115: 162–172.

    Article  Google Scholar 

  • Eftekhar Azam S, Mariani S (2013). Investigation of computational and accuracy issues in POD-based reduced order modeling of dynamic structural systems. Engineering Structures, 54: 150–167.

    Article  Google Scholar 

  • Fan Z, Zhao CJ, Li L, et al. (2010). Application situation and practice of retractable roof in China and abroad. Construction Technology, 39(08): 1–7. (in Chinese)

    Google Scholar 

  • Fu JY, Liang SG, Li QS (2007). Prediction of wind-induced pressures on a large gymnasium roof using artificial neural networks. Computers & Structures, 85: 179–192.

    Article  Google Scholar 

  • Gavalda X, Ferrer-Gener J, Kopp GA, et al. (2011). Interpolation of pressure coefficients for low-rise buildings of different plan dimensions and roof slopes using artificial neural networks. Journal of Wind Engineering and Industrial Aerodynamics, 99: 658–664.

    Article  Google Scholar 

  • Govinda Ram HS, Arakeri VH (1990). Studies on unsteady pressure fields in the region of separating and reattaching flows. Journal of Fluids Engineering, 112: 402–408.

    Article  Google Scholar 

  • Gu S, Wang J, Hu G, et al. (2021). Prediction of wind-induced vibrations of twin circular cylinders based on machine learning. Ocean Engineering, 239: 109868.

    Article  Google Scholar 

  • Haykin S (2007). Neural Networks: A Comprehensive Foundation, 3rd edn. New York: Prentice-Hall (3rd edition).

    MATH  Google Scholar 

  • He YC, He JY, Chen WC, et al. (2020). Insights from Super Typhoon Mangkhut (1822) for wind engineering practices. Journal of Wind Engineering and Industrial Aerodynamics, 203: 104238.

    Article  Google Scholar 

  • Holmes JD, Sankaran R, Kwok KCS, et al. (1997). Eigenvector modes of fluctuating pressures on low-rise building models. Journal of Wind Engineering and Industrial Aerodynamics, 69–71: 697–707.

    Article  Google Scholar 

  • Hoxey RP, Robertson AP, Richardson GM, et al. (1997). Correction of wind-tunnel pressure coefficients for Reynolds number effect. Journal of Wind Engineering and Industrial Aerodynamics, 69–71: 547–555.

    Article  Google Scholar 

  • Huang J, Guan FL, Wu KC (2007). The wind tunnel test of the roof of the Hangzhou Huanglong Sports Center Tennis Hall. Journal of Southern Yangtze University (Natural Science Edition), 6(1): 81–85. (in Chinese)

    Google Scholar 

  • Huang D, He S, He X, et al. (2017). Prediction of wind loads on high-rise building using a BP neural network combined with POD. Journal of Wind Engineering and Industrial Aerodynamics, 170: 1–17.

    Article  Google Scholar 

  • Irwin HPAH, Wardlaw RL (1979). A wind tunnel investigation of a retractable fabric roof for the Montreal Olympic Stadium. National Research Council of Canada, Quarterly Bulletin of the Division of Mechanical Engineering.

  • Ishii K (2000). Structural Design of Retractable Roof Structures. Southampton, UK: Wit Press.

    Google Scholar 

  • Ji X, Huang G, Zhang X, et al. (2018). Vulnerability analysis of steel roofing cladding: Influence of wind directionality. Engineering Structures, 156: 587–597.

    Article  Google Scholar 

  • Kassabian PE, You Z, Pellegrino S (1999). Retractable roof structures. Proceedings of the Institution of Civil Engineers — Structures and Buildings, 134: 45–56.

    Article  Google Scholar 

  • Kato Y, Kanda M (2014). Development of a modified hybrid aerodynamic vibration technique for simulating aerodynamic vibration of structures in a wind tunnel. Journal of Wind Engineering and Industrial Aerodynamics, 135: 10–21.

    Article  Google Scholar 

  • Kawai H, Nishimura G (1996). Characteristics of fluctuating suction and conical vortices on a flat roof in oblique flow. Journal of Wind Engineering and Industrial Aerodynamics, 60: 211–225.

    Article  Google Scholar 

  • Kawai H (1997). Structure of conical vortices related with suction fluctuation on a flat roof in oblique smooth and turbulent flows. Journal of Wind Engineering and Industrial Aerodynamics, 69–71: 579–588.

    Article  Google Scholar 

  • Kho S, Baker C, Hoxey R (2002). POD/ARMA reconstruction of the surface pressure field around a low rise structure. Journal of Wind Engineering and Industrial Aerodynamics, 90: 1831–1842.

    Article  Google Scholar 

  • Letchford CW, Marwood R (1997). On the influence of v and w component turbulence on roof pressures beneath conical vortices. Journal of Wind Engineering and Industrial Aerodynamics, 69–71: 567–577.

    Article  Google Scholar 

  • Li B, Yang QS, Tian YJ, et al. (2010a). Wind load characteristics of retractable roof of New National Tennis Center. China Civil Engineering Journal, 43(S2): 112–118. (in Chinese)

    Google Scholar 

  • Li SK, Li SY, Chen ZQ (2010b). Experimental investigation on wind loading of a stadium with a retractable roof. Journal of Building Structures, 31(10): 17–23. (in Chinese)

    Google Scholar 

  • Li F, Chen X (2020). POD analysis for modeling wind pressures and wind effects of a cylindrical shell roof. Wind and Structures, 30: 559–573.

    Google Scholar 

  • Li D, Liu B, Cheng Y (2020). Wind pressure coefficients zoning method based on an unsupervised learning algorithm. Mathematical Problems in Engineering, 2020: 1670128.

    Google Scholar 

  • Li JC, Hu SY, Li QS (2021a). Comparative study of full-scale and model-scale wind pressure measurements on a gable roof low-rise building. Journal of Wind Engineering and Industrial Aerodynamics, 208: 104448.

    Article  Google Scholar 

  • Li A, Xiao F, Fan C, Hu M (2021b). Development of an ANN-based building energy model for information-poor buildings using transfer learning. Building Simulation, 14: 89–101.

    Article  Google Scholar 

  • Liu W, Qian F (2010). Application and Development of Retractable roof in Sport Architecture. Journal of Architectural and Civil Engineering, 27(04): 121–126. (in Chinese)

    Google Scholar 

  • Lu GY, Wong DW (2008). An adaptive inverse-distance weighting spatial interpolation technique. Computers & Geosciences, 34: 1044–1055.

    Article  Google Scholar 

  • Lu CL, Li QS, Huang SH, et al. (2012). Large eddy simulation of wind effects on a long-span complex roof structure. Journal of Wind Engineering and Industrial Aerodynamics, 100: 1–18.

    Article  Google Scholar 

  • Lumley JL (1967). The structure of inhomogeneous turbulent flows. In: Yaglom AM, Tartarsky VI (Eds.), Atmospheric Turbulence and Radio Wave Propagation. Moscow: Nauka.

    Google Scholar 

  • Luo Z, Chen G (2018). Proper Orthogonal Decomposition Methods for Partial Differential Equations. Cambridge, MA, USA: Academic Press.

    Google Scholar 

  • Maren AJ, Harston CT, Pap RM (2014). Handbook of Neural Computing Applications. San Diego, CA, USA: Academic Press.

    MATH  Google Scholar 

  • Marwood R, Wood CJ (1997). Conical vortex movement and its effect on roof pressures. Journal of Wind Engineering and Industrial Aerodynamics, 69: 589–595.

    Article  Google Scholar 

  • Qin L, Tian YJ (2012). Research on wind load on a large-span plane roof. Building Structure, 42(02): 160–164. (in Chinese)

    Google Scholar 

  • Ricciardelli F, de Grenet ET (2002). Analysis of the wind loading of a bridge deck box section using proper orthogonal decomposition International Journal of Fluid Mechanics Research, 29: 312–322.

    Article  Google Scholar 

  • Richards PJ, Hoxey RP, Short LJ (2001). Wind pressures on a 6m cube. Journal of Wind Engineering and Industrial Aerodynamics, 89: 1553–1564.

    Article  Google Scholar 

  • Rumelhart DE, McClelland JL, PDP Research Group (1986). Parallel distributed processing: Explorations in the Microstructure of Cognition. Cambridge, MA, USA: MIT Press.

    Book  Google Scholar 

  • Shu ZR, Li QS (2017). An experimental investigation of surface pressures in separated and reattaching flows: effects of freestream turbulence and leading edge geometry. Journal of Wind Engineering and Industrial Aerodynamics, 165: 58–66.

    Article  Google Scholar 

  • Shu ZR, Li QS (2019). Wind tunnel study of separated and reattaching flows by particle image velocimetry and pressure measurements. Advances in Structural Engineering, 22: 1769–1782.

    Article  Google Scholar 

  • Shu ZR, Chan PW, Li QS, et al. (2020). Quantitative assessment of offshore wind speed variability using fractal analysis. Wind and Structures, 31: 363–371.

    Google Scholar 

  • Shu ZR, Chan PW, Li QS, et al. (2021a). Characterization of vertical wind velocity variability based on fractal dimension analysis. Journal of Wind Engineering and Industrial Aerodynamics, 213: 104608.

    Article  Google Scholar 

  • Shu ZR, Chan PW, Li QS, et al. (2021b). Investigation of chaotic features of surface wind speeds using recurrence analysis. Journal of Wind Engineering and Industrial Aerodynamics, 210: 104550.

    Article  Google Scholar 

  • Shu ZR, Chan PW, Li QS, et al. (2021c). Dynamic characterization of wind speed under extreme conditions by recurrence-based techniques: comparative study. Journal of Aerospace Engineering, 34: 04020114.

    Article  Google Scholar 

  • Solari G, Carassale L (2000). Modal transformation tools in structural dynamics and wind engineering. Wind and Structures, 3: 221–241.

    Article  Google Scholar 

  • Solari G, Carassale L, Tubino F (2007). Proper orthogonal decomposition in wind engineering — Part 1: A state-of-the-art and some prospects. Wind and Structures, 10: 153–176.

    Article  Google Scholar 

  • Sun Y, Wu Y, Lin ZX, et al. (2007). Investigation on the signature turbulence of long-span flat roof surface. Acta Aerodynamica Sinica, 25(3): 319–324. (in Chinese)

    Google Scholar 

  • Sun H, Qiu C, Lu L, et al. (2020). Wind turbine power modelling and optimization using artificial neural network with wind field experimental data. Applied Energy, 280: 115880.

    Article  Google Scholar 

  • Sun W, Zhang Q (2020). Universal equivalent static wind loads of fluctuating wind loads on large-span roofs based on compensation of structural frequencies and modes. Structures, 26: 92–104.

    Article  Google Scholar 

  • Tallet A, Liberge E, Inard C (2017). Fast POD method to evaluate infiltration heat recovery in building walls. Building Simulation, 10: 111–121.

    Article  Google Scholar 

  • Tamura Y, Suganuma S, Kikuchi H, et al. (1999). Proper orthogonal decomposition of random wind pressure field. Journal of Fluids and Structures, 13: 1069–1095.

    Article  Google Scholar 

  • Taylor ZJ, Gurka R, Kopp GA (2014). Effects of leading edge geometry on the vortex shedding frequency of an elongated bluff body at high Reynolds numbers. Journal of Wind Engineering and Industrial Aerodynamics, 128: 66–75.

    Article  Google Scholar 

  • Tse KT, Hu G, Song J, et al. (2021). Effects of corner modifications on wind loads and local pressures on walls of tall buildings. Building Simulation, 14: 1109–1126.

    Article  Google Scholar 

  • Turkkan N, Srivastava NK (1995). Prediction of wind load distribution for air-supported structures using neural networks. Canadian Journal of Civil Engineering, 22: 453–461.

    Article  Google Scholar 

  • Wang HF, Cao HL, Zhou Y (2014). POD analysis of a finite-length cylinder near wake. Experiments in Fluids, 55: 1790.

    Article  Google Scholar 

  • Weiss J (2019). A Tutorial on the Proper Orthogonal Decomposition. In: Proceedings of AIAA Aviation 2019 Forum, Dallas, Texas, USA.

  • Wu T, Kareem A (2011). Modeling hysteretic nonlinear behavior of bridge aerodynamics via cellular automata nested neural network. Journal of Wind Engineering and Industrial Aerodynamics, 99: 378–388.

    Article  Google Scholar 

  • Xu ZG, Huang BC, Lin G, et al. (2006). Wind loads on rails of Qizhong retractable tennis gymnasium roof. Spatial Structure, 12(03): 38–43. (in Chinese)

    Google Scholar 

  • Yan B, Chan PW, Li QS, et al. (2020). Characterising the fractal dimension of wind speed time series under different terrain conditions. Journal of Wind Engineering and Industrial Aerodynamics, 201: 104165.

    Article  Google Scholar 

  • Yasui H, Marukawa H, Katagiri J, et al. (1999). Study of wind-induced response of long-span structure. Journal of Wind Engineering and Industrial Aerodynamics, 83: 277–288.

    Article  Google Scholar 

  • Yu F, Xu X (2014). A short-term load forecasting model of natural gas based on optimized genetic algorithm and improved BP neural network. Applied Energy, 134: 102–113.

    Article  Google Scholar 

  • Zhang Y, Pan G, Chen B, et al. (2020). Short-term wind speed prediction model based on GA-ANN improved by VMD. Renewable Energy, 156: 1373–1388.

    Article  Google Scholar 

Download references

Acknowledgements

The authors would like to thank the anonymous reviewers for their insightful and valuable comments. This project was funded by grants from the National Natural Science Foundation of China (No. 51778072 and No. 51408062) and Practice Innovation and Entrepreneurship Enhancement Plan of CSUST (SJCX202021).

Author information

Authors and Affiliations

  1. School of Civil Engineering, Changsha University of Science and Technology, Changsha, 410082, China

    Fubin Chen & Wen Kang

  2. School of Civil Engineering, Central South University, Changsha, 410083, China

    Zhenru Shu

  3. Department of Architecture and Civil Engineering, City University of Hong Kong, Kowloon, Hong Kong, China

    Qiusheng Li & Kang Zhou

  4. Hunan Provincial Key Laboratory of Structures for Wind Resistance and Vibration Control & School of Civil Engineering, Hunan University of Science and Technology, Xiangtan, 411201, China

    Yi Li

  5. Department of Civil Engineering, The Pennsylvania State University, Middletown, PA, 17057, USA

    Y. Frank Chen

Authors
  1. Fubin Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Wen Kang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Zhenru Shu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Qiusheng Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Yi Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Y. Frank Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Kang Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to Zhenru Shu or Kang Zhou.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chen, F., Kang, W., Shu, Z. et al. Predicting roof-surface wind pressure induced by conical vortex using a BP neural network combined with POD. Build. Simul. 15, 1475–1490 (2022). https://doi.org/10.1007/s12273-021-0867-7

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12273-021-0867-7

Keywords

Search

Navigation